基于最小均方误差(MMSE)估计的因果维纳滤波的实现.
最小均方误差mmse算法

最小均方误差mmse算法温馨提示:该文档是小主精心编写而成的,如果您对该文档有需求,可以对它进行下载,希望它能够帮助您解决您的实际问题。
文档下载后可以对它进行修改,根据您的实际需要进行调整即可。
另外,本小店还为大家提供各种类型的实用资料,比如工作总结、文案摘抄、教育随笔、日记赏析、经典美文、话题作文等等。
如果您想了解更多不同的资料格式和写法,敬请关注后续更新。
Tips: This document is carefully written by the small master, if you have the requirements for the document, you can download it, I hope it can help you solve your practical problems. After downloading the document, it can be modified and adjustedaccording to your actual needs.In addition, the store also provides you with a variety of types of practical information, such as work summary, copy excerpts, education essays, diary appreciation, classic articles, topic composition and so on. If you want to know more about the different data formats and writing methods, please pay attentionto the following updates.在通信系统中,为了减小信号的传输误差和提高信号质量,通常会采用各种信号处理算法进行优化处理。
学习笔记-最小均方(LMS)自适应滤波
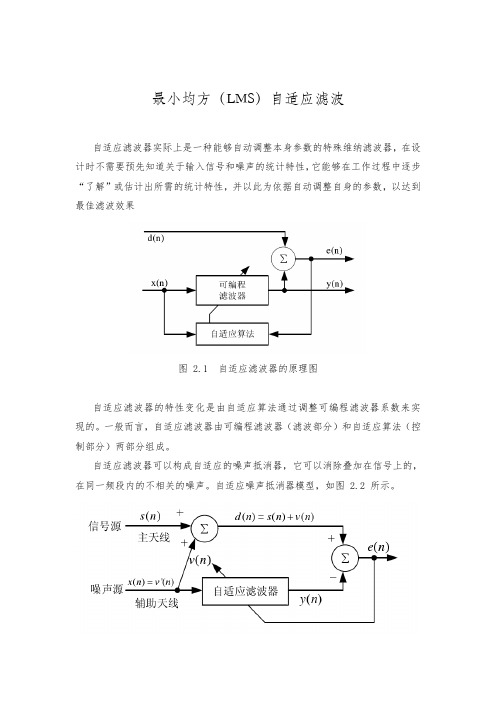
最小均方(LMS)自适应滤波自适应滤波器实际上是一种能够自动调整本身参数的特殊维纳滤波器,在设计时不需要预先知道关于输入信号和噪声的统计特性,它能够在工作过程中逐步“了解”或估计出所需的统计特性,并以此为依据自动调整自身的参数,以达到最佳滤波效果图 2.1 自适应滤波器的原理图自适应滤波器的特性变化是由自适应算法通过调整可编程滤波器系数来实现的。
一般而言,自适应滤波器由可编程滤波器(滤波部分)和自适应算法(控制部分)两部分组成。
自适应滤波器可以构成自适应的噪声抵消器,它可以消除叠加在信号上的,在同一频段内的不相关的噪声。
自适应噪声抵消器模型,如图 2.2 所示。
图 2.2 自适应噪声抵消器模型最小均方(LMS )算法是基于最小均方误差(MMSE )准则的维纳滤波器和最陡下降法的基础上,由 Widrow 和 Hoff 于 1960 年提出的。
固定步长最小均方(LMS )自适应算法也常称为标准 LMS 算法,它以期望响应和滤波输出信号之间误差的均方值最小为目标,它依据输入信号在迭代过程中估计梯度矢量,并更新权系数以达到最优的自适应迭代算法。
下面以横截型结构的自适应 FIR 滤波器为例,进行最小均方算法的公式推导。
图 2.3 自适应横截型滤波器结构框图设滤波器系数矢量为()()()()T M n w n w n w n w ][121-= ,滤波器抽头输入信号矢量为()()()()T M n x n x n x n x ]11[+--= ,自适应横截型滤波器结构框图,如图 3.1 所示。
滤波器输出信号()n y 为:()()()()()i n x n w n x n w n y M i i T-=*=∑-=10 上式中“T ”表示转置,n 为时间指针,M 为滤波器长度。
那么滤波器误差信号 e(n)表示为:()()()()()()n x n w n d n y n d n e T *-=-=基于 Widrow Hoff 的 LMS 算法,即随机梯度法,采用瞬时()()n x n e 2-来替代上式()()[]n x n e E 2-的估计运算,则有迭代公式:()()()()n x n e n w n w **+=+μ21其中 µ 是步长因子。
W-CDMA

[编辑本段]1.W-CDMA的概念:W-CDMA是一种由3GPP具体制定的,基于GSM MAP核心网,UTRAN(UMTS 陆地无线接入网)为无线接口的第三代移动通信系统。
目前WCDMA有Release 99、Release 4、Release 5、Release 6等版本。
W-CDMA(宽带码分多址)是一个ITU(国际电信联盟)标准,它是从码分多址(CDMA)演变来的,在官方上被认为是IMT-2000的直接扩展,与现在市场上通常提供的技术相比,它能够为移动和手提无线设备提供更高的数据速率。
WCDMA采用直接序列扩频码分多址(DS-CDMA)、频分双工(FDD)方式,码片速率为3.84Mcps,载波带宽为5MHz.基于Release 99/ Release 4版本,可在5MHz的带宽内,提供最高384kbps的用户数据传输速率。
W-CDMA能够支持移动/手提设备之间的语音、图象、数据以及视频通信,速率可达2Mb/s(对于局域网而言)或者384Kb/s(对于宽带网而言)。
输入信号先被数字化,然后在一个较宽的频谱范围内以编码的扩频模式进行传输。
窄带CDMA使用的是200KHz宽度的载频,而W-CDMA使用的则是一个5MHz宽度的载频。
[编辑本段]2.W-CDMA的定位:目前,3G的主流技术有W-CDMA、CDMA2000和TD-SCDMA三种。
CDMA2000由美国高通公司提出,技术成熟性最高,有着明确的提高频谱利用率的演进路线,但全球漫游能力一般,韩国已经开通了CDMA2000商用网。
W-CDMA由欧洲和日本支持,有较高的扩频增益,发展空间较大,全球漫游能力最强,但技术成熟性一般,在日本已经投入商用。
[编辑本段]3.W-CDMA的特点概要:W-CDMA由ETSI NTT DoCoMo作为无线介面为他们的3G网路FOMA开发。
后来NTTDocomo提交给ITU一个详细规范作为一个象IMT-2000一样作为一个候选的国际3G标准。
数字监控图像降噪技术详解

数字监控图像降噪技术详解数字监控系统是现代社会中广泛应用的安全保障措施之一。
然而,由于环境噪声和图像传输过程中的干扰等因素,监控图像往往会受到一定程度的干扰和噪声,影响了图像的清晰度和可视性。
为了解决这一问题,数字监控图像降噪技术应运而生。
本文将详细介绍数字监控图像降噪技术的原理、方法及应用。
一、数字监控图像降噪技术的原理数字监控图像降噪技术主要基于信号处理理论,通过去除图像中的噪声,提高图像的质量和可见性。
其原理可分为两个方面:噪声模型和滤波算法。
1. 噪声模型噪声模型是数字监控图像降噪技术的基础,它用来描述图像中噪声的类型和分布规律。
常见的噪声模型包括高斯噪声、椒盐噪声、泊松噪声等。
其中,高斯噪声是一种均值为0且方差为常数的随机噪声,椒盐噪声是指图像中出现的黑白像素点,泊松噪声则是一种与光子计数有关的噪声。
2. 滤波算法滤波算法是数字监控图像降噪技术中的核心部分,它通过对图像进行滤波操作,去除图像中的噪声。
常见的滤波算法包括均值滤波、中值滤波、维纳滤波等。
其中,均值滤波是通过求取像素点周围区域的平均灰度值来实现的,中值滤波则是通过求取像素点周围区域的中位数来实现的,维纳滤波则是一种基于最小均方误差准则的自适应滤波方法。
二、数字监控图像降噪技术的方法数字监控图像降噪技术主要有两种方法:空域降噪和频域降噪。
1. 空域降噪空域降噪是最常用的图像降噪方法之一,它直接对图像的像素进行操作。
常见的空域降噪方法有均值滤波、中值滤波、双边滤波等。
均值滤波通过计算像素周围邻域的平均值来抑制噪声,中值滤波通过计算像素周围邻域的中位数来抑制噪声,双边滤波则是一种同时考虑空间距离和像素灰度差异的滤波方法。
2. 频域降噪频域降噪是一种将图像从空域转换到频域进行滤波处理的方法。
这种方法主要包括傅里叶变换和小波变换。
傅里叶变换将图像从时域转换到频域,对频域图像进行滤波后再进行逆变换得到降噪后的图像;小波变换则是一种多尺度分析的方法,通过对图像进行分解和重构,提取出图像中的噪声信号。
基于阵列处理器的最小均方误差检测算法并行设计与实现

基于阵列处理器的最小均方误差检测算法并行设计与实现刘帅;蒋林;李远成;山蕊;朱育琳;王欣【期刊名称】《计算机应用》【年(卷),期】2022(42)5【摘要】针对大规模多输入多输出(MIMO)系统中,最小均方误差(MMSE)检测算法在可重构阵列结构上适应性差、计算复杂度高和运算效率低的问题,基于项目组开发的可重构阵列处理器,提出了一种基于MMSE算法的并行映射方法。
首先,利用Gram矩阵计算时较为简单的数据依赖关系,设计时间上和空间上可以高度并行的流水线加速方案;其次,根据MMSE算法中Gram矩阵计算和匹配滤波计算模块相对独立的特点,设计模块化并行映射方案;最后,基于Xilinx Virtex-6开发板对映射方案进行实现并统计其性能。
实验结果表明,该方法在MIMO规模为128×4、128×8和128×16的正交相移键控(QPSK)上行链路中,加速比分别2.80、4.04和5.57;在128×16的大规模MIMO系统中,可重构阵列处理器比专用硬件减少了42.6%的资源消耗。
【总页数】7页(P1524-1530)【作者】刘帅;蒋林;李远成;山蕊;朱育琳;王欣【作者单位】西安科技大学通信与信息工程学院;西安科技大学计算机科学与技术学院;西安邮电大学电子工程学院;西安科技大学电气与控制工程学院【正文语种】中文【中图分类】TP302【相关文献】1.基于循环平稳周期的交织差分最小均方误差多用户检测算法2.基于最小均方误差准则的盲多用户检测新算法3.WCDMA系统中的差分最小均方误差多用户检测算法4.基于最小均方误差的串扰消除多用户检测算法5.基于自适应阈值活动语音检测和最小均方误差对数谱幅度估计的低信噪比降噪算法因版权原因,仅展示原文概要,查看原文内容请购买。
(完整word版)自适应滤波LMS算法及RLS算法及其仿真

自适应滤波第1章绪论 (1)1.1自适应滤波理论发展过程 (1)1. 2自适应滤波发展前景 (2)1. 2. 1小波变换与自适应滤波 (2)1. 2. 2模糊神经网络与自适应滤波 (3)第2章线性自适应滤波理论 (4)2. 1最小均方自适应滤波器 (4)2. 1. 1最速下降算法 (4)2.1.2最小均方算法 (6)2. 2递归最小二乘自适应滤波器 (7)第3章仿真 (12)3.1基于LMS算法的MATLAB仿真 (12)3.2基于RLS算法的MATLAB仿真 (15)组别: 第二小组组员: 黄亚明李存龙杨振第1章绪论从连续的(或离散的)输入数据中滤除噪声和干扰以提取有用信息的过程称为滤波。
相应的装置称为滤波器。
实际上, 一个滤波器可以看成是一个系统, 这个系统的目的是为了从含有噪声的数据中提取人们感兴趣的、或者希望得到的有用信号, 即期望信号。
滤波器可分为线性滤波器和非线性滤波器两种。
当滤波器的输出为输入的线性函数时, 该滤波器称为线性滤波器, 当滤波器的输出为输入的非线性函数时, 该滤波器就称为非线性滤波器。
自适应滤波器是在不知道输入过程的统计特性时, 或是输入过程的统计特性发生变化时, 能够自动调整自己的参数, 以满足某种最佳准则要求的滤波器。
1. 1自适应滤波理论发展过程自适应技术与最优化理论有着密切的系。
自适应算法中的最速下降算法以及最小二乘算法最初都是用来解决有/无约束条件的极值优化问题的。
1942年维纳(Wiener)研究了基于最小均方误差(MMSE)准则的在可加性噪声中信号的最佳滤波问题。
并利用Wiener. Hopf方程给出了对连续信号情况的最佳解。
基于这~准则的最佳滤波器称为维纳滤波器。
20世纪60年代初, 卡尔曼(Kalman)突破和发展了经典滤波理论, 在时间域上提出了状态空间方法, 提出了一套便于在计算机上实现的递推滤波算法, 并且适用于非平稳过程的滤波和多变量系统的滤波, 克服了维纳(Wiener)滤波理论的局限性, 并获得了广泛的应用。
NB-IoT中一种改进的DFT信道估计算法

南京岬电大学学披(自然科学版)Journal of Nanjing University of Posts and Telecommunications(Natural Science Edition)Vol.40No.6 Dec.2020第40卷第6期2020年12月doi:10.14132/ki.1673-5439.2020.06.002NB-IoT中一种改进的DFT信道估计算法谭钦红,梁泽乾,于敏(重庆邮电大学通信与信息工程学院.重庆400065)摘要:在窄带物联网(Narrow Band Internet of Things,NB-loT)系统中,上行数据链路采用单载波频分多址(Single-Carrier Frequency-Division Multiple Access,SC-FDMA),由于SC-FDMA固有的解码步骤会将估计误差扩展到所有的子载波上,因此对信道估计的误差更加敏感。
在传统基于阈值的离散傅里叶变换(Discrete Fourier Transform,DFT)信道估计的基础上,利用NB-IoT的应用场景的低速性、准静态性,提出了一种基于双时隙的DFT信道估计算法。
该算法利用两时隙内的导频的线性组合进一步降低噪声的影响,在复杂度增加较小的情况下,提升了系统性能。
Matlab仿真结果表明,与基于阈值的DFT信道估计相比,在误比特率(Bit Error Ratio,BER)为1xl0〜时,文中算法相较基于阈值的DFT估计算法约有4dB的性能增益,具有一定的实用价值。
关键词:窄带物联网;信道估计;离散傅里叶变换中图分类号:TN929.5文献标志码:A文章编号:1673-5439(2020)06-0007-05An improved DFT channel estimation algorithm in NB-IoTTAN Qinhong,LIANG Zeqian,YU Min(College of Telecommunications and Information Engineering,Chongqing University of Posts and Telecommunications,Chongqing400065,China)Abstract:In the narrow band Internet of Things(NB-IoT)system,since the uplink uses single-carrier frequency・division multiple access(SC-FDMA),its decoding step will extend the estimation error to all subcarriers,thus it is more sensitive to the channel estimation error.Based on the traditional thresholdbased discrete Fourier transform(DFT)channel estimation,an improved DFT channel estimation is proposed using the low speed and quasi-static nature of NB-IoT application scenarios.The algorithm uses the linear combination of the pilots in the two slots to further reduce the impact of noise,and improves the sys・tem performance in a lower complexity extent.The Matlab simulation demonstrates that the algorithm can improve the bit error ratio(BER)performance about 4dB compared with the threshold-based DFT estimation algorithm when BER=103,thus the algorithm has a certain practical value.Keywords:narrow band Internet of Things(NB-IoT);channel estimation;discrete Fourier transform窄带物联网(Narrow Band Internet of Things, NB-I()T)是低功耗广域网(Low-Power Wide-Area Net-work,LPWAN)技术之一,是物联网的一个重要分支⑴,支持低功耗设备在LPWAN的蜂窝数据连接。
韩希珍-自适应信号处理抗干扰算法的研究-毛兴鹏

自适应信号处理抗干扰算法的研究摘要自适应信号处理(Adaptive Signal Processing)是近40年来发展起来的信号处理领域一个新的分支。
随着人们在该领域研究的不断深入,自适应信号处理的理论和技术日趋完善,其应用的范围也愈来愈广泛。
而自适应滤波算法又是自适应信号处理中的重要部分。
本论文首先从自适应信号处理的的发展过程出发,简要介绍了自适应信号处理的应用领域。
然后进一步介绍自适应滤波器原理,并根据自适应滤波算法的发展与改进,先后介绍了五种自适应滤波算法:LMS算法、NLMS算法、VS-LMS算法、MS-LMS算法和RLS算法。
并分析了各种算法的优缺点。
最后利用MATLAB软件,对这五种自适应滤波算法进行了编程与仿真,进一步通过仿真结果观察并总结各种算法的优缺点。
关键词:自适应滤波,最小均方(LMS)自适应算法,递推最小二乘(RLS)自适应算法,仿真。
Analysis of Adaptive signal processing algorithms anti-interferenceAbstractAdaptive Signal Processing is nearly 40 years since it show up a new branch in the field of signal processing . As people in the field of researching in-depth, adaptive signal processing theory and the technology develop more and more perfectly , its scope of application also become wider. And adaptive filtering algorithm is an important part of the adaptive signal processing.This paper first start from the development process of adaptive signal processing , and introduce briefly the application of adaptive signal processing. Then introduce adaptive filter principle, and according to the development and improvement of adaptive filtering algorithms, introduce five adaptive filtering algorithms on the order: LMS algorithm, NLMS algorithm, VS-LMS algorithm, MS-LMS algorithm, and RLS algorithm. And analyze the advantages and disadvantages of the various algorithms.Finally using MATLAB software, program and simulate the five adaptive filtering algorithm, and according to the simulation results to observe and summarize fatherly the advantages and disadvantages of the various algorithms.Key words: adaptive filtering algorithms, Least Mean Square (LMS)algorithm, Recursive Least Squares(RLS) algorithm,simulation.目录摘要 (I)Abstract (II)1 绪论 (1)1.1自适应信号处理的发展过程 (1)1.2自适应信号处理的研究领域 (2)1.3研究的目的和意义 (3)1.4主要研究内容 (3)1.5本文结构 (3)2自适应滤波 (4)2.1 自适应滤波器的基本原理 (4)2.2 自适应滤波理论与算法 (4)2.2.1 基于维纳滤波理论的方法 (5)2.2.2 基于卡尔曼滤波理论的方法 (5)2.2.3 基于最小二乘准则的方法 (5)2.3 本章小结 (6)3自适应滤波算法 (7)3.1 最小均方(LMS)自适应算法 (7)3.1.1 LMS算法的基本原理 (7)3.1.2 LMS算法的性能分析 (9)3.2 归一化最小均方(NLMS)算法 (10)3.3 变步长LMS(VS-LMS)算法 (12)3.4 改进的变步长LMS(MS-LMS)算法 (12)3.5 递归最小二乘(RLS)算法 (13)3.6 本章小结 (15)4软件仿真 (16)4.1 LMS算法的仿真 (17)4.2 NLMS算法的仿真 (23)4.3 VS-LMS算法的仿真 (27)4.4 MS-LMS算法的仿真 (32)4.5 RLS算法的仿真 (38)4.6 五种算法的收敛速度比较 (43)4.7 本章小结 (45)结论 (46)致谢 (47)参考文献 (48)附录 (49)1 绪论1.1自适应信号处理的发展过程自适应信号处理由优化理论发展而来,通信领域中的优化理论研究可以追溯到20世纪20年代,Nyquist及Hareley研究了频带及信噪比问题。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
基于最小均方误差(MMSE)估计的因果维纳滤波的实现
一.功能简介
基于最小均方误差(MMSE)估计的因果维纳滤波的Matlab 实现,用莱文森-德宾(Levinson-Durbin)算法求解维纳-霍夫方程(Yule-wa1ker)方程,得到滤波器系数,进行维纳滤波。
二.维纳滤波简介
信号处理的实际问题,常常是要解决在噪声中提取信号的问题,因此,我们需要寻找一种所谓有最佳线性过滤特性的滤波器,这种滤波器当信号与噪声同时输入时,在输出端能将信号尽可能精确地重现出来,而噪声却受到最大抑制。
维纳(Wiener)滤波就是用来解决这样一类从噪声中提取信号问题的一种过滤(或滤波)方法。
一个线性系统,如果它的单位样本响应为h (n ),当输入一个随机信号x (n ),且
)()()(n n s n x υ+=
其中s (n )表示信号,)(n υ表示噪声,则输出y (n )为
∑-=m
m n x m h n y )()()(
我们希望x (n )通过线性系统h (n )后得到的y (n )尽量接近于s (n ),因此称y (n )为s (n )的估计值,
用)(ˆn s
表示,即 )(ˆ)(n s
n y =
维纳滤波器的输入—输出关系
如上图所示。
这个线性系统)(⋅h 称为对于s(n)的一种估计器。
如果我们以s
s ˆ与分别表示信号的真值与估计值,而用e (n )表示它们之间的误差,即
)(ˆ)()(n s
n s n e -= 显然,e (n )可能是正的,也可能是负的,并且它是一个随机变量。
因此,用它的均方值来表达误差是合理的,所谓均方误差最小即它的平方的统计平均值最小:
[][]
22)ˆ()(s
s E n e E -=最小 已知希望输出为:
1
ˆ()()()()N m y n s
n h m x n m -===-∑ 误差为:
1
ˆ()()()()()()N m e n s n s
n s n h m x n m -==-=--∑ 均方误差为:
1
2
20()(()()())N m E e n E s n h m x n m -=⎡⎤⎡⎤=--⎢⎥⎣⎦
⎣⎦
∑ 上式对() m=0,1,,N-1h m 求导得到:
1
02(()()())()0
0,1,21N opt m E s n h m x n m x n j j N -=⎡⎤---==-⎢⎥⎣⎦
∑
进一步得:
[][]
1
()()()()()0,1,1N opt m E s n x n j h m E x n m x n j j N -=-=--=-∑
从而有:
1
()()()
0,1,2,,1N xs opt xx m R j h m R j m j N -==-=-∑
于是就得到N 个线性方程:
(0)(0)(0)(1)(1)(1)(1)1(1)(0)(1)(1)(0)(1)(2)1(1)(0)(1)(1)(2)(1)(0)
xs xx xx xx xs xx xx xx xs xx xx xx j R h R h R h N R N j R h R h R h N R N j N R N h R N h R N h N R ==+++--⎧⎪==+++--⎪
⎨
⎪⎪=--=-+-++-⎩
写成矩阵形式为:
(0)
(1)(1)(0)(0)(1)(0)(2)(1)(1)(1)(2)
(0)(1)(1)xx xx xx xs xx xx xx xs xx xx xx xs R R R N R h R R R N R h R N R N R R N h N -⎡⎤⎡⎤
⎡⎤⎢⎥⎢⎥⎢⎥-⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢
⎥⎢
⎥⎢⎥----⎣⎦⎣⎦⎣⎦
简化形式:xx xs R H R = 其中:H=[h(0) h(1)
h(N-1)]'是滤波器的系数
[](0),(1),(1)'xs xs xs xs R R R R N =-是互相关序列
(0)
(1)(1)(1)(0)(2)(1)(2)
(0)xx xx xx xx
xx xx xx xx xx xx R R R N R R R N R R N R N R -⎡⎤⎢⎥-⎢
⎥=⎢⎥⎢
⎥
--⎣⎦
是自相关矩阵
由上可见,设计维纳滤波器的过程就是寻求在最小均方误差下滤波器的单位脉冲响应或传递函数的表达式,其实质就是解维纳-霍夫(Wiener -Hopf )方程。
另外,设计维纳滤波器要求已知信号与噪声的相关函数。
三.程序求解过程
由上述可见,本程序实现的关键是在已知输入信号的自相关函数和输入信号和理想输出信号的互相关函数的情况下,求解维纳-霍夫(Wiener -Hopf )方程,从而得到滤波器系数,再进行维纳滤波。
求解步骤: 1. 初始化值
(0)(0)/(0)xd xx a r r = (0)(1)/(0)xd xx b r r =
2. 对于j=1,2,
,M-1,进行如下计算:
1
10()()()1(0)()()
j xd xx i j xx xx i r j r j i a i temp r r j i b i -=-=--=
--∑∑
()()2() i=0,1,
j-1a i a i temp b i =-⋅
()1a j temp =
1
01
0(1)(1)()2(0)()()
j xx xx i j xx xx i r j r i b i temp r r j i b i -=-=+-+=
--∑∑
()(1)2() i=1,
j b i b i temp b j i =--⋅-
(0)2b temp =
3.滤波器系数为:()() i=0,1,
M-1h i a i =
4.利用上面的得到的滤波器对输入信号进行维纳滤波,得到输出信号。
四.函数说明
函数使用方法:y=wienerfilter(x,Rxx,Rxd,M)
参数说明:x 是输入信号,Rxx 是输入信号的自相关向量,Rxx 是输入信号和理想信号的的互相关向量,M 是维纳滤波器的长度,输出y 是输入信号通过维纳滤波器进行维纳滤波后的输出。
具体程序见Matlab 的.m 文件。
五.程序示例
加载Matlab 中的语音数据handel ,人为地加入高斯白噪声,分别计算加入噪声后信号的自相关xx R 和加入噪声后信号和理想信号的互相关xd R ,取滤波器的长度为M=500,将以上参数代入函数中进行维纳滤波,得到输出。
程序如下:
load handel %加载语音信号 d=y; d=d*8; %增强语音信号强度 d=d';
fq=fft(d,8192); %进行傅立叶变换得到语音信号频频 subplot(3,1,1); f=Fs*(0:4095)/8192;
plot(f,abs(fq(1:4096))); %画出频谱图 title('原始语音信号的频域图形');
xlabel('频率f');
ylabel('FFT');
[m,n]=size(d);
x_noise=randn(1,n); %(0,1)分布的高斯白噪声
x=d+x_noise; %加入噪声后的语音信号
fq=fft(x,8192); %对加入噪声后的信号进行傅立叶变换,看其频谱变化
subplot(3,1,2);
plot(f,abs(fq(1:4096))); %画出加入噪声后信号的频谱图
title('加入噪声后语音信号的频域图形');
xlabel('频率f');
ylabel('FFT');
yyhxcorr=xcorr(x(1:4096)); %求取信号的信号的自相关函数
size(yyhxcorr);
A=yyhxcorr(4096:4595);
yyhdcorr=xcorr(d(1:4096),x(1:4096)); %求取信号和理想信号的互相关函数
size(yyhdcorr);
B=yyhdcorr(4096:4595);
M=500;
yyhresult=wienerfilter(x,A,B,M); %进行维纳滤波
yyhresult=yyhresult(300:8192+299);
fq=fft(yyhresult); %对维纳滤波的结果进行傅立叶变换,看其频谱变化subplot(3,1,3);
f=Fs*(0:4095)/8192;
plot(f,abs(fq(1:4096))); %画出维纳滤波后信号的频谱图
title('经过维纳滤波后语音信号的频域图形');
xlabel('频率f');
ylabel('FFT');
求出的频谱图如下所示:
由上述结果可见,经过维纳滤波后信号的噪声减弱,信噪比提高。
