2011年杭州市中考数学试卷及参考答案(1)

合集下载

杭州市中考数学试卷及参考答案

杭州市中考数学试卷及参考答案Company Document number：WTUT-WT88Y-W8BBGB-BWYTT-199982011年杭州市各类高中招生文化考试数学考生须知：1. 本试卷满分120分，考试时间100分钟。

2. 答题前，在答题纸上写姓名和准考证号。

3. 必须在答题纸的对应答题位置上答题，写在其它地方无效。

答题方式详见答题纸上的说明。

4. 考试结束后，试题卷和答题纸一并上交。

试题卷一. 仔细选一选（本题有10个小题，每小题3分，共30分）下面每小题给出的四个选项中，只有一个是正确的。

注意可以用多种不同的方法来选取正确答案。

1. 下列各式中，正确的是A. 3)3(2-=-B. 332-=-C. 3)3(2±=±D. 332±=2. 正方形纸片折一次，沿折痕剪开，能剪得的图形是A. 锐角三角形B. 钝角三角形C. 梯形D. 菱形 3. =⨯36)102(A. 9106⨯B. 9108⨯C. 18102⨯D. 18108⨯ 4. 正多边形的一个内角为135°，则该多边形的边数为A. 9B. 8C. 7D. 45. 在平面直角坐标系xOy 中，以点（-3，4）为圆心，4为半径的圆A. 与x 轴相交，与y 轴相切B. 与x 轴相离，与y 轴相交C. 与x 轴相切，与y 轴相交D. 与x 轴相切，与y 轴相离6. 如图，函数11-=x y 和函数xy 22=的图像相交于点M （2，m ），N （-1，n ），若21y y >，则x 的取值范围是A. 1-<x 或20<<xB. 1-<x 或2>xC. 01<<-x 或20<<xD. 01<<-x 或2>x7. 一个矩形被直线分成面积为x ，y 的两部分，则y 与x 之间的函数关系只可能是8. 如图是一个正六棱柱的主视图和左视图，则图中的=aA. 32B. 3C. 2D. 1 9. 若2-=+b a ，且a ≥2b ，则A.a b 有最小值21 B. a b有最大值1 C. b a 有最大值2 D. b a 有最小值98- 10. 在矩形ABCD 中，有一个菱形BFDE （点E ，F 分别在线段AB ，CD 上），记它们的面积分别为ABCD S 和BFDE S ，现给出下列命题：①若232+=BFDE ABCD S S ，则33tan =∠EDF ； ②若EF BD DE ⋅=2,则DF=2AD 则A. ①是真命题，②是真命题B. ①是真命题，②是假命题C. ①是假命题，②是真命题D. ①是假命题，②是假命题二. 认真填一填（本题有6个小题，每小题4分，共24分）要注意认真看清楚题目的条件和要填写的内容，尽量完整地填写答案 11. 写出一个比-4大的负．无理数_________12. 当7=x 时，代数式)1)(3()1)(52(+--++x x x x 的值为__________ 13. 数据，，，，，的众数是___________；中位数是_______________ 14. 如图，点A ，B ，C ，D 都在⊙O 上，的度数等于84°，CA 是∠OCD的平分线，则∠ABD+∠CAO=________° 15. 已知分式ax x x +--532，当2=x 时，分式无意义，则=a _______；当6<x 时，使分式无意义的x 的值共有_______个16. 在等腰Rt △ABC 中，∠C=90°，AC=1，过点C 作直线l ∥AB ，F 是l 上的一点，且AB=AF ，则点F 到直线BC 的距离为__________三. 全面答一答（本题有8个小题，共66分）解答应写出文字说明、证明过程或推演步骤。

2007-2011年杭州市中考试题数学答案

2007年杭州市中考试题数学参考答案一. 仔细选一选 (本题有10个小题, 每小题3分, 共30分)1、C2、C3、A4、D5、B6、B7、A8、C9、D 10、C 二. 认真填一填 (本题有6个小题, 每小题4分, 共24分)11、28d << 12、300 13、70,704070,55,55︒︒︒︒︒︒或 14、1 15、510x y =⎧⎨=⎩16、13111,,83224n πππ-⎛⎫- ⎪⎝⎭三. 全面答一答 (本题有8个小题, 共66分)17、（1）规律是任意一个分式除以前面一个分式恒等于2x y-；（2）第7个分式应该是157x y。

18、③有一个内角为直角；④一组邻边相等；⑤一组邻边相等；⑥有一个内角为直角； ⑦两腰相等；⑧一条腰垂直于底边。

19、（1）这个多面体是六棱柱；（2）侧面积为6ab ；全面积为2633ab b + 20、（1）略；（2）诸如公交优先；或宣传步行有利健康。

21、作图略22、（1）正确的结论是①、②、③；（2）证明略。

23、设原计划每天的行程为x 公里，由题意，应有：()()()8192200819912x x x ⎧+>⎪⎨+>-⎪⎩ 解得：256260x x >⎧⎨<⎩ 所以这辆汽车原来每天计划的行程范围是256公里至260公里。

24、（1）设动点出发t 秒后，点P 到达点A 且点Q 正好到达点C 时，BC BA t ==，则1630,102BPQ S t t ∆=⨯⨯=∴=（秒）则()()10,2BA cm AD cm ==；（2）可得坐标为()()10,30,12,30M N （3）当点P 在BA 上时，()213sin 010210y t t B t t =⨯⨯⨯=≤<；当点P 在DC 上时，()()1101859012182y t t t =⨯⨯-=-+<≤ 图象略2008年杭州市各类高中招生文化考试数学参考答案及评分标准一. 选择题(每小题3分, 共30分)二. 填空题(每小题4分, 共24分) 11. 5.0-; 12+-等, 答案不惟一12. BCD ∆ CAD ∆; 9:16 或BCD ∆ BAC ∆; 9:25 或CAD ∆ BAC ∆; 16:25 13. 说得不对, 不光看图象, 要看到纵坐标的差距不是很大. 14. 3215.r r 34;5 16. 4或7或9或12或15三. 解答题(8小题共66分) 17. (本题6分) 方程组如下: ⎩⎨⎧=+=+944235y x y x , --- 4分可以用代入消元和加减消元法来解这个方程组. --- 2分 18. (本题6分)(1) 对应关系连接如下: --- 4分(2) 当容器中的水恰好达到一半高度时, 函数关系图上t 的位置如上: --- 2分 19. (本题6分)凸八边形的对角线条数应该是20. --- 2分思考一: 可以通过列表归纳分析得到:思考二: 从凸八边形的每一个顶点出发可以作出5(8-3)条对角线, 8个顶点共40条, 但其一条对角线对应两个顶点, 所以有20条对角线. --- 4分 (如果直接利用公式: 2)3(-n n 得到20而没有思考过程, 全题只给3分) 20. (本题8分)作图如下, BCD ∠即为所求作的γ∠.--- 图形正确4分, 痕迹2分, 结论2分21. (本题8分)(1) 补全表格: --- 4分(2) 折线图: --- 4分22. (本题10分)(1) 将点),3(21P 代入函数关系式ta y =, 解得23=a , 有ty 23=将1=y 代入ty 23=, 得23=t , 所以所求反比例函数关系式为)(2323≥=t y t ;--3分再将)1,(23代入kt y =, 得32=k ,所以所求正比例函数关系式为)0(2332≤≤=t t y . --- 3分 (2) 解不等式4123<t, 解得 6>t , 所以至少需要经过6小时后，学生才能进入教室. --- 4分23. (本题10分)(1) ∵△ABC 是等腰△，CH 是底边上的高线，∴BCP ACP BC AC ∠=∠=,，又∵CP CP =, ∴△ACP ≌△BCP ，∴CBP CAP ∠=∠, 即CBF CAE ∠=∠; --- 3分 (2) ∵BCF ACE ∠=∠, CBF CAE ∠=∠，BC AC =,∴△ACE ≌△BCF ，∴BF AE =; --- 3分 (3) 由(2)知△ABG 是以AB 为底边的等腰△，∴ABG ABC S S ∆∆= 等价于AC AE =，1）当∠C 为直角或钝角时，在△ACE 中，不论点P 在CH 何处，均有AC AE >，所以结论不成立; 2）当∠C 为锐角时， =∠A -9021∠C ，而A C A E ∠<∠，要使AC AE =，只需使∠C =∠CEA ，此时，∠=CAE 180°–2∠C ，只须180°–2∠C <-9021∠C ，解得 60°<∠C < 90°. --- 4分(也可在CEA ∆中通过比较C ∠和CEA ∠的大小而得到结论)24. (本题12分)(1) ∵ 平移2tx y -=的图象得到的抛物线F 的顶点为Q ,∴ 抛物线F 对应的解析式为:b t x t y +--=2)(. --- 2分 ∵ 抛物线与x 轴有两个交点，∴0>b t . --- 1分令0=y , 得-=t OB t b，+=t OC tb , ∴ -=⋅t OC OB (|||||tb)( +t t b )|-=2|t 22|OA t tb == ,即22tt t b ±=-, 所以当32t b =时, 存在抛物线F 使得||||||2OC OB OA ⋅=.-- 2分 (2) ∵BC AQ //, ∴ b t =, 得F : t t x t y +--=2)(,解得1,121+=-=t x t x . --- 1分在∆Rt AOB 中,1) 当0>t 时,由 ||||OC OB <, 得)0,1(-t B , 当01>-t 时, 由=∠ABO tan 23=||||OB OA =1-t t , 解得3=t , 此时, 二次函数解析式为241832-+-=x x y ; --- 2分当01<-t 时, 由=∠ABO tan 23=||||OB OA =1+-t t , 解得=t 53, 此时，二次函数解析式为-=y 532x +2518x +12548. --- 2分 2) 当0<t 时, 由 ||||OC OB <, 将t -代t , 可得=t 53-, 3-=t , （也可由x -代x ，y -代y 得到）所以二次函数解析式为 =y 532x +2518x –12548或241832++=x x y . --- 2分2009年杭州市各类高中招生文化考试数学参考答案一、仔细选一选（每小题3分，芬30分）题号 1 2 3 4 5 6 7 8 9 10 答案CDACBCBDBD二. 认真填一填（本题有6个小题，每小题4分，共24分） 11、326512.)2)(2)(2(2-++x x x 13、23；2.614、14或16或2615、46-≠->m m 或16、①5∶2 ；②21三. 全面答一答（本题有8个小题，共66分） 17、（本题6分）至少会有一个整数 .因为三个任意的整数a,b,c 中，至少会有2个数的奇偶性相同，不妨设其为a ，b ，那么2ba +就一定是整数 . 18、（本题4分）（1）连接圆心O 和T 1的6个顶点可得6个全等的正三角形 . 所以r ∶a=1∶1;连接圆心O 和T 2相邻的两个顶点，得以圆O 半径为高的正三角形，所以r ∶b=3∶2;（2） T 1∶T 2的连长比是3∶2，所以S 1∶S 2=4:3):(2=b a .19、（本题6分）（1）圆锥；（2）表面积S=πππππ164122=+=+=+r rl S S 圆扇形（平方厘米）（3）如图将圆锥侧面展开，线段BD 为所求的最短路程 . 由条件得，∠BAB ′=120°，C 为弧BB ′中点，所以BD =33 .20、（本题8分）（1）作图如右，ABC ∆即为所求的直角三角形；（2）由勾股定理得，AC =52cm ，设斜边AC 上的高为h, ABC ∆面积等于h ⨯⨯=⨯⨯52212421，所以554=h 21、（本题8分）（1）补全的三张表如下：编号项目人数比例 1 经常近距离写字 360 37.50% 2 经常长时间看书 200 20.83% 3长时间使用电脑525.42%4 近距离地看电视 108 11.25% 5不及时检查视力24025.00%（表一）（2）例如：“象爱护生命一样地爱护眼睛！”等 . 22、（本题10分）（1）∵BA=AD ，∠BAE=∠ADF ，AE=DF ， ∴△BAE ≌△ADF ，∴BE=AF ；（2）猜想∠BPF=120° .∵由（1）知△BAE ≌△ADF ，∴∠ABE=∠DAF .∴∠BPF=∠ABE+∠BAP=∠BAE ，而AD ∥BC ，∠C=∠ABC=60°， ∴∠BPF=120° . 23、（本题10分）（1）9191215225++++=x y ；（2）由题意有x x >++++9191215225，解得x ＜17，所以小方在前5场比赛中总分的最大值应为17×5－1=84分；（3）又由题意，小方在这10场比赛中得分至少为18×10 + 1=181分，设他在第10场比赛中的得分为S ，则有81+（22+15+12+19）+ S ≥181 .解得S≥29，所以小方在第10场比赛中得分的最小值应为29分 .24、（本题12分）（1）设第一象限内的点B （m,n ），则tan ∠POB 91==m n ，得m=9n ，又点B 在函数xy 1= 的图象上，得m n 1=，所以m =3（－3舍去），点B 为)31,3(，而AB ∥x 轴，所以点A （31，31），所以38313=-=AB ；（2）由条件可知所求抛物线开口向下，设点A （a , a ），B （a 1，a ），则AB =a 1－ a = 38, 所以03832=-+a a ，解得313=-=a a 或 . 当a = －3时，点A （―3，―3），B （―31，―3），因为顶点在y = x 上，所以顶点为（－35，－35），所以可设二次函数为35)35(2-+=x k y ，点A 代入，解得k= －43,所以所求函数解析式为35)35(432-+-=x y .同理，当a = 31时，所求函数解析式为35)35(432+--=x y ；（3）设A （a , a ），B （a 1，a ），由条件可知抛物线的对称轴为aa x 212+= .设所求二次函数解析式为：)2)1()(2(59++--=aa x x y .点A （a , a ）代入，解得31=a ，1362=a ，所以点P 到直线AB 的距离为3或136.2010年杭州市各类高中招生文化考试数学评分标准一、仔细选一选 (本题有10个小题, 每小题3分, 共30分)题号 1 2 3 4 5 6 7 8 9 10 答案CBDAACBCDB二、认真填一填 (本题有6个小题, 每小题4分, 共24分)11. 3.422⨯106 12. m (m +2)(m – 2) 13. 118° 14. 4 15. 5.20 16. 332+三、全面答一答 (本题有8个小题, 共66分) 17．(本小题满分6分)方法1．用有序实数对(a ，b )表示.比如：以点A 为原点，水平方向为x 轴，建立直角坐标系，则B(3，3). --- 3分方法2. 用方向和距离表示.比如: B 点位于A 点的东北方向（北偏东45°等均可），距离Ａ点32处． --- 3分18. (本小题满分6分)(1) 作图如右, 点P 即为所求作的点; --- 图形2分, 痕迹2分 (2) 设AB 的中垂线交AB 于E ，交x 轴于F ，由作图可得, EF AB ⊥, EF x ⊥轴, 且OF =3, ∵OP 是坐标轴的角平分线，∴P (3，3). --- 2分19. (本小题满分6分)(1)命题n : 点(n , n 2) 是直线y = nx 与双曲线y =xn 3的一个交点(n 是正整数). --- 3分(2)把 ⎩⎨⎧==2ny n x 代入y = nx ，左边= n 2，右边= n ·n = n 2，∵左边 =右边，∴点(n ，n 2)在直线上. --- 2分同理可证：点(n ，n 2)在双曲线上，∴点(n ，n 2)是直线y = nx 与双曲线y = xn 3的一个交点，命题正确. --- 1分20. (本小题满分8分) （1）（第18题）上海世博会前20天日参观人数的频数分布直方图填频数分布表 --- 2分频数分布直方图 --- 2分（2）日参观人数不低于22万有9天, --- 1分所占百分比为45％. --- 1分（3）世博会前20天的平均每天参观人数约为2040920332625618511＝＋＋＋⨯⨯⨯⨯＝20.45（万人） ---1分20.45×184＝3762.8（万人）∴ 估计上海世博会参观的总人数约为3762.8万人. --- 1分21. (本小题满分8分)(1) 当a = 2, h = 3时， V = a 2h = 12 ;S = 2a 2+ 4ah =32 . --- 4分 (2) ∵a 2h = 12, 2a (a + 2h ) =32， ∴ 212a h =, (a + 2h ) =a16, ∴ha 12+=ah ah +2=21216aa a ⋅=34. --- 4分22. (本小题满分10分)(1) ∵ BD ∥AC ，点B ，A ，E 在同一条直线上， ∴ ∠DBA = ∠CAE , 又∵3==AEBDAC AB , ∴ △ABD ∽△CAE . --- 4分 (2) ∵AB = 3AC = 3BD ，AD =22BD ，组别（万人）组中值(万人)频数频率 7.5～14.5 11 5 0.25 14.5～21.5 18 6 0.30 21.5～28.5 25 6 0.30 28.5～35.53230.15上海世博会前20天日参观人数的频数分布表∴ AD 2 + BD 2 = 8BD 2 + BD 2 = 9BD 2 =AB 2， ∴∠D =90°, 由（1）得 ∠E =∠D = 90°, ∵ AE =31BD , EC =31AD =232BD , AB = 3BD ， ∴在Rt △BCE 中，BC 2 = (AB + AE )2 + EC 2 = (3BD +31BD )2 + (322BD )2 = 9108BD 2 = 12a 2 , ∴ BC =32 a . --- 6分23. (本小题满分10分)(1) 作BH ⊥PQ 于点H , 在Rt △BHP 中,由条件知, PB = 320, ∠BPQ = 30°, 得 BH = 320sin30° = 160 < 200,∴ 本次台风会影响B 市. ---4分 (2) 如图, 若台风中心移动到P 1时, 台风开始影响B 市, 台风中心移动到P 2时, 台风影响结束. 由（1）得BH = 160, 由条件得BP 1=BP 2 = 200,∴所以P 1P 2 = 222160200-=240, --- 4分 ∴台风影响的时间t = 30240= 8(小时). --- 2分 24. (本小题满分12分)(1) ∵OABC 是平行四边形，∴AB ∥OC ，且AB = OC = 4， ∵A ，B 在抛物线上，y 轴是抛物线的对称轴， ∴ A ，B 的横坐标分别是2和– 2，代入y =241x +1得， A(2, 2 )，B(– 2，2)， ∴M (0，2)， ---2分 (2) ① 过点Q 作QH ⊥ x 轴，设垂足为H ，则HQ = y ，HP = x –t ，由△HQP ∽△OMC ，得：42tx y -=, 即： t = x – 2y , ∵ Q(x ,y ) 在y = 241x +1上， ∴ t = –221x + x –2. ---2分当点P 与点C 重合时，梯形不存在，此时，t = – 4，解得x = 1±5, 当Q 与B 或A 重合时，四边形为平行四边形，此时，x =± 2(第22题)（第23题）（第24题）∴x 的取值范围是x ≠ 1±5, 且x ≠± 2的所有实数. ---2分 ② 分两种情况讨论：1）当CM > PQ 时，则点P 在线段OC 上， ∵ CM ∥PQ ，CM = 2PQ ，∴点M 纵坐标为点Q 纵坐标的2倍，即2 = 2(241x +1)，解得x = 0 ， ∴t = –2021+ 0 –2 = –2 . --- 2分 2）当CM < PQ 时，则点P 在OC 的延长线上， ∵CM ∥PQ ，CM =21PQ ， ∴点Q 纵坐标为点M 纵坐标的2倍，即241x +1=2⨯2，解得： x = ±32. ---2分当x = –32时，得t = –2)32(21–32–2 = –8 –32, 当x =32时，得t =32–8. ---2分2011年杭州市中考数学试卷参考答案一、选择题题号 1 2 3 4 5 6 7 8 910 答案BCDBCDABCA二、填空题11、如2-等；12、-6；13、9.10，9.15；14、48︒；15、6，2；16、312±三、解答题17、解：由已知得，直线AB 方程为26y x =+，直线CD 方程为112y x =-+ 解方程组26112y x y x =+⎧⎪⎨=-+⎪⎩，得22x y =-⎧⎨=⎩，所以直线AB ，CD 的交点坐标为（-2，2）. 18、解：（1）图略，只能选,,b c d 三边画三角形；（2）所求概率为14p =19、解：（1）222123BC AC AB +=+== ，ABC ∴∆是直角三角形，且C Rt ∠=∠.11sin sin 3023BC A AB ==>=︒ ，30A ∴∠≠︒. （2）所求几何体的表面积为()()()23262S r l r πππ=+=⨯⨯+=+20、解：（1）图略；（2）从第六届开始成交金额超百亿元，第五第六届成交金额增长最快；（3）设第五届到第七届平均增长率为x ，则265.3(1)128x += 解得40%x ≈，或 2.4x ≈-（不合题意，舍去）所以预测第八届成交金额约为128(1+40%)179⨯≈（亿元）. 21、解：（1）取出⑤，向上平移2个单位；（2）可以做到. 因为每个等边三角形的面积是134S =，所以正六边形的面积为61335622S S ==> 而615335302224S S <-=-<= 所以只需用⑤的33522⎛⎫- ⎪ ⎪⎝⎭面积覆盖住正六边形就能做到.22、解：（1）EF 是OAB ∆的中位线，1//,2EF AB EF AB ∴= 而1,//2CD AB CD AB =,,EF CD OEF OCD OFE ODC ∴=∠=∠∠=∠ FOE DOC ∴∆≅∆（2）222245AC AB BC BC BC BC =+=+=15sin sin 55BC OEF CAB AC ∴∠=∠===SERBM（3）,//AE OE OC EF CD ==A E G A C ∴∆∆ ，11,33EG AE EG CD CD AC ∴===即同理13FH CD =29533AB CD CD CD CD CD GH CD ++∴==++23、解：（1）如两个函数为21,31y x y x x =+=++，函数图形略；（2）不论k 取何值，函数2(21)1y kx k x =+++的图象必过定点(0,1),(2,1)--，且与x 轴至少有1个交点.证明如下：由2(21)1y kx k x =+++，得2(2)(1)0k x x x y ++-+=当220,10x x x y +=-+=且，即0,12,1x y x y ===-=-，或时，上式对任意实数k 都成立，所以函数的图像必过定点(0,1),(2,1)--.又因为当0k =时，函数1y x =+的图像与x 轴有一个交点；当0k ≠时，22(21)4410k k k ∆=+-=+> ，所以函数图像与x 轴有两个交点.所以函数2(21)1y kx k x =+++的图象与x 轴至少有1个交点.（3）只要写出1m ≤-的数都可以.0k < ，∴函数2(21)1y kx k x =+++的图像在对称轴直线212k x k+=-的左侧，y 随x 的增大而增大. 根据题意，得212k m k +≤-，而当0k <时，2111122k k k+-=-->- 所以1m ≤-.24、解：（1）由题意，得四边形ABCD 是菱形.由//EF BD ，得ABD AEF ∆∆ ，1565h EF -∴=，即()1655EF h =- ()2111166515255522OEFS S EF h h h h ∆⎛⎫∴==⨯=-⨯=--+ ⎪⎝⎭所以当152h =时，max 152S =. （2）根据题意，得OE OM =.如图，作OR AB ⊥于R ， OB 关于OR 对称线段为OS ，1）当点,E M 不重合时，则,OE OM 在OR 的两侧，易知RE RM =.225334AB =+= ，1534OR ∴=2215933434BR ⎛⎫∴=-= ⎪⎝⎭由////ML EK OB ，得,OK BE OL BMOA AB OA AB== 2OK OL BE BM BROA OA AB AB AB∴+=+=，即1295517h h +=124517h h ∴+=，此时1h 的取值范围为145017h <<且14534h ≠ 2）当点,E M 重合时，则12h h =，此时1h 的取值范围为105h <<.。

浙江省2011年中考数学试题分类解析1 实数(含答案)

浙江省2011年中考数学专题1：实数一、选择题1.（浙江舟山、嘉兴3分）－6的绝对值是（A ）－6（B ）6（C ）61（D ）61【答案】A 。

【考点】绝对值。

【分析】根据绝对值的性质：一个正数的绝对值是它本身；一个负数的绝对值是它的相反数；0的绝对值是0。

据此作解即可。

故选A 。

2.（浙江舟山、嘉兴3分）一个纸环链，纸环按红黄绿蓝紫的顺序重复排列，截去其中的一部分，剩下部分如图所示，则被截去部分纸环的个数可能是（A ）2010（B ）2011（C ）2012（D ）2013【答案】D 。

【考点】分类归纳。

【分析】从图中知，该纸链是5的倍数，中间截去的是剩下3+5n ，从选项中数减3为5的倍数者即为所求。

∵2013-3被5整除，故选D 。

2.（浙江温州4分）计算：（﹣1）+2的结果是A 、﹣1B 、1C 、﹣3D 、3【答案】B 。

【考点】有理数的加法。

【分析】异号两数相加，取绝对值较大加数的符号，再用较大绝对值减去较小绝对值：（﹣1）+2=+（2﹣1）=1。

故选B 。

3.（浙江绍兴4分）－3的相反数是A 、－13B 、13C 、3D 、－3【答案】C 。

【考点】相反数。

【分析】相反数的定义是：如果两个数只有符号不同，我们称其中一个数为另一个数的相反数，特别地，0的相反数还是0。

∴－3的相反数是3。

故选C 。

4.（浙江绍兴4分）明天数学课要学“勾股定理”．小敏在“百度”搜索引擎中输入“勾股定理”，能搜索到与之相关的结果个数约为12 500 000，这个数用科学记数法表示为A 、1.25×105B 、1.25×106C 、1.25×107D 、1.25×108【答案】C 。

【考点】科学记数法。

【分析】根据科学记数法的定义，科学记数法的表示形式为1010n a a <⨯≤，其中1，n 为整数，表示时关键要正确确定a 的值以及n 的值。

在确定n 的值时，看该数是大于或等于1还是小于1。

2011年中考数学试题及答案(Word版)

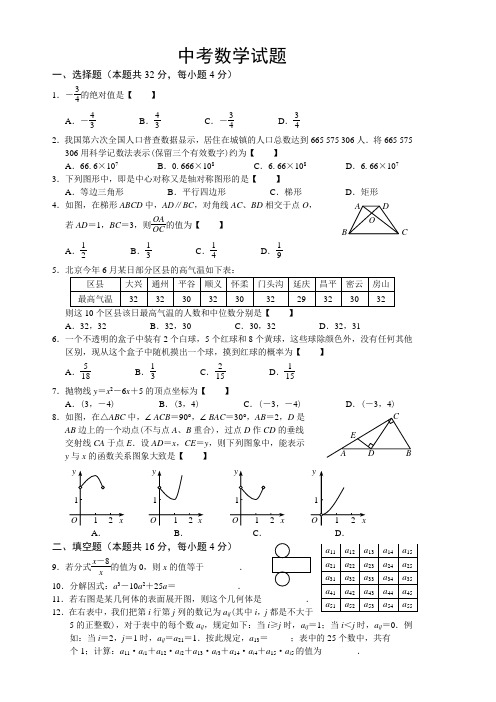
A OBCD A B C ED 中考数学试题一、选择题（本题共32分，每小题4分）1．－ 34的绝对值是【】A ．－ 4 3B ． 4 3C ．－ 3 4D ． 342．我国第六次全国人口普查数据显示，居住在城镇的人口总数达到665 575 306人．将665 575 306用科学记数法表示(保留三个有效数字)约为【】A ．66.6×107B ．0.666×108C ．6.66×108D ．6.66×107 3．下列图形中，即是中心对称又是轴对称图形的是【】A ．等边三角形B ．平行四边形C ．梯形D ．矩形 4．如图，在梯形ABCD 中，AD ∥BC ，对角线AC 、BD 相交于点O ，若AD ＝1，BC ＝3，则OAOC的值为【】 A ． 1 2 B ． 1 3 C ． 1 4 D ． 195则这10个区县该日最高气温的人数和中位数分别是【】A ．32，32B ．32，30C ．30，32D ．32，316．一个不透明的盒子中装有2个白球，5个红球和8个黄球，这些球除颜色外，没有任何其他区别，现从这个盒子中随机摸出一个球，摸到红球的概率为【】 A ．5 18 B ． 1 3 C ． 2 15 D ． 1157．抛物线y ＝x 2－6x ＋5的顶点坐标为【】A ．(3，－4)B ．(3，4)C ．(－3，－4)D ．(－3，4)8．如图，在△ABC 中，∠ACB ＝90°，∠BAC ＝30°，AB ＝2，D 是AB 边上的一个动点(不与点A 、B 重合)，过点D 作CD 的垂线交射线CA 于点E ．设AD ＝x ，CE ＝y ，则下列图象中，能表示y 与x 的函数关系图象大致是【】二、填空题（本题共16分，每小题4分）9．若分式x ―8x的值为0，则x 的值等于________． 10．分解因式：a 3―10a 2＋25a ＝______________．11．若右图是某几何体的表面展开图，则这个几何体是__________．12．在右表中，我们把第i 行第j 列的数记为a ij (其中i ，j 都是不大于5的正整数)，对于表中的每个数a ij ，规定如下：当i ≥j 时，a ij ＝1；当i ＜j 时，a ij ＝0．例如：当i ＝2，j ＝1时，a ＝a ＝1．按此规定，a ＝_____；表中的25个数中，共有_____A ．B ．C ．D ．FE x13．计算：01)2(2730cos 221π-++-⎪⎭⎫⎝⎛- ．14．解不等式：4(x －1)＞5x －6．15．已知a 2＋2ab ＋b 2＝0，求代数式a (a ＋4b )－(a ＋2b )(a －2b )的值．16．如图，点A 、B 、C 、D 在同一条直线上，BE ∥DF ，∠A ＝∠F ，AB ＝FD ．求证：AE ＝FC ．17．如图，在平面直角坐标系xOy 中，一次函数y ＝－2x 的图象与反比例函数y ＝ kx 的图象的一个交点为A (－1，n )．(1)求反比例函数y ＝ kx的解析式；(2)若P 是坐标轴上一点，且满足P A ＝OA ，直接写出点P 的坐标．18．列方程或方程组解应用题：京通公交快速通道开通后，为响应市政府“绿色出行”的号召，家住通州新城的小王上班由自驾车改为乘坐公交车．已知小王家距上班地点18千米．他用乘公交车的方式平均每小时行驶的路程比他自用驾车的方式平均每小时行驶的路程的2倍还多9千米，他从家出发到达上班地点，乘公交车方式所用时间是自驾车方式所用时间的 37．小王用自驾车方式上班平均每小时行驶多少千米？A B C D19．如图，在△ABC 中，∠ACB ＝90°，D 是BC 的中点，DE ⊥BC ，CE ∥AD ．若AC ＝2，CE ＝4，求四边形ACEB 的周长．21．以下是根据北京市国民经济和社会发展统计公报中的相关数据，绘制统计图的一部分．请根据以上信息解答下列问题：(1)2008年北京市私人轿车拥有是多少万辆(结果保留三个有效数字)？ (2)补全条形统计图；(3)汽车数量增多除造成交通拥堵外，还增加了碳排放量，为了了解汽车碳排放量的情况，小明同学通过网络了解到汽车的碳排放量与汽车排量有关．如：一辆排量为1.6L 的轿车，如果一年行驶1万千米，这一年，它碳排放量约为2.7吨．于是他调查了他所居住小区的150辆私人轿车，不同排量的轿车数量如下表所示．如果按照小明的统计数据，请你通过计算估计，2010年北京市仅排量为1.6L 的这类私人轿车(假设每辆车平均一行行驶1万千米)的碳排放总量约为多少万吨？北京市2001～2010年私人轿车拥有量的年增长率统计图北京市2001～2010年私人轿车拥有量统计图A E F 图3 22．阅读下面材料：小伟遇到这样一个问题：如图1，在梯形ABCD 中，AD ∥BC ，对角线AC 、BD 相交于点O ．若梯形ABCD 的面积为1，试求以AC 、BD 、AD ＋BC 的长度为三边长的三角形的面积．小伟是这样思考的：要想解决这个问题，首先应想办法移动这些分散的线段，构造一个三角形，再计算其面积即可．他先后尝试了翻折、旋转、平移的方法，发现通过平移可以解决这个问题．他的方法是过点D 作AC 的平行线交BC 的延长线于点E ，得到的△BDE 即是以AC 、BD 、AD ＋BC 的长度为三边长的三角形(如图2)．参考小伟同学的思考问题的方法，解决下列问题：如图3，△ABC 的三条中线分别为AD 、BE 、CF ．(1)在图3中利用图形变换画出并指明以AD 、BE 、CF的长度为三边长的一个三角形(保留画图痕迹)； (2)若△ABC 的面积为1，则以AD 、BE 、CF 的长度为三边长的三角形的面积等于_______．24．(7分)在□ABCD 中，∠BAD 的平分线交直线BC 于点E ，交直线DC 于点F ．(1)在图1中，证明：CE ＝CF ； (2)若∠ABC ＝90°，G 是EF 的中点(如图2)，直接写出∠BDG 的度数； (3)若∠ABC ＝120°，FG ∥CE ，FG ＝CE ，分别连结DB 、DG (如图3)，求∠BDG 的度数．B BADADC C EE G FABC DE GF 图1图2图3BBCADOADCEO图2图1数学试卷答案及评分参考13、解：()0122730221π-++-⎪⎭⎫⎝⎛- cos=1332322++⨯- =13332++- =332+.14、解：去括号，得6544->-x x移项，得6454->-x x合并，得2->-x 解得 2<x所以原不等式的解集是2<x . 15、解：()()()b a b a b a a 224-+-+ =()22244b a ab a --+ =244b ab +∵0222=++b ab a ∴0=+b a∴原式=()b a b +4=0. 16、证明：∵BE ∥DF ， ∴∠ABE=∠D .在△ABE 和△FDC 中，∴△ABE ≌△FDC . ∴AE =FC .17、解（1）∵A （-1，n ）在一次函数x y 2-=∴n =2-×（1-）=2.∴点A 的坐标为（-1，2）.∵点A 在反比例函数xky =的图象上，∴2-=k .∴反比例函数的解析式为xy 2-=. ∠ABE=∠D AB=FD∠A=∠F18、解：设小王用自驾车方式上班平均每小时行使x 千米. 依题意，得xx 18739218⨯=+ 解得 27=x .经检验，27=x 是原方程的解，且符合题意. 答；小王用自驾车方式上班平均每小时行使27千米. 四、解答题19、解：∵∠ACB=90°，DE ⊥BC ， ∴AC ∥DE .又∵CE ∥AD ，∴四边形ACED 的是平行四边形. ∴DE=AC=2.在Rt △CDE 中，由勾股定理得3222=-=DE CE CD . ∵D 是BC 的中点， ∴BC=2CD=34.在Rt △ABC 中，由勾股定理得13222=+=BC AC AB . ∵D 是BC 的中点，DE ⊥BC ， ∴EB=EC=4.∴四边形ACEB 的周长= AC+CE+EB+BA=10+132. 21、解（1）146×（1+19%） =173.74≈174（万辆）.∴2008年北京市私人轿车拥有量约是174万辆.（2）如右图. （3）276×15075×2.7=372.6（万吨）估计2010年北京市仅排量为1.6L的这类私人轿车的碳排放总量约为372.6万吨.22、解：△BDE 的面积等于1 . （1）如图.以AD 、BE 、CF 的长度为三边长的一个三角形是 △CFP . （2）以AD 、BE 、CF 的长度为三边长的三角形的面积等于43. . 24、（1）证明：如图1. ∵AF 平分∠BAD ， ∴∠BAF=∠DAF .∵四边形ABCD 是平行四边形， ∴AD ∥BC ，AB ∥CD .∴∠DAF=∠CEF ，∠BAF=∠F .E∴CE =CF .（2）∠BDG =45°.（3）分别连结GB 、GE 、GC （如图2） ∵AB ∥DC ，∠ABC =120°， ∴∠ECF=∠ABC=120°.∵FG ∥CE 且FG =CE ，∴四边形CEGF 是平行四边形. 由（1）得CE =CF ， ∴□CEGF 是菱形.∴EG =EC ，∠GCF=∠GCE=21∠ECF= 60°.∴△ECG 是等边三角形.∴EG =CG ， ① ∠GEC=∠EGC=60°. ∴∠GEC=∠GCF .∴∠BEG=∠DCG . ②由AD ∥BC 及AF 平分∠BAD 可得∠BAE =∠AEB . ∴AB=BE .在□ABCD 中，AB=DC . ∴BE=DC . ③ 由①②③得△BEG ≌△DCG . ∴BG=DG ，∠1=∠2.∴∠BGD=∠1+∠3=∠2+∠3=∠EGC=60°. ∴∠BDG=2180BGD∠- =60°.图2。

2011年杭州市中考数学试卷(含答案)

2011年杭州市中考数学试卷(含答案) 2011年杭州市中考数学试卷一、选择题（每小题5分，共30分）1. 若一个正方体的一条对角线长为x，那么它的一条棱长约为是多少？2. 若，则m的值为多少？3. 若集合A={1,2,3,4}，B={3,4,5,6}，C={5,6,7,8}，则。

4. 已知一个由20个正六边形面构成的多面体的表面积为360平方厘米，则这个多面体的体积是多少？5. 曲线y=x²-6x+10的图象是。

6. 乙比甲晚2小时到达终点，如果乙每小时15公里，那么甲每小时多少公里？二、填空题（每小题6分，共30分）7. 计算：35×1.1+57×0.65＝_________。

8. 若，则a=_________。

9. 数集中15个元素的众数为8，则数集中11个元素的众数是_________。

10. 一个减数是，另一个减数为，差是。

11. 一个数的三次方大于216，小于729，这个数是。

三、解答题（共40分）12. 用1元，2元，5元若干张凑成15元，共有多少种不同的凑法？13. 福建沿海应用科技学校的2010级初中生定于6月15日第一次参观都江堰，7月22日第二次参观峨眉山，这两次参观都结束后共用去了学校的4个百分之一的时间。

学校共用了几天参观这两个地方？14. 若，则x=_________。

15. 将一个四位数的个位数、千位数相加得11，十位数、百位数相加等于12，求这个四位数。

16. 对于一个十进制数，它与15倍后相差28，求这个十进制数。

2011年杭州市中考数学试卷答案一、选择题（每小题5分，共30分）1. 2x÷√32. -13. B4. 420 cm³5. 抛物线6. 30 km/h二、填空题（每小题6分，共30分）7. 76.258. -19. 810. 0.711. 6三、解答题（共40分）12. 有三种不同的凑法：a)全用1元共15张；b)一张2元，11张1元；c)三张5元共5元。

2011年浙江省中考数学试卷

2011年浙江省初中生学业考试数学I试卷….•一・•：■•!■:门:：：：''•・! \ .• • J・•・•■・/ ;・・.・考生须知：\ 、・・• •〕八; ・]1.本试卷分试题卷和答题卷两部分•满分150分，考试时间120分钟.• 2.答题时，应该古答题卷指定位置内填写学校、班级、姓名和准考证号.3.所有答案都必须做在答题卷标定的位置上，请务必注意试题序号和答题序号相对应.4・考试结束后，丄交试题卷和答题卷../參考公式:二次函数2+加化图象的顶点坐标是（-碁，驚1）.试题卷]一.选择题（本大题有10小题海小题4分，共40分.请选出各题中一个符合题意的正确选项, 将答题卡上相应的位置涂黑.不选、多选、错选均不给分）-2-1012 第1題田3. B.中国是缺水严重的国家之一，人均淡水资源为世界人均量的四分之一，所以我们为中国节水, 为世界节水•若每人每天浪费水0.32L,那么100万人每天浪费的水,用科学记数法表示为（）4. B. 3.2x1^ C. 3.2x10^1 D. 3.2x10^某校七年级有13名同学参加百米竞赛，预赛成绩各不相同，要取前6名参加决赛，小梅已经知道了自己的成绩，她想知道自己能否进入决赛,还需要知道这13名同学成绩的（） A.中位数•B.众数C.平均数A. 3.2X10T5. 如图，小华同学设计了一个圆直径的测量器，标有刻度的尺子OA 、0B 在0点钉在一起，并使它们保持垂直，在测直径时，把0点靠在圆周上,读D.极差 B 第5题图如图，直角三角形纸片的两直角边长分别为6,8,按如图那样折叠，使点 C. 16：257.已知m=l+VT t Fi=l-V^ JlJ 代数式皿话而"的值为() A. 9 B. ±3 C. 3D. 5&如图，在五边形ABCDE 中，乙以£=120。

，/■加乙E=90。

"BMC, AE=DE,在BC,DE 上分别找一点M,/V,使得ZSAMN 周长最小时，则•LAMN^LANM 的度数为( ・ ••：)• ； ' lA. 100°B. 110°C. 120。

2011年初中毕业升学考试(中考)数学试卷及答案

数学试卷第1页（共10页）准考证号：**市2011年初中毕业生学业考试数学试卷【说明】全卷分为第Ⅰ卷和第Ⅱ卷，第Ⅰ卷1－2页，第Ⅱ卷3－10页。

考试时间120分钟，满分150分。

考试结束后，第Ⅱ卷和答题卡按规定装袋上交。

第Ⅰ卷(选择题共40分)注意事项：1．答第Ⅰ卷前，考生务必将自己的学校、姓名、准考证号、考试科目填涂在答题卡上。

2．每小题选出答案后，用铅笔把答题卡上对应题目的答案标号涂黑。

如需改动，用橡皮擦干净后，再选涂其他答案，不能答在试题卷上。

3．考试结束后，本试卷由考场统一收回，集中管理。

一、选择题：本大题共10个小题，每小题4分，共40分，在每个小题给出的四个选项中，只有一个符合题目要求 1．－2的相反数A ．－2B ．2C ．2±D ．－2 2．下列分式是最简分式的Ａ．b a a 232 B ．a a a 32- C ．22b a b a ++ D ．222ba ab a -- 3．下列运算错误的是A ．235a a a ⋅=B ．347()m m =C ．3363282c b a bc a =）（ D ．624m m m ÷= 4．一幅扑克牌（不含大小王），任意抽取一张，抽中方块的概率是 A ．21 B ．521 C ．31 D ．415．函数31--=x x y 的自变量x 的取值范围是 A ．1x > B ．1x >且3x ≠ C ．1≥x D. 1≥x 且3x ≠数学试卷第2页（共10页）6．点（－2，3）关于原点对称的点的坐标是A ．(2,3)B ．(－2,－3)C ．(2,－3)D ．(－3,2) 7．如图：等腰梯形ABCD 中，AD ∥BC ，AB=DC ， AD=3，AB=4,∠B=60︒，则梯形的面积是 A.310 B.320 C.346+ D.3812+ 8．计算2sin30︒-sin 245︒+cot60︒的结果A.3321+ B.3321+ C.23+ D.23-1+ 9．如图：△ABC 中，DE ∥BC ，AD:DB=1:2,下列选项正确的是A ．DE:BC=1:2B ．AE:AC=1:3C ．BD:AB=1:3D ．S DE A ∆:S ABC ∆=1:4（第9题）（第10题）10．如图：在△ABC 中，∠ACB=90°,CD ⊥AB 于点D ，下列说法中正确的个数是①CD AB BC AC ⋅=⋅ ②DB AD AC ⋅=2③BA BD BC ⋅=2 ④DB AD CD ⋅=2A ．1个B ．2个C ．3个D ．4个CBEDABDAC数学试卷第3页（共10页）绝密★启用前【考试时间：2011年6月】**市2011年初中毕业生学业考试数学试卷第Ⅱ卷（非选择题共110分）注意事项：1．第Ⅱ卷共8页，用钢笔或中性笔直接答在试卷上。

2011年浙江杭州中考数学试题

一、仔细选一选（本题有10个小题，每小题3分，共30分）1. 下列各式中，正确的是（）A . 3)3(2-=-B . 332-=-C . 3)3(2±=±D . 332±=2. 正方形纸片折一次，沿折痕剪开，能剪得的图形是（）A . 锐角三角形B . 钝角三角形C . 梯形D . 菱形3. =⨯36)102(（）A . 9106⨯B . 9108⨯C . 18102⨯D . 18108⨯4. 正多边形的一个内角为135°，则该多边形的边数为（）A . 9B . 8C . 7D . 45. 在平面直角坐标系xOy 中，以点（-3，4）为圆心，4为半径的圆（）A .与x 轴相交，与y 轴相切B . 与x 轴相离，与y 轴相交C .与x 轴相切，与y 轴相交D . 与x 轴相切，与y 轴相离11-=x y 和函数xy 22=的6. 如图，函数图像相交于点M （2，，7. m ），N （-1，n ），若21y y >则x 的取值范围是（）A .1-<x 或20<<xB .1-<x 或2>xC .01<<-x 或20<<xD .01<<-x 或2>x7. 一个矩形被直线分成面积为x ，y 的两部分，则y 与x 之间的函数关系只可能是（）8. 如图是一个正六棱柱的主视图和左视图，则图中的=a （）A .32B .3C .2D .19. 若2-=+b a ，且a ≥2b ，则（）A .a b 有最小值21B . ab 有最大值1 C . b a 有最大值2D .b a 有最小值98- 10. 如图在矩形ABCD 中，有一个菱形BFDE （点E ，F 分别在线段AB ，CD 上），记它们的面积分别为ABCD S 和BFDE S ，现给出下列命题：①若232+=BFDE ABCD S S ，则33tan =∠EDF ； ②若EF BD DE ⋅=2,则DF =2AD 则（）A . ①是真命题，②是真命题B . ①是真命题，②是假命题C . ①是假命题，②是真命题D . ①是假命题，②是假命题二、认真填一填（本题有6个小题，每小题4分，共24分）11. 写出一个比-4大的负．无理数_________.12. 当7=x ，代数式)1)(3()1)(52(+--++x x x x 的值为_________.13. 数据9.30，9.05，9.10，9.40，9.20，9.10的众数是___________；中位数是____________.⊙O 上，的度数等于14. 如图，点A ，B ，C ，D 都在84°，CA 是∠OCD 的平分线，则∠ABD +∠CAO =________°15. 已知分式ax x x +--532，当2=x 时，分式无意义，则=a _______；当6<x 时，使分式无意义的x 的值共有_______个.16. 在等腰Rt △ABC 中，∠C =90°，AC =1，过点C 作直线l ∥AB ，F 是l 上的一点，且AB =AF ，则点F 到直线BC 的距离为__________.三、全面答一答（本题有8个小题，共66分）17. （本小题满分6分）点A ，B ，C ，D 的坐标如图，求直线AB 与直线CD 的交点坐标.18. （本小题满分6分）四条线段a ，b ，c ，d 如图，4:3:2:1:::=d c b a（1）选择其中的三条线段为边作一个三角形（尺规作图，要求保留作图痕迹，不必写出作法）；（2）任取三条线段，求以它们为边能作出三角形的概率.19.（本小题满分6分）在△ABC中，AB=3，AC=2，BC=1.（1）求证：∠A≠30°；（2）将△ABC绕BC所在直线旋转一周，求所得几何体的表面积.20.（本小题满分8分）中国国际动漫节以“动漫的盛会，人民的节日”为宗旨，以“动漫我的城市，动漫我的生活”为主题，已在杭州成功举办七届.目前，它成为国内规模最大、交易最旺、影响最广的动漫专业盛会.下面是自首届以来各届动漫产品成交金额统计图表（部分未完成）：（1）请根据所给的信息将统计图表补充完整；（2）从哪届开始成交金额超过百亿元？相邻两届中，哪两届的成交金额增长最快？（3）求第五届到第七届的平均增长率，并用它预测第八届中国国际动漫节的成交金额（精确到亿元）.21. （本小题满分8分）在平面上，七个边长为1的等边三角形，分别用①至⑦表示（如图）。

2011年浙江省杭州市各类高中招生文化考试数学试题及参考答案全word版

2011年浙江省杭州市各类高中招生文化考试数学试题及参考答案全word版2011年杭州市各类高中招生文化考试数学考生须知：1. 本试卷满分120分，考试时间100分钟。

2. 答题前，在答题纸上写姓名和准考证号。

3. 必须在答题纸的对应答题位置上答题，写在其它地方无效。

答题方式详见答题纸上的说明。

4. 考试结束后，试题卷和答题纸一并上交。

试题卷一、仔细选一选（本题有10个小题，每小题3分，共30分）下面每小题给出的四个选项中，只有一个是正确的。

注意可以用多种不同的方法来选取正确答案。

1. 下列各式中，正确的是 A.3)3(2-=- B. 332-=- C. 3)3(2±=± D. 332±= 2. 正方形纸片折一次，沿折痕剪开，能剪得的图形是A. 锐角三角形B. 钝角三角形C. 梯形D. 菱形3. =⨯36)102(A. 9106⨯B.9108⨯ C. 18102⨯D. 18108⨯ 4. 正多边形的一个内角为135°，则该多边形的边数为A. 9B. 8C. 7D. 45. 在平面直角坐标系xOy 中，以点（-3，4）为圆心，4为半径的圆A. 与x 轴相交，与y 轴相切B. 与x 轴相离，与y 轴相交C. 与x 轴相切，与y 轴相交D. 与x 轴相切，与y 轴相离6. 如图，函数11-=x y 和函数xy 22=的图像相交于点M （2，m ），N （-1，n ），若21y y>，则x 的取值范围是A.1-<x 或20<<x B. 1-<x 或2>x C.01<<-x 或20<<x D. 01<<-x 或2>x7. 一个矩形被直线分成面积为x ，y 的两部分，则y 与x 之间的函数关系只可能是8. 如图是一个正六棱柱的主视图和左视图，则图中的=aA. 32B. 3C. 2D. 19. 若2-=+b a ，且a ≥2b ，则A. a b 有最小值21B. ab 有最大值1C. b a 有最大值 2D.b a有最小值98- 10. 在矩形ABCD 中，有一个菱形BFDE （点E ，F 分别在线段AB ，CD 上），记它们的面积分别为ABCD S和BFDE S ，现给出下列命题： ①若232+=BFDE ABCD SS，则33tan =∠EDF ； ②若EF BD DE ⋅=2,则DF=2AD则A. ①是真命题，②是真命题B. ①是真命题，②是假命题C. ①是假命题，②是真命题D. ①是假命题，②是假命题二、认真填一填（本题有6个小题，每小题4分，共24分）要注意认真看清楚题目的条件和要填写的内容，尽量完整地填写答案11. 写出一个比-4大的负．无理数_________ 12. 当7=x 时，代数式)1)(3()1)(52(+--++x x x x 的值为__________13. 数据9.30，9.05，9.10，9.40，9.20，9.10的众数是___________；中位数是_______________14. 如图，点A ，B ，C ，D 都在⊙O上，的度数等于84°，CA 是∠OCD 的平分线，则∠ABD+∠CAO=________°15. 已知分式a x xx +--532，当2=x 时，分式无意义，则=a _______；当6<x 时，使分式无意义的x 的值共有_______个16. 在等腰Rt△ABC中，∠C=90°，AC=1，过点C作直线l∥AB，F是l上的一点，且AB=AF，则点F到直线BC的距离为__________三、全面答一答（本题有8个小题，共66分）解答应写出文字说明、证明过程或推演步骤。

2011年杭州市中考数学试卷及参考答案(精解版)

2011年杭州市各类高中招生文化考试数学考生须知：1. 本试卷满分120分，考试时间100分钟。

2. 答题前，在答题纸上写姓名和准考证号。

3. 必须在答题纸的对应答题位置上答题，写在其它地方无效。

答题方式详见答题纸上的说明。

4. 考试结束后，试题卷和答题纸一并上交。

试题卷一. 仔细选一选（本题有10个小题，每小题3分，共30分）下面每小题给出的四个选项中，只有一个是正确的。

注意可以用多种不同的方法来选取正确答案。

1. 下列各式中，正确的是A . 2(3)3-=-B . 233-=-C .2(3)3±=± D . 233=±答案：B解析：A 中2(3)3-=；B 正确；C 中2(3)3±=；D 中233=，故选B .2. 正方形纸片折一次，沿折痕剪开，能剪得的图形是A . 锐角三角形B . 钝角三角形C . 梯形D . 菱形答案：C解析：折一次能得到直角三角形、长方形和梯形.故选C 3. 63(210)⨯=A . 9610⨯ B . 9810⨯ C . 18210⨯ D . 18810⨯ 答案：D解析：6336318(210)210810⨯⨯=⨯=⨯4. 正多边形的一个内角为135°，则该多边形的边数为A . 9B . 8C . 7D . 4 答案：B解析：设边数为n ，正多边形也有n 个内角，180(2)135n n -=，解得8n =，选B .5. 在平面直角坐标系xOy 中，以点（-3，4）为圆心，4为半径的圆A . 与x 轴相交，与y 轴相切B . 与x 轴相离，与y 轴相交C . 与x 轴相切，与y 轴相交D . 与x 轴相切，与y 轴相离答案：C解析：因为点的横坐标34r -<=，所以与y 轴相交，点的纵坐标44r ==，所以与x 轴相切.6. 如图，函数11y x =-和函数22y x=的图像相交于点M （2，m ），N （-1，n ），若12y y >，则x 的取值范围是A . 1x <-或02x <<B . 1x <-或2x >C . 10x -<<或02x <<D . 10x -<<或2x >答案：D解析：解：根据图象得到当10x -<<或2x >时，12y y >．故答案为10x -<<或2x >．7. 一个矩形被直线分成面积为x ，y 的两部分，则y 与x 之间的函数关系只可能是答案：A解析：因为x y k +=（矩形的面积是一定值），整理得y x k =-+，由此可知y 是x 的一次函数，图象经过一、二、四象限，x 、y 都不能为0，且x ＞0，y ＞0，图象位于第一象限.8. 如图是一个正六棱柱的主视图和左视图，则图中的a =A . 23B .3 C . 2 D . 1答案：B解析：解：由正六棱柱的主视图和左视图，可得到正六棱柱的最长的对角线长是4，则边长为2，作AD ⊥BC 于D ，在△ABC 中，AB =AC =2，∠BAC =120°， ∴在直角△ABD 中，∠ABD =30°，AD =1， ∴AB =2，BD =AB •cos 30°3=，即3a =．选B9. 若2a b +=-，且a ≥2b ，则A .b a 有最小值12 B . ba有最大值1C . a b 有最大值2D . ab有最小值89-答案：C 解析：2a b +=-，所以a b 、中至少有一个负数，又有a ≥2b ，所以0b <，22a a b b ≥⇒≤. ab有最大值2 选C 10. 在矩形ABCD 中，有一个菱形BFDE （点E ，F 分别在线段AB ，CD 上），记它们的面积分别为ABCD S 和BFDE S ，现给出下列命题： ①若232ABCD BFDE S S +=，则3tan 3EDF ∠=； ②若2DE BD EF =⋅,则DF =2AD 则A . ①是真命题，②是真命题B . ①是真命题，②是假命题C . ①是假命题，②是真命题D . ①是假命题，②是假命题答案：A解析：解：①设CF =x ，DF =y ，BC =h ，则由已知菱形BFDE ，BF =DF =y 由已知得：()232x y h yh ++= 得32x y =即cos ∠BFC =32，∴∠BFC =30°，由已知 ∴∠EDF =30° ∴tan ∠EDF =33所以①是真命题．②已知菱形BFDE ，∴DF =DE1124DEFSDF AD BD EF =⋅=⋅，又2DE BD EF =⋅（已知）， ∴22DEFSDE DF ==，2DF AD DF ∴⋅=，∴DF =2AD ，所以②是真命题．故选：A ．二. 认真填一填（本题有6个小题，每小题4分，共24分）要注意认真看清楚题目的条件和要填写的内容，尽量完整地填写答案 11. 写出一个比-4大的负．无理数_________ 答案：2-解析：因为416-=-，只要根号里面比16小的都行（注意要是无理数不能是4-类似的）.如2, 1.5--等等都行.12. 当7x =-时，代数式(25)(1)(3)(1)x x x x ++--+的值为__________答案：-6解析：(25)(1)(3)(1)(8)(1)1(6)6x x x x x x ++--+=++=⨯-=- 13. 数据9.30，9.05，9.10，9.40，9.20，9.10的众数是___________；中位数是_______________ 答案：9.10，9.15解析：把数据从小到大排列9.05，9.10，9.10，9.20，9.30，9.40，所以众数为9.10，中位数为9.109.209.152+=.14. 如图，点A ，B ，C ，D 都在⊙O 上，CD 的度数等于84°，CA 是∠OCD 的平分线，则∠ABD +∠CAO =________°答案：48︒解析：∵CD 的度数等于84° ∴∠DOC =84° ∵ OC =OD ∴∠OCD =48°∵CA 是∠OCD 的平分线 ∴∠OCA =∠ACD =24°∵∠ACD 与∠ABD 是同一段弧上的圆周角 ∴∠ACD =∠ABD ∵ OA =OC ∴∠OCA =∠CAO∠ABD +∠CAO =∠OCA +∠ACD =48°15. 已知分式235x x x a--+，当2x =时，分式无意义，则a =_______；当6a <时，使分式无意义的x 的值共有_______个. 答案：6，2解析：解：分式无意义，说明当2x =时，分母为0，即4520a -⨯+=，6a =.要使250x x a -+=，2540a ∆=->，所以方程有两个实根，即使分是无意义的x 的值共有2个.16. 在等腰Rt △ABC 中，∠C =90°，AC =1，过点C 作直线l ∥AB ，F 是l 上的一点，且AB =AF ，则点F 到直线BC 的距离为__________ 答案：312± 解析：解：如图，ABC 为等腰直角三角形，且1AC =,又有等腰直角三角形的斜边是直角边的2倍，22,2AB AD ∴==，又1162,2AF DF =∴=，16222CF ∴=- 123162,222FE CF -∴==+2312F H +∴=，为312±三. 全面答一答（本题有8个小题，共66分）解答应写出文字说明、证明过程或推演步骤。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

2011年杭州市中考数学试卷参考答案一、选择题
二、填空题
11、如等；12、-6；13、，；14、48︒；15、6，2；16、1
2
三、解答题
17、解：由已知得，直线AB方程为26
y x
=+，直线CD
方程为11
2
y x
=-+解方程组
26
1
1
2
y x
y x
=+
⎧
⎪
⎨
=-+
⎪⎩
，得
2
2
x
y
=-
⎧
⎨
=
⎩
，所以直线
AB，CD的交点
坐标为（-2，2）
.
18、解：（1）
图略，只能选,,
b c d三边画三角形；（2）所求概率为
1
4
p= 19、解：（1）222
123
BC AC AB
+=+==
Q，ABC
∴∆是直角三角形，且C Rt
∠=∠.
1
sin sin30
2
BC
A
AB
==>=︒
Q，30
A
∴∠≠︒.
（2）所求几何体的表面积为
)
()2
S r l r
πππ
=+==
20、解：（1）图略；（2）从第六届开始成交金额超百亿元，第五第六届成交金额增长最快；
（3）设第五届到第七届平均增长率为x ，则265.3(1)128x += 解得40%x ≈，或 2.4x ≈-（不合题意，舍去）
所以预测第八届成交金额约为128(1+40%)179⨯≈（亿元）. 21、解：（1）取出⑤，向上平移2个单位；
（2）可以做到. 因为每个等边三角形的面积是14
S =
，
所以正六边形的面积为615
622
S S ==>
而615502
2S S <-=
-<=
所以只需用⑤的52⎫
-⎪⎪⎝⎭
面积覆盖住正六边形就能做
到.
22、解：（1）EF Q 是OAB ∆的中位线，1//,2
EF AB EF AB ∴= 而1,//2
CD AB CD AB =
（2）
AC ==Q
（3）,//AE OE OC EF CD ==Q
AEG ACD ∴∆∆:，11
,33
EG AE EG CD CD AC ∴===即同理1
3
FH CD =
23、解：（1）如两个函数为21,31y x y x x =+=++，函数图形略；（2）不论k 取何值，函数2(21)1y kx k x =+++的图象必过定点
(0,1),(2,1)--，
且与x 轴至少有1个交点.证明如下：由2(21)1y kx k x =+++，得2(2)(1)0k x x x y ++-+= 当220,10x x x y +=-+=且，即0,12,1x y x y ===-=-，或时，
O
上式对任意实数k 都成立，所以函数的图像必过定点
(0,1),(2,1)--.
又因为当0k =时，函数1y x =+的图像与x 轴有一个交点；当0k ≠时，22(21)4410k k k ∆=+-=+>Q ，所以函数图像与x
轴有两个交点.
所以函数2(21)1y kx k x =+++的图象与x 轴至少有1个交
点.
（3）只要写出1m ≤-的数都可以.
0k <Q ，∴函数2(21)1y kx k x =+++的图像在对称轴直线
212k x k
+=-
的左侧，y 随x 的增大而增大. 根据题意，得21
2k m k
+≤-
，而当0k <时，211
1122k k k
+-
=-->- 所以1m ≤-.
24、解：（1）由题意，得四边形ABCD 是菱形.
由//EF BD ，得ABD AEF ∆∆:，1565h EF -∴=
，即()16
55
EF h =- 所以当15
2
h =时，max 152
S =
. （2）根据题意，得OE OM =.
如图，作OR AB ⊥于R ， OB 关于OR 对称线段为OS ， 1）
当点,E M 不重合时，
则,OE OM 在OR 的两侧，易知RE RM =
.
AB Q ，OR ∴=
由////ML EK OB ，得
,OK BE OL BM
OA AB OA AB
==
2OK OL BE BM BR OA OA AB AB AB ∴
+=+=
，即1295517
h h += 124517h h ∴+=
，此时1h 的取值范围为145017h <<且145
34
h ≠ 2）当点,E M 重合时，则12h h =，此时1h 的取值范围为
105h <<.。