平面几何100题 70页
新平面几何100题1-60

1、设I是△ABC的内心,D是边BC上的一点,E是BC延长线上一点,且满足BDDC =BEEC.设H是D到直线IE的垂足,证明:∠AHE=∠IDE.B2、设O、H分别是△ABC的外心和垂心,点A关于直线OH的对称点是P,点P和点A不在直线BC的同侧,E、F分别在AB和AC上,满足BE=PC,CF=PB,直线AP、OH相交于点K,证明:EK⊥FK.B CP3、设正△ABC的外接圆和内切圆分别是Γ、ω,P为ω上一动点,P1、P2、P3分别为P在BC、CA、AB上的射影,圆ω1、ω2、ω3分别与BC、CA、AB切于P1、P2、P3且与Γ内切(它们的圆心与A、B、C分别在BC、CA、AB的异侧).证明:圆ω1、ω2、ω3两两外公切线的长度之和是一个定值.A4、设正△ABC内接于⊙O,E、F分别是AC,BC上一点,使得AE=2CE,BF=2CF. P为⊙O上的一点,PD⊥EF于D,交AB于K,作PS⊥BC于S,连接SK并交AO于T.证明:DS=DT.T5、设E、F分别位于△ABC的AC,AB边上,BE、CF交于D,△AEF的外接圆交△ABC的外接圆于点A、P,△AEF的外接圆在A处的切线交△ABC于A、Q两点,设N、M分别为AQ、BC的中点.证明:∠APD=∠MNQ.Q6、已知△ABC的外心为O,A′、B′、C′分别是边BC、CA、AB上的点,且满足A、B′、C′、O共圆,C、A′、B′、O共圆.以B′为圆心,B′C为半径的圆和以C′为圆心,BC′为半径的圆的根轴为l a.类似定义l b、l c.证明:直线l a、l b、l c交出的三角形垂心与△ABC的垂心重合.7、设凸四边形ABCD顶点不共圆,记点A在直线BC、BD、CD上的射影分别为P、Q、R,其中P、Q分别在BC、BD内,R在CD的延长线上.记点D在直线AC、BC、AB上的射影分别为X、Y、Z,其中X、Y分别在线段AC、BC内,Z在BA的延长线上,设△ABD的垂心为H,证明:BH的中点在△PQR外接圆和△XYZ外接圆的根轴上.8、在圆内接四边形ABCD中,AB>BC,AD>DC,I、J分别为△ABC、△ADC的内心.以AC为直径的圆与线段IB交于点X、与JD的延长线交于点Y.证明:若B、I、J、D四点共圆,则点X、Y关于直线AC对称.9、设△ABC的外接圆和内切圆的圆心分别为O、I,点M和点Q分别在边AB和AC上,点N和点P分别在边BC上(N在线段BP上),且满足五边形AMNPQ的五条边长相等.记点S为直线MN和QP的交点,l为∠MSQ的角平分线.证明:l和OI平行.S11、凸四边形ABCD中,P、Q、R、S分别是线段AB、BC、CD、DA上的点.若相交的线段PR、QS把四边形ABCD分为4个四个对角线互相垂直的凸四边形.证明:P、Q、R、S四点共圆.B12、不等腰三角形ABC的外接圆为Ω,内心为I,射线AI与BC交于D,与Ω交于除A以外的另一点M,以DM为直径的圆与Ω交于除M以外的另一点K,直线MK与BC交于点S,设N为IS的中点,L1、L2为△KID的外接圆与△MAN的外接圆的交点.证明:IL1或IL2的中点在Ω上.S113、在非等腰△ABC中,D、E、F分别为BC、CA、AB的中点.过D作△ABC的内切圆的切线(不同于直线BC),交直线EF于点X.类似定义Y和Z.证明:X、Y、Z三点共线.ZBD14、圆外切四边形ABCD的内切圆⊙I分别切DC、DA于E、F,K为BD上一点,KA、KC分别交⊙I于M、N,MF与NE交于L.证明:L在直线BD上.L15、四边形ABCD内接于⊙O,∠A、∠C的角平分线相交于点I,∠B、∠D的角平分线相交于点J,直线IJ不经过点O,且与边AB、CD的延长线分别交于点P、R,与边BC、DA分别交于点Q、S.线段PR、QS的中点分别为M、N.证明:OM⊥ON.R16、在圆内接四边形ABCD中,M、N分别是线段BC、AD的中点,对角线AC、BD交于点E. P是边BC上的点,满足PBPC =(BDAC)2.设E在PN上的投影是H,证明:△BEC的外接圆与△MPH的外接圆相切.17、圆内接四边形ABCD的对角线相交于P,存在一个圆Γ与AB、BC、AD、DC的延长线切于点X、Y、Z、T.过A、B的圆Ω与圆Γ外切于S.证明:SP⊥ST.18、对于平面上的凸四边形ABCD,设直线l交直线AB于X,交直线CD于X′,交直线BC于Y,交直线DA于Y′,交直线AC于Z,交直线BD于Z′.已知以上六点在l上按照X、Y、Z、X′、Y′、Z′的顺序排列.证明:以XX′、YY′、ZZ′为直径的三个圆共点.19、设O是三角形ABC的外心,D是AB上一点,作与⊙O内切,与线段CD、BD相切的⊙I;作与⊙O内切,与线段CD、AD相切的⊙J.证明:若A、B、I、J四点共圆,则D是三角形ABC中的∠ACB内旁切圆在AB上的切点.20、设⊙O 1与⊙O 2交于P 、Q 两点,过P 作两条割线AB 、CD ,过Q 作两条平行割线A′B′、C′D′,取△PAC 、△PBD 、△QB′D′、△QA′C′的九点圆圆心F 1、F 2、F 3、F 4.证明:四边形F 1F 2F 3F 4是矩形.D'A'C21、设⊙O是四边形ABCD的内切圆. AC、BD交于P,I、J分别是△ABC、△ADC的内心,OP,IJ交于K,T是K在BD上的射影.证明:I、J、P、T四点共圆.B22、设O、I B、I C分别是锐角三角形ABC的外接圆圆心,∠B内的旁切圆圆心和∠C内的旁切圆圆心.在AC边上取点E和Y,使得∠ABY=∠CBY,BE⊥AC,在AB边上取点F和Z,使得∠ACZ=∠BCZ,CF⊥AB,直线I B F和I C E交于点P.证明:PO⊥YZ.I B I C23、四边形ABCD内接于⊙O,AC、BD交于点P,直线AB、CD交于点Q. K是P在QO上的射影,KP、BC交于X,M是BC的中点,P′是P关于BC的对称点,K′是K关于M的对称点. P′K′分别交BC于Y,交KP于Z.证明:△XYZ的外接圆与△QBC的外接圆相切.D24、对边不平行的凸四边形ABCD中,BA延长线与CD延长线交于点E,AD延长线与BC延长线交于点F,K是△CDF的外接圆与△ADE的外接圆的交点(K≠D).设∠BAD、∠ABC、∠BCD、∠ADC的外角平分线分别为l A、l B、l C、l D,l A和l B、l B和l C、l C和l D、l D和l A分别交于点G、H、I、J.△CDF的外接圆中,弧DF(不含C)的中点为Q,直线EH与△AED的外接圆交于另一点M.设GJ中垂线与IH中垂线(不重合)交于点P.证明:P、M、Q、K四点共圆.25、设D是△ABC外接圆⊙O上任意一点,过D作⊙O的切线l.证明:l关于△ABC三边对称的直线围成的三角形的外接圆与⊙O相切.26、设O为△ABC内一点,O在BC、CA、AB上的射影分别为U、V、W.X、Y、Z分别在BC、CA、AB上,X′、Y′、Z′分别是X关于U、Y关于V,Z关于W的对称点,点X、Y、Z关于△ABC的密克点为S,点X′、Y′、Z′关于△ABC的密克点为T.证明:OS=OT.B CX'U27、点D、E、F分别在△ABC的边AB、BC、CA上,满足AD+AF=BC、BD+BE=AC、CE+CF=AB. △ADF、△BDE、△CEF的外接圆与△ABC外接圆的另一个交点分别为A1、B1、C1,P是D、E、F关于△ABC的密克点,证明:P为△A1B1C1的垂心.128、设AA′、BB′、CC′是锐角△ABC的外接圆的三条直径,P为△ABC内任意一点,点P在BC、CA、AB上的射影分别是D、E、F,X、Y、Z分别是A′关于D、B′关于E,C′关于F的对称点.证明:△XYZ∽△ABC.29、设H是锐角△ABC的外接圆的垂心,P是外接圆弧BC上一点,连接PH交弧AC于M,弧AB上一点K满足直线KM平行于点P关于△ABC的西姆松线,设Q为外接圆上一点满足30、设△ABC的内切圆⊙I分别切BC、CA、AB于点D、E、F,延长EI交DF于G,BE、CF交⊙I于另外的点X、Y.设J为△AEF外接圆的另一个交点,△XJI外接圆与⊙I的另一个交点为S,T在⊙I上满足TS⊥AI,连接YT、XS交于P,直线DP与⊙I的另一个交点为Q.证明:KQ是⊙I的直径.C31、在△ABC中,内切圆⊙I分别切BC、CA、AB于点D、E、F,M、N分别是AB、AC的中点,EF、MN交于S,DS与⊙I的另一个交点为J.证明:J在△ABC的九点圆上.B C32、过△ABC内心I任作一直线l,内切圆分别切BC、CA、AB于点X、Y、Z,边BC、CA、AB的中点分别为D、E、F,直线l分别交△BIC外接圆、△CIA外接圆、△AIB外接圆于另一点D′、E′、F′,过点X、Y、Z分别作平行于DD′、EE′、FF′的直线l1、l2、l3.证明:直线l1、l2、l3交于一点.33、已知△ABC的外接圆为⊙O,A′为点A在⊙O上的对径点.作等边△BCD,使得A、D位的于BC的异侧,过点A′作A′D的垂线,分别与AC、AB交于E、F两点.以EF为底,作底角为π6等腰△ETF,并使得A、T位于BC的异侧.证明:AT经过△ABC的九点圆圆心.ED34、设△ABC的内切圆⊙I与边BC、CA、AB分别切于点D、E、F,记⊙I B、⊙I C分别为△ABC的顶点B、C所对的旁切圆,P、Q分别为I B E,I C F的中点,若DE、DF与I B I C交于点K、J,EJ 与FK交于点M,PE与△PAC的外接圆交于另一点X,QF与△QAB的外接圆交于另一点Y.证明:BY、CX、AM三线共点.35、已知凸四边形ABCD内两动点P、Q满足∠APB=∠AQB=∠CPD=∠CQD.证明:动直线PQ要么均经过一个定点,要么相互平行.36、在凸四边形ABCD中,∠ABC=∠ADC<π,∠ABC、∠ADC的平分线交于点P,并分2别与AC交于点E、F,M为AC的中点,BM、DM与△BDP的外接圆分别交于另一点X、Y,EX与PY交于点Q.证明:AC⊥PQ.B37、凸六边形A1A2A3A4A5A6满足A1A2=A3A4=A5A6,A2A3=A4A5=A6A1,点X、Y在38、已知凸四边形ABCD内接于⊙O,⊙I切AC、BD及⊙O,E为弧BC的中点,AE与BD相交于点M,DE与AC相交于点N.证明:△EMN外接圆与⊙I相切.39、锐角△ABC 中BC >AC >AB ,I 、O 、H 分别为其内心、外心、垂心,D 、E 分别在BC 、AC 上使AE =BD ,CD +CE =AB .记K 为BE 与AD 交点,证明:KH =2IO .ABC40、在锐角△ABC中,AB>AC,设Γ为其外接圆,H为垂心,F为由顶点A处所引高的垂足,M为边BC的中点.Q、K为圆Γ上的点,使得∠HQA=∠HKQ=π.若点A、B、C、K、Q互2不相同,且按此顺序排列在Γ上,证明:△KQH的外接圆与△FKM的外接圆相切.41、设△ABC内接于⊙O,过A作⊙O的切线交BC于T,G为△ABC的重心,直线TG分别交AB、AC于E、F,AG交⊙O于K,证明:AK平分∠EKF.K42、在凸四边形ABCD中,AB≠BC,ω1和ω2分别是△ABC和△ADC的内切圆.已知存在一个圆ω与射线BA相切(切点不在线段BA上),与射线BC相切(切点不在线段BC上),且与直线AD和直线CD都相切.证明:圆ω1和ω2的两条外公切线的交点在圆ω上.43、P为△ABC内一点,L、M、N分别为边BC、CA、AB的中点,且PL∶PM∶PN=BC∶CA∶AB.延长AP、BP、CP分别交△ABC的外接圆于点D、E、F.证明:△APF、△APE、△BPF、△BPD、△CPD、△CPE的外接圆圆心六点共圆.B44、给定△ABC,求线段BC上满足下列条件的所有点P:如果X、Y是直线PA与△PAB、△PAC外接圆的两条外公切线的交点,则(PAXY )2+PB∙PCAB∙AC=1.45、在凸四边形ABCD中,∠ABC=∠CDA=π2,H是A在BD上的射影,边AB上的S和边AD上的T使H在△SCT内部,∠CHS−∠CSB=π2,∠THC−∠DTC=π2,证明:直线BD和△TSH的外接圆相切.CD46、在△ABC中,⊙O、⊙I分别为其外接圆与内切圆,⊙I与BC切于点D,M为ID中点,A0与A 关于点O对称,直线A0M交⊙O于异于点A0的一点X,证明:△ADX的外接圆与直线BC相切.47、已知P 是凸四边形ABCD 的边AB 上的一点,ω是△CPD 的内切圆,I 为其圆心,若ω分别与△APD 以及△CPB 的内切圆切于点K 和L ,AC 与BD 交于点E ,AK 、BL 交于点F .证明:E 、I 、F 共线.BAD48、在锐角△ABC中,ω、Ω、R分别表示其内切圆、外接圆及外接圆的半径.圆ωA与Ω内切于点A且与ω外切;圆ΩA与Ω内切于点A且与ω内切.设P A和Q A分别是ωA和ΩA的圆心.同样定义P B和Q B、P C和Q C.证明:8P A Q A∙P B Q B∙P C Q C≤R349、已知△ABC的垂心为H,外心为O,设A、B、C关于BC、CA、AB的对称点分别为D、E、F.证明:D、E、F共线当且仅当OH=2R,其中R为△ABC外接圆半径.FCO50、设∠XAY是一个固定的角,B、C分别是射线AX、AY上的动点,∠XAY内有一动点P满足PA、PB、PC的长度都保持不变.求△ABC面积的最小值.。
平面几何100题及答案(前80题)
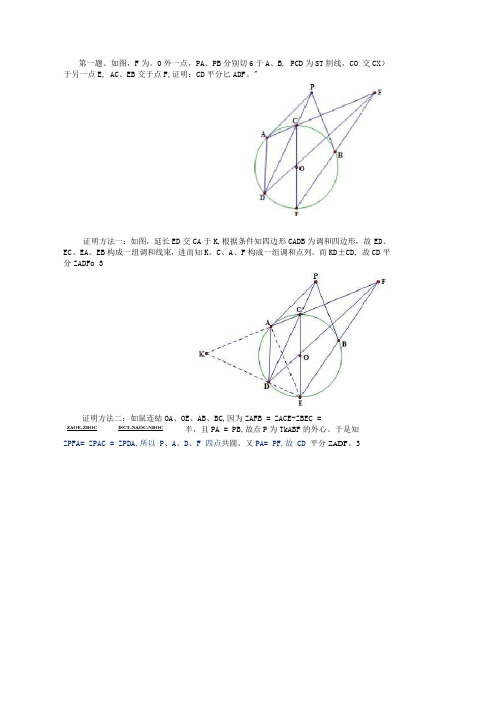
第一题、如图,F为。
0外一点,PA、PB分别切6于A、B, PCD为ST割线,CO 交CX)于另一点E, AC、EB交于点F,证明:CD平分匕ADF。
"证明方法一:如图,延长ED交CA于K,根据条件知四边形CADB为调和四边形,故ED、EC、EA、EB构成一组调和线束,进而知K、C、A、F构成一组调和点列。
而KD±CD, 故CD平分ZADFo 3证明方法二:如鼠连結OA、OE、AB、BC,因为ZAFB = ZACE-ZBEC =ZAOE-ZBOC ISCT-NAOC-NBOC 半,且PA = PB,故点P为TkABF的外心。
于是知ZPFA= ZPAC = ZPDA,所以P、A、D、F 四点共圆。
又PA= PF,故CD 平分Z A DF。
3第二题、如图,AB为©0直径,C、D为O。
上两点,且在AB同侧,。
在C、D两处的切城交于点E, BC、AD交于点F, EF交AB于证明:E、C、页、D四点共圆。
“证明:如图,延长白C、BD交于点K,则BC1AK, AD丄BK,从而知F^)AKAB的垂心。
又在圆内接六边形CCADDB中使用帕斯卡定理,知K、E、F三点共线,从而KM丄卽于価。
于是知匕CMF = ZCAF= ZCDE,所以E、C、页、D四点共圆。
K第三题、如图,AB为。
直径,C、D为伽上两点'且在AB同侧,O0在C. D两处的切线交于点E, BC、AD交于点F, EB交0。
于点G,证明;ZCEF = 2/AGF。
“证明:如图,根据条件知匕CF D =典牌=(脸-®;(i对-命)=Z CAB + / DBA = ZECF + ZEDF;且EC = ED;故点E 为△CED 外心。
于是知/EFC = ZECF = ZCAB = ZCGE,敌E、C、F、G四点共圆。
所以“ZCGF = ZCEF = 2(90° - ZECF)= 2(90° - ZCAB)= 2ZABC 二2ZAGC " 0lWZAGF = —=—,即得ZCEF = 2ZAGFo,2 2第四題、如图,AB为直径,P为AB延长线上一点,PC切于C,点C关于朋的对称点为点D, CE1AD于E, F为CE中点,AF交于K,求证:AP为ZXPCK外扬圆的切线。
高中奥林匹克竞赛数学平面几何100题——珍藏版

高中奥林匹克竞赛数学平面几何100题——珍藏版高中数学联赛的几何题目有100道,难度较高。
这些题目涉及到各种不同的几何概念和定理,需要考生具备扎实的数学基础和丰富的解题经验。
在这些题目中,有许多需要考生进行证明,需要考生熟练掌握各种证明方法和技巧。
同时,还有一些需要考生进行画图,需要考生具备良好的几何直观和手绘能力。
这些几何题目的难度不仅仅在于其题目本身,还在于考试的时间限制。
考生需要在有限的时间内解决尽可能多的问题,因此需要考生具备快速解题的能力和良好的时间管理能力。
为了更好地应对这些几何题目,考生需要在平时的研究中注重基础知识的掌握和解题技巧的训练。
同时,还需要多做一些类似的练题目,以提高自己的解题水平和应对能力。
总之,高中数学联赛的几何题目难度较高,需要考生具备扎实的数学基础、丰富的解题经验、良好的几何直观和手绘能力、快速解题的能力和良好的时间管理能力。
考生需要在平时的研究中注重基础知识的掌握和解题技巧的训练,并多做类似的练题目,以提高自己的解题水平和应对能力。
1.研究证明角平分在这一部分中,我们将研究如何证明一个角被平分。
这是一个非常基础的几何问题,但是它的应用非常广泛。
我们将介绍几种不同的证明方法,包括使用角平分线的定义、角度相等、相似三角形等。
2.研究证明四点共圆在这一部分中,我们将研究如何证明四个点共圆。
这个问题也是几何学中的基础问题之一。
我们将介绍几种不同的证明方法,包括使用圆的定义、圆心角、垂直等。
3.研究证明角的倍数关系在这一部分中,我们将研究如何证明角的倍数关系。
这是一个非常重要的几何问题,因为它在许多几何证明中都有应用。
我们将介绍几种不同的证明方法,包括使用角度相等、相似三角形等。
4.证明线与圆相切在这一部分中,我们将研究如何证明一条线与一个圆相切。
这是一个非常基础的几何问题,但是它的应用非常广泛。
我们将介绍几种不同的证明方法,包括使用切线的定义、圆心角等。
5.证明垂直在这一部分中,我们将研究如何证明两条线段垂直。
平面几何100题(1)

平面几何100题1.非等腰锐角三角形ABC 的外接圆为ω,H 为△ABC 的垂心,M 是AB 的中点。
在不含C 的圆弧AB 上取点P、Q,使得∠ACP=∠BCQ<∠ACQ,过H 分别作CQ、CP 的垂线,垂足为R、S。
证明:P,Q,R,S 共圆且点M 是该圆的圆心。
2.在△ABC 中,点M、N、K 分别在边BC、CA、AB 上且不与顶点重合,若∠BAC=∠KMN 且∠ABC=∠KNM,则称△MNK 为完美三角形。
证明:如果在△ABC 中有两个具有共同顶点且不重合的完美三角形,则△ABC 是直角三角形。
3.四边形ABCD 满足AD//BC,∠ABC>90⁰,M 是线段AB 上不同于A、B 的一点,设△MAD、△MBC 的外心分别为21,O O 。
△D MO 1的外接圆不同于M 的交点为N。
求证:点N 在直线21O O 上。
4.在凸四边形(非平行四边形)ABCD 的对角线上分别取点B′、C′,使得△ACB′、△BDC′都为正三角形,其中点B 和B′位于AC 的同侧,点C 和C′位于BD 的同侧,如果CD AB C B +='',求∠BAD+∠CDA 的值。
5.给定一个凸六边形ABCDEF,其中AB//DE,BC//EF,CD//FA。
设BD 和AE、AC 和DF、CE 和BF 的交点分别为M、N、K。
证明:过M、N、K 分别作AB、CD、EF 的垂线交于同一点。
6.圆内接四边形ABCD 的对角线交于点K,点M 和N 分别是对角线AC 和BD 的中点,△ADM 和△BCM 的外接圆交于点M、L,证明:K,L,M,N(这些点两两不重合)四点共圆。
7.圆内接四边形ABCD 的外接圆为圆Ω且AB=AD,在线段BC、CD 上分别取点M、N,使得MN=BM+DN。
直线AM 交圆Ω于点P (不同于A),直线AN 交圆Ω于点Q (不同于A)。
求证:△APQ 的垂心在MN 上。
8.给定四边形ABCD,其中∠B=∠D=90⁰,在线段AB 上取点M 使得AD=AM。
高中奥林匹克竞赛数学平面几何100题——珍藏版

高中数学联赛难度几何题100道第一题:学习证明角平分 (4)第二题:学习证明四点共圆 (5)第三题:学习证明角的倍数关系 (6)第四题:证明线与圆相切 (7)第五题:证明垂直 (8)第六题:证明线段相等 (9)第七题:证明线段为比例中项 (10)第八题:证明垂直 (11)第九题:证明线段相等 (12)第十题:证明角平分 (13)第十一题:证明垂直 (14)第十二题:证明线段相等 (15)第十三题:证明角相等 (16)第十四题:证明中点 (17)第十五题:证明线段的二次等式 (18)第十六题:证明角平分 (19)第十七题:证明中点 (20)第十八题:证明角相等 (21)第十九题:证明中点 (22)第二十题:证明线段相等 (23)第二十一题:证明垂直 (24)第二十二题:证明角相等 (25)第二十三题:证明四点共圆 (26)第二十四题:证明两圆相切 (27)第二十五题:证明线段相等 (28)第二十六题:证明四条线段相等 (29)第二十七题:证明线段比例等式 (30)第二十八题:证明角的倍数关系 (31)第二十九题:证明三线共点 (32)第三十题:证明平行 (33)第三十一题:证明线段相等 (34)第三十二题:证明四点共圆 (35)第三十三题:证明三角形相似 (36)第三十四题:证明角相等 (37)第三十五题:证明内心 (38)第三十六题:证明角平分 (39)第三十七题:证明垂直 (40)第三十八题:证明面积等式 (41)第三十九题:证明角平分 (42)第四十题:证明角相等 (43)第四十二题:证明中点 (45)第四十三题:证明角相等 (46)第四十四题:证明垂直 (47)第四十五题:证明角相等 (48)第四十六题:证明垂直 (49)第四十七题:证明四点共圆 (50)第四十八题:证明四点共圆 (51)第四十九题:证明四点共圆 (52)第五十题:证明角平分 (53)第五十一题:证明线段相等 (54)第五十二题:证明两圆外切 (55)第五十三题:证明垂直 (56)第五十四题:证明垂直 (57)第五十五题:证明垂直 (58)第五十六题:证明垂直 (59)第五十七题:证中点 (60)第五十八题:证明角相等 (61)第五十九题:证明角相等 (62)第六十题:证明四点共圆 (63)第六十一题:证明四点共圆 (64)第六十二题:证明四点共圆 (65)第六十三题:证明角相等 (66)第六十四题:证明角的倍数关系 (67)第六十五题:证明中点 (68)第六十六题:伪旁切圆 (69)第六十七题:证明垂直 (70)第六十八题:证明平行 (71)第六十九题:证明圆心在某线上 (72)第七十题:证明三线共点 (73)第七十一题:证明垂直 (74)第七十二题:证明垂直 (75)第七十三题:证明中点 (76)第七十四题:证明垂直 (77)第七十五题:证明垂直 (78)第七十六题:证明三线共点 (79)第七十七题:证明平行 (80)第七十八题:证明平行 (81)第七十九题:证明三线共点、证明垂直 (82)第八十题:证明三点共线(牛顿定理) (83)第八十一题:证明角平分 (84)第八十二题:证明角相等 (85)第八十三题:证明三点共线 (86)第八十四题:证明四圆共点 (87)第八十六题:证明线段相等 (89)第八十七题:证明角相等 (90)第八十八题:证明线段相等 (91)第八十九题:证明线段相等 (92)第九十题:证明线段相等 (93)第九十一题:证明中点 (94)第九十二题:证明四点共圆 (95)第九十三题:证明西姆松定理及逆定理 (96)第九十四题:证明线段的和差关系等式 (97)第九十五题:证明角相等 (98)第九十六题:证明托勒密定理及逆定理 (99)第九十七题:证明线段的和差关系等式 (100)第九十八题:证明角相等 (101)第九十九题:证明四点共圆 (102)第一百题:证明两三角形共内心 (103)第一题:证明角平分已知PE 、PF 是⊙O 的切线,A 、B 是一组对径点,PB 交⊙O 于另一点C ,直线AF 、BE 交于D 点。
杏坛孔门新平面几何一百题

杏坛孔门新平面几何一百题平面几何是几何学的一个分支,研究平面上的点、线、角、面积等概念以及它们之间的关系。
下面我将为你列举一些关于平面几何的题目,一共有一百道,希望能够满足你的需求。
1. 证明平行线的性质及其判定方法。
2. 证明垂直线的性质及其判定方法。
3. 证明等腰三角形的性质及其判定方法。
4. 证明等边三角形的性质及其判定方法。
5. 证明直角三角形的性质及其判定方法。
6. 证明相似三角形的性质及其判定方法。
7. 证明正方形的性质及其判定方法。
8. 证明矩形的性质及其判定方法。
9. 证明菱形的性质及其判定方法。
10. 证明平行四边形的性质及其判定方法。
11. 证明梯形的性质及其判定方法。
12. 证明圆的性质及其判定方法。
13. 证明圆内接四边形的性质及其判定方法。
14. 证明圆内切四边形的性质及其判定方法。
15. 证明圆外接四边形的性质及其判定方法。
16. 证明圆外切四边形的性质及其判定方法。
17. 证明圆锥的性质及其判定方法。
18. 证明圆台的性质及其判定方法。
19. 证明圆球的性质及其判定方法。
20. 证明圆柱的性质及其判定方法。
21. 证明圆锥的体积公式。
22. 证明圆台的体积公式。
23. 证明圆柱的体积公式。
24. 证明圆球的体积公式。
25. 证明圆锥的表面积公式。
26. 证明圆台的表面积公式。
27. 证明圆柱的表面积公式。
28. 证明圆球的表面积公式。
29. 证明正多边形的内角和公式。
30. 证明正多边形的外角和公式。
31. 证明正多边形的边长与半径的关系。
32. 证明正多边形的面积公式。
33. 证明正多边形的周长公式。
34. 证明正多边形的内切圆半径公式。
35. 证明正多边形的外接圆半径公式。
36. 证明正多边形的内接圆面积公式。
37. 证明正多边形的外接圆面积公式。
38. 证明正多边形的对角线数目公式。
39. 证明正多边形的射影长公式。
40. 证明正多边形的对称轴数目公式。
41. 证明正多边形的中心对称轴数目公式。
几何题库100题

几何题库100题1. 已知三角形ABC的面积是20平方厘米,D是AB上的一个点,且BD/AB = 1/4,E是AC上的一个点,且AE/AC = 1/3,求三角形BDE的面积。
2. 已知平行四边形ABCD的面积是24平方厘米,E是CD的中点,F是AD的中点,求三角形BEF的面积。
3. 已知正方形ABCD的边长为4厘米,E是BC的中点,F是CD上的一点,且CF = 3厘米,求三角形AEF的面积。
4. 已知矩形ABCD的长为8厘米,宽为6厘米,G是矩形对角线AC的中点,求三角形AGD的面积。
5. 已知圆O的半径为5厘米,点P在圆上,点Q在圆外,且OP=3厘米,OQ=4厘米,求三角形POQ的面积。
6. 已知梯形ABCD的上下底分别为6厘米和10厘米,高为8厘米,求梯形的中位线长度。
7. 已知菱形ABCD的边长为6厘米,点E在BC上,且BE=3厘米,求三角形ABE的面积。
8. 已知三角形ABC的边长分别为3厘米、4厘米和5厘米,求三角形ABC 的周长。
9. 已知矩形ABCD的面积是36平方厘米,对角线AC的长度为10厘米,求矩形的宽。
10. 已知圆O的面积为154平方厘米,求圆的半径。
11. 已知椭圆的长半轴为6厘米,短半轴为4厘米,求椭圆的面积。
12. 已知抛物线y=2x^2+3x-1的顶点坐标,求抛物线的对称轴。
13. 已知立方体ABCDEF的体积是125立方厘米,求立方体的表面积。
14. 已知圆柱的高为10厘米,底面半径为5厘米,求圆柱的体积。
15. 已知直角三角形ABC的直角边长分别为3厘米和4厘米,求直角三角形的斜边长。
16. 已知平面上有四个点A、B、C、D,且AB=4厘米,BC=5厘米,CD=6厘米,求四边形ABCD的周长。
17. 已知平行四边形ABCD的对角线AC=6厘米,BD=8厘米,求平行四边形的面积。
18. 已知圆O的直径为10厘米,点P在圆上,且OP=5厘米,求三角形OEP 的面积。
平面几何100题2.0版61-100,1'-30'

61.设ω是△A B C的外接圆,ΓA是与线段A B、A C相切且与ω内切的圆,ΓB是与线段B A、B C相切且与ω内切的圆,ΓC是与线段C A、C B相切且与ω内切的圆.设过B、C且与ΓA 相切的圆(不同于ω)切ΓA于X,过C、A且与ΓB相切的圆(不同于ω)切ΓB于Y,过A、B且与ΓC相切的圆(不同于ω)切ΓC于Z.证明:A X、B Y、C Z三线共点.62.设⊙I是△A B C的内切圆,⊙u、⊙v、⊙w分别是过点B和点C且与⊙I相切的圆、过点A和点C且与⊙I相切的圆、过点B和点A且与⊙I相切的圆.设P、Q、R、S、T、U分别是⊙w与B C、⊙v与B C、⊙v与A B、⊙u与A B、⊙u与C A、⊙w与A C的交点(均不同于A、B、C).I1、I2分别是△A R Q、△B S T的内心,类似定义I3、I4、I5、I6.I A是△A S T∠S A T内的旁心,类似定义I B、I C.求证∶△I A I2I3、△I B I6I1、△I C I4I5的欧拉线共点.63.以凸四边形A B C D为边长向外作正方形A E1E2B、B F1F2C、C G1G2D、D H1H2A.连接A F1、B G1、C H1、D E1交出四边形A'B'C'D',连接D F2、A G2、B H2、C E2交出四边形A''B''C''D''.证明∶A'A''、B'B''、C'C''、D'D''交出的四边形是正方形.64.圆内接四边形A B C D中,直线A C、B D交于E,直线A B、C D交于F,直线B C、D A交于G.设△A B E的外接圆与直线C B交于B、P两点,△A D E的外接圆与直线C D交于D、Q两点.设直线F P、G Q交于点M,证明∶A M⊥A C.65.设⊙X、⊙Y、⊙Z分别为△A B C∠B A C、∠A B C、∠B C A内的旁切圆,D、E、F、G、H、I分别是⊙Z与A C、⊙Z与B C、⊙X与A B、⊙X与A C、⊙Y与B C、⊙Y与A B的切点.F D、G I交于J,I E、H F交于K,E G、D H交于L,设M、N、O、P、Q、R分别是K L、L J、J K、B C、C A、A B的中点.证明∶直线M P、N Q、O R三线共点.66.已知凸六边形A B C D E F既有外接圆又有内切圆,记△A B C、△B C D、△C D E、△D E F、△E F A、△F A B的内切圆分别为ωb、ωc、ωd、ωe、ωf、ωa.l A B表示ωb、ωa的另一条外公切线(不为A B),类似定义l B C、l C D、l D E、l E F、l F A.设l F A与l A B的交点为A1,类似定义B1、C1、D1、E1、F1.若六边形A1B1C1D1E1F1为凸六边形,证明:该六边形的对角线共点.67.已知圆弧Γ1、Γ2、Γ3均过点A、C,且在直线A C同侧,Γ2在Γ1与Γ3之间,B是线段A C上一点,由B引三条射线h1、h2、h3,与Γ1、Γ2、Γ3在直线A C的同侧,且h2在h1与h3之间.设h i与Γj(i,j=1,2,3)的交点为V i j.由线段V i j V i l、V k j V k l及弧V i j V k j、弧V i l V k l构成的曲边四边形记为V i j V k j V k l V i l,若存在一个圆与其两条线段和两条弧均相切,则称这个圆为这个曲边四边形的内切圆.证明:若曲边四边形V11V21V22V12、V12V22V23V13、V21V31V32V22均有内切圆,则曲边四边形V22V32V33V23也有内切圆.68.设△A B C的内心为I,⊙I分别切边B C,C A,A B于点D、E、F,设A I与D E、D F交于点M、N,以M N为直径的圆交B C于P、Q.已知△A P Q的外接圆与⊙I切于R,△A B C 的外接圆与九点圆切于F e,设R F e与D E、D F分别交于点M'、N'.以M'N'为直径的圆交B C 于点P'、Q'.证明:△A P'Q'的外接圆与⊙I的根轴平分线段B C.69.设I是△A B C的内心,∠B A C、∠A B C、∠B C A的内角平分线分别交对边于点D、E、F.记H是△D E F垂心.证明:I H与△A B C的欧拉线平行.70.设⊙O、⊙P、⊙Q分别是△A B C∠B A C、∠C B A、∠A C B内的旁切圆,G、H、I、J、K、L分别是⊙P与A B、⊙Q与A C、⊙Q与B C、⊙O与A B、⊙O与A C、⊙P与B C的切点.证明∶△J K D、△L G E、△H I F、△A B C的欧拉线共点.71.△A B C中,O为外心,K为△A B C九点圆圆心关于△A B C的等角共轭点.K在B C、C A、A B上的射影分别为D、E、F,H是△D E F垂心.证明:O、K、H共线.72.已知H、I分别为△A B C垂心、内心,D、E、F分别在射线A H、B H、C H上,且A D=B E=C F=2r,这里r是△A B C的内切圆半径.证明:I也为△D E F内心.73.已知B、I1、I2、C是⊙M上顺次四点,B I1与C I2交于A,△I1I2M的外接圆与A B、A C 再次交于M1、M2,点O'满足M1O'∥C I1,M2O'∥B I2.X、Y为△A B C的一组等角共轭点,D、E分别在A B、A C上使得X D∥C I1、X E∥B I2,N为△B M C外接圆弧B C(不含M)的中点,X N与△B M C外接圆的另一个交点为F.证明:X、Y、O'共线当且仅当△D E F外接圆与△I1I2M的外接圆相切.74.设△A B C∠B A C内的旁切圆切A B、A C于G、F,∠A B C内的旁切圆⊙P切A B、A C于E、N,∠A C B内的旁切圆⊙Q切A B、A C于M、D.直线D E、M N分别交⊙Q于H、J,交⊙P 于I、K.H C、B I交于X,J F、K G交于Y,证明∶∠B A X=∠C A Y.75.△A B C的内切圆⊙I切B C于D,连接A D交⊙I于J,K在J D上且D K=A J,若B J⊥C J,证明:I、K关于△J B C等角共轭.76.O为△A B C外心,B C、C A上的旁切圆切点分别是X、Y,A X、B Y交于点N.圆Γ1切B A、C A延长线于E、D使得A D=A E=B C,类似地定义Γ2、Γ3.⊙U为与Γ1、Γ2、Γ3均外切的圆,证明:N、O、U共线.77.△A B C内切圆⊙I切B C于D,∠A C B内的旁切圆⊙P分别切B C、A B、C A于E、F、G,∠A B C内的旁切圆⊙Q分别切B C、C A、A B于H、J、K,C F与⊙P交于F、M两点,B J与⊙Q交于J、N两点.证明:M J、N F、A D共点.78.P为圆外切四边形A B C D内任意一点,A P、D P分别交B C于N、M.证明:△A P D、△M P N、△A B N、△C D M四个三角形的内心共圆.79.设⊙I是△A B C的内切圆,△B C D外接圆⊙O1、△C A E外接圆⊙O2、△A B F外接圆⊙O3分别与⊙I内切于点D、E、F.G H与S T、J K与N P、L M与Q R分别是⊙O2与⊙O3、⊙O1与⊙O2、⊙O3与⊙O1的外公切线(L、N、R、K在⊙O1上,P、H、J、S在⊙O2上,G、Q、T、M在⊙O3上,G H、T S与A分别在B C的同侧、异侧,L M、R Q与B分别在A C的同侧、异侧,J K、Y M与C分别在A B的同侧、异侧).设△G H F、△J K E、△L M D外接圆分别为ω1、ω2、ω3,X、Y、Z分别是ω2与ω3、ω1与ω3、ω1与ω2的交点且X、A在B C异侧,Y、C在B A异侧,Z、B在A C异侧.证明∶S△K S X•S△M N Y•S△H Q Z=S△L T X•S△G P Y•S△R J Z.80.圆外切四边形A B C D中两点P、Q满足∠D P A+∠B P C=∠D Q A+∠B Q C,I1、I2、I3、I4、I11、I22、I33、I44分别是△P A B、△P B C、△P C D、△P D A、△Q A B、△Q B C、△Q C D、△Q D A 的内心.证明:I1、I2、I3、I4共圆当且仅当I11、I22、I33、I44共圆.81.△A B C的内切圆分别切A C、A B于E、F.P、Q分别为边A C、A B上的旁切圆切点.点M 为B C中点,P Q、E F交于R.设△A B C九点圆与内切圆切于K,证明:M、R、K共线.82.凸四边形A B C D中,△A B C、△B C D、△C D A、△D A B的内心分别为I D、I A、I B、I C,∠B A C与∠B D C的角平分线交于点E,∠A B D与∠AC D的角平分线交于点F,线段ID I A、I B I C、E F的中点分别为X、Y、Z.证明:X、Y、Z三点共线.83.设ω1、ω2分别是过A、C且与△A B C内切圆内切于J的圆与过B、A且与△A B C内切圆内切于K的圆.设Q、R分别是ω1、ω2与B C的交点,ω1与A B交于P,ω2与A C交于S,X 是△C S R∠C内的旁心,Y是△B P Q∠B内的旁心,M是△B S R的内心,N是△C P Q的内心.证明:四边形X Y M N是矩形.84.设圆Γ过B,C且与△A B C的内切圆⊙I内切于点J,延长A J交B C于K,交Γ于L.证明:(K B/K C)2=(L B/L C)3.85.⊙I、⊙J、⊙K与⊙O外切于X、Y、Z,E H、F L、M G分别是⊙I与⊙K、⊙I与⊙J、⊙J 与⊙K的外公切线且均与⊙O相交,并且E、F、G、H、L、M均为切点.H G与M L、E F与H G、E F与M L分别交于点U、V、W.证明:Y W·X V·Z U=WX·V Z·U Y.86.设I、O分别是△A B C的内心、外心,U、V分别为⊙O与⊙I的外位似中心与内位似中心,设E、F、Y、Z分别是B I与A C、C I与A B、B O与A C、C O与A B的交点.证明:U、E、F 共线的充要条件是V、Y、Z共线.87.设P、Q是△A B C的一对等角共轭点且△A B C的重心G与P、Q共线.D、E、F分别是A P 与B C、B P与A C、C P与A B的交点,A Q、B Q、C Q分别与△A B C外接圆再次交于点X、Y、Z,证明:△A D X、△B E Y、△C F Z外接圆有公共的根轴.88.给定△A B C,证明:在△A B C所在平面内存在唯一的一点P,使得△A B C、△P A B、△P B C、△P C A的欧拉线互相平行.89.设N为△A B C的九点圆圆心,N在B C、C A、A B上的射影分别为D、E、F,R为N 关于△D E F的等角共轭点,X是△A E F的九点圆圆心.证明:R X垂直于B C.90.设O、I a、I b、I c分别是△A B C的外心、∠B A C内的旁心、∠A B C内的旁心、∠B C A 内的旁心.设与⊙I b、⊙I c外切且与⊙O内切的圆与⊙O切于X,类似定义Y、Z.证明:A X、B Y、C Z三线共点.91.O为△A B C外心,P、Q为△A B C的一对等角共轭点.设D、E、F分别为A P与B C、B P与C A、C P与A B的交点.设一条与O Q垂直的直线分别与B C、C A、A B交于点X、Y、Z.证明:△AD X外接圆、△BE Y外接圆、△CF Z外接圆有一条公共的根轴.92.设I、O分别为△A B C的内心、外心,D、E、F分别为A I与B C、B I与A C、C I与A B的交点.设ωa为与A B、A C相切且与⊙O内切的圆,过E,F作ωa的切线(不同于直线A B、A C)交于D1,X为ωa与⊙O切点,类似定义E1、F1、Y、Z.证明:X D1、Y E1、Z F1、O I 四线共点.93.设P为△A B C内一点,D、E、F分别是A P与B C、B P与A C、C P与A B的交点.设△D E F外接圆与直线B C另一个交点为X,O为△A B C外心,T为△D E F垂心,X'为X 关于直线E F的对称点.证明:A X'、B C、O T三线共点.94.给定△A B C及与一点P,设A P与B C、B P与C A、C P与A B的交点分别为D、E、F.证明:存在两点U、V使得V是U关于△A B C的等角共轭点,也是U关于△D E F的等角共轭点.95.△A B C的垂心为H,A H与B C交点为D.U、V为线段B C上两点使得∠B H U=∠C H V,P Q、R S为△A B C外接圆的两条弦且分别过U、V.证明:△A D P、△A D Q、△A D R、△A D S四个三角形的垂心共圆.96.△A B C的内心、外心、垂心分别是I、O、H.P为直线O I上一点,P a、P b、P c分别是P在B C、C A、A B上的射影.设A I、B I、C I与⊙O再次交于D、E、F,设D'、E'、F'分别为D关于P a、E关于P b、F关于P c的对称点.证明:D'、E'、F'、H四点共圆.97.△A B C外心为O,P为△A B C所在平面内一点,D、E、F分别为P在B C、A C、A B 上的射影,A P、B P、C P与⊙O再次交于点X、Y、Z.X'、Y'、Z'分别是X关于O D、Y关于O E、Z关于O F的对称点.证明:A X'、B Y'、C Z'三线共点.98.△A B C外心为O,共轭重心为K,D与A在直线B C同侧且△B C D为正三角形,J是A D 中垂线与B C交点,A J与⊙O再次交于T.证明:T关于△A B C的西姆松线平行于O K.99.P为△A B C内一点,D、E、F分别是A P与B C、B P与A C、C P与A B交点,X、Y、Z分别是P在B C、C A、A B上的射影.P关于△A B C的等角共轭点Q,O为△A B C外心,r为⊙O 半径.R在射线O Q上且O P·O Q=r2.△D E F外接圆与△X Y Z外接圆有两个不同的交点T1、T2.l1、l2分别为T1、T2关于△D E F的西姆松线,直线l3、l4使得l3∥l1且T1到l3的距离为T1到l1距离的两倍,l4∥l2且T2到l4的距离等于T2到l2距离的两倍(T1在l1、l3的同侧,T2在l2、l4的同侧).证明:l3、l4一条过P,一条过R.100.已知⊙O上顺次五点A、B、C、D、E,设ω1为与B C、A C相切且与⊙O内切的圆,ω2为与A D、B E相切且与⊙O内切的圆,ω3为与A D、B E相切且与⊙O外切的圆.证明:C向ω3所作的一条切线与ω1与ω2的一条公切线平行.1'.已知⊙O1与△A B C的A B、B C边相切且与△A B C的外接圆内切于E,⊙O2与△A B C的A C、B C边相切且与△A B C的外接圆内切于F,连接E O2、F O1交于X.证明:A X平分∠B A C.2'.一直线交△X1X2X3三边所在直线X2X3、X3X1、X1X2于A1、A2、A3.分别过A1、A2、A3作X2X3、X3X1、X1X2的垂线,三垂线交成△Y1Y2Y3.证明:直线A1A2A3平分△X1X2X3垂心和△Y1Y2Y3垂心的连线段.3'.设H为锐角△A B C的垂心,M为B C中点,⊙I1、⊙I2分别为△A B H、△A C H的内切圆.证明:⊙I1、⊙I2除A H外的另一条内公切线过M.4'.设△A B C的内切圆分别切B C、C A、A B于D、E、F.记D关于E F、E关于F D、F关于D E 的对称点分别为D’、E’、F’,V为△A B C的九点圆心.证明:V在△D’E’F’的欧拉线上.5'.△A B C内接与⊙O,H是△A B C的垂心,E、F分别是H关于直线A C、A B的对称点.O E与A C交于M,O F与A B交于N,作平行四边形A B D C,设X、Y、Z分别是H在M N、N D、M D边上的射影.证明:△X Y Z的外接圆与△A B C的九点圆相切.6'.已知⊙I为△A B C的内切圆,⊙U过B、C两点,⊙V与边A B、A C相切且与⊙U内切,l 为平行于B C且与⊙I相切的直线(l不与B C重合),L为⊙U上任意一点,过L作⊙I的切线交l于E、F.证明:△E F L的外接圆与⊙V相切.7'.设K是△A B C的共轭重心,P是△A B C内任意一点,P在B C、C A、A B的射影分别为X、Y、Z,G为△X Y Z的重心,D在A B C的外接圆上且满足D关于△A B C的西姆松线与直线K P平行.设直线A D、B C交于E;直线B D、A C交于F;直线E F、A B交于J.证明:J、K、G共线.8'.设H、I分别为△A B C的垂心、内心,A B、A C上的旁切圆切点分别为F、E,线段B E与C F相交于N.设H N中点为M,J在射线M I上满足J M·I M=M H²,直线I N与B C交于D,G在线段B C上且满足B G=C D.证明:G I=G J.9'.已知四边形A B C D为圆外切四边形,A C、B D的中垂线相交于P,设I1、I2、I3、I4分别为△A B P、△B C P、△C D P、△D A P的内心.证明:I1、I2、I3、I4四点共圆.10'.设四边形A B C D内接于⊙U,⊙V与线段A C、B D相切(与线段B C相交)且与⊙U内切于T,F为劣弧B C上任意一点,⊙P与线段A F、B C相切(与线段A B相交)且与⊙U内切.设M是⊙P与B C的切点,延长D M交⊙U于E.⊙Q与线段D E、B C相切(与线段C D相交)且与⊙U内切,⊙R与直线B F、C E相切且与⊙U外切于X.设N是⊙Q与B C的切点.证明:M、N、T、X四点共圆.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
61.设ω是△ABC的外接圆,ΓA是与线段AB、AC相切且与ω内切的圆,ΓB是与线段BA、BC相切且与ω内切的圆,ΓC是与线段CA、CB相切且与ω内切的圆.设过B、C且与ΓA 相切的圆(不同于ω)切ΓA于X,过C、A且与ΓB相切的圆(不同于ω)切ΓB于Y,过A、B且与ΓC相切的圆(不同于ω)切ΓC于Z.证明:AX、BY、CZ三线共点.62.设⊙I是△ABC的内切圆,⊙u、⊙v、⊙w分别是过点B和点C且与⊙I相切的圆、过点A和点C且与⊙I相切的圆、过点B和点A且与⊙I相切的圆.设P、Q、R、S、T、U分别是⊙w与BC、⊙v与BC、⊙v与AB、⊙u与AB、⊙u与CA、⊙w与AC的交点(均不同于A、B、C).I1、I2分别是△ARQ、△BST的内心,类似定义I3、I4、I5、I6.I A是△AST∠SAT内的旁心,类似定义I B、I C.求证∶△I A I2I3、△I B I6I1、△I C I4I5的欧拉线共点.63.以凸四边形ABCD为边长向外作正方形AE1E2B、BF1F2C、CG1G2D、DH1H2A.连接AF1、BG1、CH1、DE1交出四边形A'B'C'D',连接DF2、AG2、BH2、CE2交出四边形A''B''C''D''.证明∶A'A''、B'B''、C'C''、D'D''交出的四边形是正方形.64.圆内接四边形ABCD中,直线AC、BD交于E,直线AB、CD交于F,直线BC、DA交于G.设△ABE的外接圆与直线CB交于B、P两点,△ADE的外接圆与直线CD交于D、Q两点.设直线FP、GQ交于点M,证明∶AM⊥AC.65.设⊙X、⊙Y、⊙Z分别为△ABC∠BAC、∠ABC、∠BCA内的旁切圆,D、E、F、G、H、I分别是⊙Z与AC、⊙Z与BC、⊙X与AB、⊙X与AC、⊙Y与BC、⊙Y与AB的切点.FD、GI交于J,IE、HF交于K,EG、DH交于L,设M、N、O、P、Q、R分别是KL、LJ、JK、BC、CA、AB的中点.证明∶直线MP、NQ、OR三线共点.66.已知凸六边形ABCDEF既有外接圆又有内切圆,记△ABC、△BCD、△CDE、△DEF、△EFA、△FAB的内切圆分别为ωb、ωc、ωd、ωe、ωf、ωa.l AB表示ωb、ωa的另一条外公切线(不为AB),类似定义l BC、l CD、l DE、l EF、l FA.设l FA与l AB的交点为A1,类似定义B1、C1、D1、E1、F1.若六边形A1B1C1D1E1F1为凸六边形,证明:该六边形的对角线共点.67.已知圆弧Γ1、Γ2、Γ3均过点A、C,且在直线AC同侧,Γ2在Γ1与Γ3之间,B是线段AC上一点,由B引三条射线h1、h2、h3,与Γ1、Γ2、Γ3在直线AC的同侧,且h2在h1与 h3之间.设h i与Γj(i,j=1,2,3)的交点为V ij.由线段V ij V il、V kj V kl及弧V ij V kj、弧V il V kl构成的曲边四边形记为V ij V kj V kl V il,若存在一个圆与其两条线段和两条弧均相切,则称这个圆为这个曲边四边形的内切圆.证明:若曲边四边形VV21V22V12、V12V22V23V13、V21V31V32V2211均有内切圆,则曲边四边形VV32V33V23也有内切圆.2268.设△ABC的内心为I,⊙I分别切边BC,CA,AB于点D、E、F,设AI与DE、DF交于点M、N,以MN为直径的圆交BC于P、Q.已知△APQ的外接圆与⊙I切于R,△ABC 的外接圆与九点圆切于Fe,设RFe与DE、DF分别交于点M'、N'.以M'N'为直径的圆交BC 于点P'、Q'.证明:△AP'Q'的外接圆与⊙I的根轴平分线段BC.69.设I是△ABC的内心,∠BAC、∠ABC、∠BCA的内角平分线分别交对边于点D、E、F.记H是△DEF垂心.证明:IH与△ABC的欧拉线平行.70.设⊙O、⊙P、⊙Q分别是△ABC∠BAC、∠CBA、∠ACB内的旁切圆,G、H、I、J、K、L分别是⊙P与AB、⊙Q与AC、⊙Q与BC、⊙O与AB、⊙O与AC、⊙P与BC的切点.证明∶△JKD、△LGE、△HIF、△ABC的欧拉线共点.71.△ABC中,O为外心,K为△ABC九点圆圆心关于△ABC的等角共轭点.K在BC、CA、AB上的射影分别为D、E、F,H是△DEF垂心.证明:O、K、H共线.72.已知H、I分别为△ABC垂心、内心,D、E、F分别在射线AH、BH、CH上,且AD=BE=CF=2r, 这里r是△ABC的内切圆半径.证明:I也为△DEF内心.73.已知B、I1、I2、C是⊙M上顺次四点,BI1与CI2交于A,△I1I2M的外接圆与AB、AC再次交于M1、M2,点O'满足M1O'∥CI1,M2O'∥BI2.X、Y为△ABC的一组等角共轭点,D、E分别在AB、AC上使得XD∥CI1、XE∥BI2,N为△BMC外接圆弧BC(不含M)的中点,XN与△BMC外接圆的另一个交点为F.证明:X、Y、O'共线当且仅当△DEF外接圆与△I1I2M的外接圆相切.74.设△ABC∠BAC内的旁切圆切AB、AC于G、F,∠ABC内的旁切圆⊙P切AB、AC于E、N,∠ACB内的旁切圆⊙Q切AB、AC于M、D.直线DE、MN分别交⊙Q于H、J,交⊙P 于I、K.HC、BI交于X,JF、KG交于Y,证明∶∠BAX=∠CAY.75.△ABC的内切圆⊙I切BC于D,连接AD交⊙I于J,K在JD上且DK=AJ,若BJ⊥CJ,证明:I、K关于△JBC等角共轭.76.O为△ABC外心,BC、CA上的旁切圆切点分别是X、Y,AX、BY交于点N.圆Γ1切BA、 CA延长线于E、D使得AD=AE=BC,类似地定义Γ2、Γ3.⊙U为与Γ1、Γ2、Γ3均外切的圆,证明:N、O、U共线.77.△ABC内切圆⊙I切BC于D,∠ACB内的旁切圆⊙P分别切BC、AB、CA于E、F、G,∠ABC内的旁切圆⊙Q分别切BC、CA、AB于H、J、K,CF与⊙P交于F、M两点,BJ与⊙Q交于J、N两点.证明:MJ、NF、AD共点.78.P为圆外切四边形ABCD内任意一点,AP、DP分别交BC于N、M.证明:△APD、△MPN、△ABN、△CDM四个三角形的内心共圆.79.设⊙I是△ABC的内切圆,△BCD外接圆⊙O1、△CAE外接圆⊙O2、△ABF外接圆⊙O3分别与⊙I内切于点D、E、F.GH与ST、JK与NP、LM与QR分别是⊙O2与⊙O3、⊙O1与⊙O2、⊙O3与⊙O1的外公切线(L、N、R、K在⊙O1上,P、H、J、S在⊙O2上,G、Q、T、M在⊙O3上,GH、TS与A分别在BC的同侧、异侧,LM、RQ与B分别在AC的同侧、异侧,JK、YM与C分别在AB的同侧、异侧).设△GHF、△JKE、△LMD外接圆分别为ω1、ω2、ω3,X、Y、Z分别是ω2与ω3、ω1与ω3、ω1与ω2的交点且X、A在BC异侧,Y、 C 在BA异侧,Z、B在AC异侧.证明∶S△KSX•S△MNY•S△HQZ=S△LTX•S△GPY•S.△RJZ80.圆外切四边形ABCD中两点P、Q满足∠DPA+∠BPC=∠DQA+∠BQC,I1、I2、I3、I4、I11、I22、I33、I44分别是△PAB、△PBC、△PCD、△PDA、△QAB、△QBC、△QCD、△QDA 的内心.证明:I1、I2、I3、I4共圆当且仅当I11、I22、I33、I44共圆.81.△ABC的内切圆分别切AC、AB于E、F.P、Q分别为边AC、AB上的旁切圆切点.点M 为BC中点,PQ、EF交于R.设△ABC九点圆与内切圆切于K,证明:M、R、K共线.82.凸四边形ABCD中,△ABC、△BCD、△CDA、△DAB的内心分别为I D、I A、I B、I C,∠BAC与∠BDC的角平分线交于点E,∠ABD与∠ACD的角平分线交于点F,线段I D I A、I B I C、EF的中点分别为X、Y、Z.证明:X、Y、Z三点共线.83.设ω1、ω2分别是过A、C且与△ABC内切圆内切于J的圆与过B、A且与△ABC内切圆内切于K的圆.设Q、R分别是ω1、ω2与BC的交点,ω1与AB交于P,ω2与AC交于S,X 是△CSR∠C内的旁心,Y是△BPQ∠B内的旁心,M是△BSR的内心,N是△CPQ的内心. 证明:四边形XYMN是矩形.84.设圆Γ过B,C且与△ABC的内切圆⊙I内切于点J,延长AJ交BC于K,交Γ于L.证明:(KB/KC)2=(LB/LC)3.85.⊙I、⊙J、⊙K与⊙O外切于X、Y、Z,EH、FL、MG分别是⊙I与⊙K、⊙I与⊙J、⊙J 与⊙K的外公切线且均与⊙O相交,并且E、F、G、H、L、M均为切点.HG与ML、EF与HG、EF与ML分别交于点U、V、W.证明:YW·XV·ZU=WX·VZ·UY.86.设I、O分别是△ABC的内心、外心,U、V分别为⊙O与⊙I的外位似中心与内位似中心,设E、F、Y、Z分别是BI与AC、CI与AB、BO与AC、CO与AB的交点.证明:U、E、F共线的充要条件是V、Y、Z共线.87.设P、Q是△ABC的一对等角共轭点且△ABC的重心G与P、Q共线.D、E、F分别是AP 与BC、BP与AC、CP与AB的交点,AQ、BQ、CQ分别与△ABC外接圆再次交于点X、Y、Z,证明:△ADX、△BEY、△CFZ外接圆有公共的根轴.88.给定△ABC,证明:在△ABC所在平面内存在唯一的一点P,使得△ABC、△PAB、△PBC、△PCA的欧拉线互相平行.89.设N为△ABC的九点圆圆心,N在BC、CA、AB上的射影分别为D、E、F,R为N 关于△DEF的等角共轭点,X是△AEF的九点圆圆心.证明:RX垂直于BC.90.设O、I a、I b、I c分别是△ABC的外心、∠BAC内的旁心、∠ABC内的旁心、∠BCA内的旁心.设与⊙Ib、⊙I c外切且与⊙O内切的圆与⊙O切于X,类似定义Y、Z.证明:AX、BY、CZ三线共点.91.O为△ABC外心,P、Q为△ABC的一对等角共轭点.设D、E、F分别为AP与BC、BP与CA、CP与AB的交点.设一条与OQ垂直的直线分别与BC、CA、AB交于点X、Y、Z.证明:△ADX外接圆、△BEY外接圆、△CFZ外接圆有一条公共的根轴.92.设I、O分别为△ABC的内心、外心,D、E、F分别为AI与BC、BI与AC、CI与 AB的交点.设ω为与AB、AC相切且与⊙O内切的圆,过E,F作ωaa的切线(不同于直线AB、AC)交于D1,X为ωa与⊙O切点,类似定义E1、F1、Y、Z.证明:XD1、YE1、ZF1、OI四线共点.93.设P为△ABC内一点,D、E、F分别是AP与BC、BP与AC、CP与AB的交点.设△DEF外接圆与直线BC另一个交点为X,O为△ABC外心,T为△DEF垂心,X'为X 关于直线EF的对称点.证明:AX'、BC、OT三线共点.。
