重大建设工程基本自振周期估算方法探讨
结构基本自振周期计算

W
---风荷载组合系数;一般结构可不考虑,风荷载起控制作用的高层建筑应
采用0.2;
精品课件
3.8.3结构抗震承载力验算
(2)截面抗震验算
S R RE
S---包含地震作用效应的结构构件内力组合的设计值; R---结构构件承载力设计值; RE ---承载力抗震调整系数;
精品课件
3.8.3结构抗震承载力验算
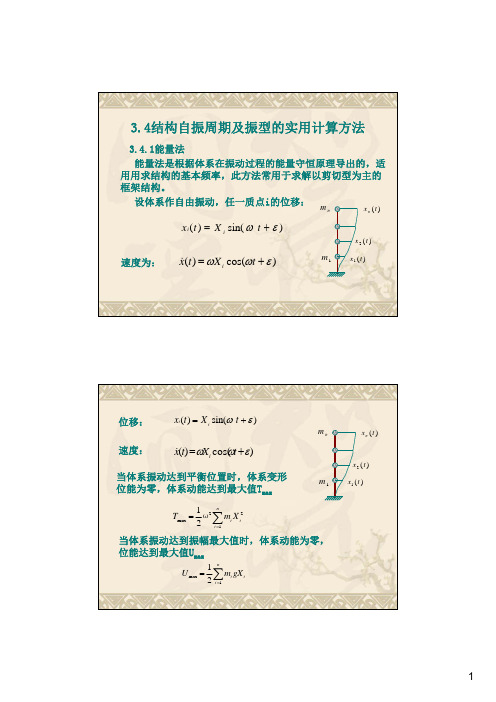
3.4.1能量法
位移: xi(t)Xisi nt()
速度: x (t)Xicots()
mn
当体系振动达到平衡位置时,体系变形
位能为零,体系动能达到最大值Tmax
Tmax12ω2 in1 miXi2
m1
xn (t)
x2 (t) x1 (t )
当体系振动达到振幅最大值时,体系动能为零,
位能达到最大值Umax
无论结构是否有偏心,地震地面运动产生的结构扭 转振动均是存在的。
★扭转作用会加重结构的震害 《规范》规定对质量和刚度明显不均匀、不对称结构 应考虑水平地震作用的扭转效应
精品课件
3.6竖向地震作用
抗震设计中,一般不考虑竖向地震作用的影响 震害表明:
1、在高烈度区,竖向地面运动的影响是明显的 2、竖向地震作用对高层建筑、高耸及大跨结构
3.4结构自振周期及振型的实用计算方法
能量法是根据体求解以剪切型为主的框架结构
mn
xn (t)
设体系作自由振动,任一质点i的位移:
xi(t)Xisi nt()
3.4.1能量法
速度为 x (t)X ico ts()
m1
精品课件
x2 (t) x1 (t )
竖向地震作用。
精品课件
3.8.1地震作用及计算方法
结构基本自振周期计算

m1
x1
xm xn
x m ---体系按第一振型振动时,相应于折算质点处的最大位移;
3.4.2折算质量法(等效质量法)
1n 2 T m ( x ) 1 max i 1 i 2i 1
1 2 T M ( x ) 2 m ax eq 1 m 2
T T 1 max 2 max
1 M e q
u [ h e e]
u e ---多遇地震作用标准值产生的楼层内最大的弹性层间位移;
h ---计算楼层层高; [ e ] ---弹性层间位移角限值,按表3.14采用。
3.8.4多遇地震作用下结构抗震变形验算
表3.14弹性层间位移角限值
结构类型 钢筋混凝土框架
钢筋混凝土框架-抗震墙、板柱-抗震墙、框架-核心筒 钢筋混凝土抗震墙、筒中筒 钢筋混凝土框支层 多、高层钢结构
结构基本自振周 期计算
3.4.1能量法
i ( t ) X t ) 位移: x isin( 速度: x ( t )
当体系振动达到平衡位置时,体系变形 位能为零,体系动能达到最大值Tmax
1 2n 2 T ω m X max i i 2 i 1
基本原理:将多质点体系用单质点体系代替。 使单质点体系的自振频率和原体系的基本频率相等或相近 等效原则:两个体系的动能相等 x x 多质点体系的最大动能为
1n 2 T m x 1 m ax i( 1 i) 2i 1
mN
n
M
eq
m
单质点体系的最大动能为
1 2 T M ( x ) 2 m ax eq 1 m 2
0.10(0.15) 0.20
3.6.3悬臂结构的竖向地震作用
7结构基本自振周期计算

Tb 1.6 b
框架结构可近似视为剪切型杆。
Ts 1.8 s
框架-抗震墙结构可近似视为剪弯型杆。
T 1.7 bs
本方法适用于质量及刚 度沿高度分布比较均匀 的任何体系结构。
补充:自振周期的经验公式
根据实测统计,忽略填充墙布置、质量分布差异等,初 步设计时可按下列公式估算
(1)高度低于25m且有较多的填充墙框架办公楼、旅馆的基本周期
T1 (0.04 ~ 0.05) N
(4)钢-钢筋混凝土混合结构
T1 (0.06 ~ 0.08) N
(5)高层钢结构
T1 (0.08 ~ 0.12) N
3.5结构的扭转地震效应
一、产生扭转地震反应的原因
两方面:建筑自身的原因和地震地面运动的原因。 m 1.建筑结构的偏心
主要原因:结构质量中心与刚度 中心不重合 质心:在水平地震作用下, 惯性力的合力中心 刚心:在水平地震作用下, 结构抗侧力的合力中心
4、8度和9度时的大跨度结构、长悬臂结构,9度时的高层建筑,应考虑 竖向地震作用。
3.8.1地震作用及计算方法
2、抗震计算方法的确定 1、高度不超过40m,以剪切变形为主且质量和刚度沿高度 分布比较均匀的结构,以及近似于单质点体系的结构, 宜采用底部剪力法等简化方法。 2、除上述以外的建筑结构,宜采用振型分解反应谱法。 3、特别不规则的建筑、甲类建筑和规范规定的高层建筑, 应采用时程分析法进行多遇地震下的补充计算。
(1)竖向反应谱及竖向振动周期 竖向地震反应谱: 与水平地震反应谱的形状相差不大 竖向反应谱的加速度峰值约为水平反应谱的1/2至2/3。 可利用水平地震反应谱进行分析。
V 0.65 H
Ⅰ类场地的竖向和水平平均反应谱
结构基本自振周期计算分解课件

竖向地震作用
竖向地震作用对高层建筑的影响较大,需要在计算中考虑竖向地震 作用的影响。
地震作用的组合
在计算中,需要考虑不同方向和不同强度地震作用的组合效应,以 更准确地评估结构的抗震性能。
06 结论与展望
本课程总结
01
结构基本自振周期计算是工程结 构分析中的重要环节,本课件详 细介绍了计算方法及其应用。
05 结构基本自振周期计算中 的注意事项
边界条件的处理
固定边界
对于固定边界,需要考虑结构在边界上的刚度,确保边界条件满 足,以减小误差。
弹性边界
对于弹性边界,需要考虑边界的弹性变形,并适当调整结构的刚 度矩阵,以更准确地模拟结构的振动。
支撑条件的模拟
在计算中,需要正确模拟结构的支撑条件,包括支撑刚度和阻尼 等参数,以确保计算结果的准确性。
02
通过案例分析,使学习者更好地 理解计算过程,掌握相关技能。
本课件注重理论与实践相结合, 帮助学习者提高解决实际问题的 能力。
03
本课件内容丰富,条理清晰,适 合作为学习资料或培训教材。
04
未来研究方向
01
深入研究结构基本自振周期的影 响因素,提高计算精度和可靠性
。
03
结合数值模拟和实验研究,进一 步验证和改进计算方法。
高层建筑结构的自振周期计算
总结词:复杂度高
详细描述:高层建筑结构的自振周期计算相对复杂,需要考虑更多的因素,如楼层高度、建筑材料、施工方法等。计算时需 要建立详细的数学模型,并进行数值分析。
大跨度结构的自振周期计算
总结词
跨度大,影响因素多
详细描述
结构自振周期及振型的实用计算方法

n
mN
n
Meq
m
∑
i =1
m i (ω 1 x i ) 2
单质点体系的最大动能为
T 2 max = 1 M 2
eq
m 1
x 1
(ω 1 x m ) 2
xm = xn
xm ---体系按第一振型振动时,相应于折算质点处的最大位移; ---体系按第一振型振动时 相应于折算质点处的最大位移; 体系按第一振型振动时,
T = 0.22 + 0.35H / 3 B 1
H---房屋总高度;B---所考虑方向房屋总宽度。 ---房屋总高度; ---所考虑方向房屋总宽度。 房屋总高度 所考虑方向房屋总宽度 (2)高度低于50m的钢筋混凝土框架-抗震墙结构的基本周期 高度低于50m的钢筋混凝土框架50m的钢筋混凝土框架
T = 0.33+ 0.00069H2 / 3 B 1
T =1.7 ∆bs
本方法适用于质量及刚 度沿高度分布比较均匀 的任何体系结构。
补充: 补充:自振周期的经验公式
根据实测统计,忽略填充墙布置、质量分布差异等, 根据实测统计,忽略填充墙布置、质量分布差异等,初 步设计时可按下列公式估算
(1)高度低于25m且有较多的填充墙框架办公楼、旅馆的基本周期 高度低于25m且有较多的填充墙框架办公楼、 25m且有较多的填充墙框架办公楼
FVi =
GiH i
n
∑G
j =1
F EVK ---质点i的竖向地震作用标准值。 ---质点 的竖向地震作用标准值。 质点i
j
j
H
规范要求: 度时 高层建筑楼层的竖向地震作用 度时, 规范要求:9度时,高层建筑楼层的竖向地震作用 效应应乘以 的增大系数。 应乘以1.5的增大系数 效应应乘以 的增大系数。
自振周期及地震作用计算讲义
n
i
根据能量守恒原理:
g
m
i 1 n i
n
i
Xi
T1
2 i
2
m
i 1
X
1
2
m X
i i 1 n
n
2 i
g
m X
i i 1
2
i
G X
i
n
2 i
G X
i i 1
i 1 n
i
一般假定:将结构重力荷载当成水平荷载作用于质点上 所得的结构弹性曲线为结构的基本振型。
T 1 max 1 2
n
i 1
m i ( 1 x i )
2
mN
xn
M
eq
xm
单质点体系的最大动能为
T 2 max 1 M 2
eq
xm xn
m1 x1
( 1 x m ) 2
x m ---体系按第一振型振动时,相应于折算质点处的最大位移;
T1max
1 n mi (1xi )2 2 i1
ห้องสมุดไป่ตู้
竖向地震作用,烟囱上 抛后下落错位。
9
德阳利森水泥厂生料均化库,受到 竖向地震作用,塔筒上抛后下落。
底部框架底层为薄弱层, 底层墙体叠合塌落。 (9度 区)
10
底部框架结构底层框架叠合塌落(北川11度区)。
中间层叠合塌落(日本阪神大地震)。
11
中间层水平裂缝 中间层水平裂缝。
3.6.1高耸结构及高层建筑的竖向地震作用
台湾省漳化县富贵 名门大楼,16层钢筋混 凝土住宅楼,平面为C 型, 平面不规整,单排 柱框架,柱子间距太大, 数量偏少。
结构自振周期计算
(4)钢-钢筋混凝土混合结构
T1 (0.06 ~ 0.08) N
(5)高层钢结构
T1 (0.08 ~ 0.12) N
3.5结构的扭转地震效应
一、产生扭转地震反应的原因
两方面:建筑自身的原因和地震地面运动的原因。 m 1.建筑结构的偏心
主要原因:结构质量中心与刚度 中心不重合 质心:在水平地震作用下, 惯性力的合力中心 刚心:在水平地震作用下, 结构抗侧力的合力中心
QKi — —第i个可变荷载的组合值系 数。
3.8.3结构抗震承载力验算
(1)构件作用效应组合
S G SGE Eh S Ehk Ev S Evk W W SWk
G---重力荷载分项系数,一般取1.2,当重力荷载效应对构件承载能力
有利时,不应大于1.0; Eh、 Ev ---分别为水平、竖向 地震作用分项系数, 按右表采用;
g
i 1 n
n
mi X i
i 2 i
m X
i 1
T1
2
1
2
m X
i i 1 n
n
2 i
g
m X
i i 1
2
i
G X
i
n
2 i
G X
i i 1
i 1 n
i
一般假定:将结构重力荷载当成水平荷载作用于质点上 所得的结构弹性曲线为结构的基本振型
3.4.2折算质量法(等效质量法)
自振周期的经验公式
在实测统计基础上,再忽略房屋宽度和层高的影响等, 有下列更粗略的公式 (1)钢筋混凝土框架结构
T1 (0.08 ~ 0.10) N T1 (0.06 ~ 0.08) N
抗震设计讲座之结构自振周期的计算
N---结构总层数。 (2)钢筋混凝土框架-抗震墙或钢筋混凝土框架-筒体结构
T1 (0.06 ~ 0.08) N
(3)钢筋混凝土抗震墙或筒中筒结构
T1 (0.04 ~ 0.05) N
(4)钢-钢筋混凝土混合结构
T1 (0.06 ~ 0.08) N
(5)高层钢结构
T1 (0.08 ~ 0.12) N
m
uT
无限自由度体系,剪切杆的的运动方程为
q
GA
y y m 0 2 2 x t
2 2
GA
悬臂杆的特解为
振型
yi ( x, t ) X i ( x) sin
X i ( x ) sin
( 2i 1) x 2l
2 t Ti
重力作为水平荷载所引起的位移为
uT ql 2 / 2GA
x1
M eq
x2 F / k1 F / k2 7.00105 1 / 10720
16.33105 m
能量法的结果为 T1=0.508s
x2
xm x2 16.3310 m
5
M eq
T1 2
m x
i 1 i 2 xm
nቤተ መጻሕፍቲ ባይዱ
2
i
400 (7 105 ) 2 300 (16.33105 ) 2 38.11t 9.8 ( 16.33105 ) 2
1 M eq (1 xm ) 2 2
mN
xn
M eq xm
m1
x1
单质点体系的最大动能为
T2 max
xm ---体系按第一振型振动时,相应于折算质点处的最大位移;
T1max T2 max
对高层建筑混凝土结构自振周期及周期比的一些见解
对高层建筑混凝土结构自振周期及周期比的一些见解[提要]通过多年来的高层结构方案分析和施工图设计,对高层建筑混凝土结构主自振周期的判定、主周期的周期比值等进行分析,提出一些自己的见解和建议,以便更准确的确定结构主自振周期,更合理的控制结构扭转刚度,保证结构的整体性能。
[关键词]高层混凝土结构,主自振周期,结构刚度,周期比值[abstract] through the years of high-rise structure scheme analysis and construction design of concrete structures of tall building Lord natural vibration period of determination, Lord cycle analysis of periodic ratio, and put forward some opinions and Suggestions, so that more accurate to determine the structure of the natural vibration period, more reasonable control structure torsional rigidity, ensure structural overall performance.[key words] top concrete structure, the natural vibration period, structure stiffness, the ratio of the cycle0 引言《高层建筑混凝土结构技术规程》[1](JGJ3)(以下简称高规)第3.4.5条规定:结构扭转为主的第一自振周期Tt与平动为主的第一自振周期T1之比,A 级高度高层建筑不应大于0.9,B级高度高层建筑、混合结构高层建筑及本规程第10章所指的复杂高层建筑不应大于0.85。
2019年结构基本自振周期计算.ppt
当体系振动达到振幅最大值时,体系动能为零,
位能达到最大值Umax
U max
1 2
n i 1
mi gX i
3.4.1能量法
Tmax
1ω 2 2
n i 1
mi
X
2 i
1 n
U max 2 i1 mi gX i
根据能量守恒原理: Tmax=Umax
3.6.1高耸结构及高层建筑的竖向地震作用
分析结果表明: 高耸结构和高层建筑竖向第一振型的地震内力与竖向 前5个振型按“平方和开方”组合的地震内力相比较, 误差仅在5%--15%。 竖向第一振型的数值大致呈倒三角形式
高耸结构和高层建筑竖向地震作用可按与底部剪力法 类似的方法计算。
3.6.1高耸结构及高层建筑的竖向地震作用
期较短,基本周期在0.1~0.2s范围内 小于场地的特征周期Tg 《建筑抗震规范》直接取竖向地震影响系数:
V max 0.65 H max
3.6.1高耸结构及高层建筑的竖向地震作用
(2)竖向地震作用计算----底部剪力法
FEVK G V m ax eq
V max 0.65 H max
质心
ug (t)
刚心
3.5结构的扭转地震效应
2.地震地面运动存在扭转分量 地震波在地面上各点的波速、周期和相位不同。建
筑结构基底将产生绕竖直轴的转动,结构便会产生扭转 振动。
无论结构是否有偏心,地震地面运动产生的结构扭 转振动均是存在的。
★扭转作用会加重结构的震害 《规范》规定对质量和刚度明显不均匀、不对称结构 应考虑水平地震作用的扭转效应
(1)竖向反应谱及竖向振动周期 竖向地震反应谱: 与水平地震反应谱的形状相差不大 竖向反应谱的加速度峰值约为水平反应谱的1/2至2/3。 可利用水平地震反应谱进行分析。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2 巨型储油罐基本自振周期估算方法
巨型储油罐主体结构的地震反应是由地面振动特性和结构本身特性两个方面决定的,准 确地掌握储油罐的自振特性(频率和振型)是储油罐抗震设计的前提。抗震设计时应避免储 油罐的自振周期接近地面运动的卓越周期,以免产生共振。影响储油罐自振周期的因素主要 包括:罐体型式、储液高度、不同高径比、地基弹性刚度和罐壁弹性模量等。因此,采用计 算精度可满足工程需要、计算结果可靠的、适用的近似估算方法,得出巨型储油罐主体结构 的自振周期是值得需要深入探讨的问题。 2.1 球形储罐基本自振周期估算方法 球形储罐常用于储存石油气、煤气和氨气等液化气体。根据 Housner 理论,液体在地震 中可分为两个部分:一部分是固定在罐壁上与罐体作一致运动(称为固定液体) ;另一部分是 独立作长周期自由晃动(称为自由液体) 。地震时,主要是固定的罐壁上的这部分液体参与结 构的整体振动。因此,引入了有效质量这一概念。同时,把球壳视为刚体,地基视为刚性, 则水平刚度是由支撑构架抵抗弯曲变形的刚度和拉杆与支柱形成的构架剪切刚度合成的。 在石油化工钢制设备(国家石油和化学工业局,1999)和石油化工构筑物(国家发展和 改革委员会,2004)的抗震设计规范中均有相关的规定,表达式的实质是一致的。对于球形 储罐基本自振周期可按下式进行计算:
230
震灾防御技术
7卷
分油气空间,浮顶对液面几乎不起约束作用,故可把浮顶罐近似地当作自由液面储罐看待。 但是,对于固定顶盖储罐,当储液上表面与顶盖之间空间小于储罐容积 4%时,则所有储液 几乎全被储罐周边约束住。根据反应谱理论,储罐地震影响系数是储罐自振周期的函数。因 此在计算储罐的地震作用时,应先计算储罐的自振周期。相关规范中均有规定,各个表达式 基本一致,但是,在实际近似计算过程中, 《立式圆筒形钢制焊接油罐设计规范(GB 50341 —2003) 》 (中华人民共和国建设部,2003)的估算方法相对简单,此规范仅针对罐壁高度与 3 直径比不大于 1.6,且容积大于或等于 100m 的常压(包括通过呼吸阀与大气相通的)圆筒 形钢制平底储罐适用,其立式圆筒形储罐的罐液耦连振动基本自振周期,应按下式计算: Tc = K c H w R
当计算罐壁底部水平地震剪力及弯距时, 采用罐液耦联振动基本自振周期 Tc, 其值在 0.1—0.5s 其值在 3—14s 的范围内。 的范围内; 当计算罐内液面晃动液高时, 采用储液晃动基本自振周期 Tw, 通常情况下,Tw 的值大于 Tc 的值。因此,在工程场地地震安全性评价工作中,根据保守性原则, 宜采用储液晃动基本自振周期 Tw 的值进行分析,相对而言是比较合理、可靠和准确的。
重大建设工程基本自振周期 估算方法探讨 1
洪海春 彭小波 毕雪梅 李细兵
(江苏省地震局,南京 210014)
摘要
在对规范和文献资料的研究和分析的基础上,本文探讨了(超)高层建筑、巨型储油罐、大跨
桥梁工程等重大建设工程基本自振周期的估算方法。在工程场地地震安全性评价工作中,可采用本文 提供的重大建设工程基本自振周期估算的公式。同时,本文为长周期地震动对工程结构作用的相关参 数的合理确定提供了依据。 关键词:基本自振周期 (超)高层建筑 巨型储油罐 大跨桥梁工程
表2 晃动周期系数
Table 2 Coefficients of sloshing period
D/Hw Ks D/Hw Ks 0.6 1.047 3.5 1.184 1.0 1.047 4.0 1.230 1.5 1.054 4.5 1.277 2.0 1.074 5.0 1.324 2.5 1.105 5.5 1.371 3.0 1.141 6.0 1.418
228
震灾防御技术
7卷
地震动对工程结构作用的相关参数的合理确定提供依据。
1 (超)高层建筑基本自振周期估算方法
对(超)高层建筑结构进行抗震设计时,其地震荷载计算主要采用基于地震反应谱理论 的底部剪力法和振型分解法,这些方法均要求先给出结构的基本自振周期。因此,基本自振 周期是工程结构抗震设计中的重要参数,是衡量一个结构质量与刚度是否匹配、刚度是否合 理的重要指标。然而,重大建设工程主体结构的实际自振周期与许多因素有关,采用各种复 杂的理论计算求得的基本自振周期数值解与实际情况有时存在较大的出入,如何相对准确而 又方便快速地估算出基本自振周期的真实值是值得探讨的问题。 近年来,国内外(超)高层建筑越来越多,然而破坏性地震常造成(超)高层建筑倒塌 和造成巨大的损失,所以(超)高层的抗震设计受到了特别的关注。对于(超)高层建筑而 言,其基本自振周期通常取值较大。虽然基本自振周期的经验公式很难反映抗震设计工程的 实际情况,但是在地震安全性评价工作中可以用于作为其估算的方法。李海涛等(2003)建 议, (超)高层建筑主体结构的基本自振周期(T1 )可以采用以下各式近似估算: 框架结构: 剪力墙结构和筒中筒结构:
−3 −3
2.0 0.435×10 5.0 0.681×10
−3 −3
2.5 0.461×10 5.5 0.736×10
−3 −3
3.0 0.502×10−3 6.0 0.791×10−3
储液晃动基本自振周期,应按下式计算: Tw = K s D (13) 式中,Tw 为储液晃动基本自振周期(s ) ;Ks 为晃动周期系数,根据 D/Hw 值由表 2 查取,中 间值采用插入法计算。
T1 = (0.12 ~ 0.15)n T1 = (0.04 ~ 0.06)n
(1) (2) (3)
框架-剪力墙结构和框架-筒体结构: T1 = (0.06 ~ 0.12)n
式中,n 为建筑物的层数。 包世华(2001)建议, (超)高层建筑主体结构的基本自振周期可以采用以下各式近似 估算: 框架或框剪结构: (4) T1 = (0.07 ~ 0.09)n 剪力墙结构的住宅和旅馆高度 20—50m、剪力墙间距 3—6m 时,若横墙间距较密,则: 横向: 纵向: 若横墙间距较疏,则: 横向: 纵向:
第7卷
第3期
震灾防御技术
Technology for Earthquake Disaster Prevention
V ol. 7, No. 3 Sep., 2012
2012 年 9 月
洪海春,彭小波,毕雪梅,李细兵,2012.重大建设工程基本自振周期估算方法探讨.震灾防御技术,7 (3) :227 —237.
3期
洪海春等:重大建设工程基本自振周期估算方法探讨
229
钢筋混凝土框架结构:
= T1 0.33 + 0.00069 H 2 / 3 B = T1 0.04 + 0.038H / 3 B
(7) (8) (9)
框架-剪力墙或框架-筒体结构: = T1 0.33 + 0.00069 H 2 / 3 B 剪力墙或筒中筒结构:
1 基金项目 中国地震局地震科技星火计划青年项目(XH12021Y)资助:中国地震局震灾应急救援司项目(CEA_EDEM-201006) [收稿日期]2012-05-15 [作者简介]洪海春,男,生于 1977 年。博士,高级工程师。主要从事地震灾害预防和岩土地震工程方面的研究。E-mail: haichunhong@
式中,H 为建筑物总高度(m) ;B 为建筑物宽度(m) 。 用底部剪力法计算高层建筑结构的水平地震作用时,建议按“假想顶点水平位移” (中 华人民共和国建设部,2002)计算:
T1 = 1.7ψ T uT
(10)
式中,ψT 为考虑非承重填充墙刚度对结构自振周期影响的折减系数;uT 为假想的结构顶点水 平位移,即假想把集中在各楼层处的重力荷载代表值 Gi 作为该楼层的水平荷载,按有关规定 计算出的结构顶点弹性水平位移(单位:m) 。 一般而言,经验公式是通过实测某类重大建设工程的主体结构的自振周期,将测得的数 据加以统计回归得出的。对于不同的重大建筑工程主体结构型式,采用以上公式的计算结果 与实测值相比,其精度并不相同。事实上,即使采用十分精确复杂的理论,用电算法求得的 数值解仍然与实际情况有较大出入。因此,为使得估算值基本接近实测值,应采用综合分析 判断的方法确定基本自振周期值。
引言
对于(超)高层建筑、巨型储油罐、大跨桥梁工程等主体结构自振周期较长的建设工程, 其对地震长周期成分响应比较强烈,在进行工程场地地震安全性评价时,应当特别仔细地考 虑长周期的地震动参数,提供能充分反映长周期地震动对工程结构作用的场地相关反应谱。 同时, (超)高层建筑、长跨桥梁、大型储油罐等对反应谱长周期部分有特殊要求,在地震动 衰减关系确定的过程中,需要专门研究长周期地震动反应谱衰减关系,应分析所选用的长周 期衰减关系是否能针对这些工程的结构特性,进一步论述衰减关系的适用性,另外还要论证 所采用地震动观测资料的长周期可靠性。此外,应根据此类大型结构的特点,合理确定地震 动持时等参数。这样才能确定科学合理的抗震设防要求,按照抗震设防要求进行严格的抗震 设计,才能保证建筑物具备一定的抗震能力,这也是重大建设工程抗震设防的关键环节(卢 寿德,2006) 。 重大建设工程的地震安全性评价工作是在项目可行性研究阶段开展的,所以,工程项目 的建设高度、容量大小、跨径规模等难以和实际情况完全相符,可能存在着稍有偏差的情况, 但是, 在这种情况下基本自振周期的变化通常很小。 总体而言, (超) 高层建筑、 巨型储油罐、 大跨桥梁工程等重大建设工程的基本自振周期,对于长周期地震动对工程结构作用的相关参 数的合理确定起着重要作用。本文探讨了重大建设工程基本自振周期的估算方法,为长周期
T1 = 0.054n T1 = 0.04n T1 = 0.06n T1 = 0.05n
(5a) (5b) (6a) (6b)
采用这些简便的经验公式计算结构基本自振周期时,应注意经验公式的局限性和适用 性,使用时对经验公式要加以选择与判断,因为经验公式一般是通过实测某类结构的自振周 期,将测得的数据加以回归得出的。 (超)高层建筑主体结构的基本自振周期取决于多个方面 的因素,例如:建筑物的高宽比、结构型式、建筑物层数、地基特征等,在不同的荷载作用 下结构的自振周期并不是一个常数,而是随着结构变形的改变而变化。同时,根据我国对高 层建筑大量实测的结果,认为影响高层建筑结构自振周期的主要因素为:对框架体系或框架剪力墙体系,主要是建筑物的高度和宽度;对剪力墙体系,则除了建筑物的高度和宽度之外, 还和剪力墙布置间距的大小有关。鉴于此,本文参考李海涛等(2003)提供的采用建筑物的 层数、高度和宽度等参数,作为确定自振基本周期的估算方法的辅助手段,以求达到相互验 证和相互判断的作用。 常用和简化的与建筑物结构形式、层数及建筑物高度和宽度有关的经验公式有:
