平行线判定拔高专题(M型)

合集下载

平行线的性质与判定大题专练

【拔尖特训】2022-2023学年七年级数学下册尖子生培优必刷题【浙教版】专题1.8平行线的性质与判定大题专练（拔高篇，重难点培优）班级：___________________ 姓名：_________________ 得分：_______________注意事项：本试卷试题解答30道，共分成三个层组：基础过关题（第1-10题）、能力提升题（第11-20题）、培优压轴题（第21-30题），每个题组各10题，可以灵活选用．答卷前，考生务必用0.5毫米黑色签字笔将自己的姓名、班级等信息填写在试卷规定的位置．一、解答题1．（2022春·浙江温州·七年级校联考阶段练习）如图，已知BC平分∠ABD交AD于点E，∠1＝∠3．(1)证明：AB∥CD；(2)若AD⊥BD于点D，∠CDA＝38°，求∠3的度数．【答案】(1)见解析(2)26°【分析】（1）由角平分线的定义得到∠1=∠2，即得∠2=∠3，即可判定AB∥CD；（2）由垂直的定义得出∠ADB=90°，可得∠CDB=128°，由平行线的性质得出∠ABD=52°，根据角平分线的定义即可得解．（1）证明：∵BC平分∠ABD∴∠1=∠2又∠1=∠3∴∠2=∠3∴AB∥CD；（2）解：∵AD⊥BD，∴∠ADB=90°，∵∠CDA=38°，2．（2022春·浙江杭州·七年级统考期末）如图，直线MN分别与直线AB和CD交于点E，F，且满足∠1+∠2=180°．(1)试判断直线AB与CD的位置关系，并说明理由．(2)作∠AEF的平分线EG交CD于点G，过点G作GH⊥EG交MN于点H．若∠DGH=40°，求∠1的度数．【答案】(1)AB∥CD，理由见解析(2)80°【分析】（1）已知∠1+∠2=180°，且∠CFE与∠2构成平角，通过等量代换即可得出互为内错角的∠1与∠CFE 相等，因此可求出AB∥CD；（2）已知GH⊥EG，通过已知条件求出∠EGF的度数，再根据平行线的性质和角平分线的性质求出∠AEF的度数，最后用180°减去∠AEF的度数即可求得∠1的度数．（1）解：AB∥CD，理由如下：∵∠1+∠2=180°又∵∠2+∠CFE=180°∴∠1=∠CFE∴AB∥CD．（2）∵GH⊥EG,∠DGH=40°，∴∠EGF=50°∵AB∥CD∴∠AEG=∠EGF=50°∵EG平分∠AEF∴∠AEF=100°∴∠1=180°−100°=80°故∠1的度数为80°．【点睛】本题考查了平行线的判定和平行线的性质，将已知角的度数通过平行线的性质转换为所求问题的相关角是本题的关键．3．（2022春·浙江绍兴·七年级统考期末）如图，CE平分∠BCF，∠DAC=126°，BC∥EF，∠ACF=∠FEC=18°．(1)求证：AD∥EF；(2)若∠AEC=72°，求∠DAE的度数．【答案】(1)证明见解析(2)54°【分析】（1）先根据平行线的性质可得∠BCE=∠FEC=18°，再根据角平分线的定义可得∠BCF=36°，从而可得∠ACB=54°，然后根据平行线的判定可得AD∥BC，最后根据平行公理推论即可得证；（2）先根据角的和差可得∠AEF=54°，再根据平行线的性质即可得．（1）证明：∵BC∥EF,∠FEC=18°，∴∠BCE=∠FEC=18°，∵CE平分∠BCF，∴∠BCF=2∠BCE=36°，∵∠ACF=18°，∴∠ACB=∠BCF+∠ACF=54°，又∵∠DAC=126°，∴∠DAC+∠ACB=180°，∴AD∥BC，又∵BC∥EF，∴AD∥EF．（2）解：∵∠AEC=72°,∠FEC=18°，∴∠AEF=∠AEC−∠FEC=54°，由（1）已证：AD∥EF，∴∠DAE=∠AEF=54°．【点睛】本题考查了平行线的判定与性质、平行公理推论、角平分线的定义等知识点，熟练掌握平行线的判定与性质是解题关键．4．（2022春·浙江湖州·七年级校联考阶段练习）已知：如图，AD∥BE，∠1＝∠2，∠3＝∠4．(1)求证：AB∥CD；(2)若∠B＝∠3＝2∠2，求∠D的度数．【答案】(1)见解析(2)72°【分析】（1）根据平行线的判定和性质即可解决问题．（2）根据三角形内角和求解即可．（1）∵AD∥BE，∴∠3=∠CAD，∵∠3=∠4，∴∠4=∠CAD，∵∠1=∠2，∴∠1+∠CAE=∠2+∠CAE，即∠BAE=∠CAD，∴∠4=∠BAE，∴AB∥CD；（2）∵∠B=∠3=2∠2，∠1=∠2，∠B+∠3+∠1=180°，∴5∠1=180°，∴∠1=36°，∴∠2=36°，∴∠3=72°，∵∠3=∠4，∠4=∠AFD，∴∠AFD=72°，∴∠D=180°-∠2-∠AFD=72°．【点睛】此题考查了平行线的判定与性质，熟记平行线的判定定理与性质定理是解题的关键．5．（2022春·浙江绍兴·七年级校联考期中）如图，已知BC平分∠ABD交AD于点E，∠1=∠3．(1)说明AB∥CD的理由；(2)若AD⊥BD交于点D，∠CDA=34°，求∠2的度数．【答案】(1)详见解析(2)28°【分析】（1）由角平分线的定义得到∠1=∠2，即得∠2=∠3，即可判定AB∥CD；（2）由垂直的定义得出∠ADB=90°，可得∠CDB=∠CDA+∠ADB=124°，由平行线的性质得出∠ABD=56°，根据角平分线的定义即可得解．（1）∵BC平分∠ABD，∴∠2=∠1，∵∠1=∠3，∴∠2=∠3，∴AB∥CD．（2）∵AD⊥BD，∴∠ADB=90°，∵∠CDA=34°，∴∠CDB=∠ADB+∠CDA=124°，∵AB∥CD．∴∠ABD=180°−∠CDB=56°，∵BC平分∠ABD，∴∠2=28°.【点睛】此题主要考查了平行线的判定与性质、角平分线的性质，熟记“内错角相等，两直线平行”及“两直线平行，同旁内角互补”是解题的关键．6．（2022春·浙江绍兴·七年级校联考期末）如图，点P在∠ABC内，点E，F分别在∠ABC的边BA，BC上，ED平分∠AEP，连结PE，PF．若∠B=∠PFC，∠PED=36°，求∠P的度数．【答案】72°【分析】根据角平分线的定义求出∠AEP=72°，由∠B=∠PFC，得出AB∥PF，然后根据平行线的性质求∠P 的度数即可．【详解】解：∵ED平分∠AEP，∴∠AEP=2∠PED，∵∠PED=36°，∴∠AEP=72°，∵∠B=∠PFC，∴AB∥PF．∴∠P=∠AEP=72°．【点睛】本题考查的是角平分线的定义，平行线的判定与性质，掌握“同位角相等，两直线平行与两直线平行，内错角相等”是解本题的关键．7．（2022春·浙江·七年级统考期末）如图，点O在直线AB上，OC⊥OD，∠D与∠1互余，F是DE上一点，连结OF．(1)ED是否平行于AB，请说明理由；(2)若OD平分∠BOF，∠OFD＝80°，求∠1的度数．【答案】(1)ED//AB，利用见详解；(2)40°【分析】（1）利用已知证得∠D+∠AOD=180°，进而得出答案；（2）由平行线的性质得到∠BOF=110°，根据角平分线的定义得到∠BOD=55°，最后根据平角的定义得出答案．8．（2021春·浙江·七年级期末）如图所示，∠ABD和∠BDC的平分线交于点E，BE交CD于点F，∠1+∠2=90°．(1)求证：AB∥CD；(2)试猜想∠2与∠3的数量关系，并说明理由．9．（2021春·浙江·七年级期中）如图，∠1＝∠BCE，∠2+∠3＝180°．(1)判断AC与EF的位置关系，并说明理由；(2)若CA平分∠BCE，EF⊥AB于F，∠1＝70°，求∠BAD的度数．【答案】(1)AC∥EF，理由见解析；(2)∠BAD＝55°【分析】（1）由∠1＝∠BCE，可得到直线AD与EC平行，可得到∠2与∠4间关系，再由∠2+∠3＝180°判断AC与EF的位置关系；（2）由（1）的结论及垂直可得到∠BAC的度数，再由平行线及角平分线的定义得到∠2的度数，利用角的和差关系可得结论．（1）解：AC∥EF．理由如下：∵∠1＝∠BCE，∴AD∥CE，∴∠2＝∠4，∵∠2+∠3＝180°，∴∠4+∠3＝180°，∴EF∥AC；（2）解：∵AD∥EC，CA平分∠BCE，∴∠ACD＝∠4＝∠2，∵∠1＝70°，∠1＝∠2+∠ACD，∴∠2＝35°，∵EF∥AC，EF⊥AB于F，∴∠BAC＝∠F＝90°，∴∠BAD＝∠BAC﹣∠2＝55°．【点睛】本题考查平行线的性质与判定，角平分线的定义，熟练掌握平行线的性质与判定定理是解题的关键．10．（2021春·浙江金华·七年级浦江县实验中学校联考期末）如图，点E，F分别在直线AB，CD上，点P，Q在直线AB，CD之间，AB//CD．(1)如图，∠P＝∠Q，①∠AEP与∠QFD的关系，并说明理由；②∠BEP和∠DFQ的角平分相交于点M，求∠EMF的度数．(2)若∠P－∠Q＝30°，∠Q＝α则∠BEP和∠DFQ的角平分相交于点M，则∠EMF的度数为．（用含α或具体数字表示）【答案】(1)①∠AEP＝∠QFD，理由见解析；②90°(2)75°【分析】（1）①根据两直线平行内错角相等，计算角的和差即可解答；②利用等角的补交相等，角平分线的定义，进行角的计算即可解答；（2）由∠P－∠Q＝30°利用（1）①得出∠AEP-∠QFD=30°，再由（1）②求∠EMF即可；（1）解：如图，过P作PG∥AB，过Q作QH∥AB，过M作MN∥AB，①∵AB∥PG，∴∠AEP=∠EPG，∵AB∥CD，QH∥AB，∴QH∥CD，∴∠QFD=∠HQF，∵PG∥AB，QH∥AB，∴PG∥QH，∴∠GPQ=∠HQP，∵∠EPQ=∠FQP，∴∠EPG+∠GPQ=∠HQF+∠HQP，∴∠EPG=∠HQF，∴∠AEP=∠QFD；②∵∠AEP=∠QFD，∠AEP+∠BEP=180°，∴∠BEP+∠QFD=180°；11．（2018秋·七年级单元测试）如图，已知∠ABC=180°-∠A，BD⊥CD于D，EF⊥CD于F．（1）求证：AD∥BC；（2）若∠1=36°，求∠2的度数．【答案】（1）见解析；（2）∠2=36°【分析】（1）求出∠ABC+∠A=180°，根据平行线的判定推出即可；（2）根据平行线的性质求出∠3，根据垂直推出BD//EF，根据平行线的性质即可求出∠2．【详解】（1）证明：∵∠ABC=180°−∠A，∴∠ABC+∠A=180°，∴AD//BC；（2）解：∵AD//BC，∠1=36°，∴∠3=∠1=36°，∵BD⊥CD，EF⊥CD，∴∠BDC=∠EFC=90°，∴BD//EF，∴∠2=∠3=36°【点睛】本题考查了平行线的性质和判定的应用，解题的关键是掌握①两直线平行，同位角相等，②两直线平行，内错角相等，③两直线平行，同旁内角互补，反之亦然．12．（2020·浙江金华·七年级期中）如图，已知BC//GE，AF//DE，∠1=45°．（1）求∠AFG的度数；（2）若AQ平分∠FAC，交BC于点Q，且∠Q=20°，求∠ACB的度数．【答案】（1）45°；（2）85°．【分析】（1）先根据BC∥EG得出∠E=∠1=45°，再由AF∥DE可知∠AFG=∠E=45°；（2）作AM∥BC，由平行线的传递性可知AM∥EG，故∠FAM=∠AFG，再根据AM∥BC可知∠QAM=∠Q，故∠FAQ=∠FAM+∠QAM，再根据AQ平分∠FAC可知∠MAC=∠QAC+∠QAM=80°，根据AM∥BC即可得出结论．【详解】解：（1）∵BC∥EG，∴∠E=∠1=45°．∵AF∥DE，∴∠AFG=∠E=45°；（2）作AM∥BC，∵BC∥EG，∴AM∥EG，∴∠FAM=∠AFG=45°．∵AM∥BC，∴∠QAM=∠Q=20°，∴∠FAQ=∠FAM+∠QAM=65°．∵AQ平分∠FAC，∴∠QAC=∠FAQ=65°，∴∠MAC=∠QAC+∠QAM=85°．∵AM∥BC，【点睛】本题考查了平行线的性质，用到的知识点为：两直线平行，同位角相等．熟记平行线的各种性质是解题的关键．13．（2020春·浙江温州·七年级统考开学考试）如图，∠ABD和∠BDC的角平分线交于点E，BE交CD于点F，∠1+∠2=90°．（1）试说明：AB//CD．（2）若∠2=28°，求∠3的度数．【答案】（1）见解析；（2）62°【分析】（1）根据角平分线的定义，结合∠1+∠2=90°，可得∠ABD+∠BDC＝180°，进而即可得到结论；（2）由∠2=28°，得∠1=62°，进而得∠ABF=62°，结合AB//CD，即可得到答案．【详解】（1）∵∠ABD和∠BDC的角平分线交于点E，∴∠ABD＝2∠1，∠BDC＝2∠2，又∵∠1+∠2=90°，∴∠ABD+∠BDC＝2(∠1+∠2)=180°，∴AB//CD；（2）∵∠2=28°，∠1+∠2=90°，∴∠1=62°，又∵BF平分∠ABD，∴∠ABF=∠1=62°，又∵AB//CD，【点睛】本题主要考查角平分线的定义，平行线的判定和性质定理，掌握“同旁内角互补，两直线平行”，“两直线平行，内错角相等”，是解题的关键．14．（2020春·浙江·七年级期中）如图所示，在ΔABC中，CE⊥AB于点E，DF⊥AB于点F，AC//FD，CE是ΔABC的角平分线.求证：∠EDF=∠BDF.【答案】详见解析【分析】先运用垂直于同一条直线的两直线平行，再根据平行线的性质进行做题．【详解】证明：∵CE⊥AB于E，DF⊥AB于F∴DF∥CE∴∠BDF=∠BCE∠FDE=∠DEC又∵AC∥ED，∴∠DEC=∠ACE∵CE是∠ACB的角平分线∴∠ACE=∠ECB∴∠EDF=∠BDF．【点睛】本题主要运用了平行线的性质和角平分线的定义，证明角的关系．15．（2021春·浙江·七年级期末）如图，AC∥EF，∠1+∠3=180°．(1)猜想AF与CD的位置关系，并说明理由．(2)若AC平分∠FAB，AC⊥EB于点C，∠4=78°，求∠BCD的度数．16．（2022春·浙江湖州·七年级校考阶段练习）已知：如图，∠1=∠C，∠E=∠B．(1)判断AB与DE的位置关系，并说明理由；(2)若AB⊥AC于点A，∠1=36°，求∠E的度数．【答案】(1)AB∥DE，见解析(2)∠E=54°【分析】（1）根据平行线的判定得出AB∥DE，根据平行线的性质得出∠E=∠EDC，求出∠B=∠EDC，根据平行线的判定得出即可；（2）求出∠BAE度数，根据平行线的性质即可求出∠E．（1）解：AB∥DE，理由如下：∵∠1=∠C，∴AE∥BC，∴∠E=∠EDC，又∵∠E=∠B，∴∠B=∠EDC，∴AB∥DE；（2）∵AB⊥AC，∠1=36°，∴∠BAE=126°，∵AB∥DE，∴∠E+∠BAE=180°，∴∠E=54°，【点睛】本题考查了平行线的性质和判定定理，垂线的性质，活运用平行线的性质和判定定理进行推理是解此题的关键．17．（2022春·浙江杭州·七年级校考期中）如图，将一张上、下两边平行（即AB∥CD）的纸带沿直线MN折叠，EF为折痕．(1)试说明∠1＝∠2；(2)已知∠2＝54°，求∠BEF的度数．18．（吉林省延边朝鲜族自治州敦化市红石乡中心校2021-2022学年七年级下学期6月月考数学试题）如图，在四边形ABCD中，∠ADC+∠ABC=180°，∠ADF+∠AFD=90°，点E、F分别在DC、AB上，且BE、DF分别平分∠ABC、∠ADC，判断BE、DF是否平行，并说明理由．19．（广东省东莞市石龙第二中学2021-2022学年七年级下学期期中数学试卷）如图，点B，C在线段AD的异侧，点E，F分别是线段AB，CD上的点，已知∠1=∠2，∠3=∠C．(1)求证：AB∥CD；(2)若∠2+∠4=180°，求证：∠BFC+∠C=180°；(3)在（2）的条件下，若∠BFC−30°=2∠1，求∠B的度数．【答案】(1)见解析(2)见解析(3)∠B=50°【分析】（1）已知∠1=∠2，所以∠3=∠2，又因为∠3=∠C，可以得出∠1=∠C即可判定AB∥CD；（2）已知∠2=∠3，∠2+∠4=180°，可以得出BF//EC，即可得出∠BFC+∠C=180°；（3）由（1）（2）可知AB∥CD，BF//EC，可以得出∠1=∠C，∠BFC+∠C=180°；可以得出∠BFC−30°=2∠1=2∠C，可以得出∠C，又因为∠C=∠1=∠B，即可求出∠B的度数．【详解】（1）证明：∵∠1=∠2，∠3=∠C，∠2=∠3，∴∠1=∠C，∴AB//CD；（2）证明：∵∠2+∠4=180°，∠2=∠3，∴∠3+∠4=180°，∴BF//EC，∴∠BFC+∠C=180°；（3）∵∠BFC+∠C=180°，∵∠BFC−30°=2∠1=2∠C，∴∠BFC=2∠C+30°，∴2∠C+30°+∠C=180°，∴∠C=50°，∴∠BFC=130°，∵AB//CD，∴∠B+∠BFC=180°，∴∠B=50°．【点睛】本题考查了对顶角相等，平行线的性质与判定，掌握平行线的性质与判定是解题的关键．20．（辽宁省鞍山市第二中学2021-2022学年七年级下学期3月月考数学试题）如图，已知点E，F为四边形ABDC的边CA的延长线上的两点，连接DE，BF，作∠BDH的平分线DP交AB的延长线于点P．若∠1=∠2，∠3=∠4，∠5=∠C．(1)判断DE与BF是否平行？并说明理由；(2)试说明：∠C＝2∠P．【答案】(1)DE∥BF，理由见解析(2)说明见解析【分析】（1）根据平行线的判定得出BD∥CE，根据平行线的性质得出∠5＝∠FAB，求出∠C＝∠FAB，根据平行线的判定得出AB∥CD，根据平行线的性质得出∠2＝∠BGD即可；（2）求出∠BDP＝∠PDH＝∠P，根据三角形的外角性质得出即可．（1）解：（1）DE∥BF，理由是：∵∠3＝∠4，∴BD∥CE，∴∠5＝∠FAB，∵∠5＝∠C，∴∠C＝∠FAB，∴AB∥CD，∴∠2＝∠BGD，∵∠1＝∠2，∴∠1＝∠BGD，∴DE∥BF；（2）∵AB∥CD，∴∠P＝∠PDH，∵DP平分∠BDH，∴∠BDP＝∠PDH，∴∠BDP＝∠PDH＝∠P，∵∠5＝∠P＋∠BDP，∴∠5＝2∠P，∵∠C＝∠5，∴∠C＝2∠P．【点睛】本题考查了平行线的性质和判定、三角形外角性质，能熟练地运用定理进行推理是解此题的关键，注意：平行线的性质有：①两直线平行，同位角相等，②两直线平行，内错角相等，③两直线平行，同旁内角互补．21．（河南省信阳市浉河区信阳文华寄宿学校2021-2022学年七年级下学期期末数学试题）如图，已知点O在直线AB上，射线OE平分∠AOC，过点O作OD⊥OE，G是射线OB上一点，连接DG，使∠ODG+∠DOG=90°．(1)求证：∠AOE=∠ODG；(2)若∠ODG=∠C，试判断CD与OE的位置关系，并说明理由．【答案】(1)证明见解析(2)CD∥OE，理由见解析【分析】（1）由OD⊥OE得到∠EOC+∠COD=∠AOE+∠DOG=90°，再利用等角的余角相等即可证明∠AOE=∠ODG；（2）证明∠EOC=∠C，利用内错角相等两直线平行，即可证明CD∥OE．【详解】（1）证明：∵OD⊥OE，∴∠EOC+∠COD=∠AOE+∠DOG=90°，∵∠ODG+∠DOG=90°，∴∠AOE=∠ODG；（2）解：CD∥OE．理由如下：由（1）得∠AOE=∠ODG，∵射线OE平分∠AOC，∴∠AOE=∠EOC，∵∠ODG=∠C，∴∠EOC=∠C，∴CD∥OE．【点睛】本题考查了角平分线定义，垂直的定义，平行线的判定，等角的余角相等，正确识图是解题的关键．22．（江苏省扬州市江都区华君外国语学校2021-2022学年七年级下学期第二次教学专项调研数学试题）如图，已知AB∥CD，∠C＝∠B．(1)求证：CF∥BD；(2)如果AB是∠FAD的平分线，且∠ADB＝96°，求∠B的度数．【答案】(1)见解析(2)42°【分析】（1）利用平行线的性质定理和判定定理可得结论；（2）由∠ADB+∠FAD=180°，可得∠FAD，易得∠FAB=42°，由CF∥BD，再根据平行线的性质推出∠B=∠FAB=42°．（1）证明：∵AB∥CD，∴∠C=∠FAB，23．（江苏省徐州市丰县2021-2022学年七年级下学期期中数学试题）如图，已知在△ABC中，∠ACB=90°，CD是AB边上的高，点E在AC上，EF⊥AB，垂足为点F，若∠1+∠2=180°，则DG与BC有怎样的位置关系？请说明理由．【答案】DG⊥BC；理由见解析【分析】根据EF⊥AB，CD⊥AB，得出CD∥EF，根据平行线的性质得出∠2+∠DCE=180°，根据∠1+∠2=180°，得出∠1=∠DCE，即可得出DG∥AC，根据∠ACB=90°，即可得出结果．【详解】解：DG⊥BC；理由如下：∵EF⊥AB，CD⊥AB，∴CD∥EF，∴∠2+∠DCE=180°，∵∠1+∠2=180°，∴∠1=∠DCE，∴DG∥AC，∵∠ACB=90°，∴∠DGB=∠ACB=90°，∴DG⊥BC．【点睛】本题主要考查了平行线的判定和性质，垂线的定义，熟练掌握内错角相等，两直线平行，两直线平行同旁内角互补，是解题的关键．24．（河北省保定市阜平县2021-2022学年七年级下学期期中数学试题）如图，点E在直线DC上，射线EF、EB分别平分∠AED、∠AEC．(1)试判断EF、EB的位置关系，并说明理由；(2)若∠A=∠5，且∠4+∠5=90°，求证：AB∥EF．25．（陕西省渭南市韩城市2021-2022学年七年级下学期期末数学试题）如图，直线BC∥OA，∠C=∠OAB=108°，E，F在线段BC上（不与点B，C重合），且满足∠FOB=∠AOB，OE平分∠COF．(1)求证：OC∥AB；(2)求∠EOB的度数．26．（广东省江门市第二中学2021-2022学年七年级下学期期中考试数学试题）已知，AB∥CD．(1)如图1，求证：∠A﹣∠C＝∠E；(2)如图2，EF平分∠AEC，CF平分∠ECD，∠F=105°，求∠A的度数．【答案】(1)证明见解析(2)150°【分析】（1）过点E作EF∥AB于点F，先根据平行线的性质可得∠A=180°−∠AEF，再根据平行公理推论可得EF∥CD，然后根据平行线的性质可得∠C=180°−∠CEF，最后计算∠A−∠C即可得证；（2）过点F作FG∥CE于点G，先根据平行线的性质可得∠EFG=180°−∠CEF，∠CFG=∠ECF，从而可得∠CEF+∠ECF=75°，再根据角平分线的定义可得∠AEC+∠ECD=150°，然后根据（1）的结论即可得．（1）证明：如图，过点E作EF∥AB于点F，∴∠A=180°−∠AEF，∵AB∥CD，∴EF∥CD，∴∠C=180°−∠CEF，∴∠A−∠C=180°−∠AEF−(180°−∠CEF)=∠AEC．（2）解：如图，过点F作FG∥CE于点G，∴∠EFG=180°−∠CEF，∠CFG=∠ECF，∵∠EFC=105°，∴∠EFG−∠CFG=180°−∠CEF−∠ECF=105°，解得∠CEF+∠ECF=75°，∵EF平分∠AEC，CF平分∠ECD，∴∠AEC=2∠CEF,∠ECD=2∠ECF，∴∠AEC+∠ECD=2(∠CEF+∠ECF)=150°，由（1）已得：∠A−∠ECD=∠AEC，∴∠A=∠AEC+∠ECD=150°．【点睛】本题考查了平行线的性质、平行公理推论、角平分线的定义，熟练掌握平行线的性质是解题关键．27．（浙江省杭州市上城区建兰中学2021-2022学年七年级下学期期中数学试题）如图，已知C为两条相互平行的直线AB，ED之间一点，∠ABC和∠CDE的角平分线相交于F．(1)当∠FDC+∠ABC=180°时：①判断直线AD与BC的关系，并说明理由．②若∠ABC=130°求∠DFB的度数．(2)当∠C=α时，直接写出∠DFB的度数（用含α的代数式表示）．【点睛】本题考查了平行线的判定和性质，平行公理的应用，作出辅助线，熟练掌握平行线的判定方法，是解题的关键．28．（湖北省宜昌市第九中学2021-2022学年七年级下学期期中考试数学试题）如图，∠1=∠2，∠D=∠CMG．(1)求证：AD∥NG；(2)若∠A+∠DHG=180°，试探索：∠ANB，∠NBG，∠1的数量关系；(3)在（2）的条件下，若∠ANB:∠BNG=2:1，∠1=100°，∠NBG=130°，求∠A的度数．【答案】(1)见解析(2)∠NBG+∠1−∠ANB=180°(3)∠A=105°【分析】（1）由∠1=∠2，∠1=∠GFC，得到∠2=∠CFG，于是得到CM∥DE，根据平行线的性质得到∠D=∠ACM，等量代换得到∠CMG=∠ACM，于是得到结论．（2）过B作BP∥AN交NG于P，由于AD∥NG，于是得到∠D=∠DHG，等量代换得到∠A+∠D=180°，得到AN∥DH，根据平行线的判定得到BP∥CM，由平行线的性质得到∠PBG+∠1=180°，等量代换即可得到结论；（3）由∠1+∠PBG=180°，∠1=100°，得到∠PBG=80°，由于∠NBG=130°，于是得到∠ANB=∠NBP=50°，根据已知条件得到∠ANB：∠BNG=2：1，即可得到结论．【详解】（1）证明：∵∠1=∠2，∠1=∠GFC，∴∠2=∠CFG，∴CM∥DE，∴∠D=∠ACM，∵∠D=∠CMG，∴∠CMG=∠ACM，∴AD∥NG；（2）解：∠NBG−∠ANB+∠1=180°；理由如下：过B作BP∥AN交NG于P，∴∠ANB=∠NBP，∵AD∥NG，∴∠D=∠DHG，∵∠A+∠DHG=180°，∴∠A+∠D=180°，∴AN∥DH，又∵CM∥DH，∴BP∥CM，∴∠PBG+∠1=180°，∵∠PBG=∠NBG−∠NBP=∠NBG−∠ANB，∴∠NBG−∠ANB+∠1=180°；（3）解：∵∠1+∠PBG=180°，∠1=100°，∴∠PBG=80°，∵∠NBG=130°，∴∠ANB=∠NBP=50°，∵∠ANB：∠BNG=2：1，∴∠BNP=25°，∴∠ANG=75°，∴∠A=105°．【点睛】本题考查了平行线的判定和性质，对顶角的性质，正确的作出辅助线是解题的关键．29．（陕西省汉中市略阳县2021-2022学年七年级上学期数学期末试题）解答下列问题(1)（问题情景）如图1，若AB∥CD，∠AEP=40°，∠PFD=130°．过点P作PM∥AB，求∠EPF的度数；(2)（问题迁移）如图2，AB∥CD，点P在AB的上方，点E，F分别在AB，CD上，连接PE，PF，过P点作PN∥AB，问∠PEA，∠PFC，∠EPF之间有何数量关系？请说明理由；(3)（联想拓展）如图3所示，在（2）的条件下，已知∠EPF=α，∠PEA的平分线和∠PFC的平分线交于点G，过点G作GH∥AB，用含有α的式子表示∠EGF的度数．30．（浙江省杭州市采荷中学教育集团2021-2022学年七年级下学期期中数学试题）将一副三角板中的两块直角三角尺顶点C按照如图①方式叠放在一起（其中∠ABC=∠CDE=90°，∠ACB=60°，∠A=30°，∠E=∠ECD=45°）设∠ACE=α．(1)若α=30°，说明AB∥CE；(2)将三角形CDE绕点C顺时针转动，若DE∥BC，求α的度数．【答案】(1)见解析(2)15°或165°【分析】（1）根据内错角相等，两直线平行证明即可；（2）分两种情形：如图②中，当DE∥CE时，如图③中，当DE∥BC时，分别求解即可．【详解】（1）解：如图①中，∵∠ACE=α=30°，∠A=30°，∴∠ACE=∠A，∴AB∥CE；（2）解：如图②中，当DE∥CE时，则∠BCE=∠E=45°，∴α=∠ACE=∠ACB−∠BCE=60°−45°=15°；如图③中，当DE∥BC时，则∠BCD=∠D=90°，∴α=∠ACE=360°−∠ACB−∠ECD−∠BCD=360°−60°−45°−90°=165°．综上所述，α的值为15°或165°．【点睛】本题考查旋转的性质，平行线的性质，直角三角形的性质等知识，解题的关键是学会用分类讨论的思想思考问题．。

人教版七年级下数学拔高专题(一) 平行线中的规律探究

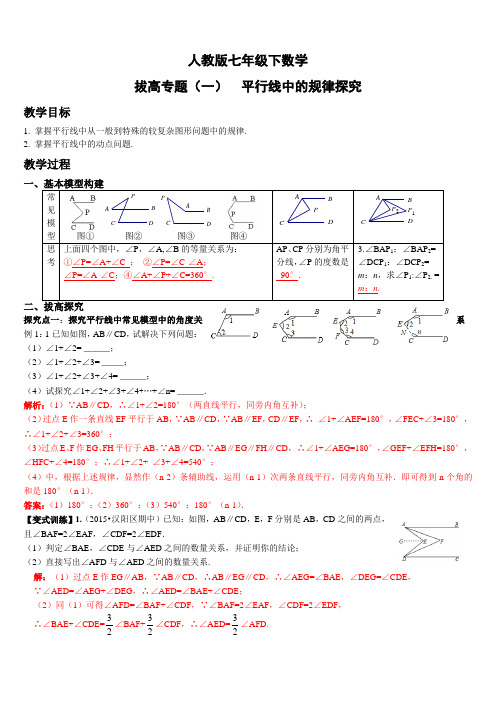
人教版七年级下数学拔高专题（一）平行线中的规律探究教学目标1. 掌握平行线中从一般到特殊的较复杂图形问题中的规律.2. 掌握平行线中的动点问题.教学过程一、基本模型构建常见模型图① 图② 图③ 图④思考上面四个图中，∠P ，∠A,∠B 的等量关系为： ①∠P=∠A+∠C ； ②∠P=∠C-∠A ；∠P=∠A-∠C ；④∠A+∠P+∠C=360°. AP 、CP 分别为角平分线，∠P 的度数是_90°.3.∠BAP 1：∠BAP 2= ∠DCP 1：∠DCP 2= m ：n ，求∠P 1:∠P 2. = m ：n.二、拔高探究探究点一：探究平行线中常见模型中的角度关系例1：1已知如图，AB ∥CD ，试解决下列问题：（1）∠1+∠2= ______；（2）∠1+∠2+∠3= _____；（3）∠1+∠2+∠3+∠4= ______；（4）试探究∠1+∠2+∠3+∠4+…+∠n= ______．解析：（1）∵AB ∥CD ，∴∠1+∠2=180°（两直线平行，同旁内角互补）；（2）过点E 作一条直线EF 平行于AB ，∵AB ∥CD ，∵AB ∥EF ，CD ∥EF ，∴ ∠1+∠AEF=180°，∠FEC+∠3=180°，∴∠1+∠2+∠3=360°；（3）过点E 、F 作EG 、FH 平行于AB ，∵AB ∥CD ，∵AB ∥EG ∥FH ∥CD ， ∴∠1+∠AEG=180°，∠GEF+∠EFH=180°，∠HFC+∠4=180°；∴∠1+∠2+ ∠3+∠4=540°；（4）中，根据上述规律，显然作（n-2）条辅助线，运用（n-1）次两条直线平行，同旁内角互补．即可得到n 个角的和是180°（n-1）．答案：（1）180°；（2）360°；（3）540°；180°（n-1）．【变式训练】1.（2015•汉阳区期中）已知：如图，AB ∥CD ，E ，F 分别是AB ，CD 之间的两点，且∠BAF=2∠EAF ，∠CDF=2∠EDF ．（1）判定∠BAE ，∠CDE 与∠AED 之间的数量关系，并证明你的结论；（2）直接写出∠AFD 与∠AED 之间的数量关系.解：（1）过点E 作EG ∥AB ，∵AB ∥CD ，∴AB ∥EG ∥CD ，∴∠AEG=∠BAE ，∠DEG=∠CDE ，∵∠AED=∠AEG+∠DEG ，∴∠AED=∠BAE+∠CDE ；（2）同（1）可得∠AFD=∠BAF+∠CDF ，∵∠BAF=2∠EAF ，∠CDF=2∠EDF ， ∴∠BAE+∠CDE=23∠BAF+23∠CDF ，∴∠AED=23∠AFD. PDCB A PDC B APDCB AP 2P 1DCB A【教师总结】无论平行线中的何种问题，都可转化到基本模型中去解决，把复杂的问题分解到简单模型中，问题便迎刃而解.探究点二探究动态中平行线中的角度关系类型一点分别在两条平行线之间、一侧判断角度之间的关系例2：如图，已知直线l 1∥l 2，直线l 3和直线l 1、l 2交于点C 和D ，在C 、D 之间有一点P ，如果P 点在C 、D 之间运动时，问∠PAC ，∠APB ，∠PBD 之间的关系是否发生变化．若点P 在C 、D 两点的外侧运动时（P 点与点C 、D 不重合），试探索∠PAC ，∠APB ，∠PBD 之间的关系又是如何？解：如图①，当P 点在C 、D 之间运动时，∠APB=∠PAC+∠PBD ．理由如下：过点P 作PE ∥l 1，∵l 1∥l 2，∴PE ∥l 2∥l 1，∴∠PAC=∠1，∠PBD=∠2，∴∠APB=∠1+∠2=∠PAC+∠PBD ；如图②，当点P 在C 、D 两点的外侧运动，且在l 1上方时，∠PBD=∠PAC+∠APB ．理由如下：∵l 1∥l 2，∴∠PEC=∠PBD ，∵∠PEC=∠PAC+∠APB ，∴∠PBD=∠PAC+∠APB ．如图③，当点P 在C 、D 两点的外侧运动，且在l 2下方时，∠PAC=∠PBD+∠APB ．理由如下：∵l 1∥l 2，∴∠PED=∠PAC ，∵∠PED=∠PBD+∠APB ，∴∠PAC=∠PBD+∠APB ．【教师总结】画出图形，点在两条直线之间、两侧，归根到基本模型一. 类型二点在平行线上移动例3：如图，直线CB ∥OA ，∠C=∠OAB=100°，E 、F 在CB 上，且满足∠FOB=∠AOB ，OE 平分∠COF.（1）求∠EOB 的度数；（2）若平行移动AB ，那么∠OBC ：∠OFC 的值是否随之发生变化？若变化，找出变化规律或求出变化范围；若不变，求出这个比值．（3）在平行移动AB 的过程中，是否存在某种情况，使∠OEC=∠OBA ？若存在，求出其度数；若不存在，说明理由. 解：（1）∵CB ∥OA ，∴∠AOC=180°-∠C=180°-100°=80°，∵OE 平分∠COF ，∴∠COE=∠EOF ，∵∠FOB=∠AOB ，∴∠EOB=∠EOF+∠FOB=1/2∠AOC=1/2×80°=40°；（2）∵CB ∥OA ，∴∠AOB=∠OBC ，∵∠FOB=∠AOB ，∴∠FOB=∠OBC ，∴∠OFC=∠FOB+∠OBC=2∠OBC ，∴∠OBC ：∠OFC=1：2，是定值；（3）存在.由（1）可知∠AOC=180°，∴∠AOC+∠OAB=180°，∴OC ∥AB ．∴∠OBA=∠COB.又BC ∥OA ，∴∠OEC=∠EOA.∴要使∠OEC=∠OBA ，只需∠EOA=∠COB,∴∠COE=∠AOB=1/2(∠AOC-∠EOB)=20°.∴∠OBA=∠COB=∠COE+∠EOB=60°.【教师点拨】遇到动点问题，先从简单开始，平行线中牢记基本图形，问题就会迎刃而解，不管点如何变动，要以不变应万变的方法解决.【变式训练】2.（2015•宜春期末）如图1，CE 平分∠ACD ，AE 平分∠BAC ，∠EAC+∠ACE=90°. （1）请判断AB 与CD 的位置关系并说明理由；（2）如图2，当∠E=90°且AB 与CD 的位置关系保持不变，移动直角顶点E ，使∠MCE= ∠ECD ，当直角顶点E 点移动时，问∠BAE 与∠MCD 否存在确定的数量关系？并说明理由. 解：（1）∵CE 平分∠ACD ，AE 平分∠BAC ，∴∠BAC=2∠EAC ，∠ACD=2∠ACE ，∵∠EAC+∠ACE=90°，∴∠BAC+∠ACD=180°，∴AB ∥CD ；图2图1M EEABCDDC B A（2）∠BAE+1/2∠MCD=90°；过E作EF∥AB，∵AB∥CD，∴EF∥AB∥CD，∴∠BAE=∠AEF，∠FEC=∠DCE，∵∠E=90°，∴∠BAE+∠ECD=90°，∵∠MCE=∠ECD，∴∠BAE+1/2∠MCD=90°.【教师点拨】对于各模型中的逆命题依然成立，作辅助线的方法相同.。

七年级数学-平行线——压轴拔高(带答案

七年级数学-平行线——压轴拔高(带答案平行线压轴拔高一、解答题1.已知：如图1，直线AB∥CD，点E是AB、CD之间的一点，连接BE、DE得到∠BED。

求证：∠BED＝∠B+∠D。

证明：通过连接EF∥AB，得到∠BEF＝∠B。

因为AB∥CD，所以EF∥CD，因此∠___∠D。

由于∠BEF+∠___∠B+∠D，所以∠BED＝∠B+∠D。

根据上述结论，可得出以下问题的解答：已知：直线AB∥CD，直线MN分别与AB、CD交于点E、F。

1）如图2，∠___和∠EFD的平分线交于点G。

猜想∠G的度数，并证明你的猜想；猜想∠G的度数为180°，因为∠___和∠EFD的平分线在点G相交，所以∠___∠DEG，而∠___∠B+∠D，所以∠BEG＋∠DEG＝∠___∠B+∠D，即2∠G＝∠B+∠D＋180°，所以∠G＝180°。

2）如图3，EG1和EG2为∠BEF内满足∠1＝∠2的两条线，分别与∠EFD的平分线交于点G1和G2.求证：∠FG1E+∠G2＝180°。

由于∠___∠DEG1，∠___∠DEG2，又因为∠1＝∠2，所以∠___∠B+∠D。

又因为∠G1EF＝∠G2EF，所以∠G1EF＋∠G2EF＝2∠FG1E。

因此，2∠FG1E＋∠B+∠D＝180°，即∠FG1E+∠G2＝180°。

2.若∠C＝α，∠EAC+∠___β。

1）如图1，若AE∥BF，则α与β有何关系？由于AE∥BF，所以∠___∠___，因此∠EAC+∠FBC＝2∠EAC＝2∠___，即β＝2α。

2）如图2，AM是∠EAC的平分线，BN是∠___的平分线，若AM∥BN，判断α与β的关系，并说明理由；由于AM∥BN，所以∠___∠___，因此∠EAC+∠FBC＝2∠EAC＝2∠___，即β＝2α。

3）若∠EAC的平分线与∠FBC平分线交于点P，试探究∠APB与α、β的关系（直接写出结果，用含α、β的代数式表示∠APB）；APB＝180°－∠EAB－∠___°－(α/2)－(β/2)＝180°－(α＋β)/2.4）如图3，若α≥β，∠EAC与∠___的平分线相交于P1，∠EAP1与∠FBP1的平分线交于P2…依此类推，则∠P4＝(α+β)/16；∠Pn＝[(n-2)(α+β)+360]/2^n。

中考数学专题复习平行线问题锯齿形(M型)

中考数学专题复习平行线问题锯齿形（M 型）学校:___________姓名：___________班级：___________考号：___________ 评卷人得分一、单选题1．如图，已知直线AB 、CD 被直线AC 所截，//AB CD ，E 是平面内任意一点（点E 不在直线AB 、CD 、AC 上），设BAE α∠=，DCE β∠=．下列各式：①αβ+，①αβ-，①a β-，①360αβ︒--，AEC ∠的度数可能是（）A ．①①B ．①①C ．①①①D ．①①①①2．如图，已知点P 是矩形ABCD 内一点（不含边界），设12,PAD θPBA θ∠=∠=，34,PCB θPDC θ∠=∠=，若80,50APB CPD ∠=∠=，则（）A ．1423()()30θθθθ+-+=B ．2413()()40θθθθ+-+=C ．1234()()70θθθθ+-+=D ．1234()()180θθθθ+++=评卷人得分二、填空题 3．如图，AB ①EF ，设①C ＝90°，那么x ，y ，z 的关系式为______．4．如图，在ABC中，24AC=，25AB=，7BC=．在AB上取一点E，AC上取一点F，连接EF，若125EFC∠=︒，过点B作//BD EF，且点D在AB的右侧，则CBD∠的度数为__________．评卷人得分三、解答题5．（1）已知：如图（a），直线DE AB∥．求证：ABC CDE BCD∠+∠=∠；（2）如图（b），如果点C在AB与ED之外，其他条件不变，那么会有什么结果？你还能就本题作出什么新的猜想？6．如图，//AB CD ，点E 在直线AB ，CD 内部，且AE CE ⊥．（1）如图1，连接AC ，若AE 平分BAC ∠，求证：CE 平分ACD∠；（2）如图2，点M 在线段AE 上，①若MCE ECD ∠=∠，当直角顶点E 移动时，BAE ∠与MCD ∠是否存在确定的数量关系?并说明理由；①若1MCE ECD n∠=∠（n 为正整数），当直角顶点E 移动时，BAE ∠与MCD ∠是否存在确定的数量关系并说明理由．7．已知AB//CD．（1）如图1，E为AB，CD之间一点，连接BE，DE，得到①BED．求证：①BED＝①B+①D；（2）如图，连接AD，BC，BF平分①ABC，DF平分①ADC，且BF，DF所在的直线交于点F．①如图2，当点B在点A的左侧时，若①ABC＝50°，①ADC＝60°，求①BFD的度数．①如图3，当点B在点A的右侧时，设①ABC＝α，①ADC＝β，请你求出①BFD的度数．（用含有α，β的式子表示）8．已知直线l1//l2，A是l1上的一点，B是l2上的一点，直线l3和直线l1，l2交于C和D，直线CD上有一点P．（1）如果P点在C，D之间运动时，问①P AC，①APB，①PBD有怎样的数量关系？请说明理由．（2）若点P在C，D两点的外侧运动时（P点与C，D不重合），试探索①P AC，①APB，①PBD之间的关系又是如何？（请直接写出答案，不需要证明）9．如图，//AB CD ，点O 在直线CD 上，点P 在直线AB 和CD 之间，ABP PDQ α∠=∠=，PD 平分BPQ ∠．（1）求BPD∠的度数（用含α的式子表示）；（2）过点D 作//DE PQ 交PB 的延长线于点E ，作DEP ∠的平分线EF 交PD 于点F ，请在备用图中补全图形，猜想EF 与PD 的位置关系，并证明；（3）将（2）中的“作DEP ∠的平分线EF 交PD 于点F ”改为“作射线EF 将DEP ∠分为1:3两个部分，交PD 于点F ”，其余条件不变，连接EQ ，若EQ 恰好平分PQD ∠，请直接写出FEQ ∠=__________（用含α的式子表示）．10．如图1，//AB CD ，130PAB ∠=︒，120PCD ∠=︒，求APC ∠的度数．小明的思路是：如图2，过P 作//PE AB ，通过平行线性质可求APC ∠的度数．（1）请你按小明的思路，写出APC ∠度数的求解过程；（2）如图3，//AB CD ，点P 在直线BD 上运动，记PAB α∠=∠，PCD β∠=∠． ①当点P 在线段BD 上运动时，则APC ∠与α∠、β∠之间有何数量关系？请说明理由；①若点P 不在线段BD 上运动时，请直接写出APC ∠与α∠、β∠之间的数量关系．11．已知，AB ①CD ．点M 在AB 上，点N 在CD 上．（1）如图1中，①BME 、①E 、①END 的数量关系为：；（不需要证明）如图2中，①BMF 、①F 、①FND 的数量关系为：；（不需要证明）（2）如图3中，NE 平分①FND ，MB 平分①FME ，且2①E ＋①F ＝180°，求①FME 的度数；（3）如图4中，①BME ＝60°，EF 平分①MEN ，NP 平分①END ，且EQ ①NP ，则①FEQ 的大小是否发生变化，若变化，请说明理由，若不变化，求出①FEQ 的度数．12．综合与探究【问题情境】王老师组织同学们开展了探究三角之间数量关系的数学活动（1）如图1，//EF MN ，点A 、B 分别为直线EF 、MN 上的一点，点P 为平行线间一点，请直接写出PAF ∠、PBN ∠和APB ∠之间的数量关系；【问题迁移】（2）如图2，射线OM 与射线ON 交于点O ，直线//m n ，直线m 分别交OM 、ON 于点A 、D ，直线n 分别交OM 、ON 于点B 、C ，点P 在射线OM 上运动，①当点P 在A 、B （不与A 、B 重合）两点之间运动时，设ADP α∠=∠，BCP β∠=∠．则CPD ∠，α∠，β∠之间有何数量关系？请说明理由．①若点P 不在线段AB 上运动时（点P 与点A 、B 、O 三点都不重合），请你画出满足条件的所有图形并直接写出CPD ∠，α∠，β∠之间的数量关系．13．请在横线上填上合适的内容．（1）如图（1）已知AB //CD ，则B D BED ∠+∠=∠．解：过点E 作直线EF //AB ． ①FEB ∠=（）．（） ①AB //CD ，EF //AB ，①（）//（）．（如果两条直线和第三条直线平行，那么这两直线平行） ①FED ∠=（）．（）． ①B D BEF FED ∠+∠=∠+∠． ①B D BED ∠+∠=∠．（2）如图①，如果AB //CD //AB CD ，则B BED D ∠+∠+∠=（）14．直线AB ①CD ，M 为AB 上一定点，N为CD 上一定点，E 为直线AB 和直线CD 之间的一点．（1）当点E 在MN 上时，如图1所示，请直接写出①MEN ，①CNE ，①AME 之间的数量关系；（2）当点E 在MN 左侧时，如图2所示，试猜想①MEN ，①CNE ，①AME 之间的数量关系，并证明；（3）当点E 在MN 右侧时，如图3所示，试猜想①MEN ，①CNE ，①AME 之间的数量关系，并证明．15．如图1，点A 、B 分别在直线GH 、MN 上，GAC NBD ∠=∠，C D ∠=∠.（1）求证：//GH MN ；（提示：可延长AC 交MN 于点P 进行证明）（2）如图2，AE 平分GAC ∠，DE 平分BDC ∠，若AED GAC ∠=∠，求GAC ∠与ACD ∠之间的数量关系；（3）在（2）的条件下，如图3，BF 平分DBM ∠，点K 在射线BF 上，13KAG GAC ∠=∠，若AKB ACD ∠=∠，直接写出GAC ∠的度数．16．已知直线AM、CN和点B在同一平面内，且AM①CN，AB①BC．（1）如图1，求①A和①C之间的数量关系；（2）如图2，若BD①AM，垂足为D，求证：①ABD＝①C；（3）如图3，已知点D、E、F都在直线AM上，且①ABD＝①NCB，BF平分①DBC，BE平分①ABD．若①FCB+①NCF＝180°，①BFC＝3①DBE，请直接写出①EBC的度数．17．已知AB①CD，线段EF分别与AB，CD相交于点E，F．（1）请在横线上填上合适的内容，完成下面的解答：如图1，当点P在线段EF上时，已知①A＝35°，①C＝62°，求①APC的度数；解：过点P作直线PH①AB，所以①A＝①APH，依据是；因为AB①CD，PH①AB，所以PH①CD，依据是；所以①APC＝（）+（）＝①A+①C＝97°．（2）当点P，Q在线段EF上移动时（不包括E，F两点）：①如图2，①APQ+①PQC＝①A+①C+180°成立吗？请说明理由；①如图3，①APM＝2①MPQ，①CQM＝2①MQP，①M+①MPQ+①PQM＝180°，请直接写出①M，①A与①C的数量关系．18．已知AB∥CD，①ABE的角分线与①CDE的角分线相交于点F．（1）如图1，若BM、DM分别是①ABF和①CDF的角平分线，且①BED＝100°，求①M的度数；（2）如图2，若①ABM＝13①ABF，①CDM＝13①CDF，①BED＝α°，求①M的度数；（3）若①ABM＝1n①ABF，①CDM＝1n①CDF，请直接写出①M与①BED之间的数量关系．19．如图1，直线AB //CD ，点P 在两平行线之间，点E 在AB 上，点F 在CD 上，连接PE ，PF ．（1）若①PEB =60°，①PFD =50°，请求出①EPF ．（请写出必要的步骤，并说明理由）（2）如图2，若点P ，Q 在直线AB 与CD 之间时，①1=30°，①2=40°，①3=70°，请求出①4= ．（不需说明理由，请直接写出答案）（3）如图3，在图1的基础上，作P 1E 平分①PEB ，P 1F 平分①PFD ，若设①PEB ＝x °，①PFD ＝y °，则①P 1= （用含x ，y 的式子表示）．若P 2E 平分①P 1EB ，P 2F 平分①P 1FD ，可得①P 2；P 3E 平分①P 2EB ，P 3F 平分①P 2FD ，可得①P 3…，依次平分下去，则①Pn ＝．（用含x ，y 的式子表示）20．如图1，点A 在直线MN 上，点B 在直线ST 上，点C 在MN ，ST 之间，且满足MAC ACB SBC ∠+∠+∠360=︒．（1）证明：//MN ST ；（2）如图2，若60ACB ∠=︒，//AD CB ，点E 在线段BC 上，连接AE ，且2DAE CBT ∠=∠，试判断CAE ∠与CAN ∠的数量关系，并说明理由；（3）如图3，若180ACB n︒∠=（n 为大于等于2的整数），点E 在线段BC 上，连接AE ，若MAE n CBT ∠=∠，则:CAE CAN ∠∠=______．21．如图，//MN GH ，点A 、B 分别在直线MN 、GH 上，点O 在直线MN 、GH 之间，若116NAO ∠=︒，144OBH ∠=︒．（1）AOB ∠= ︒；（2）如图2，点C 、D 是NAO ∠、GBO ∠角平分线上的两点，且35CDB ∠=︒，求ACD ∠ 的度数；（3）如图3，点F 是平面上的一点，连结F A 、FB ，E 是射线FA 上的一点，若MAE ∠= n OAE ∠，HBF n OBF ∠=∠，且60AFB ∠=︒，求n 的值．22．在图中，若//AB CD ，又得到什么结论？23．如图，若//AB CD ，则B D E ∠+∠=∠，你能说明为什么吗？24．在图中，//AB CD，E G+∠∠与B F D++∠∠∠又有何关系？25．如图所示，已知//AB CD，BE平分ABC∠，DE平分ADC∠，求证：1()2E A C∠=∠+∠26．（1）如图1，已知//AB CD，ABF DCE∠=∠，求证：BFE FEC∠=∠（2）如图2，已知//AB CD，14EAF EAB∠=∠，14ECF ECD∠=∠，求证：34AFC AEC∠=∠27．如图1，AB//CD，点E、F分别在AB、CD上，点O在直线AB、CD之间，且100EOF∠=︒．（1）求BEO OFD∠+∠的值；（2）如图2，直线MN分别交BEO∠、OFC∠的角平分线于点M、N，直接写出EMN FNM∠-∠的值；（3）如图3，EG 在AEO ∠内，AEG m OEG ∠=∠；FH 在DFO ∠内，DFH m OFH ∠=∠，直线MN 分别交EG 、FH 分别于点M 、N ，且50FMN ENM ∠-∠=︒，直接写出m 的值．28．如图，AB //CD ，点E为两平行线间的一点．请证明两个结论．（1）12BED ∠=∠+∠；（2）360EBM EDN BED ∠+∠+∠=．29．如图1，由线段,,,AB AM CM CD 组成的图形像英文字母M ，称为“M 形BAMCD ”．（1）如图1，M 形BAMCD 中，若//,50AB CD A C ∠+∠=︒，则M ∠=______；（2）如图2，连接M 形BAMCD 中,B D 两点，若150,B D AMC α∠+∠=︒∠=，试探求A ∠与C ∠的数量关系，并说明理由；（3）如图3，在（2）的条件下，且AC 的延长线与BD 的延长线有交点，当点M 在线段BD 的延长线上从左向右移动的过程中，直接写出A ∠与C ∠所有可能的数量关系．30．已知//EM BN ．（1）如图1，求E A B ∠+∠+∠的大小，并说明理由．（2）如图2，AEM ∠与ABN ∠的角平分线相交于点F ． ①若120A ∠=︒，140AEM ∠=︒，则EFD ∠=________． ①试探究EFD ∠与A ∠的数量关系，并说明你的理由．（3）如图3，AEM ∠与ABN ∠的角平分线相交于点F ，过点F 作FG BD ⊥交BN 于点G ，若43A EFG ∠=∠，求EFB ∠的度数．参考答案：1．D【解析】【分析】由题意根据点E有6种可能位置，分情况进行讨论，依据平行线的性质以及三角形外角性质进行计算求解即可．【详解】解：（1）如图1，由AB①CD，可得①AOC=①DCE1=β，①①AOC=①BAE1+①AE1C，①①AE1C=β-α．（2）如图2，过E2作AB平行线，则由AB①CD，可得①1=①BAE2=α，①2=①DCE2=β，①①AE2C=α+β．（3）如图3，由AB①CD，可得①BOE3=①DCE3=β，①①BAE3=①BOE3+①AE3C，①①AE3C=α-β．（4）如图4，由AB①CD，可得①BAE4+①AE4C+①DCE4=360°，①①AE 4C =360°-α-β．（5）（6）当点E 在CD 的下方时，同理可得①AEC =α-β或β-α．综上所述，①AEC 的度数可能为β-α，α+β，α-β，360°-α-β，即①①①①．故选：D ．【点睛】本题主要考查平行线的性质的运用，解题时注意两直线平行，同位角相等；两直线平行，内错角相等以及分类讨论． 2．A 【解析】【分析】依据矩形的性质以及三角形内角和定理，可得2110θθ-=︒，4340θθ-=︒，两式相减即可得到1423()()30θθθθ+-+=︒．【详解】解：矩形ABCD ，90BAD BCD ∴∠=∠=︒，190BAP θ∴∠=︒-，390DCP θ∠=︒-，ABP ∴∆中，129080180θθ︒-++︒=︒，即2110θθ-=︒，①DCP ∆中，349050180θθ︒-++︒=︒，即4340θθ-=︒，①由①-①，可得4321()()30θθθθ---=︒，即1423()()30θθθθ+-+=︒，故选：A ．【点睛】本题主要考查了矩形的性质以及三角形内角和定理的运用，解决问题的关键是掌握：矩形的四个角都是直角．3．y=90°-x+z．【解析】【分析】作CG，AB，DH，EF，由AB①EF，可得AB，CG，HD，EF，根据平行线性质可得①x=①1，①CDH=①2，①HDE=①z，由①C＝90°，可得①1+①2=90°，由①y=①z+①2，可证①y=①z+90°-①x即可．【详解】解：作CG，AB，DH，EF，①AB①EF，①AB，CG，HD，EF，①①x=①1，①CDH=①2，①HDE=①z①①BCD＝90°①①1+①2=90°，①y=①CDH+①HDE=①z+①2，①①2=90°-①1=90°-①x，①①y=①z+90°-①x．即y=90°-x+z．【点睛】本题考查平行线的性质，掌握平行线的性质，利用辅助线画出准确图形是解题关键． 4．35︒【解析】【分析】在ABC 中，由三边的长度可得出222AC BC AB +=，进而可得出ABC 为直角三角形且90ACB ∠=︒，由于平行线之间有拐点，所以过点C 作//CM EF 交AB 于点M ，则//BD CM ，利用平行的性质可得出MCF ∠的度数，结合BCM ACB MCF ∠=∠-∠可求出BCM ∠的度数，再利用“两直线平行，内错角相等”即可求出CBD ∠的度数．【详解】解：在ABC 中，24AC =，25AB =，7BC =，①22224762525+==，即222AC BC AB +=，①ABC 为直角三角形且90ACB ∠=︒．过点C 作//CM EF 交AB 于点M ，则//BD CM ，如下图所示，①//CM EF ，125EFC ∠=︒，①18055MCF EFC ∠=︒-∠=︒，①35BCM ACB MCF ∠=∠-∠=︒．又①//BD CM ，①35CBD BCM ∠=∠=︒．故答案为：35︒．【点睛】本题考查了勾股定理的逆定理以及平行线的性质，利用勾股定理的逆定理，找出90ACB ∠=︒并知道过拐点作已知直线的平行线是解题的关键．5．（1）见解析；（2）当点C 在AB 与ED 之外时，ABC CDE BCD ∠-∠=∠，见解析【解析】【分析】（1）由题意首先过点C作CF①AB，由直线AB①ED，可得AB①CF①DE，然后由两直线平行，内错角相等，即可证得①ABC+①CDE=①BCD；（2）根据题意首先由两直线平行，内错角相等，可得①ABC=①BFD，然后根据三角形外角的性质即可证得①ABC-①CDE=①BCD．【详解】解：（1）证明：过点C作CF①AB，①AB①ED，①AB①ED①CF，①①BCF=①ABC，①DCF=①EDC，①①ABC+①CDE=①BCD；（2）结论：①ABC-①CDE=①BCD，证明：如图：①AB①ED，①①ABC=①BFD，在①DFC中，①BFD=①BCD+①CDE，①①ABC=①BCD+①CDE，①①ABC-①CDE=①BCD．若点C在直线AB与DE之间，猜想360ABC BCD CDE︒∠+∠+∠=,①AB ①ED ①CF ，①180,180,ABC BCF CDE DCF ︒︒∠+∠=∠+∠=①360ABC BCD CDE ABC BCF DCF CDE ︒∠+∠+∠=∠+∠+∠+∠=.【点睛】本题考查的是平行线的性质及三角形外角的性质，熟练掌握平行线的性质是解答本题的关键，注意掌握辅助线的作法．6．（1）见解析；（2）①①BAE +12①MCD =90°，理由见解析；①①BAE +1n n +①MCD =90°，理由见解析.【解析】【分析】（1）根据平行的性质可得①BAC +①DCA =180°，再根据AE CE ⊥可得①EAC +①ECA =90°，根据AE 平分①BAC 可得①BAE =①EAC ,等量代换可得①ECD +①EAC =90°，继而求得①DCE =①ECA ；（2）①过E 作EF ①AB ，先利用平行线的传递性得出EF ①AB ①CD ，再利用平行线的性质及已知条件可推得答案；①过E 作EF ①AB ，先利用平行线的传递性得出EF ①AB ①CD ，再利用平行线的性质及已知条件可推得答案.【详解】（1）解：因为//AB CD ，所以①BAC +①DCA =180°，因为AE CE ⊥，所以①EAC +①ECA =90°，因为AE 平分①BAC ，所以①BAE =①EAC ，所以①BAE +①DCE =90°，所以①EAC +①DCE =90°，所以①DCE =①ECA ，所以CE 平分①ACD ；（2）①①BAE与①MCD 存在确定的数量关系：①BAE +12①MCD =90°，理由如下：过E 作EF ①AB ，①AB ①CD ，①EF ①AB ①CD ，①①BAE =①AEF ，①FEC =①DCE ，①①E =90°，①①BAE +①ECD =90°，①①MCE =①ECD ，①①BAE +12①MCD =90°；①①BAE 与①MCD 存在确定的数量关系：①BAE +1n n ①MCD =90°，理由如下：过E 作EF ①AB ，①AB ①CD ，①EF ①AB ①CD ，①①BAE =①AEF ，①FEC =①DCE ，①①E =90°，①①BAE +①ECD =90°，①①MCE =1n①ECD ， ①①BAE +1n n +①MCD =90°. 【点睛】本题主要考查平行线的性质和角平分线的定义，解决本题的关键是要添加辅助线利用平行性质.7．（1）见解析；（2）55°；（3）1118022αβ︒-+ 【解析】【分析】（1）根据平行线的判定定理与性质定理解答即可；（2）①如图2，过点F 作//FE AB ，当点B 在点A 的左侧时，根据50ABC ∠=︒，60ADC ∠=︒，根据平行线的性质及角平分线的定义即可求BFD ∠的度数；①如图3，过点F 作//EF AB ，当点B 在点A 的右侧时，ABC α∠=，ADC β∠=，根据平行线的性质及角平分线的定义即可求出BFD ∠的度数．【详解】解：（1）如图1，过点E 作//EF AB ，则有BEF B ∠=∠，//AB CD ，//EF CD ∴，FED D ∴∠=∠，BED BEF FED B D ∴∠=∠+∠=∠+∠；（2）①如图2，过点F 作//FE AB ，有BFE FBA∠=∠．//AB CD，//EF CD∴．EFD FDC∴∠=∠．BFE EFD FBA FDC∴∠+∠=∠+∠．即BFD FBA FDC∠=∠+∠，BF平分ABC∠，DF平分ADC∠，1252FBA ABC∴∠=∠=︒，1302FDC ADC∠=∠=︒，55BFD FBA FDC∴∠=∠+∠=︒．答：BFD∠的度数为55︒；①如图3，过点F作//FE AB，有180BFE FBA∠+∠=︒．180BFE FBA∴∠=︒-∠，//AB CD，//EF CD∴．EFD FDC∴∠=∠．180BFE EFD FBA FDC∴∠+∠=︒-∠+∠．即180BFD FBA FDC∠=︒-∠+∠，BF平分ABC∠，DF平分ADC∠，1122FBA ABCα∴∠=∠=，1122FDC ADCβ∠=∠=，1118018022BFD FBA FDC αβ∴∠=︒-∠+∠=︒-+．答：BFD ∠的度数为1118022αβ︒-+．【点睛】本题考查了平行线的判定与性质，解决本题的关键是熟练掌握平行线的判定与性质． 8．（1）PAC PBD APB ∠+∠=∠；（2）当点P 在直线1l 上方时，∠-∠=∠PBD PAC APB ；当点P 在直线2l 下方时，∠-∠=∠PAC PBD APB ．【解析】【分析】（1）过点P 作1//PE l ，由“平行于同一条直线的两直线平行”可得出12////PE l l ，再由“两直线平行，内错角相等”得出PAC APE ∠=∠、PBD BPE ∠=∠，再根据角与角的关系即可得出结论；（2）按点P 的两种情况分类讨论：①当点P 在直线1l 上方时；②当点P 在直线2l 下方时，同理（1）可得PAC APE ∠=∠、PBD BPE ∠=∠，再根据角与角的关系即可得出结论．【详解】解：（1）PAC PBD APB ∠+∠=∠．过点P 作1//PE l ，如图1所示．1//PE l ，12l l //，12////PE l l ∴，PAC APE ∴∠=∠，PBD BPE ∠=∠，APB APE BPE ∠=∠+∠，PAC PBD APB ∴∠+∠=∠．（2）结论：当点P在直线1l上方时，∠-∠=∠PBD PAC APB；当点P在直线2l下方时，∠-∠=∠PAC PBD APB．①当点P在直线1l上方时，如图2所示．过点P作1//PE l．1//PE l，12l l//，12////PE l l∴，PAC APE∴∠=∠，PBD BPE∠=∠，APB BPE APE∠=∠-∠，PBD PAC APB∴∠-∠=∠．②当点P在直线2l下方时，如图3所示．过点P作1//PE l．1//PE l，12l l//，12////PE l l∴，PAC APE∴∠=∠，PBD BPE∠=∠，APB APE BPE∠=∠-∠，PAC PBD APB∴∠-∠=∠．【点睛】本题考查了平行线的性质以及角的计算，解题的关键是根据“两直线平行，内错角相等”找到相等的角．本题属于基础题，难度不大，解决该题型题目时，根据平行线的性质得出相等（或互补）的角是关键．9．（1）2BPD α∠=；（2）画图见解析，EF PD ⊥，证明见解析；（3）452α︒-或3452α︒- 【解析】【分析】（1）根据平行线的传递性推出////PG AB CD ，再利用平行线的性质进行求解；（2）猜测EF PD ⊥，根据PD 平分,2BPQ BPD α∠∠=，推导出2BPD DPQ α∠=∠=，再根据//DE PQ 、EF 平分DEP ∠，通过等量代换求解；（3）分两种情况进行讨论，即当:1:3PEF DEF ∠∠=与:1:3DEF PEF ∠∠=，充分利用平行线的性质、角平分线的性质、等量代换的思想进行求解．【详解】（1）过点P 作//PG AB ，//,//AB CD PG AB ，////PG AB CD ∴，,BPG ABP DPG PDQ αα∴∠=∠=∠=∠=，2BPD BPG DPG α∴∠=∠+∠=．（2）根据题意，补全图形如下：猜测EF PD ⊥，由（1）可知：2BPD α∠=，PD平分,2BPQ BPDα∠∠=，2BPD DPQα∴∠=∠=，//DE PQ，2EDP DPQα∴∠=∠=，1801804DEP BPD EDPα∴∠=︒-∠-∠=︒-，又EF平分DEP∠，19022PEF DEPα∠=∠=︒-，18090EFD PEF BPD∴∠=︒-∠-∠=︒，EF PD∴⊥．（3）①如图1，:1:3PEF DEF∠∠=，由（2）可知：2,1804EPD DPQ EDP DEPαα∠=∠=∠=∠=︒-，:1:3PEF DEF∠∠=，1454PEF DEPα∴∠=∠=︒-，313534DEF DEPα∠=∠=︒-，//DE PQ，DEQ PQE∴∠=∠，180EDQ PQD∠+∠=︒，2,EDP PDQαα∠=∠=，3EDQ EDP PDQα∴∠=∠+∠=，1801803PQD EDQα∠=︒-∠=︒-，又EQ平分PQD∠，139022PQE DQE DEQ PQD α∴∠=∠=∠=∠=︒-， 331353(90)4522FEQ DEF DEQ ααα∴∠=∠-∠=︒--︒-=︒-； ①如图2，1804DEP α∠=︒-，1803PQD α∠=︒-（同①）；若:1:3DEF PEF ∠∠=，则有11(1804)4544DEF DEP αα∠=∠=⨯︒-=︒-，又113(1803)90222PQE DQE PQD αα∠=∠=∠=⨯︒-=︒-， //DE PQ ，3902DEQ PQE α∴∠=∠=︒-， 1452FEQ DEQ DEF α∴∠=∠-∠=︒-，综上所述：3452FEQ α∠=︒-或452α︒-，故答案是：452α︒-或3452α︒-．【点睛】本题考查了平行线的性质、角平分线、三角形内角和定理、垂直等相关知识点，解题的关键是掌握相关知识点，作出适当的辅助线，通过分类讨论及等量代换进行求解． 10．（1）见解析；（2）①APC αβ∠=∠+∠，见解析；①APC αβ∠=∠-∠【解析】【分析】（1）过P 作//PE AB ，利用平行线的性质即可得出答案；（2）①过P 作//PE AB ，再利用平行线的性质即可得出答案；①分P 在BD 延长线上和P 在DB 延长线上两种情况进行讨论，结合平行线的性质即可得出答案【详解】解：（1）如图2，过P 作//PE AB//ABCD ，////PE AB CD ∴，180PAB APE ∴∠+∠=︒，180PCD CPE ∠+∠=︒，130PAB ∠=︒，120PCD ∠=︒，50APE ∴∠=︒，60CPE ∠=︒，110APC APE CPE ∴∠=∠+∠=︒．（2）①、APC αβ∠=∠+∠，理由：如图3，过P 作//PE AB ，//AB CD ， ////AB PE CD ∴，APE α∴∠=∠，CPE β∠=∠，APC APE CPE αβ∴∠=∠+∠=∠+∠；①、APC αβ∠=∠-∠．如备用图1，当P 在BD 延长线上时，APC αβ∠=∠-∠；理由：如备用图1，过P 作PG//AB ，//AB CD ，////AB PG CD ∴，APG α∴∠=∠，CPG β∠=∠，APC APG CPG αβ∴∠=∠-∠=∠-∠；如备用图2所示，当P 在DB 延长线上时，APC βα∠=∠-∠；理由：如备用图2，过P 作PG//AB ，//AB CD ，////AB PG CD ∴，APG α∴∠=∠，CPG β∠=∠，APC CPG APG βα∴∠=∠-∠=∠-∠；综上所述，APC αβ∠=∠-∠．【点睛】本题考查的是平行线的性质，解题的关键是过P 作//PE AB ．11．（1）①BME ＝①MEN ﹣①END ；①BMF ＝①MFN ＋①FND ；（2）120°；（3）不变，30°【解析】【分析】（1）过E 作EH ①AB ，易得EH ①AB ①CD ，根据平行线的性质可求解；过F 作FH ①AB ，易得FH ①AB ①CD ，根据平行线的性质可求解；（2）根据（1）的结论及角平分线的定义可得2（①BME +①END ）+①BMF -①FND =180°，可求解①BMF =60°，进而可求解；（3）根据平行线的性质及角平分线的定义可推知①FEQ =12①BME ，进而可求解．【详解】解：（1）过E作EH①AB，如图1，①①BME＝①MEH，①AB①CD，①HE①CD，①①END＝①HEN，①①MEN＝①MEH＋①HEN＝①BME＋①END，即①BME＝①MEN﹣①END．如图2，过F作FH①AB，①①BMF＝①MFK，①AB①CD，①FH①CD，①①FND＝①KFN，①①MFN＝①MFK﹣①KFN＝①BMF﹣①FND，即：①BMF＝①MFN＋①FND．故答案为①BME＝①MEN﹣①END；①BMF＝①MFN＋①FND．（2）由（1）得①BME＝①MEN﹣①END；①BMF＝①MFN＋①FND．①NE平分①FND，MB平分①FME，①①FME＝①BME＋①BMF，①FND＝①FNE＋①END，①2①MEN＋①MFN＝180°，①2（①BME＋①END）＋①BMF﹣①FND＝180°，①2①BME＋2①END＋①BMF﹣①FND＝180°，即2①BMF＋①FND＋①BMF﹣①FND＝180°，解得①BMF＝60°，①①FME＝2①BMF＝120°；（3）①FEQ的大小没发生变化，①FEQ＝30°．由（1）知：①MEN＝①BME＋①END，①EF平分①MEN，NP平分①END，①①FEN＝12①MEN＝12（①BME＋①END），①ENP＝12①END，①EQ①NP，①①NEQ＝①ENP，①①FEQ＝①FEN﹣①NEQ＝12（①BME＋①END）﹣12①END＝12①BME，①①BME＝60°，①①FEQ＝12×60°＝30°．【点睛】本题主要考查平行线的性质及角平分线的定义，作平行线的辅助线是解题的关键．12．（1）360PAF PBN APB∠+∠+∠=°；（2）①CPDαβ∠=∠+∠，理由见解析；①图见解析，CPDβα∠=∠-∠或CPDαβ∠=∠-∠【解析】【分析】（1）作PQ①EF，由平行线的性质，即可得到答案；（2）①过P作//PE AD交CD于E，由平行线的性质，得到DPEα∠=∠，CPEβ∠=∠，即可得到答案；①根据题意，可对点P进行分类讨论：当点P在BA延长线时；当P在BO之间时；与①同理，利用平行线的性质，即可求出答案．【详解】解：（1）作PQ①EF，如图：①//EF MN，①////EF MN PQ，①180PAF APQ∠+∠=°，180PBN BPQ∠+∠=°，①APB APQ BPQ∠=∠+∠①360PAF PBN APB∠+∠+∠=°；（2）①CPDαβ∠=∠+∠；理由如下：如图，过P作//PE AD交CD于E，①//AD BC，①////AD PE BC，①DPEα∠=∠，CPEβ∠=∠，①CPD DPE CPEαβ∠=∠+∠=∠+∠；①当点P在BA延长线时，如备用图1：①PE①AD①BC，，，EPC=β，①EPD=α，①CPDβα∠=∠-∠；当P在BO之间时，如备用图2：①PE①AD①BC，①①EPD=α，①CPE=β，∠=∠-∠．①CPDαβ【点睛】本题考查了平行线的性质，解题的关键是熟练掌握两直线平行同旁内角互补，两直线平行内错角相等，从而得到角的关系．13．（1）①B，两直线平行，内错角相等，EF，CD，①D，两直线平行，内错角相等；（2）360°【解析】【分析】（1）过点E作直线EF①AB，则①FEB=①B，继而由EF①CD可得①FED=①D．所以①B+①D=①BEF+①FED，即①B+①D=①BED；（2）过点E作直线EF①AB，则①FEB+①B=180°，继而由EF①CD可得①FED+①D=180°．所以①B+①D+①BEF+①FED=360°，即①B+①BED+①D=360°．【详解】解：（1）解：过点E作直线EF①AB．①①FEB=①B．（两直线平行，内错角相等）①AB①CD，EF①AB，① EF①CD（如果两条直线和第三条直线平行，那么这两直线平行）．①①FED=①D（两直线平行，内错角相等）．①①B+①D=①BEF+①FED．①①B+①D=①BED．故答案为：①B，两直线平行，内错角相等，EF，CD，①D，两直线平行，内错角相等；（2）解：过点E作直线EF①AB，如图．①①FEB+①B=180°．两直线平行，内错角相等）．①AB①CD，EF①AB，① EF①CD（如果两条直线和第三条直线平行，那么这两直线平行）．①①FED+①D=180° （两直线平行，内错角相等）．①①B+①D+①BEF+①FED=360°．①①B+①BED+①D=360°．故答案为：360°．【点睛】本题考查了平行线的判定与性质，平行公理及其推论，熟练掌握平行线判定、性质说理是关键．14．（1）∠MEN＝∠CNE+∠AME；（2）∠MEN＝∠CNE+∠AME，证明见解析；（3）∠MEN+∠CNE+∠AME＝360°，证明见解析．【解析】【分析】（1）由平行线的性质及平角的定义即可得解；（2）过点E作直线EF①AB，则EF①CD，由平行线的性质即可得解；（3）过点E作直线EG①AB，则EG①CD，由平行线的性质即可得解．【详解】解：（1）如图1，∠MEN＝∠CNE+∠AME，证明如下：∵AB∥CD，∴∠CNE+∠AME＝180°，∵∠MEN＝180°，∴∠MEN＝∠CNE+∠AME；（2）如图2，∠MEN＝∠CNE+∠AME，证明如下：过点E作直线EF∥AB，则EF∥CD，∴∠AME＝∠MEF，∠CNE＝∠NEF，∵∠MEN＝∠MEF+∠NEF，∴∠MEN＝∠CNE+∠AME；（3）如图3，∠MEN+∠CNE+∠AME＝360°，证明如下：过点E作直线EG∥AB，则EG∥CD，∴∠AME+∠MEG＝180°，∠CNE+∠NEG＝180°，∴∠AME+∠MEG+∠CNE+∠NEG＝360°，∵∠MEG+∠NEG＝∠MEN，∴∠MEN+∠CNE+∠AME＝360°．【点睛】此题考查了平行线的性质，熟记“两直线平行，内错角相等”及“两直线平行，同旁内角互补”是解题的关键．15．（1）见解析；（2）3ACD GAC∠=∠，见解析；（3）54019⎛⎫⎪⎝⎭°或54023︒⎛⎫⎪⎝⎭．【解析】【分析】（1）根据平行线的判定与性质求证即可；（2）根据三角形的内角和为180°和平角定义得到AQD E EAQ ∠=∠+∠，结合平行线的性质得到BDQ E EAQ ∠=∠+∠，再根据角平分线的定义证得2CDB E GAC ∠=∠+∠，结合已知即可得出结论；（3）分当K 在直线GH 下方和当K 在直线GH 上方两种情况，根据平行线性质、三角形外角性质、角平分线定义求解即可．【详解】解：（1）如图1，延长AC 交MN 于点P ，①ACD C ∠=∠，①//AP BD ，①NBD NPA ∠=∠，①GAC NBD ∠=∠，①GAC NPA ∠=∠，①//GH MN ；（2）延长AC 交MN 于点P ，交DE 于点Q ，①180E EAQ AQE ∠+∠+∠=°，180AQE AQD ∠+∠=°，①AQD E EAQ ∠=∠+∠，①//AP BD ，①AQD BDQ ∠=∠，①BDQ E EAQ ∠=∠+∠，①AE 平分GAC ∠，DE 平分BDC ∠，①2GAC EAQ∠=∠，2CDB BDQ ∠=∠，①2CDB E GAC ∠=∠+∠，①AED GAC ∠=∠，ACD CDB ∠=∠，①23ACD GAC GAC GAC ∠=∠+∠=∠；（3）当K 在直线GH 下方时，如图，设射线BF 交GH 于I ，①//GH MN ，①AIB FBM ∠=∠，①BF 平分MBD ∠，①1(180)2DBF FBM DBN ∠=∠=-∠°， ①AIB DBF ∠=∠， ①AIB KAG AKB ∠+∠=∠，AKB ACD ∠=∠，①ACD DBF KAG ∠=∠+∠，①13KAG GAC ∠=∠，GAC NBD ∠=∠， ①11(180)332GAC DBN ACD GAC ∠+-∠=∠=∠°，即1190332GAC GAC GAC ∠+-∠=∠°，解得：54019GAC ⎛⎫∠= ⎪⎝⎭．当K 在直线GH 上方时，如图，同理可证得1(180)2AIB DBN AKB KAG ∠=-∠=∠+∠°，则有113(180)32GAC GAC GAC ∠+∠=-∠，解得：54023GAC ⎛⎫∠= ⎪⎝⎭．综上，故答案为54019⎛⎫⎪⎝⎭°或54023︒⎛⎫⎪⎝⎭．【点睛】本题考查平行线的判定与性质、角平分线的定义、三角形的外角性质、三角形的内角和定理、平角定义、角度的运算，熟练掌握相关知识的联系与运用是解答的关键．16．（1）①A+①C=90°；（2）见解析；（3）①EBC=105°．【解析】【分析】（1）通过平行线性质和直角三角形内角关系求解．（2）画辅助平行线找角的联系．（3）利用（2）的结论，结合角平分线性质求解．【详解】解：（1）如图1，①AM①CN，①①C=①AOB，①AB①BC，①①ABC=90°，①①A+①AOB=90°，①A+①C=90°，故答案为：①A+①C=90°；（2）如图2，过点B作BG①DM，①BD①AM，①DB①BG，①①DBG=90°，①①ABD+①ABG=90°，①AB①BC，①①CBG+①ABG=90°，①①ABD=①CBG，①AM①CN，①①C=①CBG，①①ABD=①C；（3）如图3，过点B作BG①DM，①AM①CN，①CN①BG，①①CBG=①BCN，①BF平分①DBC，BE平分①ABD，①①DBF=①CBF，①DBE=①ABE，①①ABD=①NCB，①①ABD=①CBG，①①ABF=①GBF，设①DBE=α，①ABF=β，则①ABE=α，①ABD=2α=①CBG，①GBF=①AFB=β，①BFC=3①DBE=3α，①BG①DM，①①DFB=①GBF=β，①①AFC=①BFC+①DFB=3α+β，①①AFC+①NCF=180°，①FCB+①NCF=180°，①①FCB=①AFC=3α+β，①BCF中，由①CBF+①BFC+①BCF=180°得：2α+β+3α+3α+β=180°，①AB①BC，①β+β+2α=90°，①α=15°，①①ABE=15°，①①EBC=①ABE+①ABC=15°+90°=105°．【点睛】本题考查平行线性质，三角形内角和定理，角平分线的定义，画辅助线，找到角的关系是求解本题的关键．17．（1）两直线平行，内错角相等；平行于同一条直线的两条直线平行；①CPH；①APH，①CPH；（2）①①APQ+①PQC＝①A+①C+180°成立，理由见解答过程；①3①PMQ+①A+①C ＝360°．【解析】【分析】（1）根据平行线的判定与性质即可完成填空；（2）结合（1）的辅助线方法即可完成证明；（3）结合（1）（2）的方法，根据①APM＝2①MPQ，①CQM＝2①MQP，①PMQ+①MPQ+①PQM＝180°，即可证明①PMQ，①A与①C的数量关系．【详解】解：过点P作直线PH①AB，所以①A＝①APH，依据是两直线平行，内错角相等；因为AB①CD，PH①AB，所以PH①CD，依据是平行于同一条直线的两条直线平行；所以①C＝（①CPH），所以①APC＝（①APH）+（①CPH）＝①A+①C＝97°．故答案为：两直线平行，内错角相等；平行于同一条直线的两条直线平行；①CPH；①APH，①CPH；（2）①如图2，①APQ+①PQC＝①A+①C+180°成立，理由如下：过点P作直线PH①AB，QG①AB，①AB①CD，①AB①CD①PH①QG，①①A＝①APH，①C＝①CQG，①HPQ+①GQP＝180°，①①APQ+①PQC＝①APH+①HPQ+①GQP+①CQG＝①A+①C+180°．①①APQ+①PQC＝①A+①C+180°成立；①如图3，过点P作直线PH①AB，QG①AB，MN①AB，①AB①CD，①AB①CD①PH①QG①MN，①①A＝①APH，①C＝①CQG，①HPQ+①GQP＝180°，①HPM＝①PMN，①GQM＝①QMN，①①PMQ＝①HPM+①GQM，①①APM ＝2①MPQ ，①CQM ＝2①MQP ，①PMQ +①MPQ +①PQM ＝180°，①①APM +①CQM ＝①A +①C +①PMQ ＝2①MPQ +2①MQP ＝2（180°﹣①PMQ ），①3①PMQ +①A +①C ＝360°．【点睛】考核知识点：平行线的判定和性质．熟练运用平行线性质和判定，添加适当辅助线是关键．18．（1）65°（2）3606α︒-︒（3）2n ①M +①BED =360° 【解析】【分析】（1）首先作EG ∥AB ，FH ∥AB ，利用平行线的性质可得①ABE +①CDE =260°，再利用角平分线的定义得到①ABF +①CDF =130°，从而得到①BFD 的度数，再根据角平分线的定义可求①M 的度数；（2）先由已知得到①ABE =6①ABM ，①CDE =6①CDM ，由（1）得①ABE +①CDE =360°-①BED ，①M =①ABM +①CDM ，等量代换即可求解；（3）先由已知得到ABF n ABM ∠=∠，CDF n CDM ∠=∠，由（2）的方法可得到2n ①M +①BED =360°．【详解】解：（1）如图1，作//EG AB ，//FH AB ，①AB CD ∥，①EG AB FH CD ∥∥∥，①ABF BFH ∠=∠，CDF DFH ∠=∠，180ABE BEG ∠+∠=︒，180GED CDE ∠+∠=︒， ①360ABE BEG GED CDE ∠+∠+∠+∠=︒，①100BED BEG DEG ∠=∠+∠=︒，①260ABE CDE ∠+∠=︒，①ABE ∠的角平分线和CDE ∠的角平分线相交于F ，①130ABF CDF ∠+∠=︒，①130BFD BFH DFH ∠=∠+∠=︒，①BM 、DM 分别是ABF ∠和CDF ∠的角平分线，①12MBF ABF ∠=∠，12MDF CDF ∠=∠，①65MBF MDF ∠+∠=︒，①1306565BMD ∠=︒-︒=︒；（2）如图2，①13ABM ABF ∠=∠，13CDM CDF ∠=∠， ①3ABF ABM ∠=∠，3CDF CDM ∠=∠，①ABE ∠与CDE ∠两个角的角平分线相交于点F ，①6ABE ABM ∠=∠，6CDE CDM ∠=∠，①66360ABM CDM BED ∠+∠+∠=︒，①BMD ABM CDM ∠=∠+∠，①6360BMD BED ∠+∠=︒，①3606BMD α︒-︒∠=；（3）①①ABM ＝1n ①ABF ，①CDM ＝1n①CDF ， ①ABF n ABM ∠=∠，CDF n CDM ∠=∠，①ABE ∠与CDE ∠两个角的角平分线相交于点F ，①2ABE n ABM ∠=∠，2CDE n CDM ∠=∠，①22360n ABM n CDM BED ∠+∠+∠=︒，①M ABM CDM ∠=∠+∠，①2360n M BED ∠+∠=︒．【点睛】本题主要考查了平行线的性质和角平分线的计算，关键在于掌握两直线平行同位角相等，内错角相等，同旁内角互补的性质．19．（1）110°；（2）80°；（3）()()11,22nx y x y ⎛⎫+︒+︒ ⎪⎝⎭【解析】【分析】（1）过点P作PH①AB①CD，根据平行线的性质：两直线平行，内错角相等即可证得；（2）同理依据两直线平行，内错角相等即可证得①1+①4=①2+①3，求得①4=80°；（3）利用（1）的结论和角平分线的性质即可写出结论；【详解】解：（1）如图1，过点P作PH①AB①CD①①1=①EPH，①2=①FPH而①EPF=①EPH+①FPH①①EPF=①1+①2=110°；（2）过点P作//PM AB,//QN AB//1PM ABEPM∴∠=//,//,////P//QN//QN AB PM AB AB CDAB M DC∴MPQ NQP∴∠=∠，2NQF∠=∠3EPM MPQ∠=∠+∠,4PQN NQF∠=∠+∠①①1+①4=①2+①3，①①1=30°，①2=40°，①3=70°，①①4=80°，故答案为：80°（3）过点P 作////PH AB CD1PE 平分PEB ∠11PEB PEP ∴∠=∠同理11DFP PFP ∠=∠ 111EPF PEB PFP ∠=∠+∠1122PFD BEP =+ ()12PFD BEP =+ ()112EPF x y ︒∠=+（用x ，y 的代数式表示）同理1()().2n n x y P ︒∠=+ 故答案为：11()2x y P ︒∠=+，1()().2n n x y P ︒∠=+ 【点睛】本题考查了平行线性质的应用，解题的关键是学会添加常用辅助线，构造平行线解决问题，学会探究规律，利用规律解决问题．20．（1）见解析；（2）见解析；（3）n -1【解析】【分析】（1）连接AB ，根据已知证明①MAB +①SBA =180°，即可得证；（2）作CF ①ST ，设①CBT =α，表示出①CAN ，①ACF ，①BCF ，根据AD ①BC ，得到①DAC =120°，求出①CAE 即可得到结论；（3）作CF ①ST ，设①CBT =β，得到①CBT =①BCF =β，分别表示出①CAN 和①CAE ，即可得到比值．【详解】解：（1）如图，连接AB ，，360MAC ACB SBC ∠+∠+∠=︒，180ACB ABC BAC ∠+∠+∠=︒，180MAB SBA ∴∠+∠=︒，//MN ST ∴（2）2CAE CAN ∠=∠，理由：作//CF ST ，则////,MN CF ST 如图，设CBT α∠=，则2DAE α∠=．BCF CBT α∠=∠=，60CAN ACF α∠=∠=︒-， //AD BC ，180120DAC ACB ∠=︒-∠=︒，12012022(60)2CAE DAE CAN αα∴∠=︒-∠=︒-=︒-=∠．即2CAE CAN ∠=∠．（3）作//CF ST ，则////,MN CF ST 如图，设CBT β∠=，则MAE n β∠=．//CF ST ，CBT BCF β∴∠=∠=，。

人教版七年级数学下《平行线的判定》拔高练习

《平行线的判定》拔高练习一、选择题（本大题共5小题，共25.0分）1．（5分）如图，点在延长线上，下列条件中不能判定BD∥AC的是（）A．∠1＝∠2B．∠3＝∠4C．∠5＝∠C D．∠C+∠BDC＝180°2．（5分）下列结论正确的是（）A．同位角相等B．同一平面内，不相交的两条直线叫做平行线C．过一点有且只有一条直线与已知直线平行D．垂直于同一条直线的两条直线互相平行3．（5分）如图，点E在AC的延长线上，下列条件能判断AB∥CD的是（）A．∠1＝∠2B．∠3＝∠4C．∠D＝∠DCE D．∠D+∠ACD＝180°4．（5分）如图，能判定a∥b的条件是（）A．∠1＝∠5B．∠2+∠4＝180°C．∠3＝∠4D．∠2+∠1＝180°5．（5分）如图，由下列条件，不能判断AB∥CD的是（）A．∠1＝∠4B．∠2＝∠3C．∠B+∠BCD＝180°D．∠BAD+∠D＝180°二、填空题（本大题共5小题，共25.0分）6．（5分）如图，两直线a、b被第三条直线c所截，若∠1＝50°，∠2＝130°，则直线a、b的位置关系是，理由是．7．（5分）如图，∠A＝70°，O是AB上一点，直线OD与AB所夹的∠AOD＝100°，要使OD∥AC，直线OD绕点O按逆时针方向至少旋转．8．（5分）如图，现给出下列条件：①∠1＝∠B，②∠2＝∠5，③∠3＝∠4，④∠BCD+∠D＝180°．其中能够得到AB∥CD的条件有．（填序号）9．（5分）如图，下列能判定AB∥CD的条件有个（1）∠B+∠BCD＝180°；（2）∠1＝∠2；（3）∠3＝∠4；（4）∠B＝∠510．（5分）如图，直线l与直线AB、CD分别相交于E、F，∠1＝120°，当∠2＝时，AB∥CD．三、解答题（本大题共5小题，共50.0分）11．（10分）已知：如图，BC＝EF，AD＝BE，AC＝DF．求证：BC∥EF．12．（10分）如图所示，∠B＝25°，∠D＝42°，∠BCD＝67°，试判断AB和ED的位置关系，并说明理由．13．（10分）如图，DE平分∠ADC，CE平分∠BCD，且∠1+∠2＝90°．试判断AD与BC的位置关系，并说明理由．14．（10分）如图，点D在△ABC的边AB上，且∠ACD＝∠A．（1）作∠BDC的平分线DE，交BC于点E．（要求：尺规作图，保留作图痕迹，但不必写出作法）；（2）在（1）的条件下，求证：DE∥AC．15．（10分）将一副直角三角尺BAC和ADE如图放置，其中∠BAC＝∠ADE＝90°，∠BCA＝30°，∠AED＝45°，若∠AFD＝75°，试判断AE与BC的位置关系，并说明理由．《平行线的判定》拔高练习参考答案与试题解析一、选择题（本大题共5小题，共25.0分）1．（5分）如图，点在延长线上，下列条件中不能判定BD∥AC的是（）A．∠1＝∠2B．∠3＝∠4C．∠5＝∠C D．∠C+∠BDC＝180°【分析】根据平行线的判定方法直接判定即可．【解答】解：选项A中，∠1与∠2是直线AC、BD被AD所截形成的内错角，因为∠1＝∠2，所以应是AC∥BD，故A选项不合题意．选项B中，∵∠3＝∠4，∴AB∥CD（内错角相等，两直线平行），不能判定BD ∥AC，所以B选项符合题意；选项C中，∵∠5＝∠C，∴BD∥AC（内错角相等，两直线平行），所以C选项不合题意；选项D中，∵∠C+∠BDC＝180°，∴BD∥AC（同旁内角互补，两直线平行），所以D选项不合题意；故选：B．【点评】本题主要考查了平行线的判定，正确识别“三线八角”中的同位角、内错角、同旁内角是正确答题的关键，不能遇到相等或互补关系的角就误认为具有平行关系，只有同位角相等、内错角相等、同旁内角互补，才能推出两被截直线平行．2．（5分）下列结论正确的是（）A．同位角相等B．同一平面内，不相交的两条直线叫做平行线C．过一点有且只有一条直线与已知直线平行D．垂直于同一条直线的两条直线互相平行【分析】根据平行线的定义、性质，即可解答．【解答】解：A、两直线平行，同位角相等，故错误；B、同一平面内，不相交的两条直线叫做平行线，正确；C、过直线外一点有且只有一条直线与这条直线平行，故错误；D、在同一平面内，垂直于同一直线的两条直线互相平行，故错误；故选：B．【点评】本题考查了平行线，解决本题的关键是熟记相关性质，注意强调同一平面内．3．（5分）如图，点E在AC的延长线上，下列条件能判断AB∥CD的是（）A．∠1＝∠2B．∠3＝∠4C．∠D＝∠DCE D．∠D+∠ACD＝180°【分析】根据平行线的判定定理即可直接作出判断．【解答】解：A．根据内错角相等，两直线平行即可证得AB∥BC；B．根据内错角相等，两直线平行即可证得BD∥AC，不能证AB∥CD；C．根据内错角相等，两直线平行即可证得BD∥AC，不能证AB∥CD；D．根据同旁内角互补，两直线平行，即可证得BD∥AC，不能证AB∥CD．故选：A．【点评】本题考查了平行线的判定定理，正确识别“三线八角”中的同位角、内错角、同旁内角是正确答题的关键，不能遇到相等或互补关系的角就误认为具有平行关系，只有同位角相等、内错角相等、同旁内角互补，才能推出两被截直线平行．4．（5分）如图，能判定a∥b的条件是（）A．∠1＝∠5B．∠2+∠4＝180°C．∠3＝∠4D．∠2+∠1＝180°【分析】根据已知条件，利用平行线判定定理：同位角相等，两直线平行；内错角相等，两直线平行；同旁内角互补，两直线平行，对4个条件逐一进行分析即可．【解答】解：A．由∠1＝∠5，不能得到a∥b；B．由∠2+∠4＝180°，可得a∥b；C．由∠3＝∠4，不能得到a∥b；D．由∠2+∠1＝180°，不能得到a∥b；故选：B．【点评】此题主要考查学生对平行线判定定理的理解和掌握，解题时注意：同旁内角互补，两直线平行．5．（5分）如图，由下列条件，不能判断AB∥CD的是（）A．∠1＝∠4B．∠2＝∠3C．∠B+∠BCD＝180°D．∠BAD+∠D＝180°【分析】根据平行线的判定定理即可直接作出判断．【解答】解：A、根据内错角相等，两直线平行即可证得，故选项错误；B、∠2和∠3是AD和BC被AC所截形成的角，因而不能证明AB∥CD，故选项正确；C、根据同旁内角互补，两直线平行，即可证得，故选项错误；D、根据同旁内角互补，两直线平行，即可证得，故选项错误．故选：B．【点评】本题考查了平行线的判定定理，正确识别“三线八角”中的同位角、内错角、同旁内角是正确答题的关键，不能遇到相等或互补关系的角就误认为具有平行关系，只有同位角相等、内错角相等、同旁内角互补，才能推出两被截直线平行．二、填空题（本大题共5小题，共25.0分）6．（5分）如图，两直线a、b被第三条直线c所截，若∠1＝50°，∠2＝130°，则直线a、b的位置关系是a∥b，理由是同位角相等，两直线平行．【分析】因为∠2与∠3是邻补角，由已知便可求出∠3＝∠1，利用同位角相等，两直线平行即可得出a，b的位置关系．【解答】解：∵∠2+∠3＝180°，∠2＝130°，∴∠3＝50°，∵∠1＝50°，∴∠1＝∠3，∴a∥b（同位角相等，两直线平行），故答案为：a∥b；同位角相等，两直线平行．【点评】本题考查了平行线的判定．解答此类要判定两直线平行的题，可围绕截线找同位角、内错角和同旁内角7．（5分）如图，∠A＝70°，O是AB上一点，直线OD与AB所夹的∠AOD＝100°，要使OD∥AC，直线OD绕点O按逆时针方向至少旋转10°．【分析】根据平行线的性质，求得∠AOD′的度数，即可确定旋转的角度，即∠DOD′的大小．【解答】解：∵OD′∥AC，∴∠AOD′＝180°﹣∠A＝110°，∴∠DOD′＝∠AOD′﹣∠AOD＝110°﹣100°＝10°．故答案为：10°．【点评】考查了平行线的判定，在旋转变换中，正确认识旋转角是解题关键，同时本题运用了平行线的性质，两直线平行，同旁内角互补．8．（5分）如图，现给出下列条件：①∠1＝∠B，②∠2＝∠5，③∠3＝∠4，④∠BCD+∠D＝180°．其中能够得到AB∥CD的条件有①②．（填序号）【分析】根据平行线的判定定理对各小题进行逐一判断即可．【解答】解：①∵∠1＝∠B，∴AB∥CD，故本小题正确；②∵∠2＝∠5，∴AB∥CD，故本小题正确；③∵∠3＝∠4，∴AD∥BC，故本小题错误；④∵∠D+∠BCD＝180°，∴AD∥CB，故本小题错误．故答案为：①②．【点评】本题考查的是平行线的判定，熟知同位角相等，两直线平行；内错角相等，两直线平行；同旁内角互补，两直线平行是解答此题的关键．9．（5分）如图，下列能判定AB∥CD的条件有3个（1）∠B+∠BCD＝180°；（2）∠1＝∠2；（3）∠3＝∠4；（4）∠B＝∠5【分析】依据平行线的判定方法进行判断：同位角相等，两直线平行；内错角相等，两直线平行；同旁内角互补，两直线平行．【解答】解：（1）由∠B+∠BCD＝180°可得AB∥CD；（2）由∠1＝∠2可得AD∥BC；（3）由∠3＝∠4可得AB∥CD；（4）由∠B＝∠5可得AB∥CD；故答案为：3．【点评】本题主要考查了平行线的判定，同位角相等，两直线平行；内错角相等，两直线平行；同旁内角互补，两直线平行．10．（5分）如图，直线l与直线AB、CD分别相交于E、F，∠1＝120°，当∠2＝60°时，AB∥CD．【分析】若AB与CD平行，利用两直线平行同旁内角互补得到一对角互补，再由对顶角相等及等量代换得到∠1与∠2互补，即可确定出∠2的度数．【解答】解：若AB∥CD，则∠2+∠3＝180°，∵∠1＝∠3，∴∠2+∠1＝180°，∵∠1＝120°，∴∠2＝60°，∴当∠2＝60°时，AB∥CD．故答案为：60°．【点评】此题考查了平行线的判定，熟练掌握平行线的判定方法是解本题的关键．三、解答题（本大题共5小题，共50.0分）11．（10分）已知：如图，BC＝EF，AD＝BE，AC＝DF．求证：BC∥EF．【分析】证明△CBA≌△FED，根据全等三角形的性质得到∠B＝∠FED，根据平行线的判定定理证明．【解答】证明：∵AD＝BE，∴AD+AE＝BE+AE，即BA＝ED，在△CBA和△FED中，，∴△CBA≌△FED（SSS），∴∠B＝∠FED，∴BC∥EF．【点评】本题考查的是平行线的性质，全等三角形的判定和性质，掌握全等三角形的判定定理和性质定理，平行线的判定定理是解题的关键．12．（10分）如图所示，∠B＝25°，∠D＝42°，∠BCD＝67°，试判断AB和ED的位置关系，并说明理由．【分析】过C作CF∥AB，据此得∠BCF＝∠B＝25°，从而知∠DCF＝∠BCD ﹣∠BCF＝42°＝∠D，依据平行线判定得CF∥ED，继而知AB∥ED．【解答】解：AB∥ED，理由：如图，过C作CF∥AB，∵∠B＝25°，∴∠BCF＝∠B＝25°，∴∠DCF＝∠BCD﹣∠BCF＝42°，又∵∠D＝42°，∴∠DCF＝∠D，∴CF∥ED，∴AB∥ED．【点评】本题主要考查平行线的判定，解题的关键是掌握内错角相等两直线平行及平行于同一直线的两直线平行的判定．13．（10分）如图，DE平分∠ADC，CE平分∠BCD，且∠1+∠2＝90°．试判断AD与BC的位置关系，并说明理由．【分析】根据角平分线的定义求出∠ADC＝2∠1，∠BCD＝2∠2，然后求出∠ADC+∠BCD＝180°，再根据同旁内角互补，两直线平行，求出AD∥BC即可．【解答】解：BC∥AD．理由如下：∵DE平分∠ADC，CE平分∠BCD，∴∠ADC＝2∠1，∠BCD＝2∠2，∵∠1+∠2＝90°，∴∠ADC+∠BCD＝2（∠1+∠2）＝180°，∴AD∥BC．【点评】本题考查了平行线的判定与性质，角平分线的定义的运用，两条直线被第三条所截，如果同旁内角互补，那么这两条直线平行．14．（10分）如图，点D在△ABC的边AB上，且∠ACD＝∠A．（1）作∠BDC的平分线DE，交BC于点E．（要求：尺规作图，保留作图痕迹，但不必写出作法）；（2）在（1）的条件下，求证：DE∥AC．【分析】（1）利用基本作图（作已知角的平分线）作∠BDC的平分线DE；（2）先根据角平分线的定义得到∠BDE＝∠CDE，再利用三角形外角性质得∠BDC＝∠A+∠ACD，加上∠ACD＝∠A，则∠BDE＝∠A，然后根据平行线的判定方法可判断DE∥BC．【解答】解：（1）如图，DE为所作；（2）DE∥AC．理由如下：∵DE平分∠BDC，∴∠BDE＝∠CDE，而∠BDC＝∠A+∠ACD，即∠BDE+∠CDE＝∠A+∠ACD，∵∠ACD＝∠A，∴∠BDE＝∠A，∴DE∥BC．【点评】本题考查了平行线的判定，基本作图：熟练掌握基本作图（作一条线段等于已知线段；作一个角等于已知角；作已知线段的垂直平分线；作已知角的角平分线；过一点作已知直线的垂线）．15．（10分）将一副直角三角尺BAC和ADE如图放置，其中∠BAC＝∠ADE＝90°，∠BCA＝30°，∠AED＝45°，若∠AFD＝75°，试判断AE与BC的位置关系，并说明理由．【分析】根据三角形外角性质，可得∠EAF＝30°，再根据∠C＝30°，可得∠EAF＝∠C，进而判定AE∥BC．【解答】解：AE与BC平行．理由：∵∠AFD是△AEF的外角，∴∠EAF＝∠AFD﹣∠E＝75°﹣45°＝30°，又∵∠C＝30°，∴∠EAF＝∠C，∴AE∥BC．【点评】本题考查了平行线的判定与性质及三角形的外角的性质的运用，平行线的判定是由角的数量关系判断两直线的位置关系；平行线的性质是由平行关系来寻找角的数量关系．。

专题01平行线(四种模型)专项训练(解析版)

专题01平行线（四种模型）专项训练题型一：M 模型（锯齿形）题型二：笔尖型题型三：“鸡翅”型题型四：“骨折”型模型一：M 模型如图，若 AB // CD ，你能确定∠B 、∠D 与∠BED 的大小关系吗？解：∠B ＋∠D ＝∠DEB ．理由如下：过点E 作 EF // AB又 ∵ AB//CD ．∴ EF//CD ．∴ ∠D =∠DEF ．∠B=∠BEF ．∴∠B ＋∠D ＝∠BEF ＋∠DEF ＝∠DEB即∠B ＋∠D ＝∠DEB ．一．选择题（共3小题）1．（2023春•临淄区期末）如图，//AB EF ，90C Ð=°，则a 、b 和g 的关系是( )A ．b a g =+B ．180a b g ++=°C ．90a b g +-=°D ．180b g a +-=°【分析】此题可以构造辅助线，利用三角形的外角的性质以及平行线的性质建立角之间的关系．【解答】解：延长DC 交AB 与G ，延长CD 交EF 于H ．在直角BGC D 中，190a Ð=°-；EHD D 中，2b g Ð=-，//AB EF Q ，12\Ð=Ð，90a b g \°-=-，即90a b g +-=°．故选：C ．【点评】本题考查的是平行线的性质，根据题意作出辅助线是解答此题的关键．2．（2023春•天宁区校级期中）如图，//AB CD ，EMNF 是直线AB 、CD 间的一条折线．若140Ð=°，260Ð=°，370Ð=°，则4Ð的度数为( )A ．55°B ．50°C ．40°D ．30°【分析】过M 作//OM AB ，//PN AB ，根据平行线的性质得到1EMO Ð=Ð，4PNF Ð=Ð，OMN PNM Ð=Ð，由角的和差得到(1)(4)14EMN MNF MNP MNP Ð-Ð=Ð+Ð-Ð+Ð=Ð-Ð，代入数据即可得到结论．【解答】解：如图2，过M 作//OM AB ，//PN AB ，//AB CD Q ，//////AB OM PN CD \，1EMO \Ð=Ð，4PNF Ð=Ð，OMN PNM Ð=Ð，(1)(4)14EMN MNF MNP MNP \Ð-Ð=Ð+Ð-Ð+Ð=Ð-Ð，6070404\°-°=°-Ð，450\Ð=°．故选：B ．【点评】本题考查的是平行线的性质，根据题意作出辅助线，构造出平行线是解答此题的关键．3．（2022春•海安市校级月考）如图，//AB EF ，90C Ð=°，则a 、b 、g 的关系为( )A ．b a g =+B ．90a b g +-=°C ．180a b g ++=°D ．90b g a +-=°【分析】此题可以构造辅助线，利用三角形的外角的性质以及平行线的性质建立角之间的关系．【解答】解：延长DC 交AB 于G ，延长CD 交EF 于H ．直角BGC D 中，190a Ð=°-；EHD D 中，2b g Ð=-，//AB EF Q ，12\Ð=Ð，90a b g \°-=-，即90a b g +-=°．故选：B ．【点评】此题主要考查了三角形的外角的性质以及平行线的性质，解题的关键是通过作辅助线，构造了三角形以及由平行线构成的内错角．二．解答题（共6小题）4．（2023春•仪征市期末）如图1，已知线段AB 、线段CD 被直线l 所截于点A 、点C ，150Ð=°，2Ð的度数是1Ð的3倍少20°．（1）求证：//AB CD ；（2）如图2，连接BD ，AB 沿BD 方向平移得到EF ，点F 在BD 上，点G 是BD 上的一点，连接AG 、EG ，30BAG Ð=°，20FEG Ð=°，求AGE Ð的度数；（3）如图3，点M 是线段BD 上一点，点N 是射线CD 上一点，CAM Ð度数为k ，AMN Ð度数为m ，MND Ð度数为n ，请直接写出k 、m 、n 之间的数量关系．（本题的角均小于180)°【分析】（1）根据已知先求得1Ð的邻补角BAC Ð的度数，得到2BAC Ð=Ð即可得结论；（2）过G 作//GQ AB ，利用平行线的性质定理和平行公理的推论即可；（3）利用平行线的性质定理和平行公理的推论即可．【解答】证明：（1）150Ð=°Q ，2Ð的度数是1Ð的3倍少20°，23120130\Ð=Ð-°=°，180250ACD \Ð=°-Ð=°，12\Ð=Ð，//AB CD \；（2）过G 作//GQ AB ，30AGQ BAG \Ð=Ð=°，//AB EF Q ，//GQ EF \，20GEF EGQ \Ð=Ð=°，50AGE AGQ EGQ \Ð=Ð+Ð=°；（3）//AB CD Q ，与（2）同理可得：AMN MAB MND Ð=Ð+Ð，AMN m Ð=Q ，MND n Ð=，m n MAB \=+Ð，150Ð=°Q ，CAM k Ð=，180118050BAM CAM k \Ð=°-Ð-Ð=°-°-，130m n k \=+°-，即130m n k -+=°．【点评】本题考查了平行线的性质定理及平行公理的推论，理解题意是解决问题的关键．5．（2022春•赣榆区期末）已知：如图，//AB CD ，BFE FEC Ð=Ð．求证：ABF DCE Ð=Ð．（1）下面是小明同学的推理过程，请按先后顺序填写空格：解：连接BC ．BFE FEC Ð=ÐQ （已知），\　BF　// （内错角相等，两直线平行）．\Ð=Ð )，FBC ECB(AB CDQ（已知），//\Ð=Ð（两直线平行，内错角相等）ABC DCB\Ð-Ð=Ð- ( )，ABC FBC DCB即ABF DCEÐ=Ð．（2）试用其他方法进行推理，并书写证明过程．【分析】（1）连接BC，根据已知，得出//AB CDÐ=Ð，再根据//BF CE，根据平行线的性质得到FBC ECB得出ABC DCBÐ-Ð=Ð-Ð即可得出答案；Ð=Ð，进而得出ABC FBC DCB ECBÐ=Ð，再利用等量代换可得H DCE （2）延长BF交DC的延长线于H，根据平行线的性质可得ABF HÐ=Ð，进而可判定//Ð=Ð．BH CE，然后可得BFE FEC【解答】（1）解：连接BC．BFE FECQ（已知），Ð=ÐBF CE\（内错角相等，两直线平行）．//FBC ECB\Ð=Ð两直线平行，内错角相等），(Q（已知），//AB CD\Ð=Ð（两直线平行，内错角相等）ABC DCBABC FBC DCB ECB\Ð-Ð=Ð-Ð等式的基本性质），(即ABF DCEÐ=Ð．故答案为：BF，CE；两直线平行，内错角相等；ECBÐ；等式的基本性质．（2）证明：延长BF交DC的延长线于H，Q，AB CD//\Ð=Ð，ABF HABF DCE Ð=ÐQ ．H DCE \Ð=Ð，//BH CE \，BFE FEC \Ð=Ð．【点评】本题考查了平行线的判定和性质，熟练应用判定定理和性质定理是解题的关键，平行线的性质：两直线平行，同位角相等；两直线平行，同旁内角互补；两直线平行，内错角相等．平行线的判定是由角的数量关系判断两直线的位置关系．平行线的性质是由平行关系来寻找角的数量关系．应用平行线的判定和性质定理时，一定要弄清题设和结论，切莫混淆．6．（2023春•天宁区校级期中）已知：如图，180ABE CEB Ð+Ð=°，12Ð=Ð，求证：M N Ð=Ð．【分析】首先证明//AB CD ，再根据平行线的性质得出ABE DEB Ð=Ð，然后结合已知条件可得到MBE NEB Ð=Ð，进而可判定//BM EN ，据此可得出结论．【解答】证明：180ABE CEB Ð+Ð=°Q ，//AB CD \，ABE DEB \Ð=Ð，即：12MBE NEB Ð+Ð=Ð+Ð，又12Ð=ÐQ ，MBE NEB \Ð=Ð，//BM EN \，M N \Ð=Ð．【点评】此题主要考查了平行线的判定和性质，解答此题的关键是准确识图，熟练掌握平行线的判定及性质：两直线平行Û同位角相等，两直线平行Û内错角相等，两直线平行Û同旁内角互补．7．（2023春•崇川区期中）如图1，已知直线EF 与直线AB 交于点E ，与直线CD 交于点F ，EM 平分AEF Ð交直线CD 于点M ，且FEM FME Ð=Ð．（1）试判断直线AB 与CD 的位置关系，并说明理由；（2）点G 是射线MD 上的一个动点（不与点M ，F 重合），EH 平分FEG Ð交直线CD 于点H ，过点H 作//HN EM 交直线AB 于点N ．设EHN a Ð=，EGF b Ð=．①如图2，当点G 在点F 的右侧，且50a =°时，求b 的值；②当点G 在运动过程中，a 和b 之间有怎样的数量关系？请写出你的猜想，并加以证明．【分析】（1）由EM 平分AEF Ð，得到AEM FEM Ð=Ð，又FEM FME Ð=Ð，所以AEM FME Ð=Ð，证得//AB CD ．（2）①由EH 平分FEG Ð，EM 平分AFE Ð，得到12HEM HEF FEM AEG Ð=Ð+Ð=Ð，由//HN EM ，//AB CD 可得，HEM EHN a Ð=Ð=，GEB EGF b =Ð=，即可得到结果．②当点G 在点F 的左侧时，由EM 平分AEF Ð，EH 平分FEH Ð，得到12HEM HEF FEM AEG Ð=Ð+Ð=Ð，由//AB CD ，//HN EM ，得到AEG b Ð=，HEM a Ð=，从而得到结果．【解答】解（1）如图1，//AB CD ，理由如下：EM Q 平分AEF Ð，AEM FEM \Ð=Ð，FEM FME Ð=ÐQ ，AEM FME \Ð=Ð，//AB CD \．（2）①如图2，EH Q 平分FEG Ð，12HEF FEG \Ð=Ð，EM Q 平分AFE Ð，12FEM AEF \Ð=Ð，12HEM HEF FEM AEG \Ð=Ð+Ð=Ð，//HN EM Q ，HEM EHN a \Ð=Ð=，//AB CD Q ，GEB EGF b \Ð=Ð=，1(180)2a b \=°-，180218025080b a \=°-=°-´°=°．②a 和b 之间的数量关系为2b a =或1802b a =°-．理由如下：当点G 在点F 的右侧时，由①得1802b a =°-，当点G 在点F 的左侧时，如图3，EM Q 平分AEF Ð，2AEF FEM \Ð=Ð，EH Q 平分FEH Ð，2GEF HEF \Ð=Ð，222AEG AEF GEF FEM HEF HEM \Ð=Ð-Ð=Ð-Ð=Ð，//AB CD Q ，AEG b \Ð=，//HN EM Q ，HEM a \Ð=，2b a \=，综上得，a 和b 之间的数量关系为2b a =或1802b a =°-．【点评】本题主要考查了平行线的判定与性质，角平分线的定义，熟练运用平行线的判定与性质是解题关键．8．（2023春•海安市期末）如图，在ABC D 中，ACB BAC Ð=Ð．过点A 作//MN BC ．（1）判断AC 是否平分BAN Ð，并说明理由；（2）如图2，点D 是射线CB 上一动点（不与点B ，C 重合），AE 平分BAD Ð交射线BC 于E ，过点E 作EF AC ^于F ．①当点D 在点B 左侧时，若20AEF Ð=°，求ADB Ð的度数；②点D 在运动过程中，AEF Ð和ADB Ð之间有怎样的数量关系？请写出你的猜想，并说明理由．【分析】（1）根据//MN BC 得ACB CAN Ð=Ð，结合已知条件得证；（2）①在直角三角形AFE 中，20AEF Ð=°，则9070EAF EAF Ð=°-Ð=°，根据19020702EAF BAC BAE DAE CAN DAN Ð=Ð+Ð=°-°=°=Ð+Ð=Ð，从而求出140DAN Ð=°，即可求出ADB Ð；②分两种情况进行讨论，当点D 在点B 左侧时和点D 在点B 右侧时，数形结合即可解答．【解答】解：（1）AC 平分BAN Ð，//MN BC Q ，ACB CAN \Ð=Ð，ACB BAC Ð=ÐQ ．BAC CAN \Ð=Ð，AC \平分BAN Ð，（2）EF AC ^Q ，9070EAF EAF \Ð=°-Ð=°，AC Q 、AE 是角平分线，DAE BAE \Ð=Ð，BAC CAN Ð=Ð，19020702EAF BAC BAE DAE CAN DAN \Ð=Ð+Ð=°-°=°=Ð+Ð=Ð，140DAN \Ð=°，40ADB \Ð=°．②设AEF a Ð=，EF AC ^Q ，90EAF a \Ð=°-，如图2，当点D 在点B 左侧时，由（1）知12NAC BAC BAN Ð=Ð=Ð，AE Q 平分BAD Ð交射线BC 于E ，12DAE BAE BAD \Ð=Ð=Ð，又1111()902222EAF BAE BAC BAD BAN BAD BAN DAN a Ð=Ð+Ð=Ð+Ð=Ð+Ð=Ð=°-Q ，1802DAN a \Ð=°-，//MN BC Q ，180ADB DAN \Ð+Ð=°，180180(1802)2ADB DAN a a \Ð=°-Ð=°-°-=，2ADB AEF \Ð=Ð；当点D 在点B 右侧时，如图：AC Q 、AE 是角平分线，12DAE BAE BAD \Ð=Ð=Ð，12BAC CAN BAN Ð=Ð=Ð，1111()902222EAF BAC BAE BAN BAD BAN BAD DAN a Ð=Ð-Ð=Ð-Ð=Ð-Ð=Ð=°-Q ，1802DAN a \Ð=°-，//MN BC Q ，1802ADB DAN a \Ð=Ð=°-，1802ADB AEF \Ð=°-Ð．综上，2ADB AEF Ð=Ð或1802AEF °-Ð．【点评】本题主要考查了平行线的性质与判定，角平分线的定义的运用，解决问题的关键是掌握两直线平行内错角相等，两直线平行同旁内角，利用角的和差关系进行推理论证．9．（2023春•姜堰区期末）已知12//l l ，李想同学将ABC D 放置在这两条平行线上展开探究，其中ABC D 三边与两条平行线分别交于点D 、E 、F 、G ．（1）【特例探究】如图1，90C Ð=°．①CED CGF Ð+Ð=　270　度；②若CED Ð与CGF Ð的角平分线相交于点P ，则EPG Ð= 度；（2）【一般探索】如图2，C a Ð=，EPG b Ð=．①若13DEP CED Ð=Ð，13FGP CGF Ð=Ð，求a 与b 的关系；②若1DEP CED n Ð=Ð，1(2FGP CGF n nÐ=Ð…且n 为整数），直接写出a 与b 的关系；（3）【拓展应用】如图3，CED Ð与CGF Ð的角平分线相交于点1P ，1PED Ð与1PGF Ð的角平分线相交于点2P ，2P ED Ð与2P GF Ð的角平分线相交于点3P ；¼，以此类推，则2023360C EP G°-ÐÐ的值是多少？（直接写出结果）【分析】（1）①作1//CM l 根据平行线的性质可得180CED ECM Ð+Ð=°，_180CGF GCM Ð+Ð=°两式相加即可得360CED CGF C Ð+Ð=°-Ð；②由①知：360CED CGF C Ð+Ð=°-Ð，再根据平行线的性质以及角平分线的定义即可得：1()2EPG CED CGF Ð=Ð+Ð化简整理即可；（2）①13DEP CED Ð=Ð，13FGP CGF Ð=Ð时，结合（1）中的结论和平行线的性质，可得a 与b 之间的关系；②类似于前面的证明，结合平行线的性质和角平分线的定义即可得结论；（3）根据角平分线的定义和平行线的性质找到规律即可得结论．【解答】解：（1）①作1//CM l，180CED ECM \Ð+Ð=°，2l Q //1l ，2//CM l \，_180CGF GCM \Ð+Ð=°，360CED ECM CGF GCM \Ð+Ð+Ð+Ð=°，90ECG ECM CGF Ð=Ð+Ð=°Q ，_90360CED CGF \Ð+Ð+°=°，270CED CGF \Ð+Ð=°，故答案为270°；②CED ÐQ 与CGF Ð的角平分线相交于点P ，2CED CEP \Ð=Ð，2CGF CGP Ð=Ð，由①知：270CED CGF Ð+Ð=°，22270CEP CGP \Ð+Ð=°，135CEP CGP \Ð+Ð=°，360CEP CGP EPG ECG Ð+Ð+Ð+Ð=°Q ，135EPF \Ð=°；（2）21//l l Q ，ECG a Ð=，由（1）①知360CED CGF ECF Ð+Ð+Ð=°，360360CED CGF ECG a \Ð+Ð=°-Ð=°-，由（1）②知若13DEP CED Ð=Ð，13FGP CGF Ð=Ð，\23CED CEP Ð=Ð，23CGF CGP Ð=Ð，2222()(360)3333CEP CGP CED CGF CED CGF a \Ð+Ð=Ð+Ð=Ð+Ð=°-，360CEP CGP EPG ECG Ð+Ð+Ð+Ð=°Q ，\2(360)3603a b a °-++=°，整理得：3360a b +=°；②若1DEP CED n Ð=Ð，1(2FGP CGF n nÐ=Ð…且n 为整数）时，由①同理可得a 与b 的关系：360n a b +=°；（3）通过前面的证明易得360360CED CGF C a Ð+Ð=°-Ð=°-，当CED Ð与CGF Ð的角平分线相交于点1P ，1PED Ð与1PGF Ð的角平分线相交于点2P ，2P ED Ð与2P GF Ð的角平分线相交于点3P ；¼，以此类推，则111111()()(360)222EPG CED CGF CED CGF a Ð=Ð+ÐÐ+Ð=°-，222111()())(360)422EP G CED CGF CED CGF a Ð=Ð+Ð=Ð+Ð==°-，333111()())(360)822EP G CED CGF CED CGF a Ð=Ð+Ð=Ð+Ð=°-，444111()())(360)1622EP G CED CGF CED CGF a Ð=Ð+Ð=Ð+Ð=°-，551(360)2EP G a Ð=°-，.....．1(360)2n nEP G a Ð=°-，当2023n =时，202320231(360)2EP G a Ð=°-，\20232023202336036021(360)2C EP G a a °-Ð°-==Ð°-，【点评】本题考查了平行线的性质，以及角平分线的定理，灵活运用所学知识找到规律是解决问题的关键．模型二、笔尖型如图，AB // CD ，探索∠B 、∠D 与∠DEB 的大小关系？解：∠B ＋∠D ＋∠DEB ＝360°．理由如下：过点E 作 EF // AB．又∵AB//CD．∴EF//CD．∴∠B+∠BEF＝180°．∠D+∠DEF＝180°．∴∠B＋∠D+∠DEB＝∠B＋∠D+∠BEF＋∠DEF ＝360°．即∠B＋∠D＋∠DEB＝360°．一．选择题（共3小题）1．（2022春•海陵区期末）如图//a b，M、N分别在a、b上，P为两平行线间一点，那么Ð+Ð+Ð= )123(A．180°B．270°C．360°D．540°【分析】首先过点P作//PA a，构造三条平行线，然后利用两直线平行，同旁内角互补进行做题．【解答】解：过点P作//a b PA，PA a，则////Ð+Ð=°，1180NPA\Ð+Ð=°，3180MPA\Ð+Ð+Ð=°．123360故选：C．【点评】两直线平行时，应该想到它们的性质，由两直线平行的关系得到角之间的数量关系，从而达到解决问题的目的．2．（2023春•沭阳县期末）如图，把一块含有30°角的直角三角板的两个顶点放在直尺的对边上．如果137Ð=°，那么2Ð的度数是( )A．30°B．25°C．23°D．37°【分析】根据平行线的性质，两直线平行，内错角相等，进而可以得出答案．【解答】解：如图，Q直尺的两条边平行，137Ð=°，\Ð=Ð=°，1337Q直角三角板的一个角为30°，\Ð+Ð=°，2360\Ð=°-°=°，2603723故选：C．【点评】本题主要考查了平行线的性质，注意隐含条件，直尺的两条对边平行和直角三角板的一个锐角是30°是解题的关键．3．（2023春•东台市月考）某小区车库门口的“曲臂直杆道闸”（如图）可抽象为如图所示模型．已知AB 垂直于水平地面AE．当车牌被自动识别后，曲臂直杆道闸的BC段将绕点B缓慢向上抬高，CD段则一直保持水平状态上升（即CD与AE始终平行），在该运动过程中ABC BCDÐ+Ð的度数始终等于( )度A．360B．180C．250D．270【分析】过点B作//Ð+Ð=°，从而可C CBGBG AE，利用平行线的性质可得180BAE ABGÐ+Ð=°，180得360BAEÐ=°，最后进行计算即可解答．Ð+Ð+Ð=°，然后根据垂直定义可得90BAE ABC BCD【解答】解：过点B作//BG AE，BAE ABG\Ð+Ð=°，180AE CDQ，//\，BG CD//\Ð+Ð=°，180C CBG\Ð+Ð+Ð+Ð=°，BAE ABG CBG C360BAE ABC BCD\Ð+Ð+Ð=°，360^Q，BA AE\Ð=°，90BAE\Ð+Ð=°-Ð=°，ABC BCD BAE360270故选：D．【点评】本题考查了平行线的性质，熟练掌握铅笔模型是解题的关键．二．填空题（共3小题）4．（2022春•崇川区校级月考）如图，直线//Ð=°，则3Ð=　78　度，Ð=°，250a b，128Ð+Ð+Ð= 度．345【分析】过3Ð的顶点作已知直线的平行线，充分运用平行线的性质，不难发现：312Ð=Ð+Ð，Ð+Ð+Ð=°345360【解答】解：如图所示：过3Ð的顶点作//c a，a bQ，//\，a b c////Ð=Ð，16\Ð=Ð，72又367Ð=Ð+Ð，\Ð=Ð+Ð=°；31278又4675180Ð+Ð=Ð+Ð=°\Ð+Ð+Ð=°．345360【点评】注意此类题中常见的辅助线：构造已知直线的平行线．根据平行线的性质发现并证明：312Ð=Ð+Ð；345360Ð+Ð+Ð=°．5．（2022春•淮安期末）如图，//Ð和AB CD，E、F分别是AB、CD上的点，EH、FH分别是AEGÐ=　125　°．GÐ=°，则HCFGÐ的角平分线．若110【分析】过点G作//CD GM，Ð+Ð=°，再结合已知可得// GM AB，根据平行线的性质可得180AEG EGM然后利用平行线的性质可得180Ð+Ð=°，再利用角平分线的定AEG CFGÐ+Ð=°，从而可得250CFG MGF义可得125Ð+Ð=°，最后利用四边形的内角和定理进行计算即可解答．HEG GFH【解答】解：过点G作//GM AB，\Ð+Ð=°，AEG EGM180Q，//AB CD//CD GM \，180CFG MGF \Ð+Ð=°，360AEG EGM CFG MGF \Ð+Ð+Ð+Ð=°，110EGF EGM MGF Ð=Ð+Ð=°Q ，360250AEG CFG EGF \Ð+Ð=°-Ð=°，EH Q 、FH 分别是AEG Ð和CFG Ð的角平分线，12HEG AEG \Ð=Ð，12GFH CFG Ð=Ð，1112522HEG GFH AEG CFG \Ð+Ð=Ð+Ð=°，360125H HEG HFG EGF \Ð=°-Ð-Ð-Ð=°，故答案为：125．【点评】本题考查了平行线的性质，根据题目的已知条件并结合图形添加适当的辅助线是解题的关键．6．（2023春•邗江区期中）将一副三角板如图1所示摆放，30BAC Ð=°，45E Ð=°，直线//GH MN ，现将三角板ABC 绕点A 以每秒1°的速度顺时针旋转，同时三角板DEF 绕点D 以每秒3°的速度顺时针旋转，如图2，设时间为t 秒，当0120t ……时，若边BC 与三角板DEF 的一条直角边（边DE ，)DF 平行，则所有满足条件的t 的值为 15或105或60　．【分析】先根据题意画出旋转后的图形，由已知条件，利用平行线的旋转，求出旋转角之间的关系，列出方程解答即可．【解答】解：由题意得：30HAC BAH BAC t Ð=Ð+Ð=°+°，3FDM t Ð=°，（1）当//BC DE 时，如图所示：延长AC 交MN 于点P ，①DE 在MN 上方，//DE BC Q ，DE DF ^，AC BC ^，//AP DF \，FDM MPA \Ð=Ð，//MN GH Q ，MPA HAC \Ð=Ð，FDM HAC \Ð=Ð，即330t t =+，15t =；②1DE 在MN 下方时，1(3180)F DP t Ð=-°，1//DE BC Q ，11DE DF ^，AC BC ^，1//AP DF \，1F DM MPA \Ð=Ð，//MN GH Q ，MPA HAC \Ð=Ð，1F DM HAC \Ð=Ð，即318030t t -=+，解之得：105t =；如图：当//BC DF 时，延长AC 交MN 于点I ，①DF 在MN 上方，(1803)FDN t Ð=-度，//DF BC Q ，AC BC ^，//AI DE \，90FDN MIA \Ð+Ð=°，//MN GH Q ，MIA HAC \Ð=Ð，90FDN HAC \Ð+Ð=°，即18033090t t -++=，解之得：60t =；②DF 在MN 下方，2(1803)F DN t Ð=-度，2//DF BC Q ，AC BC ^，22ED DF ^，2//AC DE \，2AIM MDE \Ð=Ð，//MN GH Q ，MIA HAC \Ð=Ð，2E DM HAC \Ð=Ð，即318030t t -=+，解之得：105t =，综上可知：所有满足条件的t 的值为：15或105或60，故答案为：15或105或60．【点评】本题主要考查了平行线的性质，解题关键是根据题意，画出旋转后的图形．三．解答题（共3小题）7．（2022春•海州区校级期中）如图，在ABC D 中，点D 、E 分别在AB 、BC 上，且//DE AC ，12Ð=Ð．求证：//AF BC ．【分析】根据平行线的性质得出1C Ð=Ð，求出2C Ð=Ð，根据平行线的判定得出即可．【解答】证明：//DE AC Q ，1C \Ð=Ð，12Ð=ÐQ ，2C \Ð=Ð，//AF BC \．【点评】本题考查了平行线的判定和性质，熟练应用判定定理和性质定理是解题的关键，平行线的性质：两直线平行，同位角相等；两直线平行，同旁内角互补；两直线平行，内错角相等．平行线的判定是由角的数量关系判断两直线的位置关系．平行线的性质是由平行关系来寻找角的数量关系．应用平行线的判定和性质定理时，一定要弄清题设和结论，切莫混淆．8．（2023春•盐都区期中）如图，在ABC D 中，点D 、E 分别在AB 、BC 上，//AF BC ，12Ð=Ð，求证：//DE AC ．【分析】由两直线平行内错角相等得到1C Ð=Ð，再根据同位角相等两直线平行可解题．【解答】证明：//AF BC Q ，1C \Ð=Ð，12Ð=ÐQ ，2C \Ð=Ð，//DE AC \．【点评】本题考查平行线的判定与性质，是重要考点，掌握相关知识是解题关键．9．（2022春•亭湖区校级月考）如图，已知1BDC Ð=Ð，23180Ð+Ð=°．（1）AD 与EC 平行吗？试说明理由．（2）若DA 平分BDC Ð，DA FA ^于点A ，182Ð=°，试求FAB Ð的度数．【分析】（1）直接利用平行线的判定与性质得出//AB CD ，进而得出3180ADC Ð+Ð=°，即可得出答案；（2）利用角平分线的定义结合平行线的性质得出2Ð，即可得出答案．【解答】（1）解：AD 与EC 平行，理由如下：1BDC Ð=ÐQ ，//AB CD \（同位角相等，两直线平行），2ADC \Ð=Ð（两直线平行，内错角相等），23180Ð+Ð=°Q ，3180ADC \Ð+Ð=°（等量代换），//AD CE \（同旁内角互补，两直线平行）；（2）解：1BDC Ð=ÐQ ，182Ð=°，82BDC \Ð=°，DA Q 平分BDC Ð，1412ADC BDC \Ð=Ð=°（角平分线定义），241ADC \Ð=Ð=°（已证），又DA FA ^Q ，90FAD \Ð=°（垂直定义），2904149FAB FAD \Ð=Ð-Ð=°-°=°．【点评】此题主要考查了平行线的判定与性质，正确得出90AEC FAD Ð=Ð=°是解题关键．模型三、“鸡翅”型如图，已知AB//CD ，试猜想∠A 、∠E 、∠C 的关系，并说明理由．解：∠AEC=∠A-∠C,理由如下：过点E 作 EF // AB又 ∵AB//CD ．∴EF//CD ．∴∠A+∠FEA=180°，∠C+∠FEC=180°∴ ∠AEC ＝ ∠FEC- ∠FEA= 180°- ∠C –(180°-∠A)=∠A-∠C即：∠AEC=∠A-∠C一、单选题1．（2021下·湖南株洲·七年级统考期末）①如图1，AB ∥CD ，则360A E C Ð+Ð+Ð=°；②如图2，AB ∥CD ，则P A C Ð=Ð-Ð；③如图3，AB ∥CD ，则1E A Ð=Ð+Ð；④如图4，直线AB ∥CD ∥ EF ，点O 在直线EF 上，则180a b g Ð-Ð+Ð=°．以上结论正确的个数是（）A．1个B．2个C．3个D．4个【答案】C【分析】①过点E作直线EF∥AB，由平行线的性质：两直线平行，同旁内角互补，即可得出结论；②如图2，先根据三角形外角的性质得出∠1＝∠C+∠P，再根据两直线平行，内错角相等即可作出判断；③如图3，过点E作直线EF∥AB，由平行线的性质可得出∠A+∠AEC﹣∠1＝180°，即得∠AEC＝180°+∠1﹣∠A；④如图4，根据平行线的性质得出∠α＝∠BOF，∠γ+∠COF＝180°，再利用角的关系解答即可．【详解】解：①如图1，过点E作直线EF∥AB，∵AB∥CD，∴AB∥CD∥EF，∴∠A+∠1＝180°，∠2+∠C＝180°，∴∠A+∠1+∠2+∠C＝360°，∴∠A+∠AEC+∠C=360°，故①正确；②如图2，∵∠1是△CEP的外角，∴∠1＝∠C+∠P，∵AB∥CD，∴∠A＝∠1，即∠P＝∠A﹣∠C，故②正确；③如图3，过点E作直线EF∥AB，∵AB∥CD，∴AB∥CD∥EF，∴∠A +∠3＝180°，∠1＝∠2，∴∠A +∠AEC ﹣∠1＝180°，即∠AEC ＝180°+∠1﹣∠A ，故③错误；④如图4，∵AB ∥EF ，∴∠α＝∠BOF ，∵CD ∥EF ，∴∠γ+∠COF ＝180°，∵∠BOF ＝∠COF +∠β，∴∠COF ＝∠α﹣∠β，∴∠γ+∠α﹣∠β＝180°，故④正确；综上结论正确的个数为3，故选：C ．【点睛】本题考查的是平行线的性质及三角形外角的性质，熟练掌握平行线的性质，根据题意作出辅助线是解答此题的关键．二、解答题2．（2021下·浙江台州·七年级统考期末）如图，已知AD AB ^于点A ，AE ∥CD 交BC 于点E ，且EF AB ^于点F ．求证：12C Ð=Ð+Ð．证明：∵AD AB ^于点A ，EF AB ^于点F ，（已知）∴90DAB EFB Ð=Ð=°．（垂直的定义）∴AD ∥EF ，（）∴__________1=Ð（）∵AE ∥CD ，（已知）∴C Ð=________．（两直线平行，同位角相等）∵2AEB AEF Ð=Ð+Ð，∴12C Ð=Ð+Ð．（等量代换）【答案】见解析Q 1PE l ∥，12l l ∥，\12PE l l ∥∥，PAC APE \Ð=Ð，PBD BPE Ð=Ð，APB APE BPE Ð=Ð+ÐQ ，PAC PBD APB \Ð+Ð=Ð．（2）解：结论：当点P 在直线1l 上方时，Ð-Ð=ÐPBD PAC APB ；当点P 在直线2l 下方时，Ð-Ð=ÐPAC PBD APB ．①当点P 在直线1l 上方时，如图2所示．过点P 作1PE l ∥．Q 1PE l ∥，12l l ∥，\12PE l l ∥∥，PAC APE \Ð=Ð，PBD BPE Ð=Ð，APB BPE APE Ð=Ð-ÐQ ，PBD PAC APB \Ð-Ð=Ð．②当点P 在直线2l 下方时，如图3所示．过点P 作1PE l ∥．Q 1PE l ∥，12l l ∥，\12PE l l ∥∥，PAC APE \Ð=Ð，PBD BPE Ð=Ð，APB APE BPE Ð=Ð-ÐQ ，PAC PBD APB \Ð-Ð=Ð．【点睛】本题考查了平行线的性质以及角的计算，解题的关键是根据“两直线平行，内错角相等”找到相等的角．本题属于基础题，难度不大，解决该题型题目时，根据平行线的性质得出相等（或互补）的角是关键．4．（2021下·广东东莞·七年级东莞市光明中学校考期中）（1）如图（1）AB CD P ，猜想BPD Ð与B D ÐÐ、的关系，说出理由．（2）观察图（2），已知AB CD P ，猜想图中的BPD Ð与B D ÐÐ、的关系，并说明理由．（3）观察图（3）和（4），已知AB CD P ，猜想图中的BPD Ð与B D ÐÐ、的关系，不需要说明理由．【答案】（1）360B BPD D Ð+Ð+Ð=°，理由见解析；（2）BPD B D Ð=Ð+Ð，理由见解析；（3）图（3）BPD D B Ð=Ð-Ð，图（4）BPD B DÐ=Ð-Ð【分析】（1）过点P 作EF AB ∥，得到180B BPE Ð+Ð=°，由AB CD P ，EF AB ∥，得到EF CD P ，得到180EPD D Ð+Ð=°，由此得到360B BPD D Ð+Ð+Ð=°；（2）过点P 作PE AB P ，由PE AB CD ∥∥，得到12B D Ð=ÐÐ=Ð，，从而得到结论12BPD B D Ð=Ð+Ð=Ð+Ð；（3）由AB CD P ，根据两直线平行，内错角相等与三角形外角的性质，即可求得BPD Ð与B D ÐÐ、的关系．【详解】（1）解：猜想360B BPD D Ð+Ð+Ð=°．理由：过点P 作EF AB ∥，∴180B BPE Ð+Ð=°，∵AB CD P ，EF AB ∥，∴EF CD P ，∴180EPD D Ð+Ð=°，∴360B BPE EPD D Ð+Ð+Ð+Ð=°，∴360B BPD D Ð+Ð+Ð=°；（2）BPD B D Ð=Ð+Ð．理由：如图，过点P 作PE AB P ，∵AB CD P ，∴PE AB CD ∥∥，∴12B D Ð=ÐÐ=Ð，，∴12BPD B D Ð=Ð+Ð=Ð+Ð；（3）如图（3）：BPD D B Ð=Ð-Ð．理由：∵AB CD P ，∴1D Ð=Ð，∵1B P Ð=Ð+Ð，∴D B P Ð=Ð+Ð，即BPD D B Ð=Ð-Ð；如图（4）：BPD B D Ð=Ð-Ð．理由：∵AB CD P ，∴1B Ð=Ð，∵1D P Ð=Ð+Ð，∴B D P Ð=Ð+Ð，即BPD B D Ð=Ð-Ð．【点睛】此题考查了平行线的性质，平行公理的推论，三角形的外角的性质定理，熟记平行线的性质是解题的关键．5．（2021下·浙江·七年级期末）已知//AM CN ，点B 为平面内一点，AB BC ^于B ．（1）如图1，点B 在两条平行线外，则A Ð与C Ð之间的数量关系为______；（2）点B 在两条平行线之间，过点B 作BD AM ^于点D ．①如图2，说明ABD C Ð=Ð成立的理由；②如图3，BF 平分DBC Ð交DM 于点,F BE 平分ABD Ð交DM 于点E ．若180,3FCB NCF BFC DBE ÐÐÐÐ+=°=，求EBC Ð的度数．【答案】（1）∠A +∠C =90°；（2）①见解析；②105°【分析】（1）根据平行线的性质以及直角三角形的性质进行证明即可；（2）①过点B 作BG ∥DM ，根据平行线找角的联系即可求解；②先过点B 作BG ∥DM ，根据角平分线的定义，得出∠ABF =∠GBF ，再设∠DBE =α，∠ABF =β，根据∠CBF +∠BFC +∠BCF =180°，可得2α+β+3α+3α+β=180°，根据AB ⊥BC ，可得β+β+2α=90°，最后解方程组即可得到∠ABE =15°，进而得出∠EBC =∠ABE +∠ABC =15°+90°=105°．【详解】解：（1）如图1，AM 与BC 的交点记作点O ，∵AM ∥CN ，∴∠C =∠AOB ，∵AB ⊥BC ，∴∠A +∠AOB =90°，∴∠A +∠C =90°；（2）①如图2，过点B 作BG ∥DM ，∵BD⊥AM，∴DB⊥BG，∴∠DBG=90°，∴∠ABD+∠ABG=90°，∵AB⊥BC，∴∠CBG+∠ABG=90°，∴∠ABD=∠CBG，∵AM∥CN，BG∥DM，BG CN\//,∴∠C=∠CBG，∠ABD=∠C；②如图3，过点B作BG∥DM，∵BF平分∠DBC，BE平分∠ABD，∴∠DBF=∠CBF，∠DBE=∠ABE，由（2）知∠ABD=∠CBG，∴∠ABF=∠GBF，设∠DBE=α，∠ABF=β，则∠ABE=α，∠ABD=2α=∠CBG，∠GBF=∠AFB=β，∠BFC=3∠DBE=3α，∴∠AFC =3α+β，∵∠AFC +∠NCF =180°，∠FCB +∠NCF =180°，∴∠FCB =∠AFC =3α+β，△BCF 中，由∠CBF +∠BFC +∠BCF =180°得：2α+β+3α+3α+β=180°，∵AB ⊥BC ，∴β+β+2α=90°，∴α=15°，∴∠ABE =15°，∴∠EBC =∠ABE +∠ABC =15°+90°=105°．【点睛】本题主要考查了平行线的性质的运用，解决问题的关键是作平行线构造内错角，运用等角的余角（补角）相等进行推导．余角和补角计算的应用，常常与等式的性质、等量代换相关联．解题时注意方程思想的运用．6．（2021下·福建厦门·七年级厦门市第十一中学校考期中）已知，//AE BD ，A D Ð=Ð．（1）如图1，求证：//AB CD ；（2）如图2，作BAE Ð的平分线交CD 于点F ，点G 为AB 上一点，连接FG ，若CFG Ð的平分线交线段AG 于点H ，连接AC ，若ACE BAC BGM Ð=Ð+Ð，过点H 作HM FH ^交FG 的延长线于点M ，且3518E AFH Ð-Ð=°，求EAF GMH Ð+Ð的度数．【答案】（1）见解析；（2）72°【分析】（1）根据平行线的性质得出180A B Ð+Ð=°，再根据等量代换可得180B D Ð+Ð=°，最后根据平行线的判定即可得证；（2）过点E 作//EP CD ，延长DC 至Q ，过点M 作//MN AB ，根据平行线的性质及等量代换可得出ECQ BGM DFG Ð=Ð=Ð，再根据平角的含义得出ECF CFG Ð=Ð，然后根据平行线的性质及角平分线的定义可推出,BHF CFH CFA FAB Ð=ÐÐ=Ð；设,FAB CFH a b Ð=Ð=，根据角的和差可得出2AEC AFH Ð=Ð，结合已知条件35180AEC AFH Ð-Ð=°可求得18AFH Ð=°，最后根据垂线的含义及平行线的性质，即可得出答案．AFH CFH CFA CFH FABÐ=Ð-Ð=Ð-ÐQ AFH b a \Ð=-，BHF CFH bÐ=Ð=222ECF AFH AEC EAB AFH AEC b\Ð+Ð=Ð+Ð+Ð=Ð+22ECF AFH E BHF\Ð+Ð=Ð+Ð2AEC AFH\Ð=Ð35180AEC AFH Ð-Ð=°Q 18AFH \Ð=°FH HM^Q 90FHM \Ð=°90GHM b\Ð=°-180CFM NMF Ð+Ð=°Q 90HMB HMN b\Ð=Ð=°-EAF FABÐ=ÐQ 18EAF CFA CFH AFH b \Ð=Ð=Ð-Ð=-°189072EAF GMH b b \Ð+Ð=-°+°-=°72EAF GMH \Ð+Ð=°．【点睛】本题考查了平行线的判定及性质，角平分线的定义，能灵活根据平行线的性质和判定进行推理是解此题的关键．模型四、“骨折模型”如图，已知BC//DE ，试猜想∠A 、∠B 、∠D 的关系，并说明理由．解：∠BAD=∠D-∠B ,理由如下：过点A 作 AG // BC又 ∵CB//DE ．∴AG//DE∴∠GAB+∠B=180°，∠GAD+∠D=180°∴ ∠BAD ＝ ∠GAB- ∠GAD=180°-∠B–(180°-∠D)=∠D-∠B即：∠BAD=∠D-∠B注：平行线四大模型大题不可直接使用，必须证明后再用，选择填空满足条件即可直接用！【答案】60°【分析】过点B作BD∥2CBDÐ=Ð，进而可得Ð【详解】解：如图，过点Q Rt ABC△中，30AÐ=°，\9060ABC AÐ=°-Ð=°．Q BD EF∥，\1ABDÐ=Ð．【答案】40°/40度∥【分析】过C作CF ABÐ=°即可得到答案；CDE140【点睛】本题考查平行线的判定与性质，解题的关键是作出辅助线，根据平行线性质得到角度关系．二、解答题4．（2021·全国·九年级专题练习）已知AB //CD ，求证：∠B ＝∠E ＋∠D【答案】见解析【分析】过点E 作EF ∥CD ，根据平行线的性质即可得出∠B =∠BOD ，根据平行线的性质即可得出∠BOD =∠BEF 、∠D =∠DEF ，结合角之间的关系即可得出结论．【详解】证明：过点E 作EF ∥CD ，如图∵AB ∥CD ，∴∠B =∠BOD ，∵EF ∥CD （辅助线），∴∠BOD =∠BEF （两直线平行，同位角相等）；∠D =∠DEF （两直线平行，内错角相等）；∴∠BEF =∠BED +∠DEF =∠BED +∠D （等量代换），∴∠BOD=∠E +∠D （等量代换），即∠B =∠E +∠D ．【点睛】本题考查了平行线的性质以及角的计算，解题的关键是根据平行线的性质找出相等或互补的角．5．（2021下·山西晋中·七年级统考期中）综合与探究【问题情境】王老师组织同学们开展了探究三角之间数量关系的数学活动（1）如图1，//EF MN ，点A 、B 分别为直线EF 、MN 上的一点，点P 为平行线间一点，请直接写出PAF Ð、PBN Ð和APB Ð之间的数量关系；【问题迁移】（2）如图2，射线OM 与射线ON 交于点O ，直线//m n ，直线m 分别交OM 、ON 于点A 、D ，直线n 分别交OM 、ON 于点B 、C ，点P 在射线OM 上运动，①当点P 在A 、B （不与A 、B 重合）两点之间运动时，设ADP a Ð=Ð，BCP b Ð=Ð．则CPD Ð，a Ð，Ðb 之间有何数量关系？请说明理由．②若点P 不在线段AB 上运动时（点P 与点A 、B 、O 三点都不重合），请你画出满足条件的所有图形并直接写出CPD Ð，a Ð，Ðb 之间的数量关系．【答案】（1）360PAF PBN APB Ð+Ð+Ð=°；（2）①CPD a b Ð=Ð+Ð，理由见解析；②图见解析，CPD b a Ð=Ð-Ð或CPD a bÐ=Ð-Ð【分析】（1）作PQ ∥EF ，由平行线的性质，即可得到答案；（2）①过P 作//PE AD 交CD 于E ，由平行线的性质，得到DPE a Ð=Ð，CPE b Ð=Ð，即可得到答案；②根据题意，可对点P 进行分类讨论：当点P 在BA 延长线时；当P 在BO 之间时；与①同理，利用平行线的性质，即可求出答案．【详解】解：（1）作PQ ∥EF ，如图：∵//EF MN ，∴////EF MN PQ ，∴180PAF APQ Ð+Ð=°，180PBN BPQ Ð+Ð=°，∵APB APQ BPQÐ=Ð+Ð∴360PAF PBN APB Ð+Ð+Ð=°；（2）①CPD a b Ð=Ð+Ð；理由如下：如图，过P 作//PE AD 交CD 于E ，∵//AD BC ，∴////AD PE BC ，∴DPE a Ð=Ð，CPE b Ð=Ð，∴CPD DPE CPE a b Ð=Ð+Ð=Ð+Ð；②当点P 在BA 延长线时，如备用图1：∵PE ∥AD ∥BC ，∴∠EPC=b ，∠EPD =a ，∴CPD b a Ð=Ð-Ð；当P 在BO 之间时，如备用图2：∵PE ∥AD ∥BC ，∴∠EPD =a ，∠CPE =b ，∴CPD a b Ð=Ð-Ð．【点睛】本题考查了平行线的性质，解题的关键是熟练掌握两直线平行同旁内角互补，两直线平行内错角。

平行线和相交线拔高题

平行线和相交线拔高题1、若两个角的两边分别平行，而其中一个角比另一个角的 3 倍少 40°，那么这两个角的度数是( )A ．20°或 55°B ．20°或 160°C ．20°、20°或 55°、125°D ．20°、125°或 20°、70°2、如图，BC ∥DE ，点A 在BC 上方，AF 平分∠BAD ，过点B 的直线GH ，使∠GBC 与∠GBA 互补，GH 分别交AF 于F ，交DE 的反向延长线于H ，若∠GFA+∠GHE=165°，则∠BAD= .3、如图，图①是一个四边形纸条ABCD ，其中AB ∥CD ，E ，F 分别为边AB ，CD 上的两个点，将纸条ABCD 沿EF 折叠得到图②，再将图②沿DF 折叠得到图③，若在图③中，∠FEM=26°，则∠EFC 的度数为A ．52°B ．64°C ．102°D ．128°4、如图，三角形ABC 中，∠C =90°，AC=3 cm ，CB=4 cm ，AB=5 cm ，将三角形ABC 沿直线CB 向右平移1 cm 得到三角形DEF ，DF 交AB 于点G ，则下列结论：①S 四边形ACFG =S 四边形BEDG ； ②FG=49cm ； ③43DE BG ；④点C 到直线DE 的距离为3 cm. ，其中正确的结论有( )个A ．1B ．2C ． 3D ． 4图①图②图③5、如图，AB ∥CD ，则∠1，∠2，∠3，∠4 的关系是（）A ．∠1－∠2＋∠3＋∠4＝180°B ．∠1＋∠2＋∠4＝∠3C ．∠3＋∠2＝∠4＋∠1D ．∠1＋∠2＋∠3－∠4＝180°6、如图，AE 平分∠BAD 交BC 边于点E ，AE ⊥DE ，∠EAD+∠EDC=90°，M ，N 分别是BA ，CD 延长线上的点，∠EAM 和∠EDN 的平分线相交于点F ，则∠F= °．7、如图，AB//DE ，∠ABC 的角平分线BP 和∠CDE 的角平分线DK 的反向延长线交于点P 且∠P −2∠C =57∘，则∠C 等于。

专题01平行线(四种模型)专项训练(原卷版)

七年级数学平行线性质与判定(拔高压轴题)(1)

C．第一次向右拐50°，第二次向右拐130°
D．第一次向左拐50°，第二次向左拐130°
12、如图，AB∥DE，∠ABC=70°，∠CDE=147°，求∠C的度数．
13、如图，CD∥BE，则∠2+∠3−∠１的度数等于多少？
四．复杂平行线性质与判定证明
1.如图，∠ABC=∠BCD,∠1=∠2,求证：BE∥CF.
复杂平行线分类练习（冲刺高分）拔高题目
一：平行于角平分线
1.已知:如图AB//CD, ,AE、BE分别平分、 .请求出的度数.
2.已知：如上图，AB∥CD，EF∥AB，BE、DE分别平分∠ABD、∠BDC.求证：∠1与∠2互余.
3.如下图，已知CB⊥AB，CE平分∠BCD，DE平分∠CDA，∠1+∠2＝90°.求证：DA⊥AB.
7.OB、OC分别平分∠ABC、∠ACB，已知∠A=50°，求∠B0C.(整体思想)
二．平行间有拐点
1.如图，DE∥CB，试证明∠AED＝∠A＋∠B。
2.如图所示，已知AB∥CD，分别探索下列四个图形中∠P与∠A、∠C的关系，
请你从所得的四个关系中加以说明．
(1)(2)(3)(4)
3.如图（1），MA1∥NA2，则∠A1＋∠A2＝___________度。
8.如图，∠CAB＝100°，∠ABF＝130°，AC∥MD，BF∥ME，求∠DME 的度数。
9、已知DE∥BC，CD是∠ACB的角平分线，∠B=80°，∠ACB=50°.试求∠EDC与∠BDC的度数。
10.如图，已知∠1=∠2=∠3，∠GFA= ，∠ACB= ，AQ平分∠FAC，求∠HAQ的度数．
（A）（B）
（C）（D）
5.如图，则．
第5题第6题第7题第8题

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

【“M ”型证明问题】
1.已知，如图1、2，AB ∥DE ，探究∠B 、∠D 和∠C 的关系（请用不同的方法解决问题）.
2.已知，如图3、4、5，AB ∥DE ，探究∠B 、∠D 和∠C 的关系.
B E
E
图3 图4 图5
3.已知，如图6、7、8，AB ∥DE ，探究∠B 、∠D 和∠C 、∠F 的关系.
4.如图，若AB ∥CD ，猜想∠A 、∠E 、∠D 之间的关系，并证明.
5.阅读填空：
（1）如图，AB ∥DE ，试问∠B 、∠E 、∠BCE 有什么关系．解：∠B ＋∠E ＝∠BCE 过点C 作CF ∥AB ，
则∠B=__________（）又∵AB ∥DE ，AB ∥CF ，
∴____________（）
∴∠E ＝∠____（）
∴∠B ＋∠E ＝∠1＋∠2 即∠B ＋∠E ＝∠BCE ．
图7
D
图6 图8
图
9 C
D F
（2）如右图，当∠B 、∠E 、∠BCE 有什么关系时，有AB ∥DE ．
（3）仿照上题方法解答：如图，AB ∥DE ，那么∠B 、∠BCD 、∠D 有什么关系？
【“M ”型数形结合】
4.如图10，AB ∥CD ，且∠BAP=60°-α，∠APC=45°+α，∠PCD=30°-α，则α=( )
A.10°
B.15°
C.20°
D.30° 5.如图10，CD AB //，且
25=∠A ，
45=∠C ，则P ∠的度数是（）
A.
60 B.
70 C. 110 D.
80 6.已知：如图11， AB ∥EF ∥CD ，EG 平分∠BEF ，∠B+∠BED+∠D =192°， ∠B-∠D=24°，求∠GEF 的度数。

图10
G
图11
D
F
7.如图，已知：0
)90(x A +=∠，0
)90(x B -=∠， 90=∠CED ，射线EF ∥AC ，0
2m D C =∠-∠
（1）判断AC 与BD 的位置关系，并说明理由. （2）如图8，当
30=m 时，求C ∠、D ∠的度数.
（3）如图9，求C ∠、D ∠的度数（用含m 的代数式表示）.
8.已知如图1，直线CD ∥EF ，MN 与CD 、EF 都相交，点A 、B 分别在直线CD 、EF 上，且位于MN 的两侧. (1)如图1,点P 是直线MN 上一点，试探究∠DAP 、∠FBP 、∠APB 的数量关系.
(2)若点P 在直线MN 上运动，则∠DAP 、∠FBP 、∠APB 的数量关系是否发生改变，试说明理由.
图12
图13
【“互余型”平行证明】
9．已知：如图15，DG⊥BC AC⊥BC，EF⊥AB，∠1=∠2.求证：EF∥CD.
10.如图，在△ABC中，CD⊥AB于D，FG⊥AB于G，ED//BC，试说明∠1=∠2，
11.已知，如图，CD⊥AB，GF⊥AB，∠B＝∠ADE，试说明∠1＝∠2．
C
F
图15
C F
图16
G
图17。