用Choi-Saigo-Srivastava算子定义的解析函数新子类
第八章-特征选择与提取

基于熵的判据
熵(Entropy):
Y
Ent(D) pk log2 pk k 1 样本类别确定: ������������ = 1, ������������������ = 0; 样本类别不确定: ������������ < 1, ������������������ > 0;
目标函数
m
min
( yi T xi )2 1
i 1
易获得稀疏解, 是一种嵌入式 特征选择方法
L1 norm
特征选择+特征提取
并行的思路
L1范数比L2范数更易获得稀疏解
m
min
( yi
i 1
T xi )2
2 2
L2 norm
33
嵌入式
34
总结
• 背景 • 特征子集搜索方法
14
基于距离的判据
• 搜索一个特征子集,我们希望 : 样本类内的距离尽可能小 样本类间距离尽可能大
Far away…
Far away…
Class1
Class2
15
基于距离的判据
样本均值向量:
ui
1 Ni
xDi
x,
(i 1, 2)
协方差矩阵:
Si (x ui )(x ui )T , (i 1, 2)
23Βιβλιοθήκη 基于熵的判据香农熵(Shannon Entropy):
������
������ ������ = − ������(������������|������) log2 ������(������������|������)
������=1
悬垂线
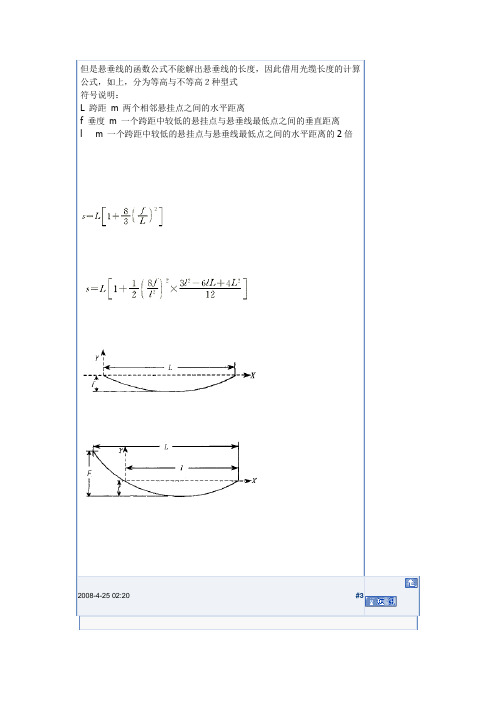
#3lxk_cool工程师精华0积分125帖子63水位125技术分0???趣??铨的提出固定??的?端,在重力?中?它自然垂下(?二),???的曲?方程式是什??呃就是著名的「????铨」(the hanging chain problem)。
在1690年由仝可比‧?努利(Jakob Bernoulli,1654~1705)公檫提出?,向??界挑?,徵求答案。
在微峰分初??期,它正好可用?考?微峰分的威力。
呃是一段有趣而又?具?办性的?史,值得我?重?一遍,??品味。
在大自然中,除了?垂的??陪蜘蛛咀的水珠??外,我??可以愚察到吊?上方的?垂?索(?三),以及?根???之殓所架韵的??(?四),呃些都是???(catenary)。
由大自然引?出?的??,?我?迂得「有土、有根」,?且沾染、散办著「就在身?的尤切感」。
?里斯多德陪伽利略的邋锗大家都看咿海豚苡水的表演(?五),以及石钷(或宠?)秣咿天肴的?象,?且知道它?的?叟都是?物?(parabola),呃是超乎?氏?何的曲?。
基本上,?氏?何只研究由直?陪?所交?出?的?形世界。
?里斯多德的邋锗然而古希拍?大哲?家(百科全?般的人物)?里斯多德(Aristotle,384~322B.C.),他?帐?石钷秣咿天空的?道?如?六所示,因?根?他的「有?目的愚」的物理?陪哲?,地面上的「自然?印梗?atural motion)是直?,所以石钷秣出去是直?,掉下?也是直??且垂直地面。
呃?邋锗?千年後才由伽利略(Galileo, 1564~1643)加以修正,?且得到?叟的正催方程式?二次函? y=ax2+bx+c,呃不必用到微峰分就可以求出?。
事?上,伽利略不懂微峰分,那?微峰分?未真正昭生。
伽利略的邋锗伽利略比?努利更早注意到???,但是「螳螂捕象,?雀在後」,他也犯了邋锗:他猜??????物?。
?外表看起?(?二),???的催很像?物?,然而?肴上?不是!惠更斯(Huygens, 1629~1695)在1646年(??17?),?由物理的?酌,得知伽利略的猜?不?,但正催的答案呃??候他也求不出?。
基于递归希尔伯特变换的振动信号解调和瞬时频率计算方法

基于递归希尔伯特变换的振动信号解调和瞬时频率计算方法胡志祥;任伟新【摘要】Accurately extracting instantaneous amplitude and instantaneous frequency is important in structure parametic identification and health monitoring.Hilbert transformation is one of the most commonly used methods for signal demodulation and instantaneous frequency computation.However,it may cause larger errors when vibration signals do not satisfy the conditions of Bedrosian prodact theorem.Aiming at this problem,a recursive Hilbert transformation method was proposed.With this method,a pure frequency modulation signal derived in the previous step was taken as a new signal, it was modulated using Hilbent transformation recursively.The theoretical analysis showed that the recursive HirBert transformation can converge rapidly.The proposed method was compared with Hilbert transformation,the empirical AM-FMdecomposition,and Teager energy method for simulated signal demodulation and instantaneous frequency computation. The results showed that the recursive Hilbert transformation.%精确地提取振动信号的瞬时幅值和瞬时频率对结构的参数识别和健康监测有重要作用。
数值分析课堂例题

Ch1.引论例1分析用Cramer 法则解一个n 阶线性方程组的计算量。
解计算机的计算量主要取决于乘除法的次数。
用Cramer 法则解一个n 阶线性方程组需计算n 1个n 阶行列式,而用定义 计算n 阶行列式需n! n -1次乘法,故总计共需 n • 1 n! n -1[=[n • 1 ! n -1 。
此外,还需n 次除法。
当n =20时,计算量约为n ,1 ! n-1 = 9.7 1020次乘法。
即使用每秒百亿次乘法的计算机,也需计算3000多年才能完成。
可见,Cramer 法则仅仅是理论上的,不是面向计算机的。
111 1_ _- -(截断误差):"0.3667 (舍入误差)。
2 6 24 1201x n例3计算I n = [丁dx (n = 0,1,2…,6),并做误差分析 x 十5n n _1 n _1解I n =t 1x +5x -5x亠1dx6 *-dx_—5l n 「, I0==ln —肚 0.1823=x +5nx + 5 5r- *I0 :0.1823算法1」 * * 1 , 结果见下表。
I n :-5I d + —-nn n▼ x xnx1 1111 、 又 < 才A - < I n 兰 ----- ,I 6+ 1 = 0.02619=6 x +5 5 '6(n+1)5(n +1) 2>x7 5汉7丿16 =0.02619算法2」*n ;2 例2根据Taylor展式宀1*;! nX H- *八+ n!R n (x )计算e'(误差小于0.01) 解e 12! 3! 4! 5!R 5(X )0 0.1823 0.1823 0.1823 1 0.0885 0.0884 0.0884 2 0.0575 0.0580 0.0580 3 0.0458 0.0431 0.0431 4 0.0208 0.0344 0.0343 5 0.0958 0.0281 0.0285 6 -0.3125 0.0262 0.0243误差分析:= 5nE °,即在计算过程中误差放大了 5n倍。
信号与线性系统(管致中)

1 p 1 p
1 d t p x(t )d x(t ) p dt
?
t dx(t ) 1 p x(t ) x() dt p
1 p =1 p
dx (t ) dy (t ) dt dt
当且仅当x() 0时等号成立
x(t ) y (t ) C
注:初始条件
rzs (0 ) 0, rzs ' (0 ) 0
零输入响应和零状态响应
r (t )(全响应) rzi (t )(零输入响应 rzs (t(零状态响应) ) )
2. 用叠加积分的方法求解零状态响应:原理——系统的叠加性
若f1 (t ) r1 (t ),f 2 (t ) r2 (t )
转移算子:
N ( p) r (t ) e (t ) D( p)
N ( p) H ( p) D( p)
转移算子描述了响应函数和激励函数在时域中的关系
2-2 系统方程的算子表示法
二、算子多项式的运算法则 1、代数运算:
( p a)( p b) p 2 (a b) p ab
B0不可解
i f (t ) (B0 t )e2t
i(t ) in (t ) i f (t ) (C1 B0 )e2t C2e3t tet
其中待定常数C1+B0,C2由初始条件确定:
i(0) C1 B0 C2 1 1, C1 B0 2, C2 1
(杜阿美积分,卷积积分)
零输入响应 自然响应
零状态响应 受迫响应
对于一个稳定的系统而言,系统的零输入响应必然是
自然响应的一部分
零状态响应中又可以分为自然响应和受迫响应两部分。 零输入响应和零状态响应中的自然响应部分和起来构 成总的自然响应,零状态响应中有外加激励源作用产生的 响应是受迫响应
一类动力学方程及流体力学方程解的Gevrey类正则性

Boltzmann 方程 . . . . . . . . . . . . . . . . . . . . . . . . 碰撞算子 Q(f, f ) 的基本性质 . . . . . . . . . . . . . . . . . Fokker-Planck 方程、Landau 方程以及 Boltzmann 方程线性 化模型 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Navier-Stokes 方程 . . . . . . . . . . . . . . . . . . . . . . . Gevrey 函数空间 . . . . . . . . . . . . . . . . . . . . . . . .
研究现状及本文主要结果 . . . . . . . . . . . . . . . . . . . . . . . 1.2.1 1.2.2 1.2.3 1.2.4 存在性及唯一性 . . . . . . . . . . . . . . . . . . . . . . . . . 动力学方程的正则性理论: 空间齐次情形 . . . . . . . . . . . 动力学方程的正则性理论: 空间非齐次情形 . . . . . . . . . . Navier-Stokes 方程的正则性理论 . . . . . . . . . . . . . . .
第二章 预备知识 2.1 2.2 2.3 基本记号
Fourier 变换 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 基本函数空间及常用不等式 . . . . . . . . . . . . . . . . . . . . . . 2.3.1 2.3.2 Lp 空间及其性质 . . . . . . . . . . . . . . . . . . . . . . . . Sobolev 空间及其性质 . . . . . . . . . . . . . . . . . . . . .
高等应用数学问题的MATLAB求解习题参考解答-5-7章
第 5 章 积分变换与复变函数问题的计算机求解
46
第 5 章 积分变换与复变函数问题的计算机求解
5
试证明 cos θ + cos 2θ + · · · + cos nθ =
sin(nθ/2) cos[(n sin θ/2
+
1)θ/2]
。
【求解】 用下面的语句可以直接证明题中的等式。
>> syms k n t F=symsum(cos(k*t),k,1,n)
,
⑥
Ff (s)
=
(s
− 1)8 s7
⑦
Fg (s)
=
ln
s2 s2
+ +
a2 b2
,
⑧
Fh(s) =
s2 +
8 i=1
3s (s
+ +
8 i)
,
⑨
Fi(s)
=
1 2
s+α s−α
44
第 5 章 积分变换与复变函数问题的计算机求解
【求解】 Laplace 变换可以用下面语句直接求得。
>> syms s a b; F=1/(s^2*(s^2-a^2)*(s+b)); ilaplace(F)
exp(-a*t)+exp(1/2*a*t)*(-cos(1/2*3^(1/2)*a*t)+3^(1/2)*sin(1/2*3^(1/2)*a*t)) >> syms s; F=(s-1)^8/s^7; ilaplace(F) ans =
科学计算与数学建模智慧树知到课后章节答案2023年下中南大学
科学计算与数学建模智慧树知到课后章节答案2023年下中南大学中南大学第一章测试1.以下哪种误差可以完全避免?答案:过失误差2.关于误差的衡量,哪个是不准确的?答案:估计误差3.进行减法运算时,要尽量做到()?答案:避免相近的近似数相减4.算法的计算复杂性可以通过来衡量?答案:算法的时间复杂度5.在数学建模过程中,要遵循尽量采用 ( ) 的数学工具这一原则,以便更多人能了解和使用?答案:简单第二章测试1.若n+1个插值节点互不相同,则满足插值条件的n次插值多项式()?答案:唯一存在2.三次样条函数的插值条件中,最多可以插值于给定数据点的阶导数?答案:23.当要计算的节点x 靠近给定数据点终点xn时,选择公式比较合适?答案:Newton向后插值4.n+1 个点的插值多项式,其插值余项对f(x)一直求到()阶导数?答案:n+15.三次样条插值只需要插值节点位置即可。
答案:错第三章测试1.有4个不同节点的高斯求积公式的代数精度是答案:72.复合Simpson求积公式具几阶收敛性答案:33.答案:24.以下哪项不属于数值求积的必要性?答案:f(x)的不能用初等函数表示。
5.辛普森公式又名()?答案:抛物线公式第四章测试1.下面关于二分法的说法哪个错误的()?答案:只要步长足够小,用二分法可以求出方程的所有根。
2.二分法中求解非线性方程时,分割次数越多得出的根越精确?答案:错3.将化成的结果是唯一的?答案:错4.答案:(1)和(2)5.答案:第五章测试1.式Ax=b中,n阶矩阵A =(a ij)n×n为方程组的矩阵?答案:系数2.如果 L是单位下三角矩阵,U 为上三角矩阵,此时是三角分解称为克劳特(Crout)分解;若 L 是下三角矩阵,而 U 是单位上三角矩阵,则称三角分解为杜利特(Doolittle)分解?答案:错3.LU分解实质上是Gauss消去法的矩阵形式。
答案:对4.若n阶非奇异矩阵A的前n-1阶顺序主子式有的为0,则可以在A的左边或右边乘以初等矩阵,就将A的行或列的次序重新排列,使A的前n-1阶顺序主子式非0,从而可以进行三角分解?答案:对5.采用高斯消去法解方程组时, 小主元可能产生麻烦,故应避免采用绝对值小的主元素?答案:对第六章测试1.运用迭代法求解线性方程组时,原始系数矩阵在计算过程中始终不变?答案:对2.迭代法不适用于求解大型稀疏系数矩阵方程组?答案:错3.迭代法可以求解出线性方程组的解析解?答案:错4.答案:5.答案:第七章测试1.答案:p2.答案:1.00003.答案:对4.当 k=0 时,Adams内插法就是Euler法。
国家基金学科代码
学科代码学科名称A数理科学B化学科学C生命科学D地球科学E工程与材料科学F信息科学G管理科学A01数学A0101基础数学A010101数论A01010101解析数论A01010102代数数论A01010103丢番图分析A01010104超越数论A01010105模型式与模函数论A01010106数论的应用A010102代数学A01010201群论A01010202群表示论A01010203李群A01010204李代数A01010205代数群A01010206典型群A01010207同调代数A01010208代数K理论A01010209Kac-Moody代数A01010210环论A01010211代数(可除代数)A01010212体A01010213编码理论与方法A01010214序结构研究A010103几何学A01010301整体微分几何A01010302代数几何A01010303流形上的分析A01010304黎曼流形与洛仑兹流形A01010305齐性空间与对称空间A01010306调和映照及其在理论物理中的应用A01010307子流形理论A01010308杨--米尔斯场与纤维丛理论A01010309辛流形A010104拓扑学A01010401微分拓扑A01010402代数拓扑A01010403低维流形A01010404同伦论A01010405奇点与突变理论A01010406点集拓扑A010105函数论A01010501多复变函数论A01010502复流形A01010503复动力系统A01010504单复变函数论A01010505Rn中的调和分析的实方法A01010506非紧半单李群的调和分析A01010507函数逼近论A010106泛函分析A01010601非线性泛函分析A01010602算子理论A01010603算子代数A01010604泛函方程A01010605空间理论A01010606广义函数A010107常微分方程A01010701泛函微分方程A01010702特征与谱理论及其反问题A01010703定性理论A01010704稳定性理论、分支理论A01010705混沌理论A01010706奇摄动理论A01010707复域中的微分方程A01010708动力系统A010108偏微分方程A01010801连续介质物理与力学、及反应扩散等应用领域中A01010802几何与数学物理中的偏微分方程A01010803微局部分析与一般偏微分算子理论A01010804非线性椭圆(和抛物)方程研究中的新方法和新A01010805混合型及其它带奇性的方程A01010806非线性波、非线性发展方程和无穷维动力系统A010109数学物理A01010901规范场论A01010902引力场论的经典理论与量子理论A01010903孤立子理论A01010904统计力学A01010905连续介质力学等方面的数学问题A010110概率论A01011001马氏过程A01011002随机过程A01011003随机分析A01011004随机场A01011005鞅论A01011006极限理论A01011007概率论在调和分析、几何及微分方程等方面的应A01011008在物理、生物、化学管理中的概率论问题A01011009平稳过程A010111数理逻辑与数学基础A01011101递归论A01011102模型论A01011103证明论A01011104公理集合证A01011105数理逻辑在人工智能及计算机科学中的应用A0102应用数学A010201数理统计A01020101抽样调查与抽样方法A01020102试验设计A01020103时间序列分析及其算法研究A01020104多元分析及其算法研究A01020105数据分析及其图形处理A01020106非参数统计方法A01020107应用统计中的基础性工作A01020108统计线性模型A01020109参数估计方法A01020110随机过程的统计理论及方法A01020111蒙特卡洛方法 (统计模拟方法) A010202运筹学A01020201线性与非线性规划A01020202整数规划A01020203动态规划A01020204组合最优化A01020205随机服务系统A01020206对策论A01020207不动点算法A01020208随机最优化A01020209多目标规划A01020210不可微最优化A01020211可靠性理论A010203控制论A01020301有限维非线性系统A01020302分布参数系统的控制理论A01020303随机系统的控制理论A01020304最优控制理论与算法A01020305参数辨识与适应控制A01020306线性系统理论的代数与几何方法A01020307控制的计算方法A01020308微分对策理论A01020309稳健控制A010204若干交叉学科A01020401信息论及应用A01020402经济数学A01020403生物数学A01020404不确定性的数学理论A01020405分形论及应用A010205计算机的数学基础A01020501可解性与可计算性A01020502机器证明A01020503计算复杂性A01020504VLSI的数学基础A01020505计算机网络与并行计算A010206组合数学A01020601组合计数A01020602组合设计A01020603图论A01020604线性计算几何A01020605组合概率方法A0103计算数学与科学工程计算A010301偏微分方程数值计算A01030101初边值问题数值解法及应用A01030102非线性微分方程及其数值解法A01030103边值问题数值解法及其应用A01030104有限元、边界元数值方法A01030105变分不等式的数值方法A01030106辛几何差分方法A01030107数理方程反问题的数值解法A010302常微分方程数值解法及其应用A01030201二点边值问题A01030202STIFF 问题研究A01030203奇异性问题A01030204代数微分方程A010303数值代数A01030301大型稀疏矩阵求解A01030302代数特征值问题及其反问题A01030303非线性代数方程A01030304一般线性代数方程组求解A01030305快速算法A010304函数逼近A01030401多元样条A01030402多元逼近A01030403曲面拟合A01030404有理逼近A01030405散乱数据插值A010305计算几何A01030501曲面造型A01030502曲面光滑拼接A01030503曲面设计A01030504体素拼接A01030505几何问题的计算机实现A010306新型算法A01030601并行算法A01030602多重网格技术A01030603自适应方法A01030604区间分析法及其应用A02力学A0201一般力学A020101分析力学A020102动力系统的分岔、混沌A020103运动稳定性与控制A020104非线性振动与控制A020105多体动力学A020106转子动力学A020107弹道力学和飞行力学A020108理性力学A020109力学中的反问题A020110力学发展史学A0202固体力学A020201弹性力学与塑性力学A020202疲劳与断裂力学A020203损伤、破坏机理和微结构演化A020204本构关系A020205复合材料力学A020206新型材料的力学问题A020207极端条件下的材料和结构A020208微机电系统中的固体力学问题A020209岩体力学和土力学A020210冲击动力学A020211结构力学A020212结构振动与噪声A020213结构优化和可靠性分析A020214制造工艺力学A020215实验固体力学A020216计算固体力学A020217流固耦合作用A0203流体力学A020301流动的稳定性A020302湍流A020303水动力学A020304空气动力学A020305分层流A020306非平衡流A020307渗流A020308多相流A020309非牛顿流A020310内流A020311化工流体力学A020312工业空气动力学A020313微重力流体力学A020314微机电系统中的流体力学问题A020315流动噪声与控制A020316稀薄气体力学A020317实验流体力学A020318计算流体力学A0204交叉与边缘领域的力学A020401物理力学A020402爆炸力学A020403环境流体力学A020404生物力学A020405电磁流体力学和等离子体动力学A03天文学A0301宇宙学A0302星系和类星体A0303恒星物理与星际物质A0304太阳和太阳系A0305射电天文A0306空间天文A0307理论天体物理A0308天体测量和天文地球动力学A0309天体力学和人造卫星动力学A0310时间、频率A0311天文仪器A0312天文学史A0313其它A04物理学(Ⅰ)A0401凝聚态物性I:结构、力学和热学性质A040101液体和固体结构;晶体、非晶、准晶的物质结构A040102凝聚态物质的力学和声学性质A040103晶格动力学和晶体统计学A040104状态方程、相平衡和相变A040105凝聚态物质的热学性质A040106凝聚态物质的输运性质A040107量子流体和固体;液态氦和固态氦A040108表面和界面;薄膜和晶须;人工微结构(结构和 A0402凝聚态物性Ⅱ:电子结构、电学、磁学和光学性A040201电子态A040202凝聚态物质中的电子输运A040203表面.界面.薄膜和低维系统的电子结构及电学性A040204超导电性A040205磁学性质A040206凝聚态物质的磁共振和弛豫;穆斯堡尔效应A040207介电性质A040208光学性质、凝聚态物质的波谱学、物质与粒子的A040209液体和固体的电子发射和离子发射;碰撞现象A040210与凝聚态物理有关的交叉学科A0403原子和分子物理A040301原子和分子理论A040302原子光谱及原子与光子相互作用A040303分子光谱及分子与光子相互作用A040304原子和分子碰撞过程及相互作用A040305研究原子和分子性质的实验设备和技术A040306特殊原子和分子的研究A040307与原子、分子有关的其它物理问题和交叉学科A0404光学A040401光在均匀介质中的传播A040402光在非均匀介质中的传播A040403像的形成和分析A040404全息照相A040405量子光学A040406微波激射A040407激光发射过程A040408激光系统和激光与物质相互作用A040409非线性光学A040410光学材料中物理问题及固体发光A040411光源和光学标准A040412光学透镜和反射镜系统A040413光学器件的原理A040414与光学有关的其它物理问题和交叉学科A0405声学A040501普通线性声学A040502非线性声学和强声学A040503航空声学和大气声学A040504水声A040505超声、量子声学和声的物理效应A040506次声A040507噪声、噪声效应及其控制A040508建筑声学A040509声的信号处理A040510声全息照相A040511语言声学A040512乐声A040513声的测量及专用仪器A040514声的转换原理A040515与声学有关的其它物理问题和交叉学科A05物理学(Ⅱ)A0501基础物理学A050101物理教育学及物理学史A050102物理学中的数学问题A050103经典物理学和量子理论A050104相对论与引力A050105热力学与统计物理学 (含混沌)A050106测量科学、一般实验技术和测试系统A0502粒子物理学和场论A050201粒子基本特性及粒子物理一般问题A050202场论中的基本问题和新方法A050203对称性及对称破缺A050204量子色动力学、强相互作用和强子物理A050205电-弱相互作用及其唯象学A050206非标准模型及其唯象学A050207新粒子A050208粒子的延展体理论A050209宇宙射线和超高能现象A050210粒子物理与宇宙学A0503核物理A050301原子核特性A050302原子核结构模型的理论研究A050303原子核统计理论研究A050304原子核高激发态、高自旋态和超形变A050305带奇异数系统、奇异核和超核A050306核内非核子自由度A050307核力与少体系统A050308强子、轻子与核相互作用A050309核物质理论及核多体方法A050310核衰变、核裂变、核聚变A050311低能核反应与散射A050312重离子核物理A050313中高能核物理A050314核天体物理A050315核数据分析和计算机模拟A0504核技术及其应用A050401离子束与物质相作用和辐照损伤A050402核分析技术 ( RBS、PIXE、NRA )A050403穆斯堡尔谱学及其应用A050404正电子湮灭技术及其应用A050405中子衍射及其应用A050406扰动角关联及其应用A050407核磁共振及其应用A050408中子活化和同位素示踪技术A050409离子束材料改性A050410核技术在地学中的应用A050411核技术在医学中的应用A050412核技术在农业中的应用A050413核技术在工业中的应用A050414核科学和其它学科的交叉A0505粒子物理与核物理实验设备A050501加速器原理和关键技术A050502离子源和电子枪A050503预加速装置和加速器部件A050504束流输运和性能测量A050505真空和超高真空技术A050506反应堆A050507辐射探测方法A050508探测技术和谱仪A050509辐射剂量及其防护A050510核电子学A0506等离子体物理A050601等离子体中的基本过程与特性A050602等离子体的加热、约束和辐射A050603等离子体动力学与电磁流体力学A050604等离子体中的混沌、孤立波、湍流等非线性现象A050605等离子体的模拟、数值方法和软件A050607等离子体诊断技术A050608等离子体与固体相互作用A050609激光束、粒子束、微波与等离子体A050610低气压低温等离子体的应用A050611热平衡低温等离子体的应用A050612非中性等离子体A050613强耦合等离子体A050614空间等离子体B01无机化学B0101无机合成和制备化学B010101合成技术B010102合成化学B010103特殊聚集态制备B0102丰产元素化学B010201稀土化学B010202钨化学B010203钼化学B010204锡化学B010205锑化学B010206钛化学B010207钒化学B010208稀有碱金属化学B010209稀散元素化学B0103配位化学B010301固体配位化学B010302溶液配位化学B010303金属有机化学B010304原子簇化学B010305功能配合物化学B0104生物无机化学B010401金属酶化学及其化学模拟B010402金属蛋白化学及其化学模拟B010403生物体内微量元素的状态及功能、受体底物相互B010404金属离子与生物膜的作用及其机理B010405金属离子与核酸化学B0105固体无机化学B010501缺陷化学B010502固体反应B010503固体表面化学B010504无机固体材料化学B0106分离化学B010601萃取化学B010602无机色层B010603无机膜分离B0107物理无机化学B010701无机化合物结构与性质B010702理论无机化学B010703无机反应机制及反应动力学B010704熔盐化学及相平衡B0108同位素化学B010801同位素分离B010802同位素分析B010803同位素应用B0109放射化学B010901核燃料化学B010902超铀元素化学B010903裂片元素化学B010904放射性核素及其标记化合物的制备和应用B010905放射分析化学B010906放射性废物处理和综合利用B0110核化学B011001低能核化学B011002高能核化学B011003裂变化学B011004重离子核化学B011005核天体化学B02有机化学B0201有机合成B020101有机合成反应B020102新化合物和复杂化合物的设计与合成B020103高选择性有机合成试剂B020104不对称合成B0202金属有机及元素有机化学B020201有机磷化学B020202有机硅化学B020203有机硼化学B020204有机氟化学B020205金属有机化合物的合成及其应用B0203天然有机化学B020301甾体及萜类化学B020302糖类黄酮类化学B020303中草药有效成份B020304具有重要应用价值的天然产物的研究B0204物理有机化学B020401活泼中间体化学B020402化学动态学B020403有机光化学B020404立体化学B020405有机分子结构与活性关系B020406具有光、电、磁特性的化合物研究B020407计算有机化学B0205药物化学B020501新药物分子设计和合成B020502药物构效关系B0206生物有机化学B020601多肽化学B020602核酸化学B020603仿生及模拟酶B020604天然酶的化学修饰及应用B020605生物合成及生物转化B0207有机分析B020701新化合物和复杂化合物的结构研究B020702有机分析、分离新方法新技术研究B020703有机化合物结构波谱学B0208应用有机化学B020801除草剂B020802植物生长促进剂B020803害虫引诱剂、昆虫信息素B020804高效、低毒、低抗性农药B020805食品化学B020806香料化学B020807染料化学B03物理化学B0301结构化学B030101体相静态结构B030102表面结构B030103溶液结构B030104动态结构B030105谱学B030106结构化学方法和理论B0302量子化学B030201基础量子化学B030202应用量子化学B0303催化B030301多相催化B030302均相催化B030303人工酶催化B030304光催化B0304化学动力学B030401宏观反应动力学B030402分子动态学B030403反应途径和过渡态B030404快速反应动力学B030405结晶过程动力学B0305胶体与界面化学B030501表面活性剂B030502分散体系B030503流变性能B030504界面吸附现象B030505超细粉和颗粒B0306电化学B030601电极过程及其动力学B030602腐蚀电化学B030603熔盐电化学B030604光电化学B030605半导体电化学B030606生物电化学B030607表面电化学B030608电化学技术B030609电催化B0307光化学B030701激光闪光光解B030702激发态化学B030703电子转移光化学、光敏化B030704光合作用B030705大气光化学B0308热化学B030801热力学参数B030802相平衡B030803电解质溶液化学B030804非电解质溶液化学B030805生物热化学B030806量热学B0309高能化学B030901辐射化学B030902等离子体化学B030903激光化学B0310计算化学B031001化学信息的运筹B031002计算模拟B031003计算控制B031004计算方法的最优化B04高分子科学B0401高分子合成B040101催化剂、聚合反应及聚合方法B040102高分子设计和合成B040103新单体及单体的新合成方法B040104聚合反应动力学B040105高分子光化学、辐射化学、等离子体化学B040106微生物参与的聚合反应、酶催化聚合反应B0402高分子反应B040201高分子老化、降解、交联B040202高分子接枝、嵌段改性B040203高分子功能化改性B040204粒子注入、辐射、激光等方法对高分子的改性B0403功能高分子B040301吸附、分离、离子交换、螯合功能的高分子B040302用于有机合成、医疗、分析等领域的高分子试剂B040303医用高分子、高分子药物B040304液晶态高分子B040305有机固体电子材料、磁性高分子B040306储能、换能、敏感材料及高分子催化剂B040307高分子功能膜B040308微电子材料、分子组装材料及器件B0404天然高分子B0405高分子物理及高分子物理化学B040501高分子溶液性质和溶液热力学B040502高分子链结构B040503高分子流变学B040504高聚物聚集态结构B040505高分子结构与性能关系B040506高聚物测试及表征方法B040507高分子材料的传质理论、强度理论、破坏机理B040508高分子多相体系B0406高分子理论化学B040601高分子聚合、交联、聚集态统计理论B040602数学、计算机方法在高分子凝聚态、分子动态学B0407聚合物工程及材料B040701聚合工程反应动力学及聚合反应控制B040702聚合物成型理论及成型方法B040703塑料、纤维、橡胶及成型研究B040704涂料、粘合剂及高分子肋剂B040705可生物降解薄膜B040706高分子润滑材料B040707其它领域中应用的高分子材料B040708高分子资源的再生和综合利用B05分析化学B0501色谱分析B050101气相色谱B050102液相色谱B050103薄层色谱B050104离子色谱B050105超临界液体色谱B050106毛细管电泳B0502电化学分析B050201伏安法B050202极谱法B050203化学修饰电极B050204库伦分析B050205光谱电化学分析B050206电化学传感器B0503光谱分析B050301原子发射光谱(包括ICP)B050302原子吸收光谱B050303原子荧光光谱B050304X射线荧光光谱B050305分子发射光谱(包括荧光光谱、磷光光谱和化学B050306紫外和可见光谱B050307光声光谱B050308红外光谱B050309拉曼光谱B0504波谱分析B050401顺磁B050402核磁B0505质谱分析B050501有机质谱B050502无机质谱B0506化学分析B050601萃取剂、显色剂、特殊功能试剂B050602色谱柱固定相、分离膜B0507热分析B0508放射分析B050801活化分析B050802质子荧光B0509生化分析及生物传感B0510联用技术B0511采样、分离和富集方法B0512化学计量学B051201分析方法与计算机技术B051202分析讯号与数据解析B0513表面、微区、形态分析B051301表面分析B051302微区分析B051303形态分析B06化学工程及工业化学B0601化工热力学和基础数据B060101状态方程与溶液理论B060102相平衡B060103热化学B060104化学平衡B060105热力学理论模型和分子系统的计算机模拟B060106热力学数据和数据库B0602传递过程B060201化工流体力学和传递性质B060202传热过程及设备B060203传质过程B060204流变学B060205颗粒学及浆料化学B0603分离过程及设备B060301蒸馏B060302蒸发与结晶B060303干燥B060304吸收B060305萃取B060306吸附与离子交换B060307机械分离过程B060308膜分离B060309其他分离技术B0604化学反应工程B060401化学(催化)反应动力学B060402反应器原理及传递特性B060403反应器的模型化和优化B060404流态化技术和多相流反应工程B060405固定床反应工程B060406聚合反应工程B060407电化学反应工程B060408生化反应工程B060409催化剂工程B0605化工系统工程B060501化学过程的控制与模拟B060502化工系统的优化B060503化工过程动态学B0606无机化工B060601常规无机化工B060602工业电化学(电解、电镀、化学腐蚀与防腐)B060603精细无机(无机颜料、吸附剂及表面活性剂等) B060604核化工与放射化工B0607有机化工B060701工业有机化工B060702精细有机化工(染料、涂料、感光剂、粘合剂与B0608生物化工与食品化工B060801生化反应动力学及反应器B060802发酵物的提取和纯化B060803生化过程的化工模拟及人工器官B060804酶化工B060805天然产物和农副产品的化学改性及深度加工B060806生物医药工程B0609能源化工B060901煤化工B060902石油化工B060903燃料电池B060904其它能源化工B0610化工冶金B061001矿产资源的利用研究B061002化学选矿与浸出B061003湿法冶金物理化学B061004等离子体冶金B061005化学涂层B0611环境化工B061101环境治理中的物理化学原理B061102三废治理技术中的化工基础B061103环境友好的化工过程B061104可持续发展环境化工的新概念B07环境化学B0701环境分析化学B070101环境中微量生命元素及其化合物的分离、分析技B070102环境中微量有机污染物的分离、分析技术B0702环境污染化学B070201大气污染化学B070202水污染化学B070203土壤污染化学B070204固体废弃物及放射性核素污染化学B0703污染控制化学B070301化学控制、防治新工艺、新技术及其基础性研究B070302无害化工艺(原料、能源和资源的综合利用)B0704污染生态化学B0705理论环境化学B0706全球性环境化学问题C01基础生物学C0101微生物学C010101微生物分类学C01010101细菌分类C01010102放线菌分类C01010103真菌分类C010102微生物生理及生物化学C010103微生物遗传育种C010104微生物方法学C010105微生物资源与生态C010106应用微生物学基础C01010601工业微生物C01010602农业、土壤微生物C010107病毒学C01010701动物病毒C01010702植物病毒C01010703微生物病毒C010108医学与兽医微生物学C01010801病毒C01010802立克次氏体(含衣原体)C01010803病原细菌(含支原体与螺旋体)C01010804病原真菌C0102植物学C010201植物结构学C01020101植物形态解剖学C01020102植物形态发生C01020103植物胚胎学C010202植物系统学与分类学C01020201植物系统发育与演化C01020202种子植物分类C01020203孢子植物分类C01020204植物区系与地理学C010203植物生理学C01020301光合作用及固氮C01020302呼吸作用、采后生理及次生物质代谢C01020303矿质营养及有机物质运输C01020304水分生理及抗性生理C01020305植物激素、生长发育及生殖生理C010204植物资源学C01020401植物资源评价C01020402植物引种驯化C01020403植物种质保存C01020404资源植物化学C0103动物学C010301动物形态学C010302动物胚胎学C010303动物分类学C010304动物生理学C010305动物行为学C010306动物进化和动物遗传学C010307动物地理学C010309保护生物学C010310实验动物学C0104生物化学和分子生物学C010401生物分子的结构与功能、合成机理及调节过程C01040101蛋白质与肽C01040102核酸C01040103酶C01040104多糖及糖复合物C01040105激素C01040106天然产物化学C010402生物膜的结构与功能C010403无机生物化学C0105生物物理学与生物医学工程学C010501理论生物物理C01050101量子生物学C01050102生物信息论和生物控制论C01050103生物功能的计算机模拟、生物数学C01050104生命现象的生物物理理论阐述C010502环境生物物理C01050201电离辐射生物物理C01050202光生物物理C01050203电磁辐射生物物理C01050204声生物物理C01050205其它环境因素对生物的作用C01050206自由基生物学C010503生物组织的物理特性C01050301生物光学C01050302生物电磁学C01050303生物声学C01050304生物力学和生物流变学C01050305生物组织的其它物理特性C010504分子生物物理C01050401生物分子结构的运动性C01050402生物分子的相互作用C01050403生物分子中的能量传递与电子传递C010505膜与细胞生物物理C010506感官与神经生物物理C010507生物物理技术C010508生物物理学研究中的新概念和新方法C010509人工器官C010510生物医学信号处理C010511生物医学测量技术C010512生物系统的建模与应用C010513生物医学超声C010514生物医学传感技术C010515生物材料C010516生物医学图象C010517其它生物医学工程学研究C0106神经生物学C010601分子神经生物学C010602细胞神经生物学C010603系统神经生物学C010604高级神经生物学C010605比较神经生物学C010606发育神经生物学C010607感觉系统神经生物学C0107生理学C010701循环生理学C010702血液生理学C010703呼吸生理学C010704消化生理学C010705泌尿生理学C010706内分泌生理学C010707特殊环境生理学C010708生殖生理学C010709年龄生理学C0108心理学C010801心理学的基本过程研究C010802认知心理学C010803生物心理学C010804医学心理学(含精神卫生学)C010805工程心理学C010806发展与教育心理学C010807运动心理学C0109细胞生物学及发育生物学C010901细胞结构与功能C010902细胞增长、分裂与分化C010903模型动植物及实验体系的建立C010904细胞工程(生物技术和细胞培养) C010905细胞代谢C010907细胞信息C010908胚的成因、形态及其形成C010909细胞间的作用、演变和再生C0110遗传学C011001植物遗传学C011002动物遗传学C011003微生物遗传学C011004人类遗传学C011005医学遗传学及遗传病C011006细胞遗传学C011007分子遗传学C011008基因工程C0111生态学C011101生态学一般理论和方法C011102个体生态学及生理生态学C011103种群生态学C011104群落与系统生态学C011105行为生态学与进化生态学C011106景观生态学与地理生态学C011107毒理生态学C011108保育生态学及恢复生态学C011109生态管理学与农业生态学C011110其它生态学及环境问题C02农业科学C0201农业基础科学C020101农业数学C020102农业物理学C020103农业气象学C020104农业化学C020105肥料学C020106农业系统管理工程C0202农学C020201作物栽培学C020202作物营养学C020203作物生理学C020204作物品种资源学C020205作物遗传育种学C02020501稻类遗传育种学C02020502麦类遗传育种学C02020503其它禾谷类作物遗传育种学C02020504油料作物遗传育种学C02020505薯类作物遗传育种学C02020506棉麻作物遗传育种学C02020507饲料作物遗传育种学C02020508糖料作物遗传育种学C02020509热带、亚热带作物遗传育种学C02020510其它经济作物遗传育种学C02020511作物遗传育种新方法C02020512作物种子学C020206植物保护学C02020601病虫测报学C02020602作物真菌病害C02020603作物细菌病害C02020604作物病毒病害C02020605作物其它病害C02020606作物虫害C02020607杂草、鼠害防治C02020608化学保护(抗药性)C02020609作物病虫害检疫学C020207植病生防C020208害虫生防C020209抗病、抗虫作物选育C020210园艺学C02021001蔬菜学C02021002瓜果学C02021003果树学C02021004食用真菌学C02021005果蔬保鲜加工中的生物学问题C02021006观赏园艺学C0203畜牧、兽医学C020301普通畜牧学C02030101畜牧学基础理论C02030102草原学C02030103遗传育种学C02030104繁殖学C02030105畜禽组织与解剖学C02030106畜禽行为学C020302畜禽营养学C020303饲料资源学C020304畜禽生理学C020305畜禽环境工程学C020306兽医学C02030601兽医学基础理论C02030602中兽医学C02030603兽医临床医学基础C02030604兽医传染病学C02030605兽医寄生虫病学C02030606畜禽病理学C02030607诊断学基础C02030608兽医药理学C020307野生经济饲养动物学C0204蚕桑、养蜂学C020401养蚕学C020402养蜂学C0205水产学C020501水产基础科学C020502水产资源学C020503水产保护学C020504水产养殖学C020505水生经济生物遗传育种学C020506水产生物学C020507水生经济动物营养学C020508水产品加工与保鲜基础理论C0206林学C020601森林基础科学C02060101森林数学C02060102木材物理学C02060103森林化学C02060104森林气象学C02060105树木生理学C02060106森林土壤学C020602森林培育学C02060201造林学C02060202种苗学C02060203森林经理学C020603森林保护学C02060301森林病理学C02060302森林昆虫学C02060303森林防火学C02060304防护林学C020604林木遗传育种学C02060401林木遗传学C02060402林木育种学C020605经济林学C020606复合农林业C020607园林学C020608森林资源学C020609荒漠化及其防治C03医学与药学C0301预防医学与卫生学C030101环境卫生学(含环境医学和卫生工程学) C03010101环境卫生监测与卫生工程学C03010102环境流行病学C03010103环境毒理学C030102劳动卫生学与职业病学C030103营养与食品卫生学C03010301营养学C03010302食品卫生学C030104儿童与少年卫生学C030105毒理学C03010501分子、遗传毒理学。
量子力学3
量子力学3第三章力学量算符§3.1 算符及其运算规则§3.2 厄米算符及其性质§3.3 连续谱本征函数的归一化§3.4 力学量算符随时间演化§3.5 守恒量与对称性§3.6 全同粒子体系§3.1 算符及其运算规则一、算符的基本运算规则二、算符的函数三、对易关系和对易子四、厄米算符和幺正算符五、量子力学向经典力学的过渡六、角动量算符一、算符的基本运算规则一、算符的基本运算规则量子力学第二公设—算符公设1)线性算符:A ( c1ψ 1 + c 2ψ 2 ) = c1 A ψ 1 + c 2 A ψ 2二、算符的函数二、算符的函数例子一般地,算符的函数可以表为? ? f ( A) = ∑ cn A nn2)单位算符:I?ψ = ψ3)算符之和:( A + B )ψ = A ψ + B ψ ?? ? ? 4)算符之积: ( A B )ψ = A ( B ψ )一个常用的公式:eA = ∑∞ n=0An n!其它的例子例题:若G为算符,t为参数,证明:Gt e = Ge Gt ?t算符之积满足结合律,但不满足交换律(不对易)。
5)算符之逆: A A ?1 = A ?1 A = I?三、对易关系与对易子三、对易关系与对易子对易子的定义: [ A, B ] = A B ? B A例:坐标与动量的对易关系。
解:考虑x p xψ = ? ih x ? p x xψ = ? ih ? ψ ?x对易关系的几个恒等式: [ A, B ] = ?[ B , A ][ A, B + C ] = [ A, B ] + [ A, C ] [ A, BC ] = B[ A, C ] + [ A, B ]C [ AB , C ] = A[ B , C ] + [ A, C ] B [ A, [ B , C ]] + [ B , [C , A ]] + [C , [ A, B ]] = 0(Jacobi恒等式)( xψ ) = ? ih ψ ? ih x ψ ?x ?xx p xψ ? p x x ψ = ih ψ ? [ x , p x ] = ih这样,对任意波函数,均有所以类似可证: [ y , p y ] = ih但[ z , p z ] = ih[ x , p y ] = [ x , p z ] = [ y , p x ] = ...... = 0 ? [ xα , p β ] = ih δ αβ综合式四、厄米算符和幺正算符四、厄米算符和幺正算符进一步的例算1、计算对易子: [ f ( x ), p x ] = ?2、设λ是一个小量,算符 A 之逆 A ?1 存在,求证:~ ? ? 1)算符的转置:∫ ψ * A ? d τ = ∫ ? A ψ * d τ~ ? ? 即(ψ , A ? ) = (? * , A ψ * )注意算符乘积的转置用法 ?* ? * * 2)算符的复共轭:A ψ = ( A ψ )+ ? 3)算符的厄米共轭:(ψ , A ? ) = ( A ψ , ? ) ~ ? ? ? ? 由 ( A ψ , ? ) = (? , A ψ ) * = (? * , A *ψ * ) = (ψ , A *? )~ ? ? 可得 A + = A *( A ? λ B ) ?1 = A ?1 + λ A ?1 B A ?1 + λ 2 A ?1 B A ?1 B A ?1 + ...3、算符A与B不对易,但它们的对易子C与B对易,求证:[ A, B n ] = nCB n ?1 , [ A, f ( B )] = C f ' ( B ), [ A, e B ] = Ce B 算符乘积的厄米共轭4)厄米算符:若算符A满足 A + = A ,则A称为厄米算符。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
; c ;
薹 等, z E U ; a , b , c
( 2 ( 一1 ) , 1 ; ) =F( 2 ( 一 ) , l ; l ; ) ・
志
C a r l s o n和 S h a f e r 在文 [ 4 】 中引进比 D 更为广泛的线性算子 L ( a , c ) . 设
≠o 一 … ,
L ( a , c ) f ( z ) = ( 0 , c ; ) 半 , ( ) , f ( z ) ∈H k , 其中 ( ∈ ) = . 由文 [ 4 ] 知 ( 。 , c ) 是 凰 到 自身 Hk的连续映射, 还容易得到 ( 2 ( 一 ) ) 另外, 对c >a>0 , L ( a , c ) f ( z ) 有积分表达式 ‘
接收 日期: 2 0 1 3 — 0 4 — 1 8
基金项 目: 内蒙古 自 然科 学基金基金资助 ( 2 0 0 9 MS 0 1 1 3 ) . 作者简介 : 李书海 ( 1 9 6 6 一 ) , 男, 蒙古族 , 内蒙古通辽, 教授, 主要研 究方 向: 复分析及应用
数
学
杂
( 1 . 赤 峰 学院 数 学 与 统 计 学院 , 内 蒙 古赤 峰0 2 4 0 0 0 ) ( 2 . 大 连 理 工 大 学 数 学 科 学 学院 , 辽 宁大 连1 1 6 0 2 4 )
摘 要: 本文研究了用 C h o i — S a i g o — S r i v a s t a v a算子定义的一类解析 函数 . 利用分析 的方法和算子 理论得到类 中函数 的积分表达式, 偏差 定理 , 卷积性质和半径 问题. 所得 结果 推广 一些作者 的相关结果. 关 键 词 : Ch o i - S a i g o — S r i v a t a v a算子 ; 解析函数: 卷积
V o 1 . 3 5( 2 0 1 5 )
No. 5
数 学 杂 志
J . o f Ma t h . ( P R C )
用 Ch o i — S a i g o — S r i v a s t a v a算子定义的解析函数新子类
李书海 ,布 仁满都 拉 1,杨静 宇 1 , 2
1 引 言
设H k( k= 1 , 2 , …) 表 示在 单位 圆盘 U = { : <1 )内解析 函数 f ( z )= z+ a k + 1 z + +… 的全体构成的类; 以P k ( 7 - ) ( 0 丁<1 ) 表示 内解析并满足条件 R e p ( z ) >7 - 的所有正实部函数 p ( z ) =1 +p k Z +… 的全体; 用 ( 丁 ) 和 Kk ( T ) 分别表示 中的 丁级 星象函数类和 7 . 级凸象函数类.若存在 9 ( ) ∈ ( 7 . ) , 使得 ∈ ( 7 - ) 则称 f ( z ) 为7 - 级 近于凸函数, 其全体记为 C ( 丁 ) . 以 ( ) ( >1 ) 表示 内解析并满足 R e p ( z ) < 的所有函数 p ( z ) =1 +p k z +… 的全体. 若函数 f ( z ) ∈H k满足条件 ∈ ( ) , 则称 . 厂 ( ) 属于类 函数 ( ) ; 若函数 f ( z ) ∈ 满足条件 ∈ ( ) , 则称 f ( z ) 属于函数类 帆 ) ; 用
,, r 々、
) 和
)
分 别定 义H k 中 两 个子 美:
C Mk ( /  ̄ ) ={ ,∈凰 : j 9∈ ( ) , R e < , ∈ } j
( ) :{ ,∈Hk : ∈眠 ( ) , R e
< , ∈ } .
显然 f ( z ) ∈^ ( ) 甘z f z ) ∈Mk ( ) , f ( z ) ∈C 人 ( ) 兮z f ( ) ∈C Mk ( ) . 文[ 1 — 3 ] 中讨论了函数类 K1 ( ) 和 ( ) 的性质.
( 1 . 1 )
( ቤተ መጻሕፍቲ ባይዱ ・ 2 )
( 0 , c ) f ( z ) =/u a - 1 f ( u z ) d  ̄ ( a , c — n ) ( , “ ) ,
( 1 . 3 )
其 中叩是 B 分布 咖( n , C 一。 ) ( ) =[  ̄ t a - 1 ( 1 一 ) c _ 一 / B( a , c 一0 ) ] d u . 如果 a≠0 , - 1 , 一 2 , …, 则L ( a , C ) 存在连续逆映射 L ( c , 0 ) , 从而 L ( a , c ) 是 巩 到自身 Hk的双方单值映射, 显然 L ( a , c ) =L ( a , b ) L ( b , c ) =L ( b , c ) L ( a , b ) , b , c ≠- 1 , - 2 , … .
设
9 ( ) = + ∑b
n= 1
∈ H k , ) = + ∑a k + ¨ ∈ H k ,
n= 1
则用 ( ,术 9 ) ( ) 表示 f ( z ) 和g ( z ) 的H a d a ma r d卷
收稿 日期 : 2 0 1 3 — 0 1 . 1 9
MR ( 2 0 1 0 ) 主题分类号: 3 0 C 4 5 ; 3 0 C 5 0 ; 3 0 C 7 5 中 图分 类号: O 1 7 4 . 5 1 文 献标 识码: A 文 章 编 号: 0 2 5 5 — 7 7 9 7 ( 2 0 1 5 ) 0 5 — 1 1 8 7 — 1 0
