安徽省六安市城南中学2014届九年级数学第一次段考试题
九年级2014第1次月考试题

九年级第一次月考数学试卷2014.9.26
一.单项选择题(每小题2分,共12分) 1.、小华在解一元二次方程x2﹣x=0时,只得出一个根x=1,则被漏掉的一个 根是( ) A、x=4 B、x=3 C、x=2 D、x=0
2. 若点(2,5),(4,5)在抛物线y=ax2+bx+c上,则它的对称轴是( )
A.abx B.x=1 C.x=2 D.x=3 3、二次函教y=x2+2x﹣5有( ) A、最大值﹣5 B、最小值﹣5 C、最大值﹣6 D、最小值﹣6
4. 对于抛物线21(5)33yx,下列说法正确的是( )
A.开口向下,顶点坐标(53), B.开口向上,顶点坐标(53), C.开口向下,顶点坐标(53), D.开口向上,顶点坐标(53),
5.已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,现有下列结论: ①b2﹣4ac>0 ②a>0 ③b>0 ④c>0 ⑤9a+3b+c<0,则其中结论 正确的个数是( )
A、2个 B、3个 C、4个 D、5个
6.若正比例函数y=mx(m≠0),y随x的增大而减小,则它和二次函数y=mx2+m的图象大致是( ) A. B. C. D.
二.填空题((每小题3分,共24分) 7. 二次函数y=2x2-1的图象与y轴的交点坐标为___________ 8.若将方程x2+6x=7化为(x+m)2=16,则m= .
9. 将抛物线2yx的图象向下平移3个单位,则平移后的抛物线的解析式为___________
10.已知关于x的一元二次方程01)1(22axxa的一个根是0,则a=______ 11.函数2yxbxc与yx的图象如图所示,有以下结论: ①240bc;②10bc;③360bc; ④当13x时,2(1)0xbxc其中结论正确的是___________ (把你认为正确的说法的序号都填上).
2014安徽中考数学试题及答案解析
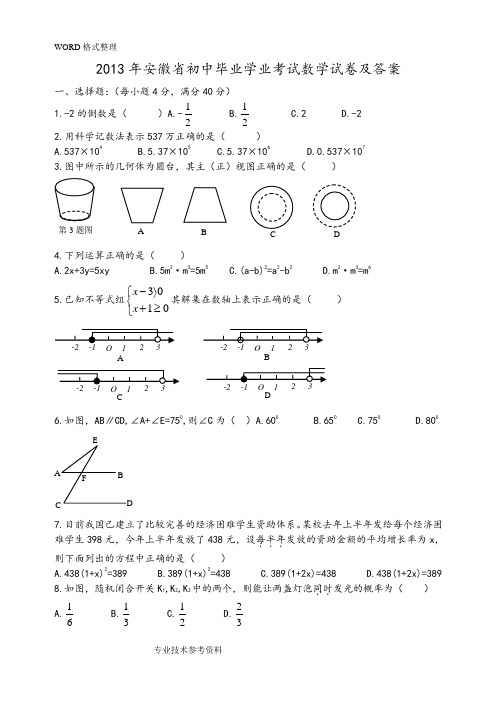
2013年安徽省初中毕业学业考试数学试卷及答案一、选择题:(每小题4分,满分40分) 1.-2的倒数是( )A.-21 B.21C.2D.-2 2.用科学记数法表示537万正确的是( )A.537×104B.5.37×105C.5.37×106D.0.537×1073.图中所示的几何体为圆台,其主(正)视图正确的是( )4.下列运算正确的是( )A.2x+3y=5xyB.5m 2·m 3=5m 5C.(a-b)2=a 2-b 2D.m 2·m 3=m 65.已知不等式组⎩⎨⎧≥+〉-0103x x 其解集在数轴上表示正确的是( )6.如图,AB ∥CD,∠A+∠E=750,则∠C 为( )A.600B.65C.750D.8007.目前我国已建立了比较完善的经济困难学生资助体系。
某校去年上半年发给每个经济困难学生398元,今年上半年发放了438元,设每半年...发放的资助金额的平均增长率为x ,则下面列出的方程中正确的是( )A.438(1+x)2=389B.389(1+x)2=438 C.389(1+2x)=438 D.438(1+2x)=389 8.如图,随机闭合开关K 1,K 2,K 3中的两个,则能让两盏灯泡同时..发光的概率为( ) A.61 B.31 C.21 D.32B12 3O -1 -2 A 12 3O -1 -2123O -1 -2 D12 3O -1-2C第3题图ABC DEAB CDF9.图1所示矩形ABCD 中,BC=x,CD=y,y 与x 满足的反比例函数关系如图2所示,等腰直角三角形AEF 的斜边EF 过点C ,M 为EF 的中点,则下列结论正确的是( ) A.当x=3时,EC <EM B.当y=9时,EC >EMC.当x 增大时,EC ·CF 的值增大D.当y 增大时,BE ·DF 的值不变10.如图,点P 是等边三角形ABC 外接圆⊙O 上点,在以下判断中,不正确...的是( ) A.当弦PB 最长时,△APC 是等腰三角形 B.当△APC 是等腰三角形时,PO ⊥ACC.当PO ⊥AC 时,∠ACP=300D.当∠ACP=300时,△BPC 是直角三角形二、填空题:11.若x 31 在实数范围内有意义,则x 的取值范围是12.分解因式:x 2y-y=13.如图,P 为平行四边形ABCD 边AD 上一点,E,F 分别是PB,PC 的中点,△PEF,△PDC,△PAB 的面积分别为S,S 1,S 2,若S=2,则S 1+S 2=·OABCPAEF ·MDB C O 33 x y第9题 图1第9题 图2 K 2K 3K 1L 1L 2第8题图14.已知矩形纸片ABCD 中,AB=1,BC=2,将该纸片折叠成一个平面图形,折痕EF 不经过A 点(E,F 是该矩形边界上的点),折叠后点A 落在点A /处,给出以下判断: ①当四边形A /CDF 为正方形时,EF=2;②当EF=2时,四边形A /CDF 为正方形; ③当EF=5时,四边形BA /CD 为等腰梯形;④当四边形BA /CD 为等腰梯形时,EF=5.其中正确的是 (把所有正确结论的序号都填在横线上)三、解答题:15.计算:2sin300+(-1)2-2216.已知二次函数图像的顶点坐标为(1,-1),且过原点(0,0),求该函数解析式。
2014年安徽省中考最新模拟考试数学试卷

2014年安徽初中毕业学业考试数 学本卷共8大题,23小题,满分150分,考试时间120分钟.一、选择题(本题共10小题,每小题4分,满分40分). 1.21-的倒数是………………………………………………………………………【 】 A .-2 B .21- C .2 D . 212. 不等式组2131x x -<⎧⎨>-⎩的解集是 …………………………………………………【 】A .2x <B .1x >-C .12x -<<D .无解3. 视力表对我们来说并不陌生.如图是视力表的一部分,其中开口向上的两个“E”之间的变换是 …………………………………………………………………………【 】 A .平移 B .旋转 C .对称 D .相似4. 图中圆与圆之间不同的位置关系有 ……………………………………………【 】 A . 2种 B . 3种 C . 4种 D . 5种5.如图,OAB △绕点O 逆时针旋转80°得到OCD △,若110A ∠=°,40D ∠=°,则∠α的度数是……………………………………………………………………【 】 A .80° B .40° C .50° D .110° 6. 在直角坐标系xOy 中, 点),4(y P 在第四象限内, 且OP 与x 轴正半轴的夹角的正切值是2, 则y 的值是……………………………………………………………【 】 A . 2 B .8 C .-2 D .-8 7. 芜湖某快餐店用米饭加配不同炒菜配制了一批盒饭(每盒米饭只配一种炒菜),配土豆丝炒肉的有25盒,配芹菜炒肉丝的有30盒,配辣椒炒鸡蛋的有10盒,配芸豆炒肉片的有15盒.每盒盒饭的大小、外形都相同,从中任选一盒,不含辣椒的概率是…………………………………………………………………………………【 】 A .78B .67 C .17D .188. 如图所示,平地上一棵树高为6米,两次观察地面上的影子,第一次是当阳光与地面成60°时,第二次是阳光与地面成30°时,第二次观察到的影子比第一次长…………………………………………………………………………………【 】 A.3 B.C.D.3-9. 由7个大小相同的正方体搭成的几何体如图所示,则关于它的视图说法正确的是…………………………………………………………………………………【 】 A .主视图的面积最大 B .俯视图的面积最大C .左视图的面积最大D .三个视图的面积一样大10.如图,在Rt ABC △中,90ACB ∠=°,3BC =,4AC =,AB 的垂直平分线DE 交AB 于点D ,交BC 的延长线于点E ,则CE 的长为 ………………………【 】 A .32 B .76 C .256D .2 二、填空题(本题共4小题,每小题5分,满分20分) 11.计算:cos 60°+tan 230°= .12.第十二届全国人民代表大会第六次会议于2013年3月16日至14日在北京人民大会堂召开,出席会议的代表为2978人,用科学记数法表示为 _______________人.(保留二位有效数字) 13. 在我们刚刚学过的九年级数学下册课本第11页,用“描点法”画某个二次函数图象时,列了如下表格:根据表格上的信息回答问题:该二次函数在x =9时,y = . 14.如图,在扇形纸片AOB 中,OA =10,∠AOB =36︒,OB 在桌面内的直线l 上.现将此扇形沿l 按顺时针方向旋转(旋转过程中无滑动),当OA 落在l 上时,停止旋转.则点O 所经过的路线长为 .三、(本题共2小题,每小题8分,满分16分)15. 计算:()()︒+--+30sin 41212.【解】标准对数视力0.1 4.0 0.1 4.1 0.14.2第3题图第4题图第5题图AD BE第8题图第9题图第10题图l第14题图16. 用配方法解方程:2x 2+x -2=0. 【解】 四、(本题共2小题,每小题8分,满分16分)17. 如图,在△ABC 中,D 是BC 边上的点(不与B ,C 重合),F ,E 分别是AD 及其延长线上的点,CF∥BE . 请你添加一个条件,使△BDE ≌△CDF (不再添加其它线段,不再标注或使用其它字母),并给出证明.(1)你添加的条件是: ;(2)【证明】:18. 已知:抛物线C 1:221(2)22y x m x m =-+++与C 2:22y x mx n =++ 具有下列特征:①都与x 轴有交点;②与y 轴相交于同一点. (1)求m ,n 的值;(2)试写出x 为何值时,y 1 >y 2?(3)试描述抛物线C 1通过怎样的变换得到抛物线C 2. 【解】五、(本题共2小题,每小题10分,满分20分)19. 某风景管理区,为提高游客到某景点的安全性,决定将到达该景点的步行台阶进行改善,把倾角由45°减至30°,已知原台阶坡面AB 的长为5m (BC 所在地面为水平面). (1)改善后的台阶坡面会加长多少?(2)改善后的台阶多占多长一段水平地面?(结果精确到0.1m1.41≈1.73≈)【解】20. .初三学生小丽、小杰为了解本校初二学生每周上网的时间,各自在本校进行了抽样调查.小丽调查了初二电脑爱好者中40名学生每周上网的时间,算得这些学生平均每周上网时间为2.5小时;小杰从全体320名初二学生名单中随机抽取了40名学生,调查了他们每周上网的时间,算得这些学生平均每周上网时间为1.2请根据上述信息,回答下列问题:(1)你认为哪位学生抽取的样本具有代表性?答: ;估计该校全体初二学生平均每周上网时间为 小时; (2)根据具有代表性的样本,把上图中的频数分布直方图补画完整; (3)在具有代表性的样本中,中位数所在的时间段是 小时/周;(4)专家建议每周上网2小时以上(含2小时)的同学应适当减少上网的时间,根据具有代表性的样本估计,该校全体初二学生中有多少名同学应适当减少上网的时间?【解】 六、(本题满分12分)21.某商场在促销期间规定:商场内所有商品按标价的80%出售;同时,当顾客在该商场内消费满一定金额后,还可按如下方案获得相应金额的奖券:320元,获得的优惠额为:400×(1-80%)+30=110(元).购买商品得到的优惠率=购买商品获得的优惠额÷商品的标价试问:(1)购买一件标价为1000元的商品,顾客得到的优惠率是多少?(2)对于标价在500元与800元之间(含500元和800元)的商品,顾客购买标价为多少元的商品,可以得到31的优惠率?A CB D F E第17题图A(每组可含最低值,不含最高值)小时/周【解】 七、(本题满分12分)22. 如图(1),∠ABC =90°,O 为射线BC 上一点,OB = 4,以点O 为圆心,21BO 长为半径作⊙O 交BC 于点D 、E .(1)当射线BA 绕点B 按顺时针方向旋转多少度时与⊙O 相切?请说明理由.(2)若射线BA 绕点B 按顺时针方向旋转与⊙O 相交于M 、N 两点(如图(2)),MN=⌒MN 的长.八、(本题满分14分)23. 几何模型:条件:如图1,A 、B 是直线l 同旁的两个定点.问题:在直线l 上确定一点P ,使PA PB +的值最小.方法:作点A 关于直线l 的对称点A ',连结A B '交l 于点P ,则PA PB A B '+=的值最小(不必证明).模型应用:(1)如图2,正方形ABCD 的边长为2,E 为AB 的中点,P 是AC 上一动点.连结BD ,由正方形对称性可知,B 与D 关于直线AC 对称.连结ED 交AC 于P ,则P B P E +的最小值是___________(填具体数值);(2)如图3,O ⊙的半径为2,点A B C 、、在O ⊙上,OA OB ⊥,60AOC ∠=°,P 是OB 上一动点,求PA PC +的最小值;(3)如图4,45AOB ∠=°,P 是AOB ∠内一点,10PO =,Q R 、分别是OA OB 、上的动点,求PQR △周长的最小值. 【解】第23题图A B A 'P l A BP R Q O A B C A BEC P P图1 图2 图3 图4图(2)图(1)(第22题)2014年数学学业模拟考试参考答案一、选择题 二、填空题11、65 12、3.0×10313、7.5 14、π12三、15、解:原式=2-1-2+21………………………………………………………… 6分 =21- ……………………………………………………………… 8分16、解:配方,得22221221⎪⎭⎫⎝⎛+=⎪⎭⎫ ⎝⎛++x x ……………………………………… 3分即 49212=⎪⎭⎫ ⎝⎛+x …………………………………………………… 4分 所以 2321=+x 或2321-=+x . …………………………………………… 6分 解得 11=x ,22-=x . ……………………………………………………… 8分 四、17、(1)DC BD =(或点D 是线段BC 的中点),ED FD =,BE CF =中任选一个即可.…………………………………………………………………………………… 3分(2)以DC BD =为例进行证明: ∵ CF ∥BE ,∴ ∠FCD ﹦∠EBD .………………………………………………………… 5分 又∵DC BD =,∠FDC ﹦∠EDB ,∴ △BDE ≌△CDF .………………………………………………………… 8分18、(1)由C 1知:△=(m +2)2-4×(12m 2+2)=m 2+4m +4―2m 2―8=―m 2+4m ―4=―(m ―2)2≥0, ∴m =2.当x =0时,y =4.∴当x =0时,n =4.(2)令y 1>y 2 时,444422++>+-x x x x ,∴x <0.∴当x <0时,y 1>y 2; (3)由C 1向左平移4个单位长度得到C 2.19. 解:(1)如图,在Rt ABC △中,52sin 45AC AB ==(m).……2分在Rt ACD △中,15 1.417.05sin 3022AC AD ==÷=≈⨯≈(m),……………4分7.055 2.1AD AB ∴-=-≈m . ………………………………5分即改善后的台阶坡面会加长2.1 m .(2)如图,在Rt ABC △中,53.322545cos ≈=︒⋅=AB BC (m).………6分在Rt ACD △中,6.10tan 302AC CD ==÷≈3(m),……………………………8分6.10 3.53 2.6BD CD BC ∴=-=-≈(m).………………………9分 即改善后的台阶多占2.6.长的一段水平地面. ……………………10分20.(1)小杰;1.2. …………………………………………………………………2分 (2)直方图正确. ………………………………………………………………………4分 (3)0~1. …………………………………………………………………………………6分 (4)该校全体初二学生中有64名同学应适当减少上网的时间 ……………………8分 21.(1)优惠额:1000×(1-80%)+130=330(元) ………………………………………2分优惠率:%33%1001000330=⨯ ……………………………………………4分 (2)设购买标价为x 元的商品可以得到13的优惠率。
2014年九年级上第一次月考数学试题

16题图(1) 16题 图(22014年九年级上第一次月考数学试题一.选择题(每小题3分,共36分) 1.下列方程中是一元二次方程的是( ) (A )3x+2=5x-3 (B )x 2=4 (C )2112x x x =-+- (D )x 2-4=(x+2)2 2. 下列解方程的过程中,正确的是( ) A .x 2=-2,解方程,得x=±2 B 。
4(x-1)2=9,解方程,得±3, x 1=47;x 2=41C .(x-2)2=4,解方程,得x-2=2,x=4D 。
(2x+3)2=25,解方程,得2x+3=±5, x 1= 1;x 2=-4 3.已知方程x 2-6x+q=0可以配方成(x-p )2=7的形式,那么q 的值是( ) A.9 B.7 C.2 D.-24. 方程(x-1)(x-3)=2的根是( )A. x 1=1,x 2=3 B.x=2±23 C.x=2±3 D.x=-2±235.关于x 的方程x 2+2k x+1=0有两个不相等的实数根,则k( ) A.k >-1 B.k ≥-1 C.k >1 D.k ≥06.2(1)31m my m xx -=+-+ 是二次函数,则m 的值为( )A .2.B 。
-1或2C 。
-2D 。
0或27、哈尔滨市政府为了申办2010年冬奥会,决定改善城市容貌,绿化环境,计划过两年时间,绿地面积增加44%,这两年平均每年绿地面积的增长率是 ( ) A. 19% B. 20% C. 21% D. 22%8. 要组织一次排球邀请赛,参赛的每个队之间都要比赛一场,根据场地和时间等条件,赛程计划安排7天,每天安排4场比赛.设比赛组织者应邀请x 个队参赛,则x 满足的关系式为( ) A . x (x +1)=28 B .x (x ﹣1)=28C .x (x +1)=28D .x (x ﹣1)=28 9. 二次函数2)1(212+-=x y 的图象可由221x y =的图象( )A.向左平移1个单位,再向下平移2个单位得到B.向左平移1个单位,再向上平移2个单位得到C.向右平移1个单位,再向下平移2个单位得到D.向右平移1个单位,再向上平移2个单位得到10.已知二次函数y=x 2﹣3x+m (m 为常数)的图象与x 轴的一个交点为(1,0),则关于x 的一元二次方程x 2﹣3x+m=0的两实数根是( ) A .x 1=1, x 2=-1. B . x 1=1, x 2=2. C . x 1=1, x 2=0 D . x 1=1, x 2=311.已知二次函数2y ax bx c =++(a ≠0)的图象如图所示,则下列结论:① ac >0; ② a –b +c <0; ③当x <0时,y <0;④方程20ax bx c ++=(a ≠0)有两个大于-1的实数根. 其中错误的结论有 ( )A .①③ B .②③ C .①④ D .②④12. 已知二次函数y =ax 2+bx +c (a ≠0)的图象如图,且关于x 的一元二次方程ax 2+bx +c ﹣m =0没有实数根,有下列结论:①b 2﹣4ac >0;②abc <0;③m >2.其中,正确结论的个数是( ) A . 0 B .1C .2D .3二.填空题(每小题3分,共18分)13. 如果(a+b-1)(a+b-2)=2,那么a+b 的值为___ _.14、若正数a 是一元二次方程x 2﹣5x +m =0的一个根,﹣a 是一元二次方程x 2+5x ﹣m =0的一个根,则a 的值是 .15、李娜在一幅长90cm 、宽40cm 的风景画的四周外围镶上一条宽度相同的金色纸边,制成一幅挂图,使风景画的面积是整个挂图面积的54%,设金色纸边的宽度为xcm ,根据题意,所列方程为: .16.图16(1)是一个横断面为抛物线形状的拱桥,当水面在l 时,拱顶(拱桥洞的最高点)离水面2m ,水面宽4m .如图16(2)建立平面直角坐标系,则抛物线的关系式是17. 我国航母舰载机某次降落触舰后滑行的距离S (m )与滑行的时间t (s )关系式为S =-5t 2+60t,则舰载机触舰后停下来需要滑行 秒。
2014九年级第一次模拟数学试题(一)
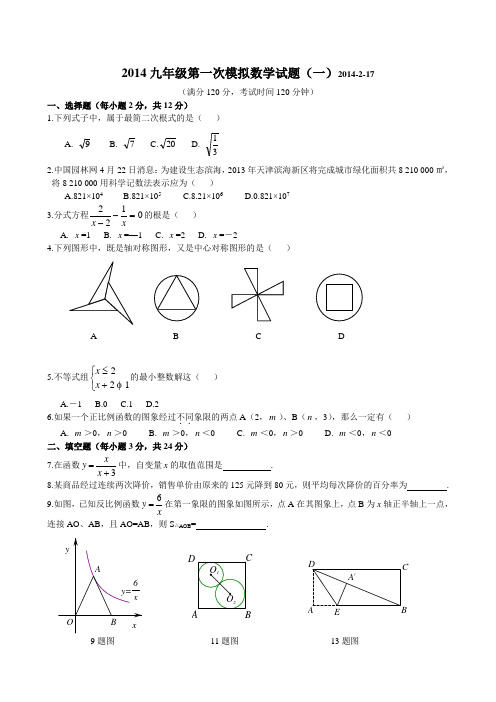
2014九年级第一次模拟数学试题(一)2014-2-17(满分120分,考试时间120分钟)一、选择题(每小题2分,共12分)1.下列式子中,属于最简二次根式的是( )A.9 B. 7 C.20 D.31 2.中国园林网4月22日消息:为建设生态滨海,2013年天津滨海新区将完成城市绿化面积共8 210 000㎡,将8 210 000用科学记数法表示应为( ) A.821×104 B.821×105 C.8.21×106 D.0.821×107 3.分式方程0122=--xx 的根是( ) A. x =1 B. x =—1 C. x =2 D. x =-24.下列图形中,既是轴对称图形,又是中心对称图形的是( )5.不等式组⎩⎨⎧+≤122x x 的最小整数解这( )A.-1B.0C.1D.26.如果一个正比例函数的图象经过不同..象限的两点A (2,m )、B (n ,3),那么一定有( ) A. m >0,n >0 B. m >0,n <0 C. m <0,n >0 D. m <0,n <0 二、填空题(每小题3分,共24分)7.在函数3+=x xy 中,自变量x 的取值范围是 . 8.某商品经过连续两次降价,销售单价由原来的125元降到80元,则平均每次降价的百分率为 . 9.如图,已知反比例函数xy 6=在第一象限的图象如图所示,点A 在其图象上,点B 为x 轴正半轴上一点,连接AO 、AB ,且AO=AB ,则S △AOB = .D A/EDCBAB C D11题图13题图10.若关于x 的函数122-+=x kx y 的图象与x 轴仅有一个公共点,则实数k 的值为 . 11.如图,在边长为3的正方形ABCD 中,⊙1O 与⊙2O 外切,且⊙1O 分别与DA 、DC 边相切,⊙2O 分别与BA 、BC 边相切,则圆心距1O 2O 为 .12.分解因式:=-+a ax ax 322 . 13.如图,在矩形纸片ABCD 中,AB =12,,BC =5,点E在AB 上,将△DAE 沿DE 折叠,使点A 落在对角线BD 上的点A ′处,则AE 的长为 .14.如图,AE 是半圆O 的直径,弦AB=BC=24,弦CD=DE=4,连接OB 、OD ,则图中两个阴影部分的面积和为 .三、解答题(每小题5分,共20分)15.化简:()11222-+-÷-a a a a a .16.如图,两条公路OA 和OB 相交于O 点,在∠AOB 的内部有工厂C 和D ,现要修一个货站P ,使货站P 到两条公路OA 、OB 的距离相等,且到两工厂C 、D 的距离相等,用尺规作出货站P 的位置.(要求:不写作法,保留作图痕迹,写出结论)O14题图 16题图17.解方程xx x --=-2112218.如图,四边形ABCD 是菱形,对角线AC 、BD 相交于点O ,DH ⊥AB 于H ,连接OH ,求证:∠DHO =∠DCO四、解答题(每小题7分,共28分) 19.如图,AB 为⊙O 的直径,C 为⊙O 上一点,AD 与过点C的直线互相垂直,垂足为D ,且AC 平分∠DAB . (1)求证:DC 是⊙O 的切线;(2)若⊙O 的半径为3,AD =4,求AC 的长.HOD C B AA 18题图 19题图20.如图,已知△ABC 和点O .(1)把△ABC 绕点O 顺时针旋转90°得到△A 1B 1C 1,在网格中画出△A 1B 1C 1;(2)用直尺和圆规作△ABC 的边AB ,AC 的垂直不平分线,并标出两条垂直平分线的交点P (要求保留作图痕迹,不写作法);指出点P 是△ABC 的内心,外心?21.天封塔历史悠久,是宁波著名的文化古迹.如图,从位于天封塔的观测点C 测得两建筑物底部A ,B 的俯角分别为45°和60°,若此观测点离地面的高度CD 为51米,A ,B 两点在CD 的两侧,且点A ,D ,B 在同一水平线上,求A ,B 之间的距离(结果保留根号).60°45°F E DC B A 21题图22.从2013年1月7日起,中国中东部大部分地区持续出现雾霾天气. 某市记者为了了解“雾霾天气的主请根据图表中提供的信息解答下列问题;(1)填空:m =________,n =_______,扇形统计图中E 组所占的百分比为_________%. (2)若该市人口约有100万人,请你估计其中持D 组“观点”的市民人数;(3)若在这次接受调查的市民中,随机抽查一人,则此人持C 组“观点”的概率是多少?五、解答题(每小题8分,共16分)23.如图,科技小组准备用材料围建一个面积为60m 2的矩形科技园ABCD ,其中一边AB 靠墙,墙长为12m ,设AD 的长为x m ,DC 的长为y m 。
2014安徽中考数学试题及答案解析

2013年安徽省初中毕业学业考试数学试卷及答案一、选择题:(每小题4分,满分40分) 1.-2的倒数是( )A.—21 B.21C.2D.—2 2.用科学记数法表示537万正确的是( )A 。
537×104B 。
5.37×105 C.5。
37×106 D.0.537×1073.图中所示的几何体为圆台,其主(正)视图正确的是( )4.下列运算正确的是( )A 。
2x+3y=5xyB 。
5m 2·m 3=5m 5 C.(a —b)2=a 2—b 2 D 。
m 2·m 3=m 65.已知不等式组⎩⎨⎧≥+〉-0103x x 其解集在数轴上表示正确的是( )6.如图,AB ∥CD,∠A+∠E=750,则∠C 为( )A.600B 。
65C 。
750D 。
8007.目前我国已建立了比较完善的经济困难学生资助体系.某校去年上半年发给每个经济困难学生398元,今年上半年发放了438元,设每半年...发放的资助金额的平均增长率为x ,则下面列出的方程中正确的是( )A 。
438(1+x)2=389 B.389(1+x)2=438 C 。
389(1+2x)=438 D 。
438(1+2x)=389 8.如图,随机闭合开关K 1,K 2,K 3中的两个,则能让两盏灯泡同时..发光的概率为( ) A.61 B 。
31 C 。
21 D.32BADC第3题图ABC DEAB CDF9.图1所示矩形ABCD 中,BC=x,CD=y,y 与x 满足的反比例函数关系如图2所示,等腰直角三角形AEF 的斜边EF 过点C ,M 为EF 的中点,则下列结论正确的是( ) A 。
当x=3时,EC <EM B 。
当y=9时,EC >EMC.当x 增大时,EC ·CF 的值增大 D 。
当y 增大时,BE ·DF 的值不变10.如图,点P 是等边三角形ABC 外接圆⊙O 上点,在以下判断中,不正确...的是( ) A.当弦PB 最长时,△APC 是等腰三角形 B 。
2014年南二外九年级第一次模拟考试数学试卷
2014年九年级数学试卷第一次模拟考试第一部分 选择题一、选择题(本部分共 小题,每小题 分,共 分,每小题给出 个选项,其中只有一个是正确的) 绝对值为 的实数是☎ ✆ ✌.5± .5 .5- 51.环境监测中 是指大气中直径小于或等于 微米的颗粒物,也称为可入肺颗粒物.数据 用科学记数法可以表示为( )✌.6105.2⨯ .5105.2-⨯ .6105.2-⨯ .7105.2-⨯.如图,下面是由四个完全相同的正方体组成的几何体,这个几何体的主视图是( )✌.....下列计算正确的是( )✌.325a a a += .222(3)9a b a b -=- .3226()ab a b -= .623a b a a b ÷= 某班抽取 名同学参加体能测试,成绩如下: , , , , , 下列表述错误..的是☎ ✆✌ 众数是 中位数是 .平均数是 极差是 .函数中,自变量⌧的取值范围是( )✌.⌧> .⌧<.51-≥x.51≥x.如图,✌ , ✌☜ , , 则 ☜的度数为( )✌.︒30 .︒20 .︒10 . ︒40.某工厂生产一种零件,计划在 天内完成,若每天多生产 个,则 天完成且还多生产 个.设原计划每天生产⌧个,根据题意可列分式方程为( ) ✌....某市今年中考体育测试,其中男生测试项目有 米跑、 米跑、立定跳远、投掷实心球、一分钟跳绳、引体向上、篮球半场来回运球上篮七个项目.考生须从这七个项目中选取两个项目,其中 米跑必选,剩下六个项目选一个,则两名男生在体育测试中所选项目完全相同的概率为( ) ✌.71 .61 .51 . 41.如右图 ,在矩形MNPQ 中,动点R 从点N 出发,沿N ❼P ❼Q ❼M 方向运动至点M 处停止.设点R 运动的路程为x ,图中阴影部分MNR △的面积为y ,如果y 关于x 的函数图象如图 所示,则矩形 ✈☠的面积为( ) ✌. . . . .以下说法正确的有( )①正八边形的每个内角都是 ②反比例函数⍓ ﹣,当⌧< 时,⍓随⌧的增大而增大 ③长度等于半径的弦所对的圆周角为 ♍分式方程13x 1=x x-的解为2x=3; ✌.个.个.个.个.如右图,在平面直角坐标系中,直线⍓ ﹣ ⌧ 与⌧轴、⍓轴分别交于✌、 两点, 以✌为边在第一象限作正方形✌,点 在双曲线( ♊)上.将正方形沿⌧轴负方向平移♋个单位长度后,点 恰好落在该双曲线上, 则♋的值是( )✌. . . .第二部分 非选择题二、填空题(本题共 小题,每小题 分,共 分).分解因式:269mx mx m -+ ♉♉♉♉♉♉♉♉♉♉♉♉♉..如图,将 沿弦✌折叠,使经过圆心 ,则✌ ..观察下列图形中点的个数,若按其规律再画下去,可以得到第⏹个图形中所有点的个数为 (用含⏹的代数式表示)..如图所示,在 ✌中,✌=✌, 、☠分别为✌、✌的中点, 、☜为 上的点,连接 ☠、☜,若✌= ♍❍, = ♍❍, ☜= ♍❍,则图中阴影部分的面积为♉♉♉♉♉♉♉♉♍❍三、解答题(本题共 小题,其中第 题 分,第 题 分,第 题 分,第 题 分,第 题 分,第 题 分,第 题 分,共 分) .计算: 02)14.3(32145sin 8-+-+⎪⎭⎫ ⎝⎛-︒⨯-π.先化简,然后♋在﹣ 、 、 三个数中选一个合适的数代入求值..某校学生准备调查初一年级学生参加❽武术类❾、❽书画类❾、❽棋牌类❾、❽器乐类❾四类校本课程的人数.( )确定调查方式时,甲同学说:❽我到初一( )班去调查全体同学❾;乙同学说:❽放学时我到校门口随机调查部分同学❾;丙同学说:❽我到初一年级每个班随机调查一定数量的同学❾.请指出哪位同学的调查方式最合理.( )他们采用了最为合理的调查方法收集数据,并绘制了如图所示的统计表和扇形统计图.请你根据以上图表提供的信息解答下列问题: ①♋ ♉♉♉♉♉♉♉♉♉ ,♌ ♉♉♉♉♉♉♉♉♉ ;②在扇形统计图中,器乐类所对应扇形的圆心角的度数是 ♉♉♉♉♉♉♉♉♉ ; ③若该校初一年级有学生 人,请你估计大约有多少学生参加武术类校本课程..钓鱼岛是我国固有领土,为测量钓鱼岛东西两端✌, 的距离,如下图,我勘测飞机在距海平面垂直高度为 千米的点 处,测得端点✌的俯角为 ,然后沿着平行于✌的方向飞行 千米到点 ,并测得端点 的俯角为 ,求钓鱼岛两端✌的距离.(结果精确到 千米,参考数据:♦♓⏹ ☟,♍☐♦ ☟,♦♋⏹ ☟,☟)类别频数(人数)频率武术类 书画类 棋牌类 ♌器乐类合计 ♋MEDB.如图,在平行四边形✌中,☜为 边上的一点,连结✌☜、 且✌☜ ✌.( )求证: ✌☜ ☜✌;( )若 ✌☜ ✌,求证:四边形✌是菱形..如图,在平面直角坐标系⌧⍓中,直线⍓ ⌧ 与坐标轴分别交于✌、 两点,过✌、 两点的抛物线为⍓ ﹣⌧ ♌⌧ ♍.点 为线段✌上一动点,过点 作 ⊥⌧轴于点 ,交抛物线于点☜.( )求抛物线的解析式. ( )当 ☜ 时,求点E的坐标.( )连接 ☜,是否存在点 ,使得△ ☜和△ ✌相似?若存在求此点 坐标;若不存在,说明理由..如图,在平面直角坐标系中, 为坐标原点,点✌的坐标为( , ),点 的坐标为( , ),点 的坐标为(﹣ , ),点 在✌上,连结 与⍓轴交于点 ,连结 .过 , , 三点作⊙✈与⍓轴的另一个交点为☜,延长 ✈交⊙✈于点☞,连结☜☞, ☞.( )求直线✌的函数解析式;( )求证:∠ ☜ ∠✌; ( )设 ☜ ⌧, ☞ ⍓.请求出⍓关于⌧的函数解析式;。
2014年安徽省中考真题数学
2014年安徽省中考真题数学一、选择题(本大题共10小题,每小题4分,满分40分)1.(4分)(-2)×3的结果是( )A. -5B. 1C. -6D. 6解析:原式=-2×3=-6.答案:C.2.(4分)x2·x3=( )A. x5B. x6C. x8D. x9解析:x2·x3=x2+3=x5.答案:A.3.(4分)如图,图中的几何体是圆柱沿竖直方向切掉一半后得到的,则该几何体的俯视图是( )A.B.C.D.解析:从几何体的上面看俯视图是,答案:D.4.(4分)下列四个多项式中,能因式分解的是( )A. a2+1B. a2-6a+9C. x2+5yD. x2-5y解析:A、C、D都不能把一个多项式转化成几个整式积的形式,故A、C、D不能因式分解;B、是完全平方公式的形式,故B能分解因式;答案:B.5.(4分)某棉纺厂为了解一批棉花的质量,从中随机抽取了20根棉花纤维进行测量,其长度x(单位:mm)的数据分布如下表所示,则棉花纤维长度的数据在8≤x<32这个范围的频率为( )A. 0.8B. 0.7C. 0.4D. 0.2解析:在8≤x<32这个范围的频数是:2+8+6=16,则在8≤x<32这个范围的频率是:=0.8. 答案:A.6.(4分)设n为正整数,且n<<n+1,则n的值为( )A. 5B. 6C. 7D. 8解析:∵<<,∴8<<9,∵n<<n+1,∴n=8,答案:D.7.(4分)已知x2-2x-3=0,则2x2-4x的值为( )A. -6B. 6C. -2或6D. -2或30解析:x2-2x-3=02×(x2-2x-3)=02×(x2-2x)-6=02x2-4x=6答案:B.8.(4分)如图,Rt△ABC中,AB=9,BC=6,∠B=90°,将△ABC折叠,使A点与BC的中点D 重合,折痕为MN,则线段BN的长为( )A.B.C. 4D. 5解析:设BN=x,由折叠的性质可得DN=AN=9-x,∵D是BC的中点,∴BD=3,在Rt△ABC中,x2+32=(9-x)2,解得x=4.故线段BN的长为4.答案:C.9.(4分)如图,矩形ABCD中,AB=3,BC=4,动点P从A点出发,按A→B→C的方向在AB和BC上移动,记PA=x,点D到直线PA的距离为y,则y关于x的函数图象大致是( )A.B.C.D.解析:①点P在AB上时,0≤x≤3,点D到AP的距离为AD的长度,是定值4;②点P在BC上时,3<x≤5,∵∠APB+∠BAP=90°,∠PAD+∠BAP=90°,∴∠APB=∠PAD,又∵∠B=∠DEA=90°,∴△ABP∽△DEA,∴=,即=,∴y=,纵观各选项,只有B选项图形符合.答案:B.10.(4分)如图,正方形ABCD的对角线BD长为2,若直线l满足:①点D到直线l的距离为;②A、C两点到直线l的距离相等.则符合题意的直线l的条数为( )A. 1B. 2C. 3D. 4解析:如图,连接AC与BD相交于O,∵正方形ABCD的对角线BD长为2,∴OD=,∴直线l∥AC并且到D的距离为,同理,在点D的另一侧还有一条直线满足条件,故共有2条直线l.答案:B.二、填空题(本大题共4小题,每小题5分,满分20分)11.(5分)据报载,2014年我国将发展固定宽带接入新用户25000000户,其中25000000用科学记数法表示为.解析:将25000000用科学记数法表示为2.5×107户.答案:2.5×107.12.(5分)某厂今年一月份新产品的研发资金为a元,以后每月新产品的研发资金与上月相比增长率都是x,则该厂今年三月份新产品的研发资金y(元)关于x的函数关系式为y= .解析:∵一月份新产品的研发资金为a元,2月份起,每月新产品的研发资金与上月相比增长率都是x,∴2月份研发资金为a×(1+x),∴三月份的研发资金为y=a×(1+x)×(1+x)=a(1+x)2.答案:a(1+x)2.13.(5分)方程=3的解是x= .解析:去分母得:4x-12=3x-6,解得:x=6,经检验x=6是分式方程的解.答案:6.14.(5分)如图,在▱ABCD中,AD=2AB,F是AD的中点,作CE⊥AB,垂足E在线段AB上,连接EF、CF,则下列结论中一定成立的是①②④.(把所有正确结论的序号都填在横线上)①∠DCF=∠BCD;②EF=CF;③S△BEC=2S△CEF;④∠DFE=3∠AEF.解析:①∵F是AD的中点,∴AF=FD,∵在▱ABCD中,AD=2AB,∴AF=FD=CD,∴∠DFC=∠DCF,∵AD∥BC,∴∠DFC=∠FCB,∴∠DCF=∠BCF,∴∠DCF=∠BCD,故此选项正确;延长EF,交CD延长线于M,∵四边形ABCD是平行四边形,∴AB∥CD,∴∠A=∠MDF,∵F为AD中点,∴AF=FD,在△AEF和△DFM中,,∴△AEF≌△DMF(ASA),∴FE=MF,∠AEF=∠M,∵CE⊥AB,∴∠AEC=90°,∴∠AEC=∠ECD=90°,∵FM=EF,∴FC=FM,故②正确;③∵EF=FM,∴S△EFC=S△CFM,∵MC>BE,∴S△BEC<2S△EFC故S△BEC=2S△CEF错误;④设∠FEC=x,则∠FCE=x,∴∠DCF=∠DFC=90°-x,∴∠EFC=180°-2x,∴∠EFD=90°-x+180°-2x=270°-3x,∵∠AEF=90°-x,∴∠DFE=3∠AEF,故此选项正确.答案:①②④.三、(本大题共2小题,每小题8分,满分16分)15.(8分)计算:-|-3|-(-π)0+2013.解析:原式第一项利用平方根定义化简,第二项利用绝对值的代数意义化简,第三项利用零指数幂法则计算,计算即可得到结果.答案:原式=5-3-1+2013=2014.16.(8分)观察下列关于自然数的等式:32-4×12=5 ①52-4×22=9 ②72-4×32=13 ③…根据上述规律解决下列问题:(1)完成第四个等式:92-4× 4 2= 17 ;(2)写出你猜想的第n个等式(用含n的式子表示),并验证其正确性.解析:由①②③三个等式可得,被减数是从3开始连续奇数的平方,减数是从1开始连续自然数的平方的4倍,计算的结果是被减数的底数的2倍减1,由此规律得出答案即可.答案:(1)32-4×12=5 ①52-4×22=9 ②72-4×32=13 ③…所以第四个等式:92-4×42=17;(2)第n个等式为:(2n+1)2-4n2=2(2n+1)-1,左边=(2n+1)2-4n2=4n2+4n+1-4n2=4n+1,右边=2(2n+1)-1=4n+2-1=4n+1.左边=右边,∴(2n+1)2-4n2=2(2n+1)-1.四、(本大题共2小题,每小题8分,满分16分)17.(8分)如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC(顶点是网格线的交点).(1)将△ABC向上平移3个单位得到△A1B1C1,请画出△A1B1C1;(2)请画一个格点△A2B2C2,使△A2B2C2∽△ABC,且相似比不为1. 解析:(1)利用平移的性质得出对应点位置,进而得出答案;(2)利用相似图形的性质,将各边扩大2倍,进而得出答案.答案:(1)如图所示:△A1B1C1即为所求;(2)如图所示:△A2B2C2即为所求.18.(8分)如图,在同一平面内,两条平行高速公路l1和l2间有一条“Z”型道路连通,其中AB段与高速公路l1成30°角,长为20km;BC段与AB、CD段都垂直,长为10km,CD段长为30km,求两高速公路间的距离(结果保留根号).解析:过B点作BE⊥l1,交l1于E,CD于F,l2于G.在Rt△ABE中,根据三角函数求得BE,在Rt△BCF中,根据三角函数求得BF,在Rt△DFG中,根据三角函数求得FG,再根据EG=BE+BF+FG即可求解.答案:过B点作BE⊥l1,交l1于E,CD于F,l2于G.在Rt△ABE中,BE=AB·sin30°=20×=10km,在Rt△BCF中,BF=BC÷cos30°=10÷=km,CF=BF·sin30°=×=km,DF=CD-CF=(30-)km,在Rt△DFG中,FG=DF·sin30°=(30-)×=(15-)km,∴EG=BE+BF+FG=(25+5)km.故两高速公路间的距离为(25+5)km.五、(本大题共2小题,每小题10分,满分20分)19.(10分)如图,在⊙O中,半径OC与弦AB垂直,垂足为E,以OC为直径的圆与弦AB的一个交点为F,D是CF延长线与⊙O的交点.若OE=4,OF=6,求⊙O的半径和CD的长.解析:由OE⊥AB得到∠OEF=90°,再根据圆周角定理由OC为小圆的直径得到∠OFC=90°,则可证明Rt△OEF∽Rt△OFC,然后利用相似比可计算出⊙O的半径OC=9;接着在Rt△OCF 中,根据勾股定理可计算出C=3,由于OF⊥CD,根据垂径定理得CF=DF,所以CD=2CF=6 .答案:∵OE⊥AB,∴∠OEF=90°,∵OC为小圆的直径,∴∠OFC=90°,而∠EOF=∠FOC,∴Rt△OEF∽Rt△OFC,∴OE:OF=OF:OC,即4:6=6:OC,∴⊙O的半径OC=9;在Rt△OCF中,OF=6,OC=9,∴CF==3,∵OF⊥CD,∴CF=DF,∴CD=2CF=6.20.(10分)2013年某企业按餐厨垃圾处理费25元/吨、建筑垃圾处理费16元/吨的收费标准,共支付餐厨和建筑垃圾处理费5200元.从2014年元月起,收费标准上调为:餐厨垃圾处理费100元/吨,建筑垃圾处理费30元/吨.若该企业2014年处理的这两种垃圾数量与2013年相比没有变化,就要多支付垃圾处理费8800元.(1)该企业2013年处理的餐厨垃圾和建筑垃圾各多少吨?(2)该企业计划2014年将上述两种垃圾处理总量减少到240吨,且建筑垃圾处理量不超过餐厨垃圾处理量的3倍,则2014年该企业最少需要支付这两种垃圾处理费共多少元?解析:(1)设该企业2013年处理的餐厨垃圾x吨,建筑垃圾y吨,根据等量关系式:餐厨垃圾处理费25元/吨×餐厨垃圾吨数+建筑垃圾处理费16元/吨×建筑垃圾吨数=总费用,列方程.(2)设该企业2014年处理的餐厨垃圾x吨,建筑垃圾y吨,需要支付这两种垃圾处理费共a 元,先求出x的范围,由于a的值随x的增大而增大,所以当x=60时,a值最小,代入求解.答案:(1)设该企业2013年处理的餐厨垃圾x吨,建筑垃圾y吨,根据题意,得,解得.答:该企业2013年处理的餐厨垃圾80吨,建筑垃圾200吨;(2)设该企业2014年处理的餐厨垃圾x吨,建筑垃圾y吨,需要支付这两种垃圾处理费共a 元,根据题意得,,解得x≥60.a=100x+30y=100x+30(240-x)=70x+7200,由于a的值随x的增大而增大,所以当x=60时,a值最小,最小值=70×60+7200=11400(元).答:2014年该企业最少需要支付这两种垃圾处理费共11400元.六、(本题满分12分)21.(12分)如图,管中放置着三根同样的绳子AA1、BB1、CC1;(1)小明从这三根绳子中随机选一根,恰好选中绳子AA1的概率是多少?(2)小明先从左端A、B、C三个绳头中随机选两个打一个结,再从右端A1、B1、C1三个绳头中随机选两个打一个结,求这三根绳子能连结成一根长绳的概率.解析:(1)三根绳子选择一根,求出所求概率即可;(2)列表得出所有等可能的情况数,找出这三根绳子能连结成一根长绳的情况数,即可求出所求概率.答案:(1)三种等可能的情况数,则恰好选中绳子AA1的概率是;(2)列表如下:所有等可能的情况有9种,其中这三根绳子能连结成一根长绳的情况有6种,则P==.七、(本题满分12分)22.(12分)若两个二次函数图象的顶点、开口方向都相同,则称这两个二次函数为“同簇二次函数”.(1)请写出两个为“同簇二次函数”的函数;(2)已知关于x的二次函数y1=2x2-4mx+2m2+1和y2=ax2+bx+5,其中y1的图象经过点A(1,1),若y1+y2与y1为“同簇二次函数”,求函数y2的表达式,并求出当0≤x≤3时,y2的最大值. 解析:(1)只需任选一个点作为顶点,同号两数作为二次项的系数,用顶点式表示两个为“同簇二次函数”的函数表达式即可.(2)由y1的图象经过点A(1,1)可以求出m的值,然后根据y1+y2与y1为“同簇二次函数”就可以求出函数y2的表达式,然后将函数y2的表达式转化为顶点式,在利用二次函数的性质就可以解决问题.答案:(1)设顶点为(h,k)的二次函数的关系式为y=a(x-h)2+k,当a=2,h=3,k=4时,二次函数的关系式为y=2(x-3)2+4.∵2>0,∴该二次函数图象的开口向上.当a=3,h=3,k=4时,二次函数的关系式为y=3(x-3)2+4.∵3>0,∴该二次函数图象的开口向上.∵两个函数y=2(x-3)2+4与y=3(x-3)2+4顶点相同,开口都向上,∴两个函数y=2(x-3)2+4与y=3(x-3)2+4是“同簇二次函数”.∴符合要求的两个“同簇二次函数”可以为:y=2(x-3)2+4与y=3(x-3)2+4.(2)∵y1的图象经过点A(1,1),∴2×12-4×m×1+2m2+1=1.整理得:m2-2m+1=0.解得:m1=m2=1.∴y1=2x2-4x+3=2(x-1)2+1.∴y1+y2=2x2-4x+3+ax2+bx+5=(a+2)x2+(b-4)x+8∵y1+y2与y1为“同簇二次函数”,∴y1+y2=(a+2)(x-1)2+1=(a+2)x2-2(a+2)x+(a+2)+1.其中a+2>0,即a>-2.∴.解得:.∴函数y2的表达式为:y2=5x2-10x+5.∴y2=5x2-10x+5=5(x-1)2.∴函数y2的图象的对称轴为x=1.∵5>0,∴函数y2的图象开口向上.①当0≤x≤1时,∵函数y2的图象开口向上,∴y2随x的增大而减小.∴当x=0时,y2取最大值,最大值为5(0-1)2=5.②当1<x≤3时,∵函数y2的图象开口向上,∴y2随x的增大而增大.∴当x=3时,y2取最大值,最大值为5(3-1)2=20.综上所述:当0≤x≤3时,y2的最大值为20.八、(本题满分14分)23.(14分)如图1,正六边形ABCDEF的边长为a,P是BC边上一动点,过P作PM∥AB交AF 于M,作PN∥CD交DE于N.(1)①∠MPN=;②求证:PM+PN=3a;(2)如图2,点O是AD的中点,连接OM、ON,求证:OM=ON;(3)如图3,点O是AD的中点,OG平分∠MON,判断四边形OMGN是否为特殊四边形?并说明理由.解析:(1)①运用∠MPN=180°-∠BPM-∠NPC求解,②作AG⊥MP交MP于点G,BH⊥MP于点H,CL⊥PN于点L,DK⊥PN于点K,利用MP+PN=MG+GH+HP+PL+LK+KN求解,(2)连接OE,由△OMA≌△ONE证明,(3)连接OE,由△OMA≌△ONE,再证出△GOE≌△NOD,由△ONG是等边三角形和△MOG是等边三角形求出四边形MONG是菱形.,答案:(1)①∵四边形ABCDEF是正六边形,∴∠A=∠B=∠C=∠D=∠E=∠F=120°又∴PM∥AB,PN∥CD,∴∠BPM=60°,∠NPC=60°,∴∠MPN=180°-∠BPM-∠NPC=180°-60°-60°=60°,故答案为;60°.②如图1,作AG⊥MP交MP于点G,BH⊥MP于点H,CL⊥PN于点L,DK⊥PN于点K,MP+PN=MG+GH+HP+PL+LK+KN.∵正六边形ABCDEF中,PM∥AB,作PN∥CD,∵∠AMG=∠BPH=∠CPL=∠DNK=60°,∴GM=AM,HL=BP,PL=PM,NK=ND,∵AM=BP,PC=DN,∴MG+HP+PL+KN=a,GH=LK=a,∴MP+PN=MG+GH+HP+PL+LK+KN=3a.(2)如图2,连接OE,∵四边形ABCDEF是正六边形,AB∥MP,PN∥DC,∴AM=BP=EN,又∵∠MAO=∠NOE=60°,OA=OE,在△ONE和△OMA中,∴△OMA≌△ONE(SAS)∴OM=ON.(3)如图3,连接OE,由(2)得,△OMA≌△ONE∴∠MOA=∠EON,∵EF∥AO,AF∥OE,∴四边形AOEF是平行四边形,∴∠AFE=∠AOE=120°,∴∠MON=120°,∴∠GON=60°,∵∠GON=60°-∠EON,∠DON=60°-∠EON,∴∠GOE=∠DON,∵OD=OE,∠ODN=∠OEG,在△GOE和∠DON中,∴△GOE≌△NOD(ASA),∴ON=OG,又∵∠GON=60°,∴△ONG是等边三角形,∴ON=NG,又∵OM=ON,∠MOG=60°,∴△MOG是等边三角形,∴MG=GO=MO,∴MO=ON=NG=MG,∴四边形MONG是菱形.。
2014学年安徽省中考数学年试题答案
11
12
… < .
x12 x22
xn2 3
18.(本小题满分 12 分)
如图,已知二面角 MN 的大小为 60 ,菱形 ABCD 在面 内, A , B 两点在棱 MN 上, BAD 60 , E 是 AB 的中点, DO⊥平面 ,垂足为 O . (Ⅰ)证明: AB⊥平面 ODE ; (Ⅱ)求异面直线 BC 与 OD 所成角的余弦值.
项是符合题目要求的.
1.设命题 p : x R , x2 1 0 ,则 p 为
上
A. x0 R , x02 1>0
B. x0 R , x02 1≤0
C. x0 R , x02 1<0
D. x R , x2 1≤0
()
2.已知集合 A {x | x>2} , B {x |1<x<3} ,则 A B
()
A. [6, 2]
B.[5, 1]
C. [4, 5]
D.[3, 6]
8.设一块石材表示的几何体的三视图如图所示,将该石材切削、打磨,加工成球,则能得到
的最大球的半径等于
()
A.1
B.2
C.3
D.4
9.若 0 x1 x2 1 ,则
()
A. ex2 ex1 ln x2 ln x1
4
3
2
A.
B.
C.
5
5
5
()
D. f (x) 2x
() 1 D. 5
6.若圆 C1 : x2 y2 1 与圆 C2 : x2 y2 6x 8y m 0 外切,则 m
效
A.21
B.19
C.9
D. 11
2014安徽中考数学
2014安徽中考数学2014年安徽中考数学试题是很多学生备战中考的重要一环。
数学是中考的一门必考科目,对学习生活中都有很大的实用价值。
下面我们将回顾一下2014年安徽中考数学试题,了解一下题目的难度和出题方向,为备战中考提供参考。
一、选择题部分选择题部分是数学试卷的重要组成部分,其特点是题目多、难度适中,考查学生运算能力和理解能力。
2014年安徽中考数学试题的选择题部分设置了30个小题,其中有10个单项选择题、15个判断题和5个填空题。
单项选择题主要考察学生对数学概念和运算方法的掌握程度。
其中的难度较大的题目多为较长的文字叙述题,需要学生仔细阅读题目,理解问题的要求。
例如:“填写下表部分空格内数字,使表中每个数字只出现一次。
”这是一道填空题,题目整体较长,要求学生按照给出的条件,填写表格中的空格。
这道题考察了学生的逻辑思维能力和数学计算能力。
判断题主要考察学生对数学概念的理解和判断能力。
题目较短,只有一句话,要求学生判断其真假。
例如:“用两条直线将一个平面分成三个部分,要求分割线不相交,则这两条直线的交点个数为1。
”这是一道判断题,考察了学生对直线分割平面的了解程度和逻辑推理能力。
填空题部分主要考察学生运算能力和解题思路。
题目简短,要求学生填写空格中的数字,使得题目的计算结果满足给定条件。
例如:“自然数42与62都能被两位数a整除,a=___。
”这是一道填空题,要求学生解方程,找出能同时整除42和62的两位数a。
二、解答题部分解答题部分是数学试卷的重点和难点,需要学生在有限的时间内综合运用所学知识和解题方法,进行分析和解答。
2014年安徽中考数学试题的解答题部分共有6个大题,涵盖了数学的各个知识点。
解答题1主要考察了学生对平行线和相交线的性质的理解和运用。
题目要求学生证明一个三角形的内心、外心和垂心共线。
这是一道较难的证明题,需要学生运用相关的定理和性质,进行推理和证明。
解答题2主要考察了学生对比例关系的运用和解题方法的掌握。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1
2013年秋城南中学九年级第一次段考数学试卷(人教版)
出题:城南中学教导处 测试内容:二次根式 测试时间:80分钟
一、选择题。(每小题4分,共32分)
1、下列式子一定是二次根式的是 ( )
A、2x B、x C、22x D、22x
2、已知一个正方形的面积是5,那么它的边长是 ( )
A、5 B、5 C、51 D、以上都不对
3、已知:aaaa112,那么a的取值范围是 ( )
A、a≤0 B、a<0 C、0<a≤1 D、a>0
4、化简aa1的结果是 ( )
A、a B、-a C、a D、-a
5、下列计算正确的是 ( )
A、532 B、632 C、48 D、3)3(2
6、若a<0,则aa2的值是 ( )
A、0 B、– a C、– 2a D、–3a
7、下列根式中,不是最简二次根式的是 ( )
A、12a B、12x C、y3.0 D、42b
8、若14x有意义,则x的最小整数值是 ( )
A、1 B、0 C、– 1 D、–4
题号 一 二 三 总分
分数
九年级数学 第1页(共4页) 九
2
二、填空题。(每小题4分,共32分)
9、若二次根式xx52有意义,则x的取值范围是_________。
10、已知322xxy,则yx=_________。
11、在实数范围内分解因式:44x=_________。
12、若024ba,则ab=_________。
13、已知:a<2,则22a=_________。
14、比较大小:56________75。
15、1112xxx成立的条件是_________。
16、三角形的三边长分别是cmcmcm45,40,20,则这个三角形的周长是_________。
三、解答题。
17、已知:a、b为实数,且421025baa,求a、b的值。
3
18、已知:231x,231y,求:xyyxyx22的值。(本小题7分)
19、计算:32275)21()1(10。(本小题7分)
20、已知:71aa,求:aa1的值。(本小题8分)
21、已知矩形的长与宽之比为5:3,它们的对角线长为68,求这个矩形的长与宽。(本小题8分)
九年级数学 第3页(共4页)
