用有限差分法和Matlab计算二维热加工温度场分析最新版本
matlab fdm算法 -回复

matlab fdm算法-回复MATLAB是一种功能强大的数学和工程计算软件,其提供了许多数值计算方法和算法。
其中,有一种被广泛应用于求解偏微分方程的数值方法称为有限差分法(FDM)。
有限差分法是一种基于数值近似和离散化的数值解法,用于将连续的偏微分方程转化为离散的代数方程组。
有限差分法的基本思想是将求解域离散化为有限个网格点,并在这些离散点上建立代数方程。
在求解过程中,通过使用近似的导数和离散化的微分方程来逼近原始偏微分方程,从而得到一个离散的线性或非线性方程组。
这个方程组可以用标准的线性代数方法(如高斯消元法)求解,从而得到原问题的数值解。
下面是使用有限差分法求解一维波动方程的一个简单示例:假设我们要求解以下一维波动方程:∂^2u/∂t^2 = c^2 ∂^2u/∂x^2其中u(t, x)表示在时刻t和位置x处的解,c是传播速度。
为了对该方程进行离散化,我们将求解域离散化为N个网格点,其中x的范围为[0, L],时间的范围为[0, T]。
我们使用Δx表示网格步长,Δt表示时间步长,有以下关系:Δx = L/N,Δt = T/M。
其中M表示时间步数。
我们在网格点(t_n, x_i)处近似偏导数,得到以下差分方程:(u^n_{i-1} - 2u^n_i + u^n_{i+1})/Δx^2 = c^2(u^{n+1}_i - 2u^n_i + u^{n-1}_i)/Δt^2其中u^n_i表示在时刻t_n和位置x_i处的解,右侧的u表示在不同时刻和位置处的解。
通过对差分方程做一些代数转换,我们可以得到以下更新方程:u^{n+1}_i = (2(1 - β) - 2μ^2)u^n_i + μ^2(u^n_{i-1} + u^n_{i+1}) - u^{n-1}_i其中β= (cΔt/Δx)^2,μ^2 = 1 - 2β。
这个更新方程可以用于迭代求解波动方程的离散解。
现在让我们使用MATLAB实现这个有限差分法算法。
二维热传导方程的可视化计算

二维热传导方程的可视化计算二维热传导方程是描述二维物体热传导过程的数学模型。
在工程领域中,通过求解二维热传导方程,可以预测物体内部的温度分布,进而进行热设计和优化。
热传导是指物体内部由高温区向低温区传递热量的过程。
二维热传导方程是基于热传导定律和能量守恒定律建立的,它可以描述物体内部温度的时空变化。
二维热传导方程的一般形式如下:∂²T/∂x² + ∂²T/∂y² = α ∂T/∂t其中,T是温度,x和y是空间坐标,t是时间,α是热扩散系数。
为了求解二维热传导方程,需要给定边界条件和初始条件。
边界条件是指在物体表面的温度分布情况,而初始条件是指在初始时刻物体内部各点的温度分布。
通常情况下,我们采用数值方法来求解二维热传导方程,其中最常用的方法是有限差分法。
有限差分法将连续的空间和时间离散化,将二维热传导方程转化为一组离散的代数方程。
在计算机中,可以使用计算软件来实现二维热传导方程的可视化计算。
首先,需要将物体的几何形状离散化为一个个小区域,然后对每个小区域进行温度计算。
在计算过程中,可以使用迭代方法来逐步求解离散方程,直到达到收敛条件。
通过迭代计算,可以得到物体在不同时间点的温度分布情况。
在可视化计算中,可以将温度用不同的颜色表示,从而直观地显示物体内部的温度分布。
通过观察温度分布的变化,可以了解物体的热传导特性,并对其进行优化设计。
除了温度分布的可视化,还可以计算物体的热流量、热传导速率等热学参数。
这些参数对于热设计和工程优化非常重要,可以帮助工程师在设计过程中做出准确的决策。
二维热传导方程的可视化计算在工程领域中具有重要的应用价值。
通过求解二维热传导方程,可以预测物体内部的温度分布,为工程设计提供参考依据。
同时,可视化计算也为工程师提供了直观的数据展示方式,帮助他们更好地理解和分析热传导过程。
二维导热物体温度场的数值模拟

金属凝固过程计算机模拟题目:二维导热物体温度场的数值模拟Solidworks十字接头的传热分析作者:张杰学号:S2*******学院:北京有色金属研究总院专业:材料科学与工程成绩:2015 年12 月二维导热物体温度场的数值模拟图1 二维均质物体的网格划分用有限差分法模拟二维导热物体的温度场,首先将二维物体划分为如图1所示的网格,x ∆与y ∆可以是不变的常量,即等步长,也可以是变量(即在区域内的不同处是不同的),即变步长。如果区域内各点处的温度梯度相差很大,则在温度变化剧烈处,网格布得密些,在温度变化不剧烈处,网格布得疏些。至于网格多少,步长取多少为宜,要根据计算精度与计算工作量等因素而定。在有限的区域内,将二维不稳定导热方程式应用于节点,)i j (可写成: ,2222 ,i jPPp i j T T T C x y ρλτ⎛⎫∂∂∂=+ ⎪∂∂∂⎝⎭,1 , ,()i jP P Pi j i jT T T οτττ+-∂⎛⎫=+∆ ⎪∂∆⎝⎭ (), 1 , , 1 ,222()i j P P P Pi j i j i j T T T T x x x ο+--+∂⎛⎫=+∆ ⎪∂⎝⎭∆ () , ,1 , ,1222()i jPP P Pi j i j i j T T T T y y y ο+--+⎛⎫∂=+∆ ⎪∂∆⎝⎭τ∆、x ∆、y ∆ 当τ∆、x ∆、y ∆较小时,忽略()οτ∆、2()x ο∆、2()y ο∆项。
当x y ∆=∆时,即x 、y 方向网格划分步长相等。最后得到节点,)i j (的差分方程: ()1 , ,0 1 , 1 , ,1 ,1 ,4P P P P P P Pi j i j i j i j i j i j i j T T F T T T T T ++-+-=++++-式中:()02p F C x λτρ∆=∆。假设边界为对流和辐射边界,对流用以下公式计算:()(),1 , ,0 1 , ,1 ,1 ,24Pc f i j P P P P P P i j i j i j i j i j i j p a T T T T F T T T T C xτρ+-+-∆-=+++-+∆MATLAB 编程模拟clc; clear;format long %% 参数输入moni_canshu=xlsread('模拟参数输入.xlsx',1,'B2:B11'); %读取excel 中的模拟参数 s=moni_canshu(1); %几何尺寸,m t0=moni_canshu(2); %初始温度,℃tf=moni_canshu(3); %辐射(空气)边界,℃ rou=moni_canshu(4); %密度,kg/m3lamda=moni_canshu(5); %导热系数,w/(m ℃) Cp=moni_canshu(6); %比热,J/(kg ℃)n=moni_canshu(7); %工件节点数,个<1000 dt=60*moni_canshu(8); %时间步长,min to s m=moni_canshu(9); %时间步数,个<100 dx=s/(n-1);%计算dxf0=lamda*dt/(rou*Cp*dx*dx);%计算f0 %% 初始参数矩阵,初始温度 for iii=1:n for jjj=1:nTold(iii,jjj)=t0; end endTold(1,:)=tf; Told(n,:)=tf; Told(:,1)=tf;Told(:,n)=tf;%% 写文件表头xlswrite('data.xlsx',{['坐标位置']},'sheet1','A1');asc=97;for ii=1:nbiaotou1={['第' num2str(ii) '点']};asc=asc+1;xlswrite('data.xlsx',biaotou1,'sheet1',[char(asc) '1']);xlswrite('data.xlsx',biaotou1,'sheet1',['A' num2str(ii+1)]);end%% 模拟运算for jj=1:2copyfile('data.xlsx','data1.xlsx')Tnew(1,1:n)=tf;Tnew(n,1:n)=tf;Tnew(1:n,1)=tf;Tnew(1:n,n)=tf;for i=2:n-1for j=2:n-1Tnew(i,j)=Told(i,j)+f0*(Told(i-1,j)-4*Told(i,j)+Told(i+1,j)+Told(i,j-1)+Told(i,j+1)); endendTold=Tnew;pcolor(Told);%绘图shading interpcolormap(jet)pause(0.1)saveas(gcf,['第' num2str(jj*0.1) 's温度图像.jpg']);xlswrite('data1.xlsx',Told,'sheet1','B2');copyfile('data1.xlsx',['第' num2str(jj*0.1) 's数据.xlsx'])delete('data1.xlsx');end图3 模拟物体的温度分布图2 模拟物体的温度等高线图和温度梯度分布图。
二维传热差分算法分析及通用计算程序实现

S a —y W A h UN Hu i u, NG Z u—mi n
( eatetfCe i l nier g Seyn steo hmcl ehooyS eyn 112 C ia Dpr n o hmc g ei , hnagI tu f e i cnl ,hnag10 4 , h ) m aE n n n it C aT g n
C ij D l
体现在不规则的几何形状和复杂的边界条件。对此
问题 的解决一般需要使用计算机进行数值求解 , 具 体方法是将要计算传热的物体分为传热网格 , 之后 对每个参加计算的节点进行热量衡算并列 出传热方 程组并求解 。在实际的计算过程 中, 手工构造 网格 比较 困难 , 而且列出方程较麻烦且不便于修改。 为了能开发较通用的传热计算程序 , 文研究 本 了节点及网格的数据描述 、 方程组 的 自动生成及求 解的计算方法 , 能够进行交互式可视化的网格设计 及方程组的 自动生成及求解 。
Ke r s h a — t n f ay i; n t d f rn e c mp tt n me o y wo d : e t — r se a l s f i ie e c ; o u i t d a rn si e a o h
工程 中经常进行的传热计算 , 一般包括物体 内 导热及物体与外界的对流传热 , 问题 的复杂性 主要
T p y e P i t y e tp on
算法分析及数据结构
11 传 热 a bo a l ns oln 此点是否是物体 内的点 n e bn a ua sBoe 否参 加计 算 lCl leA ol 是 e t n a
t sS g 温度 i l A ne xA ig s nl X坐标 S e
2有限差分法及热传导数值计算PPT演示课件

t1
1 a11
(b1
a12t2
a13t3 )
t2
1 a 22
(b2
a 21t1 a 23t3 )
1 t3 a 33 (b3 a 31t1 a 32t2 )
•24
(2)假设一组解(迭代初场),记为: t1(0)、t2(0)并、t代3(0) 入迭代方程求得第一 次解
每次计算t1(1)均、t用2(1)、最t3(1新) 值代入。
(1) 平直边界上的节点
如图所示 边界节点 (m,n) 只能代表半个元体,若边界上有向 该元体传递的热流密度为q ,据能量守恒定律对该元体有:
tm1,n tm,n ytm,n1tm,n x
x
y 2
x
2
tm,n1 tm,n y
Φm,n
2xyyqw
0
Байду номын сангаас
xy tm ,n1 4 2 tm 1 ,n tm ,n 1 tm ,n 1 x2 Φ m ,n 2 x q w
非稳态项 的离散有三种不同的格式。如果将函数在节 点(n,i+1)对点(n,i)作泰勒展开,可有
•30
•31
由式(b)可得在点(n,i)处一阶导数的一种差分表示式 , 的向前差分:
类似地,将t在点(n,i-1)对点(n,i)作泰勒展开,可得 的向后差分的表达式:
如果将t在点(n,i+1)及(n,i-1)处的展开式相加,则可得 一阶导数的中心差分的表达式:
qw
y x
•16
(3) 内部角点
如图所示内部角点代表了 3/4 个元体,在同样的假设条 件下有
tm1,ntm,ny tm,n1tm,nx tm,n1tm,n x
x
用有限差分法和Matlab计算二维热加工温度场分析最新版本
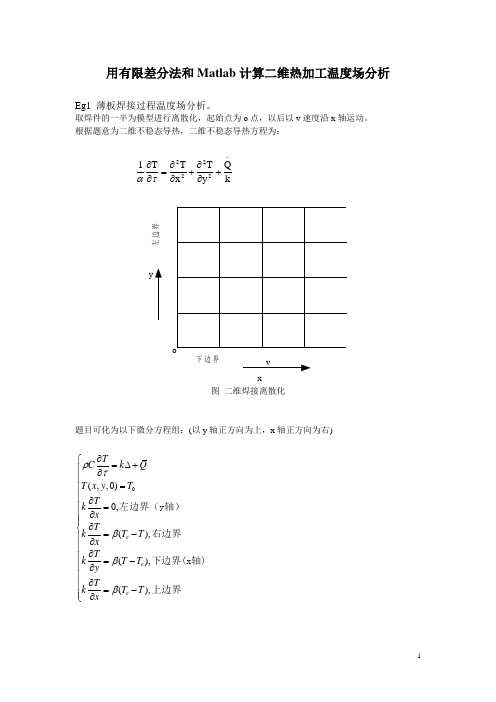
用有限差分法和Matlab 计算二维热加工温度场分析Eg1 薄板焊接过程温度场分析。
取焊件的一半为模型进行离散化,起始点为o 点,以后以v 速度沿x 轴运动。
根据题意为二维不稳态导热,二维不稳态导热方程为:k QyT x T T 12222-+∂∂+∂∂=∂∂ταyx 左边界下边界图 二维焊接离散化题目可化为以下微分方程组:(以y 轴正方向为上,x 轴正方向为右)0(,,0)0,(),(),(),e eeT C k Q T x y T Tk x Tk T T x T k T T y T k T T xρτβββ∂⎧=∆+⎪∂⎪=⎪⎪∂=⎪∂⎪⎪∂⎨=-⎪∂⎪∂⎪=-⎪∂⎪∂⎪=-⎪∂⎩左边界(y 轴)右边界下边界(x 轴)上边界需要的参数(均已cm,cal,g 为单位,所以不必换算):用PDE Tool解题步骤如下: 0.>> pdetool 1. 区域设置 单击工具,在窗口拉出一个矩形,双击矩形区域,在Object Dialog 对话框输入Left为0,Bottom 为0,Width 为2,Height 为2。
与默认的坐标相比,图形小的看不见,所以要调整坐标显示比例。
方法:选择Options->Axes Limits,把X ,Y 轴的自动选项打开。
设置Options->Application 为Heat Transfer (设置程序应用热传输模型) 2. 设置边界条件 单击 ,使边界变红色,然后分别双击每段边界,打开Boundary Conditions对话框,设置边界条件(根据边界条件)。
所有的边界都为Neumann 条件。
输入值见下表:3. 设置方程类型 单击,打开PDE Specification 对话框,设置方程类型为Parabolic (抛物型), C (比热)为0.16,a (导热系数)为0.1,d(密度)为7.82,f (热源)为4000*exp(-3*(x.^2+(y-0.4*t).^2)/0.49)。
热传导方程有限差分法的MATLAB实现
△t
n
nn
关于
t
的二阶中心差商[10]:
坠2u 坠x2
≈
uj+1
-2uj +uj-1 (△x)2
,对方
程进行离散。 离散后的方程为:
n n-1
n
nn
uj -uj △t
=a2
uj+1
-2uj +uj-1 (△x)2
。
令
:r=
a2·△t (△x)2
,即
n
n
n
n-1
(1+2r)uj -r·uj+1 -r·uj-1 =uj 。 可化为矩阵形式:
摘 要:对于有界热传导齐次方程的混合问题,用分离变量法求解往往很复杂。 为了更好地
理解热传导方程的解,使用 MATLAB 软件将方程的解用图像表示出来。 通过区域转换的思想,
利用 MATLAB 编程实现一定区域内热传导方程的有限差分方法,数值表明了方法的可行性和
稳定性。
关键词:热传导方程;有限差分;MATLAB
方法, 把控制方程中的导数用网格节点上的函数值
的差商代替进行离散,从而 建立以网格节点上的值
为未知数的代数方程组。
1 求解热传导方程的基本思想
基本思想是把连续的定解区域用有限个离散点
构成的网格来代替, 这些离散点称作网格的节点;
把连续定解区域上的连续变量的函数用在网格上定
义的离散变量函数来近似; 把原方程和定解条件中
x0(ii+1)=ii*ox; end u=sin(pi*x0/l); % t=0 时 u(x,t)的值 r=a^2*ot/(ox)^2; for ii=1:n
%数据的输入 B=zeros(M-1,1);%存放系数矩阵主对角线元素 A=zeros (M-2,1);%存放系数矩阵主对角线元素下 方次对角线的元素 C=zeros (M-2,1);%存放系数矩阵主对角线元素上 方次对角线的元素 S=zeros(M-1,1);%存放右端的常数项 for ii=1:M-2
二维热传导方程 matlab
二维热传导方程是描述二维热传导过程的数学模型,它在工程、物理、地球科学等领域都有重要应用。
在实际工程问题中,我们经常需要求解二维热传导方程,以预测物体表面的温度分布、热量传递速率等参数。
Matlab是一个强大的数学软件,通过Matlab我们可以很方便地求解二维热传导方程,并得到预期的结果。
一、二维热传导方程的基本形式二维热传导方程可以用偏微分方程的形式表示为:∂u/∂t = k(∂²u/∂x² + ∂²u/∂y²)其中,u(x, y, t)是温度分布随时间和空间的变化,k是热传导系数。
二、Matlab中求解二维热传导方程的方法在Matlab中,我们可以采用有限差分法(finite difference method)求解二维热传导方程。
有限差分法将偏微分方程离散化,转化为代数方程组,然后通过迭代求解得到数值解。
具体步骤如下:1. 离散化空间和时间变量,将连续的空间区域和时间区间分割成若干个小区间。
2. 利用二阶中心差分格式对二维热传导方程进行离散化,得到代数方程组。
3. 利用Matlab中的矩阵运算和迭代方法,求解代数方程组,得到数值解。
三、Matlab代码示例下面是一个简单的Matlab代码示例,用于求解二维热传导方程:```matlab定义参数和初始条件Lx = 1; Ly = 1; 区域大小Nx = 100; Ny = 100; 离散化网格数T = 1; 总时间Nt = 100; 时间步数k = 1; 热传导系数dx = Lx/Nx; dy = Ly/Ny;dt = T/Nt;x = 0:dx:Lx; y = 0:dy:Ly;[X, Y] = meshgrid(x, y);u = sin(pi*X).*sin(pi*Y); 初始温度分布迭代求解for n = 1:Ntun = u;for i = 2:Nx-1for j = 2:Ny-1u(i, j) = un(i, j) + k*dt/dx^2*(un(i+1, j)-2*un(i, j)+un(i-1, j)) + k*dt/dy^2*(un(i, j+1)-2*un(i, j)+un(i, j-1));endendend可视化结果figure;surf(X, Y, u);xlabel('x'); ylabel('y'); zlabel('Temperature');```以上代码首先定义了区域大小、离散化网格数、总时间、热传导系数等参数,然后利用有限差分法进行迭代求解,最后利用Matlab绘制了温度分布的三维图像。
热传导方程有限差分法的MATLAB实现
万方数据万方数据万方数据万方数据热传导方程有限差分法的MATLAB实现作者:史策作者单位:西安建筑科技大学,理学院,陕西,西安,710055刊名:咸阳师范学院学报英文刊名:JOURNAL OF XIANYANG NORMAL UNIVERSITY年,卷(期):2009,24(4)被引用次数:0次1.曹钢,王桂珍,任晓荣.一维热传导方程的基本解[J].山东轻工业学院学报,2005,19(4):76-80.2.万正苏,方春华,张再云.关于热传导方程有限差分区域分解并行算法精度的注记[J].湖南理工学院学报(自然科学版),2007,20(3):12-14.3.StephenJ.Chapman.MATLAB编程[M].邢树军,郑碧波,译.北京:科学出版社,2008.4.田兵.用MATLAB解偏微分方程[J].阴山学刊,2006,20(4):12-13.5.王飞,裴永祥.有限差分方法的MATLAB编程[J].新疆师范大学学报(自然科学版),2003,22(4):21-27.6.王宝红.热传导方程的可视化探讨[J].忻州师范学院学报,2008,24(2):31-36.7.李先枝.热传导方程差分解法的最佳网格[J].河南大学学报(自然科学版),2004,34(3):16-18.8.赵德奎,刘勇.MATLAB在有限差分数值计算中的应用[J].四川理工学院学报,2005,18(4):61-64.9.谢焕田,吴艳.拉普拉斯有限差分法的MATLAB实现[J].四川理工学院学报,2008,21(3):1-2.10.南京大学数学系计算数学专业.偏微分方程数值解法[M].北京:科学出版社,1979.1.学位论文申卫东热传导方程有限差分区域分解算法研究2003区域分解算法是在并行机上求解偏微分方程数值解的一种较自然的方法.该方法先将偏微分方程求解区域划分为若干个子区域,然后在各个子区域并行求解.全文共五章.第一章为引言,简要介绍了热传导方程并行算法的概况及该文所讨论的基本内容.在第二章,我们在内边界点为等距分划的多子区域条件下,得到Dawson等人关于求解热传导方程区域分解算法差分解的误差估计.在第三章,我们以Saul'yev非对称格式作内边界处理,发展了新的区域分解算法,得到了差分解的先验误差估计,并与Dawson等人的算法作了比较.给出了关于算法计算精度的数值结果.在第四章,我们发展了一些新技术,在子区域的边界处采用小时间步长古典显式格式求解,构造了新的区域分解算法,得到了差分解的先验误差估计.给出了关于算法计算精度的数值结果.在第五章,我们在二维热传导方程求解上扩充了Dawson等人的区域分解算法.给出了关于算法计算精度的数值结果.第六章为该研究工作的主要结论.2.期刊论文张守慧.王文洽.ZHANG Shou-hui.WANG Wen-qia热传导方程有限差分逼近的数学Stencil及其新型迭代格式-山东大学学报(理学版)2006,41(6)将Stencil应用于偏微分方程有限元差分逼近过程,以两类差分格式为基础建立了求解热传导方程的两种新型迭代算法.此两种算法与经典的Jacobi方法同样具有并行的性质,但比Jacobi方法收敛快.给出的算例说明方法的适用性.3.期刊论文吕桂霞.马富明.Lü Guixia.Ma Fuming二维热传导方程有限差分区域分解算法-数值计算与计算机应用2006,27(2)本文讨论了一类数值求解二维热传导方程的并行差分格式.在这个算法中,通过引进内界点将求解区域分裂成若干子区域.在子区域间内界点上采用非对称格式计算,一旦这些点的值被计算出来,各子区域间的计算可完全并行.本文得到了稳定性条件和最大模误差估计.它表明我们的格式有令人满意的稳定性,并且有着较高的收敛阶.4.学位论文田源地下煤火三维数理模型正演数值模拟2006本文首先给出了几个地下煤火随空间、温度变化的动态和稳态热数学物理模型及其简化模型。
基于有限元法的切削加工温度场数值分析
基于有限元法的切削加工温度场数值分析胡艳娟;王占礼;李静;卢凯【摘要】为了研究切削加工过程中的温度场分布情况,基于有限元理论,建立了正交切削有限元模型,并对其关键技术进行了探讨。
利用ABAQUS软件对切削AISI1045钢的温度场进行数值模拟,并得出影响切削温度场的变化规律。
研究结果表明:该方法可以有效模拟金属加工过程中因热力耦合作用下的工件、刀具及切屑中的非均匀温度场分布情况。
这为深入研究金属切削原理、切削温度场、预测切削热等提供了理论依据。
【期刊名称】《制造业自动化》【年(卷),期】2013(000)024【总页数】5页(P46-49,60)【关键词】有限元分析;热力耦合模型;切削热预测;温度场模拟【作者】胡艳娟;王占礼;李静;卢凯【作者单位】长春工业大学机电工程学院,长春 130012;长春工业大学机电工程学院,长春 130012;长春工业大学机电工程学院,长春 130012;长春工业大学机电工程学院,长春 130012【正文语种】中文【中图分类】TG501.40 引言金属切削加工过程是一个非常复杂的动态性、非线性的工艺过程,常伴随着切削力、切削热和刀具磨损等物理现象。
其中,切削热是一个重要的物理参数标志,它直接影响着刀具的磨损、刀具的使用寿命、工件的加工精度以及加工表面的完整性[1,2]。
因此,切削温度场的理论研究对分析金属加工原理、预测工件的加工精度以及刀具磨损机理等方面具有重要的意义。
目前,常用的切削温度场研究方法主要有:试验法(如:人工热电偶测温法、红外热像仪法等)、解析法(如:积分变化法、拉普拉斯变化法)和有限元数值法(如:有限差分法、有限元法[3])。
试验法可以得到可靠的数据,但是试验法无法直接得到温度场的分布情况,只能测得某点处的平均温度(如:人工热电偶法);解析法常常基于各种假设,与实际情况不符;有限元法在解决由材料性质、变形状态和多耦合场引起的非线性问题时,往往表现出其独特的优点,更加接近于实际,同时有限元法可以快速地得到精确的仿真结果[4,5]。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
用有限差分法和Matlab 计算二维热加工温度场分析
Eg1 薄板焊接过程温度场分析。
取焊件的一半为模型进行离散化,起始点为o 点,以后以v 速度沿x 轴运动。
根据题意为二维不稳态导热,二维不稳态导热方程为:
k Q
y
T x T T 122
22-
+∂∂+∂∂=∂∂τα
y
x 左边界
下边界
图 二维焊接离散化
题目可化为以下微分方程组:(以y 轴正方向为上,x 轴正方向为右)
0(,,0)0,(),(),(),e e
e
T C k Q T x y T T
k x T
k T T x T k T T y T k T T x
ρτβββ∂⎧=∆+⎪∂⎪
=⎪⎪∂=⎪∂⎪⎪
∂⎨=-⎪∂⎪
∂⎪=-⎪∂⎪
∂⎪=-⎪∂⎩左边界(y 轴)右边界下边界(x 轴)
上边界
需要的参数(均已cm,cal,g 为单位,所以不必换算):
用PDE Tool
解题步骤如下: 0.>> pdetool 1. 区域设置 单击
工具,在窗口拉出一个矩形,双击矩形区域,在Object Dialog 对话框输入Left
为0,Bottom 为0,Width 为2,Height 为2。
与默认的坐标相比,图形小的看不见,所以要调整坐标显示比例。
方法:选择Options->Axes Limits,把X ,Y 轴的自动选项打开。
设置Options->Application 为Heat Transfer (设置程序应用热传输模型) 2. 设置边界条件 单击 ,使边界变红色,然后分别双击每段边界,打开Boundary Conditions
对话框,
设置边界条件(根据边界条件)。
所有的边界都为Neumann 条件。
输入值见下表:
3. 设置方程类型 单击
,打开PDE Specification 对话框,设置方程类型为Parabolic (抛物型), C (比热)为0.16,a (导热系数)为0.1,d(密度)为7.82,f (热源)为
4000*exp(-3*(x.^2+(y-0.4*t).^2)/0.49)。
22
2223
40000exp(3())/exp()
13(())/exp(.)
0.49
44000m Q h r
cal cm cm r
x y cal c m τ=
∙-=∙--+-=∙则:
4.网格划分
单击,或者加密网格,单击。
5.初值和误差的设置
单击Solve菜单中Parameters…选项,打开Solve Parameters对话框,输入Time为0:0.5:5,u(t0)为20,其他不变。
6.解方程
单击,开始解方程。
7.整理数据
单击Mesh->Export Mesh…输出p e t 的数值,单击Solve->Export Solution…输出u.
回到Matlab主窗口执行下面两条命令:
u1=[p',u(:,7)] %将节点坐标和其在3s时的温度组成新矩阵
u2=sortrows(u1,3) %将u1按温度值大小升序排列。
u1=[p',u(:,4)] %将节点坐标和其在1.5s时的温度组成新矩阵
u2=sortrows(u1,3) %将u1按温度值大小升序排列。
8.温度场分布:
点plot >>parameters 勾选相关项目,右下角的时间选为1.5S,然后点plot 即可。
1.5s时
1.5s 时的三维图
3
Time=1.5 Color: u Height: u Vector field: -grad(u)
50100150200250
300
350
400450
500
3s 时的温度场:
3s时的三维图:。
