理论力学 第2章 平面力系的简化和平衡
理论力学 第2章力系的简化习题解答

第二章 力系的简化 习题解答2-1在立方体的顶点A 、H 、B 、D 上分别作用四个力,大小均为F ,其中1F 沿AC ,2F 沿IG ,3F 沿BE ,4F 沿DH 。
试将此力系简化成最简形式。
解:各力均在与坐标平面平行的面内,且与所在平面的棱边成45°角。
将力系向A 点简化,主矢'R F 在坐标轴上的投影为045cos 45cos '21=-=F F F Rx ,FF F F F F Ry 245cos 45cos 45cos 45cos '4321=+-+=,F F F F Rz 245cos 45cos '43=+= 。
用解析式表示为: ()k j F +=F R 2'设立方体的边长为a ,主矩A M 在坐标轴上的投影为 045cos 45cos 32=⋅+⋅-=a F a F M Ax , Fa a F a F M Ay 245cos 45cos 42-=⋅-⋅-= ,Fa a F a F M Az 245cos 45cos 42=⋅+⋅= 。
用解析式表示为:()k j M +-=Fa A 2。
因为,0'=⋅A R M F ,所以,主矢和主矩可以进一步简化为一个力,即力系的合力。
合力的大小和方向与主矢相同,'R R F F =;合力作用点的矢径为()i MF r a F R R =⨯=2'',所以,合力大小为2F ,方向沿对角线DH 。
2-2三力321,F F ,F 分别在三个坐标平面内,并分别与三坐标轴平行,但指向可正可负。
距离c b a ,,为已知。
问:这三个力的大小满足什么关系时力系能简化为合力?又满足什么关系时能简化为力螺旋?解:这力系的主矢为k j i 321'F F F F R ++=; 对O 点的主矩为k j i a F c F b F M O 213++=。
当主矢与主矩垂直时,力系能简化为合力。
理论力学2.2、平面任意力系的合成与平衡

m F1 OA F2 OB F1 ( OA OB ) F1 AB
3
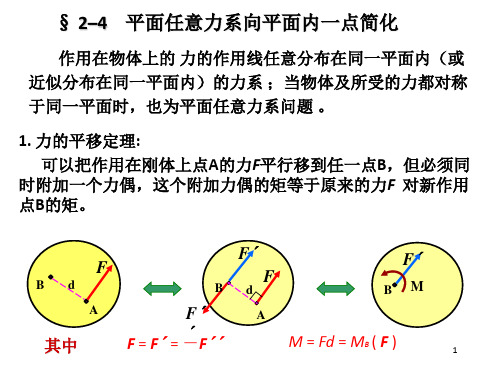
力 线 作用在刚体上的力可以离开其作用线而平 平 行移动到刚体上任意位置处,但必须对刚体 移 附加一个力偶,附加力偶的力偶矩等于原力 定 对平移后所得新力作用点的力矩。 理
求细绳的拉力和A、B两处的支持力。
解、研究对象:AB,受力 如图所示,则有:
Fix Fiy mD
0 0
(Fi )
0
FB FD G FA c
FA
os
sin 0
FB
BD
G
AB 2
0 sin
FA
AD
0
FA 115.5(N) FB 72.2(N ) FD 129.9(N) 12
例2.2-6、匀质细杆AB长度为L,重量为mg,静 止在半径为r的光滑半圆槽内(图2.2-17),
L=3r;求AB杆与水平线之间的夹角
解、研究对象:AB杆,受力如 图所示,则有:
Fix 0 Fiy 0 mO (Fi ) 0
FB FB
cos(2 ) FD sin sin(2 ) FD cos
d mO 2402 3.39(m) FR 709 .5
xE
d
sin
3.39 sin 70.8
3.59(m)
y yE tan 70.8 (x xE ) y 2.87x 10.31 0
10
课堂练习题(图示):
四川大学 理论力学 课后习题答案 第3周习题解答(第2章习题)

解:
S dxdy dx
S 0
魏
π
y sin x
0
dy sin xdx 2
0
泳
π
涛
yC
π y sin x 1 1 π 2 π y d x d y d x y d y sin xdx 0 0 0 S S 2S 8
由对称性, xC
魏
MO FR
泳
涛
0 , M O 0 ,原平面力系简化成通过简化中心 O 的合力。 3). FR 0 , M O 0 ,原平面力系可简化成一个合力。由于 O 位于力系平 4). FR M O 0 。在这种情况下,合力作用线距简化中心 O 的距离 面内,因此必有 FR
椭圆的面积为: π 3r
7 πr 2 0 πr 2 r r 2 2 7 πr πr 6 2 2 7 πr 0 πr r r 图形形心 y 坐标: 2 2 7 πr πr 6
图形形心 x 坐标:
四川大学 建筑与环境学院 力学科学与工程系 魏泳涛
静力学习题及解答—力系的简化
形心坐标 y mm 325 140 20
图形形心: yC
S y S
i i
i
193.06mm
将第二个平面图形分解成四部分。
四川大学 建筑与环境学院 力学科学与工程系 魏泳涛
静力学习题及解答—力系的简化
魏
图形 1 图形 2 图形 3 图形 4
面积 Si mm 2 320000 208000 80000 -70685.8
2.10 将图示均质梯形薄板 ABCD 在点 C 挂起,设 AD a 。欲使 AD 边保持水平, BC 应等于多少。
《理论力学》第二章力系的简化习题解

第二章力系的简化习题解[习题2-1] 一钢结构节点,在沿OA,OB,OC的方向上受到三个力的作用,已知,,,试求这三个力的合力.解:作用点在O点,方向水平向右.[习题2-2] 计算图中已知,,三个力分别在轴上的投影并求合力. 已知,,.解:合力的大小:方向余弦:作用点:在三力的汇交点A.[习题2-3] 已知,,,,求五个力合成的结果(提示:不必开根号,可使计算简化).解:合力的大小: 方向余弦:作用点:在三力的汇交点A.[习题2-4] 沿正六面体的三棱边作用着三个力,在平面OABC内作用一个力偶. 已知,,,.求力偶与三个力合成的结果.解:把,,向平移,得到:主矢量:的方向由E指向D.主矩:方向余弦:[习题2-5] 一矩形体上作用着三个力偶,,.已知,,,,求三个力偶合成的结果.解:先把在正X面上平行移动到x轴.则应附加力偶矩:把沿轴上分解:主矩:方向余弦:[习题2-6] 试求图诸力合成的结果.解:主矢量:竖向力产生的矩顶面底面斜面-0.76 0.2 0.75 主矩:方向余弦:[习题2-7] 柱子上作有着,,三个铅直力, 已知,,,三力位置如图所示.图中长度单位为,求将该力系向点简化的结果.解:主矢量:竖向力产生的矩3.5 1.7 0主矩:方向余弦:[习题2-8] 求图示平行力系合成的结果(小方格边长为)解:主矢量:ABCD8.4 -4.35主矩:方向余弦:[习题2-9] 平板OABD上作用空间平行力系如图所示,问应等于多少才能使该力系合力作用线通过板中心C.解:主矢量:由合力矩定理可列出如下方程:[习题2-10] 一力系由四个力组成。
已知F1=60N,F2=400N,F3=500N,F4=200N,试将该力系向A点简化(图中长度单位为mm)。
解:主矢量计算表0 0 600 200 0300 546.41 -140方向余弦:-110.564 120 0 主矩大小:方向余弦:[习题2-11]一力系由三力组成,各力大小、作用线位置和方向见图。
理论力学第二章(力系的等效与简化)

z
x c
F
b
o
o x
a
M y ( F ) M o ( F ) Fc
F
M z ( F ) M o ( F ) Fa
15
2019年4月16日星期二
《理论力学》
3、力对点之矩与力对通过 该点的轴之矩的关系 (转动效果的度量)
z
Fz F
y
x A
o
y
力对点之矩矢:
M o (F ) r F
Fx Fxy cos Fx F sin cos
Fy
F
O Fx x
Fy Fxy sin
y F y F sin sin
Fxy
2019年4月16日星期二
Fz F cos
6
力的分解:
F Fx Fy Fz
力F在直角坐标系中的
Fz z
F
O x
Fy
解析式
Fx
2019年4月16日星期二
力矩的符号
M O F
2019年4月16日星期二
力偶矩的符号
M
27
《理论力学》
力偶系和力偶系的合成
MR =M1+M2+…+Mn
M
力偶系
2019年4月16日星期二 28
《理论力学》
§2-3 力系等效定理
1.力系的主矢和主矩 Fn 。 设刚体上作用一平面任意力系F 1 、F 2 · · · · · ·
的夹角可为任意值。 的夹角为90o。
36
在平面任意力系, M与 R
2019年4月16日星期二
思考: 主矢,主矩与简化中心的位置有无关系?
主矢:作用在简化中心,大小和方向却与中心的位 置无关; 主矩:作用在该刚体上,大小和方向一般与中心的 位置有关。
理论力学第二章(2)

合力FR 的大小等于原力系的主矢
合力FR 的作用线位置
MO FR
小结:平面任意力系简化结果讨论
主矢
FR 0
FR 0
主矩
MO 0
MO 0 MO 0
MO 0
最后结果
说明
合力 合力作用线过简化中心
合力 合力偶
合力作用线距简化中心M O FR
与简化中心的位置无关
平衡
与简化中心的位置无关
21
简化为一个力:
c os (FR
,
i)
Fx FR
,
cos(FR ,
j)
Fy FR
原力系的主矢与简化中心O的位置无关
主矩: 原力系中各力对简化中心O之矩的代数和称为原力
系对点O的主矩。
n
M O M O (F1) M O (F2 ) ...... M O (Fn ) M o (Fi ) i 1
主矩与简化中心的选择有关
称点O为简化中心 F1’、F2’、….Fn’平面汇交力系,合力为FR’
M1、M2、….Mn平面力偶系,合力偶矩为MO
10
1、主矢和主矩
FR’=F1’+F2’+….+Fn’=F ’= F
主矢:量(简平称面为力主系矢中)所有各力的矢量和FR′称为该力系的主矢
主矢FR′的大小和方向余弦为:
FR (Fx )2 (Fy )2
11
平面任意力系向作用面内一点简化
一般力系(任意力系)向一点简化汇交力系+力偶系
(复杂力系)
(两个简单力系)
汇交力系 力偶系
力,FR‘(主矢) , (作用在简化中心)
力偶 ,MO (主矩) , (作用在该平面上)
理论力学第2章平面任意力系
空载时轨道A 、 B的约束反力,并问此起重机在使用过程中有无翻
倒的危险。
解:
(1)起重机受力图如图
(2)列平衡方程 :
MA 0:
Q
Q(6 2) RB 4 W 2 P(12 2) 0
MB 0:
Q(6 2) W 2 P(12 2) RA 4 0
6m
解方程得:
W
P
12m
RA 170 2.5P
FR' Fi Fxi Fy j
MO MO (Fi )
3. 平面任意力系的简化结果
(1)FR´= 0,Mo ≠ 0, (2)FR´ ≠ 0,Mo = 0, (3)FR´≠ 0,Mo ≠ 0, (4)FR´= 0,Mo = 0,
合力偶,合力偶矩,MO MO (Fi )
合力,合力作用线通过简化中心O。
3
F2
j
F3
x
(437.6)2 (161.6)2
F1
1 1
100
Oi
1 2
466.5N
200
MO 21.44N m
y
合力及其与原点O的距离如图(c) 。 MO
x
y
d
x
O
FR FR′ 466.5N FR´
FR
O
d MO 45.96mm
(b)
(c)
FR
10
例11 水平梁AB受按三角形分布的载荷作用,如图示。载荷的
M
l
l
30
B
D
° F
3l
P
q
A
21
解:T字形刚架ABD的受力如图所示。
M
l
l
Fx 0
30
B
FAx 1 • q • 3a Fcos30 0
理论力学常见问题解答:第2章

理论力学常见问题及解答第2单元:力系的简化1. 任意力系亦可由力平行四边形法则(或力多边形法则)得到简化结果吗? 解答:不能。
因为平行四边形法则(或力多边形法则)只能应用于汇交力系。
参考资料:贾启芬,刘习军. 《理论力学》,机械工业出版社2011第2版萧龙翔等.《理论力学》,天津大学出版社1995关键词:任意力系,力的平行四边形法则,力的多边形法则,汇交力系2. 如何应用力的平移定理解释偏心力对立柱的作用效果?解答:将力平移到立柱的轴线上,得到一个力和一个附加力偶,该力使立柱产生受压变形,而该力偶使立柱产生弯曲变形。
参考资料:贾启芬,刘习军. 《理论力学》,机械工业出版社2011第2版萧龙翔等.《理论力学》,天津大学出版社1995范钦珊. 《理论力学》,清华大学出版社2004(美)施皮格尔(M.R.Spiegel ). 《理论力学 • 理论和习题》,科学出版社1983关键词:力的平移定理,立柱,作用效果3. 如何理解力系的两个不变量?解答:主矢量'R 和主矢量与主矩的标量积O M R '均与简化中心O 无关,是力系的固有属性,因此称为力系的不变量。
参考资料:贾启芬,刘习军. 《理论力学》,机械工业出版社2011第2版萧龙翔等.《理论力学》,天津大学出版社1995范钦珊. 《理论力学》,清华大学出版社2004洪嘉振,杨长俊. 《理论力学》,高等教育出版社2008(第3版) 关键词:力系的不变量,主矢量,主矩,简化中心4.如何从力系简化,理解固定端约束反力的表达方法?解答:固定端约束的反力是空间分布力系,将该力系向梁与基础连接点简化,得到一个力(主矢量)和一个力偶(主矩),将该力和力偶矩矢量向三个方向正交分解,得到固定端约束反力的表达方式,如图。
参考资料:贾启芬,刘习军. 《理论力学》,机械工业出版社2011第2版萧龙翔等.《理论力学》,天津大学出版社1995范钦珊. 《理论力学》,清华大学出版社2004洪嘉振,杨长俊. 《理论力学》,高等教育出版社2008(第3版)(美)施皮格尔(M.R.Spiegel). 《理论力学•理论和习题》,科学出版社1983关键词:固定端,反力,力系简化5.当力系第二不变量为零时,共有几种简化结果?解答:共3种:力系平衡,力,力偶。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
l 0
xq
(
x ) dx
FR'0,MO0;故可合成为一个合力,且
FR=
FR'=
l 0
q
(
x ) dx
FR大小等于分布载荷图形的面积
合力FR的作用线到O的距离为:
h=MO/FR'=
l xq
0
(x)dx
/
lq
0
(x ) dx
FR的作用线通过分布载荷图形的形心。 33
情况 向O点简化的结果 力系简化的最终结果
分类 主矢FR' 主矩MO (与简化中心无关)
1
FR’=0 MO=0 平衡状态(力系对物体的移动
和转动作用效果均为零)。
2
FR'=0
MO0 一个合力偶,M=MO。
3
FR0
MO=0 合力FR=FR,作用线过O点。
4
FR‘0
MO0 一个合力,其大小为 FR=FR,
m
求得: RA AB cos30 144N
0.24
对CD杆:m 0 m Rc 0.182 0.242 0.2322 0
§2–3 平面任意力系的合成与平衡
平面任意力系:各力的作用线在同一平面内,既不汇交为一点 又不相互平行的力系叫∼。
[例]
力系向一点简化:把未知力系(平面任意力系)变成已知 力系(平面汇交力系和平面力偶系)
现mo (R ) mo (F1)mo (F2 )证毕
3、平面汇交力系合成与平衡的解析法
从前述可知:平面汇交力系平衡的必要与充分条件是该力系
的合力为零。 即:
R 0 Rx2 Ry2 0
Rx X 0 Ry Y 0
为平衡的充要条件,也叫平衡方程 11
例2.2 求图示作用在O点之共点力系的合力。
h=M0
/FR=1.09
(m)
;
位置由Mo
的正负确定,如图。
32
讨论2 同向分布平行力系合成
h FR
qo
q(x)
设载荷集度为q(x),在距O点x 处取
微段dx, 微段上的力为q(x)dx。
O
以O点为简化中心,主矢和主矩为: x dx l
x
FR=q(x)dx=
l
0
q
(
x
)
dx ;MO=xq(x)dx=
②
由①得
cos
T1 T2
P 2P
1 2
600
由②得NDQ-T2sin Q-2Psin 600Q 3P
15
解题技巧及说明: 1、一般地,对于只受三个力作用的物体,且角度
特殊时用 几 何法(解力三角形)比较简便。
2、一般对于受多个力作用的物体,且角度不特殊或 特殊,都用解析法。
Rx
X
作用点: 为该力系的汇交点
3、合力矩定理
定理:平面汇交力系的合力对平面内任一点的矩,等于所
有各分力对同一点的矩的代数和
即:
n
mO (R )mO (Fi )
i1
10
[证] 由合力投影定理有: od=ob+oc
又∵ M o (F1)2oABoAob M o (F2 )2oAC oAoc M o (R )2oADoAod
空间力系: 包括空间汇交力系,空间平行力系,空间力偶系和 空间一般力系(空间任意力系)
平面力系: 包括平面汇交力系,平面平行力系,平面力偶系和 平面一般力系(平面任意力系)
3
平面汇交力系:各力的作用线都在同一平面内且汇交于一点 的力系。
平面平行力系:各力的作用线都在同一平面内且互相平行 的力系。
平面力偶系:所有的力偶都作用在同一个平面内
0.4 1.2
1 3
SCD
sin
450
P cos450
tg
4.24
kN
;
RA
SCD
cos450
cos
3.16 kN
14
[例2.5] 已知如图P、Q, 求平衡时 =? 地面的反力
ND=? 解:研究球受力如图,
选投影轴列方程为
X 0 T2cos T10 ①
Y 0T2 sin Q N D 0
在工程中常见的
雨搭
车刀
29
固定端(插入端)约束
20
说明
①认为Fi这群力在同一 平面内;
② 将Fi向A点简化得一 力和一力偶;
③RA方向不定可用正交 分力YA, XA表示;
④ YA, XA, MA为固定端 约束反力;
⑤ YA, XA限制物体平动,
MA为限制转动。
30
y
FR h
FR'
讨论1 平面一般力系简化的最终结果 MO O x
(未知力系)
(已知力系)
汇交力系
力 , R'(主矢) , (作用在简化中心)
力偶系
力偶 ,MO (主矩) , (作用在该平面上)
27
主矢R ' F1 F2 F3 Fi
主矩 MO m1 m2 m3
mO (F1)mO (F2 )mO (Fi )
大小:R' R'x2 R'y2 ( X )2 (Y )2
力偶是矢量(自由矢) 平面力偶是代数量
共点力系可合成为 一个合力。
平面力偶系可合成 为一个合力偶。
合力投影定理有: 合力偶定理:
FRx=F1x+F2x+…+Fnx=Fx FRy=F1y+F2y+…+Fny=Fy
M=Mi
20
[例2.6] 在一钻床上水平放置工件,在工件上同时钻四个等 直径的孔,每个钻头的力偶矩为m1 m2 m3 m4 15Nm 求工件的总切削力偶矩和A 、B端水平反力?
用点B的矩。
[证] 力F
力系 F ,F , F 力F 力偶(F,F )
25
说明: ①力线平移定理揭示了力与力偶的关系:力 力+力偶
(偶断丝连) ②力平移的条件是附加一个力偶m,且m与d有关,m=F•d ③力线平移定理是力系简化的理论基础。
26
2. 平面一般力系向一点的简化
一般力系(任意力系)向一点简化汇交力系+力偶系
即:
Rx X1 X2 X4 X
Ry Y1 Y2 Y3 Y4 Y
Rx X Ry Y
合力投影定理:合力在任一轴上的投影,等于各分力在同一 轴上投影的代数和。
9
合力的大小: R Rx2 Ry2
x2 y2
方向:
tg
Ry Rx
∴ tg1 Ry tg1 Y
解:取坐标如图。
合力ห้องสมุดไป่ตู้坐标轴上的投影为:
Rx=X=-400+250cos45-200×4/5 =-383.2 N
Ry=Y=250sin45-500+200×3/5 =-203.2N
y
F4 =200N
F3=500N
F 2 =250N
5
3 4
45 F1 =400N
O
x
R
合力为: R Rx2 Ry2 =433.7N;
23
研究思路:
受
y
力
如 共点力系可合
M2
何 成为一个力
简
分 析
M1
化 力偶系可合成
一般力系 x
? 为一个合力偶
问题:如何将力移到同一个
作用点上?
O
或者说力如何移到任一点O?
F
力向一点平移
力系的简化
平衡条件
24
1.力的平移定理
可以把作用在刚体上点A的力 F平行移到任一 点B,但必须 同时附加一个力偶。这个力偶的矩等于原来的力 F 对新作
3、投影轴常选择与未知力垂直,最好使每个方程中 只有一个未知数。
16
4、对力的方向判定不准的,一般用解析法。 5、解析法解题时,力的方向可以任意设,如果求出
负值,说明力方向与假设相反。对于二力构件, 一般先设为拉力,如果求出负值,说明物体受压 力。
17
§2-2 平面力偶系的合成与平衡
平面力偶 等效定理
mo (Q ) Ql
13
[例2.4] 已知 P=2kN 求SCD , RA
解:①研究AB杆
②画出受力图
③列平衡方程
X 0 RAcos SCDcos4500 Y 0 PRA sin SCD sin450 0
④解平衡方程 由EB=BC=0.4m,
解得:
tg
EB AB
主矢 R 方向: tg1 Ry tg1 Y
(移动效应)
Rx
X
简化中心 (与简化中心位置无关) [因主矢等于各力的矢量和]
28
大小: M O mO (Fi )
主矩MO 方向: 方向规定 +
—
(转动效应) 简化中心: (与简化中心有关)
(因主矩等于各力对简化中心取矩的代数和)
固定端(插入端)约束
6
结论: R F1 F2 F3 F4
即: R F
即:汇交力系的合力等于力系中各分力的矢量和,合力的作 用线通过力系的汇交点。
二、汇交力系平衡的几何条件
汇交力系平衡的充要条件是:
R F 0
在几何法求力系的合力中,合力为零意
味着力多边形自行封闭。所以汇交力系
平衡的必要与充分的几何条件是:
力多边形自行封闭
或
力系的合力等于零
力系中各力的矢量和等于零
7
三 合成的解析法
1、力在平面坐标轴上的投影
X=Fx=F·cos :
