实验三函数的数值逼近
数值分析实验报告2

实验报告实验项目名称函数逼近与快速傅里叶变换实验室数学实验室所属课程名称数值逼近实验类型算法设计实验日期班级学号姓名成绩512*x^10 - 1280*x^8 + 1120*x^6 - 400*x^4 + 50*x^2 - 1并得到Figure,图像如下:实验二:编写程序实现[-1,1]上n阶勒让德多项式,并作画(n=0,1,…,10 在一个figure中)。
要求:输入Legendre(-1,1,n),输出如a n x n+a n-1x n-1+…多项式。
在MATLAB的Editor中建立一个M-文件,输入程序代码,实现勒让德多项式的程序代码如下:function Pn=Legendre(n,x)syms x;if n==0Pn=1;else if n==1Pn=x;else Pn=expand((2*n-1)*x*Legendre(n-1)-(n-1)*Legendre(n-2))/(n);endx=[-1:0.1:1];A=sym2poly(Pn);yn=polyval(A,x);plot (x,yn,'-o');hold onend在command Windows中输入命令:Legendre(10),得出的结果为:Legendre(10)ans =(46189*x^10)/256 - (109395*x^8)/256 + (45045*x^6)/128 - (15015*x^4)/128 + (3465*x^2)/256 - 63/256并得到Figure,图像如下:实验三:利用切比雪夫零点做拉格朗日插值,并与以前拉格朗日插值结果比较。
在MATLAB的Editor中建立一个M-文件,输入程序代码,实现拉格朗日插值多项式的程序代码如下:function [C,D]=lagr1(X,Y)n=length(X);D=zeros(n,n);D(:,1)=Y';for j=2:nfor k=j:nD(k,j)=(D(k,j-1)- D(k-1,j-1))/(X(k)-X(k-j+1));endendC=D(n,n);for k=(n-1):-1:1C=conv(C,poly(X(k)));m=length(C);C(m)= C(m)+D(k,k);end在command Windows 中输入如下命令:clear,clf,hold on;k=0:10;X=cos(((21-2*k)*pi)./22); %这是切比雪夫的零点Y=1./(1+25*X.^2);[C,D]=lagr1(X,Y);x=-1:0.01:1;y=polyval(C,x);plot(x,y,X,Y,'.');grid on;xp=-1:0.01:1;z=1./(1+25*xp.^2);plot(xp,z,'r')得到Figure ,图像如下所示:比较后发现,使用切比雪夫零点做拉格朗日插值不会发生龙格现象。
数值分析讲义第三章 函数逼近

P ( xk ) f ( xk ) 1 f , Pn* , 1
k
n2
b, s.t.
(充分性):设[a, b]上至少有n 2个点a x1 x2 x P ( xk ) f ( xk ) 1 f , Pn* , 1
一致逼近或 均匀逼近 均方逼近或 平方逼近
max a x b f ( x) P( x)
f ( x) P( x) 2
b
a
f ( x) P( x) dx
2
存在性问题: f(x)C[a,b], 是否存在
Pn(x) f(x)(uniformly)?
Th1. (Weierstrass定理)设f(x)C[a,b], >0, 多项式P(x), s.t. f ( x) P( x) 在[a,b]上一致成立。 Weierstrass,德,
3个重要推论
推论1
证
最佳逼近多项式唯一
设f ( x)有两个最佳逼近多项式P( x), Q( x), 则x [a, b] - En P( x) f ( x) En , - En - En Q( x) f ( x) En , P( x) Q( x) f ( x) En 2 P( x) Q( x) R( x) 也是f ( x)的最佳逼近多项式, 2 且R ( x) f ( x)的n 2个交错点组x1 x2 x n 2 满足 R ( xk ) f ( xk ) 1 En
k
En R( xk ) f ( xk )
P( xk ) f ( xk ) Q( xk ) f ( xk ) 2 2
(*)
数值分析实验(3)

实验三函数逼近与快速傅里叶变换P95专业班级:信计131 班姓名:段雨博学号:2013014907一、实验目的1、熟悉 matlab 编程。
2、学习最小二乘法及程序设计算法。
二、实验题目1、对于给函数f x1在区间1,1 上取 x i 1 0.2i i0,1,10 ,试求3次125x2曲线拟合,试画出拟合曲线并打印出方程,与第二章计算实习题 2 的结果进行对比。
2、由实验给出数据表x0.00.10.20.30.50.8 1.0y 1.00.410.500.610.91 2.02 2.46试求 3 次、 4 次多项式的曲线拟合,再根据数据曲线形状,求一个另外函数的拟合曲线,用图示数据曲线及相应的三种拟合曲线。
3.给定数据点 x i , y i如表所示00.50.60.70.80.91x x i1 1.75 1.96 2.19 2.44 2.71 3.00y i用最小二乘法求拟合数据的二次多项式,并求平方误差。
三、实验原理与理论基础1.最小二乘原理与线性拟合:在函数的最佳平方逼近中 f ( x)C[ a,b] ,如果 f ( x) 只在一组离散点集 { x i , i 0,1..., m} 上给出,这就是科学实验中经常见到的实验数据{{( x i, y i ), i 0,1...m} }的曲线拟合,这里y i f (x i)(i0,1...m) ,要求一个函数y S * ( x) 与所给数据 {( x i , y i ), i 0,1...m} 拟合,若记误差(01 ,... m ) T,设0 ( x),1 (x),... n (x) 是C[a,b]上线性无关函数族,在span{0 ( x),1 ( x),...n (x)} 中找一函数 S * (x) 使误差平方和m m m222[ S * ( x)y i ]2min[ S( x i )y i ] ,这2ii 0i0i 0里S(x)a0 0 ( x)a0 1 ( x)... a n n ( x) ( n m )。
函数的数值逼近-拟合
课程名称 计算方法实验项目名称 函数的数值逼近-拟合实验成绩 指导老师(签名 ) 日期一. 实验目的和要求1. 通过实例学习如何用拟合方法解决实际问题。
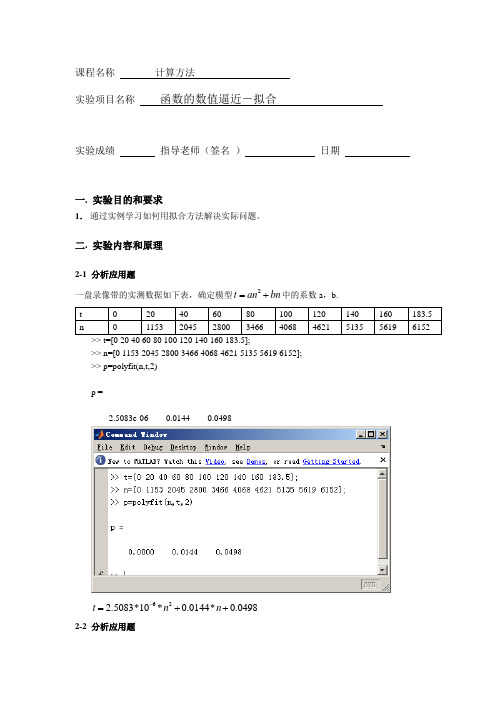
二. 实验内容和原理2-1 分析应用题一盘录像带的实测数据如下表,确定模型2t an bn =+中的系数a ,b.>> t=[0 20 40 60 80 100 120 140 160 183.5];>> n=[0 1153 2045 2800 3466 4068 4621 5135 5619 6152]; >> p=polyfit(n,t,2) p =2.5083e-06 0.0144 0.0498622.5083*10*0.0144*0.0498t n n -=++2-2 分析应用题旧车价格预测:某年美国旧车价格的调查资料如下表,其中i x 表示轿车的使用年数,i y 表示相应的平均价格。
试分析用什么形式的曲线来拟合上述的数据,并预测使用4.5年后轿车的平均价格大致为多少。
>> x=1:10;>> y=[2615 1943 1494 1087 765 538 484 290 226 204]; >> p=polyfit(x,y,2); >> a=p(1); >> b=p(2); >> c=p(3);>> Y=polyval(p,x); >> plot(x,y,'b',x,Y ,'r') >> z=polyval(p,4.5) z =955.70472-3分析应用题>> t=1790:10:1980;>> x=[3.9 5.3 7.2 9.6 12.9 17.1 23.2 31.4 38.6 50.2 62.9 76.0 92.0 106.5 123.2 131.7 150.7 179.3 204.0 226.5];>> p=polyfit(t,log(x),1);>> r=p(1)r =0.0214>> x0=exp(p(2))x0 =1.2480e-016>> x1=x0.*exp(r.*t);>> plot(t,x,'r',t,x1,'b')三. 操作方法与实验步骤(包括实验数据记录和处理)四. 实验结果与分析。
实验指导书_函数逼近

实验指导书_函数逼近与曲线拟合曲线拟合:由一组实验数据},,2,1),,{(n i y x i i =,选择一个较简单的函数)(x f (如多项式),在一定准则下,最接近这组数据.函数逼近:已知一个较为复杂的连续函数],[),(b a x x y ∈,要求选择一个较简单的函数)(x f ,在一定准则下最接近)(x y .掌握内容:切比雪夫零点插值、最佳平方逼近、曲线拟合的最小二乘法的Matlab 实现一、切比雪夫零点插值1.算法原理设1[,],()+∈n n f C a b L x 是以,0,1,,22-+=+= k k b a a bx t k n 为插值节点的Lagrange 插值多项式,其中21cos,0,1,,2(1)π+==+ k k t k n n 是Chebyshev 多项式1()n T x +的零点,此时插值误差最小,误差(余项)估计公式为:1(1)21()()()()max ()2(1)!+++≤≤-=-≤+n n n n n a x bb a R x f x L x f x n2.实例例1(P64例4) 求()x f x e =在[0,1]上的四次Lagrange 插值多项式4()L x ,插值节点用5()T x 的零点,并估计误差401max ().x x e L x ≤≤-首先编写Lagrange 插值主程序,并保存为lagrange.mfunction[L ,C, l ,L1]= lagrange (X,Y)%输入的量:n+1个节点(xi,yi)的横坐标向量X ,纵坐标向量Y ;%输出的量:n 次拉格朗日插值多项式L 及其系数向量C ,基函数l 及其系数矩阵L1 m=length(X); L=ones(m,m); for k=1: m V=1; for i=1:m if k~=iV=conv(V ,poly(X(i)))/(X(k)-X(i)); end endL1(k,:)=V; l(k,:)=poly2sym (V); endC=Y*L1; L=Y*l; l=vpa(l,4); L=vpa(L,4);然后编写如下程序,并保存为lc_P64eg4.m%P64eg4求Lagrange- Chebyshev 多项式的程序lc_P64eg4.m %X 为插值节点%L 为Lagrange- Chebyshev 多项式的表达式%C 为按降幂排列的Lagrange- Chebyshev 多项式的系数 %R 为误差限 clear;format short g s=1;for k=0:4X(k+1)=(1+cos((2*k+1)*pi/10))/2; Y(k+1)=exp(X(k+1)); s=s*(k+1); end X,[L ,C, l ,L1]= lagrange(X,Y); L, C,R=2.71828/(s*2^9)x=linspace(X(1), X(5),50); y=polyval(C,x); y1=exp(x);plot(X,Y,'r*',x,y,'r-') figure,plot(X,Y,'r*',x,y1,'b-') figure,plot(X,Y,'r*',x,y,'r-',x,y1,'b-')在Matlab 窗口中运行程序lc_P64eg4.m >> lc_P64eg4 X =0.97553 0.79389 0.5 0.20611 0.024472 L =.9988*x+.1403*x^3+.6942e-1*x^4+.5098*x^2+1.000 C =0.069416 0.14028 0.50978 0.99876 1 R =4.4243e-005图1.()xf x e 在[0,1]上的四次Lagrange- Chebyshev 插值多项式例2 (P65例5)设211()f x x =+,在[-5,5]上利用11()T x 的零点作插值点,构造10次拉格朗日插值多项式 10()L x ,并与等距节点的10()L x 近似()f x 作比较. 首先编写如下程序,并保存为lc_P65eg5.m%P64eg4求Lagrange- Chebyshev 多项式的程序lc_P65eg5.m%X 为Chebyshev 零点%L 为Lagrange- Chebyshev 多项式的表达式%C 为按降幂排列的Lagrange- Chebyshev 多项式的系数 %L1为等距节点多项式的表达式%C1为按降幂排列的等距节点多项式的系数 clear;format short for k=0:10X(k+1)=(10*cos((2*k+1)*pi/22))/2; Y(k+1)=1/(1+X(k+1)^2); end X,[L ,C, l ,L1]= lagrange(X,Y); L,C,x=linspace(X(1), X(11),100); y=polyval(C,x); y1=1./(1+x.^2);X1=linspace(-5,5,11); Y1=1./(1+X1.^2);[L1 ,C1, l1 ,L11]= lagrange(X1,Y1); L1,C1,X2=-5:0.1:5;Y2=polyval(C1,X2);plot(X,Y ,'r*',x,y,'r-',x,y1,'b-',X1,Y1,'O',X2,Y2,'k-') gtext('切比雪夫插值点r*') gtext('切比雪夫插值曲线r-') gtext('被插函数曲线b-') gtext('等距节点插值点o')gtext('等距节点插值多项式k-')在Matlab 窗口中运行程序lc_P65eg5.m,得如下图形结果(这里,数值结果略,请自己运行观察)图2. 211()f x x=+在[-5,5]上的插值多项式 10()L x 与10()L x二、最佳平方多项式逼近1.求定义在区间[a ,b ]上的已知函数最佳平方逼近多项式的算法(1)设已知函数()f x 的最佳平方逼近多项式为01()n n p x a a x a x =+++ ,由最佳平方逼近的定义有:010012(,,)(,,,,)n iF a a a i n a ∂==∂其中()20101(,,)()()b nn n aF a a a f x aa x a x dx =-+++⎰(2)求多项式()p x 系数的法方程:Ca D =,其中1211222111212()(),()(b bb bbn na aa a a bbb b b n n a aa aa b bb b b n n n n n a aa aa bbb bn n n n naaa a dx xdx x dx x dx f x dx xdx x dx x dx x dx xf x dx C D x dx x dxx dx x dx x f x dx x dx x dx x dx x dx x f x -+----+-⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥==⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰)b a dx ⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎰2.求定义在区间[a ,b ]上的已知函数最佳平方逼近多项式的主程序function [coff,d]=ZJPF(func,n,a,b) %func:已知函数%n:最佳平方逼近多项式的最高次数 %a:逼近区间的左端点 %b:逼近区间的右端点%coff:按升幂排列的逼近多项式的系数 % d:法方程的右端项 C = zeros(n+1,n+1);var = findsym(sym(func)); func = func/var; for i=1:n+1C(1,i)=(power(b,i)-power(a,i))/i; %算法中的C 矩阵的第一行 func = func*var;d(i,1)=int(sym(func),var,a,b); %算法中的D 向量的第一行 endfor i=2:n+1C(i,1:n)=C(i-1,2:n+1); f1 = power(b,n+i); f2 = power(a,n+i);C(i,n+1)=(f1-f2)/(n+i); %形成C 矩阵 endcoff = C\d; %求解逼近多项式的系数3.例题(教材P68例6)设211()f x x =+,求[0,1]上的一次最佳平方逼近多项式.首先编写被逼近函数的M 文件,并保存为funcp68eg6.m function f=funcp68eg6() syms xf=sqrt(1+x^2);然后编写如下程序,并保存为p68_eg6.m %p68_eg6.m clear;[coff,d]=ZJPF(funcp68eg6,1,0,1); coff=vpa(coff)x = findsym(sym(funcp68eg6)); func=funcp68eg6*funcp68eg6;PFWC=vpa(int(sym(func),x,0,1)-coff'*d,4)运行结果>> p68_eg6 coff =[ .9343200492928959528618412015402] [ .4269470508068461683106156461091] PFWC = .12e-2三、曲线拟合的最小二乘法1. 多项式拟合及其MATLAB 程序面对一组数据,,,2,1),,(n i y x i i = 用线性最小二乘法作曲线拟合时,如果选取一组函数02(),(),,()m x x x ϕϕϕ 为)(,,,,12n m x x x m < ,则拟合曲线为多项式11++++=m m m a x a x a y .一般m = 2,3, 不宜过高.对于指数曲线,拟合前需作变量代换,化为系数参数的线性函数.2. 用MATLAB 作线性最小二乘拟合的多项式拟合用MATLAB 作线性最小二乘拟合的多项式拟合有现成程序. 调用格式为: a=polyfit(x,y,m)其中输入参数 x ,y 为要拟合的数据,是长度自定义的数组,m 为拟合多项式的次数,输出参数a 为拟合多项式:11++++=m m m a x a x a y的系数向量a ),,,(11+=m m a a a .(注意:按降幂排列)3. 多项式在x 处的值y 的计算: y=polyval(a,x)例 给出一组数据点),(i i y x 列入下表中,试用线性最小二乘法求拟合曲线,.解(1)首先根据给出的数据点),(i i y x ,用下列MATLAB 程序画出散点图. 在MATLAB 工作窗口输入程序>> x=[-2.9 -1.9 -1.1 -0.8 0 0.1 1.5 2.7 3.6];y=[53.94 33.68 20.88 16.92 8.79 8.98 4.17 9.12 19.88]; plot(x,y,'r*'), legend('数据点(xi,yi)') xlabel('x'), ylabel('y'),title('例7.4.1的数据点(xi,yi)的散点图')运行后屏幕显示数据的散点图,见图3.(2)因为数据的散点图3的变化趋势与二次多项式很接近,所以选取一组函数2,,1x x ,令3221)(a x a x a x f ++=,其中k a 是待定系数)3,2,1(=k .(3)用作线性最小二乘拟合的多项式拟合的MATLAB 程序求待定系数k a)3,2,1(=k .输入程序>> a=polyfit(x,y,2)运行后输出按拟合多项式的系数a =2.8302 -7.3721 9.1382故拟合多项式为2138.91372.72830.2)(2+-=x x x f .(4)编写下面的MATLAB 程序估计其误差,并做出拟合曲线和数据的图形.输入程序>> xi=[-2.9 -1.9 -1.1 -0.8 0 0.1 1.5 2.7 3.6];y=[53.94 33.68 20.88 16.92 8.79 8.98 4.17 9.12 19.88]; n=length(xi); f=2.8302.*xi.^2-7.3721.*xi+9.1382 x=-2.9:0.001:3.6;F=2.8302.*x.^2-7.3721.*x+8.79; fy=abs(f-y); fy2=fy.^2; Er=sqrt((sum(fy2)/n)), plot(xi,y,'r*', x,F,'b-'),legend('数据点(xi,yi)','拟合曲线y=f(x)') xlabel('x'), ylabel('y'), 运行后屏幕显示数据),(i i y x 与拟合函数f 的均方根误差E 2及其数据点(x i ,y i )和拟合曲线y =f (x )的图形,见图4.图3图4。
《函数的数值逼近》PPT课件

精选课件ppt
7
2、插值多项式的存在唯一性
定理 若插值结点 x0,x1,…, xn是(n+1)个互异点,则满足插值条件 P(xk)= yk (k = 0,1,…,n)
精选课件ppt
10
§2 代数多项式插值
一、线性插值与抛物线插值
1. 线性插值(n =1)
设已知区间[ xk , xk+1]端点处的函数值yk= f (xk),yk+1 = f (xk+1),
求线性插值多项式L 1(x ) ,使其满足
L1 ( xk ) yk
L1
(
xk
1
)
yk 1
x 0 xk
y = L1(x)
P(x) = a0 + a1 x + ⋯ + an xn
则称P( x)为n 次插值多项式. 相应的插值法称为多项式插 值法(代数插值法)。
x
y = f (x) •
(xi, yi)
y = P(x) 曲线 P ( x)
近似 f ( x)
0 a=x0 x1 x2 x3
xn=b y
精选课件ppt
6
研究问题:
构造法:
先求 插值基函数l k-1(x), l k (x), l k+1(x) (二次函数), 满足:
lk1(xk1)1, lk1(xk)lk1(xk1)0;
lk(xk)1,
lk(xk1)lk(xk1)0;
(4)
lk1(xk1)1, lk1(xk1)lk1(xk)0,
函数的数值逼近-插值
课程名称计算方法实验项目名称函数的数值逼近-插值实验成绩指导老师(签名)日期2011-9-16一. 实验目的和要求1.掌握用Matlab计算Lagrange、分段线性、三次样条三种插值的方法,改变节点的数目,对三种插值结果进行初步分析。
2.通过实例学习如何用插值方法解决实际问题。
二. 实验内容和原理1)编程题2-1要求写出Matlab源程序(m文件),并对每一行语句加上适当的注释语句;2)分析应用题2-2,2-3,2-4,2-5要求将问题的分析过程、Matlab源程序、运行结果和结果的解释、算法的分析等写在实验报告上。
2-1分析应用题用12y x=在0,1,4,9,16x=产生5个节点15,,P P。
用以下五种不同的节点构造Lagrange插值公式来计算5x=处的插值,与精确值比较并进行分析。
function y=lagr(x0,y0,x)n=length(x0);m=length(x);L=zeros(1,n);y=zeros(1,m);for k=1:ms=0;for i=1:nL(i)=1;for j=1:nif j~=iL(i)=L(i)*(x(k)-x0(j))/(x0(i)-x0(j));endends=s+y0(i)*L(i);endy(k)=s;end1) 用34,P P 构造;>> x0=[4,9]; >> y0=[2,3]; >> lagr(x0,y0,5) ans =2.20002) 用234,,P P P 构造;>> x0=[1,4,9]; >> y0=[1,2,3]; >> lagr(x0,y0,5) ans =2.26673) 用2345,,,P P P P 构造;>> x0=[1,4,9,16]; >> y0=[1,2,3,4]; >> lagr(x0,y0,5) ans =2.25404) 用1245,,,P P P P 构造;>> x0=[0,1,9,16]; >> y0=[0,1,3,4]; >> lagr(x0,y0,5) ans =2.95245) 用全部插值节点12345,,,,P P P P P 构造。
函数逼近实验报告
一、实验目的1. 理解函数逼近的基本概念和方法。
2. 掌握常见的逼近方法,如泰勒级数、傅里叶级数等。
3. 通过实际操作,加深对逼近理论的理解和应用。
二、实验内容1. 泰勒级数逼近- 实验步骤:1. 选择一个函数,如$f(x) = e^x$,在$x_0 = 0$处展开泰勒级数。
2. 根据所需的精度,确定展开的项数。
3. 利用泰勒级数公式计算逼近值。
4. 将逼近值与原函数值进行比较,分析误差。
- 实验结果:- 当展开3项时,逼近值与原函数值的最大误差约为$1.3 \times 10^{-4}$。
- 当展开5项时,逼近值与原函数值的最大误差约为$3.5 \times 10^{-6}$。
2. 傅里叶级数逼近- 实验步骤:1. 选择一个周期函数,如$f(x) = \sin x$,进行傅里叶级数展开。
2. 根据所需的精度,确定展开的项数。
3. 利用傅里叶级数公式计算逼近值。
4. 将逼近值与原函数值进行比较,分析误差。
- 实验结果:- 当展开3项时,逼近值与原函数值的最大误差约为$0.015$。
- 当展开5项时,逼近值与原函数值的最大误差约为$0.003$。
3. 实验比较- 泰勒级数与傅里叶级数的比较:- 泰勒级数适用于函数在一点附近展开,而傅里叶级数适用于周期函数的展开。
- 泰勒级数的逼近效果在函数变化剧烈的区间可能较差,而傅里叶级数对周期函数的逼近效果较好。
三、实验结论1. 函数逼近是数学和工程中常用的一种方法,可以有效地将复杂函数简化为易于计算的形式。
2. 泰勒级数和傅里叶级数是常见的函数逼近方法,各有优缺点,应根据具体问题选择合适的方法。
3. 在实际应用中,应根据所需精度和计算复杂度,合理选择逼近方法的项数。
四、实验心得1. 通过本次实验,我对函数逼近的基本概念和方法有了更深入的理解。
2. 实验过程中,我学会了如何选择合适的逼近方法和确定逼近项数,提高了我的数学建模能力。
3. 本次实验让我认识到,函数逼近在工程和科学研究中的应用非常广泛,具有重要的实际意义。
函数的数值逼近
函数的数值逼近用比较简单的函数代替复杂的函数,是函数逼近。
函数最佳逼近,即不满足插值条件而整体具有好的逼近效果的函数拟合方法。
下面先讨论函数的数值逼近的基本理论与方法,例如最佳平方逼近函数的存在性、惟一性以及最佳平方逼近函数的求法。
最后讨论曲线拟合的最小二乘解问题。
1、 预备知识1.1正交多项式的概念及几个重要性质定义1.1 设有C [a,b]中的函数组,),(,),(),(10 x x x n ΦΦΦ若满足{)1.1()()()(),(,0,⎰≠=>=ΦΦ=ΦΦbak j k j A k j k j k dx x x x ρ其中)(x ρ为权函数,则称此函数组为在区间[a,b]上带权)(x ρ的正交函数组,其中k A 为常数,若k A =1,称该函数组是标准正交的.定理1.1 设函数组{}∞=Φ0)(k k x 正交,则它们一定线性无关.证 设),,2,1()(n i x i =Φ为{}∞=Φ0)(k k x 中任意n 个函数,令,0)()()(2211=Φ++Φ+Φx C x C x C n n 上式两边与)(x k Φ作内积,由内积的性质和正交性有 ).,,2,1(0),(n k C k k k ==ΦΦ因为,0),(≠ΦΦk k 故有),,2,1(0n k C k==.得证.定理1.2 设{}],,[)(0b a C x nk k ∈Φ=它们线性无关的充分必要条件是其Gram 行列式,0≠n G 其中)2.1(),(),(),(),(),(),(),(),(),(101110101000n n n n n n n G ΦΦΦΦΦΦΦΦΦΦΦΦΦΦΦΦΦΦ=证 我们主要在实内积空间讨论问题.由内积的定义可知),,(),(k j j k ΦΦ=ΦΦ故n G 对应的矩阵是对称矩阵.考虑以n a a a ,,,10 为未知元的线性方程组∑===ΦΦnk k j kn j a)3.1().,,1,0(0),(其系数行列式为n G .由线性代数知识知道:式(1.3)仅有零解),,1,0(0n k a k ==的充要条件是,0≠n G充分性 设,0≠n G 要证明{}n k k x 0)(=Φ线性无关. 作线性组合∑==Φnk kk a 0,0显然有∑∑∑=====ΦΦ=ΦΦ=ΦΦnk nk nk k j k j k k j k k n j a a a 0).,,1,0(0),(),(),(这表明),,1,0(n k a k =满足式(1.3).又因,0≠n G 故有),,1,0(0n k a k ==,按线性无关的定义知{}nk k x 0)(=Φ线性无关.必要性 设{}nk k x 0)(=Φ线性无关.要证明.0≠n G设),,1,0(n k a k =满足式(1.3).即 ∑===ΦΦnk k j kn j a).,,1,0(0),(则有 ∑∑====ΦΦ=ΦΦnk j k k nk j k kn j a a),,,1,0(0),(),(从而有 .0),(0∑∑===ΦΦnk nk kkkka a由上式可知.00∑==Φnk kk a由于{}nk k x 0)(=Φ线性无关,则有),,1,0(0n k a k ==,即齐次线性方程组(1.3)仅有零解,故.0≠n G定义1.2 给定区间[a,b]和对应的权函数)(x ρ及多项式序列∑===kj jjk k x ax g 0),,2,1,0()(其中首项系数,0≠k a 若满足{)9.1()()()(),(,0,⎰≠=>==ba k j k j A k j k j k dx x g x g x g g ρ则称之为在区间[a,b]上带权)(x ρ的正交多项式序列, )(x g k 称为k 次正交多项式. 没说明时,认为权函数)(x ρ≡1.2、最佳平方逼近2.1 最佳平方逼近函数的概念定义2.1 设],[)(b a C x f ∈及],[b a C 中的子集},,,,{10n span ΦΦΦ=Γ 其中n ΦΦΦ,,,10 线性无关. 若存在Γ∈*)(x S 使得)1.2()]()()[(min ||)()(||min ||)()(||22222⎰-=-=-Γ∈Γ∈*ba S S dxx S x f x x S x f x S x f ρ 成立,则称)(x S *为f(x)在Γ中的最佳平方逼近函数.特别地,当},,,,1{nx x span =Γ满足式(2.1)的Γ∈*)(x S n 称为f(x)的n 次最佳平方逼近多项式,简称n 次最佳平方逼近.2.2 最佳平方逼近函数的求法定理 2.1 对于任意的函数],[)(b a C x f ∈,其在Γ中的最佳平方逼近函数)(x S *是存在且唯一的.证 Γ中的函数形如∑=Φ=nj jj x a x S 0),()(由式(2.1)可知,求f(x)的最佳平方逼近函数等价于求多元函数∑⎰=Φ-=nj j j ban dxx a x f x a a a I 0210)2.2()]()()[(),,,(ρ的最小值问题.由极值存在的必要条件有)3.2(),,,1,0(0n k a Ik==∂∂积分与求导交换次序有: ∑⎰==Φ-Φ-nj k j j badx x x a x f x 0.0))()](()()[(2ρ故∑⎰===ΦΦ-nj k j j ban k dx x x a x f x 0)4.2(),,,1,0(0)()]()()[( ρ∑⎰⎰=Φ=ΦΦnj babak j k j dx x x f x dx x x x a 0.)()()()()()(ρρ所以∑==Φ=ΦΦnj k j j kn k f a 0)5.2().,,1,0(),(),(这是以n a a a ,,10为未知元的线性方程组,因为n ΦΦΦ,,,10 线性无关,其系数行列式,0≠n G 故式(2.5)有唯一解.设其解为),,,1,0(n i a i =*则∑=**Φ=ni iia x S 0)6.2(.)(下面证明)(x S *满足式(2.1).即需证明,)(Γ∈∀x S⎰⎰-≤-*babadx x S x f x dx x S x f x 22)]()()[()]()()[(ρρ成立.为此只需证明 ⎰⎰≥---=*babax S x f x dx x S x f x D .0)]()()[()]()()[(22ρρ由于⎰⎰*-=b abadxx S x dx x S x D 22)]()[()]()[(ρρdx x S x f x dx x S x f x bab a⎰⎰*+-)()()(2)()()(2ρρ⎰*-=badx x S x S x 2)]()()[(ρ⎰**--+badx x S x f x S x S x ,)]()()][()()[(2ρ由于,)()(Γ∈-*x S x S 由(2.4)知上式第二项为零. 故 .0)]()()[(2⎰≥-=*badx x S x S x D ρ这表明)(x S *为f(x)在Γ中的最佳平方逼近函数.由于式(2.5)的解),,,1,0(n i a i =*存在且唯一,所以f(x)在Γ中的最佳平方逼近函数)(x S *存在且唯一. 最佳平方逼近函数的误差由式(2.4)知 22||)()(||x S x f *-),(),(),(),(f S f S S f f S f S f S f ******-=---=--= ),(||||),(),(022∑=**-=-=nk k k f a f f S f f φ)7.2(.),(||||022∑=*-=k k k f af φ例 2.1 求函数x e x f =)(在区间[0,1]上的一次最佳平方逼近多项式)(1x S *,并计算22||)()(||x S x f *-.解 设,)(101x a a x S +=*1,1)(,,1},,1{10===Φ=Φ=Γn x x x span ρ,由式(2.5)知⎩⎨⎧Φ=ΦΦ+ΦΦΦ=ΦΦ+ΦΦ),(),(),(),(),(),(11110010110000f a a f a a ⎰==ΦΦ1000,11),(dx⎰==ΦΦ=ΦΦ10110,21),(),(xdx ⎰⎰-==Φ==ΦΦ10010211,1),(,31),(e dx e f dx x x ⎰==Φ11,1),(dx xe f x所以 ,11312121110⎥⎦⎤⎢⎣⎡-=⎥⎦⎤⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡e a a⎩⎨⎧-=-=.618,10410e a e a 故.)618(104)(1x e e x S -+-=*由式(2.7)知22||)()(||x S x f *-=∑=-=122),(||||k k k f a f φ.1094.3)618()1)(104(132⎰-⨯=-----=e e e dx e x 3、用正交多项式作函数的最佳平方逼近设},,,,{10n span ϕϕϕ =Γ{}ni i 0=ϕ在[a,b]上带权)(x ρ正交。
函数逼近与曲线拟合实验报告
数值分析实验报告一、实验题目:函数逼近与曲线拟合二、目的和意义:1.掌握曲线拟合的最小二乘法2.最小二乘法亦可用于解超定线性代数方程组3.探索拟合函数的选择与拟合精度间的关系三、计算公式(算法):由已知的离散数据点选择与实验点误差最小的曲线)(...)()()(1100x a x a x a x S n n ϕϕϕ+++= 称为曲线拟合的最小二乘法。
若记),()()(),(0i k i j m i i k j x x x ϕϕωϕϕ∑==k i k i mi i k d x x f x f ≡=∑=)()()(),(0ϕωϕ 上式可改写为),...,1,0(;),(n k d a k j no j j k -=∑=ϕϕ这个方程成为法方程,可写成矩阵形式.d Ga =其中,),...,,(,),...,,(1010T n T n d d d d a a a a ==⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=),(),(),()(),(),(),(),(),(101110101000n n n n n n G ϕϕϕϕϕϕϕϕϕϕϕϕϕϕϕϕϕϕ 。
它的平方误差为:.)]()([)(||||2022i i mi i x f x S x -=∑=ωδ 1) 按照最小二乘法的性质构造Gram 矩阵G ,并求解Ga=d ;构造的时候首先构造一个零矩阵A ;2)然后开始构造Gram 矩阵(在下面程序里我们把克莱姆矩阵用A来表示)3)然后求列矩阵b,因为Aa=b,所以求a=A\b;(d就是列矩阵b); 4)然后找对应数据的最小二乘拟合方程和画出它的图像;四、结构程序设计:n=3M=zeros(n,12)%三行十二列的零矩阵M(1,:)=[0:5:55];%输入x值for i=2:nM(i,:)=power(M(1,:),i);end%内积求φiA=zeros(n,n);%n行n列零矩阵for i=1:nfor j=1:nA(i,j)=M(i,:)*M(j,:)'endend%Gram矩阵y=[0 1.27 2.16 2.86 3.44 3.87 4.15 4.37 4.51 4.58 4.02 4.64];y=y.*10.^(-4);b=[];for i=1:nb(i)=M(i,:)*y';endformat long;c=[];b=b'c=A\b%输出系数d=[];for i=1:nd(i)=c(n-i+1);endd(n+1)=0plot(M(1,:),y,'*');hold on x1=[0:1:55];plot(x1,polyval(d,x1)); legend('数据点','二次拟合') title('二次拟合')set(gcf,'color','w');%画图error=0,e=[];e=polyval(d,M(1,:))-y; error=e*e';e=sqrt(error)%求误差五、输出结果:首先是关于原问题的拟合拟合图像再考虑四次项时的拟合,即当n=4时输出结果如图所示可见四次拟合时误差会更小一些六、讨论和分析:拟合方程的选取至关重要,它决定了最大误差、平均误差的大小,即拟合曲线的接近程度。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验三函数的数值逼近-插值与曲线拟合
【实验目的】
(一)学习MATLAB中多项式的表示及多项式运算;
(二)学习用典型的插值和拟合方法求函数的近似值或近似表达式;(三)掌握拉格朗日、牛顿插值法的基本理论及MATLAB实现,解决一些实际问题;
【实验内容】
(一)多项式表示及运算;
(二)拉格朗日插值法、Newton插值理论的MATLAB实现;
(三)函数拟合理论的MATLAB实现;
【实验性质】设计型
【实验步骤】
(一)多项式表示及运算
1、在MATLAB命令窗口中输入以下语句,观察结果,分析语句功能
(1)p=[1,-5,6,-33],poly2sym(p)
(2)syms x
f=4*x^3+6*x
sym2poly(f)
分析函数poly2sym和sym2poly的功能。
2、多项式运算
在MATLAB命令窗口中输入以下语句,观察结果
p=[3,2,1]; a=1:2:5;polyval (p,a),分析函数polyval功能
(二)拉格朗日插值法、Newton插值理论的MATLAB实现
Lagrange插值的参考程序:
X=[];Y=[]; %X,Y存放已知数据点
syms x s
n=length(X);
s=0.0;
for k=1:n
p=1.0;
for j=1:n
if j~=k
p=p*(x-X(j))/(X(k)-X(j));
end
end
s=s+p*Y(k);
end
s; s=simplify(s);
Newton插值的参考程序:
X= [];Y= [];
n=length(X);
for i=1:1:n-1
CS(i,1)=(Y(i+1)-Y(i))/(X(i+1)-X(i));
end
for j=2:1:n-1
for i=j:1:n-1
CS(i,j)=(CS(i,j-1)-CS(i-1,j-1))/(X(i+1)-X(i+1-j));
end
end
syms N x b
N=Y(1);
a=0;
b=(x-X(1));
for i=1:1:n-1
a=CS(i,i);
N=N+a*(b);
b=(b)*(x-X(i+1));
end
fprintf('插值多项式为')
N
用Lagrange或Newton插值完成课本P48 第2题, P34例5,P28 例2.
(三)函数拟合理论的MATLAB实现
1、多项式拟合的MATLAB实现
(1)学习多项式拟合函数polyfit的使用,其调用格式为:
p=polyfit(x,y,n)
其中,参数x代表已知数据点自变量组成的向量;参数y代表已知数据点函数值组成的向量;
参数n代表所求得拟合多项式系数向量;参数p代表拟合多项式的系数。
(2)在对问题求解过程中,如需计算多项式p在某点x处的值f,可用以下语句:
f=polyval(p, x)
(3)在多项式拟合过程中,如需画出数据点的散点图,可用MATLAB绘图函数plot,plot函数的调用格式:plot(x,y,s),其中,参数x,y的意义同多项式拟合polyfit(),参数s为用于修饰图形线型的字符串,详情寻求MATLAB在线帮助:>>help plot
试验举例
对向量X=[-2.8 -1 0.2 2.1 5.2 6.8]和Y=[3.1 4.6 2.3 1.2 2.3 -1.1]分别进行阶数为3、4、5 的多项式拟合,并画出图形进行比较。
参考程序:
>> x=[-2.8 -1 0.2 2.1 5.2 6.8];>> y=[3.1 4.6 2.3 1.2 2.3 -1.1];
% 用不同阶数的多项式拟合x 和y
>> p3=polyfit(x, y, 3); p4=polyfit(x, y, 4); p5=polyfit(x, y, 5);
>> xcurve= -3.5:0.1:7.2; % 生成x 值
% 计算在这些x 点的多项式值
>> p3curve=polyval(p3, xcurve);
>> p4curve=polyval(p4, xcurve);
>> p5curve=polyval(p5, xcurve);
>> plot(xcurve,p3curve,'--',xcurve,p4curve,'-.',xcurve,p5curve,'-',x,y,'*');
上机习题:
例已知某乡镇企业1990-1995年的生产利润如下表所示
问题:试预测该企业1996、1997年利润.
2、用MATLAB实现非线性拟合
(1)调用MATLAB非线性拟合函数fit,fit函数的调用格式:
f = fit(x,y,model)
其中,参数x代表已知数据点自变量组成的列向量,参数y代表已知数据点函数值组成的列向量,参数model代表根据需要自定义得拟合模型,参数f代表所选模型的待定参数.
model为由函数fittype所定义的字符串描述的模型类型,如
model=fittype('a*exp(b*x) ')
定义了指数模型bx
=
y ae
(2)实验实例
例在某次阻尼振荡试验中测得如下表3所列的18组数据点,用阻尼振荡对应的函数w x
kx
e)
)x(f=作为拟合函数,求拟合函数的待定参数w
a
cos(
,.
a,
k
参考程序.
解:输入已知数据
x=[];y=[];
用fittype()函数定义模型
model=fittype('a*cos(k*x)*exp(w*x)')
调用fit()求解参数a,k,w,f= fit(x',y',model)
执行语句plot(x,y,'r*',x,f(x))可得的拟合效果图.。
