2第二十六章 26.1.2二次函数Y=ax2的图象
合集下载
26.1.2二次函数图像和性质00
演示
向上
顶点从(0,0)移到了 (0,–2)，即x=0时， y取最大值–2
5 4 3 2 1
y
顶点从(0,0)移到了 (0, 2)，即x=0时， y取最大值2
x 1 2 3 4 5
–5 –4 –3 –2 –1 O –1 –2 1 2 y x 2 –3 3 –4 –5
1 2 y x 2 3 1 2 y x 3
下 3、函数y =-2(x+1)2的图象开口向____，对称轴 (-1,0) 是____________，顶点坐标是________，当 直线x=-1
大 < -1 0 -1 x=____时，函数有最____值为____；当x_____
> -1 时，y随x的增大而增大，当x_____时， y随x的 增大而减小。 4、抛物线y=3x2-4，y=3(x-1)2与抛物线y=3x2 位置 形状 的_______相同，_______不同。抛物线y=3x2-4 是由抛物线y=3x2向____平移____单位而得到； 下 4 右 抛物线y=3(x-1)2是由抛物线y=3x2向____平移 1 ____单位而得到。
y=a(x-h)2 (a≠0) 开口方向 顶点坐标 对称轴 增 减 性
a>0
a<0
向上 (h ,0) x=h
当x<h时， y随着x的增大而减小。 当x>h时， y随着x的增大而增大。
向下 (h ,0) x=h
当x<h时, y随着x的增大而增大。 当x>h时， y随着x的增大而减小。
极值
x=h时,y最小值=0
1y 2x 3
2
向上
2
直线x=3 直线x= –1
直线x=0 (Y轴)
向上
顶点从(0,0)移到了 (0,–2)，即x=0时， y取最大值–2
5 4 3 2 1
y
顶点从(0,0)移到了 (0, 2)，即x=0时， y取最大值2
x 1 2 3 4 5
–5 –4 –3 –2 –1 O –1 –2 1 2 y x 2 –3 3 –4 –5
1 2 y x 2 3 1 2 y x 3
下 3、函数y =-2(x+1)2的图象开口向____，对称轴 (-1,0) 是____________，顶点坐标是________，当 直线x=-1
大 < -1 0 -1 x=____时，函数有最____值为____；当x_____
> -1 时，y随x的增大而增大，当x_____时， y随x的 增大而减小。 4、抛物线y=3x2-4，y=3(x-1)2与抛物线y=3x2 位置 形状 的_______相同，_______不同。抛物线y=3x2-4 是由抛物线y=3x2向____平移____单位而得到； 下 4 右 抛物线y=3(x-1)2是由抛物线y=3x2向____平移 1 ____单位而得到。
y=a(x-h)2 (a≠0) 开口方向 顶点坐标 对称轴 增 减 性
a>0
a<0
向上 (h ,0) x=h
当x<h时， y随着x的增大而减小。 当x>h时， y随着x的增大而增大。
向下 (h ,0) x=h
当x<h时, y随着x的增大而增大。 当x>h时， y随着x的增大而减小。
极值
x=h时,y最小值=0
1y 2x 3
2
向上
2
直线x=3 直线x= –1
直线x=0 (Y轴)
22.1.2二次函数y=ax2图像与性质
y=ax2+c (a≠0) 开口方向 顶点坐标 对称轴 增 减 性 极值
a>0 向上 (0 ,c) y轴
当x<0时， y随着x的增大而减小。 当x>0时， y随着x的增大而增大。
a<0 向下 (0 ,c) y轴
当x<0时, y随着x的增大而增大。 当x>0时， y随着x的增大而减小。
x=0时,y最小=c
x y = x2 · · · · · · －3 －2 －1 0 1 2 3 · · · · · ·
9
4
1
0
1
9
4
9
2. 根据表中x,y的数值在 坐标平面中描点（x,y） 3.连线 如图，再用平 滑曲线顺次连接各点， －3 2 就得到y = x 的图象．
y = x2
6
3 3
二次函数 y = x2的图象是一条曲线，它的形状类似 于投篮球时球在空中所经过的路线，只是这条曲线 开口向上，这条曲线叫做抛物线 y = x2 ， 二次函数的图象都是抛物线， 它们的开口或者向 上或者向下． 一般地，二次函数 y = ax2 + bx + c （a≠0）的图象叫做抛物线y = ax2 + bx + c y = x2
m2+m
解②得:m1=－2, m2=1 由①得:m>－1 ∴ m=1 此时,二次函数为: y=2x2,
x ….. y=x2 …… y=x2+1 ……
-2 4
-1 1
0 0
y
8
1 1
2 4
…… ……
5
2
0
2
5
y=x2+1
函数y=x2+1的图象与y=x2的 图象的位置有什么关系? 函数y=x2+1的图 象与y=x2的图象 的形状相同吗?
九年级数学下第26章二次函数26.1二次函数及其图象2二次函数y=ax2的图象习题新人教
•1、书籍是朋友,虽然没有热情,但是非常忠实。2022年3月27日星期日2022/3/272022/3/272022/3/27 •2、科学的灵感，决不是坐等可以等来的。如果说，科学上的发现有什么偶然的机遇的话，那么这种‘偶然的机遇’只能给那些学有素养的人，给那些善于独 立思考的人，给那些具有锲而不舍的人。2022年3月2022/3/272022/3/272022/3/273/27/2022 •3、做老师的只要有一次向学生撒谎撒漏了底，就可能使他的全部教育成果从此为之失败。 2022/3/272022/3/27March 27, 2022
x＞ 0时 ， y随 x的 增 大 而 增 大 ， x＜ 0时 ， y随 x的 增 大 而 减 小 .
2.a＜0⇔开口向下⇔有最大值⇔
x＞ 0时 ， y随 x的 增 大 而 减 小 ， x＜ 0时 ， y随 x的 增 大 而 增 大 .
知识点 2 求二次函数y=ax2的解析式
【例2】(2013·山西中考)如图是我省某地一座抛物线形拱桥,
(1)求此抛物线的解析式. (2)过点P作CB所在直线的垂线,垂足为点R, 求证:PF=PR.
【解析】(1)由题意可得:点A的坐标为(2,-1),
∵抛物线的顶点为坐标原点O,
∴可设抛物线的解析式为:y=ax2, 将点A(2,-1)代入可得:4a=-1,解得a=- 1 ,
4
∴抛物线的解析式为y=- 1 x2.
【例1】函数 ym2xm 2m 4 是关于x的二次函数,求:
(1)满足条件的m的值. (2)m为何值时,抛物线有最低点?求出这个最低点,这时当x为何 值时,y随x的增大而增大? (3)m为何值时,抛物线的开口方向向下?这时当x为何值时,y随x 的增大而减小?
【解题探究】(1)函数是二次函数的条件是自变量的最高次数
26.1 二次函数y=ax2的图象与性质 精品作业课件(课程配套练习) 公开课一等奖课件
1 2 解：(1)y＝ x (2)图略 (3)抛物线；当 x＞0 时，y 随 x 4 的增大而增大 (4)有最小值为 0
18． (10 分)如图所示， 某桥洞的截面是抛物线形， 在图中 建立的直角坐标系中，抛物线所对应的二次函数的关系式为 1 2 y＝－ x ，当桥洞中水面宽 AB 为 12 米时，求水面到桥拱顶 4 点 O 的距离．
解：水面到桥拱顶点 O 的距离为 9 米
【综合运用】 19．(12 分)已知点 A(－3，－9)是顶点在原点的抛物线上 的一点 ，点 P(x，y)是抛物线上的一个动点 ，且在第四象限 内．点 B 在 x 轴正半轴上，且 OB＝4，△OPB 的面积为 S. (1)求抛物线的函数关系式； (2)分别求 S 和 y，S 和 x 之间的函数关系式，并判断它们 是什么函数，直接写出自变量的取值范围．
)
3．(4分)某课外兴趣小组为了了解所在地区老年人的健康状况，分别做了四种不 同的抽样调查，你认为抽样比较合理的是( D ) A．在某个公园调查了1 000名老年人的健康状况 B．在医院调查了1 000名老年人的健康状况 C．调查了10名老年邻居的健康状况 D．利用派出所的户籍网随机调查了该地区10%的老年人的健康状况 4．(4分)下列调查的样本缺乏代表性的是( C ) A．在大学生中调查大学生课余时间娱乐的主要方式 B．调查学号为3的倍数的学生，以了解学生对学校某项新举措的意见和建议 C．在老年活动中心调查市民对春节联欢会的喜好程度 D．在某校九年级中调查全市九年级学生的身体发育情况
解： (1)y＝－x2 (2)S＝－2y， 它是一次函数， 自变量 y＜ 0；S＝2x2，它是二次函数，自变量的取值范围为 x＞0.
抽样调查时 ， 所选取的样本要有 __ 代表性 __ ， 样本容量要足够 __大__．仅仅增加调查人数不一定能够提高调查质量 ，开展调查 之前，要仔细检查总体中的每个个体是否都有可能成为 _调查对象 __．
26.1 二次函数 华师大版数学九年级下册 课件
增加 ycm²,试写出y与x的函数关系式.
答:(1)y=-x²+10x; (2)S=r²; (3)y=x²+7x.共同特点:都是关于自变量的二次式.
2.探究新知
问题 1 要用长为20m的铁栏杆,一面靠墙(墙足够长),围成一个矩 形的花圃.
(1)设垂直于墙面的边AB为xm,矩形的面 积为ym².y能用含x的代数式来表示吗?
第26章 二次函数
26.1 二次函数
一 教学目标
1.通过对实际问题情境的分析,让学生经历二次函数概念的 形成过程,学会用类比思想学习二次函数知识. 2.掌握二次函数的概念,列出实际问题中的二次函数关系式.
二 重难点
重点：掌握二次函数的概念,列出二次函数关系式. 难点：理解变量之间的对应关系,并会求自变量的取值范围.
问题 2 某商店将每件进价为8元的某种商品按每件10元出售,一天 可售出100件.该店想通过降低售价、增加销售量的办法来提高利润. 经市场调查,发现这种商品每件每降低0.1元,每天销售量可增加10 件.将这种商品的售价降低多少时,能使每天销售利润最大?
(1)设每件商品降低x元(0≤x≤2),该商品每天的利润为y,y是x的 函数吗?为什么要限定x的值?
(2)试填写下面的表格. (3)x的值可以任意取吗?有限定范围吗? (4)我们发现y是x的函数,试写出这个函数的关系式.
解:(1)能. (2)如表所示.
AB的边长 x（m）
1
2
3
4
5
6
7
8
9
BC的边长 x（m）Fra bibliotek1816
14
12
10
8
6
4
2
面积y （m²）
18
答:(1)y=-x²+10x; (2)S=r²; (3)y=x²+7x.共同特点:都是关于自变量的二次式.
2.探究新知
问题 1 要用长为20m的铁栏杆,一面靠墙(墙足够长),围成一个矩 形的花圃.
(1)设垂直于墙面的边AB为xm,矩形的面 积为ym².y能用含x的代数式来表示吗?
第26章 二次函数
26.1 二次函数
一 教学目标
1.通过对实际问题情境的分析,让学生经历二次函数概念的 形成过程,学会用类比思想学习二次函数知识. 2.掌握二次函数的概念,列出实际问题中的二次函数关系式.
二 重难点
重点：掌握二次函数的概念,列出二次函数关系式. 难点：理解变量之间的对应关系,并会求自变量的取值范围.
问题 2 某商店将每件进价为8元的某种商品按每件10元出售,一天 可售出100件.该店想通过降低售价、增加销售量的办法来提高利润. 经市场调查,发现这种商品每件每降低0.1元,每天销售量可增加10 件.将这种商品的售价降低多少时,能使每天销售利润最大?
(1)设每件商品降低x元(0≤x≤2),该商品每天的利润为y,y是x的 函数吗?为什么要限定x的值?
(2)试填写下面的表格. (3)x的值可以任意取吗?有限定范围吗? (4)我们发现y是x的函数,试写出这个函数的关系式.
解:(1)能. (2)如表所示.
AB的边长 x（m）
1
2
3
4
5
6
7
8
9
BC的边长 x（m）Fra bibliotek1816
14
12
10
8
6
4
2
面积y （m²）
18
26.1.2二次函数y=ax2的图象和性质
y
Q(0,b)
(-,+) o (-,-)
(+,+)
P(a,0)
x (+,-)
3. 点的位置及其坐标特征: ①.各象限内的点: ③.对称于坐标轴的两点: y
C(m,n) M(a,b)
②.各坐标轴上的点: ④.对称于原点的两点:
N(a,-b) A(x,y)
o
x
D(-m,-n) B(-x,y)
试学活动一
二次函数y=ax 二次函数y=ax2的图象和性质
y
x
平面直角坐标系: 一. 平面直角坐标系 1. 有关概念: 2. 平面内点的坐标:
你还记得有关 y 平面直角坐标 P (a,b) b 系的相关知识 吗? a o
(纵轴) 第二象限 第一象限 第三象限 第四象限
x(横轴)
3. 点的位置及其坐标特征: ①.各象限内的点: ②.各坐标轴上的点:
y=－ 2 3 x
2
试学活动二
2
，
的图象。
x
y= 1 2 x y=x2 2
... ... ... ...
-4 -3 8 4.5
-2 -1 2 0.5
0 0 0 0 0 0
1 0.5 0.5 0.5 1
− 2 3
2 2 1 2 1.5 1.5
3 4.5 1.5 4.5 2
− 8 3
4 8 2 8 3 -6
y = 2x2
y = − x2
2 y = − x2 3
二次函数y=ax2的图象形如物体抛射时 所经过的路线，我们把它叫做抛物线。 抛物线。 抛物线 这条抛物线关于y轴 这条抛物线关于 轴 这条抛物线关于y轴 这条抛物线关于 轴 这条抛物线关于y轴 这条抛物线关于 轴 对称， 轴就是它的 对称，y轴就是它的 对称， y轴就是它的 对称，y轴就是它的 对称， 对称， 轴就是它的 对称轴。 对称轴。轴就是它的 对称轴。 对称轴。 对称轴。 对称轴。 对称轴与抛物线 抛物线的交点 对称轴与抛物线的交点 对称轴与抛物线的交点 叫做抛物线的顶点。 叫做抛物线的顶点
26.1 二次函数及其图像 课件4(数学人教版九年级下册)
y=a(x-h)2+k(a>0)
y=a(x-h)2+k(a<0)
h，k
直线x h
向上
当x h时, 最小值为 k
h，k
直线x h
向下
当x h时，最大值为 k
练习1
说出下列抛物线的开口方向、对称轴及顶点：
（ 1 ）y （ 2 x 3） 5；（2）y （ 3 x 1 ） 2；
-5 -4 -3 -2 -1 o 1 2 3 4 5
x
抛物线y=x2+1:
开口向上,对称轴是y轴, 顶点为(0,1). 抛物线y=x2－1: 开口向上,对称轴是y轴, 顶点为(0, －1).
(1) 抛物线 2 2 y=x +1,y=x －1 的开口方向、对 称轴、顶点各是 什么?
10 9 8 7 6 5 4 3 2 ● 1
y
三、观察三条抛物线：
2 (2)开口大小有没有 1 变化？ -3 -2 -1 0 1 2 3 x -1 -2 没有变化 -3 1 2 -4 y x -5 2 1 1 2 y ( x 1) -6 y ( x 1) 2 2 -7 2 -8
y
三、观察三条抛物线：
2 (3)对称轴是什么？ 1 -3 -2 -1 0 1 2 3 x -1 -2 -3 y 轴 x=-1 x=1 1 2 -4 y x -5 2 1 1 2 y ( x 1) -6 y ( x 1) 2 2 -7 2 -8
抛物线y a ( x h) 2 k有如下特点： （1）当a 0时，开口向上 ____；当a 0，开口向下 ___； x=h ； （2）对称轴是直线____ （3）顶点坐标是 ______ 。 （ h，k）
二次函数y=a(x-h)2的图象及性质
• 左右平移时：左加右减（抛物线左移，高度 不变，左移后x变小了，要使y不变，则需要 加；类似的抛物线右移，高度不变，右移后x 变大了，要使y不变，则需要x 减。）
1.抛物线y=ax2+k、抛物线y=a(x－h)2和抛物线y=ax2 的形状完全相同,开口方向一致;
当a>0时, 开口向上; 当a<0时,开口向上.
(1) y=5x2 向上，y轴 （0, 0) (2) y=-3x2 +2 向下，y轴 （0, 2) (3) y=8x2+6 向上，y轴 （0, 6)
(4) y= -x2-4 向下，y轴 （0, - 4)
下面，我们探究二次函数 y = a﹙x-h﹚2的图 像和性质,以及与y=ax2的联系与区别.
探究
y=－
1 2
﹙x+1﹚2
－4
－6
24
y=－ 21﹙x-1﹚2
可以看出，抛物线 y 1 x 1 的2 开口向下，对称轴是
2
经过点（－1，0）且与x轴垂直的直线，我们把它记住直线
x=－1，顶点是（－1，0）；抛物线 y 1 x 12 的开
2 口向______下___，对称轴是_直线_______x__=__1____，顶点是
（2）对称轴： 对称轴直线x=h;
（3）顶点坐标：顶点坐标是（h，0） （4）函数的增减性：
当a＞0时，对称轴左侧(x ﹤ h时)y随x增大而减小，
对称轴右侧(x ≥ h时)y随x增大而增大； 当a＜0时， 对称轴左侧y随x增大而增大，
对称轴右侧y随x增大而减小。 （5）最值
• 上下平移时：上加下减（抛物线上移，高度 变高，要使y变大，则需要加；类似的抛物线 下移，高度变低，要使y变小，则需要减。）
1.抛物线y=ax2+k、抛物线y=a(x－h)2和抛物线y=ax2 的形状完全相同,开口方向一致;
当a>0时, 开口向上; 当a<0时,开口向上.
(1) y=5x2 向上，y轴 （0, 0) (2) y=-3x2 +2 向下，y轴 （0, 2) (3) y=8x2+6 向上，y轴 （0, 6)
(4) y= -x2-4 向下，y轴 （0, - 4)
下面，我们探究二次函数 y = a﹙x-h﹚2的图 像和性质,以及与y=ax2的联系与区别.
探究
y=－
1 2
﹙x+1﹚2
－4
－6
24
y=－ 21﹙x-1﹚2
可以看出，抛物线 y 1 x 1 的2 开口向下，对称轴是
2
经过点（－1，0）且与x轴垂直的直线，我们把它记住直线
x=－1，顶点是（－1，0）；抛物线 y 1 x 12 的开
2 口向______下___，对称轴是_直线_______x__=__1____，顶点是
（2）对称轴： 对称轴直线x=h;
（3）顶点坐标：顶点坐标是（h，0） （4）函数的增减性：
当a＞0时，对称轴左侧(x ﹤ h时)y随x增大而减小，
对称轴右侧(x ≥ h时)y随x增大而增大； 当a＜0时， 对称轴左侧y随x增大而增大，
对称轴右侧y随x增大而减小。 （5）最值
• 上下平移时：上加下减（抛物线上移，高度 变高，要使y变大，则需要加；类似的抛物线 下移，高度变低，要使y变小，则需要减。）
26.1.2二次函数
小结 的图象及性质： 二次函数 y = ax 的图象及性质：
2
(1)形状、对称轴、顶点坐标； 形状、对称轴、顶点坐标； 形状 (2)开口方向、极值、开口大小； 开口方向、极值、开口大小； 开口方向 (3)对称轴两侧增减性。 对称轴两侧增减性。 对称轴两侧增减性
x=0时,y最小=0
x=0时,y最大=0
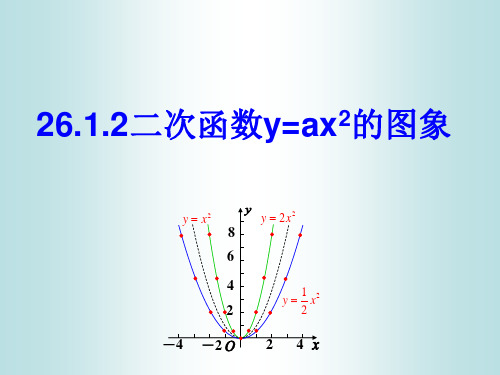
越小, 越小 2.形状是由 确定 |a|越大 抛物线的开口就越小 |a|越小 形状是由|a|确定 越大 抛物线的开口就越小. 形状是由 确定, 越大, 抛物线的开口就越大. 抛物线的开口就越大
3.抛物线 抛物线y=ax2 与y=-ax2 的图象关系： 的图象关系： 抛物线 关于x轴对称 关于 轴对称
1 函数y= 的图象与函数y= 函数 =－ x22 y=－2x2的图象与函数 =－x2 , = 图中蓝线图形)的图象相比,有什么共同点和不同点? (图中蓝线图形)的图象相比,有什么共同点和不同点?
共同点: 开口都向下 共同点: 开口都向下; 顶点是原点 原点而且是抛物线 顶点是原点而且是抛物线 的最高 的最高点，对称轴是 y 轴 在对称轴的左侧， 在对称轴的左侧， 随着x 增大而增大。 y随着x的增大而增大。 在对称轴的右侧， 在对称轴的右侧， 而减小。 随着x 增大而减小 y随着x的增大而减小。 不同点: 开口大小不同; 不同点: 开口大小不同;
2
范例 例1、在同一平面直角坐标系中，画出 、在同一平面直角坐标系中， 下列二次函数的图象： 下列二次函数的图象：
(1) y = 2x
2
(2) y = −2x
2
函数y= 2 =2 的图象 =2x 函数 = x2,1y=2 2的图象 与函数y= 图中虚线图形) 与函数 =x2(图中虚线图形) 的图象相比, 的图象相比,有什么共同点 和不同点? 和不同点? 开口都向上 开口都向上; 共同点: 共同点: 顶点是原点 原点而且是抛物线 顶点是原点而且是抛物线 的最低 的最低点，对称轴是 y 轴
九年级下册知识点(第二十六章)
九年级下册知识点（第二十六章）温习关于先生提高是很关键的，接上去看看查字典数学网为大家引荐的九年级下册知识点(第二十六章)，会不会对大家起到协助呢?第二十六章二次函数26.1 二次函数及其图像二次函数(quadratic function)是指未知数的最高次数为二次的多项式函数。
二次函数可以表示为f(x)=ax^2+bx+c(a不为0)。
其图像是一条主轴平行于y轴的抛物线。
普通的，自变量x和因变量y之间存在如下关系：普通式y=ax+bx+c(a0,a、b、c为常数)，顶点坐标为(-b/2a，-(4ac-b2)/4a) ; 顶点式y=a(x+m)2+k(a0,a、m、k为常数)或y=a(x-h)2+k(a0,a、h、k为常数)，顶点坐标为(-m，k)对称轴为x=-m，顶点的位置特征和图像的启齿方向与函数y=ax2的图像相反，有时标题会指出让你用配方法把普通式化成顶点式; 交点式y=a(x-x1)(x-x2) [仅限于与x轴有交点A(x1，0)和 B(x2，0)的抛物线] ;重要概念：a，b，c为常数，a0，且a决议函数的启齿方向，a0时，启齿方向向上，a0时，启齿方向向下。
a的相对值还可以决议启齿大小,a的相对值越大启齿就越小,a的相对值越小启齿就越大。
牛顿插值公式(三点求函数解析式)y=(y3(x-x1)(x-x2))/((x3-x1)(x3-x2)+(y2(x-x1)(x-x3)) /((x2-x1)(x2-x3)+(y1(x-x2)(x-x3))/((x1-x2)(x1-x3) 。
由此可引导出交点式的系数a=y1/(x1*x2) (y1为截距)求根公式二次函数表达式的左边通常为二次三项式。
求根公式x是自变量，y是x的二次函数2x1,x2=[-b((b^2-4ac))]/2a (即一元二次方程求根公式)(如右图) 求根的方法还有因式分解法和配方法在平面直角坐标系中作出二次函数y=2x的平方的图像，可以看出，二次函数的图像是一条永无止境的抛物线。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
驶向胜利 的彼岸
（2）因为 4 2(1) 2 ,所以点B（-1 ，-4） 不在此抛物线上. （3）由-6=-2x2 ,得x2=3, x 3 所以纵坐标为-6的点有两个，它们分别是
( 3 ,6)与( 3 ,6)
当堂测试
耐心填一填
1、函数y=4x2的图象的开口 ,对称轴 向上 是 y轴,顶点是 (0,0) ; 2、函数y=－3x2的图象的开口向下 ,对称轴 (0,0) 是 y轴 ,顶点是___ ;
2 2 y x 3
y随着x的增大而增大；在 对称轴的左 侧， y随着x的增大而减小，当x= 0 时， 函数y的值最小，最小值是 0 ,抛物 线y=2x2在x轴的 上 方（除顶点外）。
2 y x 2在x轴的 （2）抛物线 3
下 方（除顶点外），在对称轴的
左侧，y随着x的 增大而增大 ；在对称轴的右侧，y随着x的 增大而减小 ，当x=0时，函数y的值最大，最大值是 0 当x ，
课题:2Βιβλιοθήκη .1.2二次函数y=ax2的图象
学习
目标
1．知道二次函数的图象是一条抛物线； 2．会画二次函数y＝ax2的图象； 3．掌握二次函数y＝ax2的性质，并会灵活应用．
预习
探路
1.二次函数的定义是什么？
二次函数的定义：一般地，形如 y ax 2 bx c
(a、b、c是常数，a≠0)，的函数叫做二次函数，其 中a为二次项系数，b为一次项系数，c为常数项。
3 (3) y x
一条直线 一条直线
双曲线
创设情境
※、正比例函数、一次函数的图象：
函数图象画法：
(1)列表 (2)描点
y
y
4 2 x 33 2 1
y 2x
(3)连线
-4 -3 -2 -1 0 1 2 3 4 -1 -2 -3 -4
x
创设情境
※、反比例函数的图象：
y
4 3 2 1
3 y x
3、函数y= 3x2的图象的开口 ,对称轴 向上 是y轴 ,顶点是 ; (0,0) 4、函数y= －0.2x2的图象的开口向下 ,
y轴 对称轴是___,顶点是(0,0);
当堂测试
5.已知 y =(m+1)x 是二次函数,且其图象开口 向上,求m的值和函数解析式. 解: 依题意有:
m2+m
m+1>0 ① m2+m=2 ②
y=x2的图像叫做抛物线y=x2. y=－x2的图像叫做抛物线y=－x2.
o
o
x
y=x2
x 实际上,二次函数的图像 它们的开口向上或者向下. 都是抛物线. 一般地,二次函数y=ax2+bx+c 的图像叫做抛物线y=ax2+bx+c. 还可以看出,二次函数y=x2和y=－x2的图 像都是轴对称图形,y轴是它们的对称轴. 抛物线与对称轴的交点叫做抛物线的顶点. 抛物线y=x2的顶点(0,0)是它的最低点. 抛物线y=－x2的顶点(0,0)是它的最高点.
-4 -3 -2 -1 0 -1 -2 -3 -4
1 2 3 4
x
理性提升
画函数y=x2的图像
x … -3 -2 -1 0 y … 9 4 1 0
10 9 8 7 6 5 4 3 2 1
解: (1) 列表
(2) 描点 (3) 连线
1 1
y
2 3 … 4 9 …
y=x2
还记得如何用 根据表中x,y的数 描点法画一个函数 值在坐标平面中描点 的图像吗?
a<0
小结归纳
请同学们把所学的二次函数图象 的知识归纳小结。 图象 左侧 右侧
y=ax2 顶点 对称轴 开口
x y x y
(0,0) 增 减 增增 大 小 大大
a＞0
最低点
y轴
向上
(0,0) a＜0 最高点
y轴
向下
增 增 增减 大 大 大小
独立 作业
教材P14
龙门学案P 拓展探究
习题26.1: 3,4.
(x,y),再用平滑曲线顺 次连接各点,就得到 y=x2的图像.
-5 -4 -3 -2 -1 o 1 2 3 4 5
x
理性提升
观察思考： 1. y=x2的图像是什 么形状？ 2.图像是轴对称图形 吗？如果是，对称 轴是？ 3.图像有最低点吗？ 如果有，其坐标是？
10 9 8 7 6 5 4 3 2 1
解②得:m1=－2, m2=1 由①得:m>－1 ∴ m=1 此时,二次函数为: y=2x2.
中考链接
1
1．(2009．浙江嘉兴)已知a≠0，在同一直角坐标系中，函数 y=ax与y=ax2的图象有可能是（ C ）
y y
1 1
y
y
1
O
x
1
O
1
x
O
A．
1
x
1
O
B．
1
x
C．
D．
2．(2009．河北)某车的刹车距离y（m）与开始刹车时的速度 x（m/s）之间满足二次函数y= x2(x＞0)（x＞0），若该 车某次的刹车距离为5 m，则开始刹车时的速度为（ C ） 1 A． 40 m/s B． 20 m/s 20 C． 10 m/s D． 5 m/s
预习
探路
2.下列函数：
、 、 (2) y 3x 1
2 2
(1) y 3x 1
(3) y 3x 2 x
3
。 4) y 2 x 2 x 1 (
2
其中二次函数的有( B )个 A. 1 B. 2 C. 3 D. 4
创设情境
※、你知道下列函数的图象分别是什么吗？
(1) y 2 x (2) y 2 x 3
理性提升
解: (1) 列表 (2) 描点
例1.在同一直角坐标系中画出函数 1 y= 2x2和y=2x2的图像
x
y= 2 x2
1
… -4 -3 -2 -1 0 1 2 3 4 … … 8 4.5 2 0.5 0 0.5 2 4.5 8 …
x … -2 -1.5 -1 -0.5 0 0.5 1 1.5 2 … y=2x2 … 8 4.5 2 0.5 0 0.5 2 4.5 8 …
-4
小结归纳
1. 二次函数的图像都是抛物线. 2. 抛物线y=ax2的图像性质: (1) 抛物线y=ax2的对称轴是y轴,顶点是原点. (2)当a>0时,抛物线的开口向上,顶点是 抛物线的最低点; 当a<0时,抛物线的开口向下,顶点是 抛物线的最高点; |a|越大,抛物线的开口越小;
o y
a>0
x
中考链接
2
3. (2009．衢州)如图，已知点A(-4，8)和点B(2，n)在抛物 线y=ax2上． (1) 求a的值及点B关于x轴对称点P的坐标，并在x轴 上找一点Q，使得AQ+QB最短，求出点Q的坐标；
A y
8
6
1 a= , 2
点Q的坐标是(
4
4 5
2
B
2 4 x
，0)
D -4
C -2 O -2
3、观察函数y=x2的图象,则下列判断中正确的( A ) (A) 若a,b互为相反数,则x=a与x=b的函数值相等; y (B) 对于同一个自变量x,有两个函数值与它对应. (C) 对任一个实数y,有两个x和它对应. (D) 对任意实数x,都有y＞0.
o
x
y 2x 2
4、根据左边已画好的函数图象填空： （1）抛物线y=2x2的顶点坐标是 （0，0）, 对称轴是 y轴 ，在 对称轴的右 侧，
在同一坐标系内,抛物线 y=ax2与抛物线y=－ax2是关于轴 对称的.
a<0
y 1 -5-4 -2-1 o1 2 3 4 5 x -3 -1 -2 -3 -4 -5 -6 -7 -8 -9 -10
随堂练习
1、函数y=2x2的图象的开口 向上 ,对称 轴 ,顶点是 (0,0) ; y轴 2、函数y=－3x2的图象的开口 向下 ,对 称轴 y轴 ,顶点是 (0,0) ;
0时，y<0.
理性提升
例.已知抛物线y=ax2经过点A（-2，-8）. （1）求此抛物线的函数解析式； （2）判断点B（-1，- 4）是否在此抛物线上. （3）求出此抛物线上纵坐标为-6的点的坐标. 解：（1）把（-2，-8）代入y=ax2,得-8=a(-2)2, 解得a= -2,所求函数解析式为y= -2x2.
解: (1) 列表 (2) 描点 (3) 连线
根据表中x,y的数 值在坐标平面中描点 (x,y),再用平滑曲线顺 次连接各点,就得到 y=x2的图像.
从图像可以看出,二次函数y=x2和y= －x2的图像都是一条曲线,它的形状类似于投篮球或投掷铅球时 y y 球在空中所经过的路线.
理性提升
这样的曲线叫做抛物线.
(3) 连线
1 函数y=2 x2,y=2x2的 图像与函数y=x2(图中虚线 图形)的图像相比,有什么共 同点和不同点? 共同点: 开口向上; 除顶点外,图像都在x轴上方 不同点: 开口大小不同;
10 9 8 7 6 5 4 3 2 1
y
-5 -4 -3 -2 -1 o 1 2 3 4 5
x
理性提升
(3) 连线 x2,y=－2x2的 图像与函数y=－x2(图中虚线图 形)的图像相比,有什么共同点和 不同点? 共同点: 开口向下; 除顶点外,图像都在x轴下方 不同点: 开口大小不同;
1 函数y=－2
1
y x
-5 -4 -3 -2 -1 o 1 2 3 4 5 -1 -2 -3 -4 -5 -6 -7 -8 -9 -10
y
y=x2
-5 -4 -3 -2 -1 o 1 2 3 4 5