管柱屈曲研究现状及存在问题分析
屈曲约束支撑研究进展综述_王凤欣

第29卷第4期河北工程大学学报(自然科学版)Vol.29No.42012年12月Journal of Hebei University of Engineering (Natural Science Edition )Dec.2012收稿日期:2012-05-30作者简介:王凤欣(1988-)女,河北保定市人,硕士,从事大跨钢结构方面研究。
文章编号:1673-9469(2012)04-0028-04屈曲约束支撑研究进展综述王凤欣1,陈银2,王高峰3,张玉鹏4(1.上海大学土木工程系,上海100020;2.河北工程大学土木工程学院,河北邯郸056038;3.中交第三公路工程局有限公司第四工程分公司,重庆401120;4.中国葛州坝集团股份有限公司西南分公司,云南昆明650000)摘要:本文旨在对屈曲约束支撑做一个综合性分析。
文章从两方面展开对国内外近几年在屈曲约束支撑方面的研究成果的分析总结。
一方面是此种支撑受力机理的研究,另一方面是新型支撑形式的介绍。
同时对于此种支撑形式在一般通用软件的建模做了简要介绍,并对目前仍不能在国内广泛应用做了原因分析。
关键词:屈曲约束支撑;滞回曲线;纤维单元中图分类号:TU393.3文献标识码:AReview on the development of buckling -restrained bracedWANG Feng -xin 1,CHEN Yin 2,WANG Gao -feng 3,ZHANG Yu -peng 4(1.Department of Civil Engineering ,Shanghai University ,Shanghai 100020,China ;College of Civil Engineering ,Hebei Universityof Engineering ,Hebei Handan 056038,China ;3.The Fourth Engineering Company ,Chinese Transportation of Third Road Construction Bureau ,Chongqing 406120,China ;4.Gezhouba Southwest Company Limited ,Yunnan Kunming 650000,China )Abstract :This article is aimed at make a comprehensive analysis on the buckling -restrained braced.The paper summarized the research of BRB in recent years both at home and abroad.The stress mechanism of such brace has been studied at first ,and then some new forms of such braces are intro-duced.And modeling in different common software also been given.At last ,analyzed reasons of not been able to used widely in our country.All of the work is hoping to make a full understanding of the new form of brace for the engineers.Key words :buckling -restrained braced ;hysteretic curve ;fiber unit 屈曲约束支撑是一种新型的无粘结耗能支撑,支撑的中心是芯材,芯材被置于一个钢套管内,然后在套管内灌注混凝土或砂浆或者设置侧向板支撑,从而克服了传统支撑受压屈曲的缺点。
碳纤维薄壁圆管屈曲性能试验研究与有限元分析

碳纤维薄壁圆管屈曲性能试验研究与有限元分析【摘要】本文对三种不同直径和壁厚的薄壁碳纤维圆管进行了屈曲试验,得出了三种管件在两端铰支条件下的屈曲临界载荷;利用ANSYS软件建立了三维薄壁圆管模型,用层合壳单元模拟薄壁圆管的叠层结构,建立了适当的位移和载荷边界条件,用特征值屈曲分析方法分析了三种不同直径和壁厚圆管的屈曲性能;试验和分析结果表明:有限元分析所得屈曲临界载荷和试验结果吻合较好,对此种形式的碳纤维圆管,特征值屈曲分析有较高的精度。
接头对屈曲临界载荷的影响也做了相应的讨论。
【关键词】碳纤维圆管;层合壳单元;特征值屈曲分析;有限元碳纤维复合材料具有比强度高、比刚度大、抗疲劳性好、减震性好等特点,被广泛应用于航空航天飞行器的结构。
碳纤维复合材料薄壁圆管也被广泛应用于航空航天器的支撑杆件。
对于受压作用下的细长型杆件,其稳定性是结构设计者首要考虑的问题。
本文针对细长型碳纤维圆管的屈曲性能进行了试验研究和有限元分析。
1碳纤维圆管屈曲性能试验研究本文研究的碳纤维圆管都由T300/Epoxy碳纤维预浸布卷铺制作而成,T300/Epoxy单层布的力学性能如表1所示[1-2],这是一种横观各向同性材料。
表1T300/Epoxy单层板性能本文研究的三种规格的碳纤维圆管的铺层信息如表2所示。
表2不同直径、壁厚圆管的铺层信息碳纤维圆管通过两端粘接的两个铝合金接头连接在试验机上,试验临界长度为1105mm,如图1所示,每种规格的试件选择5根进行屈曲试验。
图1碳纤维圆管屈曲试验件简图试验在微控电子万能试验机上进行,加载速度控制在3mm/min内,试验现场如图2(a)所示,两端约束条件为铰接,如图2(b)所示。
(a)屈曲试验试验件安装图(b)两端铰接约束条件图2碳纤维圆管屈曲试验在试验机上安装好试件之后,开始加载,由试验机自动记录试验数据试验,加载至试件屈曲破坏。
其破坏形式如图3所示,破坏位置均为杆件中点,为典型的两端铰接的压杆一阶失稳破坏模式,试验结果如表3所示。
屈曲分析实例解析

屈曲分析屈曲分析- 分析内容屈曲分析主要用于研究结构在特定载荷下的稳定性以及确定结构失稳的临界载荷,屈曲分析包括:线性屈曲和非线性屈曲分析。
线弹性失稳分析又称特征值屈曲分析;线性屈曲分析可以考虑固定的预载荷,也可使用惯性释放;非线性屈曲分析包括几何非线性失稳分析,弹塑性失稳分析,非线性后屈曲(Snap-through)分析。
欧拉屈曲buckling结构丧失稳定性称作(结构)屈曲或欧拉屈曲。
L.Euler从一端固支另一端自由的受压理想柱出发.给出了压杆的临界载荷。
所谓理想柱,是指起初完全平直而且承受中心压力的受压杆。
设此柱是完全弹性的,且应力不超过比例极限,若轴向外载荷P小于它的临界值,此杆将保持直的状态而只承受轴向压缩。
如果一个扰动(如—横向力)作用于杆,使其有一小的挠曲,在这一扰动除去后。
挠度就消失,杆又恢复到平衡状态,此时杆的直的形式的弹性平衡是稳定的。
若轴向外载荷P大于它的临界值,柱的直的平衡状态变为不稳定,即任意扰动产生的挠曲在扰动除去后不仅不消失,而且还将继续扩大,直至达到远离直立状态的新的平衡位置为止,或者弯折。
此时,称此压杆失稳或屈曲(欧拉屈曲)。
屈曲分析- 分析分类线性屈曲:是以小位移小应变的线弹性理论为基础的,分析中不考虑结构在受载变形过程中结构构形的变化,也就是在外力施加的各个阶段,总是在结构初始构形上建立平衡方程。
当载荷达到某一临界值时,结构构形将突然跳到另一个随遇的平衡状态,称之为屈曲。
临界点之前称为前屈曲,临界点之后称为后屈曲。
侧扭屈曲:梁的截面一般都作成窄而高的形式,对截面两主轴惯性矩相差很大。
如梁跨度中部无侧向支承或侧向支承距离较大,在最大刚度主平面内承受横向荷载或弯矩作用时,荷裁达一定数值,梁截面可能产生侧向位移和扭转,导致丧失承载能力,这种现象叫做梁的侧向弯扭屈曲,简称侧扭屈曲。
理想轴向受压直杆的弹性弯曲屈曲:即假定压杆屈曲时不发生扭转,只是沿主轴弯曲。
但是对开口薄壁截面构件,在压力作用下有可能在扭转变形或弯扭变形的情况下丧失稳定,这种现象称为扭转屈曲或弯扭屈曲。
管道的屈曲分析
可以求得
EI
4
K0 D 1
2
D
Pcr
2
Ku D 1
1 D
EIK0
D
1
2 D
• 失稳时,轴向位移与横向位移相比只是一个二 阶小数,可忽略不计。
4 EI
K0D Pcr 2 EIK0D
适用于直线管道(或曲率半 径1000D的弯曲管道)。
土壤的压缩抗力系数K0
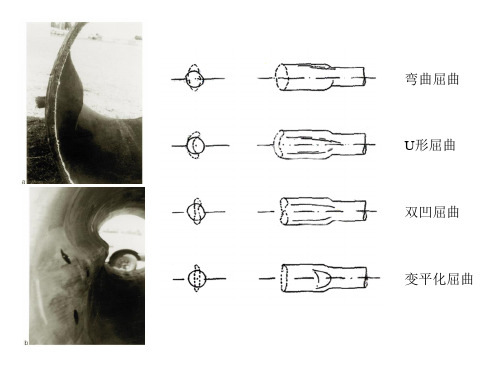
弯曲屈曲 U形屈曲 双凹屈曲 变平化屈曲
屈曲分析的内容
轴向屈曲 地下埋设管道
屈 曲
上浮屈曲
局部屈曲
地下埋设管道 海底埋设管道
机械作用 外压
屈曲传播
4-1 地下管道的轴向稳定性
• 在嵌固段,管道所受到的最大轴向力为:
P pD ET A
2t
• 管道轴向稳定性的验算条件
P nPcr
n——安全系数,可取n=0.6~0.75。
• 压扁深度大于管道直径8%时,影响管道的爆破 强度;
• 压扁处容易在疲劳载荷下产生裂纹。
压扁分析的Wierzbicki(维兹比基)模式
• 忽略了环向弯曲和轴向拉伸的塑性相互作用; • 忽略了弹塑性变形的相互作用; • 忽略了应变硬化; • 假定冲击载荷作用于垂直于管道的平面内。
塑性铰
压扁处的位移
2 210 103 (1 0.32 )
6
3
273
4.90MPa
4-5 海底管道的屈曲传播
• 局部屈曲 • 屈曲传播 • 止屈措施
1、局部屈曲
• 对管子局部屈曲可定义为:管子截面扁平化或翘 曲折皱超过规定的限度。
• 实际管子存在残余的椭圆度,而且还可能产生显 著的塑性变形。因此,管道的失稳的临界外压是 材料屈服极限的函数。
管桩及应用和研究现状分析

管桩的应用和研究现状分析1前言管桩作为一种地基处理及桩基础形式从上个世纪初产生到现在已经得到了很大的发展,在各种建筑基础中得到广泛地应用,并发挥着巨大的作用。
从国外管桩的发展来看,从1920年澳大利亚发明了离心法制作混凝土制品、1925年日本引进这种技术用于钢筋混凝土管桩,在1962年开发预应力混凝土管桩(PC管桩),到现在已有八九十年的历史,目前管桩已朝着全面取代传统实心桩方向发展。
我国是1944年开始生产混凝土离心(RC)管桩,到SO 年代末期研究成功预应力抽筋管桩,即采用后X法对桩身混凝土施加预应力。
近15年,我国生产的预应力混凝土管桩无论从产品性能和产量上都达到了世界前列,呈现出布局面广,产品品种、规格齐全,生产技术成熟,配套应用技术日趋完善等特点。
据资料反映,2004年福建省实际利用预制高强混凝土管桩就达2500万米。
为了更合理利用管桩这一技术、有效地推广使用管桩,对管桩进行研究是极为必要的。
管桩的种类分为:钢管桩、预制混凝土管桩及钢管混凝土管桩。
钢管桩及钢管混凝土管桩具有高强度、抗冲击疲劳性能好、贯入能力强、便于割接、质量可靠、运输方便、沉桩速度快及挤土影响小等优点,但造价高,约为预应力混凝土管桩的3-10倍。
因此,一般只在必须穿越砂层或其它桩型无法施工和质量难以保证、或工期紧迫等情况下使用,或者是一些重要的特种工程的基础上,如海上钻井平台,港口平台等工程中使用。
预制混凝土管桩之所以得到迅速发展和广泛的应用,主要是由于具有以下优点:(a)施工工期短,施工方便、不受季节限制,工业化生产:(b)对施工场地无污染,若采用静压式施工更无噪音,符合绿色环保施工要求;(c)经济效益可观,同样的地基处理效果(竖向承载力及水平承载力)所使用的混凝土比实心桩节省30%-60%且抗腐蚀能力强,工作性能同钢管桩基本相似。
(d)对持力层起伏变化较大的地质条件适应性强,一般情况下,软土、粘性土、粉土、砂土及全风化岩体等地层条件均可采用。
12-屈曲分析

Fapp
用载荷控制能达到 Fapp吗?
u
3、非线性特征值屈曲
载荷控制:
Training Manual
Advanced Contact & Fasteners
• 使用 Newton-Raphson 载荷控制的困难是求解不能通过不稳定点。 在不稳定点 (Fcr), 切线刚度矩阵 KT 是奇异的,使用载荷控制, Newton-Raphson 法不收敛。然而, 该类型的分析对描述结构的前 屈曲 行为是有用的。
分叉点 极限点
理想载荷路径 有缺陷结构的载荷路径
理想静态行 为
实际动态响应
前屈曲
后屈曲
u
3、非线性特征值屈曲
Training Manual
Advanced Contact & Fasteners
有几种分析技术用于计算结构的非线性 静力变形响应,这些技术包括: -载荷控制 -位移控制 -弧长法 载荷控制: 如下图所示, 考虑浅拱的快速通过分析,当以增量载荷 (F) 求解该问题时, 求解采用载荷控制来完成。
2、线性特征值屈曲
Training Manual
Advanced Contact & Fasteners
• 然而, 缺陷和非线性行为阻止大多数实际结构达到理想的弹性屈曲 强度,特征值屈曲一般产生非保守 解, 使用时应谨慎。 F
极限载荷 分叉点 理想载荷路径 有缺陷结构的载荷路径
前屈曲
u
尽管特征值屈曲一般产生非保守的结果, 线性屈曲分析仍有两个优点: -相对不费时(快捷)的分析。 -为了提供更真实的结果, 屈曲模态形状可用作非线性屈曲分析的初始几 何缺陷
2、线性特征值屈曲
Training Manual
关于海底管线屈曲剧变特性研究

关于海底管线屈曲剧变特性研究摘要:上世纪七十年代以来,管道在液、固、流态物质的运输渠道中得到越来越广泛的应用。
这是因为管道运输不受时间的限制,运输量大,运输安全性高,运输成本低廉。
海底管线是管道运输的一个重要组成部分,在海底进行运输方面同样发挥着不可替代的作用。
本文主要对海底管线经常出现屈曲剧变问题做出介绍,深入分析研究了屈曲剧变的特性,为完善海底管线提供了宝贵经验。
关键词:海底管线;屈曲剧变;特性分析目前,铺设海底管道线这项工程刚兴起几十年的时间,由于海底作业难度大,在铺设海底管道线时,时常发生一些技术故障,即使在海底管道线铺设完成后,铺设好的管道也会发生一些故障。
例如海底管线发生屈曲剧变等问题。
而此时对海底管道线的修建技术还处于发展阶段,这需要对这项技术不断地进行完善,以便使其更好地应对海底管道线出现的问题。
1.海底管线屈曲剧变1.1.海底管线屈曲剧变概念作为海洋油气集输与储运系统的一个重要组成部分,海底管线起着不可替代的作用。
但海底管线的屈曲剧变问题容易造成管线失效,使海底管线在发挥作用时受限。
管线屈曲的内容主要指管线在内外温差和压差较大时,由于受到地基土的约束作用,无法自由变形,在管线的内部产生附加应力,使管线发生竖向或水平向的弯曲。
这种弯曲给海底管线造成很大影响。
不仅对管线的安全运营造成威胁,而且还给海底管道运输业造成重大经济损失。
1.2.海底管线屈曲剧变的形态根据管线屈曲特点,可将管线的屈曲剧变可分成两类,一是水平向屈曲模式,二是竖直向屈曲模式。
竖直向屈曲模式,是指管线在温度应力和内部压力的作用下由于受到地基土体的约束,无法自由变形而产生的垂直向上隆起,常发生于全埋管线或半埋管线中。
水平向屈曲模式,是指管线在温度应力和内部压力的作用下由于受到地基土体的约束,无法自由变形而产生的水平方向的蛇形位移,常发生于半埋管线或不埋管线中。
从这两种屈曲形态定义中可以看出影响管线变形的一些因素,这为分析管线屈曲原因提供了参考。
钻井用连续管的屈曲分析

钻井用连续管的屈曲分析张辛1, 徐兴平1, 王龙庭2,王雷1(1.中国石油大学(华东)机电学院,山东东营,207061;2. 胜利油田高原石油装备有限责任公司研发中心)摘要:连续管弯曲可能会出现在任何井段。
但是,在不同的井段开始形成弯曲的临界压缩载荷不同。
本文在总结国内外学者研究的基础上,以垂直井段为例,对已有公式的适用条件进行了探讨。
采用能量守恒原理,对垂直井段的连续管进行临界屈曲载荷分析,得到连续管的临界屈曲载荷。
利用拉格朗日乘子方法分别对管柱处于不同屈曲形式下进行管柱与套管壁的接触载荷计算。
并对管柱的屈曲行为进行了ABAQUS计算机模拟分析。
关键词:连续管屈曲分析计算模型计算机模拟Buckling Analysis of Drilling Coiled TubingZhang Xin1, Xu Xingping1, Wang Longting2, Wang Lei1(1. College of Mechanical and Electronic Engineering, China University of Petroleum, Dongying, Shandong, 257061, China; 2. Shengli Oilfield Highland Petroleum Equipment Co., Ltd. R&Dcenter)Abstract:The bend of coiled tubing may appear in any hole section. However, the critical compressive load is different in different interval when the bend is generated. On the base of the research of domestic and foreign scholars, applicable conditions to the existed formulas are researched in this paper with the example of vertical interval. Using energy method, equations are derived to predict the axial compression force required to produce buckling in vertical wells. Utilizing the Lagrange multiplier method, the unit lateral contact force corresponding to straight, sinusoidal, and helical configurations between CT and casing are obtained in vertical, inclined, and curved wells, respectively. The buckling of CT is also discussed on the basis of ABAQUS computer simulations.Keywords: Coiled tubing Buckling analysis Computation model Computer simulation前言在连续管下入过程中,由于管柱本身重力的影响和管柱与井壁摩擦的影响,使得管柱在受压时由初始的近似直线状态变为曲线状态,这就是管柱的屈曲。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
I 管柱屈曲研究现状及存在问题分析 摘要:对20世纪五十年代后期以来有关油气井管柱屈曲方面的文献进行系统检索,从弯曲力、临界屈曲、后屈曲平衡等方面介绍了在管柱屈曲领域的最新研究成果和应用现状,在管柱屈曲中,考虑了温度变形、鼓胀变形、轴向力变形和螺旋弯曲变形,并指出了今后油气井管柱屈曲的重点发展方向。 关键词 管柱 屈曲 正弦屈曲 螺旋屈曲 管柱(包括钻柱、套管柱、测试管柱、抽油杆管柱、连续油管等)的屈曲行为是石油工程中的关键问题,对石油工程中的诸多方面(如钻井、完井、测井、压裂、采油等)都有不良影响,会引起钻头方向改变及井下摩阻和扭矩显著增加(甚至使管柱“锁死”),导致钻具疲劳破坏、油管密封失效、管柱连接失效、连续油管无法下入以及采油杆管柱偏磨等。特别是随着水平井、大位移井、多分支井和连续油管技术的推广应用,受井眼约束管柱的屈曲问题更加突出,已成为油气钻采工程中的关键问题之一。 80年代以前,研究工作主要侧重于管柱在垂直井眼中的稳定性和螺旋屈曲分析。80年代以后,特别是90年代以来,由于定向井、水平井、大位移井等工程应用的需要,研究重点转向了斜井、水平井以及弯曲井眼中管柱的稳定性、屈曲以及自锁分析。国内外学者分别利用解析方法、能量方法、数值方法和试验方法对管柱在垂直井、斜直井、水平井和弯曲井眼中的稳定性和屈曲行为进行了理论和试验研究。理论和试验研究表明,管柱在井眼中有4中不同的平衡状态和空间构型:稳定状态、正弦弯曲状态、螺旋弯曲状态和自锁状态。在这4种不同的平衡状态之间,存在3个临界点。 一般情况下,当结构受到载荷超过其临界载荷,将导致结构损坏。由于井壁为管柱的后屈曲平衡提供了约束条件,管柱都是在高于其临界载荷条件下工作的,要计算管柱的载荷、变形和应力,必须先知道实际工况条件下管柱的屈曲形态。 井下管柱的变形包括横向变形和纵向变形,由于管柱横向尺寸(数量级一般
为110m)与纵向尺寸(数量级一般为310m)相比很小,横向变形量与纵向变形 II
量相比也很小。因此,分析井下管柱的变形主要是指轴向(纵向)变形。管柱的轴向变形对作业的成败起着至关重要的作用——若管柱轴向变形过大,会引起封隔器失封或过大的螺旋弯曲而使管柱塑性破坏或降低管柱的密封性。目前,国内外比较一致的做法是:将井下管柱的变形分为温度变形、鼓胀变形、轴向力(包括活塞力)变形、螺旋弯曲形变四个分量;将坐封工况下上述四种变形的数值作为“零点”,其它工况下管柱的各个变形分量与“零点”分量的差值对应地称作“温度效应”、“鼓胀效应”、“活塞效应”(本文称为“轴力效应”)和“螺旋弯曲效应”;上述四种“效应”的代数和就是因工况改变,井下管柱的变形变化量。根据结构力学理论,若该变形变化量受到限制,将转化为轴向力;若该变形变化量不受到限制,将影响到封隔器的封隔性能。 一、弯曲力 轴向压力可能导致管柱发生屈曲。当管柱受到内外流体压力作用力,用弯曲力来替换真实轴力,即 22()()baiiiiooooFFpvApvA
(1)
式中:bF——弯曲力; aF——真实轴力;
ip,op——内外压力;
iA,oA——管柱内、外圆面积;
2v
——流体流动动量的影响;
——流体密度;
v——横截面平均速度;
下标i,o——管柱内部和外部。 由(1)式得在内外流体压力作用下管柱单位长度重量为()bppiioowwAAg (2)
式中:pw——管柱在空气中单位长度重量; i,o——管柱内、外部流体密度; III
g——重力加速度。 通过弯曲力的定义,可以发现内部流体压力加剧管柱屈曲,而外部流体压力有助于管柱保持直线稳定状态。 二、临界屈曲 欧拉最早提出了压杆稳定性分析方法,铁摩辛柯在欧拉公式的基础上建立了弹性稳定理论。Greenhill分析了扭转条件下杆柱的弯曲。鲁宾斯基在细长直管柱的假设条件下,对管柱的螺旋弯曲行为进行了分析。理论分析中,常假设在井眼管柱中有两种屈曲状态:正弦屈曲和螺旋屈曲。在轴向压力作用下,管柱首先发生正弦屈曲,随着弯曲力增加过渡到螺旋弯曲。在实际情况下,油管屈曲可能比这复杂得多。试验结果表明,螺旋屈曲旋向为逆时针方向。 2.1 正弦临界屈曲 Dawson和Paslay分析了在斜直井中管柱正弦屈曲临界载荷,即 4sinsbpFEIw (3)
式中:EI——弯曲模量; ——管柱与井壁间的径向间隙;
——井斜角。
He and Kyllingstad将Dawson和Paslay的结果推广到弯曲井眼中,即 4scFEIw (4)
其中 22(sin)(sin)cbpbbwwFF
(5)
式中:cw——管柱与井壁之间的接触力; ——方位角;
*——深度s的微分。
(5)式由Sheppard在拉扭模型屈曲分析中首次建立。对于弯曲井眼,(5)式可表示为 222()cbpzbbpzwwnFwb
(6) IV
式中:zn,zb——曲线的主法线、副法线; ——曲率。
2.1.1 摩擦力的影响 当管柱相对井壁未发生转动,随着摩擦力不断增加,在任意小的侧向扰动条件下,管柱正弦临界屈曲载荷为
24csoEIwGJ
Fd
(7)
式中:G——剪切模量; J——极惯性矩;
od——管柱外径。
当管柱相对井壁发生滑动,摩擦力对屈曲产生影响。此时,正弦屈曲临界载荷为 4cfsEIwF
(8)
其中
21ccfww
(9)
式中:cfw——滑动接触力; ——滑动摩擦系数。
2.1.2 井眼弯曲的影响 在弯曲井眼中,2EI等效于弯曲力bF。在这种情况下,正弦屈曲临界载荷为 2bsFEIF
(10)
sF由(4)式、(7)式或(9)式确定。
2.2螺旋临界屈曲 Chen和Cheatham首次提出斜井管柱螺旋屈曲临界载荷,即 F2hsF (11) V
Mitchell在数值分析的基础上,给出了螺旋屈曲临界载荷为 F2.8hsF (12)
当2.8F2sbsFF时,管柱可能发生螺旋屈曲或正弦屈曲。2.8sF是正弦屈曲临界载荷的上限;而2sF是螺旋屈曲临界载荷的下限。 Mitchell通过解析法得到了正弦屈曲临界载荷和螺旋屈曲临界载荷,即
正弦屈曲 1.382.6sbsFFF (13) 螺旋屈曲 3.88sbFF (14) (14)式中,螺旋屈曲临界载荷的求解考虑了接触力的影响。这表明,当2.63.88sbsFFF时,管柱屈曲构型近似于一个螺旋。正弦解的区间接近(11)
式和(12)式构成的区间。
理论上,正弦屈曲稳定解的最大值为2. 8 sF。在实践中,由于不规则的几何形状,管柱将在区间(2sF,2.8sF)从正弦屈曲过渡到螺旋屈曲。Suryanarayana的实验验证了这一结果。 三、后屈曲平衡 3.1 螺旋屈曲 油管屈曲微分方程是非线性的,边界条件复杂,方程求解困难。Lubinski首次提出受井眼约束细长无重管柱螺旋弯曲几何方程,即
1cosu (15)
1cosu (16)
其中 s (17)
与螺旋螺距p的关系为
22212p
(18)
(注:近似方程假定2224p) VI
(15)式、(16)式和(17)式带入平衡方程,得 222()cEIw
(19)
因接触力为正,22。 和的表达式为
bFEI (20)
lwb=F2EI (21)
2bp8EIF
(22)
式中;EI——弯曲刚度; p——螺距。 联立(19)式、(22)式得到接触力为 2222()4bclwlwFwEIEI
(23)
考虑扭矩的影响,Miska-Cunha和He、Halsey、Kyllingstad进一步修正了上
述结果。假设tMEI是小量,可得 38tlwWEI
(24)
接触力为 242btbclwFMFwEIEI
(25)
3.2斜井后屈曲 斜井中,屈曲方程是非线性的,求解非常困难,不适合设计计算的需要,可通过数值分析结果拟合出简单的计算公式。 3.2.1弯曲角最大值 (1)正弦屈曲时
0.040.46max1.1227()2bbsFFFEI
(26)
(2)螺旋屈曲时
