狼群算法介绍

合集下载

狼群算法原理

狼群算法原理狼群算法（Wolf Pack Algorithm）是一种模仿狼群行为的优化算法，它是基于自然界中狼群协同捕食的行为模式而发展起来的。

狼群算法通过模拟狼群中狼之间的协作与竞争关系，以寻找最优解或近似最优解的方式来解决优化问题。

狼群算法的核心思想是将问题空间映射到一个虚拟的狼群空间中，每个个体（狼）代表着一个潜在的解。

狼群中的每只狼都有自己的位置和适应度值，适应度值表示了该位置的解的优劣程度。

狼群算法通过模拟狼群的协作与竞争过程，不断迭代更新每只狼的位置，从而逐步接近最优解。

狼群算法包含三个主要的行为模式：寻找猎物、狼群协作和狼群竞争。

在寻找猎物的行为中，狼群中的每只狼会根据自身的位置和适应度值来搜索周围的解空间，以找到更优的解。

狼群协作的行为模式指的是狼之间会相互交流信息，通过共享有用的信息来提升整个狼群的搜索效果。

而狼群竞争的行为模式则是指狼群中的狼会相互竞争，通过竞争来筛选出适应度值更高的个体，并且淘汰适应度值较低的个体。

狼群算法的核心优势在于其强大的全局搜索能力和快速的收敛速度。

由于每只狼都具有寻找猎物、狼群协作和狼群竞争等行为模式，狼群算法能够充分利用群体智慧，有效地避免陷入局部最优解。

同时，狼群算法通过狼群协作和狼群竞争的机制，能够在搜索过程中迅速收敛到最优解附近，从而提高了算法的收敛速度。

狼群算法在实际应用中具有广泛的适用性。

它可以用于解决各种优化问题，如函数优化、组合优化、路径规划等。

狼群算法还可以应用于机器学习中的特征选择、参数优化等问题。

此外，狼群算法还可以与其他优化算法相结合，形成混合算法，以进一步提升搜索效果。

狼群算法是一种模仿狼群行为的优化算法，通过模拟狼群的协作与竞争关系，以寻找最优解或近似最优解的方式来解决优化问题。

狼群算法具有全局搜索能力强、收敛速度快等优势，并且在各种优化问题中具有广泛的应用价值。

通过研究和应用狼群算法，我们可以更好地理解和利用自然界中的智慧，为解决复杂的优化问题提供有力的工具和方法。

蚁群算法

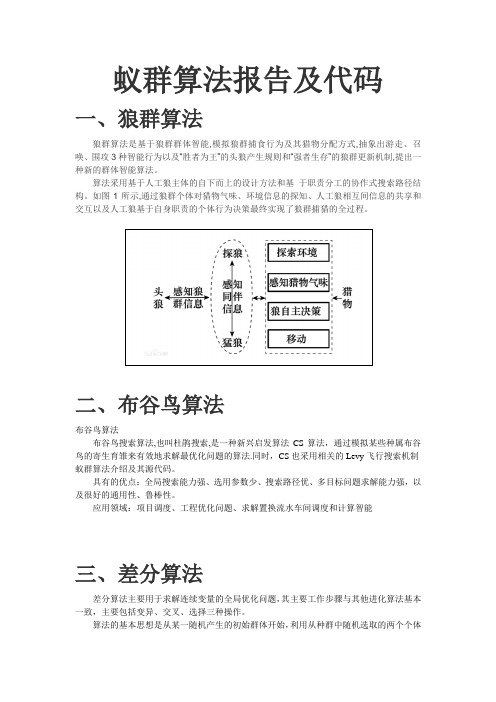
蚁群算法报告及代码一、狼群算法狼群算法是基于狼群群体智能,模拟狼群捕食行为及其猎物分配方式,抽象出游走、召唤、围攻3种智能行为以及“胜者为王”的头狼产生规则和“强者生存”的狼群更新机制,提出一种新的群体智能算法。

算法采用基于人工狼主体的自下而上的设计方法和基于职责分工的协作式搜索路径结构。

如图1所示,通过狼群个体对猎物气味、环境信息的探知、人工狼相互间信息的共享和交互以及人工狼基于自身职责的个体行为决策最终实现了狼群捕猎的全过程。

二、布谷鸟算法布谷鸟算法布谷鸟搜索算法,也叫杜鹃搜索,是一种新兴启发算法CS算法，通过模拟某些种属布谷鸟的寄生育雏来有效地求解最优化问题的算法.同时，CS也采用相关的Levy飞行搜索机制蚁群算法介绍及其源代码。

具有的优点：全局搜索能力强、选用参数少、搜索路径优、多目标问题求解能力强，以及很好的通用性、鲁棒性。

应用领域：项目调度、工程优化问题、求解置换流水车间调度和计算智能三、差分算法差分算法主要用于求解连续变量的全局优化问题，其主要工作步骤与其他进化算法基本一致，主要包括变异、交叉、选择三种操作。

算法的基本思想是从某一随机产生的初始群体开始，利用从种群中随机选取的两个个体的差向量作为第三个个体的随机变化源，将差向量加权后按照一定的规则与第三个个体求和而产生变异个体，该操作称为变异。

然后，变异个体与某个预先决定的目标个体进行参数混合，生成试验个体，这一过程称之为交叉。

如果试验个体的适应度值优于目标个体的适应度值，则在下一代中试验个体取代目标个体，否则目标个体仍保存下来，该操作称为选择。

在每一代的进化过程中，每一个体矢量作为目标个体一次，算法通过不断地迭代计算，保留优良个体，淘汰劣质个体，引导搜索过程向全局最优解逼近。

四、免疫算法免疫算法是一种具有生成+检测的迭代过程的搜索算法。

从理论上分析，迭代过程中，在保留上一代最佳个体的前提下，遗传算法是全局收敛的。

五、人工蜂群算法人工蜂群算法是模仿蜜蜂行为提出的一种优化方法，是集群智能思想的一个具体应用，它的主要特点是不需要了解问题的特殊信息，只需要对问题进行优劣的比较，通过各人工蜂个体的局部寻优行为，最终在群体中使全局最优值突现出来，有着较快的收敛速度。

一种新的群体智能算法——狼群算法

中图分类号：ＴＰ１８文献标志码：ＡＤＯｌ：１０．３９６９／ｊ．ｉｓｓｎ．１００１～５０６Ｘ．２０１３．１１．３３
Ｎｅｗｓｗａｒｍｉｎｔｅｌｌｉｇｅｎｃｅａｌｇｏｒｉｔｈｍ－ｗｏｌｆｐａｃｋａｌｇｏｒｉｔｈｍ
ｕｔｉｖｅｍｏｄｅｆｏｒｐｒｅｙ，ｔｈｉｓｐａｐｅｒａｂｓｔｒａｃｔｓｔｈｒｅｅｉｎｔｅｌｌｉｇｅｎｔｂｅｈａｖｉｏｒｓ，ｓｃｏｕｔｉｎｇ，ｓｕｍｍｏｎｉｎｇａｎｄｂｅｌｅａｇｕｅｒｉｎｇ，ａｎｄ
ｄｅｄｕｃｅｓａｐｒｏｄｕｃｔｉｖｅｒｕｌｅｆｏｒｌｅａｄｉｎｇｗｏｌｆｔｈａｔｔｈｅｗｉｎｎｅｒｃａｎｄｏｍｉｎａｔｅｉｔｓａｌｌａｎｄａｒｅｎｅｗａｂｌｅｍｅｃｈａｉｓｍ，ｎａｍｅｄｓｕｒｖｉｖａ【ｏｆｔｈｅｓｔｒｏｎｇｅｒ，ｆｏｒａｐａｃｋｏｆｗｏｌｖｅｓ．Ｆｒｏｍｔｈｅａｂｏｖｅ，ａｎｅｗｈｅｕｒｉｓｔｉｃｓｗａｒｍｉｎｔｅｌｌｉｇｅｎｔｍｅｔｈｏｄ，ｗｏｌｆ
２．ＭａｔｅｒｉｅｌＥｎｇｉｎｅｅｒｉｎｇＣｏｌｌｅｇｅ，ＡｒｍｅｄＰｏｌｉｃｅＦｏｒｃｅＥｎｇｉｎｅｅｒｉｎｇＵｎｉｖｅｒｓｉｔｙ，Ｘｉ ’ ａｎ７１００８６，Ｃｈｉｎａ；

灰狼优化算法 ( G W O ) 原理

灰狼优化算法--简单易懂附python代码ps:本博文为个人理解，如有错误请不吝赐教本博文部分引用了1、算法原理：简单的讲，狼群中有 Alpha、Beta、Delta三只灰狼做头狼，Alpha是狼王，Beta、Delta分别排第二第三，Beta要听老大Alpha 的，Delta要听Alpha、Beta的。

这三头狼指导着狼群里其他的狼寻找猎物。

狼群寻找猎物的过程就是我们寻找最优解的过程。

2、公式方面大家可以看另一博主的博文。

3、代码如下：import randomimport numpydef GWO(objf, lb, ub, dim, SearchAgents_no, Max_iter):# 初始化 alpha, beta, and delta_posAlpha_pos = numpy.zeros(dim) # 位置.形成30的列表Alpha_score = float("inf") # 这个是表示“正负无穷”,所有数都比 +inf 小；正无穷：float("inf"); 负无穷：float("-inf") Beta_pos = numpy.zeros(dim)Beta_score = float("inf")Delta_pos = numpy.zeros(dim)Delta_score = float("inf") # float() 函数用于将整数和字符串转换成浮点数。

# list列表类型if not isinstance(lb, list): # 作用：来判断一个对象是否是一个已知的类型。

其第一个参数（object）为对象，第二个参数（type）为类型名，若对象的类型与参数二的类型相同则返回Truelb = [lb] * dim # 生成[100，100，.100]30个if not isinstance(ub, list):ub = [ub] * dim# Initialize the positions of search agents初始化所有狼的位置Positions = numpy.zeros((SearchAgents_no, dim))for i in range(dim): # 形成5*30个数[-100，100)以内Positions[:, i] = numpy.random.uniform(0, 1, SearchAgents_no) * (ub[i] - lb[i]) + lb[i] # 形成[5个0-1的数]*100-（-100）-100Convergence_curve = numpy.zeros(Max_iter)#迭代寻优for l in range(0, Max_iter): # 迭代1000for i in range(0, SearchAgents_no): # 5# 返回超出搜索空间边界的搜索代理for j in range(dim): # 30Positions[i, j] = numpy.clip(Positions[i, j], lb[j], ub[j]) # clip这个函数将将数组中的元素限制在a_min(-100),a_max(100)之间，大于a_max的就使得它等于 a_max，小于a_min,的就使得它等于a_min。

求解柔性作业车间调度问题的两段式狼群算法

柔性作业车间调度问题由Bucker和Schlie提出[1]，相比于经典的作业车间调度问题，它的每一道工序可以在多台机器上加工，不同机器上的加工时间亦不相同，且已被证明是NP难问题[2]；其调度目标是以某个加工性能指标为目标函数确定各机器上各个工件工序的加工次序，通常以总流经时间、最迟完工时间、最小化最大完工时间等为目标函数。

赵博选等[3]提出对策略融合的Pareto人工蜂群算法求解柔性作业车间调度问题；Azzouz等[4]用遗传算法求解柔性作业车间调度问题；Xu等[5]提出改进混合免疫算法求解柔性作业车间调度问题；姜天华[6]提出一种混合灰狼算法求解柔性作业车间问题；徐华等[7]提出混合遗传蝙蝠算法求解单目标柔性作业车间调度问题；石小秋等[8]提出了一种自适应变级遗传算法求解以最小化最大完工时间为目标的柔性作业车间调度问题；王春等[9]提出了一种多目标进化算法，以优化区间柔性作业车间调度问题；Nouiri等[10]提出分布粒子群算法求解柔性作业车间调度问题；尽管各种元启发式算法在FJSP问题中已得到广泛的研究，但目前仍没有任何一种算法能够获得所有问题的最优解，因此学者们仍在不断积极探索，以获得更丰富且更有效的方法。

狼群算法（Wolf Pack Algorithm，WPA）是近年来提出的一种模拟自然界中狼群分工协作捕猎的群体智能优化算法[11]。

针对WPA的相关研究表明，该算法具有较强的全局搜索能力和计算鲁棒性。

目前，WPA已在复杂连续优化函数问题上得到了研究与应用[11]。

在离散问题方面，狼群算法已在无人机航线规划问题[12]、多配送中心车辆路径[13]、TSP[14]、矩形件排样[15]等问题中获求解柔性作业车间调度问题的两段式狼群算法谢锐强，张惠珍上海理工大学管理学院，上海200093摘要：针对以最小化最大完工时间为目标函数的柔性作业车间调度问题，建立其数学模型并提出了一种两段式狼群算法加以求解。

狼群智能算法简述

狼群分工协作
猎物分配规则:捕获猎物后狼群并不是平均分配猎物而是按“论功行赏、由强到弱” （按劳分配)的方式分配。尽管这种近乎残酷的食物分配方式会使得少数弱狼由于食物缺乏而饿死但此规则可保证有能力捕到猎物的狼获得充足的食物进而保持其强健的体质，在下次捕猎时仍可顺利地捕到猎物，从而维持着狼群主体的延续和发展。
探狼：寻找猎物时，狼群不会全体出动而是派出少数精锐的探狼在猎物的可能活动范围内游猎，根据空气中猎物留下的气味进行自主决策，气味越浓表明狼离猎物越近探狼始终就朝着气味最浓的方向搜寻会立即向头狼报告，头狼视情通过嚎叫召唤周围的猛狼来对猎物进行围攻周围的猛狼闻声则会自发地朝着该探狼的方向奔袭向猎物进一步逼近。
• 步骤 3 人工猛狼据式(2)向猎物奔袭,若途中猛狼感知的猎物气味浓度Yi > Ylead则Yi = Ylead，替代头狼并发起召唤行为；若Yi < Ylead则人工猛狼续奔袭直到dis<dnear,转步骤4。
• 步骤 4 按式(4)对参与围攻行为的人工狼的位置进行更新;执行围攻行为。
• 步骤 5 按胜者为王的头狼产生规则对头狼位置进行更新;再按照强者生存的狼群更新机制进行群体更新。
智能算法概述
• 步骤 1 数值初始化。初始化狼群中人工狼位置Di及其数目N,最大迭代次数kmax,探狼比例因子α,最大游走次数Tmax,距离判定因子w,步长因子S,更新比例因子。
• 步骤 2 选取最优人工狼为头狼"除头狼外最佳的S_num匹人工狼为探狼并执行游走行为，直到某只探狼i侦察到的猎物气味浓度Yi大于头狼所感知的猎物气味浓度Ylead或达到最大游走次数Tmax,则转步骤3。
狼群智能算法简述
目录

灰狼算法和粒子群算法

灰狼算法和粒子群算法灰狼算法和粒子群算法是两种常用的进化计算算法，它们在优化问题中具有广泛的应用。

本文将分别介绍灰狼算法和粒子群算法的原理和特点，并通过比较它们的优缺点，探讨其适用的场景。

1. 灰狼算法灰狼算法是由灰狼群体的行为和特性启发而来的一种群体智能算法。

灰狼群体中的每只狼都有一个适应度值，适应度值越高表示狼的位置越好。

算法的核心思想是模拟灰狼群体中的寻食行为，通过迭代更新每只狼的位置，最终找到最优解。

灰狼算法的具体步骤如下：1）初始化灰狼群体的位置和适应度值；2）通过适应度值的大小确定群体中的Alpha狼、Beta狼和Delta 狼；3）根据Alpha狼的位置和其他狼的位置，更新每只狼的位置；4）更新每只狼的适应度值；5）重复步骤3和4，直到满足停止条件。

灰狼算法的优点是简单易实现，收敛速度快，适用于解决复杂的非线性优化问题。

然而，灰狼算法在处理高维优化问题时，容易陷入局部最优解。

2. 粒子群算法粒子群算法是一种模拟鸟群觅食行为的群体智能算法。

算法中的每个粒子都有一个位置和速度，通过更新粒子的速度和位置，最终找到最优解。

粒子群算法的核心思想是通过个体和群体的交互合作来搜索最优解。

粒子群算法的具体步骤如下：1）初始化粒子群体的位置和速度；2）根据粒子的适应度值，更新局部最优解；3）根据局部最优解和全局最优解，更新粒子的速度和位置；4）更新粒子的适应度值；5）重复步骤2、3和4，直到满足停止条件。

粒子群算法的优点是容易实现，具有较好的全局搜索能力，适用于解决多峰优化问题。

然而，粒子群算法在处理高维优化问题时，易陷入局部最优解。

3. 算法比较与适用场景灰狼算法和粒子群算法都是基于群体智能的优化算法，它们在某些方面具有相似之处，但也存在一些差异。

灰狼算法与粒子群算法相比，优点是收敛速度快，适用于解决复杂的非线性优化问题；缺点是在处理高维优化问题时，容易陷入局部最优解。

粒子群算法与灰狼算法相比，优点是具有较好的全局搜索能力，适用于解决多峰优化问题；缺点是在处理高维优化问题时，易陷入局部最优解。

利用改进的二进制狼群算法求解多维背包问题

ｄｅｍｏｎｓｔｒａｔｅｔｈｅｅｆｆｅｃｔｉｖｅｎｅｓｓａｎｄｃｏｍｐｕｔａｔｉｏｎａｌｒｏｂｕｓｔｎｅｓｓｏｆｔｈｅｐｒｏｐｏｓｅｄａｌｇｏｒｉｔｈｍ．
数的目标函数，减小了由于惩罚参数过大而导致算法陷入局部最优的风险；并受狼群的繁衍方式的启发，在二进
制狼群算法的基础上提出了求解多维背包问题的改进二进制狼群算法（ｉｍｐｒｏｖｅｂｉｎａｒｙｗｏｌｆｐａｃｋａｌｇｏｒｉｔｈｍ，ＩＢ～
限制下具有最大价值的物品装载方案。如金融产品组合投
资、无人机任务分配、物料资源分配、货运装载等很多实际
问题都可抽象为背包问题，应用非常广泛。背包问题有
收稿Ｅｔ期：２０１４一Ｏ４— ２５；修回日期：２ｏ１４—１０—２ｏ；网络优先出版日期：２０１４—１１ —１９。
３．空军工程大学空管领航学院，陕西西安７１００５１）
摘要：狼群算法启发于狼群群体生存智慧，已被用于复杂函数寻优和０ —１普通背包问题求解。针对多维背包问题特点，设计了试探装载式的修复机制有效修复和改进人工狼群中的不可行解，改进了传统基于大惩罚参

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

2017/6/19
实验仿真
4种典型非线性函数
2017/6/19
实验仿真
典型函数不同优化算法对比结果
2017/6/19
实验结较好的鲁棒性和全局收敛性能，可有效避免常用智能算法所出现的算法早熟收敛问题。特别对多峰、高维的复杂函数寻优效果较好，可以给大量非线性、多峰值的复杂优化问题的求解提供新的思路和解决方法。
2017/6/19
狼群算法介绍
2017/6/19
基本内容
算法简介算法实现实验仿真实验结论
2017/6/19
算法简介
复杂非线性优化
群体智能算法
粒子群（鸟群扑食）蚁群、鱼群、细菌觅食（大肠杆菌在食道）
早熟、收敛精度不高
易陷入局部最优
狼群算法
模拟游猎行为：独立的局部精细搜索；模拟召唤行为：局部最优解的搜索效率; 模拟攻击行为：全局最优解
2017/6/19
算法简介
三种行为
游走行为召唤行为围攻行为
两条准则
强者生存
2017/6/19
胜者为王
算法实现
几点说明：初始目标函数值最大的作为头狼；选取除头狼外最佳的部分人工狼为探狼；剩余的作为猛狼；奔袭和围攻行为是由猛狼执行的。按“胜者为王”的头狼规则对头狼位置进行更新；按照“强者生存”的狼群更新机制进行群体更新。终止条件包括：优化精度或最大迭代次数