线性回归的不确定度问题

线性回归的不确定度问题

一 基本概念

两个变量Y 与X 相关，并可能接近线性相关，希望找出这种戏相关关系：Y=aX+b

这是可能的，但只能是近似的而且不会是唯一的，用最小二乘法可以找到最佳线性相关关系。具体方法如下：

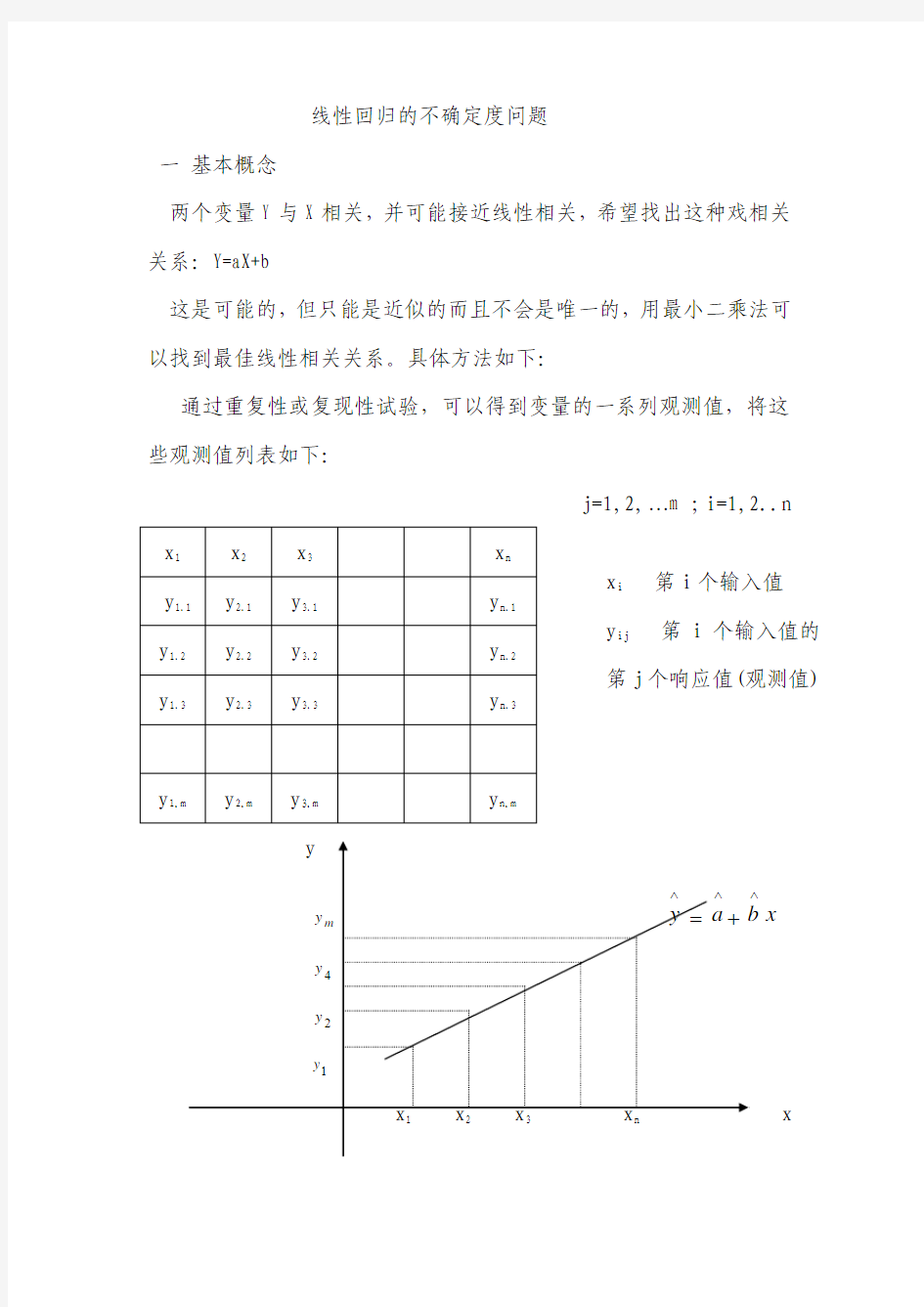
通过重复性或复现性试验，可以得到变量的一系列观测值，将这些观测值列表如下：

j=1,2,…m ；i=1,2..n

x x

x i 第i 个输入值 y ij 第i 个输入值的第j 个响应值(观测值)

散点图（说明：由于本人在计算机上作图的能力有限，所以此图有很多信息未表达甚至有误，请注意。）

用这一系列输入值与观测值，根据最小的乘法原理可以回归出一条最佳直线：

x b a y

???+= y

?——y 的估计值（最佳） a

?——a 的估计值（最佳） b

?——b 的估计值（最佳） 理论上可以证明，这条直线通过散点图的几何重心（x ?.y ?）所

谓最佳直线，是指y 的各点观测值y i 与回归后的估计值i y ?的残差平方和最小。（散点距回归直线距离最近）

一般情况下输入量x i 是标准值，其不确定度相对y 来说很小，可忽略。

二、各项参数计算

1.计算y 的平均值

∑=

=m

j ij i y m y 1

1

2.计算变量x 、y 的平均值

∑=

∑===n

i i

n

i i

y n

y x n x 1

111

3.计算L xx , L xy , L yy （用各点观测值的平均值来回归的方法）

L xx =2

2

2

1)

(1)(∑-

∑=-∑=i i n

i i x n

x x x

L xy =∑∑-

∑=--∑=i i i i i n

i i y x n

y x y y x x 1))((1

L yy =2

2

1

2

)

(1)(∑-

∑=∑-=i i n

i i y n

y y y

4.计算a ?、b

? b

?=xx

xy L L a

?=x b y ?- 5.得到回归函数（回归方程）

x b a y

???+= 三、利用回归方程（在很多情况下，特别是测量领域，直线回归方程是作为校准直线来使用的）来求x 或y 的值。

x b a y

???+= 在回归时，x 是输入量（标准值）y 是输出（相应值）

b a y x

?)?(?-= 回归方程得到后，在使用它时，往往y 是输入量（已知量），x

?是未知量，y 可能是单次测量值，也可能是多次测量值

接下来的问题在于：

① 回归函数的“质量”如何？y 与x 间是否确有较好的线性关系？ ② 利用回归函数来估计x 或y 时的不确定度？如何确定 四、回归函数的“质量”检验——显著性检验

1.三个方差

① S 总=2

1)(y y n

i i -∑=——反映了i y 的总的分散程度

② S 回=2

1)?(y y n

i i -∑=——反映了回归值i y ?的分散程度

③ S 余=2

1

)?(i n

i i y

y -∑=——反映了观测值i y 偏离回归直线的程度 2.回归函数的标准偏差 2

2

)?(2

-=

-∑-=

n s n y

y s i i 余 ——残余标准偏差

xx

l s b

s =)?( ——b

?的标准偏差 3.相关关系 yy

xx xy l l l =

γ

4.显著性检验

① 当05.0γγ≤时， y 与x 的线性相关关系不显著 ② 当01.005.0γγγ≤≤时，y 与x 的线性相关关系显著 ③ 当01.0γγ>时， y 与x 的线性相关关系特别显著 那么，05.0γ=？01.0γ=？ 查相关系数显著性检验表

根据)01.005.0(或=α及自由度n-2可查出05.0γ或01.0γ，如n-2=8时，05.0γ=0.632，01.0γ=0.765

五、当利用回归方程（校准直线）求x 的估计值时的不确定度

已知观测值0y ，求0x （0y 是由p 次测量得到的平均直）

∑--+

+

=∑--+

+=

-===n i i c n i i c x x x x n p s

y u x x x x n p b

s

x u b a y x 1

2

2

001

2

2

0000)

()

(11)()()

(11?)(?/)?(

六 特别说明

以上计算是用观测点的平均值求回归方程以及标准偏差。在《化学分析中不确定度的评估指南》的例A5中使用观测点的平均值求回归方程，而用各观测点的值求标准偏差，。故计算公式有所不同。此外该《指南》的公式可能有错误，在下面的应用实例中予以指出，供参考。

七 应用实例（《化学分析中不确定度的评估指南》例A5）

用原子吸收光谱法测量陶瓷中镉溶出量 1. 方法简述

用4%醋酸水溶液（体积浓度）浸泡陶瓷，陶瓷中所含的有害金属镉将会溶出，然后用原子吸收光谱仪（AAS ）测量溶液的吸光率。根据吸光率来判断镉溶液浓度。但AAS 的吸光率与镉溶液浓度的关系事先要用最小二乘法回归以产生校准直线。 2 程序

① 被测样品（陶瓷器皿）在（22±2）℃的条件下保存，测量其表面积。本例为a V =2.37dm 3 ;

② 将（22±2）℃的4%醋酸溶液倒入被测样品容器（陶瓷器皿）

中，溶液高度距陶瓷器皿上口1mm;; ③ 记录4%醋酸溶液的量，本例V L =332ml; ④ 样品在（22±2）℃的条件下放置24h(黑暗中)

⑤ 搅拌溶液使其均匀。取一部分溶液稀释，稀释系数为d 。 ⑥ 选用适当的波长在AAS 上进行分析。校准直线已事先建立； ⑦ 计算结果，报告在总浸取液中镉的含量（mg/dm 2）。 3 数学模型 temp time acid V

L f f f d a V c r ??=

式中：r ---每单位面积镉溶出量 (mg ﹒dm -2 ) 0c ---浸取液中镉含量 (mg ﹒l -1)

d

---稀释系数

L V ---浸取液体积 (l)

V

a ----容器的表面积 (dm 2)

acid f ----酸浓度的影响 time

f ----浸泡时间的影响

temp f ----温度的影响 4 识别和分析不确定度来源 4.1浸取液中镉含量0c

用原子吸收光谱法测定，并用校准溶液事先校准。

1

00B B A c -=

0A

----浸取液中金属的吸光度

0B ----校准直线的截距 1B ----校准直线的斜率

校准直线在拟合时有不确定度，浸泡时间、溶液浓度、温度对浸取液中镉含量0c 均有影响。 4.2 体积L V

浸取液体积测量，受浸泡液体高度、温度、校准、读数影响。 4.3容器的表面积V a

容器的表面积测量，受长度测量影响及浸泡深度影响。 4.4稀释系数d

本例无须稀释浸取液，故可不考虑其影响。 根据以上分析画出因果图：

L V 0c

直线拟合 酸浓度 浸泡液高度 温度

浸泡时间 浸泡温度 校准 读数

r 长度2

长度2 d v a

5 不确定度来源量化

5.1浸取液中镉含量0c 的不确定度 5.1.1 校准直线拟合的影响

用(500±0.5)mgl -1的镉标准溶液配制5个标准溶液，其浓度分别为0.1、0.3、0.5、0.7、0.9 mgl -1。对每个标准溶液分别测量3次，

共得到15个测量值：

说明：5个标准溶液的排序为i=1、2、3、4、

5 n=5

每个标准溶液测量3次的排序为j=1、2、3 m=3

校准直线的公式为： 0

1B B C A i j

+=

j A ----对第i 个标准溶液的第j 次吸光度测量值

i C

----第i 个标准溶液的浓度

1B ----斜率 0B ----截距 拟合的结果为：

用AAS 测量浸泡陶瓷容器的溶液两次,得到浓度26

.00

=c mgl -1,而

标准不确定度： 018

.02

.1)

5.02

6.0(15

12

1241

.0005486.0)(11)(2

2

01

0=-+

+

=

-+

+=

xx

s c c N P B s c u mgl -1

残余标准偏差为：

005486

.02

)]([1

2

10=-+-=∑=N c B B A

s N

J i J

2.1)

(2

1

=-=

∑=N

J i

xx

c c

s

式中：P ---测量0c 的总次数（2

=P

）

N ---测量校准溶液的总次数（15

==mn N ）（3=m ，5=n ）

J ---测量校准溶液的序数（N

J

????=321、、），注意：J 与j 不同。

i ----校准溶液的序数（54321、、、、=i ）

c ----5=n 个校准溶液浓度的平均值 1B ----斜率

0c ----浸出液中镉的浓度 i c ----第i 个校准溶液的浓度

注：在《化学分析中不确定度的评估指南》第78页中，上述3个公式可能有错误或表

达混乱！第111页最后一个公式可能也有错误。（编者自注，仅供参考）

5.1.2温度影响

研究给出：在25℃附近金属溶出量随温度变化呈线性，其斜率约为：5%℃-1，试验时温度变化范围为±2℃,按均匀分布考虑，故而：

06

.03

2

05.0)(=?=

temp f u

5.1.3 时间影响

研究给出：在浓度为86mgl -1时，浸出量与浸泡时间的关系约为0.3%/h 。试验时浸泡时间有±0.5h 的允许变化范围，按均匀分布考虑，故而：

001

.03

5

.0003.0)(=?=

time f u

5.1.4 酸浓度影响

一个研究表明：酸浓度每变化1%，acid f 约有0.1的变化；另一个研究表明：当酸浓度约为4%时，酸浓度的不确定度为0.008%。所以：

0008

.01.0008.0)(=?=acid f u

5.2 面积测量的不确定度 5.2.1 长度测量的影响

测量样品容器的尺寸，计算其总的表面积为2.37dm 2

（高1.45dm,

宽1.64dm ）。由于样品容器几何形状不是很规则，其尺寸测量的不确定度约为1mm(95%置信概率)。 5.2.2 面积计算的影响

由于样品容器几何形状不是很规则，所以面积计算也有不确定度，本例面积计算的相对扩展不确定度约为5%（95%置信概率）。

面积测量和计算的标准不确定度为： 06

.0)

96

.137

.205.0(

01.001.0)(2

2

2

=?++=

V a u dm 2

5.3 体积测量的不确定度

5.3.1 液体灌满样品容器的体积影响

经验方法要求液体灌满样品容器至上口边沿1mm 之内，1mm 约为

样品容器内高的1%，本例灌满样品的液体体积为332升，因此样品容器被液体灌满的体积的变化范围的半宽为±0.5%×332升,按三角分布考虑。 注：液体灌满样品容器的程度与实际浸泡部分的表面积有关，所以这一影

响应在面积计算的不确定度中考虑，而不是在体积计算中考虑。体积测量是用量筒进行的，并非依据液体灌满样品容器的程度。（编者自注，仅供参考）

5.3.2 温度影响

样品容器的体膨胀系数比液体的体膨胀系数要大得多，为2.1×10-4 允许的温度变化范围为±2℃，假定为均匀分布，则332升体积的不确定度为：

08

.03

233210

1.24

=???-ml

5.3.3 读数影响

用量筒测量浸泡液体体积，可以有1%的误差，按三角分布考虑。 5.3.4 校准影响

根据制造商的技术说明，500ml 量筒有±2.5ml 的偏差，设为三角分布。

体积测量的不确定度为：

83

.1)6

5.2(

)6

332

01.0(

08

.0)6

332

005.0(

)(2

2

2

2

=+?++?=

L V u ml

6 计算合成标准不确定度

6.1 计算样品单位表面积的镉溶出量 在没有稀释的情况下

036

.00.10.10.137

.2332

.026.0=????=

r mg 〃dm -2

6.2 计算合成标准不确定度

2

2

2

2

2

2

0]

)([

])([

])([

])([

])([

])([

)(temp

temp time

time acid

acid V

V L

L c f f u f f u f f u a a u V V u c c u r

r u +++++=

095

.006.0001.0008

.0025

.00054.0069.02

2

2

2

2

2

=+++++=

0034

.0095.0)(==r r u mg 〃dm -2

7 计算扩展不确定度 取包含因子为2，则：

007

.00034.02=?=U mg 〃dm -2

8 结果

用该方法测量镉溶出量为：)007.0036.0(± mg 〃dm

-2

,k=2

9 不确定度分量列表（略）

从不确定度分量表可以看出镉溶出量测量不确定度影响最大的是直线拟合不确定度及温度影响。

不确定度评定（完整）步骤

一技术规定

描述试验方法、步骤、要求、所用仪器设备等，给出结果计算公式（或建立数学模型）

二不确定度来源的确定和分析

确定主要不确定度的来源，了解其对被测量及其不确定度的影响，画出因果图（鱼刺图）。测量的许多环节都可能有重复性影响，可考虑将这些重复性合并成一个总试验的分量，并且利用方法确认的数值将其量化。

影响量2 影响量1

被测量

影响量1的重复性

影响量2的重复性

重复性（rep）影响量3

三 不确定度分量的定量（评定） 1 写出不确定度传播率

2 对各不确定度分量分别采用A 类或B 类评定，有时可以直接利用方法确认的结果（如总的重复性rep ）。

3 编制测量数据和不确定度分量表

说明：在一个完整的数学模型

?

+?=rep x x x f y )(321、、

中，rep 代表试验的总重复性 ，?代表试验偏差。rep 的数学期望应为1（即无限多次重复测量的平均值应为理想值），但rep 的标准不确定度（总重复性标准偏差——表征试验的精密度）却不为零。?是用标准物质或标准样品进行试验得到的，是用标准物质或标准样品

复现的量值减去测量值。

四计算合成标准不确定度

按不确定度传播率公式计算合成标准不确定度，对于复杂的运算过程可以利用“电子表格”的形式。

五计算扩展不确定度

六重新评估显著性不确定度分量

1 画出各不确定度分量的统计直方图

rep

x1

x2

x3

y

2 对比各分量的大小，对相对大的分量进行充分研究，找出减少影响该量的因素加以解决。