曲线桥梁 自重 内外侧扭矩
曲线梁桥结构设计及内力计算课程设计报告书

五跨预应力混凝土曲线梁桥结构设计与力计算: +++++++++学号: +++++++++班级:桥梁 1202指导老师:++++老师五跨预应力混凝土曲线梁桥结构设计与力计算摘要曲线梁桥又称弯梁桥,受力特点不同于其他形式,在外荷载作用下出现弯扭耦合,外边缘的挠度一般大于边缘的挠度,对于设有抗扭支座的弯梁桥,外弧侧的支座反力大于弧侧的支座反力,由于抗扭支座的存在而使结构为超静定结构,在结构设计与力计算中比一般的梁桥复杂,因此,在处理这类问题时,可以借助有限元软件进行结构受力分析,如迈达斯,ansys,桥博,sap2000等。
MIDAS/Civil 是针对土木结构,特别是分析象预应力箱型桥梁、悬索桥、斜拉桥等特殊的桥梁结构形式,同时可以做非线性边界分析、水化热分析、材料非线性分析、静力弹塑性分析、动力弹塑性分析。
为能够迅速、准确地完成类似结构的分析和设计的软件。
关键词:曲线梁桥结构设计力分析迈达斯AbtractCurved girder is also called the curved girder bridge, the mechanical characteristics are different from other forms, the outer loads appear crankle coupling, outside the edge of the deflection generally greater than in the edge of the deflection, for curved girder bridge with torsion bearing, bearing reaction force is greater than the inner arc of the outer arc side side bearing reaction force, due to the existence of the torsional support and make the structure is statically indeterminate structure, the structural design and complex than the average in the calculation of internal force of bridge, therefore, in dealing with this kind of problem, can undertake structural stress analysis by finite element software, such as Midas, ansys, bridge, sap2000, etc.MIDAS/Civil is for Civil structures, especially the analysis of prestressed concrete box bridge, suspension bridge, cable-stayed bridge, such as special forms of bridge structure, and can do a nonlinear boundary, hydration heat, the material nonlinear analysis, the static elastoplastic analysis, the dynamic elastic-plastic analysis.To quickly and accurately finishanalysis and design of software of similar structures.Keywords: curve beam bridge structure design, internal force analysis of Midas目录一:设计资料 (4)二:截面及防护栏设计及相关技术参数的确定...................5-6三:五跨曲线梁建模.........................................7-10四:结构力计算...........................................10-263.1 计算结构自重(一期恒载+二期恒载)、整体升温、整体降温作用下的支座反力、主梁力(弯矩、剪力、扭矩)和变形(竖向、扭转)结果;3.2 分别计算边跨跨中、次边跨跨中、中跨跨中及其中间支点截面力(弯矩、剪力、扭矩)影响线(注:分中载、偏和外偏三工况进行计算);3.3 计算公路-I级荷载作用下不同荷载工况下(中载、偏载和外偏载)的弯矩、剪力、扭矩包络图和各支座的支反力包络值;3.4 根据荷载组合原则,计算桥梁结构承载能力极限状态下对应的弯矩、剪力、扭矩包络图和支反力包络值。
连续曲线梁桥设计浅谈
的超高布置方式
曲线梁桥结构受力特点
梁体的弯扭耦合作用 曲梁 在外荷载 的作用下会 同时 产生弯矩和扭矩, 并且互 相影 响, 使梁 截面处 于弯 扭耦合 作 用的状态, 其 截面主拉应 力往 往比 相应的 直梁 桥大得 多, 这 是曲梁独有的受力 特点。曲 线梁 桥由 于受到 强大 的扭矩 作 用, 产生扭 转变形, 其 曲线外 侧的 竖向 挠度大 于同 跨径的 直 桥; 由于弯扭耦合作 用, 在梁端可能出 现翘曲; 当梁端横 桥向 约束较弱时, 梁体有向弯道外侧 “ 爬移” 的趋势 。
结构设计与研究应用 � � � � � 《 四川建材》 年第 期
【文章编号】 : ( ) -
连 续 曲 线 梁 桥 设 计 浅 谈
欧阳尚贤
(佛山市顺德区规划设计院有限公司)
【摘 要】 : 本文 介绍了曲 线桥梁 的受力 特点, 分析了 曲 内 梁和外 梁受力 不均 在曲线 梁桥中, 由于 存在较 大
曲线梁桥的结构设计
直梁桥受 “弯、 剪” 作用, 而曲线 梁桥处 于 “ 弯、 剪、 扭” 的 复合受力状态, 故上 、 下部结构必须构成有利于 抵抗 “ 弯、 剪、 扭” 的措施。 ( ) 曲线梁桥的弯扭刚度比对结构的受力状态和变 形状 态有着直接的关系: 弯扭 刚度 比越 大, 由 曲率 因素 而导致 的 扭转弯形越大, 因 此, 对于曲 线梁 桥而言 在满 足竖 向变形 的 前提下, 应尽可 能减 小抗 弯刚度、 增 大抗扭 刚度。所 以在 曲 线桥梁中, 宜选用 低高度梁和抗扭惯矩较大的箱形截面。 ( ) 在曲线梁桥截 面设计时, 要 在桥跨范 围内 设置一 些 横隔板, 以加强横 桥向刚度并保持全桥稳 定性。在截面 发生 较大变化的位置, 要设渐变段过渡, 减小应力集中效应。 ( ) 在进行配筋设 计时要充 分考虑 扭矩效 应, 弯梁应 在 腹板侧面布置较多受力钢筋, 其截面上下缘钢 筋也比同 等跨 径的直桥多, 且应 配置较多的抗扭箍筋。 ( ) 城市立交桥中的弯箱梁桥中墩多布置成独柱支 承构
预设支座偏心对曲线梁桥的内力影响研究

在恒载的作用下 , 各支座反力列于表 1 从 。 表 中可以看出,支座偏心对端部支座总支反力 影 响较小 , 变化幅度在 6 %以内 , 但可以改变端 明 。 部支座 内外侧支 反力 的分配 , 处支座反力随 z 1 4结论 图 4各截面总弯矩 随支座偏心的 ̄d -意 图5 端部总扭矩随支座偏心的 变化示意 g, T , v 着支座 的偏心距 的增加 而增加 , 处支座反力 z 2 设 置 支 座 则相应的减小 ,所以通过预偏心 可以改善端支 偏心距 , 可改善端部支座内外侧支反力的分配 , 箱 形 M】 京 : 国铁 道 出版 社 ,9814 . _b 中 19 . 5 — 座反力。而 z 的支座反力有所减小 , 3处 但变化 使端部内外侧支座反力趋 于平衡 ,可避免不利 [】 4郭金 琼 . 形 梁桥 设 计 理 论 [ . 京 : 民 交 箱 M] 北 人 幅度不大 , 23 %, 图 2 仅 . 4 见 。端部 内外侧 支座 荷载作 用下支座脱空 ; 同时, 端部支座的反扭矩 通 出版 社 , 9 1 19 . 反力趋 于均衡 , 这有利于支座 的设计 。 随偏心 e的增大呈线性减小趋势。支座偏心对 [】 玲 森 , 线 梁 [ . 京 : 民 交 通 出 版 社 , 5姚 曲 M】 北 人 22剪力 _ 98 剪力的影 响很小 。合理 的偏心距可以使最大扭 1 9. 随着支座偏心 的增加 ,在恒载作用下 , 截 矩等于最小扭矩的绝对值 。预偏心只是内力 的 面的剪力变化很小 ,截 面的总剪力变化 最大 约 重分布, 不能完全消除外扭矩的作用。 为 1% , 图 3 5 见 。 寻找一种确定合适偏心值的公式是非常 困 23弯矩 - 难 的, 但是可以借助计算机 、 用试算的方法确定 随着支座偏心的增加 , 恒载弯矩有微小变 偏心值是非常简单快速 的。 化, 各跨最大正弯矩略有增加 。 — 2 2截面处的弯 参 考 文 献 矩 由 2 2 . N・ 增 大 到 34 . K m,— 『l] 6 99 K m 0 88 N・ 4 4 l, g、 广华, 曲线 梁桥计算. 第一版[ . MI 北京 : 民 人 截 面处 的弯 矩 由 1 1.K m增 大 到 16 . 交 通 出版 社 .99 . 2 54 N・ 5 1 9 1 5 KN・ , 图 4 i见 n 。 『]l 光 , 淦 . 凝 土 弯 梁桥 『 . 京 : 民 交 2g 容  ̄ 夏 混 M1 北 人 2 扭 矩 . 4 通 出版 社 . 9 4 19 . 端部支座 的反扭 矩随偏心距 的增大 呈线 [] 责 任 编 辑 : 依 凡 袁 3黄剑 源. 薄壁结构的扭转分析一 曲线 梁与斜 支
浅谈曲线梁桥设计中应注意的几个问题

浅谈曲线梁桥设计中应注意的几个问题论文导读:近年来,随着我们交通事业和城市建设事业的蓬勃发展,由于受地形、地物的限制等诸多原因,城市立交和公路交叉工程等结构出现弯、坡、斜、异型等特点,曲线梁桥便应运而生。
本文将对曲线梁桥设计中应注意的几个问题进行简要的探讨。
在进行曲线桥梁总体布置时,应考虑到两方面问题:(1)结构受力方面,要注意调整梁内的扭矩分布,控制扭矩峰值,使梁截面以及支座受力较均匀。
关键词:曲线梁桥,设计,问题近年来,随着我们交通事业和城市建设事业的蓬勃发展,由于受地形、地物的限制等诸多原因,城市立交和公路交叉工程等结构出现弯、坡、斜、异型等特点,曲线梁桥便应运而生。
相比于直线梁桥,曲线梁桥对地形地貌的适应性较强。
本文将对曲线梁桥设计中应注意的几个问题进行简要的探讨。
1.总体布置在进行曲线桥梁总体布置时,应考虑到两方面问题:(1)结构受力方面,要注意调整梁内的扭矩分布,控制扭矩峰值,使梁截面以及支座受力较均匀;(2)结构变形方面,要注意控制梁端纵横向变位及翘曲变形。
使之符合规范要求。
要得到这些结果,主要是靠调整跨径划分和处理边界条件。
1.1分孔问题因曲线梁桥其特殊的结构构造,其梁内侧支座反力较小甚至可能出现负值,为了避免可能出现梁端内侧支座脱空现象,可使内侧支座处于受压状态,并考虑给予一定的压力储备。
达到此目的比较有效的方法是控制边跨跨径,使边跨跨径与中跨比较接近。
当受实际条件限制,边跨跨径与中跨差距较大时,也可考虑采取其他一些措施,如调整边跨与中跨的自重等。
1.2支承方式(边界条件)曲线梁桥的支承方式一般分为两种类型:抗扭支承和独柱点铰支承。
其中抗扭支承具有较强的抗扭能力,而独柱点铰支承具有墩位布设灵活的特点。
一般在曲线梁桥的两端常用抗扭支承,此支承方式可有效地提高主梁截面的横向抗扭性能,保证桥梁横向稳定性;此外,在梁桥的中间支承处仅设置一个支座即为独柱点铰支承,这两种支承方式应用均较普遍。
桥梁工程中小半径曲线梁桥的设计要点

桥梁工程中小半径曲线梁桥的设计要点摘要:随着我国城市交通压力的不断增加,大量的高架桥和立交桥被兴建,但是由于城市交通功能的要求和地形环境的诸多限制,这些桥梁多采用的是曲线型构造。
曲线型结构的桥梁受力比较复杂,其中以小半径梁桥最为特别,除了一般的受力外,还要承受扭矩和翘曲双力矩的共同作用,所以小半径曲线梁桥出现的问题较多。
本文就小半径曲线梁桥出现的问题做了相应的说明,并就这些问题进行了深入的探讨并着重说明了设计中要注意的要点。
关键词:桥梁工程;小半径曲线梁桥;设计要点Abstract: Along with the urban traffic increase of pressure, a lot of viaduct and flyovers be built, but because the city traffic function requirements and terrain environment many of the limitations of the Bridges take the form of a curve type structure. The structure of the bridge type curve stress is more complex, among them with small radius of the most special bridge, in addition to the stress of the general, but also bear torque and warp the joint action of double moment, so small radius of the problem of the curved girder Bridges is more. This paper is small radius of the problem of the curved girder Bridges related instructions, and these problems thoroughly discussed and the focus on the design to the main points of attention.Key Words: Bridge engineering; Small radius curve beam bridge; Design key points of the小半径曲线梁桥,虽说在现实生活中有了很广泛的应用,但是由于其承载量,预应力及温差引起的弯矩、扭矩等作用力的受力较复杂,因此很容易产生设计考虑不全面,支座脱空、移位甚至崩塌的问题,给人民生命财产安全带来了极大的隐患。
自重作用下曲线连续刚构桥扭转效应初探

Ab ta t Ba e nac niu u uv dbig n t emeh do f t lm e t r c d r ia ii, rd esmulto d li etbih d By s rc : sdo o t o sc r e r ea dwi t to f mieee n o e ueM d s vlab g i n d hh p c i ainmo e s sa lse . c a gn uv a isa d a ay ig te b a c noron wi ifrn uv du n t e sle C I erdu u ifrn irh ihs o h n ig c rer du n lzn h e m o t t t d fee tc rer isa d wi t an H V isb td f e tpe eg t,s me n i h a h h a e
2 1.O 8第 1 卷 总 第 1 6 02 . N 1 0 期
d i1 .9 9 i n1 7 - 1 72 1 .80 1 o 03 6 4.s 6 1 9 0 0 20 .4 s
道桥工程 4 1
自重 作 用 下 曲线 连 续 刚构 桥 扭 转效 应 初 探
On T ri n l f c f Co t u u u v d Br g n e e f a i o so a e t n i o sC r e i eu d rS l Gr vt Ef o n d - y
半径 为 2 0 4 0 8 0 、 5 0 0 m、 0 m、 0 m 2 0 m的 直 线 桥 的有 限 元 仿真 模
型 .用 以分 析 随 着 曲 率半 径 的变 化 .对 刚构 桥 扭 转 效 应 的 影 响 。 文 中所 涉 及 的 模 型 上部 结 构 和 下 部 结 构 共被 划 分 成 16 论 3 个单 元 .其 中8 个 单 元为 上部 结 构 单 元 . 8 单 元 为 下 部 单 8 4个 元 。 当 曲线 半 径 一定 时 ( 2 0 以 0 m曲线 半 径 为例 )本 文 分 析 了 ,
小半径曲线桥梁设计要点探析

小半径曲线桥梁设计要点探析一、小半径曲线桥梁的结构受力特点小半径曲线桥梁由于主梁的平面弯曲使得下部结构墩柱的支承点不在同一条直线上,形成了其独有的受力特点:(1)主梁受曲率影响,梁截面发生竖向弯曲的同时会产生扭转,而产生的弯矩和扭矩相互影响,使梁处于弯扭耦合状态;(2)由于弯扭耦合作用,弯桥的变形比同跨径的直桥要大,主梁外边缘的挠度大于内边缘的,而且曲率半径越小,桥越宽,这一趋势越明显。
同时在梁端可能出现翘曲,当梁端横桥向约束较弱时,梁体有向弯道外侧“爬移”的趋势;(3)曲线桥梁上汽车荷载的偏心布置及其行驶时的离心力,也会造成曲线梁桥向外偏转并增加主梁扭矩和扭转变形。
另外,曲线桥梁即使在对称荷载作用下也会产生较大的扭矩,该扭矩通常会使得外梁超载,内梁卸载;(4)主梁的扭转传递到梁端部时,会造成端部各支座横向受力分布严重不均,通常呈曲线外侧支反力变大,内侧变小的趋势,有时内侧支座甚至会出现负反力。
(5)曲线桥的中横梁是保持全桥稳定的重要构件,与直线桥相比,其刚度一般较大。
(6)采用连续梁体系的曲线桥,预应力效应对支反力的分配有较大的影响,在计算支座反力时必须考虑预应力效应的影响。
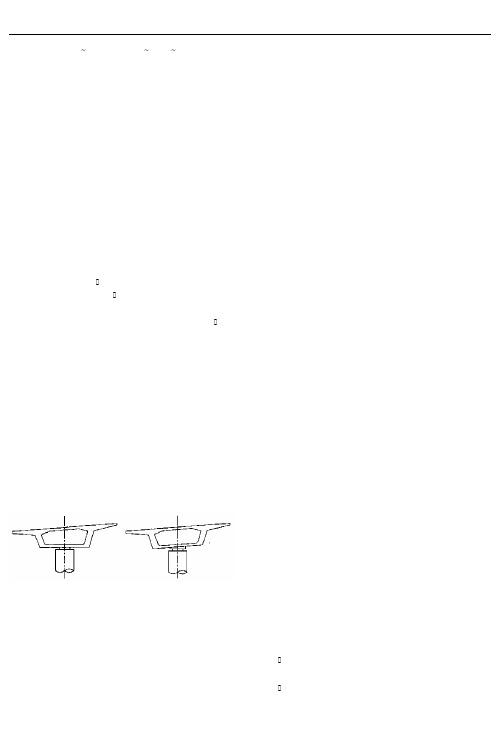
二、小半径曲线桥梁的设计要点(一)小半径曲线桥梁支座的布置形式曲线箱梁桥支座的布置型式通常采用三种形式(如下图):a. 全部采用抗扭支承, b. 两端设置抗扭支承,中间设单支点铰支承,c.两端设置抗扭支承,中间既有单支点铰支承,又有抗扭支承的混合式支承。
近年来,在曲线箱梁桥工程实际应用中,两端为抗扭支座(双支座),联内安置几个单点铰支座,即中支点下部采用独柱支承的曲线桥多次发生侧倾事故。
其主要原因多为主梁在偏心荷载作用下发生扭转,当转角大到一定程度时,支反力的下滑分力将超过支座侧向的约束能力,扭矩将全部转移到梁端造成曲线内侧支座脱空,主梁发生倾覆。
所以此类支座布置的形式在工程应用中已不多见。
对于小半径的曲线箱梁,通常全部采用抗扭支承。
曲线桥设计思路

曲线桥设计思路一、概要目前白线箱梁桥在现代化的公路及城市道路立交中的数量逐年增加,应用已非常普遍。
尤其在互通式立交的匝道桥设计中应用更为广泛。
因预应力混凝土白线箱梁具有较大的抗扭刚度、较好的适应地形地物、线条平顺流畅等优点。
在公路立交及城市高架桥的曲线桥上得到了广泛的应用。
但由线箱梁作为一种空问结构,在荷载、预应力、温度徐变中等产生的弯矩、担矩、剪力、轴力及二次矩等作用下受力十分复杂,千艮难直接计算,若设计考虑不周,会发生支座脱空、移位、崩脱等事故,导致在工程施工结束后不久就需要进行加固维修,造成不良的社会影响。
据有关报道,深圳市40座立交桥中,有19座立交桥存在大小不同的问题。
产生问题的原因是多方面的,有的在连续梁曲线内侧端支座脱空:有的白线梁体向由线外侧径向整体侧移:有的墩梁固结处在立柱顶部(与梁底街接处)产生水平环形裂缝等危及桥梁正常使用的现象。
但总的来说届于在探索和设计过程中认识不足和尚未认识的天误。
国此针对小半径曲线梁桥进行设计分析。
对工程设计和施工都具有很大的意义。
二、曲线梁桥结构受力特点2.1预应力混凝土曲线箱梁中的扭矩众所周知,白线梁与直线梁的主要区别在于曲线梁具有如下特征:外缘弯由应力大于内缘弯由应力;2)外缘挠度大于内缘挠度,且随着自率半径的减小,挠度差不断增大;3)无论采用何种支座布置方案,曲线梁内总存在扭矩;4)各主梁恒载内力不均匀,因此,曲线梁总是处于弯、扭耦合的受力状态下。
对于非预应力白线箱梁,恒载产生的扭矩主要白内外缘目重差异引起: 对于预应力曲线箱梁,除了内外缘自重差异产生扭矩外,预应力钢束在空间方向的分布对于剪心(即扭转中心)会产生很大的力矩,且为主要扭矩。
钢束在箱梁的腹板中有若十个上弯白和下弯白,同时在水平方向还有一个大弯曲。
底板内的钢束主要为水子面内的弯由。
考虑到中腹板内钢束向上的竖直分力与剪心的力矩基本平衡,而向弯白中心方向的分力对梁体有一个逆时针方向的根矩,底板钢束产生逆时针方向的扭矩,腹板中钢束水平分力产生了顺时针方向的扭矩,因此在支座附近由钢束产生的扭矩要远小于跨中部分的扭矩。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
曲线桥梁的自重和内外侧扭矩
本文将探讨曲线桥梁的自重和内外侧扭矩的相关概念和计算方法。
我们将
首先介绍曲线桥梁的基本结构和工作原理,然后详细讨论自重和内外侧扭
矩的计算方法,并给出实际案例进行说明。
1. 曲线桥梁的基本结构和工作原理
曲线桥梁是一种在曲线轨道上搭建的桥梁结构,用于跨越地形的高低起伏或河流等障碍物。
它通常由桥墩、梁体和支座等组成。
桥墩是支撑梁体的垂直结构,通常由混凝土或钢材制成。
梁体是曲线桥梁的主要承载构件,承担车辆荷载和自重等作用。
支座则用于连接桥墩和梁体,使其能够自由伸缩和旋转,以适应曲线轨道的变化。
曲线桥梁的工作原理是通过将车辆荷载传递到桥墩上,再由桥墩通过支座传递到梁体上,最终通过梁体将荷载分散到地基上。
在曲线轨道上,由于曲率的存在,梁体会受到额外的内外侧扭矩作用。
2. 曲线桥梁的自重计算方法
曲线桥梁的自重是指桥梁本身所受到的重力作用。
为了确保桥梁的安全性和稳定性,需要对其自重进行准确的计算。
自重计算通常分为以下几个步骤:
2.1 确定桥梁结构参数
首先需要确定桥梁的结构参数,包括梁体的几何形状、材料属性和荷载标准等。
这些参数将直接影响到自重的计算结果。
2.2 计算梁体的体积
根据桥梁的几何形状,可以计算出梁体的体积。
对于简单的矩形梁体,可以使用基本几何公式进行计算;对于复杂的曲线梁体,可以使用数值积分或离散化方法进行近似计算。
2.3 估算梁体的材料密度
根据梁体所采用的材料类型和密度,可以估算出梁体的总质量。
常用的桥梁材料有混凝土、钢材和预应力混凝土等,它们的密度可以通过实验或文献资料获取。
2.4 计算梁体的自重
最后,将梁体的体积乘以材料的密度,即可得到梁体的自重。
自重的单位通常为牛顿或千克,可以根据需要进行单位转换。
3. 曲线桥梁的内外侧扭矩计算方法
曲线桥梁在曲线轨道上运行时,会受到内外侧扭矩的作用。
内侧扭矩是指桥梁在曲线内侧受到的扭矩作用,外侧扭矩则相反。
内外侧扭矩的计算方法如下:
3.1 确定曲线半径和车辆参数
首先需要确定曲线的半径和车辆的参数。
曲线半径是曲线的圆心到曲线轨道中心线的距离,车辆参数包括车辆的质量、速度和轨道半径等。
3.2 计算内外侧加速度
根据车辆的速度和曲线半径,可以计算出车辆在曲线上的内外侧加速度。
加速度的计算可以使用几何关系或动力学模型进行。
3.3 计算内外侧扭矩
根据内外侧加速度和车辆的质量,可以计算出内外侧扭矩。
内侧扭矩是由于离心力和摩擦力的作用而产生的,外侧扭矩则相反。
3.4 考虑桥梁的刚度和支座的特性
最后,需要考虑桥梁的刚度和支座的特性对内外侧扭矩的影响。
桥梁的刚度会影响扭矩的传递和分配,支座的特性则会影响扭矩的传递和桥梁的变形。
4. 实际案例分析
下面以一座具体的曲线桥梁为例,进行自重和内外侧扭矩的计算和分析。
4.1 桥梁结构参数
假设该曲线桥梁的梁体为矩形截面,长为20米,宽为3米,高为1.5米。
材料为混凝土,密度为2400千克/立方米。
4.2 自重计算
根据梁体的几何形状和材料密度,可以计算出梁体的体积为90立方米。
将体积乘以材料密度,即可得到梁体的自重为216000牛顿。
4.3 内外侧扭矩计算
假设曲线半径为100米,车辆质量为5000千克,速度为30米/秒。
根据几何关系和动力学模型,可以计算出内外侧加速度分别为2.7米/秒2和0.9米/秒2。
将加速度乘以车辆质量,即可得到内外侧扭矩分别为13500牛顿米和4500牛顿米。
4.4 桥梁刚度和支座特性的影响
考虑到桥梁的刚度和支座的特性,内外侧扭矩可能会产生额外的变形和反力。
这些影响需要通过详细的结构分析和计算来确定。
结论
本文介绍了曲线桥梁的自重和内外侧扭矩的计算方法,并以一个实际案例进行了分析。
自重和内外侧扭矩的准确计算对于桥梁的设计和施工具有重要意义,可以保证桥梁的安全性和稳定性。
在实际工程中,还需要考虑其他因素的影响,如温度变化、风荷载等,以进一步完善计算结果。
参考文献:
[1] 张三, 李四. 曲线桥梁设计手册. 北京:人民交通出版社,2010.
[2] 中国桥梁设计规范. GB 50010-2010. 北京:中国建筑工业出版社,2010.。
