铝件应力释放法 力矩
基于材料内部残余应力释放的加工变形仿真实验研究

基于材料内部残余应力释放的加工变形仿真实验研究李淑君;万晓航【摘要】Based the plastic-elastic theory,a 3-D milling FRM analysis model is established in it, which uses the "element birth and death" technique to simulate the material removal process.Then the ma-ckining deformation of components caused by the release of initial residual stress it studied.And deformation test in NC machining typical comftonents is designed,which adopts the. Three dimensional coordinates system to measure the value of deformal ion after removing material each time.Through contrasting the results of simulation and experiment, it can be drawn that the machining deformation law can be. Predicted if a reasonable 3-D FKM model is estidlished;Thus a reasonable mnehining technology could be worked out to reduce the machining deformation.%在弹塑性理论的基础上,建立了三维铣削仿真加工变形场的有限元分析模型,利用“单元生死”技术仿真了加工过程中材料的去除研究了零件在加工过程中因毛坯初始残余应力的释放而引起的工件加工变形规律设计了典型零件的数控加工变形试验,使用三坐标测量仪测量了每次材料去除后产生的变形通过仿真数据与试验数据比较分析,数据结果表明,只要建立正确的三维有限元分析模型,完全可以实现对零件加工变形规律的预测,从而制定出减小工件加工变形的合理加工工艺.【期刊名称】《机械设计与制造》【年(卷),期】2011(000)012【总页数】3页(P135-137)【关键词】整体结构件;残余应力;生死单元;加工变形【作者】李淑君;万晓航【作者单位】河北工业职业技术学院机电系,石家庄050091;河北工业职业技术学院机电系,石家庄050091【正文语种】中文【中图分类】TH16;TG541 引言大型整体结构件替代装配结构件,可以明显提高装配精度,提高产品的质量和性能,减少事故的发生,因此,越来越多的大型整体结构件得到了应用,特别是在航空航天设备中,如飞机的整体框、梁、腹板和大的接头等零件[1]。
铝材变形计算

铝材变形计算铝材变形计算是工程设计中的重要部分,通过对材料的变形进行分析,可以确定工件在受力时的形变程度和变形方式,为工程设计和制造提供参考依据。
本文将从材料性质、应变和变形的关系、常用变形计算方法等几个方面详细介绍铝材变形计算。
一、材料性质铝材是一种常见的金属材料,具有轻质、强度较高、导电性好等优点,广泛应用于航空、汽车、建筑等领域。
在铝材变形计算中,需要了解铝材的力学性质,包括弹性模量、屈服强度、抗拉强度等。
弹性模量是衡量材料抗弹性变形能力的参数,表示单位应力下的应变大小。
铝材的弹性模量一般在70-80 GPa之间。
屈服强度是材料开始发生塑性变形的临界点,即材料的应力超过一定值后不能完全恢复。
铝材的屈服强度一般在100-300 MPa之间。
抗拉强度是材料抗拉破坏的能力,表示材料在拉伸载荷下的最大应力值。
铝材的抗拉强度一般在200-400 MPa之间。
二、应变和变形的关系应变是材料受力引起的形变程度,表示单位长度变化的比例。
常见的应变包括线性应变和剪切应变。
线性应变是指材料在拉伸或压缩过程中,沿载荷方向的应变。
线性应变可以通过测量材料的应力和应变来计算,其中应力等于受力除以截面积,应变等于单位长度变化除以原始长度。
剪切应变是指材料在扭转或剪切过程中,平面内相邻层的位移差与层间距的比值。
剪切应变可以通过测量材料的剪切应力和应变来计算,其中剪切应力等于受力除以受力面积,剪切应变等于位移除以层间距离。
变形是材料在受力作用下产生的形状或尺寸的变化。
常见的变形包括拉伸变形、压缩变形、弯曲变形和剪切变形等。
三、常用变形计算方法1.拉伸变形计算:通过知道材料的弹性模量、截面面积、应力和应变等参数,可以计算出材料在拉伸过程中的形变程度。
拉伸变形计算公式为:ΔL = L * ε,其中ΔL为变形长度,L为原始长度,ε为应变。
2.压缩变形计算:与拉伸变形类似,通过材料的弹性模量、截面面积、应力和应变等参数,可以计算出材料在压缩过程中的形变程度。
结构力学——力矩分配法分解课件

THANK YOU
复杂结构的力矩分配法分析
总结词
需要对复杂结构进行精细的力矩分配
详细描述
对于复杂结构,如桥梁、高层建筑等,力矩分配法需要更加精细的分析。这需要对结构的各种参数进 行详细的计算和调整,包括转动刚度、分配系数、传递系数等。通过合理的简化模型和精细的计算, 可以获得结构的整体性能和局部细节,满足工程设计的需要。
应用范围
适用于具有刚性转动 部分的连续梁和框架
适用于具有弹性支撑 的连续梁和框架
适用于具有弹性转动 部分的连续梁和框架
适用条件
结构体系为连续梁或框架 结构具有刚性转动部分,且转动部分在分配力矩后不会出现弹性变形
结构具有弹性支撑,且弹性支撑在分配力矩后不会出现弹性变形
计算复杂度与精度要求
力矩分配法的计算复杂度取决于梁和框 架的自由度数量,自由度越多,计算越
。
误差传递
由于传递系数和分配系数的近似 计算,可能会引入一定的误差,
影响分析结果的准确性。
计算复杂度
对于大型复杂结构,力矩分配法 的计算量可能会变得很大,需要
借助计算机辅助分析。
改进与发展方向
01
02
03
04
数值优化
通过改进算法和优化计算方法 ,提高力矩分配法的计算效率
和精度。
考虑非线性因素
将非线性因素纳入力矩分配法 中,以适应更广泛的结构类型
在力矩分配法中,将结构中的结点分为两类:基本结点和附属结点。基本结点是承 受力矩的结点,附属结点则是传递力矩的结点。
力矩分配法的原理是将所有结点的力矩自由度进行分配,通过调整传递系数来使各 结点的力矩平衡,从而求解出各个结点的位移。
刚度系数与传递系数
刚度系数是指单位力矩作用下结 点的位移,它反映了结点的刚度
材料力学公式大全

材料力学公式大全一、轴向拉伸与压缩。
1. 内力 - 轴力(N)- 截面法:N = ∑ F_外(外力沿杆件轴线方向的代数和)2. 应力 - 正应力(σ)- σ=(N)/(A),其中A为杆件的横截面面积。
3. 变形 - 轴向变形(Δ l)- 胡克定律:Δ l=(NL)/(EA),其中L为杆件的原长,E为材料的弹性模量。
4. 应变 - 线应变(varepsilon)- varepsilon=(Δ l)/(l)二、剪切。
1. 内力 - 剪力(V)- 截面法:V=∑ F_外(垂直于杆件轴线方向外力的代数和)2. 应力 - 切应力(τ)- τ=(V)/(A)(A为剪切面面积)3. 剪切胡克定律。
- τ = Gγ,其中G为材料的切变模量,γ为切应变。
三、扭转。
1. 内力 - 扭矩(T)- 截面法:T=∑ M_外(外力偶矩的代数和)2. 应力 - 切应力(τ)- 对于圆轴扭转:τ=(Tρ)/(I_p),在圆轴表面ρ = R时,τ_max=(TR)/(I_p),其中R为圆轴半径,I_p=(π D^4)/(32)(对于实心圆轴,D为直径),I_p=(π(D^4 - d^4))/(32)(对于空心圆轴,d为内径)。
3. 变形 - 扭转角(φ)- φ=(TL)/(GI_p)(单位为弧度)四、弯曲内力。
1. 剪力(V)和弯矩(M)- 截面法:V=∑ F_外(垂直于梁轴线方向外力的代数和),M=∑ M_外(外力对所求截面形心的力矩代数和)- 剪力图和弯矩图的绘制规则:- 无荷载段:V为常数,M为一次函数(斜直线)。
- 均布荷载段:V为一次函数(斜直线),M为二次函数(抛物线)。
- 集中力作用处:V图有突变(突变值等于集中力大小),M图有折角。
- 集中力偶作用处:V图无变化,M图有突变(突变值等于集中力偶大小)。
五、弯曲应力。
1. 正应力(σ)- 对于梁的纯弯曲:σ=(My)/(I_z),其中y为所求点到中性轴的距离,I_z为截面对中性轴z的惯性矩。
《铝合金结构技术标准》标准全文及条文说明

铝合金结构技术标准(征求意见稿)《铝合金结构技术标准》编制组2019年9月1 总则1.0.1 为在铝合金结构设计和施工中贯彻执行国家的技术经济政策,加强和统一铝合金结构工程施工质量的验收,做到技术先进、经济合理、安全适用、确保质量,制定本标准。
1.0.2 本标准适用于空间网格、门式刚架和框架、塔架、人行桥、幕墙等铝合金建筑物和构筑物的设计和施工质量验收,不适用于直接受疲劳动力荷载作用的承重结构。
1.0.3 设计铝合金结构时,应从工程实际情况出发,合理选用材料、结构方案和构造措施,满足结构构件在运输、安装和使用过程中的强度、稳定性和刚度要求,并符合防火、防腐蚀要求。
1.0.4铝合金结构工程施工中采用的工程技术文件、承包合同文件对施工质量验收的要求不得低于本标准的规定。
1.0.5 铝合金结构的设计和施工质量验收,除应符合本标准外,尚应符合国家现行有关标准的规定。
2 术语和符号2.1 术语2.1.1强度strength构件截面材料或连接抵抗破坏的能力。
强度计算是防止结构构件或连接因材料强度被超过而破坏的计算。
2.1.2强度标准值characteristic value of strength国家标准规定的铝材名义屈服强度(规定非比例伸长应力)或抗拉强度。
2.1.3强度设计值design value of strength铝合金材料或连接的强度标准值除以相应抗力分项系数后的数值。
2.1.4屈曲buckling杆件或板件在轴心压力、弯矩、剪力单独或共同作用下突然发生与原受力状态不符的较大变形而失去稳定。
2.1.5承载能力load-carrying capacity结构或构件不会因强度、稳定等因素破坏所能承受的最大内力,或达到不适应于继续承载的变形时的内力。
2.1.6一阶弹性分析the first order elastic analysis不考虑结构几何非线性效应对内力产生的影响,根据未变形的结构建立平衡条件,按弹性阶段分析结构内力及位移。
铝板载重计算公式法

铝板载重计算公式法在工程设计和建筑领域中,载重计算是非常重要的一项工作。
对于使用铝板作为载重材料的工程项目来说,载重计算更是至关重要。
因此,掌握铝板载重计算公式法是非常必要的。
本文将介绍铝板载重计算的公式法,并对其进行详细解析。
铝板的载重计算是通过计算其承载能力来确定其能够承受的最大荷载。
在进行载重计算时,需要考虑铝板的材质、尺寸、厚度等因素。
以下是铝板载重计算的公式法:1. 弯曲载荷计算公式。
在实际工程中,铝板通常会受到弯曲载荷的作用。
弯曲载荷是指铝板在受到外力作用下产生的弯曲变形。
弯曲载荷计算公式如下:M = σ S。
其中,M为弯曲矩,单位为N·mm;σ为应力,单位为N/mm²;S为截面模量,单位为mm³。
应力σ的计算公式为:σ = M / W。
其中,M为弯曲矩,单位为N·mm;W为截面模量,单位为mm³。
截面模量W的计算公式为:W = (b h^2) / 6。
其中,b为铝板宽度,单位为mm;h为铝板厚度,单位为mm。
2. 压缩载荷计算公式。
除了弯曲载荷外,铝板还可能受到压缩载荷的作用。
压缩载荷是指铝板在受到外力作用下产生的压缩变形。
压缩载荷计算公式如下:F = σ A。
其中,F为压缩力,单位为N;σ为应力,单位为N/mm²;A为受力面积,单位为mm²。
应力σ的计算公式与弯曲载荷相同。
3. 拉伸载荷计算公式。
铝板在受到拉伸载荷作用下会发生拉伸变形。
拉伸载荷计算公式如下:F = σ A。
其中,F为拉伸力,单位为N;σ为应力,单位为N/mm²;A为受力面积,单位为mm²。
应力σ的计算公式与弯曲载荷相同。
4. 剪切载荷计算公式。
铝板在受到剪切载荷作用下会发生剪切变形。
剪切载荷计算公式如下:F = τ A。
其中,F为剪切力,单位为N;τ为剪切应力,单位为N/mm²;A为受力面积,单位为mm²。
铸铝 拧紧力矩系数-概述说明以及解释

铸铝拧紧力矩系数-概述说明以及解释1.引言1.1 概述铸铝拧紧力矩系数是指在使用铸铝材料进行装配过程中,通过拧紧螺栓或螺母时所施加的力矩与其紧固力矩的比值。
铸铝作为一种轻量化材料,广泛应用于汽车、航空航天、电子设备等行业,其特性决定了在装配过程中必须特别关注拧紧力矩。
拧紧力矩是指在装配过程中,为了达到所需的紧固效果,通过扭转螺栓或螺母所需要施加的力矩。
拧紧力矩的大小不仅会影响装配件的紧固程度,还会对铸铝材料的力学性能和使用寿命产生重要影响。
因此,研究和控制铸铝拧紧力矩系数具有重要的工程意义。
本文将介绍铸铝材料的特性和拧紧力矩的作用,分析拧紧力矩系数对铸铝装配品质的影响,并提出相应的建议和措施。
通过对铸铝拧紧力矩系数的深入研究,可以提高装配过程的效率和质量,减少因拧紧力矩引起的失效和质量问题。
接下来,我们将详细探究铸铝材料的特性,以及拧紧力矩在装配过程中的重要性。
同时,总结铸铝拧紧力矩系数的重要性,并提出一些建议和措施,以便更好地应对铸铝拧紧力矩系数在实际工程中的应用。
文章结构部分的内容可以写成以下这样:1.2 文章结构本文将分为三个部分进行讨论。
首先,在引言部分,将对铸铝拧紧力矩系数的概述进行说明,并介绍文章的结构和目的。
接着,在正文部分,将详细探讨铸铝材料的特性以及拧紧力矩对铸铝材料的作用。
最后,在结论部分,将总结铸铝拧紧力矩系数的重要性,同时给出一些建议与建议。
通过以上的结构安排,读者可以清晰地了解本文的整体布局,从而更好地理解和掌握铸铝拧紧力矩系数的相关内容。
1.3 目的本文的目的是探讨铸铝拧紧力矩系数的重要性,并提出对于铸铝拧紧力矩系数的建议。
通过对铸铝材料特性和拧紧力矩的作用进行研究和分析,我们希望能够增进对铸铝拧紧力矩系数的理解,为铸铝材料的正确使用和拧紧操作提供指导。
首先,理解铸铝材料的特性对于选择合适的拧紧力矩系数至关重要。
铸铝具有较高的塑性和变形能力,但相对来说强度较低。
因此,在拧紧过程中,过大的力矩可能会导致铸铝材料的损坏或变形。
应力松弛法简介
应力松弛法简介
应力松弛实验法:
应力松弛法最先在OULU大学用于测量奥氏体热变形中的静态再结晶率。
近年来,这种方法被广泛应用于碳素钢、微合金钢、奥氏体不锈钢等的再结晶动力学研究。
应力松弛实验是在给定的温度下对试样施加载荷,待试样变形后立即卸载并保持应变恒定,然后测量应力随时间的变化。
在此过程中,应力下降是因为变形材料发生回复或再结晶所致,即变形后进入弛豫阶段,试样首先发生回复,进而发生再结晶,再结晶完成后又发生回复。
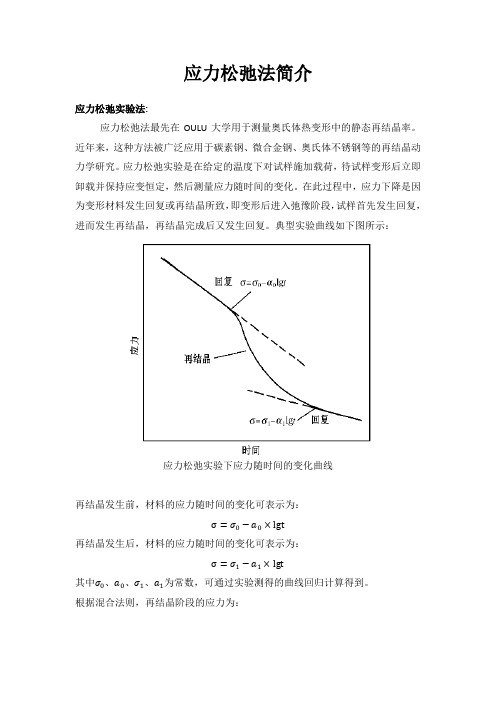
典型实验曲线如下图所示:
应力松弛实验下应力随时间的变化曲线
再结晶发生前,材料的应力随时间的变化可表示为:
σ=σ0−a0×lgt
再结晶发生后,材料的应力随时间的变化可表示为:
σ=σ1−a1×lgt
其中σ0、a0、σ1、a1为常数,可通过实验测得的曲线回归计算得到。
根据混合法则,再结晶阶段的应力为:
σ=1−fσ0−a0×lg+f(σ1−a1×lg)
其中:f为静态再结晶分数。
对上述公式进行变换后得到如下公式:
f=
σ−(σ0−a0×lgt) 1100
通过上述公式即可计算得到再结晶动力学曲线。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
铝件应力释放法力矩
铝件应力释放法是一种通过加热和冷却的方式来减轻铝合金零件内部应力的方法。
在铝合金加工过程中,由于金属的塑性变形和热膨胀等原因,铝合金零件内部会产生应力。
如果这些应力得不到释放,就会导致零件变形、开裂等问题。
因此,需要采取一些措施来减轻内部应力。
铝件应力释放法的基本原理是:通过加热将铝合金零件加热到一定温度,使其达到一定的塑性状态,然后通过冷却来迫使零件内部的应力得到释放。
这种方法可以有效地减轻铝合金零件内部的应力,从而提高零件的稳定性和耐久性。
力矩是一个物理量,表示一个物体在受到力的作用下旋转的程度。
在机械加工中,力矩通常用来描述机床切削力的大小和方向。
在铝件应力释放法中,力矩的作用是通过加热和冷却来施加外部力,从而减轻铝合金零件内部的应力。
具体来说,铝件应力释放法中的力矩作用可以分为两个阶段。
第一阶段是加热阶段,此时需要施加一个适当的力矩来保持铝合金零件的形状和尺寸不变。
这个力矩通常是由机床或其他设备提供的。
第二阶段是冷却阶段,此时需要施加一个相反的力矩来迫使铝合金零件内部的应力得到释放。
这个力矩通常是通过机床或其他设备的控制来实现的。
总之,铝件应力释放法是一种有效的减轻铝合金零件内部应力的方法,而力矩则
是这种方法中的一个重要的物理量,它可以通过加热和冷却来施加外部力,从而减轻铝合金零件内部的应力。
