11.2_全等三角形的判定(SSS)同步练习
人教版八年级数学上册同步练习题及答案+八年级数学下册同步练习题及答案

人教版八年级数学上册同步练习题及答案+八年级数学下册同步练习题及答案人教八年级数学上册同步练习题及答案第十一章全等三角形11.1全等三角形1、已知⊿ABC≌⊿DEF,A与D,B与E分别是对应顶点,∠A=52°,∠B=67 °,BC =15cm,= ,FE = .则F2、∵△ABC≌△DEF∴AB= ,AC= BC= ,(全等三角形的对应边)∠A= ,∠B= ,∠C= ;(全等三角形的对应边)3、下列说法正确的是()A:全等三角形是指形状相同的两个三角形 B:全等三角形的周长和面积分别相等C:全等三角形是指面积相等的两个三角形 D:所有的等边三角形都是全等三角形4、如图1:ΔABE≌ΔACD,AB=8cm,AD=5cm,∠A=60°,∠B=40°,则AE=_____,∠C=____。
C课堂练习1、已知△ABC ≌△CDB ,AB 与CD 是对应边,那么AD= ,∠A= ;2、如图,已知△ABE ≌△DCE ,AE=2cm ,BE=1.5cm ,∠A=25°∠B=48°; 那么DE= cm ,EC= cm ,∠C= 度.3、如图,△ABC ≌△DBC ,∠A=800,∠ABC=300,则∠DCB= 度;(第1小题) (第2小题) (第3小题) (第4小题)4、如图,若△ABC ≌△ADE ,则对应角有 ; 对应边有 (各写一对即可);11.2.1全等三角形的判定(sss )课前练习1、如图1:AB=AC ,BD=CD ,若∠B=28°则∠C= ;2、如图2:△EDF ≌△BAC ,EC=6㎝,则BF= ;3、如图,AB ∥EF ∥DC ,∠ABC =900,AB =DC ,那么图中有全等三角形 对。
第2题图EDCBA(第1小题) (第2小题) (第3小题)课堂练习4、如图,在△ABC 中,∠C =900,BC =40,AD 是∠BAC 的平分线交BC 于D ,且DC ∶DB =3∶5,则点D 到AB 的距离是 。
全等三角形的判定精选练习题(分SSS、SAS、AAS、ASA、HL分专题)
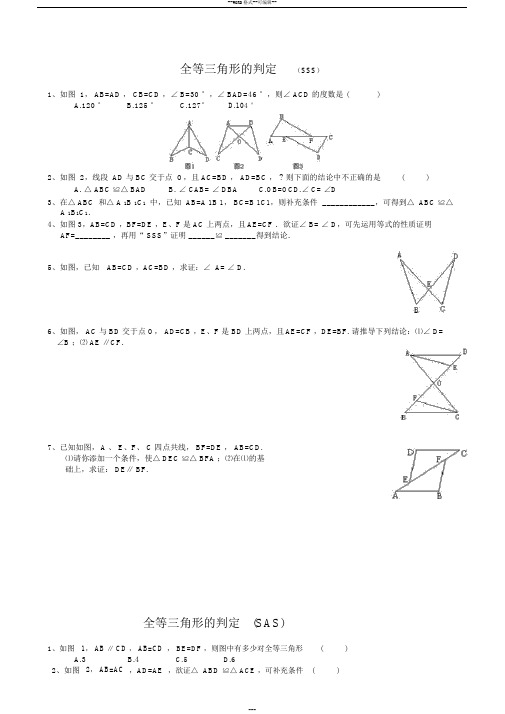
全等三角形的判定(SSS)1、如图 1, AB=AD , CB=CD ,∠ B=30 °,∠ BAD=46 °,则∠ ACD 的度数是 ()A.120 °B.125 °C.127°D.104 °2、如图 2,线段 AD 与 BC 交于点 O,且 AC=BD , AD=BC , ? 则下面的结论中不正确的是()A. △ ABC ≌△ BADB. ∠ CAB= ∠ DBAC.OB=OCD.∠ C= ∠D3、在△ ABC 和△ A 1B 1C1中,已知 AB=A 1B 1, BC=B 1C1,则补充条件 ____________,可得到△ ABC ≌△A 1B1C1.4、如图 3,AB=CD ,BF=DE ,E、F 是 AC 上两点,且AE=CF .欲证∠ B= ∠ D,可先运用等式的性质证明AF=________ ,再用“ SSS”证明 ______≌ _______得到结论.5、如图,已知AB=CD ,AC=BD ,求证:∠ A= ∠ D.6、如图, AC 与 BD 交于点 O, AD=CB ,E、F 是 BD 上两点,且AE=CF ,DE=BF. 请推导下列结论:⑴∠ D=∠B ;⑵ AE ∥CF.7、已知如图,A 、 E、F、 C 四点共线, BF=DE , AB=CD.⑴请你添加一个条件,使△ DEC ≌△ BFA ;⑵在⑴的基础上,求证: DE∥ BF.全等三角形的判定(SAS)1、如图1, AB ∥ CD , AB=CD, BE=DF ,则图中有多少对全等三角形()A.3B.4C.5D.62、如图2, AB=AC,AD=AE,欲证△ABD≌△ ACE ,可补充条件()A. ∠ 1= ∠23、如图 3, AD=BCA.AB ∥ CDB.∠ B= ∠ C,要得到△ ABDB.AD ∥ BCC.∠ D= ∠ ED. ∠BAE= ∠CAD 和△CDB 全等,可以添加的条件是 ( C.∠A=∠ C D. ∠ABC= ∠ CDA)4、如图 4, AB 与 CD 交于点 O, OA=OC , OD=OB ,∠ AOD=________ , ? 根据 _________可得到△ AOD≌△ COB,从而可以得到AD=_________ .5、如图 5,已知△ ABC 中, AB=AC , AD 平分∠ BAC ,请补充完整过程说明△∵ AD 平分∠ BAC ,∴∠ ________=∠ _________(角平分线的定义).在△ ABD 和△ ACD 中,∵ ____________________________ ,∴△ ABD≌△ ACD(ABD)≌△ ACD的理由.6、如图 6,已知 AB=AD , AC=AE ,∠ 1= ∠ 2,求证∠ ADE= ∠ B.7、如图,已知AB=AD ,若 AC 平分∠ BAD ,问 AC 是否平分∠ BCD ?为什么?BA CD8、如图,在△ABC 和△ DEF 中, B 、 E、 F、 C,在同一直线上,下面有 4 个条件,请你在其中选 3 个作为题设,余下的一个作为结论,写一个真命题,并加以证明.①AB=DE ;② AC=DF ;③∠ ABC= ∠ DEF ;④ BE=CF.9、如图⑴, AB ⊥ BD , DE⊥ BD ,点 C 是 BD 上一点,且BC=DE , CD=AB .⑴试判断AC 与 CE 的位置关系,并说明理由.⑵如图⑵,若把△CDE 沿直线 BD 向左平移,使△CDE 的顶点 C 与 B 重合,此时第⑴问中的位置关系还成立吗?(注意字母的变化)AC与BE全等三角形(三) AAS和 ASA【知识要点】1.角边角定理( ASA):有两角及其夹边对应相等的两个三角形全等.2 .角角边定理( AAS):有两角和其中一角的对边对应相等的两个三角形全等.【典型例题】例 1.如图, AB∥ CD, AE=CF,求证: AB=CDD FC O例 2.如图,已知: AD=AE,ACD ABE ,求证:BD=CE.AE BAD E例 3.如图,已知:CD . BAC ABD ,求证:OC=OD.B CD COA B例 4.如图已知: AB=CD,AD=BC,O是 BD中点,过 O点的直线分别交DA和 BC的延长线于E,F. 求证: AE=CF.FDCOAB例 5.如图,已知123 ,AB=AD.求证:BC=DE.EA2E1OB D 3C例6.如图,已知四边形 ABCD中, AB=DC,AD=BC,点 F 在 AD 上,点 E 在 BC上, AF=CE, EF 的对角线 BD 交于 O,请问 O点有何特征?A F DOB EC【经典练习】1. △ ABC和△A B C中,A A' , BC B C ,C C 则△ABC与△ A B C.2.如图,点 C,F 在 BE上,12, BC EF ,请补充一个条件,使△ABC≌DFE,补充的条件是.A DB 12EC F3.在△ ABC和△A B C中,下列条件能判断△ABC和△A B C全等的个数有()① A AB B , BC B C② AA , B B , AC A C③ A AB B , AC B C④ AA , B B , AB A CA . 1 个 B. 2 个 C. 3 个 D. 4 个4.如图,已知 MB=ND,MBA NDC ,下列条件不能判定是△ABM≌△CDN的是()A.M NB. AB=CD M NC. AM=CND. AM∥ CN5.如图 2 所示,∠E=∠ F=90°,∠ B=∠ C, AE=AF,给出下列结论:①∠ 1=∠2② BE=CF③△ ACN≌△ ABM④ CD=DN A C B D 其中正确的结论是_________ _________ 。
11.2.1全等三角形的判定(SSS)

2.分别以B’,C’为圆心,线段AB, 判定两个三角形全等的过程叫 做证明三角形全等。 AC为半径画弧,两弧交于A’,
3.(简写成“边边边” 或“SSS”)
马小虎家的衣橱上镶有两块全等的三 角形玻璃,他打碎了其中一块,妈妈让他到 玻璃店配一块回来,请你说说他该怎么办?
在CMO和CNO中,
OM=_____ CM=_____ O CO=_____ CMO≌ CNO(____) _____ = _____ OC是AOB的平分线 .
M A C N B
我 悟 , 我 练
1.三边对应相等的两个三角形全等
(边边边或SSS); 2.证明全等三角形书写格式(4步):
C
D
同学们,音乐能激发人的情 怀,绘画能使人赏心悦目,诗歌 能动人心弦,哲学能使人获得智 慧, 科学可以改善物质生活,但 数学能给予以上的一切,让我们 热爱数学吧!
C
巩固练习
1.如图,AB=DC,AC=DB,△ABC和△DCB是否全等? 试说明理由。 A D
答: △ABC≌△DCB 理由如下: B AB = DC ( 已知 ) ∵ AC = DB ( 已知 )
C
我 悟 , 我 练
BC = CB (公共边 )
∴
△ABC
≌
△DCB (
SSS
)
巩固练习
2.如图,已知点B、E、C、F在同一条直线上, AB=DE,AC=DF,BE=CF。 试说明∠A=∠D的理由。
∵BE=CF(已知) 解: ∴ BE+EC=CF+EC 即 BC=EF 在△ABC和△DEF中 AB=DE(已知) B
A
D
我 悟 , 我 练
E
第11章《全等三角形》易错题集(02):11.2+三角形全等的判定

第11章《全等三角形》易错题集(02):11.2三角形全等的判定第11章《全等三角形》易错题集(02):11.2 三角形全等的判定选择题1.(2002•鄂州)下列命题:①有两个角和第三个角的平分线对应相等的两个三角形全等;②有两条边和第三条边上2.如图所示,∠1=∠2,AE⊥OB于E,BD⊥OA于D,交点为C,则图中全等三角形共有()3.下列说法中,正确的有()①三角对应相等的2个三角形全等;②三边对应相等的2个三角形全等;③两角、一边相等的2个三角形全等;④两边、4.如图,D在AB上,E在AC上,且∠B=∠C,则在下列条件:①AB=AC;②AD=AE;③BE=CD.其中能判定△ABE≌△ACD 的有()5.△ABC中,AB=AC,三条高AD,BE,CF相交于O,那么图中全等的三角形有()6.有以下四个说法:①两边和其中一边上的中线(或第三边上的中线)对应相等的两个三角形全等;②两角和其中一角的角平分线(或第三角的角平分线)对应相等的两个三角形全等;③两边和其中一边上的高(或第三边上的高)对应相等的两个三角形全等;④刘徽计算过π的值,认为其为.其中正确的有()7.如图,在△ABC与△ADE中,∠BAD=∠CAE,BC=DE,且点C在DE上,若添加一个条件,能判定△ABC≌△ADE,这个条件是()8.给出下列各命题:①有两边和它们的夹角对应相等的两个三角形一定全等;②有两边和一角对应相等的两个三角形一定全等;③有两条直角边对应相等的两个直角三角形一定全等;④有两条边分别相等的两个直角三角形一定全等;10.如图,已知AB=AC,D是BC的中点,E是AD上的一点,图中全等三角形有几对()11.如图,FD⊥AO于D,FE⊥BO于E,下列条件:①OF是∠AOB的平分线;②DF=EF;③DO=EO;④∠OFD=OFE.其中能够证明△DOF≌△EOF的条件的个数有()12.下列说法中,正确的个数是()①斜边和一直角边对应相等的两个直角三角形全等;②有两边和它们的对应夹角相等的两个直角三角形全等;③一锐角和斜边对应相等的两个直角三角形全等;13.对于条件:①两条直角边对应相等;②斜边和一锐角对应相等;③斜边和一直角边对应相等;④直角边和一锐角对14.(2008•鄂州)如图,已知△ABC中,∠ABC=45°,AC=4,H是高AD和BE的交点,则线段BH的长度为().D15.(2007•玉溪)如图,AE⊥AB且AE=AB,BC⊥CD且BC=CD,请按照图中所标注的数据,计算图中实线所围成的图形的面积S是()16.如图,AB=AC,AD=AE,∠B=50°,∠AEC=120°,则∠DAC的度数等于()17.如果两个三角形的两条边和其中一条边上的高对应相等,那么这两个三角形的第三条边所对的角的关系是18.如图,已知△ABC中,AB=AC,BD=DC,则下列结论中一定错误的是()19.如图,AB.CD相交于O,O是AB的中点,∠A=∠B=80°,若∠D=40°,则∠C=()20.如图,AB∥FC,DE=EF,AB=15,CF=8,则BD等于()21.如图,在△ABC中,AD是∠A的外角平分线,P是AD上异于A的任意一点,设PB=m,PC=n,AB=c,AC=b,则(m+n)与(b+c)的大小关系是()22.长为3cm,4cm,6cm,8cm的木条各两根,小明与小刚分别取了3cm和4cm的两根,要使两人所拿的三根木填空题23.(2009•遂宁)已知△ABC中,AB=BC≠AC,作与△ABC只有一条公共边,且与△ABC全等的三角形,这样的三角形一共能作出_________个.24.(2007•南宁)如图是用七巧板拼成的一艘帆船,其中全等的三角形共有_________对.25.在△ABC和△DEF中,①AB=DE,②BC=EF,③AC=DF,④∠A=∠D,从这四个条件中选取三个条件能判定△ABC≌△DEF 的方法共有_________种.26.如图,∠B=∠D=90°,BC=DC,∠1=40°,则∠2=_________度.27.如图所示,在四边形ABCD中,CB=CD,∠ABC=∠ADC=90°,∠BAC=35°,则∠BCD的度数为_________度.28.(2009•道里区一模)△ABC中,∠C=90°,AC=BC,分别过A、B向过C的直线CD作垂线,垂足分别为E、F,若AE=5,BF=3,则EF=_________.第11章《全等三角形》易错题集(02):11.2 三角形全等的判定参考答案与试题解析选择题1.(2002•鄂州)下列命题:①有两个角和第三个角的平分线对应相等的两个三角形全等;②有两条边和第三条边上2.如图所示,∠1=∠2,AE⊥OB于E,BD⊥OA于D,交点为C,则图中全等三角形共有()3.下列说法中,正确的有()①三角对应相等的2个三角形全等;②三边对应相等的2个三角形全等;③两角、一边相等的2个三角形全等;④两边、4.如图,D在AB上,E在AC上,且∠B=∠C,则在下列条件:①AB=AC;②AD=AE;③BE=CD.其中能判定△ABE≌△ACD 的有()5.△ABC中,AB=AC,三条高AD,BE,CF相交于O,那么图中全等的三角形有()6.有以下四个说法:①两边和其中一边上的中线(或第三边上的中线)对应相等的两个三角形全等;②两角和其中一角的角平分线(或第三角的角平分线)对应相等的两个三角形全等;③两边和其中一边上的高(或第三边上的高)对应相等的两个三角形全等;④刘徽计算过π的值,认为其为.其中正确的有()的值,认为其为7.如图,在△ABC与△ADE中,∠BAD=∠CAE,BC=DE,且点C在DE上,若添加一个条件,能判定△ABC≌△ADE,这个条件是()8.给出下列各命题:①有两边和它们的夹角对应相等的两个三角形一定全等;②有两边和一角对应相等的两个三角形一定全等;③有两条直角边对应相等的两个直角三角形一定全等;④有两条边分别相等的两个直角三角形一定全等;10.如图,已知AB=AC,D是BC的中点,E是AD上的一点,图中全等三角形有几对()11.如图,FD⊥AO于D,FE⊥BO于E,下列条件:①OF是∠AOB的平分线;②DF=EF;③DO=EO;④∠OFD=OFE.其中能够证明△DOF≌△EOF的条件的个数有()12.下列说法中,正确的个数是()①斜边和一直角边对应相等的两个直角三角形全等;②有两边和它们的对应夹角相等的两个直角三角形全等;③一锐角和斜边对应相等的两个直角三角形全等;13.对于条件:①两条直角边对应相等;②斜边和一锐角对应相等;③斜边和一直角边对应相等;④直角边和一锐角对14.(2008•鄂州)如图,已知△ABC中,∠ABC=45°,AC=4,H是高AD和BE的交点,则线段BH的长度为().D15.(2007•玉溪)如图,AE⊥AB且AE=AB,BC⊥CD且BC=CD,请按照图中所标注的数据,计算图中实线所围成的图形的面积S是()(16.如图,AB=AC,AD=AE,∠B=50°,∠AEC=120°,则∠DAC的度数等于()17.如果两个三角形的两条边和其中一条边上的高对应相等,那么这两个三角形的第三条边所对的角的关系是18.如图,已知△ABC中,AB=AC,BD=DC,则下列结论中一定错误的是()19.如图,AB.CD相交于O,O是AB的中点,∠A=∠B=80°,若∠D=40°,则∠C=()20.如图,AB∥FC,DE=EF,AB=15,CF=8,则BD等于()21.如图,在△ABC中,AD是∠A的外角平分线,P是AD上异于A的任意一点,设PB=m,PC=n,AB=c,AC=b,则(m+n)与(b+c)的大小关系是(),22.长为3cm,4cm,6cm,8cm的木条各两根,小明与小刚分别取了3cm和4cm的两根,要使两人所拿的三根木填空题23.(2009•遂宁)已知△ABC中,AB=BC≠AC,作与△ABC只有一条公共边,且与△ABC全等的三角形,这样的三角形一共能作出7个.24.(2007•南宁)如图是用七巧板拼成的一艘帆船,其中全等的三角形共有2对.25.在△ABC和△DEF中,①AB=DE,②BC=EF,③AC=DF,④∠A=∠D,从这四个条件中选取三个条件能判定△ABC≌△DEF 的方法共有2种.26.如图,∠B=∠D=90°,BC=DC,∠1=40°,则∠2=50度.27.如图所示,在四边形ABCD中,CB=CD,∠ABC=∠ADC=90°,∠BAC=35°,则∠BCD的度数为110度.28.(2009•道里区一模)△ABC中,∠C=90°,AC=BC,分别过A、B向过C的直线CD作垂线,垂足分别为E、F,若AE=5,BF=3,则EF=8或2.参与本试卷答题和审题的老师有:zhangmin;郭静慧;ln_86;zxw;zhangCF;117173;蓝月梦;星期八;zhjh;Liuzhx;csiya;py168;MMCH;zhqd;wenming;CJX;wdxwwzy;trista;110397;yingzi;lanchong;Linaliu;王岑(排名不分先后)菁优网2014年8月7日。
全等三角形的性质与判定(SSS、SAS、ASA、AAS)练习题

全等三角形的性质与判断(SSS、SAS、ASA 、AAS )练习题1.如图,在△2.如图,把△则∠ A=A ABC中,∠ A=90°, D、 E 分别是 AC、 BC上的点,若△ ADB≌△ EDB≌△ EDC,则∠ C= ABC 绕点 C 顺时针旋转35°,获得△ A′ B′ C, A′ B′交 AC 于点 D,若∠ A′ DC=90°,A' BEDAD D A' C FCB'B'AB E CB CO A B1题图2题图3题图4题图3.如图,△ AOB 中,∠ B=3 0°,将△ AOB 绕点 O 顺时针旋转 52°,获得△ A′ OB′,边 A′B′与边OB交于点 C( A′不在 OB上),则∠ A′ CO=4.如图,△ AB C≌△ ADE , BC 的延伸线过点 E,∠ ACB= ∠ AED=10 5°,∠ CAD=1 0°,∠ B=50°,则∠ DEF=5.如图, Rt △ ABC中,∠ BAC=90°, AB=AC,分别过点 B、 C 作过点 A 的垂线 BC、CE,垂足分别为 D、E,若 BD=3 , CE=2 ,求 DE 的长 .BCD A E6.如图, AD 是△ ABC的角均分线, DE⊥AB, DF⊥AC,垂足分别是 E、 F,连结 EF,交 AD 于 G,试判断AD与 EF的关系,并证明你的结论。
AEGFBDC7.如下图,在△ ABC 中, AD 为∠ BAC 的角均分线, DE⊥ AB 于 E, DF⊥ AC 于 F,△ ABC 的面积是28cm2,AB=20cm,AC=8cm,求 DE的长。
AE FB D C8.如图, AD=BD , A D⊥ BC于 D, BE⊥ AC于 E, AD与 BE 订交于点 H,则 BH与 AC相等吗?为何?AEH- 1 -B D C1 / 49.已知: BD 、 CE 是△ ABC 的高,点 F 在 BD 上, BF=AC ,点 G 在 CE 的延伸线上, CG=AB ,求证: A G⊥AFG AE DFB C10.如图:在△ ABC中, BE、 CF 分别是 AC、AB 两边上的高,在 BE 上截取 BD=AC,在 CF 的延伸线上截取CG=AB,连结 AD、 AG.试判断 AD与 AG的关系怎样?并证明之.AGF EDHB C11.已知,如图:AB=AE,∠ B=∠ E,∠ BAC=∠ EAD,∠ CAF=∠ DAF,求证:AF⊥ CDAEBC F DA12.已知:∠ B=∠ E,且AB=AE。
11.2全等三角形的判定复习[1]
![11.2全等三角形的判定复习[1]](https://img.taocdn.com/s3/m/db127b24cfc789eb172dc824.png)
二:利用全等三角形证明线的垂直关系
例:如图:BF是Rt△ABC的角平分线,∠ACB=90°, CD是高,BF与CD交于点E,EG∥AC交AB于G 求证:FG⊥AB 证明:∵BF平分∠ABC
C F 3 E
1 ∴∠1=∠2 2 4 ∵CD⊥AB A G D B ∴∠3+∠ABC=90° ∴BG=BC (全等三角形的对应边相等) 又∵∠ACB=90° ∴∠A+∠ABC=90° 在△BFG与△BFC中 ∴∠3=∠A BG=BC 又∵EG∥AC ∠1=∠2 ∴∠A=∠4 BF=BF ∴∠3=∠4 ∴△BFG≌△BFC (SAS) 在△BEG与△BEC中 ∠1=∠2 ∴∠FGB=∠FCB=90°(全等三角形的对应角相等 ∠3=∠4 ∴FG⊥AB BE=BE ∴△BEG≌△BEC (AAS)
牛道口中学 曹兰华 2012.9
知识梳理:
1、 什么是全等三角形?一个三角形经过哪些变化可以得到它的全等形? 。
能够完全重合的两个三角形叫做全等三角形。
一个三角形可以通过平移、翻折、旋转得到它的全等形。 2、两个全等三角形有什么特征?
两个全等三角形的对应边相等,对应角相等。 3、例:如图,已知Δ ABC≌ ΔDEF,找出其中相等的边和角。
A E B
O
F
C
如图:AB=DC,AC=DB 求证:∠ABO=∠DCO 证明: 在△ABC和△DCB中 AB=DC AC=DB BC=CB
A
D
O
∴ △ABC△DCB (SSS) ∴ ∠A=∠D (全等三角形的对应角相等) 在△AOB和△DOC中 ∠A=∠D ∠AOB=∠DOC AB=CD ∴ △AOB≌△DOC (AAS) ∴ ∠ABO=∠DCO (全等三角形的对应角相等)
11.2 三角形全等的判定(ASA,AAS)(含答案)
11.2 三角形全等的判定(ASA,AAS)◆课堂测控测试点 ASA,AAS1.三角形对应相等的两个三角形______全等,•即两个三角形全等的条件中至少有_______相等.2.已知在△ABC与△A′B′C′中,∠A=∠A′,∠B=∠B′,•则在下列条件中不能确定△ABC与△A′B′C′全等的是()A.AB=A′B′ B.BC=B′C′ C.AC=A′C′ D.∠C=∠C′3.如图,已知AB=A′B′,∠A=∠A′,若△ABC≌△A′B′C′,还需要()A.∠B=∠B′ B.∠C=∠C′ C.AC=A′C′ D.以上都对4.如图,已知△ABC的六个元素,则下面甲,乙,丙三个三角形中和△ABC全等的图形是()A.甲和乙 B.乙和丙 C.只有乙 D.只有丙5.如图,某同学把一块三角形的玻璃打碎成了三块,•现在要到玻璃店去配一块完全一样的玻璃,那么最省事的办法是()A.带①去 B.带②去 C.带③去 D.带①和②去◆课后测控6.如图,在△ABC中,D是BC上一点,AB=AD,∠1=•∠2,•∠B=•∠ADE,•根据______可判定△ABC≌△ADE.7.如图,AD=AB,∠C=∠E,∠ADC=125°,则∠ABE=_____.8.如图,在△ABC中,∠C=90°,AD是∠BAC的平分线,交BC于D,•且DC=15,则点D到AB的距离DE长为_______.EDC BA(第6题) (第7题) (第8题)9.如图,∠E=∠F=90°,∠B=∠C ,AE=AF ,给出下列结论:①∠1=∠2;②BE=CF ;③△ACN ≌△ABM ,其中正确的结论是_______.(注:将你认为正确的结论都填上)(第9题) (第11题)10.在△ABC 与△A ′B ′C ′中,∠A=44°,∠B=67°,∠C ′=69°,∠B ′=44°,且AC=B ′C ′.那么这两个三角形(提醒:画出草图)( )A .一定不全等B .一定全等C .不一定全等D .以上都不对11.如图,在△ABC 与△DEF 中,已有条件AB=DE ,•还需添加两个条件才能使△ABC ≌△DEF ,不能添加的一组条件是( )A .∠B=∠E ,BC=EFB .BC=EF ,AC=DFC .∠A=∠D ,∠B=∠E D .∠A=∠D ,BC=EF12.如图,AB=AC ,CD ⊥AB 于D ,BE ⊥AC 于E ,求证:AD=AE .13.如图,AC和BD相交于点E,AB∥CD,AB=CD,求证:E为BD的中点.14.已知:如图,B,C,E三点在同一条直线上,AC∥DE,AC=CE,∠ACD=∠B.求证:△ABC≌△CDE.◆拓展测控15.(教材变式探究题)如图(1),在△ACB中,∠ACB=90°,AC=BC,直线L经过点C,AD ⊥L于D,BE⊥L于E.(1)求证:①△ADC≌△CEB;②DE=AD+BE.(2)当直线L绕点C旋转到图(2)的位置时,DE,AD,BE具有怎样的等量关系?说出你的猜想,并证明你的猜想.答案:1.不一定一对对应边2.D (点拨:没有一对对应边相等)3.D (点拨:根据ASA可选A,根据AAS可选B,根据SAS可选C)4.B (点拨:根据SAS可知乙,根据AAS可知丙)5.C (点拨:依据ASA)[总结反思]证明三角形全等的方法增加了ASA和AAS.6.ASA (点拨:由∠1=∠2可得∠BAC=∠DAE)7.125°(点拨:易知△ADC≌△ABE)8.15 (点拨:易证△ACD≌△AED,DE=CD)9.①②③(点拨:根据已知条件易证△ABE≌△ACF,△ABM≌△ACN)10.B (点拨:画出草图后,确定对应边和角)11.D (点拨:三角形全等条件中边边角不成立)12.证明:∵CD⊥AB,BE⊥AC,∴∠ADC=∠AEB=90°.在△ADC和△AEB中,,,,A AAD C AEB AC AB∠=∠⎧⎪∠=∠⎨⎪=⎩∴△ADC≌△AEB,∴AD=AE.[解题规律]有两角及其一角对边相等的两个三角形全等.13.证明:∵AB∥CD,∴∠A=∠C,∠B=∠D.在△ABE和△CDE中,,,,A C ABC DB E ∠=∠⎧⎪=⎨⎪∠=∠⎩∴△ABE≌△CDE(ASA).∴BE=DE,即E为BD的中点.[解题规律]有两角及其夹边对应相等的两个三角形全等.14.证明:∵AC∥DE,∴∠ACD=∠D,∠ACB=∠E.又∵∠ACD=∠B,∴B=∠D.在△ABC和△CDE中,,,,B DAC B E AC C E∠=∠⎧⎪∠=∠⎨⎪=⎩∴△ABC≌△CDE(AAS).[解题技巧]充分利用AC∥DE得到∠ACB=∠E和∠ACD=∠D,即一线二用.15.(1)证明:∵AD⊥L,BE⊥L,∴∠ADC=∠CEB=90°.∵∠ACB=90°,∴∠ACD+∠ECB=90°.又∠1+∠ACD=90°,∴∠1=∠ECB.在△ADC和△CEB中,, 1,,AD C C EBEC BAC BC∠=∠⎧⎪∠=∠⎨⎪=⎩∴△ADC≌△CEB(AAS),∴AD=CE,DC=BE.∴DE=CE+DC=AD+BE.(2)结论:DE=AD-BE.证明:同(1)可证△ADC≌△CEB.∴AD=CE,DC=BE,∴DE=CE-CD=AD-BE.[解题方法]解决问题(2)的关键是弄清图(2)中哪些量发生了变化,•哪些没有发生变化,本题在证明过程中要发现∠ACD=90°的用法,即由∠ACB=90°可得∠ACD+∠BCE=90°.。
11.2.1三角形全等的条件——SSS
②△ABE≌△ACD吗?理由正确书写的能力。
A
B
C
D
E
4、如图所示,AB=AC,AD=AE,EC、DB、BD与CE学生独立思考,当堂完成
A
B
E
D
C
相交于点O。求证:∠CAB=∠EAD及时了解学生学习效果。
四、想一想(你能独立完成吗?)通过学生独立思考,进行
3、尝试探索三角形全等的条件,得出第一个条件——SSS
4、课堂练习,巩固判定
5、利用个别习题,检测学生书写
6、小结与作业
7、课后检测
教学任务
一组————学一学
二组————试一试
三组————练一练1,2
四组————练一练3
五组————练一练4
六组————想一想
如图,AB=CD,AD=BC,那么AD∥BC,AB∥BC,你能说明其自我评价,培养学生良好的学
中的道理吗?习习惯
五、归纳总结:___________________________________________。
教学
后反思
教学流程
1、提前一天发学案,布置学生预习
2、检查学生预习(利用书上课后习题)
课题
11.2 .1三角形全等的条件——“SSS”
课型
自学互学展示课
时间
班级
学习目标
1、掌握应用“边边边”判定全等三角形的方法;
2、利用全等三角形的判定方法解决较为简单的问题。
学习环节
1、课前检测52、质疑讨论5 3、明标1 4、展示质疑26 5、测评8
学习过程
一、学一学:(看,别人都学完了)
(2021年整理)三角形全等的判定SSS例题及练习题
三角形全等的判定SSS例题及练习题编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(三角形全等的判定SSS例题及练习题)的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为三角形全等的判定SSS例题及练习题的全部内容。
全等三角形的判定(SSS )练习题1.如图,ABE ∆≌DCF ∆,点A 和点D 、点E 和点F 分别是对应点,则AB= ,=∠A ,AE= ,CE= ,AB// ,若BC AE ⊥,则DF 与BC 的关系是 .2.如图,ABC ∆≌AED ∆,若=∠︒=∠︒=∠︒=∠BAC C EAB B 则,45,30,40 ,=∠D ,=∠DAC .3.已知ABC ∆≌DEF ∆,若ABC ∆的周长为23,AB=8,BC=6,则AC=,EF= .4.如图,若AB=AC ,BE=CD ,AE=AD ,则ABE ∆ ACD ∆,所以=∠AEB ,=∠BAE ,=∠BAD .B第1题图D第2题图第4题图5.如图,ABC ∆≌ADC ∆,点B 与点D 是对应点,︒=∠26BAC ,且︒=∠20B ,1=∆ABC S ,求ACD D CAD ∠∠∠,,的度数及ACD ∆的面积.6.如图,ABC ∆≌DEF ∆,cm CE cm BC A 5,9,50==︒=∠,求DEF ∠的度数及CF 的长.7.如图,已知:AB=AD ,AC=AE ,BC=DE,求证:CAD BAE ∠=∠8.如图,在,90︒=∠∆C ABC 中D 、E 分别为AC 、AB 上的点,且BE=BC ,DE=DC ,求证:(1)AB DE ⊥;(2)BD 平分ABC ∠9.如图,已知AB=EF ,BC=DE ,AD=CF,求证:①ABC ∆≌FED ∆;②AB//EFDF。
人教版初二数学上册11.2三角形全等的判定配套练习(SAS).2三角形全等的判定(SAS)
11.2三角形全等的判定配套练习(SAS♦随堂检测1. 如图OA 平分/ BOC 并且 OB=OC 青指出AB=AC 的理由.2. 如图,已知△ ABC 中,AB=AC,D 、E 分别是 AB AC 的中点,且CD=BE △人。
与厶AEB 全等吗?3. 如图,OA=OB OC=OD / AOB=/ COD 请说明 AC=BD 的理由.4.如图为某市人民公园中的荷花池 ,现要测量此荷花池两旁 A 、B 两棵树间的距离(我们不能直接量得).请你根据所学知识,以卷尺和测角仪为测量工具设计一种测量方案要求:(1)画出你设计的测量平面图; (2)简述测量方法,并写出测量的数据(长度用a,b,c,…表示;角度用 ,,…表示);(3)根据你测量的数据,计算A 、B 两棵树间的距离小明是这样分析的:因为 AB=AC,BE=CD, BAE K CAD 所以△ ADC^^ AEB( 确吗?请说明理由CSSA ),他的思路正D?A?B♦典例分析例:如图所示,铁路上A, B两站(视为线上两点)相距25km, C, D为铁路同旁的两个村庄(视为两点),DAL AB于A点,CB丄AB于B点,DA=15km, BC=10km,现在要在铁路AB 上建一个土特产品收购站E,使C, D两村到E站的距离相等,则E站应建在距A站多少千米处?解析:若C, D两村到E站的距离相等,则有DE=EC,又因为ADbBC=AEbEB=25km,由此想到收购站应建在距A点10km处,此时则有EB=15km,又DAI AB CB1AB则厶DAE^^ EBC根据全等三角形的质知DE=EC这样通过构造全等三角形就找到了收购站地址.♦课下作业•拓展提高1. 如图,AC与BD交于0点,若OA=OD用“ SAS证明△ AOB^A DOC还需()A、AB=DC;B、OB=OC;C、/ A=Z D;D、/ AOB=/ DOC2. 如图,AB平分/ CAD E为AB上一点,若AC=AD则下列结论错误的是()A、BC=BD; B 、CE=DE;BC、BA平分/ CBD;D、图中有两对全等三角形3. 如图,点B、E、C F在同一直线上,AC=DF BE=CF只要再找出边=边,或/ = / ,或 // , 就可以证得△ DEF^A ABC.4 .如图,AE=AF / AEF=Z AFE BE=CF 说明AB=AC5. 如图,A、D、F、B 在同一直线上,AD=BF,AE=BC, 且AE // BC.说明:(1 )△ AEF^A BCD (2) EF // CD.•体验中考1. (2009年湖南省娄底市)如图,在△ ABC中,AB=AC D是BC的中点,连结AD在AD的延长线上取一点E,连结BE CE求证:△ ABE^A ACE2. (2008 年遵义市)如图,OA = OB , OC =OD , . 0=50;, .D = 35,则.AEC 等于()A. 60B. 50C. 45D. 30。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
全等三角形的判定
(SSS)
1、如图1,AB=AD,CB=CD,∠B=30°,∠BAD=46°,则∠ACD的度数是( )
A.120° B.125° C.127° D.104°
2、如图2,线段AD与BC交于点O,且AC=BD,AD=BC,•则下面的结论中不正确的是( )
A.△ABC≌△BAD B.∠CAB=∠DBA C.OB=OC D.∠C=∠D
3、在△ABC和△A1B1C1中,已知AB=A1B1,BC=B1C1,则补充条件____________,可得
到△ABC≌△A1B1C1.
4、如图3,AB=CD,BF=DE,E、F是AC上两点,且AE=CF.欲证∠B=∠D,可先运用
等式的性质证明AF=________,再用“SSS”证明______≌_______得到结论.
5、如图,AB=AC,BD=CD,求证:∠1=∠2.
6、如图,已知AB=CD,AC=BD,求证:∠A=∠D.
7、如图,AC与BD交于点O,AD=CB,E、F是BD上两点,且AE=CF,DE=BF.请推导
下列结论:⑴∠D=∠B;⑵AE∥CF.
8、已知如图,A、E、F、C四点共线,BF=DE,AB=CD.
⑴请你添加一个条件,使△DEC≌△BFA;
⑵在⑴的基础上,求证:DE∥BF.
