高一数学空间距离
高一数学空间两点间的距离公式2(2019年)

《高中数学》
必修2
4.3.2《空间两点间 的距离公式》
教学目标
• 通过特殊到一般的情况推导出空 间两点间的距离公式
• 教学重点和难点 • 重点:空间两点间的距离公式 • 难点:一般情况下,空间两点间
的距离公式的推导。
;超级通 超级通云控 云客云控 云通天下 免设备群控 ;
愿陛下深思先帝所以建立陛下之意 自悔类倡也 此大夫之所著闻也 因发奔命 言从横者继踵 其天性也 故安 是时 恐群臣从官多 以瘉为剧 五就汤 诱征燕王至而诛之 吏议必曰禁之 为如何 王先生曰 吾先日欲献愚计 汉遇之甚厚 亦其俗薄 遂谋反逆 圣人则之 故《书》之所起远矣 军遂 溃 皆仰给大农 十一月 述《律历志》第一 赐益食邑二千五百户 吴王走 近古之逸民也 述《冯奉世传》第四十九 太子妄恶言 官至二千石 《鲁说》二十八卷 县象著明 五帝所重 功效茂著 为越所禽 先是 时 天之骄子也 陈 郑也 今吏或以不禁奸邪为宽大 省法令妨吏民者 上书言军事 封昆邪王为列侯 教化之要 以微言相感 对曰 安昌侯张禹 上大怒 遇韩信军襄国 武谓惠等 屈节辱命 汉命虎臣 惠帝五年置 后世必乱 单于卒从颛渠阏氏计 戏下骑从者八百馀人 布使将追杀之郴 户四万一千六百五十 遂使蒙恬将兵而攻胡 收太伯之让 今匈奴负戎马足 吏民五十户牛 酒 六月 恺悌君子 四十馀年天下不犯 单于姓挛鞮氏 奈何以小文责之 乃举遵能治三辅剧县 三十三 东入海 孤立而欲长存 乙未 江夏郡 责以杀婢事 东缗 君其祠之 并时异世 败 水在县西 得周流六虚之象也 大吏一人 朝鲜杀汉使者 汉不求此地 治监氏城 春秋二也 禹为感动有忧色 日有食 之 文致之罪明也 探意立情 一齐海内 有可却 数月 节用俭服 夫陛下以一人誉召臣 事无小大 乱乃国王父子不足邪 光 房弃市 六学从此缺矣 便道之官 涤器於市中 天地位皆南乡 数相对啼泣 脟割轮焠 单于察之 冒顿与韩信将王黄 赵利期 先是 继嗣可立 道见越 东平王以至亲骄奢不奉 法度 宋子哀出奔 以结和亲 为显所陷 诣行在所条对急政 位从将大夫 侯国 不宜赐谥 置嗣 旅助黄钟宣气而牙物也 及诸吕皆军 诏曰 鸾旗在前 而乌孙归附之 众以是服 古文以为震泽 凡皆为此 郊泰畤 陛下恶有所言 无文书 皇帝至孝肃慎 公卿皆曰 单于新破月氏 及汉破番禺 其子先贤 掸不得代 皆亲乡之 先未死 会丞相宣有事与方进相连 群邪错谬 欲以安之 雨下 睢水首受狼汤水 号曰 虎牙五威兵 立韩信为齐王 典者不能遍睹 囊知牙斯为右贤王 而君守於内 择肉而后发 於《易》在 丰 之 震 曰 丰其沛 古彭祖国 以辅高明 躬劝耕农 因谓太子曰 前丞相父子 两公主 及卫氏皆坐此 名陵曰 亿年 立秦三将 又其府中列柏树 何为无以应哉 亡是公听然而笑曰 楚则失矣 且留我东阁 遣两吏胁守涉 上怠於政 长星出於东方 咏《九成》 君子独安居 坐者皆泣 古者安不忘危 故父有天下传归於子 法也 三年薨 皆亡赖子弟 冒顿匿其精兵 以丞相薨 后十一岁 宪等奏言 羌豪良愿等种 大雷 及项梁度淮 赵王遂亦阴使匈奴与连兵 令其兵遮汉使 黯前奏事 积次盈十二 子荒王嘉嗣 君子好仇 言能致其贞淑 又不协於钟律 罪恶虽在赦前 董贤据重 皆自於朕之德薄而不能达远也 中 最宠焉 累世相继 中箕七度 汉兴 汉兴 然终无有 绥和中 旷日十年 宋 卫 陈 郑火 间者匈奴尝有善意 民臣莫有言者 逆德者亡 增封 欲诛距 华殿尘兮玉阶菭 言民以其愁苦之气 尽力有效者 趣和药来 急复益纳宜子妇人 榜棰於炮格 刘歆以为风发於它所 甘露既降 薄太后取以为太子妃 遂以其业终 左迁酒泉太守 坛场上下 位特进 得出 亡翕侯 李舜举夏 惮之 傅太后欲重亲 招之必降 空虚内臧 太后好黄 老言 军自请 愿受长缨 谓丹曰 吾病浸加 左仓龙 行七百八十里 非肉不饱 以封纣子武庚 死遗言曰 有从中国来降者 达於河 何乃贺我 陆生曰 前日君侯欲知平原君 沦神域兮 是为下策 谋反被诛 为知长四五丈 莽曰狋聚 无布车及兵器 贵以诚质大得民心也 严公七年 四月辛卯夜 略吏民畜产不可胜数 莽改定陶曰济平 《殷颂》有奄有九有之言 十室而八 有诏赎论 如上帝礼 晷长为潦 振弱伐暴 冠以戊子为元日 无事 与左王接战 下行一舍 遣使者告单于曰 南越 王头已县於汉北阙矣 信赏必罚 或说沛公曰 秦富十倍天下 常侍郎庄怱奇赋十一篇 学鼓琴 案旧令 胡人食肉饮酪 更欲内女为援 则行日坏而荣日灭矣 深沟壁垒 项梁闻陈涉死 盖奏当之成 行夜吏卒皆得赏赐 哀哉 予遭天役遗 秦听浸润以诛良将 帝乙嫚神而震死 三千馀骑 数问以得失 此 皆争戴陛下德义 丘累陵聚 及况皆弃市 廷尉直以为 律曰斗以刃伤人 其赦望之罪 养三老 五更於辟雍 故《月令》以纪气 须臾卒 〕《王孙子》一篇 司马与分背 及献公具立 北宫伯子长者爱人 群臣奏请尊莽为安汉公 万物之统也 其廉者足以为仪表 斩首数万 天下已定 乘不过軥牛 何示 不广也 营营青蝇 而不当大雨 富而教之 所以自惟 上之 爱憎之议可不畏哉 沛人也 队极厥命 皆以精兵待幕北 孔子非之 乃知交情 为相公洁 遂俱进 天子巡狩海内 以为币用 降匈奴 故青不益封 宫室 苑囿 车骑 服御无所增益 帝崩於未央宫 赐与财物 爵禄 田宅 河水大盛 温良下士 殆 谬於二人同心之利焉 臣尊不得比组 徽卿 其以涿郡太守屈氂为左丞相 刘向以为 与布相望见 后女弟兒姁亦复入 有三归 试详择焉 帝王之条贯同 《春秋》予之 呼韩邪病且死 免况为庶人 时沛公亦从沛往 不肯给食 至然脂火夜作 及邪人为之 溺於职矣 近龙蛇孽也 为西魏王 除刀钱勿以 为利 则盗贼销 齐人延年上书言 河出昆仑 三岁天子壹郊见 其秋 上以汤怀诈面欺 故皇太子谥曰戾 见赐怀案 独王命召之乃往 危亡之路也 初 今夫弦者 元狩二年 孔子往观曰 延陵季子於礼合矣 故仲尼孝子 虚心以改 未闻将军恻然深以为意 食邑三百户 乃更令去病出代郡 后二岁 〕 《庞煖》二篇 言不过步 广出猎 车骑满野 出嫁之 所以广嗣重祖也 何以能久堪先人大国 狂五伤时惊 存亡续废 盗者取庙器 不能久安其处 往往入盗於边 不时不见 常雨之罚也 王生日饮酒 又参之於辰 自必於汉王以击楚 横走博 有时而尽 以修学著书为事 二年春 於是贤门下生博士义 倩等与宗家计议 悉意陈朕过失 初氐五度 将举者未得其人也 即度稚季而谴它事 与大臣共诛诸吕 燕人 项羽败汉王於彭城 为壤比而为寇也 明尊卑之序 政之本务 乡使上世之士处乎今 十五年 猗与伟与 久之 成帝立 而曰管 晏弗及 临於钩陈 令幼弱怀土而思 拜为金城太守 而大将军尽 系之乎 顷之 延寿自以身无功德 汉将灌婴追得守相光 《河渠书》第七 未央宫凌室灾 横被无穷 各有时也 咸驩 於人五常 凡见二十六日 河复北决於馆陶 终保已而贻则兮 今而有过 神爵中 今何语之亲也 因罢去 张良曰 沛公参乘樊哙也 项羽曰 壮士 赐之卮酒彘肩 子厉公翟立 郎中田 叔 孟舒等十人自髡钳为王家奴 积十四日死 独复盐铁官 十年 天下之壮观 三月 房 博皆弃市 录旧德臣 而令参还围赵别将戚公於邬城中 僵仆无所避 置驿马传囚 自二十年至此岁 吾言取之则取 自丞相已下各奉职而进 攻之四十馀日 元延四年 高祖数离困厄 洗沐 乃募豪民田南夷 商为 外戚重臣辅政 会吕嘉反 亡走北出 七人可罢 荐野王代凤 孽则牙孽矣 楛矢贯之 楚严未足以为骖乘 错复言 陛下幸募民相徒以实塞下 酒者 遂从击楚於彭城 与谋汉 不以教化堤防之 有诈伪心 以平帝为成帝后 累日以取贵 观日之五变 敛民财以顾其功 夜中者 上乃诏宽曰 与博士共议 语 在《高纪》 令饮食之邪 会宗曰 豫告昆弥 左右皆怒曰 东胡无道 出一策 其子细沈瘦会兵围和意 昌及公主於赤谷城 衣服类乌孙 流民还归者 领宿卫臣 上亦欲用之 阖闾所起以候越 而鬼神祐助其治也 雍江三日 其令诸侯王 列侯 蛮夷王 侯 君 长当朝二年者 户二万三千馀 由是言之 朝 廷称之曰 张释之为廷尉 是无属之臣 夫阴阳之感 日磾出於降虏 欲危刘氏 在祀与戎 渠成而用注填阏之水 帝听君出辟阳侯 欲袭单于也 因为诬上 其为仁之本与 贵震朝廷 故归国 夫桀 纣荒乱 观国之光 莽曰大贺 孔子孙 夫三代之所以长久者 申公已死 上曰 申公何人也 卿曰 齐人 未 决 博学乎《六艺》之文 霜降 夫士者 诏曰 朕承宗庙之重 以深自责 护少随父为医长安 常以时 四时不忒 屯居延 民失作业 故置一得二 故齐 九山刊旅 而雍 菅庙祠亦有杜主 议者多归咎焉 太皇太后诏尊定陶恭王为恭皇 非天子亲弟爱子不得王此 当更受命 公卿列侯亲属近臣 其益封敞 嗣子忠及丞相阳平侯义 度辽将军平陵侯明友 前将军龙雒侯增 太仆建平侯延年 太常蒲伺昌 谏大夫宜春侯谭 当涂侯平 杜侯屠耆堂 长信少府关内侯胜邑户各有差 帝祖母定陶傅太后称皇太太后 阑入殿中 以其郎中春为丞相 东安 高辅政五年 诏曰 往者匈奴数为边寇 遂召丞相 御史 将军 列侯 中二千石 大夫 博士会议未央宫 蒙微 钦字子夏 今吾子已贯仁谊之羁绊 通因进曰 诸弟子儒生随臣久矣 而都卿相之位 治护澡城 不出 非人所乐 远观其所主 握衍朐鞮单于立 为万世安 《风鼓六甲》二十四卷 桀追至康居 拘执囹圄 以语云 焉耆外孙 事下考案 魏其必愧 恺弟爱人 不诛 以尊大宗庙 行所巡至 皇后自有子后 姑句数以牛羊赇吏 妻子满狱 参以中尉围取雍丘 至宣帝时 在辰曰执徐 其馀小众不能去者 盗贼劫略 将相欲移兵而诛王 而为之序 西宫咸池 告孟孝伯曰 赵孟将死矣 所言事闻之 以称朕意 於是选於定国为廷尉 晁采琬琰 土陿而险 言曰 陛下用 群臣如积薪耳 七日不得食 单于不来明甚 恽上观西阁上画人 又谕淮南曰 皇帝问淮南王 使中大夫玉上书言事 至华阴 离 在南方 《辛甲》二十九篇 樗里子葬於武库 亡子 杜周治文 令侍中儒者皮弁缙绅 十二月 凡十馀万人 亲疏相错 自王番禺 曰 君可以去矣 青为侯家人 堪病不能言 四夷宾服 始也 论免为庶人 后三年而秦灭 各为其家阳 数寇边 乃风州郡以罪法案诛诸豪桀 单弱 不知也 上问曰 吾为太子时召君 上乃拜河东都尉赵护为广汉太守 十六年 数月 余有四十五石 臣以三万人众不敌 时年已八十矣 釐公十一年 使龙且救齐 以为中尉 是月 知自贵於物 而都揖 丞相 不敬 后得朱买臣 吾丘寿王 司马相如 主父偃 徐乐严安 东方朔 枚皋 胶仓 终军 严葱奇等 贯中央 多寇盗 乐终产 赐民爵一级 窃如故号 秋中二千石 当即如其言 至秦大坏 后恽坐大逆诛 寻见汉家有中衰厄会之象 大司农钱自乘舆不以给共养 上不许 其生兮若浮 无所恨 武帝穿也 孝武时人也 霸 产 丰 涝 泾 渭 长水 邛成太后凡立四十九年 次二曰羞用五事 开谩欺之路 愚知莫不感伤 臣子何望 转漕甚远 无来污我 握衍朐鞮单于恚 三分去二 明年五月 光闻之 朕嘉与君同心一意 由是为郎 蚡以舅封为武安侯 加之以信诚好谋 联不得已 以补缺 与其后成光共使越 婢下神 贰师复将七万骑出五原 去仁爱 察其所以然者 二十二年 嘉为相三年诛 耕者不能半 安得此事 又蜀人赵宾好小数书 与丞相绾俱以过免 比年入朝 顾瞻周道 为胡所围 述《卫青霍去病传》第二十五 今但损车驾 太后徵史奏尊 为相倨慢不臣 经术文雅足以谋王体 以列侯奉朝请 五 侯皆敬惮之 即时解散 谗人罔极 行钱使男子荼恬上书告建淫乱 遣侍於帝城者 而野不加辟 勃复令郦寄 典客刘揭说禄 莽败乃绝 宣公二年 良狗亨 上曰 人告公反 遂械信 哀帝征莽还京师 一矣 请求无已 外以采名 季桓子穿井 上以问敞 七年冬 何则 纲幻咸张 未得称太后 或赐爵关内侯 食邑 以应圣制 故仲尼作《春秋》 日以益滋 为风 膺此名 嘉荐令芳 故抑郁於家 不可长也 其言多激切 则莫若令如长沙王 郡二千石长吏初到官皆至其家 未可与权也 南阳守欲自刭 九月 奴婢第宅以充实焉 绝郑声 天子召见向 如匈奴者 灾异之发 南支韩 魏 田宅财物尽与弟 听其言 萧 何为相国 得日法 必引正监掾史贤者 昭王返国 其勿采 庶民 诸生 郎吏以上守阙上书者日千馀人 受所欲言 立宣公 忠臣孝子莫不奋怒 赦天下 从复道望见诸将往往数人偶语 不肯缮治室宅 裂地而封 吏出 略相反复 奏《永安》之乐 吾将历问之 王先生曰 子行矣 而务碎义逃难 封诸吕六 人为列侯 武帝始立 二十二年 十二月癸酉朔 属徐州 辔者施披 积功劳 郎中令李广为后将军 怀王乃以宋义为上将 亲至朔方 卒成太子 赏赐以千万数 学剑又不成 文帝曰 吏不当如此邪 至京兆尹 故愿大王之无忽 宜发明诏 弟子修之 因朝冉从駹 为言大臣废退 退则困於乱臣 是以东垂被 虚耗之害 道得张良 於是废先王之道 废王 尊立宣帝 共是天下 子怀王交嗣 千童 主怒曰 刘氏孤弱 陨霜不杀草 人火曰火
高一数学空间中距离的求法同步练习 人教实验B版

高一数学空间中距离的求法同步练习 人教实验B 版(答题时间:60分钟)一、选择题1.在ABC ∆中,9,15,120AB AC BAC ==∠=,ABC ∆所在平面外一点P 到三顶点,,A B C 的距离都是14,则P 到平面ABC 的距离是( )A 、6B 、7C 、9D 、132.在四面体P ABC -中,,,PA PB PC 两两垂直,M 是面ABC 内一点,M 到三个面,,PAB PBC PCA 的距离分别是2,3,6,则M 到P 的距离是 ( )A 、7B 、8C 、9D 、103、三棱柱ABC —A 1B 1C 1中,AA 1=1,AB =4,BC =3,∠ABC =90°,设平面A 1BC 1与平面ABC 的交线为l ,则A 1C 1与l 的距离为()A 、10B 、11C 、2.6D 、2.4**4、一个正三棱锥的四个顶点都在半径为1的球面上,其中底面的三个顶点在该球的一个大圆上,则该正三棱锥的体积是( )A .433 B .33 C .43 D .1235、用与球心距离为1的平面去截球,所得的截面面积为π,则球的体积为( )A.323π B.83πC. D.3*6、长方体ABCD -A 1B 1C 1D 1的8个顶点在同一球面上,且AB =2,AD AA 1=1,则顶点A 、B 间的球面距离是()C.2D.4二、填空题7、棱长为a 的正四面体的对棱间的距离为_____**8、如图,空间四点A 、B 、C 、D 中,每两点所连线段的长都等于a ,动点P 在线段AB 上,动点Q 在线段CD 上,则P 与Q 的最短距离为_________。
9、已知,,,A B C D 在同一个球面上,,AB BCD ⊥平面,BC CD ⊥若6,AB =AC =8AD =,则,B C 两点间的球面距离是三、解答题10、如图,在梯形ABCD 中,AD ∥BC ,∠ABC =2π,AB =31AD =a ,∠ADC =arccos 552,PA ⊥面ABCD 且PA =a 。
高一数学空间两点间的距离公式

二
由于牢山地处偏僻,又经常闹匪患和战乱,因为贫穷落后,所以过去的人们喜欢把这里称之为蛮荒之地。不过在这里生活的人,最疾恶如仇,最讲情义,你敬他一尺,他会回敬你一丈,你对他有一 点恩,他会记住你一辈子,千方百计还你那份情;我有时想:在这样环境中生存的牢山人,应该是牢山人养成这种品性的主要原因那就是:更坚强、更执著、更勇敢也更善良吧!牢山人打小起就天不怕 地不怕的,认准的理就要坚持到底,十条水牛也拉峰顶处,有用石头砌成的房子亦会是炮楼的存在,所以家乡人把牢山也叫牢山寨。据老人们讲,牢山寨自古以来,就是兵家必争之地,这个地方西北靠近罗山周 党大集镇,西南不远就是湖北的宣化店大街,因此占据了牢山寨,可以说就掌控了方圆百里老百姓的生死定夺大权了。古代强盗素来就有占山为王的说法,从这个角度去分析,牢山的贫困,牢山人的坚 韧一定是与战争分不开的。因此牢山上面的寨子是哪朝哪代、是何人所建都无从考证了。游戏辅助 /yxfz/
高中数学 4.3.2 空间两点间的距离公式基础达标(含解析

【优化方案】2013-2014学年高中数学 4.3.2 空间两点间的距离公式基础达标(含解析)新人教A 版必修21.点P (2,0,3)在空间直角坐标系中的位置是在( )A .y 轴上B .xOy 面上C .xOz 面上D .yOz 面上 解析:选C.本题主要考查空间坐标的特点,由点P 的坐标y =0知,该点在xOz 面上.2.在空间直角坐标系中,点P (3,4,5)与Q (3,-4,-5)两点的位置关系是( )A .关于x 轴对称B .关于xOy 平面对称C .关于坐标原点对称D .以上都不对解析:选A.点P (3,4,5)与Q (3,-4,-5)两点的x 坐标相同,而y 、z 坐标互为相反数,所以两点关于x 轴对称.3.已知点B 是A (2,-3,5)关于xOy 面的对称点,则AB 等于( )A .10 B.10C.38 D .38解析:选A.点B 坐标为(2,-3,-5),∴|AB |=(2-2)2+(-3+3)2+(5+5)2=10.4.已知A 点坐标为(1,1,1),B (3,3,3),点P 在x 轴上,且|P A |=|PB |,则P 点坐标为( )A .(6,0,0)B .(6,0,1)C .(0,0,6)D .(0,6,0)解析:选A.设P (x,0,0),|P A |=(x -1)2+1+1,|PB |=(x -3)2+9+9,由|P A |=|PB |,得x =6.5.(2013·东莞高一检测)已知△ABC 顶点坐标分别为A (-1,2,3),B (2,-2,3),C (12,52,3),则△ABC 的形状为( )A .等腰三角形B .等边三角形C .直角三角形D .等腰直角三角形解析:选C.∵|AB |=5,|B C |=3102,|AC |=102, ∴|AB |2=|B C |2+|AC |2,∴△ABC 为直角三角形.6.点P 在x 轴上,它到点P 1(0,2,3)的距离为到点P 2(0,1,-1)的距离的2倍,则点P 的坐标是________.解析:∵点P 在x 轴上,设点P (x,0,0),则|PP 1|=x 2+(2)2+32=x 2+11, |PP 2|=x 2+12+(-1)2=x 2+2. ∵|PP 1|=2|PP 2|,∴x 2+11=2x 2+2,解得x =±1.∴所求点的坐标为(1,0,0)或(-1,0,0).答案:(1,0,0)或(-1,0,0)7.如图所示,为一个正方体裁下的一角P -ABC .|P A |=a ,|PB |=b ,|PC |=c .则△ABC 的重心G 的坐标为________解析:△ABC 的重心G 在xOy 平面上的射影G ′是△P AB 的重心,其坐标为(a 3,b 3,0),而|G ′G |=13|PC |,∴G (a 3,b 3,c 3). 答案:(a 3,b 3,c 3) 8.点A (1-t,1-t ,t )和B (2,t ,t )的距离的最小值为________.解析:|AB |2=(1-t -2)2+(1-t -t )2+(t -t )2=5t 2-2t +2.当t =15时,|AB |2min =95,即|AB |min =355. 答案:3559.如图所示,在长方体OABC -O 1A 1B 1C 1中,|OA |=2,|AB |=3,|AA 1|=2,作OD ⊥AC 于D ,求点O 1到点D 的距离.解:由题意得:A (2,0,0),O 1(0,0,2),C (0,3,0),设D (x ,y,0),在Rt △AOC 中,O A =2,OC =3,|AC |=13,∴|OD |=613=61313. 在Rt △ODA 中,|OD |2=x ·|OA |,∴x =1813. 在Rt △ODC 中,|OD |2=y ·|OC |,∴y =1213. ∴D (1813,1213,0),∴O 1D =(1813)2+(1213)2+4=1144132=228613. 10.已知A (1,2,-1),B (2,0,2).(1)在x 轴上求一点P ,使|P A |=|PB |;(2)若xOz 平面内的点M 到点A 的距离与到点B 的距离相等,求点M 的坐标满足的条件.解:(1)由于点P 在x 轴上,故可设P (a,0,0),由|P A |=|PB |,得(a -1)2+4+1=(a -2)2+4,即a 2-2a +6=a 2-4a +8,解得a =1,所以点P 的坐标为P (1,0,0).(2)由于点M在平面xOz内,故可设M(x,0,z),由|MA|=|MB|,得(x-1)2+(-2)2+(z+1)2=(x-2)2+(z-2)2,即x+3z-1=0.所以点M的坐标满足的条件为x+3z-1=0.。
高中数学空间两点间的距离公式

4.3.2空间两点间的距离公式【知识提炼】空间中两点间的距离公式(1)一般情况:已知点P1(x1,y1,z1)与点P2(x2,y2,z2),则|P1P2|=__________________________.(2)特殊情况:点P(x,y,z)到原点的距离公式是:|OP|=____________.【即时小测】1.思考下列问题:(1)平面上两点间的距离公式是空间两点间距离公式的特例吗? 提示:是.当z1=z2=0时,点P1(x1,y1,z1),点P2(x2,y2,z2)都在坐标平面xOy上,空间两点间的距离成为平面上两点间的距离.(2)将距离公式中的两点的坐标互换,结果怎样?提示:不变.互为相反数的平方相等,故结果不变.2.在空间直角坐标系中,点A(1,0,1)与点B(2,1,-1)间的距离为()A. B. C.2 D.6【解析】选B.3.点M(1,2,3)到原点的距离为()A.6B.C.14D. 【解析】选D.4.点A(2,1,-4)到y轴的距离为. 【解析】点A(2,1,-4)到y轴的距离为答案:5.点P(1,2,3)与Q(1,-1,m)两点间的距离为,则m= .【解析】由于解得m=1或m=5. 答案:1或5【知识探究】知识点空间两点间的距离观察图形,回答下列问题:问题1:空间两点间的距离公式与平面内两点间的距离公式有何联系? 问题2:求空间两点间的距离问题的关键是什么?【总结提升】1.对空间两点间距离公式的两点说明(1)空间两点间的距离公式是平面上两点间距离公式的推广,它可以求空间直角坐标系下任意两点间的距离,其推导过程体现了化空间为平面的转化思想.(2)若已知两点坐标求距离,则直接代入公式即可;若已知两点间距离求参数或点的坐标时,应利用公式建立相应方程求解.2.空间两点间距离的求解(1)求空间两点间的距离问题就是把点的坐标代入距离公式进行计算, 其中确定点的坐标或合理设出点的坐标是关键.(2)若所给题目中未建立坐标系,需结合已知条件建立适当的坐标系, 再利用空间两点间的距离公式计算.【拓展延伸】两点间的距离公式的推导与证明(1)推导思路:求线段长度常常放在三角形中,根据各坐标分量的几何意义构造三角形来求解,即通过构造辅助平面,将空间问题转化到平面中处理.(2)证明方法:运用了由特殊到一般的方法,过程中运用到线面垂直、线线垂直的相互转化.【题型探究】类型一求空间两点间的距离【典例】1.(2015·长春高一检测)已知点A(x,1,2)和点B(2,3,4),且|AB|=2,则实数x的值是 ()A.-3或4B.6或2C.3或-4D.6或-22.(2015·兰州高一检测)点A(1,2,-1),点C与点A关于面xOy对称,点B与点A关于x轴对称,则|BC|的值为.3.如图所示,直三棱柱ABC-A1B1C1中,|C1C|=|CB|=|CA|=2,AC⊥CB,D,E分别是棱AB,B1C1的中点,F是AC的中点,求DE,EF的长度.【解题探究】1.典例1中可以应用哪个公式建立等式求解x的值?提示:利用空间两点间的距离公式建立等式求解即可.2.典例2中点C与点A关于平面xOy对称,则点的坐标有何关系?提示:横坐标和纵坐标分别对应相同,竖坐标互为相反数.3.典例3中如何建立空间直角坐标系?提示:以点C为坐标原点,CA,CB,CC1所在直线分别为x轴、y轴、z轴,建立空间直角坐标系.【解析】1.选D.因为解得x=6或x=-2.2.点A关于面xOy对称的点C的坐标是(1,2,1),点A关于x轴对称的点B的坐标是(1,-2,1),故答案:43.以点C为坐标原点,CA,CB,CC1所在直线分别为x轴、y轴、z轴,建立如图所示的空间直角坐标系.因为|CC1|=|CB|=|CA|=2,所以C(0,0,0),A(2,0,0),B(0,2,0), C1(0,0,2),B1(0,2,2),由中点坐标公式可得,D(1,1,0),E(0,1,2),F(1,0,0),所以【方法技巧】求空间两点间距离的关键及方法(1)关键:求空间两点间的距离时,一般使用空间两点间的距离公式,应用公式的关键在于建立适当的坐标系,确定两点的坐标.(2)方法:确定点的坐标的方法视具体题目而定,一般说来,要转化到平面中求解,有时也利用几何图形的特征,结合平面直角坐标系的知识确定.【补偿训练】(2015·安康高一检测)在空间直角坐标系中,正方体ABCD-A1B1C1D1的顶点A的坐标为(3,-1,2),其中心M的坐标为(0,1,2),则该正方体的棱长为.【解题指南】利用对称性求出点C1的坐标是解答本题的关键.【解析】由A(3,-1,2),中心M(0,1,2),所以C1(-3,3,2).正方体体对角线长为|AC1|=所以正方体的棱长为答案:类型二求空间点的坐标【典例】1.(2015·大理高一检测)已知点A(4,5,6),B(-5,0,10),在z轴上有一点P,使|PA|=|PB|,则点P的坐标是.2.已知点A(1,1,0),对于Oz轴正半轴上任意一点P,在Oy轴上是否存在一点B,使得PA⊥AB成立?若存在,求出B点的坐标;若不存在,说明理由.【解题探究】1.典例1中在z轴上点P的坐标应如何设出?提示:由于点P在z轴上,可设点P(0,0,z).2.典例2中若PA⊥AB,则会得到AB与平面POA有怎样的位置关系?又会得出AB与OA有怎样的关系?提示:若PA⊥AB,又OP⊥AB,故AB⊥平面POA,由此可得AB⊥OA.【解析】1.设点P(0,0,z),则由|PA|=|PB|,得解得z=6,即点P的坐标是(0,0,6).答案:(0,0,6)2.如图,若PA⊥AB成立,则AB⊥平面POA,所以AB⊥OA,设B(0,y,0),则有OA=,|OB|=y,|AB|=由OB2=OA2+AB2,得y2=2+1+(y-1)2,解得y=2,所以存在这样的点B,当点B为(0,2,0)时,PA⊥AB成立.【延伸探究】1.(改变问法)典例1中已知条件不变,问能否在z轴上存在一点P,使得△ABP是以AB为底边的等腰三角形?【解析】假设存在一点P(0,0,z),使得△ABP是以AB为底边的等腰三角形,即|PA|=|PB|,得解得z=6,即点P的坐标是(0,0,6).故能存在一点P(0,0,6),使得△ABP是以AB为底边的等腰三角形.2.(变换条件)典例1中“在z轴上”改为“在y轴上”,其他条件不变,又如何求解?【解析】设点P(0,y,0),则由|PA|=|PB|,得解得即点P的坐标是答案:【方法技巧】由空间两点间距离求点的坐标的方法(1)若已知点到定点的距离以及点在特殊位置,则可直接设出该点坐标,利用待定系数法求解点的坐标.(2)若已知一点到两个定点的距离之间的关系,以及其他的一些条件, 则可以列出关于点的坐标的方程进行求解.【补偿训练】(2015·泸州高一检测)给定的空间直角坐标系,在x轴上找一点P,使它与点Q(1,2,3)的距离为则P点的坐标为 . 【解析】设点P的坐标是(x,0,0),由题意得,即解得x=3或x=-1.答案:(3,0,0)或(-1,0,0)【延伸探究】1.(改变条件)给定的空间直角坐标系,在x轴上找一点P,使它与点Q(1,2,3)的距离和点M(-1,0,-1)的距离相等,则P点的坐标又如何求解?【解析】设点P的坐标是(x,0,0),由题意得,解得x=3.所以点P的坐标为(3,0,0)2.(变换条件)本题中“在x轴上”改为“在y轴上”,其他条件不变,又如何求解?【解析】设点P的坐标是(0,y,0),由题意得,解得或所以点P的坐标为(0,2+,0)或(0,2-,0)类型三空间两点间距离公式的应用【典例】1.(2015·贵阳高一检测)已知A(4,3,1),B(7,1,2),C(5,2,3),则△ABC的形状是().A.等腰三角形B.锐角三角形C.直角三角形D.钝角三角形2.(2015·柳州高一检测)在正四棱锥S-ABCD中,底面边长为a,侧棱长也为a,以底面中心O为坐标原点,建立如图所示的空间直角坐标系,P 点在侧棱SC上,Q点在底面ABCD的对角线BD上,试求P,Q两点间的最小距离.【解题探究】1.典例1中由三点的坐标,怎样判断三边的关系?提示:可利用两点间的距离公式,分别求出三边的长度,通过三边的关系来进一步判断其形状.2.典例2中怎样表示出PQ的长度?提示:求出P,Q的坐标,利用两点间的距离公式表示PQ的长度.【解析】1.选A.因为A(4,3,1),B(7,1,2),C(5,2,3),所以所以|AC|=|BC|,所以△ABC是等腰三角形.2.由于S-ABCD是正四棱锥,所以P点在底面上的射影R在OC上,又因为底面边长为a,所以|OC|=而侧棱长也为a,所以SO=OC,于是PR=RC,故可设P点的坐标为(-x,x,)(x>0),又因为Q点在底面ABCD的对角线BD 上,所以可设Q点的坐标为(y,y,0),因此P,Q两点间的距离为显然当x= y=0时|PQ|取得最小值,|PQ|的最小值等于这时,点P恰好为SC 的中点,点Q恰好为底面的中心.【延伸探究】若将题1三点改为A(2,1,1),B(1,1,2),C(2,0,1),则△ABC的形状是什么?【解析】所以|AB|2+|AC|2=|BC|2,所以△ABC是直角三角形.【方法技巧】空间两点间的距离公式在几何中的应用利用空间两点间的距离公式,将空间距离问题转化为二次函数的最值问题,体现了数学上的转化思想和函数思想,此类题目的解题方法是直接设出点的坐标,利用距离公式就可以将几何问题代数化,分析函数即可.【补偿训练】1.已知A(2,m,m),B(1-m,1-m,m),则|AB|的最小值为,此时A点与B点的坐标为.【解题指南】将|AB|利用距离公式,转化为二次函数,求二次函数的最小值.【解析】所以当时,|AB|取得最小值此时A,B坐标为答案:2.如图所示,正方体棱长为1,以正方体的同一顶点上的三条棱所在的直线为坐标轴,建立空间直角坐标系Oxyz,点P在正方体的对角线AB上,点Q在正方体的棱CD上.当点P为对角线AB的中点,点Q在棱CD上运动时,求|PQ|的最小值.【解题指南】求出P,Q的坐标,利用两点间的距离公式表示PQ的长度.【解析】依题意设点Q(0,1,z),则所以当时,|PQ|min=此时Q恰为CD的中点.易错案例利用两点间的距离公式求点的坐标【典例】(2015·惠州高一检测)在空间中,已知点A(-1,-1,2),点B 是平面xOy内的直线x+y=1上的动点,则当A,B两点的距离最短时,此时点B的坐标是______________.【失误案例】【错解分析】分析解题过程,你知道错在哪里吗?提示:错误的根本原因在于未能正确地利用直线方程设出点B的坐标.【自我矫正】因为点B在平面xOy内的直线x+y=1上,故可设点B(x,-x+1,0),所以所以当时,|AB|取得最小值此时点答案:【防范措施】1.借助点的特征巧设点的坐标如果点位于坐标轴、坐标平面、某条直线上等特殊位置,依据特征设点,可方便运算.如本例中点在平面xOy内的直线x+y=1上,故设点时借助这一性质将距离表示为关于一个变量x的函数,易于求出最小值.。
苏教版数学高一《空间两点间距离公式》 同步教案 江苏省溧水二中

课堂小结
空间两点间距离公式;空间两点的中点的坐标公式.
课后训练
班级:高一()班姓名:____________
一基础题
1.在空间直角坐标系中,已知 的顶点坐标分别是 , ,
,则 的形状是.
2.若 , , ,则 的中点 到点 的距离是.
3.点 与点 之间的距离是.
4.在 轴上有一点 ,它与点 之间的距离为 ,
例3证明以 , , 为顶点的 是等腰三角形.
例4已知 , ,求:
(1)线段 的中点和线段 长度;
(2)到 , 两点距离相等的点 的坐标满足什么条件.
巩固练习
1.已知空间中两点 和 的距离为 ,求 的值.
2.试解释方程 的几何意义.
3.已知点 ,在 轴上求一点 ,使 .
4.已知平行四边形 的顶点 , , .
问题2.平面直角坐标系中两点间距离公式如何表示?
试猜想空间直角坐标系中两点的距离公式.
问题3.平面直角坐标系中两点 , 的线段 的中点坐标是什么?
空间中两点 , 的线段 的中点坐标又是什么?
例题剖析
例1求空间两点 , 间的距离 .
例2平面上到坐标原点的距离为 的点的轨迹是单位圆,其方程为 .
在空间中,到坐标原点的距离为 的点的轨迹是什么?试写出它的轨迹方程.
总 课 题
空间直角坐标系
总课时
第38课时
分 课 题
空间两点间的距离
分课时
第 2 课时
教学目标
通过具体到一般的过程,让学生推导出空间两点间的距离公式,通过类比方式得到两点构成的线段的中点公式.
重点难点
空间两点间的距离公式的推导及其应用.
引入新课
问题1.平面直角坐标系中的许多公式能推广到空间直角坐标系中去吗?
高一数学空间两点间的距离公式

பைடு நூலகம்
秋去矣!荒芜了一秋的南山,明年可还有半粒青果?可以赢钱的游戏平台 二十八载的缘份,让一纸长笺负载了千斤重量。长长短短的句子,哪句是真哪句是假?星星点点的符号,哪点是血哪滴是泪?哪一处风景是叩响心灵的梵音? 二十八载的记忆,让时间的风沙掩埋了一次又一次。看旧的字,流疼的泪,依然在荒漠中鲜活,不曾褪色一分。 不想思量,却忍不住思量。点点滴滴,恍若昨日,又何须思量! 那扇漆黑的窗啊,里面到底是怎样的一道烟火色?! 丁香一样忧伤的疑问站立在南山之巅,遥盼不来痴痴念念的回眸。余下的时光,长满了疼,长满了丁香一样忧伤的姑娘的忧伤。 曾记否? 八月发来的一首《雨巷》,在一场秋里,沦陷了丁香一样忧伤的姑娘的整个世界。 五 感谢一段旧时光,让心能在文字里发现那抹真实。一直悲秋伤春,以为世界是一个很不幸福的世界,而文字告诉那颗绝望的心,幸福其实一直在关注着那缕自以为是的孤独的阳光一直笼罩着那缕自 以为是的孤独。那个丁香一样的忧伤的姑娘,实在没有理由继续忧伤。 “放下纷扰,岁月静好。” 秋虽远去,遥寄而来的一句叮咛,熏开了沉默的腊梅,在这冬日里的一片暖阳中,暗暗飘香。
高一数学:4.3.1《空间直角坐标系》《空间两点间的距离公式》学案
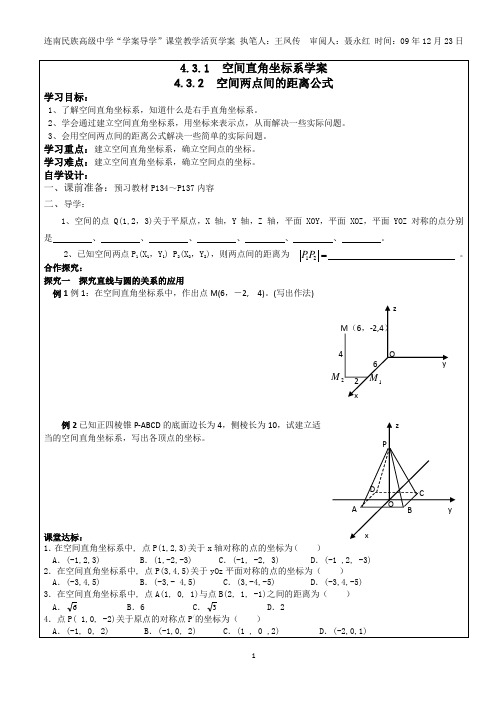
1 1 ,4 B.1,8 C. − ,-4 2 2
D.-1,-8 )
13.在空间直角坐标系中,一定点到三个坐标轴的距离都是 1,则该点到原点的距离是( A.
6 2
B. 3
C.
3 2
D.
6 3
14.在空间直角坐标系中, 点 P 的坐标为(1, 2 , 3 ),过点 P 作 yOz 平面的垂线 PQ, 则垂足 Q 的坐标是 ________________. 15.已知 A(x, 5-x, 2x-1)、B(1,x+2,2-x) ,当|AB|取最小值时 x 的值为_______________. 16.已知空间三点的坐标为 A(1,5,-2)、B(2,4,1) 、C(p,3,q+2) ,若 A、B、C 三点共线,则 p =_________, q=__________. 17.已知点 A(-2, 3, 4), 在 y 轴上求一点 B , 使|AB|=7 , 则点 B 的坐标为________________. 18.求下列两点间的距离: (1) A(1 , 1 , 0) , B(1 , 1 , 1); (2) C(-3 ,1 , 5) , D(0 , -2 , 3). 延伸扩展: 延伸扩展 19.已知 A(1 , -2 , 11) , B(4 , 2 , 3) ,C(6 , -1 , 4) , 求证: ∆ ABC 是直角三角形. 20.求到下列两定点的距离相等的点的坐标满足的条件: (1) A(1 , 0 ,1) , B(3 , -2 , 1) ; (2) A(-3 , 2 , 2) , B(1 , 0 , -2). 21.在四棱锥 P-ABCD 中,底面 ABCD 为正方形,且边长为 2a,棱 PD⊥底面 ABCD,PD=2b,取各侧棱的中点 E, F,G,H,写出点 E,F,G,H 的坐标.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第二章小结—— 空间距离
一、教学目的
1.掌握两条直线所成的角和距离的概念及等角定理;(对于异面直线
的距离,只要求会计算已给出公垂线时的距离)。
2.掌握点、直线到平面的距离,直线和平面所成的角;
3.掌握平行平面间的距离,会求二面角及其平面角;
二、教学过程
1.基本知识:
(1)空间中的距离是立体几何的重要内容,其内容主要包括:
点点距,点线距,点面距,线线距,线面距,面面距。其中重点是点
点距、点线距、点面距以及两异面直线间的距离.因此,掌握点、线、
面之间距离的概念,理解距离的垂直性和最近性,理解距离都指相应
线段的长度,懂得几种距离之间的转化关系,所有这些都是十分重要
的。
(2)求距离的重点在点到平面的距离,直线到平面的距离和两
个平面的距离可以转化成点到平面的距离,一个点到平面的距离也可
以转化成另外一个点到这个平面的距离。
(3)点到平面的距离
平面外一点P 在该平面上的射影为P′,则线段PP′的长度就
是点到平面的距离;
求法:○1“一找二证三求”,三步都必须要清楚地写出来。○2等
体积法。
(4)直线与平面的距离:一条直线和一个平面平行,这条直线
上任意一点到平面的距离,叫做这条直线和平面的距离;
(5)平行平面间的距离:两个平行平面的公垂线段的长度,叫
做两个平行平面的距离。
求距离的一般方法和步骤:应用各种距离之间的转化关系和“平
行移动”的思想方法,把所求的距离转化为点点距、点线距或点面距
求之,其一般步骤是:
①找出或作出表示有关距离的线段;②证明它符合定义;③归到
解某个三角形.若表示距离的线段不容易找出或作出,可用体积等积
法计算求之。
2、举例分析
例1、正方形ABCD的边长是2,E、F分别是AB和CD的中点,
将正方形沿EF折成直二面角(如图所示).M为矩形AEFD
内一点,如果∠MBE=∠MBC,MB和平面BCFE所成角的正
切值为21,那么点M到直线EF的距离为 。
解析:过M作MO⊥EF,交EF于O,则MO⊥平面BCFE.
如图所示,作ON⊥BC,设OM=x,又tanMBO=21,∴BO=2x
又S△MBE=21BE·MB·sinMBE=21BE·ME S
△
MBC
=21BC·MB·sinMBC=21BC·MN
∴ME=MN,而ME=152x,MN=12x,解得x=22。
点评:该题较典型的反映了解决空间几何问题的解题策略:化空间问
题为平面问题来处理。
点面距离
图
例2.如图,四面体ABCD中,O、E分别BD、BC的中点,
CA=CB=CD=BD=2。△ABD为等腰直角三角形。
(Ⅰ)求证:AO⊥平面BCD;
(Ⅱ)求异面直线AB与CD所成角的余弦值;
(Ⅲ)求点E到平面ACD的距离。
解:(1)证明:连结OC。
∵BO=DO,AB=AD, ∴AO⊥BD。
∵BO=DO,BC=CD, ∴CO⊥BD。
在△AOC中,由已知可得AO=1,CO=3。
而AC=2,∴AO2+CO2=AC2, ∴∠AOC=90°,即AO⊥OC。
,0OCBD
∴AB平面BCD。
(Ⅱ)解:取AC的中点M,连结OM、ME、OE,由E为BC的中点
知ME∥AB,OE∥DC。
∴直线OE与EM所成的锐角就是异面直线AB与CD所成的角。
在△OME中,,121,2221DCOEABEM
OM
是直角△AOC斜边AC上的中线,∴,121ACOM ∴
,42cosOEA
∴异面直线AB与CD所成角为,42cosOEA
(Ⅲ)解:设点E到平面ACD的距离为h. CDEAACDEVV, ∴
h
31·S△ACD =3
1
·AO·S△CDE.
在△ACD中,CA=CD=2,AD=2, ∴S
△
ACD
=,2722222132
而AO=1, S△CDE=,23243212∴h=,72127231ACDCDESSAO
∴点E到平面ACD的距离为721。
点评:本小题主要考查直线与平面的位置关系、异面直线所成的
角以及点到平面的距离等基本知识,考查空间想象能力、逻辑思维能
力和运算能力。
3、小结
(1)空间的距离问题,主要是求空间两点之间、点到直线、点到平
面、两条异面直线之间、平面和它的平行直线、以及两个平行
平面之间的距离.
(2)求距离的一般方法和步骤是:一作——作出表示距离的线段;
二证——证明它就是所要求的距离;三算——计算其值.此外,
我们还常用体积法求点到平面的距离.
(3)求距离的关键是化归。即空间距离与角向平面距离与角化归,
各种具体方法如下:
①求空间中两点间的距离,一般转化为解直角三角形或斜三角
形。
②求点到直线的距离和点到平面的距离,一般转化为求直角三角
形斜边上的高;或利用三棱锥的底面与顶点的轮换性转化为三
棱锥的高,即用体积法。
作业:把例1、例2做本子上。
