第二部分最小二乘法OLS和线回归模型资料讲解
(9)12.9两阶段最小二乘法

ˆ Qt = β 0 + β 1 P t + β 2 W t +
u∗ t 2
(12.9.11)
其中 Pt 的数值由第一阶段的OLS估计式(12.9.10)算 ˆ 出(见表12.9.1)。 再用OLS法分别对模型(12.9.11)中每个方程进行估计, 得出模型(12.9.11)的2SLS估计式,如图12.9.2和图12.9.3 所示:
y1t = Π 11 x1t + Π 12 x 2t + v1t y 2t = Π 21 x1t + Π 22 x 2t + v 2t
(12.9.2)
对约简型的每个方程应用OLS法,得
ˆ ˆ ˆ y1t = Π 11 x1t + Π 12 x 2t ˆ ˆ ˆ y 2t = Π 21 x1t + Π 22 x 2t
(12.9.3)
于是有
ˆ y1t = y1t + ε 1t ˆ y 2t = y 2t + ε 2t
(12.9.4)
其中ε1t,ε2t分别为v1t,v2t的OLS估计量。 第二阶段 将(12.9.4)代入被估计的结构方程(12.9.1)的右边的 内生变量:
ˆ y1t = β 2 y 2t + γ 1 x1t + ε
Qt = α 0 + α 1 Pt + α 2 Y t + u1t Qt = β 0 + β 1 Pt + β 2 W t + u 2t
(12.9.8)
可以证明两个方程皆可恰好识别。样本数据列表于 表12.9.1。 第一阶段: 写出约简式: Pt=Π10 + Π11Yt + Π12Wt + v1t (12.9.9)
普通最小二乘回归法

普通最小二乘回归法第1页普通最小二乘回归法普通最小二乘回归法(Ordinary Least Squares,OLS)是一种统计学方法,它把拟合直线的不确定性归入到残差的不确定性中,使拟合直线尽可能接近数据的偏差。
就是把一组样本数据,用最佳拟合函数来解释它,使参数矩阵的乘积最小化。
普通最小二乘回归法是一种简单的线性回归方法,它假设样本的特征之间没有相互关系,因此忽略了任何影响模型拟合程度的复杂性。
OLS的基本原理是通过最小化残差的平方来最小化总体模型预测的误差平方。
残差指观测值和预测值之间的差值。
普通最小二乘回归的模式是一个线性回归模型,它把数据表示为一个函数,数据拟合的效果要比最大似然法好得多。
普通最小二乘回归的优点1. 简单:能够用少量的步骤完成。
2. 快速:有算法可以用来更快地计算最小二乘回归。
3. 准确:可以更准确地预测数据。
4. 稳定:抗噪声能力较强。
第2页普通最小二乘回归的应用普通最小二乘回归是一种非常有用的数据拟合方法,它有很多应用领域,包括经济学、工程学、生物学、计算机科学、物理学等等。
1. 经济学:普通最小二乘回归经常被用来拟合研究经济问题,比如薪水、物价、汇率等数据。
2. 生物学:普通最小二乘回归可以用来拟合特定基因的表达水平与某种疾病的相关性等。
3. 计算机科学:可以用来判断计算机程序的性能和执行速度。
4. 工程学:用来估算各种物料的力学特性、汽车、飞机的性能等等。
普通最小二乘回归的缺点1. 拟合时关系必须是线性的:普通最小二乘法假定样本的特征之间的关系必须是一元或多元线性关系。
如果关系是非线性的,则模型效果可能不好。
2. 数据需要服从正态分布:最小二乘回归的假设之一就是数据服从正态分布,但在实际应用中常常会出现非正态分布的数据,这时最小二乘回归可能就不再有效了。
3. 方程解受多元共线数据的影响大:多元共线数据会严重影响方程解的收敛性,导致模型无法正确拟合。
2.2 多元回归模型的OLS 估计

2.2 多元回归模型的OLS 估计多元回归模型在实际问题中经常被用来对一个因变量与两个或两个以上自变量的关系进行建模和预测。
常用的估计方法是OLS(最小二乘)估计。
本文将对多元回归模型的OLS 估计进行详细介绍。
1. 多元线性回归模型的建立$Y = \beta_0 + \beta_1X_1 + \beta_2X_2 + \cdots + \beta_kX_k + \epsilon$其中,$Y$ 为因变量,$X_1, X_2,\cdots, X_k$ 为自变量,$\beta_0, \beta_1,\beta_2,\cdots, \beta_k$ 为回归系数,$\epsilon$ 为误差项。
利用最小二乘估计,我们可以通过拟合一条直线或曲线使估计误差最小,来估计模型中的未知参数。
最小二乘法的目标就是使残差平方和最小。
OLS 估计是多元线性回归中最常用、最有效的方法之一。
OLS 估计方法就是按照最小二乘法的思想,通过最小化误差平方和来求出回归方程中的估计参数。
具体来说,我们可以利用正规方程(normal equation)来求解参数估计值。
设 $X$ 是 $n \times k$ 的样本自变量数据矩阵,$Y$ 是 $n$ 维因变量向量,$b$ 是 $k$ 维参数向量,我们可以通过最小化误差平方和,找到回归系数的最优解:$\min_{b} \ \sum_{i=1}^{n}(Y_i-X_ib)^2$我们对 $b$ 求导并令导数为 0,可以得到正规方程:$X^TXb=X^TY$其中,$X^T$ 表示 $X$ 的转置矩阵。
对于非满秩矩阵 $X$,正规方程可能无解或者存在无数解。
因此,我们需要在实际应用中注意检查矩阵的秩。
(1)OLS 估计是一种无偏的估计方法,即在样本量足够大时,估计值的期望等于真实值。
这使得 OLS 估计在实际应用中更具有可靠性。
(2)OLS 估计是一种最优的线性无偏估计方法,可以最小化在误差平方和最小的情况下使得估计值最接近真实值。
ols原理

ols原理OLS原理,即最小二乘法原理,是统计学中常用的一种参数估计方法。
它的核心思想是通过最小化残差平方和,来确定模型中的参数估计值。
本文将从最小二乘法的基本原理、应用领域以及优缺点等方面进行阐述。
最小二乘法的基本原理是建立在一系列假设条件下的。
假设我们有一个线性回归模型,其中自变量与因变量之间存在线性关系,即因变量可以通过自变量的线性组合来表示。
最小二乘法的目标是找到最优的参数估计值,使得模型预测值与观测值之间的差距最小。
具体而言,我们可以通过求解最小化残差平方和的优化问题,得到参数的估计值。
最小二乘法在许多领域都有广泛的应用。
首先,在经济学中,最小二乘法常用于估计经济模型中的参数。
例如,在计量经济学中,我们可以通过最小二乘法来估计供求模型中的价格弹性。
其次,在工程学中,最小二乘法可以用于信号处理、图像处理等领域。
例如,在图像处理中,我们可以通过最小二乘法来实现图像的去噪和恢复。
此外,在金融学、医学、社会学等学科中,最小二乘法也有着广泛的应用。
最小二乘法具有一些优点,但也存在一些缺点。
首先,最小二乘法是一种直观、易于理解的方法,能够得到解析解,计算相对简单。
其次,最小二乘法在假设条件满足的情况下,可以得到无偏、有效的参数估计值。
然而,最小二乘法也有一些局限性。
首先,最小二乘法对异常值敏感,异常值的存在可能会对参数估计结果产生较大的影响。
其次,最小二乘法要求模型满足线性关系的假设,对于非线性关系的数据拟合效果可能较差。
此外,最小二乘法还要求模型的误差项满足独立同分布的假设,若误差项的分布存在异方差性或自相关性,可能会导致参数估计的偏误。
OLS原理是一种常用的参数估计方法,通过最小化残差平方和来确定模型中的参数估计值。
最小二乘法在经济学、工程学等领域有着广泛的应用。
虽然最小二乘法具有一些优点,如直观、易于理解,但也存在一些缺点,如对异常值敏感、对非线性关系的拟合效果较差等。
因此,在使用最小二乘法时,需要根据具体问题的特点和要求,权衡其优缺点,选择合适的参数估计方法。
简单线性回归模型 PPT课件

• y = b0 + b1x + u…………(2.1)
• 且假定方程(2.1)在我们所关注的某个总体 中成立,它定义了一个简单线性回归模型 (simple linear regression model)。因为它把 两个变量x和y联系起来,所以又把它叫做 两变量或者双变量线性回归模型。我们现 在来讨论等式(2.1)中每个量的含义。
• 在写出用x解释y的模型时,我们要面临三 个问题。
– 首先,既然两个变量之间没有一个确切的关系, 那么我们应该如何考虑其他影响y的因素呢? – 第二,y和x的函数关系是怎样的呢? – 第三,我们怎样知道是否抓住了在其他条件不 变的情况下y和x之间的关系(如果这是我们所 追求的目标的话)呢?
简单回归模型的定义
关于u和x的关系的关键性假定
• 需要一个关键假设来约定u和x之间 的关系。我们希望关于x的信息不会 透露关于u的任何信息,也就是说, 两者应该是完全无关的。
关于u和x的关系的关键性假定
• 因为u和x是随机变量,所以我们能够在任 何给定的x值下得到u的条件分布。具体地 说,对于任何一个x值,我们都能够在x的 值所描述的总体剖面上求得u的期望(或平 均)值。因此,一种好的方法是对给定x时 u的期望值作出假定。 • 故关键的假定是:u的平均值不依赖于x值。 也即: E(u|x) = E(u) = 0…… (2.6) • 也就意味着: E(y|x) = b0 + b1x
y ie ld b 1 fe r tiliz e r
• 例2.2 一个简单的工资方程 • 以下模型表示一个人的工资水平与他的可测教育水 平及其他非观测因素的关系:
计量经济学 第二章 一元线性回归模型
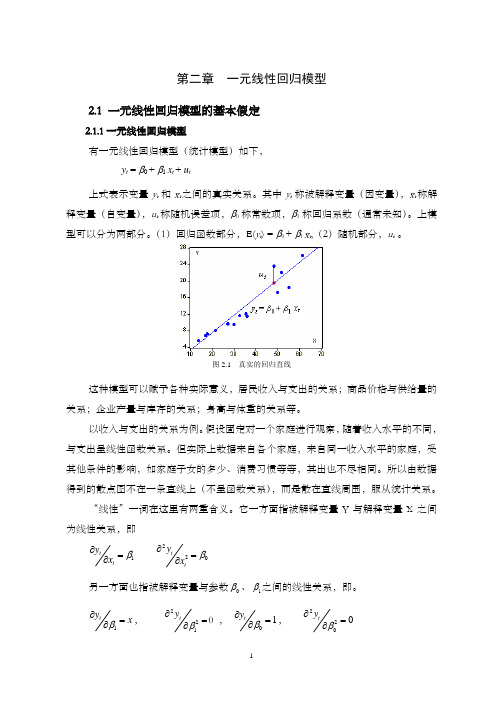
第二章 一元线性回归模型2.1 一元线性回归模型的基本假定2.1.1一元线性回归模型有一元线性回归模型(统计模型)如下, y t = β0 + β1 x t + u t上式表示变量y t 和x t 之间的真实关系。
其中y t 称被解释变量(因变量),x t 称解释变量(自变量),u t 称随机误差项,β0称常数项,β1称回归系数(通常未知)。
上模型可以分为两部分。
(1)回归函数部分,E(y t ) = β0 + β1 x t ,(2)随机部分,u t 。
图2.1 真实的回归直线这种模型可以赋予各种实际意义,居民收入与支出的关系;商品价格与供给量的关系;企业产量与库存的关系;身高与体重的关系等。
以收入与支出的关系为例。
假设固定对一个家庭进行观察,随着收入水平的不同,与支出呈线性函数关系。
但实际上数据来自各个家庭,来自同一收入水平的家庭,受其他条件的影响,如家庭子女的多少、消费习惯等等,其出也不尽相同。
所以由数据得到的散点图不在一条直线上(不呈函数关系),而是散在直线周围,服从统计关系。
“线性”一词在这里有两重含义。
它一方面指被解释变量Y 与解释变量X 之间为线性关系,即1tty x β∂=∂220tt y x β∂=∂另一方面也指被解释变量与参数0β、1β之间的线性关系,即。
1ty x β∂=∂,221ty β∂=∂0 ,1ty β∂=∂,2200ty β∂=∂2.1.2 随机误差项的性质随机误差项u t 中可能包括家庭人口数不同,消费习惯不同,不同地域的消费指数不同,不同家庭的外来收入不同等因素。
所以在经济问题上“控制其他因素不变”是不可能的。
随机误差项u t 正是计量模型与其它模型的区别所在,也是其优势所在,今后咱们的很多内容,都是围绕随机误差项u t 进行了。
回归模型的随机误差项中一般包括如下几项内容: (1)非重要解释变量的省略, (2)数学模型形式欠妥, (3)测量误差等,(4)随机误差(自然灾害、经济危机、人的偶然行为等)。
eviews两阶段最小二乘法步骤
eviews两阶段最小二乘法步骤最小二乘法(OLS)是一种常用的线性回归参数估计方法。
然而,有时候样本数据可能同时受到外部因素和内部因素的影响,导致OLS估计出的参数具有偏误。
为了应对这个问题,经济学家和统计学家提出了两阶段最小二乘法(2SLS)。
两阶段最小二乘法是基于一种被称为工具变量的技术。
在使用OLS 估计线性回归模型时,我们经常会面对内生性问题,即自变量和误差项之间可能存在内生性关系,导致OLS估计结果不准确甚至出现偏误。
这时候,我们就需要引入一个工具变量来解决内生性问题。
两阶段最小二乘法的步骤大致可以分为两个阶段:第一阶段:工具变量的选择在两阶段最小二乘法中,首先需要确定一个或多个工具变量。
工具变量应当满足两个条件:第一,与内生自变量相关;第二,与回归方程的误差项不相关。
通常情况下,工具变量的选择需要通过经验和理论知识来确定。
例如,如果我们想要研究教育对收入的影响,而教育受家庭背景的影响,那么我们可以选择父母教育水平作为工具变量。
第二阶段:两阶段最小二乘法的估计在第一阶段确定了工具变量之后,接下来就是进行两阶段最小二乘法的估计。
这个过程可以分为两个步骤。
在第一步中,我们使用工具变量来估计内生自变量,得到估计值。
在第二步中,我们将这些估计值代入原始回归方程中,然后利用OLS对整个模型进行估计,得到最终的参数估计结果。
两阶段最小二乘法的步骤相对于OLS来说更为复杂,但它能够有效地解决内生性问题,得到更加准确的参数估计结果。
然而,同时也需要注意的是,在使用两阶段最小二乘法时需要满足一些前提条件,比如工具变量的有效性和外生性等。
如果这些前提条件不满足,那么两阶段最小二乘法的结果可能会出现偏误。
总之,两阶段最小二乘法是一种强大的工具,能够有效地应对内生性问题,提高线性回归模型的参数估计准确性。
在实际应用中,研究者需要根据具体情况来选择合适的工具变量,并严格遵守两阶段最小二乘法的步骤,以获得可靠的结果。
普通最小二乘法
选择合适的回归模型,如线性回归、多项式回归等。
设定模型假设
确保满足回归分析的基本假设,如误差项独立同分布、误差项无系统偏差等。
建立模型
利用最小二乘法计算回归参数的最优估计值。
分析估计量的性质,如无偏性、有效性等,确保估计结果可靠。
参数估计
检验估计量性质
计算最小二乘估计量
03
模型选择与优化
普通最小二乘法的历史与发展
02
普通最小二乘法的原理
01
02
03
线性回归模型是一种预测模型,通过找到最佳拟合直线来预测因变量的值。
在线性回归模型中,自变量和因变量之间存在线性关系,即因变量可以表示为自变量的线性组合。
线性回归模型的一般形式为:y = β0 + β1x1 + β2x2 + ... + βpxp + ε,其中y是因变量,x1, x2, ..., xp是自变量,β0, β1, β2, ..., βp是参数,ε是误差项。
详细描述
主成分回归是一种基于主成分分析的回归方法,通过提取解释变量中的主要成分,降低数据的维度,提高模型的解释性和稳定性。
总结词
主成分回归首先对解释变量进行主成分分析,提取出解释变量中的主要成分,然后将这些主成分作为新的解释变量进行回归分析。由于主成分能够反映原始变量中的大部分信息,因此这种方法能够减少数据的维度,降低多重共线性的影响,提高模型的稳定性和解释性。
无偏性
普通最小二乘法估计的参数具有无偏性,即估计的期望值等于真实值。
最佳线性无偏估计
普通最小二乘法能得到最佳线性无偏估计,即估计的方差最小。
优点
异方差性
普通最小二乘法对数据的异方差性敏感,可能导致估计结果失真。
普通最小二乘法
对随机扰动项u的假定
假定1:零均值假定:
u 在给定X的条件下, 的条件期望为零 i
E(ui Xi ) 0
假定2:同方差假定:
在给定X的条件下, 的条件
方差为某个常数 ui
2
Y
E(Y Xi )
Var(ui X i ) E[ui E(ui X i )]2 2
第14页/共33页
23
第23页/共33页
概
率
密
度
f ( )
f (ˆ )
f (*)
估计值
24
第24页/共33页
3、渐近性质(大样本性质)
思想:当样本容量较小时,有时很难找到方差最小的无偏估计,
需要考虑样本扩大后的性质(估计方法不变,样本数逐步增大)
一致性:
当样本容量 n 趋于无穷大时,如果
数的真实值,就称这个估计ˆ式 是
解得模型的参数估计量为:
ˆ
0
ˆ1
X
2 i
Yi
X iYi
nX
2 i
(X
i
)2
nYi X i YiX
nX
2 i
(X i
)2
X
i
i
可见,在满足一系列基本假设的情况下,模型 结构参数的最大或然估计量与普通最小二乘估计 量是相同的。
第11页/共33页
简单线性回归模型的最小二乘估计
用样本去估计总体回归函数,总要使用特定的方法,而任 何估
Xi X
14
假定3:无自相关假定:
随机扰动项 u i的逐次值互不相关
Cov(ui ,u j ) E[ui E(ui )][u j E(u j )]
E(uiu j ) 0
计量经济学第二章
y ˆ0 ˆ1x
ˆ0 y ˆ1x
由cov(x,u)=E(xu)=0 得E[x(y – 0 – 1x)] = 0
对于给定的数据样本,有
n
n1 xi yi ˆ0ˆ1xi 0
i1
n
xi yi y ˆ1x ˆ1xi 0
i 1
n
n
xi yi y ˆ1 xi xi x
OLS的无偏性 OLS估计量的方差
计量
38
OLS的无偏性
我们首先在一组简单假定的基础上构建 OLS的无偏性。
假定SLR.1 线性于参数 在总体模型中,因变量y与自变量x的误差项u的
关系如下: y 0 1x u
其中, 0 和 1 分别表示总体的截距和斜率参数。
计量
39
OLS的无偏性
假定SLR.2 随机抽样 我们具有一个服从从整体模型方程
E(yxi)01xi
yi 01xi ui
yˆi ˆ 0 ˆ1 xi
yi ˆ0 ˆ1 xi ei
如果能够通过某种方式获得
ˆ
1 和ˆ
的数值,显然:
0
● ˆ 1 和 ˆ 0是对总体回归函数参数 1 和 0 的估计
●
yˆ
是对总体条件期望
i
E ( y x i ) 的估计
● e i 在概念上类似总体回归模型中的u i ,可视
yi y 2 yi yˆi yˆi y 2 uˆi yˆi y 2
uˆi2 2uˆi yˆi y yˆi y 2 SSR 2uˆi yˆi y SSE 又因为uˆi yˆi y 0,所以得证
计量
31
拟合优度
拟合优度(又称判定系数)
我们定义R2 = SSE/SST = 1 – SSR/SST为拟合 优度,又称判定系数,总是介于0到1之间
