第63炼立体几何中的建系设点问题

合集下载

立体几何中的各种建系

直角建系
•以三条相互垂直的线为坐标轴。

•常用于简单多面体，例如长方体、正方体和菱形十二面体。

极坐标系
•以一个点为极点，一个线段为极轴。

•坐标由极点到点的距离（极径）和极轴与线段之间的夹角（极角）表示。

•常用于球体和圆柱体。

柱面坐标系
•以一个轴为 z 轴，与该轴相交的两条平行线为 x 轴和 y 轴。

•坐标由点到 z 轴的距离（柱面半径）、点到 x 轴的投影与 z 轴的夹角（柱面角）和点到 z 轴投影到 x-y 平面的距离（高度）表示。

•常用于圆柱体和圆锥体。

球面坐标系
•以一个点为极点，两个相互垂直的半径为经线和纬线。

•坐标由极点到点的距离（极径）、纬线与极点连线的夹角（纬度）和经线与参考经线的夹角（经度）表示。

•常用于球体。

双极坐标系
•以两个点为焦点的双曲线的一个分支。

•坐标由点到两焦点的距离之差和点到该分支的距离之和表示。

•常用于轨迹和电磁场问题。

椭圆柱坐标系
•以三个相互正交的椭圆为坐标轴。

•坐标由点到三个椭圆的距离表示。

•常用于椭圆柱体和椭圆锥体。

抛物柱坐标系
•以一个抛物线的一个分支和该抛物线的准线为坐标轴。

•坐标由点到抛物线分支的距离和点到准线的距离之差表示。

•常用于抛物柱体和抛物锥体。

柱面-球面坐标系
•极坐标系和柱面坐标系的组合。

•坐标由极径、极角、柱面半径和高度表示。

•常用于圆柱球体和球冠。

立体几何解题建系策略(有答案)

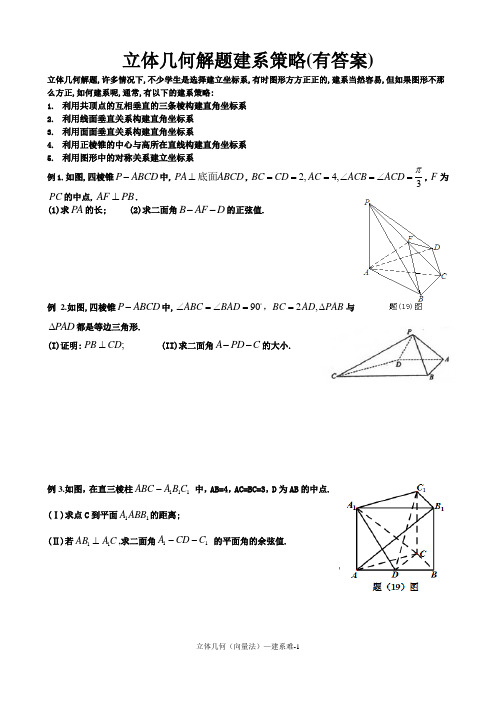
立体几何解题建系策略(有答案)立体几何解题,许多情况下,不少学生是选择建立坐标系,有时图形方方正正的,建系当然容易,但如果图形不那么方正,如何建系呢,通常,有以下的建系策略: 1. 利用共顶点的互相垂直的三条棱构建直角坐标系 2. 利用线面垂直关系构建直角坐标系 3. 利用面面垂直关系构建直角坐标系4. 利用正棱锥的中心与高所在直线构建直角坐标系5. 利用图形中的对称关系建立坐标系例1.如图,四棱锥P ABCD -中,PA ABCD ⊥底面,2,4,3BCCD AC ACB ACD π===∠=∠=,F 为PC 的中点,AF PB ⊥.(1)求PA 的长; (2)求二面角B AF D --的正弦值.例 2.如图,四棱锥P ABCD -中,902,ABC BAD BC AD PAB ∠=∠==∆，与PAD ∆都是等边三角形.(I)证明:;PB CD ⊥ (II)求二面角A PD C --的大小.例3.如图，在直三棱柱111C B A ABC - 中，AB=4，AC=BC=3，D 为AB 的中点. (Ⅰ)求点C 到平面11ABB A 的距离;(Ⅱ)若11AB A C ⊥,求二面角11A CD C -- 的平面角的余弦值.例4.如图，在三棱柱ABC －A 1B 1C 1中，已知AB ＝AC ＝AA 1＝5，BC ＝4，点A 1在底面ABC 的投影是线段BC 的中点O .(1)证明在侧棱AA 1上存在一点E ，使得OE ⊥平面BB 1C 1C ，并求出AE 的长； (2)求平面A 1B 1C 与平面BB 1C 1C 夹角的余弦值．例5.平面图形ABB 1A 1C 1C 如图(1)所示，其中BB 1C 1C 是矩形，BC ＝2，BB 1＝4，AB ＝AC ＝2，A 1B 1＝A 1C 1＝ 5.现将该平面图形分别沿BC 和B 1C 1折叠，使△ABC 与△A 1B 1C 1所在平面都与平面BB 1C 1C 垂直，再分别连接A 1A ，A 1B ，A 1C ，得到如图(2)所示的空间图形．对此空间图形解答下列问题． (1)证明：AA 1⊥BC ； (2)求AA 1的长；(3)求二面角A －BC －A 1的余弦值．例6.如图,四棱锥S-ABCD 中,,AB CD BC CD ⊥,侧面SAB 是等边三角形,AB=BC=2,CD=SD=1. ⑴证明:SD ⊥面SAB ;⑵求AB 与平面SBC 所成角的正弦值.例7.如图,在多面体ABCDEF 中,四边形ABCD 是正方形,//EFAB ,EF FB ⊥,2AB EF =,90BFC ∠=︒,BF FC =,H 为BC 的中点. ⑴求证://FH 面EDB ;⑵求证: ACEDB ⊥面;⑶求二面角B-DE-C 的大小.例8.如图,BCD ∆与MCD ∆都是边长为2的正三角形,平面MCD ⊥平面BCD ,AB ⊥面BCD ,AB=23.⑴求点A 到平面MBC 的距离;⑵求平面ACM 与平面BCD 所成二面角的正弦值.例9.在如图所示的几何体中,四边形ABCD 为平行四边形,90ACB ∠=︒,EA ⊥面ABCD ,//,EF AB //,FG BC //,2.EG AC AB EF =⑴若M 是线段AD 的中点,求证://ABFE GM 面; ⑵若AC=BC=2AG,求二面角A-BF-C 的大小.例10.如图,四棱锥P ABCD -中,底面ABCD 是菱形,PA ⊥面ABCD ,22,2,AC PA ==E 是PC 上的一点,2PE EC =.⑴证明:PC ⊥面BED ;⑵设二面角A-PB-C 为90︒,求PD 与平面PBC 所成角的大小.例11.如图,在三棱锥P ABC -中,90APB ∠=︒,60PAB ∠=︒,AB BC CA ==,面PAB ⊥面ABC .⑴求直线PC 与平面ABC 所成角的大小; ⑵求二面角B-AP-C 的大小.例12.如图，在四棱锥中,, 且6,PB BC BD ===222CD AB ==,120PAD ∠=︒.（1）求证：平面平面；（2）求直线与平面所成的角的正弦值．例13.如图，在三棱锥P −ABC 中，△ABC 是正三角形，面PAB ⊥面ABC ，∠PAB =30°，AB =PB =2，△ABC 和△PBC 的重心分别为D ，E .(1)证明：DE ∥面PAB ;(2)求AB 与面PDE 所成角的正弦值.例14.如图,AB 是圆的直经,PA 垂直圆所在的平面,C 是圆上的点, ⑴求证:平面PAC ⊥面PBC ;⑵若AB=2,AC=1,PA=1,求二面角C-PB-A 的余弦值.例15.已知两个正四棱锥P －ABCD 与Q －ABCD 的高都为2，AB ＝4．（1）证明：PQ ⊥平面ABCD ；（2）求异面直线AQ 与PB 所成的角；（3）求点P 到平面QAD 的距离．例16.如图，三棱锥P —ABC 的底面ABC 是等腰直角三角形，AB ⊥BC ，AB=BC=2,PA=PC=22,二面角P —B C —A 等于︒45.（Ⅰ）求证：AC ⊥PB ；（Ⅱ）求PA 与面PBC 所成角的大小.PED CBA例17.如图，三棱台DEF —ABC 中，面ADFC ⊥面ABC ，∠ACB =∠ACD =45°，DC =2BC ．（I ）证明：EF ⊥DB ；（II ）求DF 与面DBC 所成角的正弦值．例18.如图，已知二面角βα--l 的大小为045,直角ABC ∆的两条直角边22=AB ，3=AC ，边AB在平面β内，且l AB ⊥，点C 在平面α内.将直角ABC ∆绕AC 边转动到ACP ∆,且AP 在平面β内，045=∠BAP .(Ⅰ)求证：⊥l 平面ABC ；(Ⅱ)求直线CP 与平面α所成角的正弦值.参考答案:例1 （2013年普通高等学校招生统一考试重庆数学（理）试题（含答案））如图,四棱锥P ABCD-中,PA ABCD ⊥底面,2,4,3BC CD AC ACB ACD π===∠=∠=,F 为PC 的中点,AF PB ⊥.(1)求PA 的长; (2)求二面角B AF D --的正弦值.【答案】解：(1)如图，联结BD 交AC 于O ，因为BC ＝CD ，即△BCD 为等腰三角形，又AC 平分∠BCD ，故AC ⊥BD .以O 为坐标原点，OB →，OC →，AP →的方向分别为x 轴，y 轴，z 轴的正方向，建立空间直角坐标系O －xyz ，则OC ＝CD cos π3＝1，而AC ＝4，得AO ＝AC －OC ＝3.又OD ＝CD sin π3＝3，故A (0，－3，0)，B (3，0，0)，C (0，1，0)，D (－3，0，0)．因P A ⊥底面ABCD ，可设P (0，－3，z )，由F 为PC 边中点，得F ⎝⎛⎭⎫0，－1，z 2，又AF →＝⎝⎛⎭⎫0，2，z 2，PB →＝(3，3，－z )，因AF ⊥PB ，故AF →·PB →＝0，即6－z 22＝0，z ＝2 3(舍去－2 3)，所以|P A →|＝2 3.(2)由(1)知AD →＝(－3，3，0)，AB →＝(3，3，0)，AF →＝(0，2，3)．设平面F AD 的法向量为1＝(x 1，y 1，z 1)，平面F AB 的法向量为2＝(x 2，y 2，z 2)．由1·AD →＝0，1·AF →＝0，得⎩⎨⎧－3x 1＋3y 1＝0，2y 1＋3z 1＝0，因此可取1＝(3，3，－2)．由2·AB →＝0，2·AF →＝0，得⎩⎨⎧3x 2＋3y 2＝0，2y 2＋3z 2＝0，故可取2＝(3，－3，2)．从而向量1，2的夹角的余弦值为 cos 〈1，2〉＝n 1·n 2|n 1|·|n 2|＝18.故二面角B －AF －D 的正弦值为3 78.例2（2013年普通高等学校招生统一考试大纲版数学（理）WORD 版含答案（已校对））如图,四棱锥P ABCD-中,902,ABC BAD BC AD PAB ∠=∠==∆，与PAD ∆都是等边三角形. (I)证明:;PB CD ⊥ (II)求二面角A PD C --的大小.【答案】解：(1)取BC 的中点E ，联结DE ，则四边形ABED 为正方形．过P 作PO ⊥平面ABCD ，垂足为O . 联结OA ，OB ，OD ，OE .由△P AB 和△P AD 都是等边三角形知P A ＝PB ＝PD ，所以OA ＝OB ＝OD ，即点O 为正方形ABED 对角线的交点，故OE ⊥BD ，从而PB ⊥OE .因为O 是BD 的中点，E 是BC 的中点，所以OE ∥CD .因此PB ⊥CD .(2)解法一：由(1)知CD ⊥PB ，CD ⊥PO ，PB ∩PO ＝P ，故CD ⊥平面PBD .又PD ⊂平面PBD ，所以CD ⊥PD .取PD 的中点F ，PC 的中点G ，连FG . 则FG ∥CD ，FG ⊥PD .联结AF ，由△APD 为等边三角形可得AF ⊥PD . 所以∠AFG 为二面角A －PD －C 的平面角．联结AG ，EG ，则EG ∥PB . 又PB ⊥AE ，所以EG ⊥AE .设AB ＝2，则AE ＝2 2，EG ＝12PB ＝1，故AG ＝AE 2＋EG 2＝3，在△AFG 中，FG ＝12CD ＝2，AF ＝3，AG ＝3.所以cos ∠AFG ＝FG 2＋AF 2－AG 22·FG ·AF ＝－63.因此二面角A －PD －C 的大小为π－arccos63. 解法二：由(1)知，OE ，OB ，OP 两两垂直．以O 为坐标原点，OE →的方向为x 轴的正方向建立如图所示的空间直角坐标系O －xyz .设|AB →|＝2，则A (－2，0，0)，D (0，－2，0)， C (2 2，－2，0)，P (0，0，2)，PC →＝(2 2，－2，－2)，PD →＝(0，－2，－2)， AP →＝(2，0，2)，AD →＝(2，－2，0)．设平面PCD 的法向量为1＝(x ，y ，z )，则 1·PC →＝(x ，y ，z )·(2 2，－2，－2)＝0，1·PD →＝(x ，y ，z )·(0，－2，－2)＝0，可得2x －y －z ＝0，y ＋z ＝0.取y ＝－1，得x ＝0，z ＝1，故1＝(0，－1，1)．设平面P AD 的法向量为2＝(m ，p ，q )，则 2·AP →＝(m ，p ，q )·(2，0，2)＝0， 2·AD →＝(m ，p ，q )·(2，－2，0)＝0，可得m ＋q ＝0，m －p ＝0.取m ＝1，得p ＝1，q ＝－1，故2＝(1，1，－1)．于是cos 〈，2〉＝n 1·n 2|n 1||n 2|＝－63.由于〈，2〉等于二面角A －PD －C 的平面角，所以二面角A －PD －C 的大小为π－arccos63. 例3（2012高考真题重庆理19）（本小题满分12分如图，在直三棱柱111C B A ABC 中，AB=4，AC=BC=3，D 为AB 的中点（Ⅰ）求点C 到平面11ABB A 的距离;（Ⅱ）若11AB A C 求二面角的平面角的余弦值.【答案】解：(1)由AC ＝BC ，D 为AB 的中点，得CD ⊥AB .又CD ⊥AA 1，故CD ⊥面A 1ABB 1，所以点C 到平面A 1ABB 1的距离为CD ＝BC 2－BD 2＝ 5.(2)解法一：如图，取D 1为A 1B 1的中点，连结DD 1，则DD 1∥AA 1∥CC 1.又由(1)知CD ⊥面A 1ABB 1，故CD ⊥A 1D ，CD ⊥DD 1，所以∠A 1DD 1为所求的二面角A 1－CD －C 1的平面角．因A 1D 为A 1C 在面A 1ABB 1上的射影，又已知AB 1⊥A 1C ，由三垂线定理的逆定理得AB 1⊥A 1D ，从而∠A 1AB 1、∠A 1DA 都与∠B 1AB 互余，因此∠A 1AB 1＝∠A 1DA ，所以Rt △A 1AD ∽Rt △B 1A 1A .因此AA 1AD ＝A 1B 1AA 1，即AA 21＝AD ·A 1B 1＝8，得AA 1＝2 2. 从而A 1D ＝AA 21＋AD 2＝2 3.所以，在Rt △A 1DD 1中， cos ∠A 1DD 1＝DD 1A 1D ＝AA 1A 1D ＝63.解法二：如图，过D 作DD 1∥AA 1交A 1B 1于点D 1，在直三棱柱中，易知DB ，DC ，DD 1两两垂直．以D 为原点，射线DB ，DC ，DD 1分别为x 轴、y 轴、z 轴的正半轴建立空间直角坐标系D －xyz .设直三棱柱的高为h ，则A (－2,0,0)，A 1(－2,0，h )，B 1(2,0，h )，C (0，5，0)，C 1(0，5，h )，从而AB 1→＝(4,0，h )，A 1C →＝(2，5，－h )．由AB 1→⊥A 1C →，有8－h 2＝0，h ＝2 2. 故DA 1→＝(－2,0,22)，CC 1→＝(0,0,22)，DC →＝ (0，5，0)．设平面A 1CD 的法向量为m ＝(x 1，y 1，z 1)，则m ⊥DC →，m ⊥DA 1→，即 ⎩⎨⎧ 5y 1＝0，－2x 1＋22z 1＝0，取z 1＝1，得m ＝(2，0,1)，设平面C 1CD 的法向量为n ＝(x 2，y 2，z 2)，则n ⊥DC →，n ⊥CC 1→，即 ⎩⎨⎧ 5y 2＝0，22z 2＝0，取x 2＝1，得n ＝(1,0,0)，所以cos 〈m ，n 〉＝m·n |m ||n |＝22＋1·1＝63. 所以二面角A 1－CD －C 1的平面角的余弦值为63. 例4（2012高考真题江西理20）（本题满分12分）如图1－5，在三棱柱ABC －A 1B 1C 1中，已知AB ＝AC ＝AA 1＝5，BC ＝4，点A 1在底面ABC 的投影是线段BC 的中点O .(1)证明在侧棱AA 1上存在一点E ，使得OE ⊥平面BB 1C 1C ，并求出AE 的长；(2)求平面A 1B 1C 与平面BB 1C 1C 夹角的余弦值．图1－5【答案】解：(1)证明：连接AO ，在△AOA 1中，作OE ⊥AA 1 于点E ，因为AA 1∥BB 1，所以OE ⊥BB 1.因为A 1O ⊥平面ABC ，所以A 1O ⊥BC .因为AB ＝AC ，OB ＝OC ，所以AO ⊥BC ，所以BC ⊥平面AA 1O .所以BC ⊥OE ，所以OE ⊥平面BB 1C 1C ，又AO ＝AB 2－BO 2＝1，AA 1＝5，得AE ＝AO 2AA 1＝55.(2)如图，分别以OA ，OB ，OA 1所在直线为x ，y ，z 轴，建立空间直角坐标系，则A (1,0,0)，B (0,2,0)，C (0，－2,0)，A 1(0,0,2)，由AE →＝15AA 1→得点E 的坐标是⎝ ⎛⎭⎪⎫45，0，25，由(1)得平面BB 1C 1C 的法向量是OE →＝⎝ ⎛⎭⎪⎫45，0，25，设平面A 1B 1C 的法向量＝(x ，y ，z )，由⎩⎪⎨⎪⎧ ·AB →＝0，n ·A 1C →＝0得⎩⎨⎧－x ＋2y ＝0，y ＋z ＝0，令y ＝1，得x ＝2，z ＝－1，即＝(2,1，－1)，所以cos 〈OE →，〉＝OE →·n |OE →|·|n |＝3010. 即平面BB 1C 1C 与平面A 1B 1C 的夹角的余弦值是3010.例5（2012高考真题安徽理18）（本小题满分12分）平面图形ABB 1A 1C 1C 如图1－4(1)所示，其中BB 1C 1C 是矩形，BC ＝2，BB 1＝4，AB ＝AC＝2，A 1B 1＝A 1C 1＝ 5.图1－4现将该平面图形分别沿BC 和B 1C 1折叠，使△ABC 与△A 1B 1C 1所在平面都与平面BB 1C 1C 垂直，再分别连接A 1A ，A 1B ，A 1C ，得到如图1－4(2)所示的空间图形．对此空间图形解答下列问题．(1)证明：AA 1⊥BC ；(2)求AA 1的长；(3)求二面角A －BC －A 1的余弦值．【答案】解：(向量法)：(1)证明：取BC B 1C 1的中点分别为D 和D 1，连接A 1D 1，DD 1，AD .由BB 1C 1C 为矩形知，DD 1⊥B 1C 1，因为平面BB 1C 1C ⊥平面A 1B 1C 1，所以DD 1⊥平面A 1B 1C 1，又由A 1B 1＝A 1C 1知，A 1D 1⊥B 1C 1.故以D 1为坐标原点，可建立如图所示的空间直角坐标系D 1－xyz . 由题设，可得A 1D 1＝2，AD ＝1.由以上可知AD ⊥平面BB 1C 1C ，A 1D 1⊥平面BB 1C 1C ，于是AD ∥A 1D 1. 所以A (0，－1,4)，B (1,0,4)，A 1(0,2,0)，C (－1,0,4)，D (0,0,4)．故AA 1→＝(0,3，－4)，BC →＝(－2,0,0)，AA 1→·BC →＝0，因此AA 1→⊥BC →，即AA 1⊥BC . (2)因为AA 1→＝(0,3，－4)，所以||AA 1→＝5，即AA 1＝5. (3)连接A 1D ，由BC ⊥AD ，BC ⊥AA 1，可知BC ⊥平面A 1AD ，BC ⊥A 1D ，所以∠ADA 1为二面角A －BC －A 1的平面角．因为DA →＝(0，－1,0)，DA 1→＝(0,2，－4)，所以 cos 〈DA →，DA 1→〉＝－21×22＋(－4)2＝－55. 即二面角A －BC －A 1的余弦值为－55.(综合法)(1)证明：取BC ，B 1C 1的中点分别为D 和D 1，连接A 1D 1，DD 1，AD ，A 1D . 由条件可知，BC ⊥AD ，B 1C 1⊥A 1D 1，由上可得AD ⊥面BB 1C 1C ，A 1D 1⊥面BB 1C 1C . 因此AD ∥A 1D 1，即AD ，A 1D 1确定平面AD 1A 1D . 又因为DD 1∥BB 1，BB 1⊥BC ，所以DD 1⊥BC . 又考虑到AD ⊥BC ，所以BC ⊥平面AD 1A 1D ，故BC ⊥AA 1.(2)延长A 1D 1到G 点，使GD 1＝AD ，连接AG . 因为AD 綊GD 1，所以AG 綊DD 1綊BB 1.由于BB 1⊥平面A 1B 1C 1，所以AG ⊥A 1G .由条件可知，A 1G ＝A 1D 1＋D 1G ＝3，AG ＝4，所以AA 1＝5.(3)因为BC ⊥平面AD 1A 1D ，所以∠ADA 1为二面角A －BC －A 1的平面角．在Rt △A 1DD 1中，DD 1＝4，A 1D 1＝2，解得sin ∠D 1DA 1＝55，cos ∠ADA 1＝cos ⎝ ⎛⎭⎪⎫π2＋∠D 1DA 1＝－55. 即二面角A －BC －A 1的余弦值为－55.向量法（建系困难）412、（杭州市学军中学2016届高三5月模拟考试）如图，在四棱锥中, , 且.（1）求证：平面平面；（2）求直线与平面所成的角的正弦值．答案412、解：证明：（1）为中点,, , 且四边形是矩形, ,又平面,且,在平面中,平面平面,又平面平面,平面平面.（2）以A 为原点，为轴,为轴,建立空间直角坐标角系，,则设平面的法向量,则,取,得, 设直线与平面所成的角为, , 直线与平面所成的角的正弦值为.14.(15分)如图，在三棱锥P−ABC中，△ABC是正三角形，面PAB⊥面ABC，∠PAB=30°，AB=PB=2，△ABC和△PBC的重心分别为D，E .(1)证明：DE∥面PAB;P(2)求AB与面PDE所成角的正弦值.例15.如图,AB是圆的直经,PA垂直圆所在的平面,C是圆上的点, ⑴求证:平面PAC 面PBC;⑵若AB=2,AC=1,PA=1,求二面角C-PB-A的余弦值.例15.已知两个正四棱锥P －ABCD 与Q －ABCD 的高都为2，AB ＝4．（1）证明：PQ ⊥平面ABCD ；（2）求异面直线AQ 与PB 所成的角；（3）求点P 到平面QAD 的距离．（2）由题设知，ABCD 是正方形，且AC ⊥BD ．由（1），PQ ⊥平面ABCD ，故可分别以直线CA DB QP，，为x ，y ，z 轴建立空间直角坐标系（如图1），易得(2202)(0222)AQ PB =--=-，，，，，，1cos 3AQ PB AQ PB AQ PB<>==，．所求异面直线所成的角是1arccos 3．（3）由（2）知，点(0220)(22220)(004)D AD PQ -=--=-，，，，，，，，．设n =（x ，y ，z ）是平面QAD 的一个法向量，则00AQ AD ⎧=⎪⎨=⎪⎩，，n n 得200x z x y ⎧+=⎪⎨+=⎪⎩，，取x ＝1，得(112)--，，n =．点P 到平面QAD 的距离22PQ d ==n n．。

立体几何(向量法)—建系讲义之欧阳与创编

立体几何（向量法）—建系引入空间向量坐标运算，使解立体几何问题避免了传统方法进行繁琐的空间分析，只需建立空间直角坐标系进行向量运算，而如何建立恰当的坐标系，成为用向量解题的关键步骤之一．所谓“建立适当的坐标系”，一般应使尽量多的点在数轴上或便于计算。

一、利用共顶点的互相垂直的三条线构建直角坐标系例1（2012高考真题重庆理19）（本小题满分12分如图，在直三棱柱111C B A ABC - 中，AB=4，AC=BC=3，D 为AB 的中点（Ⅰ）求点C 到平面11ABB A 的距离;（Ⅱ）若11AB A C ⊥求二面角的平面角的余弦值.【答案】解：(1)由AC ＝BC ，D 为AB 的中点，得CD ⊥AB .又CD ⊥AA 1，故CD ⊥面A 1ABB 1，所以点C 到平面A 1ABB 1的距离为CD ＝BC 2－BD 2＝ 5.(2)解法一：如图，取D 1为A 1B 1的中点，连结DD 1，则DD 1∥AA 1∥CC 1.又由(1)知CD ⊥面A 1ABB 1，故CD ⊥A 1D ，CD ⊥DD 1，所以∠A 1DD 1为所求的二面角A 1－CD －C 1的平面角．因A 1D 为A 1C 在面A 1ABB 1上的射影，又已知AB 1⊥A 1C ，由三垂线定理的逆定理得AB 1⊥A 1D ，从而∠A 1AB 1、∠A 1DA 都与∠B 1AB 互余，因此∠A 1AB 1＝∠A 1DA ，所以Rt △A 1AD ∽Rt △B 1A 1A .因此AA 1AD ＝A 1B 1AA 1，即AA 21＝AD ·A 1B 1＝8，得AA 1＝2 2. 从而A 1D ＝AA 21＋AD 2＝2 3.所以，在Rt △A 1DD 1中，cos ∠A 1DD 1＝DD 1A 1D ＝AA 1A 1D ＝63. 解法二：如图，过D 作DD 1∥AA 1交A 1B 1于点D 1，在直三棱柱中，易知DB ，DC ，DD 1两两垂直．以D 为原点，射线DB ，DC ，DD 1分别为x 轴、y 轴、z 轴的正半轴建立空间直角坐标系D －xyz .设直三棱柱的高为h ，则A (－2,0,0)，A 1(－2,0，h )，B 1(2,0，h )，C (0，5，0)，C 1(0，5，h )，从而AB1→＝(4,0，h )，A 1C →＝(2，5，－h )．由AB 1→⊥A 1C →，有8－h 2＝0，h ＝2 2.故DA1→＝(－2,0,22)，CC 1→＝(0,0,22)，DC →＝ (0，5，0)．设平面A 1CD 的法向量为m ＝(x 1，y 1，z 1)，则m ⊥DC→，m ⊥DA1→，即 ⎩⎪⎨⎪⎧ 5y 1＝0，－2x 1＋22z 1＝0，取z 1＝1，得m ＝(2，0,1)，设平面C 1CD 的法向量为n ＝(x 2，y 2，z 2)，则n ⊥DC→，n ⊥CC1→，即 ⎩⎪⎨⎪⎧5y 2＝0，22z 2＝0，取x 2＝1，得n ＝(1,0,0)，所以cos 〈m ，n 〉＝m·n |m ||n |＝22＋1·1＝63. 所以二面角A 1－CD －C 1的平面角的余弦值为63.二、利用线面垂直关系构建直角坐标系例2.如图所示，AF 、DE 分别是圆O 、圆1O 的直径，AD 与两圆所在的平面均垂直，8AD =.BC 是圆O 的直径，6AB AC ==,//OE AD .(I)求二面角B AD F --的大小；(II)求直线BD 与EF 所成的角的余弦值.19.解：(Ⅰ)∵AD 与两圆所在的平面均垂直,∴AD ⊥AB, AD ⊥AF,故∠BAD 是二面角B —AD —F 的平面角，依题意可知，ABCD 是正方形，所以∠BAD ＝450.即二面角B —AD —F 的大小为450；(Ⅱ)以O 为原点，BC 、AF 、OE 所在直线为坐标轴，建立空间直角坐标系（如图所示），则O （0，0，0），A （0，23-，0），B （23，0，0）,D （0，23-，8），E （0，0，8），F （0，23，0）所以，)8,23,0(),8,23,23(-=--=FE BD设异面直线BD 与EF 所成角为α，则1082|,cos |cos =><=EFBD α直线BD 与EF 所成的角为余弦值为10．三、利用图形中的对称关系建立坐标系例3（2013年重庆数学（理））如图,四棱锥P ABCD-中,PA ABCD ⊥底面,2,4,3BC CD AC ACB ACD π===∠=∠=,F 为PC 的中点,AF PB ⊥.(1)求PA 的长; (2)求二面角B AF D --的正弦值.【答案】解：(1)如图，联结BD 交AC 于O ，因为BC ＝CD ，即△BCD 为等腰三角形，又AC 平分∠BCD ，故AC ⊥BD .以O 为坐标原点，OB→，OC →，AP →的方向分别为x 轴，y 轴，z 轴的正方向，建立空间直角坐标系O －xyz ，则OC ＝CD cos π3＝1，而AC ＝4，得AO ＝AC －OC ＝3.又OD ＝CD sin π3＝3，故A (0，－3，0)，B (3，0，0)，C (0，1，0)，D (－3，0，0)．因P A ⊥底面ABCD ，可设P (0，－3，z )，由F 为PC 边中点，得F ⎝ ⎛⎭⎪⎫0，－1，z 2，又AF →＝⎝ ⎛⎭⎪⎫0，2，z 2，PB →＝(3，3，－z )，因AF ⊥PB ，故AF →·PB →＝0，即6－z 22＝0，z ＝23(舍去－23)，所以|P A →|＝2 3.(2)由(1)知AD→＝(－3，3，0)，AB →＝(3，3，0)，AF →＝(0，2，3)．设平面F AD 的法向量为1＝(x 1，y 1，z 1)，平面F AB 的法向量为2＝(x 2，y 2，z 2)．由1·AD →＝0，1·AF→＝0，得 ⎩⎪⎨⎪⎧－3x 1＋3y 1＝0，2y 1＋3z 1＝0，因此可取1＝(3，3，－2)．由2·AB →＝0，2·AF→＝0，得 ⎩⎪⎨⎪⎧3x 2＋3y 2＝0，2y 2＋3z 2＝0，故可取2＝(3，－3，2)．从而向量1，2的夹角的余弦值为cos 〈1，2〉＝n 1·n 2|n 1|·|n 2|＝18. 故二面角B －AF －D 的正弦值为378.四、利用正棱锥的中心与高所在直线，投影构建直角坐标系例4-1（2013大纲版数学（理））如图,四棱锥P ABCD - 中,902,ABC BAD BC AD PAB ∠=∠==∆，与PAD ∆都是等边三角形.(I)证明:;PB CD ⊥ (II)求二面角A PD C --的余弦值.【答案】解：(1)取BC 的中点E ，联结DE ，则四边形ABED为正方形．过P作PO⊥平面ABCD，垂足为O.联结OA，OB，OD，OE.由△P AB和△P AD都是等边三角形知P A＝PB＝PD，所以OA＝OB＝OD，即点O为正方形ABED对角线的交点，故OE⊥BD，从而PB⊥OE.因为O是BD的中点，E是BC的中点，所以OE∥CD.因此PB⊥CD.(2)解法一：由(1)知CD⊥PB，CD⊥PO，PB∩PO＝P，故CD⊥平面PBD.又PD⊂平面PBD，所以CD⊥PD.取PD的中点F，PC的中点G，连FG.则FG∥CD，FG⊥PD.联结AF，由△APD为等边三角形可得AF⊥PD.所以∠AFG为二面角A－PD－C的平面角．联结AG，EG，则EG∥PB.又PB⊥AE，所以EG⊥AE.设AB＝2，则AE＝22，EG＝12PB＝1，故AG＝AE2＋EG2＝3，在△AFG中，FG＝12CD＝2，AF＝3，AG＝3.所以cos ∠AFG ＝FG 2＋AF 2－AG 22·FG ·AF ＝－63.解法二：由(1)知，OE ，OB ，OP 两两垂直．以O 为坐标原点，OE→的方向为x 轴的正方向建立如图所示的空间直角坐标系O －xyz .设|AB→|＝2，则 A (－2，0，0)，D (0，－2，0)， C (22，－2，0)，P (0，0，2)，PC→＝(22，－2，－2)，PD →＝(0，－2，－2)， AP→＝(2，0，2)，AD →＝(2，－2，0)．设平面PCD 的法向量为1＝(x ，y ，z )，则1·PC →＝(x ，y ，z )·(22，－2，－2)＝0， 1·PD →＝(x ，y ，z )·(0，－2，－2)＝0，可得2x －y －z ＝0，y ＋z ＝0.取y ＝－1，得x ＝0，z ＝1，故1＝(0，－1，1)．设平面P AD 的法向量为2＝(m ，p ，q )，则2·AP →＝(m ，p ，q )·(2，0，2)＝0， 2·AD →＝(m ，p ，q )·(2，－2，0)＝0，可得m ＋q ＝0，m －p ＝0.取m ＝1，得p ＝1，q ＝－1，故2＝(1，1，－1)．于是cos 〈，2〉＝n 1·n 2|n 1||n 2|＝－63. 例4-2如图1－5，在三棱柱ABC －A 1B 1C 1中，已知AB ＝AC ＝AA 1＝5，BC ＝4，点A 1在底面ABC 的投影是线段BC 的中点O .(1)证明在侧棱AA 1上存在一点E ，使得OE ⊥平面BB 1C 1C ，并求出AE 的长；(2)求平面A 1B 1C 与平面BB 1C 1C 夹角的余弦值．图1－5【答案】解：(1)证明：连接AO ，在△AOA 1中，作OE ⊥AA 1 于点E ，因为AA 1∥BB 1，所以OE ⊥BB 1.因为A 1O ⊥平面ABC ，所以A 1O ⊥BC .因为AB ＝AC ，OB ＝OC ，所以AO ⊥BC ，所以BC ⊥平面AA 1O .所以BC ⊥OE ，所以OE ⊥平面BB 1C 1C ，又AO ＝AB 2－BO 2＝1，AA 1＝5，得AE ＝AO 2AA 1＝55. (2)如图，分别以OA ，OB ，OA 1所在直线为x ，y ，z 轴，建立空间直角坐标系，则A (1,0,0)，B (0,2,0)，C (0，－2,0)，A 1(0,0,2)，由AE →＝15AA 1→得点E 的坐标是⎝ ⎛⎭⎪⎫45，0，25，由(1)得平面BB 1C 1C 的法向量是OE →＝⎝ ⎛⎭⎪⎫45，0，25，设平面A 1B 1C 的法向量＝(x ，y ，z )，由⎩⎨⎧ ·AB →＝0，n ·A 1C →＝0得⎩⎪⎨⎪⎧ －x ＋2y ＝0，y ＋z ＝0，令y ＝1，得x ＝2，z ＝－1，即＝(2,1，－1)，所以cos 〈OE →，〉＝OE →·n |OE →|·|n |＝3010. 即平面BB 1C 1C 与平面A 1B 1C 的夹角的余弦值是3010三、利用面面垂直关系构建直角坐标系例5（2012高考真题安徽理18）（本小题满分12分）平面图形ABB 1A 1C 1C 如图1－4(1)所示，其中BB 1C 1C 是矩形，BC ＝2，BB 1＝4，AB ＝AC ＝2，A 1B 1＝A 1C 1＝5.图1－4现将该平面图形分别沿BC 和B 1C 1折叠，使△ABC 与△A 1B 1C 1所在平面都与平面BB 1C 1C 垂直，再分别连接A 1A ，A 1B ，A 1C ，得到如图1－4(2)所示的空间图形．对此空间图形解答下列问题．(1)证明：AA 1⊥BC ；(2)求AA 1的长；(3)求二面角A －BC －A 1的余弦值．【答案】解：(向量法)：(1)证明：取BC B 1C 1的中点分别为D 和D 1，连接A 1D 1，DD 1，AD . 由BB 1C 1C 为矩形知，DD 1⊥B 1C 1，因为平面BB 1C 1C ⊥平面A 1B 1C 1，所以DD 1⊥平面A 1B 1C 1，又由A 1B 1＝A 1C 1知，A 1D 1⊥B 1C 1.故以D 1为坐标原点，可建立如图所示的空间直角坐标系D 1－xyz .由题设，可得A 1D 1＝2，AD ＝1.由以上可知AD ⊥平面BB 1C 1C ，A 1D 1⊥平面BB 1C 1C ，于是AD ∥A 1D 1.所以A (0，－1,4)，B (1,0,4)，A 1(0,2,0)，C (－1,0,4)，D (0,0,4)．故AA 1→＝(0,3，－4)，BC →＝(－2,0,0)，AA 1→·BC→＝0，因此AA1→⊥BC →，即AA 1⊥BC .(2)因为AA1→＝(0,3，－4)，所以⎪⎪⎪⎪AA 1→＝5，即AA 1＝5.(3)连接A 1D ，由BC ⊥AD ，BC ⊥AA 1，可知BC ⊥平面A 1AD ，BC ⊥A 1D ，所以∠ADA 1为二面角A －BC －A 1的平面角．因为DA →＝(0，－1,0)，DA 1→＝(0,2，－4)，所以cos 〈DA →，DA 1→〉＝－21×22＋－42＝－55.即二面角A －BC －A 1的余弦值为－55.(综合法)(1)证明：取BC ，B 1C 1的中点分别为D 和D 1，连接A 1D 1，DD 1，AD ，A 1D .由条件可知，BC ⊥AD ，B 1C 1⊥A 1D 1，由上可得AD ⊥面BB 1C 1C ，A 1D 1⊥面BB 1C 1C .因此AD ∥A 1D 1，即AD ，A 1D 1确定平面AD 1A 1D . 又因为DD 1∥BB 1，BB 1⊥BC ，所以DD 1⊥BC .又考虑到AD ⊥BC ，所以BC ⊥平面AD 1A 1D ，故BC ⊥AA 1.(2)延长A 1D 1到G 点，使GD 1＝AD ，连接AG .因为AD 綊GD 1，所以AG 綊DD 1綊BB 1.由于BB 1⊥平面A 1B 1C 1，所以AG ⊥A 1G .由条件可知，A 1G ＝A 1D 1＋D 1G ＝3，AG ＝4，所以AA 1＝5.(3)因为BC ⊥平面AD 1A 1D ，所以∠ADA 1为二面角A －BC －A 1的平面角．在Rt △A 1DD 1中，DD 1＝4，A 1D 1＝2，解得sin ∠D 1DA 1＝55，cos ∠ADA 1＝cos ⎝ ⎛⎭⎪⎫π2＋∠D 1DA 1＝－55.即二面角A －BC －A 1的余弦值为－55.。

2020年高考数学立体几何建系困难问大题精做

2020年高考数学立体几何建系困难问大题精做1.已知三棱锥P ABC -（如图一）的平面展开图（如图二）中，四边形ABCD 的正方形，ABE △和BCF △均为正三角形，在三棱锥P ABC -中：（1）证明：平面PAC ⊥平面ABC ；（2）若点M 在棱PA 上运动，当直线BM 与平面PAC 所成的角最大时，求二面角P BC M --的余弦值．图一图二2．矩形ABCD 中，1AB =，2AD =，点E 为AD 中点，沿BE 将ABE △折起至PBE △，如图所示，点P 在面BCDE 的射影O 落在BE 上．（1）求证：面PCE ⊥面PBE ；（2）求平面PCD 与平面PBE 所成锐二面角的余弦值．3．如图1，在矩形ABCD 中，AB =BC =点E 在线段DC 上，且DE ，现将AED △沿AE 折到AED '△的位置，连结CD '，BD '，如图2．（1）若点P 在线段BC 上，且BP =，证明：AE D P ⊥'；（2）记平面AD E '与平面BCD '的交线为l ．若二面角B AE D --'为2π3，求l 与平面D CE '所成角的正弦值．4．如图，在四棱锥P ABCD-中，已知底面ABCD是边长为1的正方形，侧面PAD⊥平面ABCD，=，PA与平面PBC．PA PD（1）求侧棱PA的长；（2）设E为AB中点，若PA AB≥，求二面角B PC E--的余弦值．【解析】（1）设AC 的中点为O ，连接BO ，PO ．由题意，得PA PB PC ==1PO =， 1AO BO CO ===．∵在PAC △中，PA PC =，O 为AC 的中点，∴PO AC ⊥，∵在POB △中，1PO =，1OB =，PB =，222PO OB PB +=，∴PO OB ⊥． ∵ACOB O =，AC ，OB ⊂平面，∴PO ⊥平面ABC ，∵PO ⊂平面PAC ，∴平面PAC ⊥平面ABC ．（2）由（1）知，BO PO ⊥，BO AC ⊥，BO ⊥平面PAC ， ∴BMO ∠是直线BM 与平面PAC 所成的角，且1tan BO BMO OM OM∠==， ∴当OM 最短时，即M 是PA 的中点时，BMO ∠最大．由PO ⊥平面ABC ，OB AC ⊥，∴PO OB ⊥，PO OC ⊥，于是以OC ，OB ，OD 所在直线分别为x 轴，y 轴，z 轴建立如图示空间直角坐标系，则()0,0,0O ，()1,0,0C ，()0,1,0B ，()1,0,0A -，()0,0,1P ，11,0,22M ⎛⎫- ⎪⎝⎭，()1,1,0BC =-，()1,0,1PC =-，31,0,22MC ⎛⎫=- ⎪⎝⎭．设平面MBC 的法向量为()111,,x y z =m ，则由00BC MC ⎧⋅=⎪⎨⋅=⎪⎩m m 得：1111030x y x z -=⎧⎨-=⎩．令11x =，得11y =，13z =，即()1,1,3=m ．设平面PBC 的法向量为()222,,x y z =n ，由00BC PC ⎧⋅=⎪⎨⋅=⎪⎩n n 得：222200x y x z -=⎧⎨-=⎩，令1x =，得1y =，1z =，即()1,1,1=n ．cos ,⋅===⋅n m m n n m ．由图可知，二面角P BC M --2．【答案】（1）详见解析；（2）11．【解析】（1）在四棱锥P BCDE -中，BE CE ==，2BC =，从而有CE BE ⊥，又∵PO ⊥面BCDE ，而CE ⊂面BCDE ，∴CE PO ⊥，而PO 、BE ⊂面PBE ，且POBE O =，由线面垂直定理可证CE ⊥面PBE ，又CE ⊂面PCE ，由面面垂直判断定定理即证面PCE ⊥面PBE ．（2）由条件知OP ⊥面BCDE ，过点E 做OP 的平行线EZ ，又由（1）知EC ⊥面PBE ，以EB 、EC 、EZ 分别为x 、y 、z 轴建立空间直角坐标系，如图所示：P ⎝⎭，()C，D ⎛⎫ ⎪ ⎪⎝⎭，22CP ⎛=⎝⎭，22DC ⎛⎫= ⎪ ⎪⎝⎭，面PBE 的一个法向量为()10,1,0=n ，设面PCD 的法向量为()2,,x y z =n，则有00xx y +==，设平面PCD 与平面PBE 所成锐二面角为θ，与12,n n 互补，则cos θ，故平面PCD 与平面PBE 所成二面角的余弦值为11． 3．【答案】（1）详见解析；（2．【解析】证明：（1）先在图1中连结DP ，在Rt ADE △中，由AD BC ==，DE得1tan2DAE ∠=，在RtPCD △中，由DC AB ==，PC BC BP ====，得1tan 2PDC ∠=，∴tan tan PDC DAE ∠=∠，则PDC DAE ∠=∠，∴90DOE ∠=︒，从而有AE OD ⊥，AE OP ⊥，即在图2中有'AE OD ⊥，AE OP ⊥， ∴AE ⊥平面'POD ，则AE D P ⊥'；解：（2）延长AE ，BC 交于点Q ，连接'D Q ，根据公理3得到直线'D Q 即为l ，再根据二面角定义得到2π'3D OP ∠=．在平面'POD 内过点O 作底面垂线，以O 为原点，分别为OA ， OP ，及所作垂线为x 轴、y 轴、z 轴建立空间直角坐标系，则(0,D '-，()1,0,0E -，()11,0,0Q -，()3,4,0C -， ('11,1,D Q =-，()2,4,0EC =-，('1,ED =-，设平面D EC '的一个法向量为(),,x y z =n ，由240'0EC x y ED x y⎧⋅=-+=⎪⎨⋅=-=⎪⎩n n ，取1y =，得2,1,⎛= ⎝⎭n ． ∴l 与平面'D CE 所成角的正弦值为'15cos ,'5'D Q D Q D Q⋅==⋅n nn ． 4．【答案】（1）1PA =或PA ；（2．【解析】（1）取AD 中点O ，BC 中点M ，连结OP ，OM ，∵PA PD =，∴OP AD ⊥，又∵平面PAD ⊥平面ABCD ，OP 平面PAD ，平面PAD 平面ABCD AD =，∴OP ⊥平面ABCD ，∴OP OA ⊥，OP OM ⊥，又∵ABCD 是正方形，∴OA OM ⊥，以O 为原点OA ，OM ，OP 为x ，y ，z 轴建立空间直角坐标系O xyz -（如图），则1,0,02A ⎛⎫ ⎪⎝⎭，1,0,02D ⎛⎫- ⎪⎝⎭，1,1,02B ⎛⎫ ⎪⎝⎭，1,1,02C ⎛⎫- ⎪⎝⎭，设()()0,0,0P c c >，则1,1,2PB c ⎛⎫=- ⎪⎝⎭，()1,0,0CB =，设平面PBC 的一个法向量为()1111,,x y z =n ，则有1111120x y cz x ⎧+-=⎪⎨⎪=⎩，取11z =，则1y c =，从而()10,,1c =n ，设PA 与平面PBC 所成角为α，∵1,0,2PA c ⎛⎫=- ⎪⎝⎭，∴111sin cos ,PA PA PA α⋅====⋅n n n 234c =或213c =， ∴1PA =或PA =．（2）由（1）知，1PAAB ≥=，∴1PA =，c ，由（1）知，平面PBC 的一个法向量为()10,,1c ⎛⎫== ⎪ ⎪⎝⎭n ，设平面PCE的一个法向量为()2x y z =，，n ，而11,,02CE ⎛⎫=- ⎪⎝⎭，1,1,2PC ⎛=- ⎝⎭，∴102102x y x y ⎧-=⎪⎪⎨⎪-+=⎪⎩取1x =，则2y =，z =(2=n ，设二面角B PC E --的平面角为β，∴12cos cos ,β===n n ，根据图形得β为锐角，∴二面角B PC E --．。

立体几何建系方法

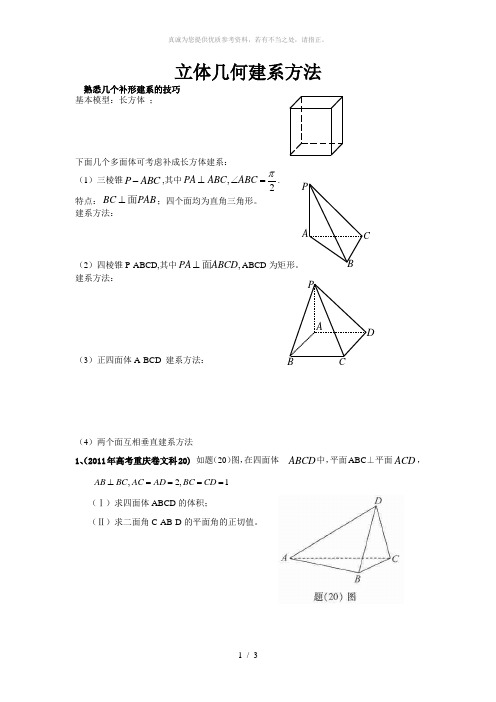
立体几何建系方法熟悉几个补形建系的技巧基本模型：长方体；下面几个多面体可考虑补成长方体建系：（1）三棱锥P ABC -,其中,2PA ABC ABC π⊥∠=.特点：BC PAB ⊥面；四个面均为直角三角形。

建系方法：（2）四棱锥P-ABCD,其中,PA ABCD ⊥面ABCD 为矩形。

建系方法：（3）正四面体A-BCD 建系方法：（4）两个面互相垂直建系方法1、（2011年高考重庆卷文科20) 如题（20）图，在四面体ABCD 中，平面ABC ⊥平面ACD ，,2,1AB BC AC AD BC CD ⊥====（Ⅰ）求四面体ABCD 的体积；（Ⅱ）求二面角C-AB-D 的平面角的正切值。

PA BCA B CDP2、（06山东），已知四棱锥P-ABCD的底面ABCD为等腰梯形，AB∥DC,AC⊥BD,AC与BD相交于点O，且顶点P在底面上的射影恰为O点，又BO=2,PO=2,PB⊥PD.(Ⅰ)求异面直线PD与BC所成角的余弦值；(Ⅱ)求二面角P－AB－C的大小；3、在直三棱柱ABC－A1B1C1中，AB＝BC，D、E分别为BB1、AC1的中点．（Ⅰ）证明：ED为异面直线BB1与AC1的公垂线；（Ⅱ）设AA1＝AC＝2AB，求二面角A1－AD－C1的大小．A BCD EA1B1C14．如图，已知四棱锥P ABCD -，底面ABCD 为菱形，PA ⊥平面ABCD ，60ABC ∠=，E F ，分别是BC PC ，的中点．（Ⅰ）证明：AE PD ⊥；（Ⅱ）若H 为PD 上的动点，EH 与平面PAD 所成最大角的正切值为2E AF C --的余弦值．5、（08安徽）如图，在四棱锥O ABCD -中，底面ABCD 四边长为1的菱形，4ABC π∠=,OA ABCD ⊥底面, 2OA =,M 为OA 的中点.（1）求异面直线AB 与MD 所成角的大小；（2）求点B 到平面OCD 的距离.P BECD FA。

高中数学立体几何建系技巧

高中数学立体几何建系技巧
高中数学立体几何的建立技巧有以下几点：
1、认真阅读教材，仔细理解立体几何的概念，了解几何定义以及各种定理的意思；
2、认真学习各种几何图形，了解各种几何体的定义、三视图及各种视图之间的关系；
3、多思考，多动手，做足够多的例题，及时纠正自己的错误，以加深对立体几何的理解；
4、多读书，查阅实用性强的教材，提高自己的计算能力，学会熟练运用各类几何计算方法；
5、多操作，学会用实物来模拟立体几何的各种定理，加强对理论的认知；
6、多总结，经常总结自己前面学习的知识点，帮助记忆自己所学的内容；
7、认真参加课堂教学，积极参与课堂练习，用实操来加深对立体几何的理解。

立体几何圆锥建系技巧 -回复

立体几何圆锥建系技巧-回复立体几何圆锥是我们在学习数学时经常会遇到的一个重要概念。

圆锥的特点是其底面是一个圆形，并且从顶点出发的任意一条直线都会与底面相交。

在解题过程中，我们经常需要使用建系的技巧来进行推导和证明。

本文将一步一步回答有关立体几何圆锥建系技巧的问题，帮助读者更好地理解和掌握这一概念。

第一步：理解基本概念在介绍建系技巧之前，我们首先需要清楚圆锥的基本概念。

圆锥由一个圆形的底面和一个相交于底面的顶点的侧面组成。

底面的半径和圆锥的高度是圆锥的基本参数，它们决定了圆锥的形状和大小。

此外，当我们讨论圆锥时，我们常常需要涉及到圆锥的几何性质，如圆锥的表面积和体积等。

第二步：建系的概念建系是一种解题方法，它通过引入一个适当的坐标系，将问题转化为代数方程的求解问题。

在圆锥建系中，我们通常会将圆锥放置在合适的坐标系中，引入坐标变量来描述圆锥的几何性质。

通过建立和求解代数方程，我们可以得到圆锥的各项性质的具体数值。

第三步：选择适当的建系方法在具体的解题过程中，我们需要根据问题的要求选择适合的建系方法。

例如，当要求计算圆锥的体积时，我们可以在直角坐标系中建立一个以圆锥的顶点为原点的三维坐标系，并选择适当的坐标变量来描述圆锥的高度和底面的半径。

而当要求计算圆锥的表面积时，我们可以选择在极坐标系中建立一个以圆锥的顶点为极点的二维坐标系，并选择适当的坐标变量来描述圆锥的高度和底面半径。

第四步：应用建系技巧解题在解题过程中，我们需要根据问题的具体要求和建系方法，应用建系技巧求解。

例如，当要求计算圆锥的体积时，我们可以使用解析几何和微积分等知识，建立代数方程来求解。

具体步骤可以如下：1. 建立圆锥的几何模型，确定选择合适的坐标系。

2. 引入合适的坐标变量来描述圆锥的高度和底面半径。

3. 根据圆锥的几何特性，建立体积的代数方程。

4. 求解代数方程，得到圆锥的体积。

第五步：验证和应用结果在解题过程中，我们需要对结果进行验证和应用。

立体几何建系步骤

立体几何建系步骤嘿，咱今儿就来唠唠立体几何建系那些事儿！你说立体几何，就像是个神秘的城堡，而建系呢，就是打开城堡大门的钥匙！咱得一步步来，可不能马虎。

首先啊，你得找个好的原点。

这原点就像是城堡的根基，得稳稳当当的。

你得寻思寻思，放在哪儿能让后面的计算最方便，最顺溜。

就好比你去一个陌生的地方，得找个最合适的起点一样。

然后呢，确定坐标轴。

这坐标轴就像是城堡里的通道呀，得给它们安排得明明白白的。

X 轴、Y 轴、Z 轴，各有各的方向，可不能乱套了。

这就好像你走路，得知道东西南北吧，不然不就晕头转向啦？接着，得给每个轴定个合适的长度单位。

这可不能瞎搞，得根据题目情况来。

就跟你买衣服得选对尺码一样，大了小了都不合适呀。

再之后，把那些关键的点都在这个坐标系里标出来。

这一个个点就像是城堡里的宝藏位置，你得清楚它们在哪儿。

想象一下，要是标错了，那不就跟找宝藏找错地方一样，白费力气嘛！还有哦，那些线啊，面啊，都得和坐标系联系起来。

它们就像是城堡里的各种机关，你得搞清楚它们和坐标系的关系。

不然怎么去破解谜题，找到答案呢？在这个过程中，可得细心细心再细心。

一个小错误，都可能让你后面的计算全错啦。

这就像走钢丝，一步都不能错呀！建系完成后，你就会发现，哇，原本那些复杂得让人头疼的立体几何问题，好像突然就变得清晰了。

就像是拨开了云雾，见到了青天。

总之啊，立体几何建系可不是个简单的事儿，但只要你一步一步慢慢来，细心认真，就一定能把这把钥匙拿到手，打开立体几何城堡的大门！加油吧！。

用向量法解立体几何题，建系求点是关键

用向量法解立体几何题，建系求点是关键发布时间：2021-08-17T17:13:25.967Z 来源：《中小学教育》2021年11期4月作者：梁业兴[导读] 利用空间向量法解立体几何题，可把抽象的空间图形关系转化为具体的数量运算梁业兴中山市龙山中学广东省中山市 528471摘要：利用空间向量法解立体几何题，可把抽象的空间图形关系转化为具体的数量运算，并有很强的规律性和可操作性，但在实际教学中发现，学生对某些几何体存在建系求点上的困难.本文主要通过实例探讨解决问题的办法.关键词：立体几何、向量法、建系求点向量是近代数学中最重要和最基本的数学概念之一，是具有几何形式和代数形式的“双重身份”的概念，是沟通代数与几何的桥梁.将空间向量引入高中数学，为解决三维空间中图形的位置关系与度量问题提供了一个十分有效的工具.解题时，只需建立合适的空间直角坐标系，求出相关点的坐标，然后化为向量问题，通过进行向量运算，即可转化为几何问题.在这里，建系求点将是解决问题的关键.一、问题的提出学生用向量法解如下高考真题（例1）时容易求错或无法求出点P的坐标.二、问题分析学生用向量法解立体几何题主要的错误有两个：一是建系不合理，二是求错甚至不会求点的坐标.主要原因有两个方面：一方面是图形认知障碍.平面几何图形反映图形的真实情况，但在立体几何中，由于是用斜二侧画法画成的直观图，图形往往不能反映原形的真实结构和全部特点.例如在“水平放置的平面图形的直观图画法”中，正方形、矩形在水平放置后呈平行四边形，以及在图中看上去明显不垂直的两条线段却偏要证明他们互相垂直，明显是锐角的实际上却是一个钝角等；另一方面是缺乏空间想象能力.由于空间想象能力是一个比较复杂、抽象的思维过程，想象能力从二维到三维的拓展难度较大，在实际教学中，学生往往不易建立空间概念，在脑海中难以形成较为准确、直观的几何模型，不能灵活运用一些重要元素之间的位置关系，没掌握一些解题技巧（如局部图形建立平面直角坐标系作平面化处理），造成点的坐标求错，甚至求不出来等.三、解决问题之建系方法研究学生建系不合理，主要集中在x轴与y轴的建立，原因就是对图形的认知有障碍.所以主要方法就是把图形还原——局部平面化处理.画出底面的平面图，把建x，y轴的问题放在平面几何里完成.分析：作底面平面图如图3，图4，图5所示.由此平面图可以比较清楚地看到以那两条互相垂直的直线分别为x 轴、y 轴为宜，且方便写出平面内各点的坐标.可以看到建系的方法并不唯一，要根据题意选用一个合适的坐标系.点评：平面内常见的垂直关系有:菱形、正方形的对角线；等腰、等边三角形的中线与底边（三线合一）；直径所对圆周角的两边；或在某个三角形中知道两边一角，先用余弦定理求出第三边，再用勾股定理证明线线垂直等.四、解决问题之求点方法研究（一）垂线法在空间直角坐标系中，有些点的坐标可以通过向坐标平面或坐标轴作垂线，再求出垂线段的长，从而写出点的坐标.点评：点E为线段PD的三等分点，个别学生可能会类比中点坐标公式，容易犯“将P、D坐标相加除以3得到E点坐标”这样的错误.此题还可以用下面的向量法解决.（二）向量法在空间直角坐标系中，利用两向量相等，可以求出点的坐标.点评：在线上是否存在一个点满足某个要求的题型通常可以利用三点共线设，再利用向量相等用表示出未知点的坐标，再根据已知条件待定.利用向量相等对处理比较难作垂线或容易作错垂线的题目来说，效果更好.如例3.（三）待定系数法设出所求点的坐标，再利用题目给出的已知条件，如：线段的长度、线线角、线面角、面面角等，列出方程组，解方程组即可求出所求点的坐标.用向量法来解决例1，如下：证明：（1）连接 AC 、BD，设AC 与BD相交于点O，则AC⊥BD.以O为坐标原点，OA、OB所在直线分别为 x 轴、y 轴建立如图11所示的空间直角坐标系，由图观察可知，此二面角为钝角，所以二面角的余弦值为.点评：因为底面ABCD是菱形，对角线 AC 与 BD 互相垂直，所以可以以对角线的交点O为坐标原点，OA、OB所在直线分别为 x 轴、y轴建立空间直角坐标系，那么点P的坐标将是解决问题的关键.这里采用待定系数法，根据题目给出的线段的长度：，列方程组求解即可求出P点的坐标，使得问题迎刃而解.参考文献[1]徐晓宇,屈黎明.向量法解立体几何题的点坐标求法——2017年高考浙江卷立体几何解答题的方法总结. 《数学教学》,2018（8）：33~36.[2]卢学渊.向量法解立体几何题时动点的设法.《数学学习与研究：教研版》，2012（11）：107~107.。

高二新学案立体几何如何建系找坐标

B 1C 1BCDAD 1A 1EFEADBCP空间立体，寻求建系的方法，学会找坐标一、标准化的正方体，长方体，四棱锥问题1.正方体ABCD-A 1B 1C 1D 1，建立适当的坐标系，并表示图中所有点的坐标。

解;以A 为坐标原点.以AB ，AD ，AA 1所在直线为x,y,z 轴，建立如图空间直角坐标系，设正方体棱长为1，则ABCD是直角梯形，90=∠=∠BAD ABC ，2.如图，四边形ABCD SA 平面⊥，1===BC AB SA ，21=AD ，SC 中点是P ，建立适当的坐标系，表示图中所有点的坐标。

解;以A 为坐标原点.以AD ，AB ，AS 所在直线为x,y,z 轴，建立如图空间直角坐标系，则3.在五面体ABCDEF 中，FA ⊥平面ABCD ，AD ∥BC ∥FE ，AB ⊥AD ，M 为EC 的中点，AF=AB=BC=FE= 21AD=1，建立适当的坐标系，表示图中所有点的坐标。

解;以A 为坐标原点.以AB ，AD ，AF 所在直线为x,y,z 轴，建立如图空间直角坐标系，则4：如图，四棱锥P ABCD-中，底面ABCD为矩形，PA ⊥底面ABCD，6,3PA AB AD ===，点E 为棱PB 的中点。

建立适当的坐标系，表示图中所有点的坐标。

解;以A 为坐标原点.以AB ，AD ，AP 所在直线为x,y,z 轴，建立如图空间直角坐标系，则5..如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AB//CD,∠DAB=90°,PA=AD=DC=1,AB=2,M 为PB 的中点. 建立适当的坐标系，表示图中所有点的坐标。

解;以A 为坐标原点.以AD ，AB ，AP 所在直线为x,y,z 轴，建立如图空间直角坐标系，则6.多面体EDABC 中,AD ⊥平面ABC , AC ⊥ＢＣ，,ＡＤ＝21ＣＥ＝１，ＡＣ＝１.BC=2，M 为BE 中点.，建立适当的坐标系，表示图中所有点的坐标。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

- 598 - Oy

FEGHI

Oyx

zA'C'BB'C

第63炼立体几何解答题的建系设点问题在如今的立体几何解答题中，有些题目可以使用空间向量解决问题，与其说是向量运算，不如说是点的坐标运算，所以第一个阶段：建系设点就显得更为重要，建立合适的直角坐标系的原则有哪些？如何正确快速写出点的坐标？这是本文要介绍的内容。一、基础知识：（一）建立直角坐标系的原则：如何选取坐标轴 1、z轴的选取往往是比较容易的，依据的是线面垂直，即z

轴要与坐标平面xOy垂直，在几何体中也是很直观的，垂直底面高高向上的即是，而坐标原点即为z轴与底面的交点 2、,xy轴的选取：此为坐标是否易于写出的关键，有这么几个原则值得参考：（1）尽可能的让底面上更多的点位于,xy轴上（2）找角：,xy轴要相互垂直，所以要利用好底面中的垂直条件（3）找对称关系：寻找底面上的点能否存在轴对称特点 3、常用的空间直角坐标系满足,,xyz轴成右手系，所以在标,xy轴时要注意。

4、同一个几何体可以有不同的建系方法，其坐标也会对应不同。但是通过坐标所得到的结论（位置关系，角）是一致的。 5、解答题中，在建立空间直角坐标系之前，要先证明所用坐标轴为两两垂直（即一个线面垂直底面两条线垂直），这个过程不能省略。 6、与垂直相关的定理与结论：（1）线面垂直： ① 如果一条直线与一个平面上的两条相交直线垂直，则这条直线与该平面垂直 ② 两条平行线，如果其中一条与平面垂直，那么另外一条也与这个平面垂直 ③ 两个平面垂直，则其中一个平面上垂直交线的直线与另一个平面垂直 ④ 直棱柱：侧棱与底面垂直（2）线线垂直（相交垂直）： - 599 -

① 正方形，矩形，直角梯形 ② 等腰三角形底边上的中线与底边垂直（三线合一） ③ 菱形的对角线相互垂直

④ 勾股定理逆定理：若222ABACBC，则ABAC （二）坐标的书写：建系之后要能够快速准确的写出点的坐标，按照特点可以分为3类 1、能够直接写出坐标的点（1）坐标轴上的点，例如在正方体（长度为1）中的,,'ACD点，坐标特点如下： x轴：,0,0x y轴：0,,0y z轴：0,0,z

规律：在哪个轴上，那个位置就有坐标，其余均为0 （2）底面上的点：坐标均为,,0xy，即竖坐标0z，由于底面在作立体图时往往失真，所以要快速正确写出坐标，强烈建议在旁边作出底面的平面图进行参考：以上图为例：则可快速写出,HI点的坐标，位置关系清晰明了 111,,0,,1,022HI



2、空间中在底面投影为特殊位置的点：如果'11,,Axyz在底面的投影为22,,0Axy，那么

1212,xxyy（即点与投影点的横纵坐标相同）

由这条规律出发，在写空间中的点时，可看下在底面的投影点，坐标是否好写。如果可以则直接确定了横纵坐标，而竖坐标为该点到底面的距离。例如：正方体中的'B点，其投影为B，而1,1,0B所以'1,1,Bz，而其到底面的距离为1，故坐标为'1,1,1B 以上两个类型已经可以囊括大多数几何体中的点，但总还有一些特殊点，那么就要用到第三个方法： 3、需要计算的点

① 中点坐标公式：111222,,,,,AxyzBxyz，则AB中点121212,,222xxyyzzM，图中的,,,HIEF等中点坐标均可计算 ② 利用向量关系进行计算（先设再求）：向量坐标化后，向量的关系也可转化为坐标的关系，

AB - 600 -

进而可以求出一些位置不好的点的坐标，方法通常是先设出所求点的坐标，再选取向量，利用向量关系解出变量的值，例如：求'A点的坐标，如果使用向量计算，则设',,Axyz，

可直接写出'1,0,0,1,1,0,1,1,1ABB，观察向量''ABABuuuuruuur，而0,1,0ABuuur ，

''1,1,1ABxyz

uuuur 101110101xxyyzz '1,0,1A

二、典型例题：例1：在三棱锥PABC中，PA平面ABC，90BACo，,,DEF分别是棱,,ABBCCD的中点，1,2ABACPA，试建立适当的空间直角坐标系并确定各点坐

标解：PAQ平面ABC ,PAABPAAC 90BACoQ

,,PAABAC两两垂直

以,,APABAC为轴建立直角坐标系坐标轴上的点：0,0,0,1,0,0,0,1,0,0,0,2ABCP

中点：:DAB中点1,0,02 :EBC中点11,,022 :FPC中点10,,12 综上所述：11111,0,0,0,1,0,0,0,2,,0,0,,,0,0,,12222BCPDEF 小炼有话说：本讲中为了体现某些点坐标的来历，在例题的过程中进行详细书写。这些过程在解答题中可以省略。例2：在长方体1111ABCDABCD中，,EF分别是棱1,BCCC上的点，2CFABCE，

1::1:2:4ABADAA，建立适当的直角坐标系并写出点的坐标

FEDAC

P - 601 -

思路：建系方式显而易见，长方体1,,AAABAD两两垂直，本题所给的是线段的比例，如果设1,2,4ABaADaAAa等，则点的坐标都含有a，不

便于计算。对待此类问题可以通过设单位长度，从而使得坐标都为具体的数。解：因为长方体1111ABCDABCD

1,,ABADAA两两垂直

以1,,ABADAA为轴如图建系，设AB为单位长度

112,4,1,2ADAACFCE

11111,0,0,1,2,0,0,2,0,1,0,4,0,0,4,1,2,4,0,2,4BCDBACD

31,,0,1,2,12EF



例3：如图，在等腰梯形ABCD中，ABCD∥，1,60ADDCCBABCo，CF 平面ABCD，且1CF，建立适当的直角坐标系并确定各点坐标。思路：本题直接有一个线面垂直，所以只需在平面ABCD找过C的相互垂直的直线即可。由题意，BCD不是直角。所以可以以其中一条边为轴，在底面上作垂线即可构造出两两垂直的条件，进而可以建立坐标系方案一：（选择BC为轴），连结AC 可知120ADCo 在ADCV中 2222cos3ACADDCADDCADC

3AC

由3,1,60ACBCABCo可解得2,90ABACBo ACBC CFQ平面ABCD ,CFACCFBC

B1C

A1D

DABC

DCAB - 602 -

以,,ACCFBC为坐标轴如图建系： 310,1,0,3,0,0,,,0,0,0,122BADF



方案二（以CD 为轴）过C作CD的垂线CM CFQ平面ABCD ,CFCDCFCM

以,,CDCFCM为坐标轴如图建系：

（同方案一）计算可得：3,22CMAB 3331,,0,,,0,0,1,0,0,0,12222ABDF



小炼有话说：建立坐标系的最重要的条件就是线面垂直（即z轴），对于,xy轴的选取，如果没有已知线段，可以以垂足所在的某一条直线为坐标轴，然后作这条轴的垂线来确定另一条轴，本题中的两个方案就是选过垂足C的直线为轴建立的坐标系。例4：已知四边形ABCD满足1,2ADBCBAADDCBCa∥，E是BC中点，将BAEV翻折成1BAEV，使得平面1BAE平面

AECD，F为1BD中点

思路：在处理翻折问题时，首先要确定在翻折的过程中哪些量与位置关系不变，这些都是作为已知条件使用的。本题在翻折时，BAEV是等边三角形，四边形AECD为60o的菱形是不变的，寻找线面垂直时，根据平面'BAE平面AECD，结合'BAEV是等边三角形，可取AE中点M，则可证'BM平面AECD，再在四边形AECD找一组过M的垂线即可建系解：取AE中点M，连结'BM

ABE

DCAB