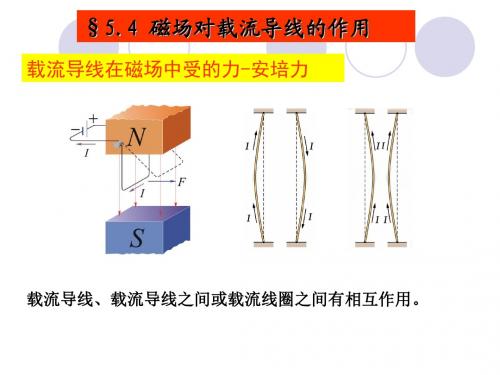
7-8载流导线在磁场中所受的力
第七章 磁力

*在均匀磁场中的闭合载流回路整体 上不受磁力
三、磁场对载流线圈的作用(磁力矩) 1.匀强磁场对载流线圈的作用 d l1 线段 ad和bc受安培力等大、 F 反向,可抵消;线段ab, dc 受力 a 相大、反向, 不在一条直线对oo/ B l2 n 轴形成力矩: c F Fab Fdc Il2 B,
11
交流电源
带电粒子的动能 q EK B2R2 2m
2
应用3-霍尔效应 ——若 B I ,则导体的上
下面之间会出现电势差。
12
b
实验规律
IB UH K b
U
霍尔效应的理论解释 空穴导电 f qvB qU H qU H 平衡时 qvB Fe qE d d S dq I q svn dt I v qnvbd v qnbd
(b ) F I dl B (a) (b) I ( d l ) B
(a)
a
载流导线上任意 位置取电流元 l Id
I ab B
BI ab
22
推论:在均匀磁场(大小相等,方向相同)中,载 流导线所受安培力与导线形状无关,只与始 末两点的直线距离成正比。
一段直线电流
qv方向与dl 方向相同, v qvdl qdl
Nqv B nsqdl v B
I
Idl
B
F BIl sin
L
L
F Idl B
L
20
安培力的实质:磁场通过洛仑兹力而施于导体的 作用力。
l1 l1 M Fab sin Fdc sin 2 2 Il1l2 B sin ISBsin
第四讲安培力共20页

解 B0
I1
2π dRcos
dFB2d Il0 2Iπ 1I2dR dlco sI 1
B
dy dFyd dF dFx
I2dl
dlRd
OR
x
dF0I1I2
2π
Rd dRcos
I2
d F xd F co s0 2 Iπ 1I2d R cR o c d o s s d F yd F sin 0 2 Iπ 1I2d R sR ic n d o s
. Fx02 I1πI2R02πdcR ocdsos
B
y
d
dFy
dF
0I1I2(1
d) d2R2
I1
F y02 I1 π I2R0 2πdsR ic d no s0
d OR
dFx I2dl
x
I2
Fx02 I1 π I2R02πdcR o cdso s0I1I2(1
为0.08T,方向沿 x 轴正向.问线圈受力情况怎样? 线
圈所受的磁力矩又为多少?
y
解 把线圈分为JQP和PKJ两部分
B
J
F JQ B P (2 R I )k 0 .6k N 4I
x
R
F P K B J ( 2 R ) I k 0 .6 k N 4 Q o d K x
I2dl2
dF1
dF2
B1
d
dF2 dF1 0I1I2
dl2 dl1 2πd
B1
0 I1
2π d
B2
0I2
2π d
d F 2B 1I2d l2sin
5 .5安培力、洛伦兹力
Fab
l1
b
B
Fbc
l 2 o'
ˆ n Pm
考虑方向: M P m B
Pm B sin
上述结论具有普遍 意义(也适用于带电
粒子沿任意闭合回路 的运动或自旋磁矩在 磁场中受的力矩) 。
Pm 右旋 力矩方向为:四指从 到 B ,大拇指指向。
§5.5 洛仑兹力 霍尔效应 1. 洛仑兹力
R
dl Rd
Fx
0
IB cos Rd 0
IB sinRd IB2R
0
例2 计算半径为R的半圆导线在均匀磁场 B中所受的力。
半径为R的半圆导线的安培力: 大小: F BI 2R
B
I
F
R
方向: 沿平面竖直向上
等效于长度为2R,电流为I的直导线所 (起点和终点重合)受的力 推广: 任何载流导线在均匀磁场中受力等效 于一直导线(起点和终点重合)所受 的力
IB VH h B
+
I
VH
定量分析:
h b
A - - - - + + + + + B
B
I
+ VH
A -
f B B
-
-
+
v
+
q
-
B
fE
+
+
I
运动电荷 所受洛仑兹力:
U A U B EH b v Bb f B qv B q e I nqv S nev bh 电场力: f E qEH I 二者平衡时: vb neh qv B qEH
大学物理磁学部分复习资料..

41 磁 学基本内容一、稳恒磁场 磁感应强度1. 稳恒磁场电流、运动电荷、永久磁体在周围空间激发磁场。
稳恒磁场是指不随时间变化的磁场。
稳恒电流激发的磁场是一种稳恒磁场。
2. 物质磁性的电本质无论是永磁体还是导线中的电流,它们的磁效应的根源都是电荷的运动。
因此,磁场是运动电荷的场。
3. 磁感应强度磁感应强度B是描述磁场的基本物理量,它的作用与E 在描述电场时的作用相当。
磁场对处于其中的载流导线、运动电荷、载流线圈、永久磁体有力及力矩的作用。
可以根据这些作用确定一点处磁场的强弱和方向——磁感应强度B。
带电q 的正点电荷在磁场中以速度v运动,若在某点不受磁力,则该点磁感应强度B 的方向必与电荷通过该点的速度v平行。
当该电荷以垂直于磁感应强度B 通过该点时受磁力⊥F ,则该点磁感应强度大小qvF B ⊥=,且⊥F ,v ,B两两互相垂直并构成右手系。
二、毕奥—萨伐尔定律 运动电荷的磁场1. 磁场的叠加原理空间一点的磁感强度等于各电流单独存在时在该点产生磁感应强度的矢量和:∑=ii B B 可推广为 ⎰=B d B42B d是电流强度有限而长度无限小的电流元l d I 或电流强度无限小而空间大小不是无限小的元电流的磁场。
上式中矢量号一般不能略去,只有当各电流产生磁场方向相同时,才能去掉矢量号。
2. 毕奥—萨伐尔定律电流元l d I 在空间一点产生的磁场B d为: 304rr l d I B d πμ⨯= 大小: 02I sin(I ,r)dB 4r dl dl μπ∠=方向:B d 垂直于电流元l d I 与r 所形成的平面,且B d与l d I 、r构成右手螺旋。
3. 电流与运动电荷的关系导体中电荷定向运动形成电流,设导体截面积为S ,单位体积载流子数为n 。
每个载流子带电q ,定向运动速率为v ,则nqvS I =。
电量为q 的带电体作半径为R 、周期为T 的匀速圆周运动相当于半径为R 、电流强度T q I /=的圆电流,具有磁矩TqR I R p m 22ππ==。
磁力的功
I
y J Idl
θ
R Q O P
B
方向与Oz轴的正向相同 垂直 方向与 轴的正向相同.垂直 轴的正向相同 纸面向外.因此 因此,作用在圆形载 纸面向外 因此 作用在圆形载 流线圈上的合力为零. 流线圈上的合力为零
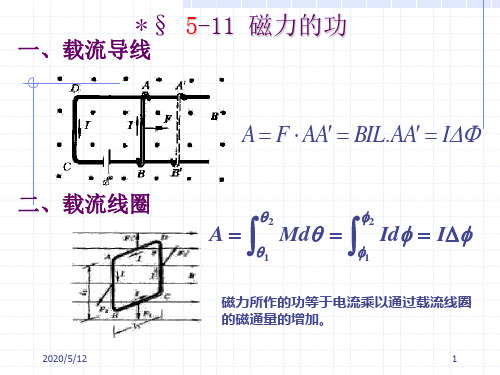
*§ 5-11 磁力的功
一、载流导线
A = F ⋅ AA′ = BIL.AA′ = I∆Φ
二、载流线圈
A=
θ2
1
∫θ
Mdθ =
∫φ
φ2
1
Idφ = I∆φ
磁力所作的功等于电流乘以通过载流线圈 的磁通量的增加。 的磁通量的增加。
2012-5-24 1
11在磁感强度为B的均匀磁场中,通过一半径为R 例 11 - 7 : 在磁感强度为 B 的均匀磁场中 , 通过一半径为 R 的 半圆导线中的电流为I 若导线所在平面与B 垂直, 半圆导线中的电流为 I。 若导线所在平面与 B 垂直 , 求该导 线所受的安培力。 线所受的安培力。 解:
F2 = BIr ∫
sin θ dθ
= BIr[cos θ 0 − cos(π − θ 0 )] = BI (2r cos θ 0 ) 2r cos θ 0 = LAB , r ) F2 = BILAB j
2012-5-24 5
闭合回路所受的磁场力F 的和为零. 即F1=-F2,闭合回路所受的磁场力 1与F2的和为零 闭合回路所受的磁场力 上述结论不仅对图所示的闭合回路是正确的,而且对其他形 上述结论不仅对图所示的闭合回路是正确的 而且对其他形 状的闭合回路也是正确的. 状的闭合回路也是正确的
大学物理第五版马文蔚课后答案(上)7-8

7-1 分析与解 在两根通过电流相同的螺线管中,磁感强度大小与螺线管线圈单位长度的匝数成正比.根据题意,用两根长度相同的细导线绕成的线圈单位长度的匝数之比21==R r n n r R 因而正确答案为(C )。
7-2 分析与解 作半径为r 的圆S ′与半球面构成一闭合曲面,根据磁场的高斯定理,磁感线是闭合曲线,闭合曲面的磁通量为零,即穿进半球面S 的磁通量等于穿出圆面S ′的磁通量;S B ⋅=mΦ.因而正确答案为(D ).7-3 分析与解 由磁场中的安培环路定律,磁感强度沿闭合回路的积分为零时,回路上各点的磁感强度不一定为零;闭合回路上各点磁感强度为零时,穿过回路的电流代数和必定为零。
因而正确答案为(B ).7-4 分析与解 由磁场中的安培环路定律,积分回路外的电流不会影响磁感强度沿回路的积分;但同样会改变回路上各点的磁场分布.因而正确答案为(C ).7-5 分析与解 利用安培环路定理可先求出磁介质中的磁场强度,再由M =(μr-1)H 求得磁介质内的磁化强度,因而正确答案为(B )7-6 分析 一个电子绕存储环近似以光速运动时,对电流的贡献为cI e I /Δ=,因而由lNe c I =,可解出环中的电子数。
解 通过分析结果可得环中的电子数10104⨯==ecIlN 7-7 分析 一个铜原子的质量A N M m /=,其中N A 为阿伏伽德罗常数,由铜的密度ρ可以推算出铜的原子数密度m ρn /=根据假设,每个铜原子贡献出一个自由电子,其电荷为e ,电流密度d m ne j v =.从而可解得电子的漂移速率v d .将电子气视为理想气体,根据气体动理论,电子热运动的平均速率em kT π8=v其中k 为玻耳兹曼常量,m e 为电子质量.从而可解得电子的平均速率与漂移速率的关系. 解 (1)铜导线单位体积的原子数为M ρN n A /=电流密度为j m 时铜线内电子的漂移速率14s m 1046.4//--⋅⨯===e ρN M j ne j A m m d v(2)室温下(T =300K)电子热运动的平均速率与电子漂移速率之比为81042.2π81⨯≈=ed d m kTv v v 室温下电子热运动的平均速率远大于电子在恒定电场中的定向漂移速率.电子实际的运动是无规热运动和沿电场相反方向的漂移运动的叠加.考虑到电子的漂移速率很小,电信号的信息载体显然不会是定向漂移的电子.实验证明电信号是通过电磁波以光速传递的.7-8 分析 如图所示是同轴柱面的横截面,电流密度j 对中心轴对称分布.根据恒定电流的连续性,在两个同轴导体之间的任意一个半径为r 的同轴圆柱面上流过的电流I 都相等,因此可得rl I j π2/=解 由分析可知,在半径r =6.0mm 的圆柱面上的电流密度2m mA 3.13π2/-⋅==rl I j7-9 解 设赤道电流为I ,则由教材第7-4节例2知,圆电流轴线上北极点的磁感强度()RIμR R IR μB 24202/3220=+=因此赤道上的等效圆电流为A 1073.12490⨯==μRBI 由于在地球地磁场的N极在地理南极,根据右手螺旋法则可判断赤道圆电流应该是由东向西流,与地球自转方向相反.7-10 分析 根据叠加原理,点O 的磁感强度可视作由ef 、be 、fa 三段直线以及acb 、a d b 两段圆弧电流共同激发.由于电源距环较远,0=ef B .而be 、fa 两段直线的延长线通过点O ,由于0Idl r ⨯=,由毕-萨定律知0b e f a ==B B .流过圆弧的电流I 1、I 2的方向如图所示,两圆弧在点O 激发的磁场分别为21101π4r l I μB =,22202π4r l I μB =其中I 1、I 2分别是圆弧acb 、a d b 的弧长,由于导线电阻R 与弧长l 成正比,而圆弧acb 、a d b 又构成并联电路,故有2211l I l I =将B1、B2叠加可得点O 的磁感强度B .解 由上述分析可知,点O 的合磁感强度0π4π42220211021=-=-=rl I μr l I μB B B 7-11 分析 应用磁场叠加原理求解.将不同形状的载流导线分解成长直部分和圆弧部分,它们各自在点O 处所激发的磁感强度较容易求得,则总的磁感强度∑=i B B 0解 (a)长直电流对点O 而言,有0=⨯r l Id ,因此它在点O 产生的磁场为零,则点O 处总的磁感强度为1/4圆弧电流所激发,故有RIμB 800=B 0的方向垂直纸面向外.(b)将载流导线看作圆电流和长直电流,由叠加原理可得RIμR I μB π22000-=B 0的方向垂直纸面向里.(c )将载流导线看作1/2圆电流和两段半无限长直电流,由叠加原理可得RIμR I μR I μR I μR I μB 4π24π4π4000000+=++=B 0的方向垂直纸面向外.7-12 分析 由教材7-4节例题可知,圆弧载流导线在圆心激发的磁感强度R αI μBπ40=,其中α为圆弧载流导线所张的圆心角,磁感强度的方向依照右手定则确定;半无限长载流导线在圆心点O 激发的磁感强度RI μB π40=,磁感强度的方向依照右手定则确定。
磁场的作用力
一、 安培定律
1. 磁场对电流元的作用
安培力:
dF
Idl
B
安培定律
大小 dF IdlBsin
I
arcsin( Idl ,B )
方向判断: 右手螺旋
r
Idl
B
dF
2. 载流导线所受磁场力
F L dF L Idl B
均匀磁场中载流直导线所受安培力
例 计算长为 L 的载流直导线在均匀磁场 B中所受的力。
由于等离子体温度太高必须使用磁约束装置来充当容器
带电粒子的速度v和磁感强度B成 任意夹角时,此带电粒子在磁场 中作螺旋线运动,且回旋半径R 与磁感强度B成反比,磁场越强, 半径越小,这样一来,在很强的 磁场中,每个带电粒子的运动便 被约束在一根磁感线附近的很小 的范围内
两个电流方向相同的 线圈产生中央弱两端 强的不均匀磁场
2
d
三、磁场对载流线圈的作用
设均匀磁场,矩形线圈
F1
F1
BIl1
sin( 2
)
BIl1 cos
F1 F1 且在同一直线上
F2
F2
BIl 2
sin 2
BIl 2
F2 F2 但不在同一直线上
整个线圈 F 0
F1 l1 d
a
2
IB
l2 b
c F1' n
a(b)
F2
F2'
d(c)
n
B
还用于继电器、电机、以及各种高频电磁元件 的磁芯、磁棒。
(2)硬磁材料——作永久磁铁 钨钢,碳钢,铝镍钴合金
B
HC
HC H
矫顽力(Hc)大(>102A/m),剩磁Br大 磁滞回线的面积大,损耗大。
安培力-高考物理知识点
安培力-高考物理知识点
(1)在安培力的公式中,I、B、l均采用国际单位制单位,则安培力的单位是牛顿。
(2)安培力(包括方向)可用矢量公式表示为F=Il×B。
(3)一般形式的安培力公式,用电流元Idl在磁场B中所受力的矢量和表示,即有F=∫Idl×B,
式中积分是对通电导线作线积分,B可为一般分布之非均匀磁场。
(4)通电线圈在匀强磁场中所受力矩的大小,不论形状如何,均等于M=ISBsinθ,式中θ为线圈磁矩方向与B之间的夹角。
通电线圈在磁场中受力矩作用而转动,以线圈磁矩沿B方向为(稳定)平衡位置。
(5)安培力与洛仑兹力两者既有联系又有区别。
载流导线在磁场中所受的安培力,实质上是导线内自由电子所受洛仑兹力的宏观表现。
但是,洛仑兹力的方向始终与运动电荷的速度方向垂直,因此它永远不作功,而载流导线在磁场中运动时,安培力是作功的,这两者并不矛盾。
洛仑兹力沿导线垂直方向的分力所作功的和正是安培力所作的功。
而另一沿平行于导线方向的分力所作的功一定为负功。
且数值与上述功相等,所以,洛仑兹力作的总功等于零,即洛仑兹力f与V垂直,不作功。
从物理意义上说,f∥所作的负功,即为外电源ε提供的电场力,维持电子向上运动所作的功。
从能量转化角度来说,此电路中通过电源把其他形式的能转化为电能。
当电流流过回路时,一部分电能通过电阻转化为焦耳热,另一部分在通过磁场时,由洛仑兹力的一个分力转变为安培力而作功,实现由电能向机械能的转化。
磁 力 的 功
沿 OPQRO,线圈所在处的磁场是均匀的,磁感应强度为 0.02 T,方向平行于 Ox 轴。② 线圈由这个位
置转至平衡位置时,求磁场力的功。 【解】 ② 线圈在 30 时,通过线圈平面的磁通量为m1 BS cos 0.02 0.06 0.08 cos30 4.8105 (Wb)
线圈转至平衡位置时 0 时,
大学物理
磁力的功 , ,
1.载流导线在磁场中运动时磁场力所做的功
设有一均匀磁场,磁感应强度 B 的方向垂直于纸面向外,如图所示。假定当 AB 滑动时,电路中电流 I 保持不变,按安培定律,载流导线 AB 在磁场中所受的安培力 F 在纸面上,指向如图所示。
F 的大小为 F BIL 在导线移动中,磁场力所做的功为W Im
RO 所受的磁场力(沿 Oy 轴负方向)为 F4 BIl1 sin( 90) 0.6 102 (N) 。
磁力矩为 M F2l1 cos30 8.3104 (N m) ,磁力矩使线圈顺时针转动(面对 Oy 轴方向看去)。
磁力的功
, ,
,
,
例题讲解 14
如图所示,长方形线圈 OPQR 可绕 y 轴转动,边长 l1 6 cm ,l2 8 cm 。线圈中的电流为 10 A,方向
当载流导线在磁场中运动时,如果电流保持不变,磁场力所做的功等于电流乘以通过回路所环绕的面 积内磁通量的增量。
磁力的功 , ,
2.载流线圈在磁场内转动时磁场力所做的功
如图所示,设载流线圈在磁场内转过极小的角度 d ,使en 与 B 之间的夹角从 增为 d 。
磁力矩 M BIS sin ,所以磁力矩所做的功为 dW Md BIS sind BISd(cos) Id(BS cos)
OP 所受的磁场力(沿 Oz 轴负方向)为 F1 BIl2 sin 90 1.6 102 (N) ; QR 所受的磁场力(沿 Oz 轴正方向)为 F2 BIl2 sin 90 1.6 102 (N) ; PQ 所受的磁场力(沿 Oy 轴正方向)为 F3 BIl1 sin 0.6 102 (N) ;
磁场中的运动和磁力的方向
磁场中的运动和磁力的方向磁场是一个无形的力场,具有方向和强度,能够对物体施加力。
当物体在磁场中运动时,会受到磁力的作用。
本文将探讨在磁场中的运动以及磁力的方向。
一、磁场中的电荷运动磁场中的电荷运动受到洛伦兹力的影响。
洛伦兹力的方向与磁场方向、电荷的速度方向以及电荷的正负有关。
根据右手定则,可以知道洛伦兹力的方向为电荷速度方向、磁场方向以及电荷正负的叉乘方向。
二、磁场中的载流导线运动当载流导线处于磁场中时,导线内的电流会受到磁场力的作用。
根据右手定则,可以确定电荷受到的洛伦兹力的方向。
如果将右手的食、中、拇三指分别指向磁场方向、电流方向及已知的力方向,那么拇指的方向就是洛伦兹力的方向。
三、磁场中的带电粒子运动带电粒子包括质子、电子等,它们在磁场中受到的磁力也遵循洛伦兹力的定律。
当带电粒子以一定的速度进入磁场时,受到的磁力将使其发生轨道弯曲。
而弯曲方向则根据右手定则来决定,即以右手的拇指指向速度方向,当四指弯曲的方向与磁场方向一致时,拇指的方向即为磁力的方向。
四、磁场中的力的方向根据前述内容可知,磁场中运动的物体所受力的方向与物体速度方向、磁场方向以及物体电荷正负相关。
总而言之,根据右手定则可以得出磁力的方向。
总结:磁场中的运动和磁力的方向是通过右手定则来确定的。
对于电荷、载流导线以及带电粒子等物体在磁场中的运动,可以根据洛伦兹力的定律来确定所受磁力的方向。
通过应用右手定则可以理解和推导这些运动和磁力的方向关系。
请君牢记:运动的基础是力,而在磁场中的运动则受到磁力的支配。
了解磁场对运动的影响对于理解电磁现象和应用磁场具有重要意义。
