图的k-顶点着色与k-边着色的Groebner基求解
第6章 着色问题

图论及其应用
9
6.2 Vizing定理
(B)iq = ik 某 1 k q-1 : 重新进行边着色如下 , vk(ik) 将uvj 改着色ij 1jk no 并抹去边uvk+1 上的色 ik 。 ik 易见, H = 的每个分支是路或圈,由色i0与ik的 i3 u(i0) 边交错组成,且 v3(i3) i 2 u,vk+1,vq 在H中的度 1。 iq-1 i1 从而,该三顶点不可能同时在H的一分支中。这时 vq(iq) v2(i2) 以下二情形至少有一个为真, v1(i1) ① u 与vk+1不在H的同一分支中:将H的含vk+1 分支中的色i0 与ik对换,得G 的除uvk+1外的正常( +1)-边着色, 其中u与vk+1上色i0都未表 现。从而,G有一正常( +1)-边着色。 ② u与vq不在H的同一分支中: 再继续调整边着色如下, 将uvj 改着色ij k+1 j q-1 并抹去边uvq上的色 (iq-1 ) 易见,上述更动并未涉及色i0与ik ,因此H 保持不变。将H中含vq分 支的色i0 与 ik 对换,得G 的除uvq外的正常( +1)-边着色,其 中在u与vq上色i0都未表现。从而,G有一正常( +1)-边着色。
图论及其应用 2
6.1 边色数
例:n个人举行一些两两会谈,每次会谈用一个单元时 间。问最少要多少单元时间,才能安排完所有会谈?
解:作一n顶点图G,其中两顶点相邻当且仅当对应 的两人间要安排一次会谈。易见,所需时间单元数 ’(G) 。
称色i表现(represented)于顶点v 与v相关 联的某一边有色i。
由归纳假设,G’ 有一 (G’)-正常边着色 C’={E1’,...,E(G’)}。 若 (G’) < (G),则G显然有(G)-正常边着色,证完; 否则,(G’) = (G)。令Au与Av各表示C’中不表现于u与v的色 集。由于在G’中u与v都不是其最大度顶点,从而有Au,Av ① 当 Au∩ Av 时:将Au ∩ Av 之一色着在边e上,即得 G的(G)-正常边着色。 ② Au Av = 时:任取色i Au 及色j Av 。令H为 G[Ei’ Ej’] 中含u的分 支。易见,H是一条路,由色i与色j边交 替组成。因此,v一定不在H上(不然,由于H的第一条边有色j, 最后一边有i,其长为偶数。这导致G中含一奇圈H + e,矛盾。) 对换H上的色i与j,得G’的另一正常 (G’)-边着色,其中在u与v上 色j都不表现。 再将色j着在e上,即得G的正常 (G)-边着色 。
基本数学模型-顶点着色

Petersen 图
'(G) 4
3
排课表问题
• 有 m 位教师和 n 个班级,教师 i 每天为班级 j 授
课 pij 个学时,如何安排一张课表,可使每天课
时数最少
• 构造有平行边的二部图 G ,顶点集 V X Y ,X 为教师集,Y 为班级集,X 中顶点 i 和 Y 中顶点 j 有 pij 条边相连
Appel, K., Haken, W., Every Planar Map is Four Colorable, Illinois Journal of Mathematics
Part I. Discharging, 21, 429–490, 1979 Part II. Reducibility, 21, 491–567,1979
p
6
排课表问题
1234
x1 y4 y1 y3 y1
x2 y2
y4
x3 y3 y4
y2
x4
y5
y4
三间教室
123456
x1 y4 y3 y1
y1
x2 y2 y4
x3ቤተ መጻሕፍቲ ባይዱ
y4 y3 y2
x4
y4
y5
两间教室
7
运筹与统计
着色
顶点着色
• 图顶点G的用顶k 点种颜k着色色之是一指着将色图,G使的得每相一邻个的
顶点不染同一种颜色
• 将 G的顶点按上述要求着色所需的最少 颜色数称为图 G的色数(chromatic
number),记为 (G) • 对任意简单图 G ,(G) Δ(G) 1,若G
连通且不是奇圈或完全图,(G) Δ(G)
可约构形组成的不 可免完备集(部分)
一类图中k-圈的Grobner基求解方法

∑‰) P 令T 中 ( 为Y 非零坐 集合 那么T 标的 ・ 可分
解 为
T = P () u Tl U u … U , ≥ 0 s
时 和J<i 时该路径. 此种约定显然是唯一确定的. 令 G中所有无 向边 的多元多项式的集合为 层, 即
=
其中 P 为 到 的一条无环 闭路径 .
为无向图. 以下 讨 论 的 图 均 为 无 环 无 重 边 的 有 限 无 向 图 ( 不
一
方 组,将 ( ∑ 圳 , ) 离 来 性方 组 程 记 ∞ 分 出 线 程 为
( )WY : F I
其 中 W = ( )为 系数 阵 ,
∈ { ,, } Y = ( -10 1 , Y)
为未 知元 阵 , : ( 为 常 数 列 阵 , e { , l . 方 程 F r) r 一l0,{ 记 组 ( ) 一 步 转 化 后 的 齐 次方 程 组 为 I进
( I )WY : 0
定 连 通 ) 后文 不再 加 以说 明 . ,
2 无 向 闭路径 与 多元 多项 式 环 n Y ,: … , Y , Y ]的 r 转化
第2 6卷
第 5期
长
沙
大
学
学
报
V0 . 6 No 5 I 2 .
2012年 9月
J OURN F CHANGSHA ALO UNl VERSI TY
S p.20 12 e
一
类 图 中 k一圈 的 Grb e 基 求解 方 法 6nr
张 蕊青 , 雪玮 熊
进行变化 , 将两端 的系数合 并之 后得 到关 于 Y 的线性 ,
个图可用 一个 图形表示 . 若把图中边 e 看作总是与两
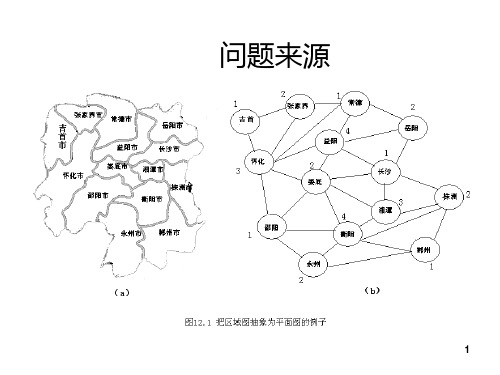
图的着色问题

问题来源
图的着色
通常所说的着色问题是指下述两类问题: 通常所说的着色问题是指下述两类问题: 1.给定无环图G=(V,E),用m种颜色为图中 的每条边着色,要求每条边着一种颜色, 的每条边着色,要求每条边着一种颜色,并 使相邻两条边有着不同的颜色, 使相邻两条边有着不同的颜色,这个问题称 为图的边着色问题。 为图的边着色问题。 2.给定无向图G=(V,E),用m种颜色为图中 的每个顶点着色,要求每个顶点着一种颜色, 的每个顶点着色,要求每个顶点着一种颜色, 并使相邻两顶点之间有着不同的颜色, 并使相邻两顶点之间有着不同的颜色,这个 问题称为图的顶着色问题。 问题称为图的顶着色问题。
化简得
( a + bd )(b + aceg )(c + bdef )( d + aceg )(e + bcdf )( f + ceg )( g + bdf )
求极小覆盖法- 求极小覆盖法-布尔代数法
Step3:从中挑选所用极大独立集个数最小者, Step3:从中挑选所用极大独立集个数最小者, 即为X 即为X(G) 但上述子集的颜色数都不是X ),正确的应 但上述子集的颜色数都不是X(G),正确的应 该是X =3,该子集为: {b,d,f}中的 该是X(G)=3,该子集为:给{b,d,f}中的 b,d,f涂颜色 涂颜色1 {a,e,g}中a,e,g涂颜色 涂颜色2 b,d,f涂颜色1,为{a,e,g}中a,e,g涂颜色2为 {a,c,g}中的 涂颜色3 中的c {a,c,g}中的c涂颜色3。 由此可见, 由此可见,求色数其需要求极大独立集以 及一切若干极大独立集的和含所有顶点的子 对于大图, 集,对于大图,因为图计算量过大而成为实 际上难以凑效的算法,所以不是一个好算法, 际上难以凑效的算法,所以不是一个好算法, 一般我们采用贪心法等近似算法来求解 。
第五节 着色问题

第五节 着色问题定义1. 图G 的顶点着色(V erter Colouring)是给每个顶点赋予一种颜色,使得相邻顶点的颜色不同,给图G 进行顶点着色需要的颜色的最小值称为G 的色数(Chromatic Number),记为)(G χ. 若κχ=)(G ,则称G 是κ-色的(κ-chromatic);若κχ≤)(G ,则称G 是可κ-着色的(κ-colourable).例1. 在下图中2)(1=G χ,3)(2=G χ,4)(3=G χ. 注意1G 即为2κ,2G 即为5κ1111111111111111v 1v 2v 1v 2u 1u 2ωG 1G 2G 3v 1v 2v 3v 4v 5u 1u 3u 4u 5ω11u 2111111下面讨论)(G χ的上界和下界,先给出下面的定义.定义2. 图G 中两两不相邻的顶点组成的集合称为独立集(Independent Set),用)(G α来表示G 中最大独立集的元素个数. 图G 中两两相邻的顶点构成的集合称为团(Clique),用)(G ω表示G 中最大团的元素个数.注记:(1)显然,G 是可κ-着色的当且仅当)(G V 是κ个独立集的并. 特别的,G 是可2-着色的当且仅当G 是二部图. (2))()(G G ωχ≥且)()()(G G n G αχ≥(习题1). (3)对于完全图n κ有:n n n ==)()(κωκχ. 但一般来说)(G χ可以远大于)(G ω. 下面介绍一种构造任意色数的三角形无关图(即不含3κ为子图)的方法,这种方法归功于Mycielski,1955.定义3(Mycielski 构造). 由简单图G 产生一个以G 为子图的简单图'G . 从顶点集为}v ,...,v ,{v n 21的图G开始添加顶点}u ,...,u ,{u n 21和ω;添加边,使得i u 与)(i G v N 中的顶点相邻,ω与}u ,...,u ,{u n 21中的所有顶点相邻.例1中,以2-色图1G 开始,进行二次Mycielski 构造,分别得到3-色图2G 和4-色图3G . 下面的定理告诉我们可以构造一个色数任意大的图G 且2)(=G ω.定理1(Mycielski 1955). 由一个κ-色三角形无关图G ,Mycielski 构造可得到一个1+κ-色三角形无关图'G .定义4. 图G 称为κ-临界的(κ-critical),如果κχ=)(G 且1)(-=-κχv G))((G V v ∈∀.也即去掉G 的任何一个顶点会使G 的色数减少.下面介绍κ-临界图的一个重要性质.定理2. 如果G 是κ-临界的,则1)(-≥κδG .证明:令G 是κ-临界的且2)(-≤κδG . 设)(G V v ∈且)()(G v d δ=. 由于G 是κ-临界的,故1)(-=-κχv G .由于2)(-≤κv d ,故在对v G -着色的1-κ种颜色中,存在一种颜色没有被v 的至多2-κ个邻接点使用,将这种颜色对v 着色就得到G 是1-κ-着色的. 与κχ=)(G 矛盾.推论①:如果κδ=)(G ,则G 至少有κ个顶点的度数不小于1-κ.证明:如果κδ=)(G ,则G 就有一个κ-临界子图H (删除G 中不影响)(G χ的顶点,直到不能继续为止).由于κχ=H)(,故H 至少有κ个顶点. 由定理2,1)H (-≥κδ,所有H 至少有κ个顶点的度数不小于1-κ,即这κ个顶点在G 中的度数不小于1-κ.推论②:1)()(+∆≤G G χ.证明:假设1)()(+∆>G G χ,即)(1)(G G ∆>-χ,与定理2矛盾.上述推论中的等号在G 是完全图或奇环时成立,除这两类图之外,我们有下面的结论. 定理3(Brooks,1941). 如果G 是连通图,并且G 既不是完全图也不是奇环,则)()(G G ∆≤χ.习题:1. 证明:)()(G G ωχ≥且)()()(G G n G αχ≥2. 下列各图是否可以3-着色?确定它们的色数.gfedcabfedbacd a111111b 1e111111c3. 新学期安排补考,下表是上学期考试不及格的情况.“×”表示某门课不及格.学生 数分 高代 解析几何英语 张三 × × 李四 × × 王五 × × 赵六 × × × 陈七××问至少需要安排几场考试,使得这五个同学参加完所有的考试(注:每场考试一个学生只能考一门,但考场中的学生可以考不同的科目) 4. 如果G 的度序列为n d d d ≥≥≥ (21),则}1,{min max 1)(},..,1{-+≤∈i d G i n i χ.5. 图G 的边着色是指将颜色赋予G 的边,如果相邻边的颜色不同,则称这种边着色为正常边着色(proper edge colouring). 边色数记为)('G χ,是对G 进行正常边着色所需要的最小颜色数量.①证明:)()('G G ∆≥χ.举例说明某些图可以取到下界.②证明:对于完全图12-n κ,12)('12-=-n n κχ;对完全图n 2κ,有12)('2-=n n κχ(因此对于任意完全图n κ,有n n n n n =+∆≤≤-=∆1)()('1)(κκχκ. 这个结果不是偶然的,因为更强的一个结果(Vizing 定理)是:对任意图G ,1)()(')(+∆≤≤∆G G G χ)③证明:如果G 是二部图,则)()('G G ∆=χ(Konig,1916).。
图着色问题
ac b ed c g e bgd b ed f b ec f df
故G的极小覆盖为 { a , c , e , g } { b , c , , d , e , g } { b , d , , e ,f } { b , c , , d ,f } 取• 其S补te集p2,:得求到出G一的切所若有干极极大大独独立立集集:和所{ 有b ,顶d ,点f} 的{ a 子,,f 集} { a ,, c ,g } { a ,, e ,g }
回溯法
14
回溯法
step two:以颜色1为顶点B着色生成结点3时,产生 (1,1,0,0,0),是个无效着色,结点3为d_结点。
Step three:以颜色2为顶点B着色生成结点4,产 生(1,2,0,0,0),是个有效着色。
Step four:分别以颜色1和2为顶点C着色生成结点 5和6,产生(1,2,1,0,0)和(1,2,2,0,0),都是无效着 色,因此结点5和6都是d_结点。
9
穷举法-Welch Powell着色法
• 给定图G,用Welch Powell法对图G着
色1
A2 3
2
A3
1
A4
A5
A6 3
10
穷举法-Welch Powell着色法
• 第一步:将图G中的结点按度数的递减顺序排
列: A 5,A 3,A 7,A 1,A 2,A 4,A 6,A 8
• 第二步:用第一种颜色对A5着第一种颜色, 并对与A5不邻接的结点A1也着第一种颜色。
//搜索下一个颜色
•
if (color[k]<=m && k= =n)
//求解完毕,输出解
•
{ for (i=1; i<=n; i++)
图的顶点着色问题的DNA算法

图的顶点着色问题的DNA 算法高 琳1,许 进2(1.西安电子科技大学雷达信号处理国家重点实验室,陕西西安710071;2.华中科技大学系统科学研究所,湖北武汉430074)摘 要: 图的顶点着色问题是指无向图中任意两个相邻顶点都分配到不同的颜色,这个问题是著名的NP -完全问题,没有非常有效的算法.但在1994年Adleman [1]首次提出用DNA 计算解决NP -完全问题,设计出一种全新的计算模式)模拟生物分子DNA 的结构并借助于分子生物技术进行计算,使得NP -完全问题的求解可能得到解决.本文首先提出了基于分子生物技术的图的顶点着色问题的DNA 算法,算法的关键是对图中的顶点和顶点的颜色进行恰当的编码,以便于使用常规的生物操作及生物酶完成解的产生及最终解的分离,依据分子生物学的实验方法,本文提出的算法是有效和可行的;其次指出了该算法的优点、存在的问题及将来进一步的研究方向.关键词: DNA 计算;NP -完全问题;顶点着色问题;限制酶中图分类号: TP18 文献标识码: A 文章编号: 0372-2112(2003)04-0494-04A DNA Algorithm for Graph Vertex Coloring ProblemGAO Lin 1,XU Jin 2(1.National Ke y Lab.o f Radar Si gnal Processing ,Xidian U niv ,Xi .an ,Shanxi 710071,China ;2.System Science Research Instit ute ,Huazhong Unive rsity o f Science and Tec hnology ,Wuhan,Hube i 430074,China)Abstract: Given an undirected graph,the vertex coloring problem is to assign a different color for vertex mutually adjacent.This problem is an NP -complete one and has no effective solving method.But Adleman [1]in troduced firstly the DNA computing in 1994,with which the NP -complete problems are likely to be solved.DNA -based algorithm simulates molecular biology structure of DNA by means of molecular biology technological computation.This paper first introduces the DNA algor i th m for the vertex colori ng problem based on bio -molecular technology.T he key of the algorithm is coding for the vertex and the color of the vertex The problem is solved by tube operation that performs the basic core processing and extraction that makes the results visible.On the basis of the experi mental bio -molecular method,the algorith m is an effective method.Fi nally,the advantage and di sadvantage are di scussed,and the future re -search directions are poi nted out.Key words: DNA computation;NP -complete problem;vertex color i ng p roblem;endonucleases1 引言图的着色问题是一个著名的组合优化问题,是现代图论中的一个主要的研究课题之一,它无论在理论上还是工程应用上均有良好的应用背景,诸如电路布局问题,工序问题,排课表问题以及存储问题[2]等均有直接的应用.然而,无论是图G 的色数x (G)还是对一个图G 进行正常k -顶点着色,k -边着色以及k -全着色问题都是NP -完全问题[3].因此,不管是从事数学研究的图论学者们,还是从事电路与系统等工程技术方面研究的图论学家们,或者是其它领域的科学家们,都对图的着色问题很感兴趣.由于用k \x (G )种颜色对图G 进行正常k -顶点着色算法是一个NP -完全问题,NP -完全问题的求解一直困扰着人们.近些年,人们用神经计算,进化计算等方法来求解NP -完全问题也取得了一些进展.基于分子生物技术的DNA 计算是一种模拟生物分子DNA 的结构并借助于生化反应作为计算工具的超大规模并行计算,而且DNA 的双螺旋结构具有巨大的信息存储容量.1994年Adleman [1]开拓性地采用现代分子生物技术,在试管中进行了DNA 的实验,解决了有向图的哈密尔顿路问题(Hamiltonian Path Problem ,简记为HPP ).虽然在实验室进行了7天的实验,才使一个只有7个顶点的有向图的哈密尔顿路问题得到解决.但是由于他首先提出DNA 计算的方法来解决NP -完全问题,这一结果不但激发了人们对分子生物计算进一步研究的兴趣,对NP -完全问题产生了新的希望与信心,而且开创了用分子生物技术研究组合优化问题的新途径,因而在国际上引起了巨大的轰动.其后有许多学者沿此/路0而行,用DNA 计算求解SAT 问题[4,5]、图的最大团问题[6]、图的最大独立集问题[7]、最小集覆盖[8]问题等.收稿日期:2001-10-26;修回日期:2002-07-31基金项目:国家自然科学基金(No 169971018,60071026);陕西省自然科学基金(2001X05)第4期2003年4月电 子 学 报ACTA ELECTRONICA SINICA Vol.31 No.4Apr. 2003本文首先讨论了图的3-顶点着色的DNA算法,对图的每个顶点用任意碱基排列的寡聚核苷酸片段编码,对顶点的颜色用具有特殊酶切位点的片段进行编码,通过并行重叠放大技术POA(Parallel Overlap Assembly)建立数据池,然后运用分子生物操作如连接反应,聚合酶链式反应PCR(Polymerase Ch-i na Reaction),酶切反应,凝胶电泳对数据池进行运算,最终通过分子检测得到问题的解;其次分析了算法的优、缺点,并指出进一步的研究方向.2DNA分子的计算特性生物的各种生命活动都有它的物质基础,生物的遗传和变异也是这样.根据现代细胞学和遗传学的研究得知[9],控制生物性状遗传的主要物质是脱氧核糖核酸DNA(deoxyribonu-cleic acid).DNA是一种高分子化合物,组成它的基本单位是脱氧核苷酸.每个脱氧核苷酸是由一分子磷酸、一分子脱氧核糖和一分子含氮碱基组成的.含氮碱基有四种A(Adenine,腺嘌呤)、G(Guanine,鸟嘌呤)、C(Cytosine胞嘧啶)和T(Thymine,胸腺嘧啶).DNA不仅具有一定的化学组成,还具有规则的双螺旋结构.这一结构的主要特点是:(1)DNA分子是由两条平行的脱氧核苷酸长链盘旋而成的;(2)两条链上的碱基通过氢键连接起来,形成碱基对,碱基对的组成有一定的规律,这就是嘌呤与嘧啶配对,而且腺嘌呤(A)一定与胸腺嘧啶(T)配对,鸟嘌呤(G)一定与胞嘧啶(C)配对.组成DNA的碱基虽然只有四种,而且这四种碱基的配对方式只有两种,但由于碱基对具有多种不同的排列顺序,因而就构成了DNA分子的多样性.在分子生物计算中,通常都采用DNA这种高分子化合物,这不仅因为DNA是生命信息的载体,而且在遗传工程实验中DNA易于操作.DNA算法解决计算问题的基本思想是:利用DNA特殊的双螺旋结构和碱基互补配对原则对问题进行编码,把要运算的对象映射成DNA分子链,在DNA溶液的试管里,在生物酶的作用下,生成各种数据池(Data Pool),然后按照一定的规则将原始问题的数据运算高度并行地映射成DNA分子链的可控的生化过程.最后,利用分子生物技术获得运算结果.从DNA的原理来看,它与数学操作非常类似.DNA的单链可看作由四个不同符号A、G、C和T组成的串.它在数学上就像计算机中的编码/00和/10一样,可表示成四个字母的集合E={A,G,C,T}来译码信息.DNA串可作为译码信息.酶可看作模拟在DNA序列上简单的计算.不同的酶相当于作用在DNA串上的不同的算子[10].3DNA算法311问题描述本文所言之图皆指无环、无重边的无向简单图,通常用V(G)和E(G)分别表示图G的顶点集和边集,图G的一个正常k-顶点着色,简称为图的k-点着色[2],是指用k种颜色1,2,,,k对G的各顶点都分配(或称着)不同的颜色.换句话讲,简单图G的一个正常k-点着色,就是把V(G)划分成k个独立集的一个分类{V1,V2,,V k},其中V i(i=1,,,k)是G 的独立集.我们用C(k)表示k种颜色,即C(k)={1,2,,, k}.现在我们可以更确切地给出图G的k-点着色的定义:图G的k-点着色,是从V(G)到C(k)的一个映射R,当且仅当u,v I V(G)且(u,v)I E(G)时,R(u)X R(v),全体G的k-点着色R构成的集合通常记作C R k(G),简记为C k(G).若C k(G) X<(空集),既G至少有一个正常k-点着色,就称G是k-点可着色的.如图1所示为一个6顶点的图及其两种着色模式.图1顶点的编号及两种着色模式312图的着色问题的DNA算法对于具有n个顶点的图,图的每一种可能的3-顶点着色方案都可以表示为由0、1和2组成的n位数字串,其中0、1和2分别表示三种颜色,如图1所示的一种着色方案表示为021021.用这样的方法,我们可以把具有n个顶点的图可能的各种着色方案转化为由0、1和2组成的n位数字串的集合,称其为完全数据池.依照上述思想,为了求解图的着色问题,首先对图中的每个顶点及顶点的颜色用寡聚核苷酸片段进行编码,然后将这些寡聚核苷酸片段放在溶液中进行生化反应,生成问题的解,最终通过凝胶电泳分离问题的解.具体的计算步骤如下:Step1:对运算对象编码,建立完全数据池,将其作为DNA分子计算的输入数据.对图G的n个顶点进行编码,每个顶点的编码由三部分构成,如图2所示,第一段的P i和第三段的P i+1表示位置,目的是为了在生化反应中各顶点的DNA片段通过并行重叠装配技术形成长的DNA链,中间部分V i表示各顶点颜色的编码.对每个顶点而言,有三种不同的编码,用来表示每个顶点的三种颜色,因此这三种编码除了中间的颜色链不同外,两边表示位置的链是完全相同的,如图1所示的顶点1的三种编码分别为:CCCTGGGTAC TGGATGC tcgaattcat AATGC TGAATGGCCCTTCCCTGGGTAC TGGATGC tctgacga AATGC TGAATGGCCC TTCCCTGGGTAC TGGATGC ggatcc AATGCTGAATGGCCCTT图2顶点编码示意图为了区分每个顶点的颜色,中间颜色段的编码采用了具有特殊酶切位点的寡聚核苷酸序列,为了解的分离,序列的长度不同,采用这种方法建立的完全数据池有3n个元素.Step2搜索满足着色条件的数据集.对数据池中所有的串进行筛选,相邻顶点不能着同样的颜色,即在相应的数字串中对应位不能同时为0、1或2,从数据池中删除(去掉)顶点相邻且相应的串值同时为0、1或2的所有数字串,如图1所示的顶点a和b相邻,不能着同样的颜色,因此a和b对应的串值不能相同,必须从数据池中删除这样的串,如图3所示.Step3输出运算结果.495第4期高琳:图的顶点着色问题的DNA算法图3 相邻顶点着色示意图4 算法的生物实现Step 1 建立数据池,以双链DNA 表示数据结构,数字串中的每一位在DNA 链上由三段组成,用i 表示所处的位置,当i 为奇数时表示为P i V m i P i +1(m =0,1,2),当i 为偶数时表示为P i +1V m i P i[6],上划线表示补序列,例对图1所示的例子,数字串长度为6位,在相应的DNA 链上,有6个位的值序列V 1到V 6,依次间隔插入7个位置序列P 1到P 7,其中P i (i =1,,,6)表示V 1的位置,P 7用于生化反应过程中聚合酶链反应的引物,如图4(a)所示.初始序列随机产生,但为了避免反应过程中错配现象的发生,不同序列具有相同碱基的长度不能超过4bp ,其次为了有效地识别顶点的不同颜色,必须加入表1 顶点的编码序列具有特殊酶切位点的限制性序列,这样就可以区分顶点的颜色.采用并行重叠技术建立数据池[11],开始时用18个寡聚核苷酸片段,每个寡聚核苷酸片段的编码如表1所示.18个寡聚核苷酸片段放在一起进行热循环,在热循环过程中,一个寡聚核苷酸片段的位置串与另一个具有互补位置串的寡聚核苷酸片段退火,在聚合酶的作用下沿3c 方向延伸形成长的双链,最终形成了V 1V 2V 3V 4V 5V 6的各种组合的数据池,如图4(b)所示.随后以P 1和 P 7作为引物,利用多聚酶链式反应技术PC R 进行扩增,就可以选择性地扩增那些以P 1开始,P 7结束的DNA 链.图4 D NA 链编码的数据Step 2 对数据池中的串用限制性内切酶进行筛选.根据图的着色的定义,有边相连的顶点不能着同样的颜色,为了满足这个要求,用限制性酶的特殊酶切位点来完成.限制性内切酶是一类能识别双链DNA 分子中特异核苷酸序列的水解酶,如果某一核苷酸序列含有限制酶的识别序列,当加入这种酶后,就会将双链的DNA 分子在酶切点切开,如EcoRII [11]的识别序列为GAATTC ,酶切点在G 与A 之间,不同的酶具有不同的识别序列及相应的切割点,因此在图的着色中,为了区分不同的颜色,分别用含有不同酶的序列来表示这些颜色的特征.,两条相邻的顶点有相同的颜色,用限制内切DNA 链切开,在引物P 1和P 7的作用下进行会被扩增.如图1所示a 和b 相邻,),将试管中的液体分为两个试管t 1和t 2,切断含V 01的串,在t 2中用KpnI 切断含的V 02试管中的液体进行合并,得到的数据池不含1(表示蓝色),将试管中的液体重新分为t 2,在t 1中用PstI 切断含V 12的串,在t 2中用的串,然后将两个试管中的液体进行合并,得11@@@@,若同为2(表示绿色),类似的操和SphI ,得到的数据池将不含22@@@@,最3所示.对于其它相邻的顶点,如果具有,只不过每次针对限制性内切酶,每个顶点不同颜色所对中小写字母所示..上述运算结束后,剩余的DNA 分色.为了将这些DNA 链分离酰胺凝胶电泳鉴定酶解产物[11],聚丙烯酰胺500bp)的效果较好,甚至可以分辨相差1bp 根据我们的编码设计,图1中第一种着色方案496 电 子 学 报2003年021021的编码链长为171bp,第二种着色方案212010的编码链长为161bp,通过凝胶电泳将其分离开.为了进一步知道每个顶点的着色情况,必须对DNA链进行序列测定,采用基因工程的方法进行,将目的DNA片段克隆于适当的载体(如M13噬菌体),产生一个能方便地进行测序的重组DNA分子,然后将重组子导入E.Coli(大肠杆菌),进行克隆和测序,根据基因的测序结果就可知道每个顶点的着色情况.5结束语本文讨论了图的3-顶点着色的DNA算法,对图的每个顶点用任意碱基排列的寡聚核苷酸片段编码,顶点的颜色用具有特殊酶切位点的片段进行编码,通过并行重叠放大技术建立数据池,然后运用分子生物操作如连接反应,聚合酶链式反应PCR,酶切反应,凝胶电泳对数据池进行运算,最终通过DNA测序得到问题的解.本文的算法编码思想充分利用DNA分子结构的特征及常规的生物操作,将数学问题的求解同生物技术密切结合起来,但在具体的生物实现过程中仍有不足之处,具体表现为: (1)在PCR过程中,有可能产生单链DNA,而限制性内切酶不能作用于单链DNA;(2)内切酶的切除不完全.由以上两个因素可能导致非法解的出现,但随着现代分子生物学技术的发展,这个问题会逐步得到克服,使得差错率控制在一定的范围内.(3)DNA计算的最大特点是大规模的并行运算及巨大的信息存储能力,但编码过程中DNA链的数目随顶点数呈指数形式增长(3n),这是目前困扰DNA计算的一个障碍,也是DNA 计算理论研究工作的一个研究问题[10].(4)酶的种类为顶点个数的3倍,随着顶点数的增加,需要种类更多的酶,计算代价比较大,这个问题可以通过不同的生物操作过程得到改善,我们在这方面将做进一步的研究工作.目前,DNA计算的研究涉及到:(1)DNA计算的能力及数学基础[13];(2)对于各种计算问题,怎样寻找一种直接的翻译方式,变换成DNA计算系统,也即DNA生物化学反应的运算途径,以至鉴别和输出最优解技术路线,使得DNA计算适应广阔的问题面,并具有实用性[14];(3)DNA计算的复杂性、生物复杂性和可实现的衡量尺度[15];(4)基于DNA计算求解问题的装置并使之自动化,研究未来DNA计算机的可行性;(5)将DNA计算与遗传算法、神经网络等智能计算方法相结合[16,17].参考文献:[1]L Adle man.Molec ular Computation of Sol ution to Combinatorial prob-le ms[J].Science,1994,266(11):1021-1024.[2]J A Bondy,U S R M urty.Graph theory with application,the Mac millanpress LTD[M].London:Basingtoke and Ne w York,1976.[3]A Gibbons.Al gori thmic graph Theory,Cambridge Universi ty dres s[M].London:Cambridge,1985.[4]Richard J Li pton.DN A Solution of Computation Proble ms[J].Sc-ience,1995,268(4):542-545.[5]Qinghua Liu,et al.D NA Computing on Surface[J].Nature,.2000,403(13):175-179.[6]Q Ouyang,et al.Solution of the Maximal Clique Problem[J].Science,1997,278(17):446-449.[7]T Head,e t puting with D NA by Operating on Plasmids[J].Bios ys te m,2000,57:87-93.[8]S Rowi se,et al.A sticker Based model s for D NA computation[EB/O L].http://www.corninfo.c [9]黄翠芬,主编.遗传工程理论与方法[M].北京:科学出版社,1987.[10]高琳,许进,张军英.D NA计算的研究进展与展望[J].电子学报,2001,29(7):945-949.[11]P C Turner,A G M c Lennan,A D Bates,M R H Whi te.Molecular Bio-logy[M].Bios Scientific Publishers Li mited.2001.[12]姜泊,张亚历,周殿元,主编.分子生物学常用实验方法[M].北京,人民军医出版社,2000.[13]D Boneh,et al.On the Computation Power of DN A[R].USA:Pri nec-ton Uni versity,1995.[14]M H Garz on,et al.Biomolecular Computing and Programming[J].IEEE Trans.On Evolutionary Computati on,1999,3(3):236-250. [15]H Garzon.The Bounded Complexity of DNA Computi ng[J].Bios ys-tems,1999,52:63-72.[16]Deaton R,et al.A D NA Based Implementation of an EvolutionarySearch for Good Encodings for DN A Computation[A].Proceedi ng of1997IEEE Internati onal Conference on Evoluti onary Computation,In-dianapolis[C].USA:IEEE,1997[17]Russo M F,et al.An Improved DN A Encoding Scheme for Neural Net-work Modeling,World Congress on Neural ne tworks San die go[A].1994International Neural networks Society Annual Meeti ng[C].USA:CA,1994.354-359.作者简介:高琳女,1964年生于陕西,1987获西安交通大学数学系理学士学位,1990年获西安电子科技大学数学系硕士学位,现为西安电子科技大学计算机学院副教授,该校雷达信号处理国家重点实验室博士生,感兴趣的研究领域为DNA分子生物计算、神经网络、遗传算法及其在组合优化问题中的应用.许进男,1958年生于陕西,教授,博士生导师,西安交通大学管理学院管理工程专业工学博士,北京理工大学应用数学系应用数学专业理学博士,西安电子科技大学电路与系统专业博士后,现任华中理工大学系统工程专业特聘教授,感兴趣的研究领域为神经网络、遗传算法、图论以及D NA计算等.497第4期高琳:图的顶点着色问题的DNA算法。
图论 图的着色

X(G(V1,V2))=
X(G)=2 G为二部图
Th5.1:如果图G的顶点次数≤ρ,则G是ρ+1可着色的。
Th5.2:如果G是一个简单连通的非完全图,如果它的最大顶点次 数为ρ(ρ≥3),则称G为ρ可着色的。
下面的讨论的图为平面图:
Th5.3:每个平面图都是6可着色的。 Th5.4:每个平面图都是5可着色的。 Th5.5:每个平面图都是4可着色的。
ρ ≤ X’(G)≤ ρ+1
对任意图判断X’(G)= ρ 或X’(G)= ρ+1没有解决,但对于一些特殊图, 答案是清楚的。
对于n个点圈图: 2 or 3
.13:对于n(n>1)的完全图,
X’(kn)=n (n为奇数)X’(kn)=n-1(n为偶数) Th5.15:如G为具有最大顶点次数ρ的二部图,则X’(G)= ρ。
Corollary 5.9:地图4色定理 平面图的4色定理。 Th5.10:设G为一张每个顶点都是3次的地图,则 G为3可面着色G的每个面皆被偶数条边所围 Th5.11:如果每个3正规的地图是4可面着色的,则4色定理成立。
5.3 边的着色
G是k可边着色的:如果图G的所有的边皆可用k种颜色着色,使得 任何两条相邻的边均具有不同的颜色,则称G是k边着色的。 k为G的边色数:如果G为k可边着色的,但不是k-1可边着色的,则 称k为G的边色数,记为:X’(G)。 Th5.12:如果G为简单图且它的最大顶点次数为ρ
第五章 图的着色
5.1 色数 5.2 地图的着色 5.3 边的着色
5.1 色数
G为k可着色的:设G是一个无自环图,如果对它的每个顶点可以用 k种颜色之一着色,使得没有两个相邻的顶点有相同的颜色,则称G 是k可着色的。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2 9 6
海 南 大 学 学 报 自 然 科 学 版
2 0 1 3正
显然 i 的值为 { 1 , 2 , …, k } 中的一个 , 即 的取值是满足方程( 一 1 ) ( 一 2 ) …( i — k ) = 0 , i = 1 , 2 , …, / ' L .因为相邻的顶点不能染相同的颜色 , 故任意一对相邻顶点 i 与 , 其着色分别为 i 和 , 满足 1 ≤ 一
l ≤七一1 .不 等式 1 ≤l 一 I ≤ 一1等价 于方程 (I x — I —1 ) ( 1 一 l 一 2 ) …( I — I 一( k一1 ) )= 0 的 根 .又 因为方 程 ( I x — l 一1 ) ( 一 I 一2 ) …( — 。 l 一( k一1 ) )= 0等价 于 方程 ( ( — ) 一1 ) ( ( — ) 一 2 ) …( ( — ) 一( k一1 ) )= 0 .综 上可知 , 得 到关 于 , , …, 的多元多项 式方 程组
1 预 备 知 识
主要介 绍 图着色 的基 本概 念 , 参 见 文献 [ 1— 4 ] . 给定 图 G=( , E) , 其 中 G的顶 点集 V={ 一 , 1 3 } , 边集 E={ e 一, e } . 定义 1 一 顶 点着 色是 指 k 种 颜色 { 1 , 2 , …, k } 对 于 G的各 顶 点 的一 种 分 配 , 使得 任 意 2个 相 邻 的顶
对 图 G的 一 顶点 着色 引入 向量 X :( , , …, ) , 其 中
1 , 顶点 v i 染颜色 1 2 ,顶点 染 颜色 2
,
.
k ,顶点 v i 染颜 色 k
收 稿 日期 : 2 0 1 3— 0 8— 0 1
基金项 目:国家 自然科 学基金资助项 目( 1 0 9 7 1 0 4 4 ) 作者简介 : 尹杰杰 ( 1 9 9 0~) , 男, 广东韶关人 , 海南 大学信 息科 学技术学院 2 0 1 2级硕士研 究生
点被染上不同的颜色. 也就是 , G的一个顶点着色 : ( G ) { 1 , 2 , …, k } , 使对每一个 i ( i = 1 , 2 , …, k) ,
( ) 是 独立 集或 空集.
定 义 2 若 存 在 G的一个 k顶点 着 色则称 图 G是 k可着 色的. 令 ( G)= ai r n { k I G是 k可着 色 的 } , 称 ( G ) 为 G的点色数 , 简 称为 色数 .若 ( G)= k , 则 称 G为 k色 的. 定义 3 一 边 着色 是指 k种颜 色 { 1 , 2 , …, k } 对 E( G) 中元 素 的一种 分配 , 使得 相邻 2条边 所染 颜色 不 同. 即 G中的 k 边 着色 是 映射 c : E( G) 一{ 1 , 2 , …, k } , 使得 对每 一个 i ( 1 , 2 , …, k ) , c ( i ) 是 匹配 或者
图的 k 一 顶点着色与 k 一 边着色的 G r 6 b n e r 基 求解
尹 杰 杰
( 海南大学 信息科学技术 学院 , 海南 海 口 5 7 0 2 2 8 )
摘 要 :利用 G r 6 b n e r 基方法给 出了任意有 限图的 一 顶点着 色与 七 . 边着 色的求解 方案 , 从而求得 图的 . 顶点
定理 1 给出( S ) 的解与 图 G的 . 顶点 着色方 案 的对应 关系. 定理 1 ( S ) 的每个解 对应 图 G的一个 J j } . 顶点着 色 , 反 之亦 然 , 且该ቤተ መጻሕፍቲ ባይዱ对应 是一一 对应. 证明
, 、
『 ( i —1 ) ( 一 2 ) …( f 一 )= 0 , l ≤ ≤n ,
, . 、
I ( ( — ) 一 1 ) ( ( 一 ) 一 2 ) …( ( 一 X t ) 一 ( k 一 1 ) ) = 0 , V v 与 相邻 .
空集 .
定义4 若存在 G的一种 后 . 边着色 , 则称 G是 J j } 一 边可着色的. ( G ) = m i n { k I G是 k 边可着色的 } 称为 G的边 色 数.
2 图的 k - 顶 点 着 色 与 多 元 多项 式 方 程 组 的 解
考察 G的 k . 顶点 着色 问题 , 并 给 出该 问题 的一个 多项式 方程 组 的求解 模型.
着 色方案和顶点色数 , 一 边 着色方案和边色数. 关键 词 :图; k - 顶点着色 ; k - 边着色 ; 色数 ; G r O b n e r 基
中 图 分 类 号 :0 1 5 7 . 5 文 献 标 志 码 :A
给 出 了任意有 限图 G的 . 顶点 着色 与 . 边 着色 问题 分 别 等价 于一 个 多元 多 项式 方 程 组 在 { 1 , 2 , …, k }范 围 内的求解 问题 . 因为多元 多项 式 方程 组在 { 1 , 2 , …, k }范 围 内的解 ( 若 存在 ) 是 有 限 的 ,由 G r t i b n e r 基 方法 , 就 能通 过计算 得 出 图的 | j } 一 顶点着色与 . 1 } . 边 着 色 的有 效 判别 与求 解方 法 , 从 而 求得 图 的 . 1 } 一 顶 点 着 色 方案 和顶 点 色数 , k . 边 着 色方案 和边 色数 .
第3 1 卷 第4期
2 0 1 3年 l 2月
海 南 大 学 学 报 自 然 科 学 版
NATURAL S CI ENCE J OURNAL oF HAI NAN I i Ⅳ ERS I T Y
V0 J . 31 No . 4
De C . 2 01 3
文章编号 : 1 0 0 4—1 7 2 9 ( 2 0 1 3 ) 0 4— 0 2 9 5— 0 5
