典型例题:圆锥曲线的对称问题
圆锥曲线之对称问题

圆锥曲线之对称问题包括两种情形:①、中心对称问题:常利用中点坐标公式求解;②、轴对称问题:主要抓住以下两个条件去处理-----➊垂直,即已知点与对称点的连线与对称轴垂直;➋中点,即连结已知点和对称点的线段的中点在对称轴上1.(本小题满分14分)设,A B 是椭圆22:143x y W +=上不关于坐标轴对称的两个点,直线AB 交x 轴于点M (与点,A B 不重合),O 为坐标原点.(I )如果点M 是椭圆W 的右焦点,线段MB 的中点在y 轴上,求直线AB 的方程; (II )设N 为x 轴上一点,且4OM ON ⋅=uuu r uuu r,直线AN 与椭圆W 的另外一个交点为C ,证明:点B 与点C 关于x 轴对称.2.在平面直角坐标系xOy 中,动点P 到定点1(0,)4F 的距离比点P 到x 轴的距离大14,设动点P 的轨迹为曲线C ,直线:1l y kx =+交曲线C 于,A B 两点,M 是线段AB 的中点,过点M 作x 轴的垂线交曲线C 于点N .(Ⅰ)求曲线C 的方程;(Ⅱ)证明:曲线C 在点N 处的切线与AB 平行;(Ⅲ)若曲线C 上存在关于直线l 对称的两点,求k 的取值范围.解析1.(本小题满分14分)(Ⅰ)解:椭圆W 的右焦点为(1,0)M , ……………… 1分因为线段MB 的中点在y 轴上,所以点B 的横坐标为1-, 因为点B 在椭圆W 上,将1x =-代入椭圆W 的方程,得点B 的坐标为3(1,)2-±. ……………… 3分所以直线AB (即MB )的方程为3430x y --=或3430x y +-=.…………… 5分(Ⅱ)证明:设点B 关于x 轴的对称点为1B (在椭圆W 上),要证点B 与点C 关于x 轴对称, 只要证点1B 与点C 重合,.又因为直线AN 与椭圆W 的交点为C (与点A 不重合),所以只要证明点A ,N ,1B 三点共线. ……………… 7分以下给出证明:由题意,设直线AB 的方程为(0)y kx m k =+≠,11(,)A x y ,22(,)B x y ,则122(,)B x y -.由 223412,,x y y kx m ⎧+=⎨=+⎩得 222(34)84120k x kmx m +++-=, ……………… 9分所以 222(8)4(34)(412)0km k m ∆=-+->,122834kmx x k +=-+,212241234m x x k -=+. (10)分在y kx m =+中,令0y =,得点M 的坐标为(,0)mk-, 由4OM ON ⋅=u u u u r u u u r ,得点N 的坐标为4(,0)k m-, (11)分设直线NA ,1NB 的斜率分别为NA k ,1NB k ,则 1211122121212444444()()NA NB k k x y y x y y y y m m k k k k k k x x x x m m m m +⨯++⨯--=-=++++ ,………12分 因为 21112244k kx y y x y y m m+⨯++⨯ 21112244()()()()k kx kx m kx m x kx m kx m m m=+++⨯++++⨯2121242()()8k kx x m x x k m=++++ 2222412482()()()83434m k kmk m k k m k -=⨯++-+++ 22323824832243234m k k m k k k k k ---++=+0=, (13)分所以 10NA NB k k -=, 所以点A ,N ,1B 三点共线,即点B 与点C 关于x 轴对称. ……………… 14分2. 19.(共13分)(Ⅰ)解:由已知,动点P 到定点1(0,)4F 的距离与动点P 到直线14y =-的距离相等.由抛物线定义可知,动点P 的轨迹为以1(0,)4为焦点,直线14y =-为准线的抛物线.所以曲线C 的方程为2y x =. ………………3分 (Ⅱ)证明:设11(,)A x y ,22(,)B x y .由2,1,y x y kx ⎧=⎨=+⎩得210x kx --=. 所以12x x k +=,121x x =-. 设00(,)M x y ,则02k x =. 因为MN x ⊥轴,所以N 点的横坐标为2k . 由2y x =,可得2y x '=所以当2kx =时,y k '=. 所以曲线C 在点N 处的切线斜率为k ,与直线AB 平行.…………8分 (Ⅲ)解:由已知,0k ≠.设直线l 的垂线为l ':1y x b k =-+.代入2y x =,可得210x x b k+-= (*)若存在两点3344(,),(,)D x y E x y 关于直线l 对称,则34122x x k +=-,342122y y b k +=+ 又3434(,)22x x y y ++在l 上, 所以211()122b k k k +=-+, 21122b k =-.由方程(*)有两个不等实根所以21()40b k ∆=+>,即221220k k+->所以212k <,解得k <或k . ………………13分。
圆锥曲线上存在轴对称点的充分必要条件

—
—
—
=
4 a 2 b 2 ( k 2 b 2 + k
—
Z n2
-
a 2 )
—
—
=
4 a 2 b 2 { b 2 + ( kb y k 一 I ] 一 1 J >
J
… 、
2 b 2 - a 2 ) 2 m 2
一
堡:
k 2 k
4
+
: — 4 [ k  ̄ p 2 + 2 k p (
—
Pk 3 + pk+ m
k 2
) ]
>
k
z +
。
: o .
( 2 ) 若双 曲线环 同支上存 在相异的两点 , 则J j } 2 6 2 _ a 2 >
n由 对 曲 结 不 同 专 卜存 存 两 占 千 古 终 对 称 台
『 a Z m 1
学1 ]
=
k
1 + a 2 } 珊毕 .
般情形—— 圆锥 曲线上存在两点关于直线对称的充分必 要 条件 , 供教师们教学参考.
一
定 理 2 : 设 双 曲 线 , 1 : 一 吾 D 1 ( 。 > 0 , 6 > 0 ) , 直 线 z : y
k x + m( k ≠0 ) , 则 双曲线,同一支上存在相异两点A ( Y ) , B( )关 于直线z 对 称的充分 必要条件是 2 6 一 < 0 且 ; 不 同支上存在相异两点A( y ) , B ( y 2 )
学 谋
, 内 铮 < 2 p ( - p | j 2 ) z < 2 p ( 一 )
> 甘 , § m <一
2 a 2 6 2 ( n 2 + b 2 ) ( k a 2 ) 此 时式 ② 的判 别 式△= 4 n 2 a 4 +4
对一道圆锥曲线中对称问题解法的探究

思路探寻圆锥曲线中的对称问题较为复杂,较多,如对称轴、对称中心、系、圆锥曲线的几何性质等.灵活运用解析几何知识,化思想、方程思想来辅助解题.讨一下求解圆锥曲线中对称问题的方法.题目:已知椭圆C:x22+y23=1与直线l:直线l与椭圆C交于A,B两点.椭圆C上有两点关于直线l对称,求m的取值范围.本题主要考查了椭圆的方程、几何性质以及轴对称图形的特点、性质.解答本题的关键,在于根据椭圆C上有两点关于直线l对称以及椭圆的几何性质,系式,从而求得m的取值范围.一、点差法线的方程中,然后将两式相减,法.点差法常用于求解与中点、关的问题.若两个点的坐标为()x1,y1、(x2,y2后便可得到含有x1+x2,y1+y2,y1-y2x1-x2子,这样就联系了中点和直线的斜率,即可求得直线的斜率、中点坐标.采用点差法来求解,代入椭圆方程中,再将两式作差,标,根据椭圆的范围即可求得m的取值范围解:设两个对称点为D()x1,y1,E()x2,y2中点为M()x0,y0,则x0=x1+x22,y0=y1+y22,ìíîïïïïx212+y213=x222+y223=将()1-()2得x0y0=23.又因为点M()x0,y0也在直线AB上,所以联立方程组ìíîïïy0=x0+m,x0y0=23,得{x0=2m,y0=3m,由题意得点M()x0,y0在椭圆内,所以()2m22+()3m23<1,解得m的取值范围为æèçø.二、利用二次函数的性质圆锥曲线的方程都是二次方程,所以在解答圆锥曲线中的对称问题时,我们可以根据题意构造二次函数,利用二次函数的图象、性质来解题.对于含参问题,我们可以直接讨论二次函数的根的分布情况,建立关于参数的关系式即可解题.对于本题,我们可以将直线与椭圆的方程联立,消去y,构造出关于x的一元二次函数,从而将问题转化为函数问题.在消去y后,可得到一元二次方程,根据弦DE所在直线与椭圆C有两个交点,便可确定一元二次方程有两个实根,再结合椭圆的范围,便可确定根的分布情况,建立关于m的关系式.解:设椭圆C上关于直线l对称的两点分别为D()x1,y1,E()x2,y2,弦DE的中点为M()x0,y0,又因为M()2m,3m,由题意可得直线DE的斜率为-1,所以直线DE与椭圆C联立方程组可得ìíîïïy=-x+5m,x22+y23=1,消去y得5x2-20mx+50m2-6=0,x∈[]-2,2.令f()x=5x2-20mx+50m2-6,则问题转化为二次函数f()x=0在x∈[]-2,2上有两个不相等的实根,则ìíîïïïïf()-2≥0,f()2≥0,f()2m<0,解得m的取值范围为æèçø.我们通过对一道椭圆中对称问题的探讨,明确了求解圆锥曲线中对称问题的两种方法:点差法和利用二次函数的性质.这两种解法中都用到了数形结合思想、转化思想、方程思想,可见在解答圆锥曲线中的对称问题时,灵活运用数学思想来辅助解题,能有效地提升解题的效率.(作者单位:江苏省大丰高级中学)52。
高考复习:圆锥曲线焦点三角形与对称问题

《圆锥曲线与方程》题型归纳小结一、焦点三角形问题【例1】 已知双曲线的焦点在x 轴上,离心率为2,12,F F 为左右焦点, P 是双曲线上一点,且1260,F PF ∠= 12PF F S ∆=. 【解析】设双曲线方程为()222210,0x y a b a b-=>> 2,2e c a =∴=令1122||,||PF r PF r ==,在12PF F ∆中,由余弦定理,22212121242cos c r r r r F PF =+-∠221212r r r r =+-21212()+r r r r =-222121244+12c a r r r r a =∴=即12212121sin 2PF F S r r PF F ∴=∠= 所以,2224,16,12a c b ===,双曲线标准方程为221412x y -=. 【评析】(1)12PF F ∆由两焦点和曲线上一点形成,我们把这种三角形叫焦点三角形. 焦点三角形问题的主要类型有:周长、面积、角度等,通常会用到圆锥曲线的定义、正弦定理、余弦定理、面积公式等.(2)焦点三角形的面积主要有两种求法:1212121211sin =2c |y |22PF F PF F P S r r F PF S =∠和; (3)涉及到焦点、顶点、曲线上点(顶点以外)等问题,抓住几个特征三角形,举一反三.这是一个考察重点,容易出现离心率的值(或范围)的运算.【变式1】(复习参考题B 组第1题)已知点P 是椭圆2216251600xy +=上一点,且在x 轴上方,F 1,F 2分别是椭圆的左、右焦点,直线PF 2的斜率为-12PF F ∆的面积. 【解析】椭圆即22110064x y +=,所以右焦点()26,0F直线PF 2为)6y x =--,代入椭圆方程,消去x 得2197680y --=因为0y >,所以y =P 的纵坐标P y =,所以12122PF FP S c y ∆=⨯⨯=.三、中点弦问题(对称问题)【例1】已知双曲线方程2222x y -=.(1) 求以A(2,1)为中点的双曲线的弦所在直线方程;(2) 过点B(1,1)能否作直线l ,使l 与所给双曲线交于Q 1、Q 2两点,且点B 是弦Q 1Q 2的中点?这样的直线l 如果存在,求出它的方程;如果不存在,说明理由.【解析】(1)即设)1,2(A 的中点弦两端点为),(),,(222111y x P y x P ,则有关系2,42121=+=+y y x x .又据对称性知21x x ≠,所以2121x x y y --是中点弦21P P 所在直线的斜率,由1P 、2P 在双曲线上,则有关系22,2222222121=-=-y x y x .两式相减是:0))(())((221212121=-+--+y y y y x x x x∴0)(2)(422121=---⋅y y x x ∴42121=--x x y y 所求中点弦所在直线为)2(41-=-x y ,即074=--y x .(法二)当直线斜率不存在时,A 不是弦的中点;设直线斜率为k ,则直线方程为()12y k x -=-,代入曲线方程,得()22222(21)4430k x k k x k k -+--+-=,(*) 设)1,2(A 的中点弦两端点为),(),,(222111y x P y x P ,则()12222142k k x x k -+==- 所以,4k =.代入(*)式,知0∆>,所以,所求中点弦所在直线为)2(41-=-x y ,即074=--y x .(2)可假定直线l 存在,而求出l 的方程为)1(21-=-x y ,即012=--y x方法同(1),联立方程⎪⎩⎪⎨⎧=--=-0122222y x y x ,消去y,得03422=+-x x 然而方程的判别式08324)4(2<-=⋅⋅--=∆,无实根,因此直线l 与双曲线无交点,这一矛盾说明了满足条件的直线l 不存在.【评析】(1)通过将弦端点的坐标代入曲线方程,再将两式相减的过程,称为代点相减.这里,代点相减后,适当变形,出现弦的斜率和中点坐标,是实现设而不求(即点差法)的关键.两种解法都要用到“设而不求”,它对简化运算的作用明显,用“点差法”解决弦中点问题更简洁.(2)实际上,若给的定点P 在椭圆内或抛物线内、双曲线内(含焦点的区域),则0∆>,即一定存在以P 为中点的弦;若定点P 在双曲线外,则有可能不存在以P 为中点的弦.【变式1】在抛物线24y x =上恒有两点关于直线3y kx =+对称,求k 的取值范围.【解析】解法一:设B 、C 关于直线3+=kx y 对称,直线BC 方程为m ky x +-=,代入x y 42=得,0442=-+m ky y ,设),(11y x B 、),(22y x C ,BC 中点),(00y x M ,则m k x k y y y +=-=+=202102,22∵点),(00y x M 在直线l 上,∴3)2(22++=-m k k k∴k k k m 3223++-=,代入016162>+=∆m k ,得0323<++k k k ,即0)3)(1(2<+-+kk k k 解得01<<-k解法二:设),(11y x B ,),(22y x C 关于l 对称,中点),(00y x M ,则⎪⎩⎪⎨⎧==22212144x y x y 相减得:)(4))((212122x x y y y y -=-+ ∴k y ky 2,4)1(200-==-⋅,则k k x 320--= ∵),(00y x M 在抛物线x y 42=内部,∴0204x y < 化简而得0323<++k k k ,即0)3)(1(2<+-+kk k k ,解得01<<-k . 【变式2】已知椭圆方程为13422=+y x ,试确定实数m 的取值范围,使得椭圆上有不同的两点关于直线m x y +=4对称。
圆锥曲线对称问题

圆锥曲线的对称问题问题1:点P(x,y)、P′(x′,y′)关于点Q(x0,y0)对称,那么它们的坐标应满足什么条件?Q点是P与P′的中点,即满足00'',22x x y yx y++==问题2:P(x,y),P′(x′,y′)关于原点对称,那么它们的坐标满足什么条件?P和P′的中点是原点.即x=-x′且y=-y′.问题3:若P和P′关于x轴对称,它们的坐标又怎样呢?x=x′且y=-y′.问题4:若P和P′关于y轴对称,它们的坐标有什么关系?y=y′且x=-x′.问:若P和P′关于直线y=x对称,它们的坐标又会怎样?y=x′且x=y′.问题5:双曲线22221x ya b-=与22221y xa b-=的位置如何?它们关于直线y=x对称.问题6:若P与P′关于直线Ax+By+C=0对称,它们在位置上有什么特征?P和P′必须在直线Ax+By+C=0的两侧且与直线垂直就能对称,及P和P′到直线Ax+By+C=0的距离相等问题7:P与P′到直线Ax+By+C=0的距离相等的含义是什么?就是P与P′的中点落在直线Ax+By+C=0上,换句话说P与P′的中点坐标满足直线方程Ax+By+C=0.问题8:两点P(x,y)、P′(x′,y′)关于直线Ax+By+C=0对称应满足的条件?应满足两个条件.第一个条件是PP′的连线垂直于直线Ax+By+C=0,第二个条件是P,P′的中点应落在直线Ax+By+C=0上.这两个条件能否用方程表示:方程组:'1'''22y y Ax x Bx x y yA B C⎧-⎛⎫∙-=-⎪⎪⎪-⎝⎭⎨++⎪∙+∙+=⎪⎩方程组中含有x′,y′,也可认为这是一个含x′,y′的二元一次方程组.换句话说,给定一个点P(x,y)和一条定直线Ax+By+C=0,可以求出P点关于直线Ax+By+C=0的对称点P′(x′,y′)的坐标.今后有很多有关对称问题都可以用此方法处理,很有代表已知直线1l和2l关于直线2x-2y+1=0对称(如图2-73),若1l的方程是3x-2y+1=0,求2l的方程.(选题目的:熟悉对称直线方程)先求出已知两直线的交点,设2l的斜率为k,由两条直线的夹角公式可求出k,再用点斜式求得2l的方程.解:由22103210x yx y-+=⎧⎨-+=⎩得交点(0,12),设2l的斜率为k,由两直线的夹角公式得:31123112kk--=++∴k=23由点斜式,l2的方程为4x-6y+3=0.另解:在直线1l上任取一点,求出这点关于2x-2y+1=0对称的点,然后再利用交点,两点式可求出2l的直线方程。
巧用点差法解决圆锥曲线中的对称问题高二上学期数学北师大版选择性必修第一册
圆锥曲线中的直线对称问题
已知椭圆E:x2 y2 1 ,试确定 m 的取值范围,使得对于直线l:y=4x+m, 23
椭圆E上有不同的两点关于这条直线对称.
y
O
x
金题精讲
圆锥曲线中的点对称问题
如图,在平面直角坐标系xOy中,椭圆
F2 (
3, 0)
,且经过点 (
3, 1) . 2
x2 a2
y2 b2
设点、作差、求斜率.
注意事项
如果是曲线的存在性问题,判断点的位置至关重要,如果点在曲线外,中点弦将 不存在.
金题精讲
圆锥曲线中的直线对称问题
已知椭圆E:x2 y2 1 ,试确定 m 的取值范围,使得对于直线l:y=4x+m, 23
椭圆E上有不同的两点关于这条直线对称.
y
【思路分析】
O
x
金题精讲
【解】假设这样的直线存在,不妨
设Q1(x1,y1) ,Q2(x2,y2) ,则
2x12 y12 2 ①
2
x22
y22
2
②
x1
x2
1③
2
y1
y2
1④
2
①–②得:2(x12 – x22)=y12 – y22
即:2(x1 + x2) (x1 – x2)=(y1 + y2)(y1 – y2)
即:2×2(x1 – x2)=2(y1 – y2)
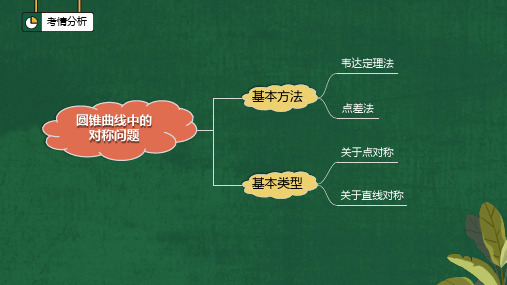
考情分析
圆锥曲线中的 对称问题
基本方法 基本类型
韦达定理法 点差法 关于点对称 关于直线对称
金题精讲
应用点差法解决中点弦问题
已知双曲线方程2x2-y2=2. (1)求以A(2,1)为中点的双曲线的弦所在的直线方程.
圆锥曲线中关于直线的对称问题解法探究

例谈圆锥曲线中存在点关于直线的对称问题解法探究崇信县第一中学尹军民我们先看一道例题:(2010年云南省第二次质检)已知实轴长为2a,虚轴长为2b的双曲线S的焦点在x轴上,直线是双曲线S的一条渐近线,而且原点O,点A(a,0)和点B(0,-b)使等式·成立.(I)求双曲线S的方程;(II)若双曲线S上存在两个点关于直线对称,求实数k的取值范围.解:(I)根据题意设双曲线S的方程为且解方程组得所求双曲线的方程为解法一(设而不求法):(II)当k=0时,双曲线S上显然不存在两个点关于直线当时,设又曲线S上的两点M、N关于直线对称,由直线MN的方程为则M、N两点的坐标满足方程组消去y得显然即设线段MN中点为则在直线即即的取值范围是【评注】由此解题过程不难归纳出步骤如下:1.假设这样的对称点M、N存在,利用对称中的垂直关系设出两点M、N所在的直线方程.2.联立MN所在直线方程与圆锥曲线方程,求出中点P的坐标.3.把P的坐标代入对称直线,求出两个参数之间的等式.4.利用联立后方程的△求出其中需求参数的范围.解法二(点差法):当k=0时,双曲线S上显然不存在两个点关于直线当时,设两式相减整理得的取值范围是【评注】这种解法的步骤是:1o设出两点和中点坐标(x,y);2o用“点差法”根据垂直关系求出x,y满足的关系式;3o联立直线方程,求出交点,即中点;4o由中点位置及对应范围求出参数取值范围.另外,这里还需要说明两个问题:1o弦中点位置问题椭圆双曲线抛物线弦中点在内部弦中点在Ⅰ(交点在同一支上)弦中点在抛物线“内部”或Ⅱ(交点不在同一支上)2o范围问题椭圆+=1 双曲线抛物线M(x0,y0)为中点,则 M(x0,y0)为中点,则 M(x0,y0)为中点,则+<1 - >1或-<0 y2-2px<0 (p>0(焦点在x轴上 y2+2px<0 (p>0->1或-<0 x2-2py<0 (p>0(焦点在y轴上) x2+2py<0 (p>0对于此类问题有一种通法,即抓住两点对称中体现的两要点:垂直(斜率之积为-1)和两点连线中点在对称直线上,至于参数的范围则是由联立后方程的△产生。
圆锥曲线中的对称问题

圆锥曲线中的对称问题上海西南位育中学 叶春怡我们常常会遇到这样的问题:第一类是整个曲线关于某点(或直线)对称,第二类是圆锥曲线上的两点关于某直线对称。
这就是本文讨论的“圆锥曲线中的对称问题”。
例1. 求椭圆1422=+y x 关于点M (3,5)对称的曲线方程。
1-1解:设所求曲线上任一点),(y x P ,如图1-1,根据中心对称的性质,P 、P /关于M (3,5)对称,得)10,6('yx P --的坐标是,它应在椭圆1422=+y x 上,于是有1)10(4)6(22=-+-y x , 即P 点坐标需满足的方程是1)10(4)6(22=-+-y x 。
本例是圆锥曲线对称问题中一类非常典型的问题,即求某一曲线关于定点的对称曲线的方程。
这一类型问题的基本解法和结论:求曲线0),(=y x f 关于点M ),(b a 第一步,设所求曲线上任一点),(y x P ;第二步,易得P 点关于M 的对称点为,2('x a P -第三步,)2,2('y b x a P --在已知曲线上,满足已知曲线方程,代入得0)2,2(=--y b x a f ;第四步,作结论0)2,2(=--y b x a f 即为所求曲线方程。
事实上对其它曲线方程,上面的步骤和结论同样成立。
例2. 求曲线C :2x y =关于直线l :x+y-1=0对称的曲线C ’的方程。
解:在曲线C ’任取一点P (x,y ).设其关于直线l 对称的点P /(x /,y /),则点P /在曲线C :2x y =上。
由对称的性质知直线l 垂直平分线段PP /,即线段PP /的中点(2/x x +,2/y y +)在直线l 上,且直线PP /的斜率xx yy --//与直线l 的斜率-1之积为-1。
通过解方程组xx yy --//(-1)=-1 2/x x ++2/y y +-1=0得x /=1+-y y /=-1+-x将P /(x /,y /)的坐标代入曲线C :2x y =中即得曲线C ’的方程为022=+-y y x 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
圆锥曲线中存在点关于直线对称问题
在直线与圆锥曲线的位置关系中,常出现这样一类问题:一个圆锥曲线上存在两点A,B关于直线L对称,求方程中参数的范围
对于此类问题抓住两点A,B关于直线L对称,对称中体现的两要点:垂直(斜率之积为-1或1,2中一个为0,一个不存在)和两点连线中点C在对称直线L上也是L与L AB的交点,分析一:(第一种通法)由于L AB与圆锥曲线交于两点AB,所以L AB与圆锥曲线方程联立方程组,得一元二次方程,△>0求参数的范围,步骤如下:
1.假设这样的对称点A、B存在,利用对称中的垂直关系设出两点A、B所在的直线方程
2.联立AB所在直线方程与圆锥曲线方程,求出中点C的坐标
3.把C的坐标代入对称直线,求出两个参数之间的等式
4.利用联立后方程的△求出其中需求参数的范围
分析二:(第二种通法)由于中点C为相交弦AB的中点,所以可用点差法,求出参数与中点的关系,又中点C在对称直线L 上,故可用参数表示中点的坐标代入不等式,求出参数的范围第二种通法,不过首先说明以下问题:
弦中点位置问题
“内部”
或Ⅱ(交点不在同一支上)
步骤如下:1设出两点和中点坐标(,y);
2用“点差法”根据垂直关系求出,y满足的关系式;
3联立直线方程,求出交点,即中点;
4由中点位置及对应范围求出参数取值范围
例1:已知椭圆C:1
3
2
2
2
=
+
y
x,试确定m的取值范围,使得对于直线l:y=4+m,椭圆C上有不同两点关于这条直线对称解法一:设存在两点A(1,y1)、B2,y2关于l对称,中点为C (0,y0),
则AB所在直线为y=-+b与椭圆联立得:
8
252-b+2b2-6=0,
∴0==
25
4b
y0==-
4
1×
25
4b b=
25
24b∵C在y=4+m上,
∴
25
24b=
25
4b×4+m,b=
8
25m又∵△=b2-4×
8
252b2-6>0,
故b2<
8
25,即-
8
25m2<
8
25,解得:-
5
2
2<m<
5
2
2
由上可知:
当-5
22<m<
5
22时,椭圆C 上有不同两点关于直线y=4+m ,
对称
解法二:设存在两点A (1,y 1)、B 2,y 2关于l 对称,中点为C (,y ),则
312
+2y 12
=6
32
2+2y 2
2
=6,得=-)(2)
(32121y y x x ++=-
023y x =-,∴y 0=60
联立y 0=40+m,解的0=2
m
,y 0=3m,
∵M 在椭圆内部,∴()13
3222
2
〈+⎪⎭⎫
⎝⎛m m 即-522<m<
5
2
2 由上可知: 当-5
2
2<m<
5
22时,椭圆C 上有不同两点关于直线y=4+m
对称
例2.已知双曲线2
-=1,双曲线存在关于直线l :y=+4的对称点,求的取值范围
注:对于此类求斜率范围要考虑=0和≠0,因为要用到- 解法一:由题意≠0:设存在两点A (1,y 1)、B 2,y 2关于l 对称,中点为C (0,y 0),
则AB 所在直线为y=-k
1+2-=1得:32-12+2b -b 232
=0, 显然32
-1≠0,即2≠310==
1
32
--k kb
y 0==-k 1×1
32--k kb
b=13322-k b k
∵C 在y=+4上,∴13322-k b k =×1
32--k kb
+4,∴2b=32-1∴b=2213k k -
又∵△=42b 24×32-1b 232>0,∴2b 232
-1>0∴2b 22
b>0∴b 2
b>0∴b>0或b<-1
2213k k ->0或2
213k
k -<-1解得:<-33或>33或-21<<0或0<<21
由上可知:当<-
33或>33或-2
1
<<0或0<<2
1
时,
双曲线2
-=1存在关于直线l :y=+4的对称点
解法二:由题意≠0:设存在两点A (1,y 1)、B 2,y 2关于l 对称,中点为C (0,y 0),
3
12-y 12
=3 322-y 22
=3,得=2121)(3y y x x ++=0
3y x =-k
1
,∴y 0=-30
联立y 0=0+4 解得
0=-
k
1
y 0=3,20x -32
0y >1(交点AB 在同一支上)或20x -
3
2
y <0(交点AB 在两支上) ∴2
<41或2
>3
1且≠0解得:<-
3
3
或>
3
3或-21<<0或0<<
2
1 由上可知:当<-
3
3或>
3
3或-2
1<<0或0<<2
1时,
例3.为何值时,抛物线y 2
=上总存在两点关于直线l :y=(-1)+1对称同上
另外,由于抛物线方程形式的特殊性,对于抛物线此类问题,
还有一种简洁解法:
例:在抛物线y=a2-1上存在两点关于直线+y=0对称,求a的范围
解:显然a≠0
设存在两点为A(1,y1)、B2,y2,
==a(1+2)=1,即1+2=,
+=0,即12=,这种方法巧之处在于利用抛物线方程的一次式设点,利用斜率和中因为存在这样的两点,点关系求出两根之和、两根之积
故方程2-+=0的△>0,当然,不管是两种通法还是针对抛物线的特殊法,都无非紧紧抓住两根
即-4>0,a>点关于直线对称所产生的垂直及,构造方程,利用△求出参数范围中点问题,不过在有关范围关系式的产生上有差别。
