同济大学高等数学第七版1-7无穷小的比较 PPT
合集下载
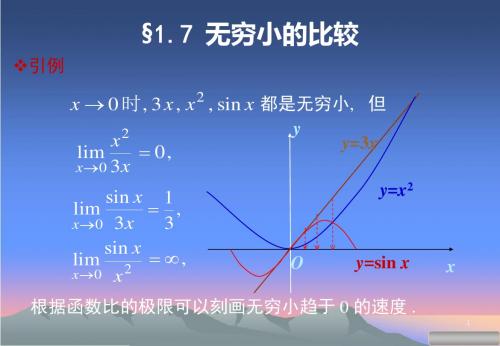
高数同济17无穷小的比较
注意 对于代数和中各等价无穷小一般不能替换.
若 ~ , ~ 且 与 不等价 , 则 - ~ - ,
下页
13
常用等价无穷小:
sin x ~ x , ln( 1 + x ) ~ x ,
当x 0时,
arctan x ~ x ,
arcsin x ~ x , tan x ~ x ,
例13
x 0
lim
1 x si n x lim2 3 lim 1 x 0 x 0 2 x x
15
结束
内容小结 1. 无穷小的比较
设 , 对同一自变量的变化过程为无穷小, 且
0
是 的高阶无穷小 是 的低阶无穷小 是 的同阶无穷小 是 的等价无穷小 是 的 k 阶无穷小
1 2 e - 1 ~ x , 1 - cos x ~ x , (1 + x ) - 1 ~ x . 2
注意 对于代数和中各等价无穷小一般不能替换.
若 ~ , ~ 且 与 不等价 , 则 - ~ - ,
下页
12
常用等价无穷小:
sin x ~ x , ln( 1 + x ) ~ x ,
下页
9
常用等价无穷小:
sin x ~ x , ln( 1 + x ) ~ x ,
当x 0时,
arctan x ~ x ,
arcsin x ~ x , tan x ~ x ,
x
1 2 e - 1 ~ x , 1 - cos x ~ x , (1 + x ) - 1 ~ x . 2
例9
tan2 2 x 求 lim . x 0 1 - cos x
若 ~ , ~ 且 与 不等价 , 则 - ~ - ,
下页
13
常用等价无穷小:
sin x ~ x , ln( 1 + x ) ~ x ,
当x 0时,
arctan x ~ x ,
arcsin x ~ x , tan x ~ x ,
例13
x 0
lim
1 x si n x lim2 3 lim 1 x 0 x 0 2 x x
15
结束
内容小结 1. 无穷小的比较
设 , 对同一自变量的变化过程为无穷小, 且
0
是 的高阶无穷小 是 的低阶无穷小 是 的同阶无穷小 是 的等价无穷小 是 的 k 阶无穷小
1 2 e - 1 ~ x , 1 - cos x ~ x , (1 + x ) - 1 ~ x . 2
注意 对于代数和中各等价无穷小一般不能替换.
若 ~ , ~ 且 与 不等价 , 则 - ~ - ,
下页
12
常用等价无穷小:
sin x ~ x , ln( 1 + x ) ~ x ,
下页
9
常用等价无穷小:
sin x ~ x , ln( 1 + x ) ~ x ,
当x 0时,
arctan x ~ x ,
arcsin x ~ x , tan x ~ x ,
x
1 2 e - 1 ~ x , 1 - cos x ~ x , (1 + x ) - 1 ~ x . 2
例9
tan2 2 x 求 lim . x 0 1 - cos x
新无穷小比较1-7

tan 2 x ~ 2 x .
若未定式的分子或分母为若干个因子的乘积,则 可对其中的任意一个或几个无穷小因子作等价无 穷小代换,而不会改变原式的极限.
例6
( x 1) sin x 求 lim . x0 arcsin x
当 x 0时 , sin x ~ x , arcsin x ~ x .
x cos( a bx )
lim f ( x ) f ( 1) .
练习题答案
3
一、1、 ; 2
0, m n 2、 1, m n ;3、2; , m n
a 6、 ; n
e ; 2、
4、 ;
5、 x ;
1
7、3;
1 8、 , 2. 2
二、1、 ; 2
2
1 2
,
故当 x 0 时, cos x与 x 2是同阶的无穷小. 1
( 2) 因为lim
x 2
tan( x-2) ( x-2)
4 3
lim
x 2
tan( x-2)
4 3
4 3
( x-2)
1 3
0
( x-2) 所以当 x 2时, tan( x- 2) 是x- 2的高阶无穷小,
x ~ sin x ~ tanx ~ arcsin x ~ arctan x ~ ln(1 x ) ~ e x 1 a 1 ~ x ln a , 1 cosx ~
x
1 2
x ,
2
(1 x ) 1 ~
1 n
x n
二、等价无穷小代换
定理2(等价无穷小代换定理) 设在自变量 x的同一 变化趋势下, ,,,都是无穷小,且 ~ , ~ , lim f ( x )存在或为无穷大, 则 lim f ( x ) lim f ( x ). 证 lim f ( x ) lim( ) f ( x )
高数课件1-7PPT课件

2
作单位圆的切线,得ACO .
扇形OAB的圆心角为x , OAB的高为BD,
于是有 sin x BD, x 弧 AB, tan x AC ,
函数与极限
8
sin x x tan x, 即 cos x sin x 1,
x
上式对于 x 0也成立. 当 0 x 时,
2
2
0 cos x 1 1 cos x 2sin 2 x 2( x)2 x2 , 22 2
lim x2 0, lim(1 cos x) 0,
x0 2
x0
lim cos x 1, 又lim1 1, lim sin x 1.
x0
x0
x0 x
函数与极限
9
例3
求
lim
x0
1
cos x2
x
.
解
2sin2 x
原式 lim x0
2 x2
1
lim
sin 2
x 2
2 x0 ( x)2
lim (1 1 )x e.
x
x
函数与极限
13
令 t x,
lim (1 1 )x lim (1 1)t lim (1 1 )t
x
x
t
t
t t 1
lim (1 1 )t1(1 1 ) e.
t t 1
t 1
lim(1 1 )x e
x
x
令t 1, x
lim(1
1
1
1
1 2!
1 n!
1
1
1 2
1 2n1
3
1 2n1
3,
xn是有界的;
lim n
xn
存在.
作单位圆的切线,得ACO .
扇形OAB的圆心角为x , OAB的高为BD,
于是有 sin x BD, x 弧 AB, tan x AC ,
函数与极限
8
sin x x tan x, 即 cos x sin x 1,
x
上式对于 x 0也成立. 当 0 x 时,
2
2
0 cos x 1 1 cos x 2sin 2 x 2( x)2 x2 , 22 2
lim x2 0, lim(1 cos x) 0,
x0 2
x0
lim cos x 1, 又lim1 1, lim sin x 1.
x0
x0
x0 x
函数与极限
9
例3
求
lim
x0
1
cos x2
x
.
解
2sin2 x
原式 lim x0
2 x2
1
lim
sin 2
x 2
2 x0 ( x)2
lim (1 1 )x e.
x
x
函数与极限
13
令 t x,
lim (1 1 )x lim (1 1)t lim (1 1 )t
x
x
t
t
t t 1
lim (1 1 )t1(1 1 ) e.
t t 1
t 1
lim(1 1 )x e
x
x
令t 1, x
lim(1
1
1
1
1 2!
1 n!
1
1
1 2
1 2n1
3
1 2n1
3,
xn是有界的;
lim n
xn
存在.
同济大学高等数学第七版1-7无穷小的比较省公开课获奖课件说课比赛一等奖课件

lim
lim
A(或).
证
lim
lim(
)
lim
lim
lim
lim A(或).
17
定理2(等价无穷小替代定理)
设
~
,
~
且
lim
A(或),
则
lim
lim
A(或).
替代意义??
lim
lim
复杂
简朴
将常用旳等阶无穷小列举如下: 当 x0时
sin x ~ x
(4)
如果
lim
k
C
(C 0, k 0),
就说是关于 的 k 阶无穷小.
(5) 如果 lim 1, 则称与是等价无穷小,
记作 ~ .
6
因为lim 3x 2 0 ,所以当x 0时,3x 2是比x 高阶旳无穷小, x0 x
即3x 2o(x)( x 0).
例
比较无穷小:
1, n
1 n2
(n )
tan x x o( x),
arcsin x ~ x,所以 当x 0时有 arcsin x x o( x),
1 - cos x ~ 1 x2 , 所以 当x 0时有 2
1 - cos x 1 x2 o( x2 ). 2
16
定理2(等价无穷小替代定理)
设
~
,
~
且
lim
A(或),
则
8.
2
27
小结
1. 无穷小旳比较 反应了同一过程中, 两无穷小趋于零旳速度
快慢, 但并不是全部旳无穷小都可进行比较. 高(低)阶无穷小; 同阶(等价)无穷小; 无穷小旳阶. 2. 等价无穷小旳替代
同济大学高等数学第一章无穷小比较

n
n
~
机动 目录 上页 下页 返回 结束
定理1.
证:
~
o( )
lim 1 lim( 1) 0, 即 lim 0
~
o( ) , 即 o( )
例如, x 0 时,
~
tan x ~x , 故
tan x x o( x)
机动
目录
上页
下页
返回
结束
说明: 设对同一变化过程 , , 为无穷小 , 由等价
无穷小的性质, 可得简化某些极限运算的下述规则.
(1) 和差取大规则: 若 = o() , 则 ~ 1 x sin x lim 例如, lim 3 3 x 0 3 x x 0 x 3 x (2) 和差代替规则: 若 ~ , ~ 且 与 不等价 , lim , 则 ~ , 且 lim
x 0 时,
机动
目录
上页
下页
返回
结束
定理2 . 设
且
存在 , 则
lim
证:
lim lim lim lim lim lim
例如,
2x 2 tan 2 x lim lim x 0 5 x 5 x 0 sin义. 设 , 是自变量同一变化过程中的无穷小,
若 lim 0 , 则称 是比 高阶的无穷小, 记作 o( ) 若 lim , 则称 是比 低阶的无穷小; 若 lim C 0 , 则称 是 的同阶无穷小;
若 lim k C 0 , 则称 是关于 的 k 阶无穷小; 若 lim 1, 则称 是 的等价无穷小, 记作 ~ 或 ~
高等数学的教学课件1-7无穷小的比较

0
0
定义3 如果x 时 ( x)是无穷小, 且lim ( x) L 0,
1 xk
则x 时 ( x)是关于 1 x的k阶的无穷小;
二、等价无穷小的性质
性质1 ~ o( ).
证 lim 1 lim( 1) lim
lim 1 lim 0
~ o( ).
v
1 v1
lim lim u1 lim 1
1
v 1
lim u1 . v 1
说明: 在求极限的过程中,分子或分母中的因子, 可用其等价无穷小替换。
常用等价无穷小:
假设( x)是不取0值的无穷小,则:
~ sin ~ tan ~ arcsin ~ arctan, ~ e 1 ~ ln(1 ), (1 ) 1 ~ , 1 cos ~ 1 2.
x0
sin 3x
解 tan 5x ~ 5x, sin 3x ~ 3x, 1 cos x ~ 1 x2.
2
原式 lim tan 5x lim1 cos x
x0 sin 3x x0 sin 3x
lim
5x
lim
1 2
x2
5 0 5.
x0 3x x0 3x 3
3
原式X
5x lim
x0
1 2
3x
x2
5 3
例4 求 lim ln(e x sin2 x) x . x0 ln(e 2 x x 2 ) 2 x
解 ln(e x sin2 x) x ln e x (1 ex sin2 x) x ln(e2x x 2 ) 2 x ln e2x (1 e2x x 2 ) 2 x
2
例1 求 lim tan2 2x . x0 1 cos x
同济版高数课件ch1-7
α
定理 1 β 与 α 是等价无穷小的充分必 要条件 的主要部分. 为 β = α + o(α ).称 α 是 β 的主要部分.
注: 由此定理知
1) 若 β ~ α , 则 β − α = o(α ).
2) 若 β = α + o(α ), 则 β ~ α .
如
β = x 3 + x 4 , ( x → 0) . α = x3
x
1− 1− x + x 5. lim x →0 x
3
2
cos x(e sin x − 1)2 ; 6. lim x →0 tan 2 x
;
1 + cos πx 7. lim ; 2 x →1 ln x
第一章
第七节 无穷小的比较
一、无穷小的比较
1 例如, 例如 当x → 0时, x , x , sin x , x sin 都是无穷小. x 2 x 观 lim = 0, x 2比3 x要快得多 ; 察 x→0 3 x 各 sin x 极 sin x x ; = 1, lim x→0 x 限 1 2 x sin x = lim sin 1 0 lim 比. 比 . 2 x→0 x→0 x x 0 , 快 .
故当 x → +∞ 时 f ( x ) 和 g ( x ) 不能比较 不能比较.
练习
求极限: 求极限:
2
1 − 2x − 1 ; 2. 1. lim x →0 x ln(1 − x )
3. lim x →0
x arcsin x e− x − 1
2
;
ln(1 + 3 ) lim ; x x →−∞ ln(1 + 2 ) 1 x arcsin x ⋅ sin x ; 4. lim x→ x →0 sin x
《高等数学》无穷小与无穷大、无穷小的比较 ppt课件
取 Xma X 1,x X2 { }当 , x X时,恒有
, 22
0 (x )
注意 无穷多个无穷小的代数和未必是无穷小.
例如 ,n时,1是无穷小, n
但n个1之和1不 为是无.穷小 n
定理 3
有界函数与无穷小的乘积是无穷 小.
证 设函u在 数 U(x0,1)内有界,
则 M 0 ,10 ,使0 得 x当 x 01 时 恒u 有 M .
2. 函数的极限与无穷小量的关系
分析
若 x l x 0 i f ( x ) m a ,则 0 ,当 0 |x x 0 | 时 , |f ( x ) a | |( f ( x ) a ) 0 | ,
即x当 x0时 , f(x)a是一个.无穷 令 ( x ) f ( x ) a , 则 ( x ) 0 ( x x 0 ) , 且 f( x ) a ( x )( x x 结论 ?
定理1
limf (x)a f(x) a (x),
xx0 (x)
其 ,( x ) 0 中 ( x x 0 , ( x ) .)
由此可看出, 寻找函数极限运算法则 可归结为寻找无穷小量的运算法则.
意义
1.将一般极限问题转化为特殊极限问题(无穷 小);
2.给出了函 f(x数 )在x0附近的近似表 f(x)A,误差为 (x).
3.无穷小的运算性质:
定理2
在同一极限过程中,有限个无穷小的代 数和仍是无穷小.
定理2在同一过程中,有限个无穷小的代数和仍 是无穷小.
证 设及是当 x时的两个, 无穷小
0, X 10,X 20,使得
当xX1时恒 有 2; 当xX2时恒 有 2;
limx2 .
x
(ii) y x3,
limx3 . (iii), (iv) 自己画
, 22
0 (x )
注意 无穷多个无穷小的代数和未必是无穷小.
例如 ,n时,1是无穷小, n
但n个1之和1不 为是无.穷小 n
定理 3
有界函数与无穷小的乘积是无穷 小.
证 设函u在 数 U(x0,1)内有界,
则 M 0 ,10 ,使0 得 x当 x 01 时 恒u 有 M .
2. 函数的极限与无穷小量的关系
分析
若 x l x 0 i f ( x ) m a ,则 0 ,当 0 |x x 0 | 时 , |f ( x ) a | |( f ( x ) a ) 0 | ,
即x当 x0时 , f(x)a是一个.无穷 令 ( x ) f ( x ) a , 则 ( x ) 0 ( x x 0 ) , 且 f( x ) a ( x )( x x 结论 ?
定理1
limf (x)a f(x) a (x),
xx0 (x)
其 ,( x ) 0 中 ( x x 0 , ( x ) .)
由此可看出, 寻找函数极限运算法则 可归结为寻找无穷小量的运算法则.
意义
1.将一般极限问题转化为特殊极限问题(无穷 小);
2.给出了函 f(x数 )在x0附近的近似表 f(x)A,误差为 (x).
3.无穷小的运算性质:
定理2
在同一极限过程中,有限个无穷小的代 数和仍是无穷小.
定理2在同一过程中,有限个无穷小的代数和仍 是无穷小.
证 设及是当 x时的两个, 无穷小
0, X 10,X 20,使得
当xX1时恒 有 2; 当xX2时恒 有 2;
limx2 .
x
(ii) y x3,
limx3 . (iii), (iv) 自己画
高等数学-无穷小的比较
x x0 1
若
~ 1,
~
1
且 lim x x0
1 1
存在 ,
例1 求 lim tan2 2x .
x0 1 cos x
则
lim
lim 1 .
x x0
x x0 1
解 当x 0时, 1 cos x ~ 1 x2 , 2
原式
lim x0
(2 x )2 1 x2
8.
2
tan 2x ~ 2x.
另例 :
第六节
第一章
无穷小的比较
一、无穷小的比较 二、等价无穷小替换
一、无穷小量的比较
定义 设 与 是同一过程中的无穷小量,即
lim 0,lim 0.
xx0
xx0
❖ 如果lim 0,则 是比 较高阶无穷小;
xx0 记作 ( ).
lim o( ) ? x x0
❖ 如果lim ,则 是比 较低阶无穷小. xx0
x0 (2 x)3
0.
解 当x 0时, sin 2x ~ 2x,
tan x sin x tan x(1 cos x) ~ 1 x3 ,
原式 lim
1 0 (2 x)3 16
② 等价替换不能离开 “定理所允许的框架”
例3 lim(1 3 tan2 x)cot x .
x0
四、等价无穷小替换
定理3 (等价无穷小替换定理)
若
~ 1,
~
1
且 lim x x0
1 1
存在 ,
则 lim lim 1 .
x x0
x x0 1
证: lim
lim (
1 1 )
x x0
x x0 1 1
lim lim 1 lim 1 lim 1 .
经典高等数学课件D1-6两个重要极限;1-7无穷小的比较
16
1 例1. 证明:当x 0时, 1 x 1 x . n
n
证:
= lim
x 0
( n 1 x )n 1 1 n x[ (1 x )n1 n (1 x )n 2 1] n
lim
n (1 x )n1 n (1 x )n 2 1
7
arcsin x 例4. 求 lim . x 0 x t arcsin x lim t 解: 式 原 t 0
x sin t
sin t
arcsin x lim 1 x 0 x
1 1 si nt lim t 0 t
0 经验:含有三角函数,反三角函数的 型的极限问题常用 0 第一个重要极限解决.
2
第六节 极限存在准则
一、极限存在准则 夹逼准则 ;单调有界准则 二、两个重要极限
两个重要极限
sin x lim 1 x 0 x
1 x lim(1 ) e x x
3
一、极限存在准则 1. 夹逼准则
准则I: yn xn zn ( n 1, 2, ) (1)
(2) lim yn lim zn a
1 1 ln e
即有等价关系: e x 1 ~ x ( x 0) 说明: 1)上述证明过程也给出了关系: ln(1 x ) ~ x ( x 0) 2) 常用等价无穷小:当x 0时, sin x ~ x , tan x ~ x, arcsin x ~ x, arctan x ~ x , ln(1 x ) ~ x, 1 2 x e 1 ~ x, 1 cos x ~ x , (1 x)a 1 ~ ax (a 0) 2
x 0 n
1
1 则 当x 0时, 1 x 1 x . n
1 例1. 证明:当x 0时, 1 x 1 x . n
n
证:
= lim
x 0
( n 1 x )n 1 1 n x[ (1 x )n1 n (1 x )n 2 1] n
lim
n (1 x )n1 n (1 x )n 2 1
7
arcsin x 例4. 求 lim . x 0 x t arcsin x lim t 解: 式 原 t 0
x sin t
sin t
arcsin x lim 1 x 0 x
1 1 si nt lim t 0 t
0 经验:含有三角函数,反三角函数的 型的极限问题常用 0 第一个重要极限解决.
2
第六节 极限存在准则
一、极限存在准则 夹逼准则 ;单调有界准则 二、两个重要极限
两个重要极限
sin x lim 1 x 0 x
1 x lim(1 ) e x x
3
一、极限存在准则 1. 夹逼准则
准则I: yn xn zn ( n 1, 2, ) (1)
(2) lim yn lim zn a
1 1 ln e
即有等价关系: e x 1 ~ x ( x 0) 说明: 1)上述证明过程也给出了关系: ln(1 x ) ~ x ( x 0) 2) 常用等价无穷小:当x 0时, sin x ~ x , tan x ~ x, arcsin x ~ x, arctan x ~ x , ln(1 x ) ~ x, 1 2 x e 1 ~ x, 1 cos x ~ x , (1 x)a 1 ~ ax (a 0) 2
x 0 n
1
1 则 当x 0时, 1 x 1 x . n
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
x
解错 当x 0时, tan x ~ x,sin x ~ x,
原式
lim
x0
x- x (2 x)3
0.
解 当x 0时, sin 2x ~ 2x,
tan x - sin x tan x(1 - cos x) ~ 1 x3 ,
原式
lim
x0
1 x3 2 (2x)3
1. 16
9
10
1
11
t -1
n
lim
t 1
(t
-
1)( t
n-1
t
n-2
t
1)
n 1 1 n
12
13
二、利用等价无穷小替换求极限
定理1 ~ - o().
即 两个等价无穷小的差一定是一个更高 阶的无穷小,反之亦然。
原因? 他们太接近了,所以它们的差远远小于 它们之中的任何一个。
无穷小的比较
定义 设, 是同一过程中的两个无穷小, 且 0.
(4)
如
果lim
k
C
(C 0, k ቤተ መጻሕፍቲ ባይዱ 0),
就说是关于 的 k 阶无穷小.
(5) 如果lim 1, 则称与是等价无穷小,
记作 ~ .
6
因为lim 3x 2 0 ,所以当x 0时,3x 2是比x 高阶的无穷小, x0 x
lim
lim(
)
lim
lim
lim
lim A(或).
17
定理2 (等价无穷小替换定理)
设
~ ,
~
且
lim
A(或),
则
lim
lim
A(或).
2
注:加、减项的无穷小不要用等价无穷小代换.
23
例5
求
lim
x0
arc 2(1 -
sin x cos 2 x
)
.
解
lim
x0
arc 2(1 -
sin x cos2 x
)
arcsin x
~
x
lim
x0
2(1
-
x cos 2
x)
lim
x
x0 2(1 - cos x)(1 cos x)
lim
x
lim 1
x0 2(1 - cos x) x0 1 cos x
1-cos
x
~
1 2
x
2
lim
x
1
x x0 2 lim(1 cos x)
x0
24
例6 求 lim ln 1 x 2sin x
lim
lim
o( )
lim1
o( )
1,
因此 ~ .
15
例 当x 0时,
sin x ~ x, 所以 当x 0时有 sin x x o( x), tan x ~ x, 所以当x 0时有
tan x x o( x), arcsin x ~ x,所以 当x 0时有
定理1 ~ o().
14
定理1 ~ o().
证 设 ~ , 则
lim
-
lim
- 1
lim
-1
0,
因此 - o( ), 即 o( ).
设 o( ), 则
x0 x
4
无穷小的比较
定义 设, 是同一过程中的两个无穷小, 且 0.
(1) 如果lim 0, 就说是比 高阶的无穷小;
记作 o( );
(2) 如果lim
,
就说 是比 低阶的无穷小;
(3) 如果lim
C(C
0),就说与是 同阶无穷小;
2
1 x -1~ x 2
tan x - sin x ~ x3 2
其中 , m , n N , a 0 .
19
例2 求 lim tan2x . x0 sin5x
解 当x 0时, tan2x ~ 2x, sin5x ~ 5x, 原式 lim 2x 2 . x0 5x 5
20
1
arcsin x x o( x),
1 - cos x ~ 1 x2 , 所以 当x 0时有 2
1- cos x 1 x2 o( x2 ). 2
16
定理2 (等价无穷小替换定理)
设
~ ,
~
且
lim
A(或),
则
lim
lim
A(或).
证
即3x 2o(x)( x 0).
例
比较无穷小:
1, n
1 n2
(n )
1
因为lim n ,所以当 n 时,1
n 1
n
n2
是比 1 低阶的无穷小. n2
7
因为lim 1 - cos x 1 ,
x0 x 2
2
所以当x 0时,1-cos x 与x2 的同阶无穷小。 当x 0时,1-cos x 是x 的二阶无穷小。
例3
求
lim (1 x2 )3 -1. x0 cos x -1
解:
21
练习
求
lim x2 ln1
x
2 x3
解
lim x2 ln1
x
2 x3
lim x2
x
2 x3
lim 2 0 x x
22
例4
求
lim
x0
tan x - sin sin3 2x
x0 x
如何比较两个无穷小??
x
lim
x0
x2
3
例 考察 x 0时, x x2 趋于零的快慢
x
0.1
0.01 0.001
…
x2
0.01 0.0001 0.000001 …
lim x 2 0,
x0 x
x2 0比x 0要快得多;
lim sin x 1, sin x 0与x 0快慢相仿;
替换意义??
lim
lim
复杂
简单
将常用的等阶无穷小列举如下: 当 x0时
sin x ~ x
arcsinx ~ x
tan x ~ x
arctanx ~ x
ln(1 x) ~ x
ex -1~ x
ax -1 ~ xln a m1 x -1~ x
m
(1 x)n -1 ~ nx 1 - cos x ~ x2
第七节 无穷小的比较
无穷小的比较 利用等价无穷小替换求极限
1
一、无穷小的比较
2
无穷小+无穷小=无穷小 无穷小-无穷小=无穷小 无穷小×无穷小=无穷小
无穷小 但: 无穷小 =?
如,当x 0时, x, x 2 , sinx 是无穷小.
lim x 2 0,
x0 x
lim sin x 1,
