6.1非参数计量经济学模型
计量经济学的起源

计量经济学的起源、发展的历史和发展程度
西方发达资本主义国家经济危机爆发后,在众多经济学家对经济现象“质”的认识趋于统一后,部分经济学家开始用数量分析开始探索经济问题,即从经济现象的“量”方面研究。
第二次世界大战后,统计学中的回归分析方法被广泛运用到预测经济指标中并引入众多通积分和检验方法。
上述两方面的结合形成了计量经济学,其主要含义是对经济的测度。
世界计量经济学学会于1930年12月29日成立,并创立会刊《计量经济学》,该学会的成立及会刊创刊是计量经济学发展史上的重要里程碑,标志着该学科的正式诞生。
上世纪计量经济学的研究自单方程模型、联立方程模型方向向分布滞后模型、受限因变量模型、非线性计量经济学模型以及之后的时间序列分析、结合计算机密集技术、非参数与半参数方法、贝叶斯方法进行深入发展。
目前为计量经济学研究提供大量高频数据的是实际金融部门,该领域已经成为学科研究的新热点。
目前ARCH模型基本被随机波动模型取代,同时基于正态性假设的传统计量经济学技术在金融数据领域的应用仍受到限制,对此,在计量经济学家的努力下,资产定价模型和期权定价模型的检测和估计等问题已被攻。
计量经济学作为一门实用性很强的学科其发展原动力来源于世纪经济生活中产生的大量原始数据。
对可利用价值越来越大的金融数据进行有效加工会促进未来计量经济学发展得更远。
经济学院金融学1202班
121002215 吕齐安。
(超全)计量经济学框架图
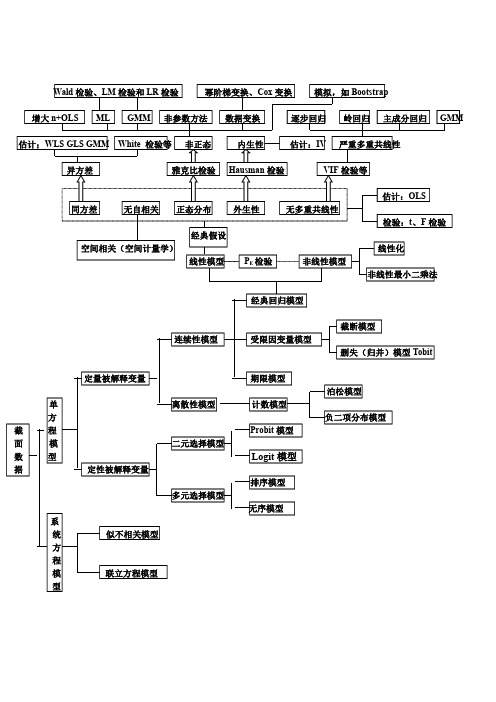
面
模
二元选择模型
数
型
Logit 模型
据
定性被解释变量
排序模型
多元选择模型
无序模型
系
统
似不相关模型
方
程
模
联立方程模型
型
泊松模型 负二项分布模型
平稳序列 ARMA 模型
单变量序列
非平稳序列
ARIMA 模型 SARMA 模型
单方程模型
平稳序列 建模方法同截面数据
多变量序列 单位根检验
时
协整(同阶单整)
间
Wald 检验、LM 检验和 LR 检验
幂阶梯变换、Cox 变换 模拟,如 Bootstrap
增大 n+OLS ML GMM 非参数方法 数据变换
逐步回归 岭回归 主成分回归 GMM
估计;WLS GLS GMM White 检验等 非正态
内生性
估计:IV 严重多重共线性
异方差
雅克比检验 Hausman 检验
VIF 检验等
同方差
无自相关 正态分布 外生性
无多重共线性
空间相关(空间计量学)
经典假设 线性模型
PE 检验
非线性模型
估计:OLS 检验:t、F 检验 线性化 非线性最小二乘法
经典回归模型
连续性模型
受限因变量模型
截断模型 删失(归并)模型 Tobit
定量被解释变量
期限模型
单
离散性模型
计数模型
方
截
程
Probit 模型
随机效应模型
面
时间效应模型
板
数
据
PVAR
类似时间序列数据的方法
面板单位根
(2024年)完整版李子奈计量经济学版第四版课件

• 三阶段最小二乘法(3SLS):三阶段最小二乘法是对二阶段最小二乘法的改进。 该方法在第二阶段估计时,不仅考虑了残差作为解释变量,还考虑了其他所有 内生变量的估计值作为解释变量。这样可以进一步提高参数估计量的效率。
在社会科学领域,这些方法可用于分析人口 统计数据、经济指标等,揭示社会经济现象 背后的复杂关系。
2024/3/26
30
THANKS
感谢观看
2024/3/26
31
多重共线性的检验
相关系数矩阵法、方差膨胀因子 法、条件指数法等。
14
04
时间序列计量经济学模型
Chapter
2024/3/26
15
时间序列基本概念与性质
01
02
03
时间序列定义
按时间顺序排列的一组数 据,反映现象随时间变化 的发展过程。
2024/3/26
时间序列构成要素
现象所属的时间(年、季、 月、日等)和反映现象在 各个时间上的统计指标数 值。
28
半参数回归分析方法
部分线性模型
模型中既包含参数部分也包含非参数部分,参数部分用于描述主要 影响因素,非参数部分用于捕捉其他未知影响因素。
单指标模型
通过投影寻踪方法将高维数据降维到一维,然后利用非参数方法进 行回归分析。
变系数模型
模型系数随着某个或多个变量的变化而变化,可以灵活捕捉变量间的 动态关系。
不可识别的情况 当联立方程模型中的某个方程不能被任何其他方程所替代 时,该方程就是不可识别的。此时,无法对该方程的参数 进行一致估计。
计量经济学4非线性模型

Yi Z i1 Z iP
ˆ0 ˆ1
ˆP
计量经济学
1、多项式函数
Y 0 1X 2 X 2 3 X 3 P X P u
令:Zi X i,(i 1,2, ,P)
则:Y 0 1Z1 2 Z 2 3Z3 P Z P u
2、双曲函数
1 a b
K dY
;
Y
Y
dL
dM
劳力贡献率: L ;土地贡献率: M
dY
dY
Y
Y
计量经济学
例:给定生产函数Y AK L,其中,Y、K、L分别
为产量、资本、劳力,若 1 , 3 ,在某期间
4
4
Y、K、L的增长率分别为5%,4%,2%,求技术进步、
资本、劳力在产品增长中的贡献份额。
解:技术进步率 5% 1 4% 3 2% 2.5%
mY ,
1,
mY ,
1,
规模报酬递减 规模报酬不变 规模报酬递增
计量经济学
二、非线性回归模型的处理 (一)变换法 适用于Y与解释变量非线性,但与参数线性的情形。
Y 0 1 f(1 X1,X 2, ,X l) 2 f(2 X1,X 2, ,X l) P f(P X1,X 2, ,X l) u
4
4
技术进步贡献率 2.5% 50%; 5%
资金贡献率 0.25 4% 20% 5%
劳力贡献率 0.75 2% 30% 5%
计量经济学
α、β、γ的求法: ①利用截面数据进行回归; ②利用时间序列数据进行回归; ③利用混合数据进行回归; ④利用类似地区的α、β、γ。
(三)Taylor展开法(略)
计量经济学
第四章 非线性模型
一、问题的提出 多元线性回归模型为:
计量经济学6虚拟变量模型

年薪 Y
2 0
男职工 女职工
工龄 X
又例:在横截面数据基础上,考虑个人保健支出 对个人收入和教育水平的回归。
教育水平考虑三个层次:高中以下, 高中, 大学及其以上
这时需要引入两个虚拟变量:
1 D1 0
高中 其他
1 D2 0
大学及其以上 其他
模型可设定如下:
Yi 0 1 X i 2 D1 3 D2 i
例。已知冷饮的销售量Y除受k种定量变量Xk的影 响外,还受春、夏、秋、冬四季变化的影响,要考察 该四季的影响,只需引入三个虚拟变量即可:
1 春季 D1t 0 其他
1 夏季 D2t 0 其他
1 秋季 D3t 0 其他
则冷饮销售量的模型为:
Yt 0 1 X1t k X kt 1D1t 2 D2t 3 D3t t
90年前 1979 1980 1981 1982 1983 1984 1985 1986 1987 1988 1989 1990
表 5.1.1
储蓄 281 399.5 523.7 675.4 892.5 1214.7 1622.6 2237.6 3073.3 3801.5 5146.9 7034.2
于是,不同性别、不同学历职工的平均薪金分别为: •女职工本科以下学历的平均薪金:
E(Yi | X i , D1 0, D2 0) 0 1 X i
•男职工本科以下学历的平均薪金:
E(Yi | X i , D1 1, D2 0) (0 2 ) 1 X i
•女职工本科以上学历的平均薪金:
X k1 X k2 X k3 X k4 X k5 X k6
1 0 0 0 0 1 0 0
0
0
1
0
0 0 0 1
计量经济学ppt课件(完整版)

在进行模型选择与比较时,需要注意避免过拟合和欠拟合问题,以及确保模型的稳定性和可靠性。此外 ,还需要关注模型的异方差性、共线性等问题,以确保模型的准确性和有效性。
04
时间序列分析及应用
时间序列基本概念及性质
01
时间序列定义
按时间顺序排列的一组数据,反映 现象随时间变化的发展过程。
时间序列类型
03
广义线性模型与非线性模型
广义线性模型介绍
定义
广义线性模型是一类用于描述响 应变量与一组预测变量之间关系 的统计模型,其特点在于响应变 量的期望值通过一个连接函数与 预测变量的线性组合相关联。
连接函数
连接函数是广义线性模型中一个 关键组成部分,它将响应变量的 期望值与预测变量的线性组合连 接起来。常见的连接函数包括恒 等连接、对数连接、逆连接等。
模型的统计性质
深入探讨多元线性回归模型的统计性质,包括无偏性、有效性和一致性等,并解释这些 性质在多元回归分析中的重要性。
多重共线性问题
详细讲解多重共线性的概念、产生原因、后果以及诊断和处理方法,如逐步回归、岭回 归等。
回归模型检验与诊断
模型的拟合优度 介绍衡量模型拟合优度的指标, 如可决系数、调整可决系数等, 并解释这些指标在实际应用中的 意义。
微观计量经济学在因果推断和政策评 估方面发挥着重要作用。目前,研究 者们关注于如何运用实验设计、工具 变量、双重差分等方法识别和处理内 生性问题,以更准确地估计因果关系 和评估政策效果。
高维数据处理与机器 学习
随着大数据时代的到来,高维数据处 理成为微观计量经济学面临的新挑战 。目前,研究者们正在探索如何将机 器学习等先进的数据分析技术应用于 微观计量经济学中,以处理高维数据 和挖掘更多的有用信息。
第六章联立方程计量经济学模型理论与方法(计量经济学
§6.1 问题的提出
一、经济研究中的联立方程计量经济学问题 二、计量经济学方法中的联立方程问题
一、经济研究经济系统,而不是单个经济活动 “系统”的相对性
• 相互依存、互为因果,而不是单向因果关系 • 必须用一组方程才能描述清楚
⒉一个简单的宏观经济系统
⒊例题3
Ct 0 1Yt 2Ct1 1t I t 0 1Yt 2Yt1 2t
例如,在上述模型中存在如下关系:
21
2 12 1 1 1
2
12 1 1 1
Π21反映Yt-1对It的直接与间接影响之和; 而其中 的β2正是结构方程中Yt-1对It的结构参数,显然, 它只反映Yt-1对It的直接影响。 • 在这里,β2是Yt-1对It的部分乘数,Π21反映Yt-1对It 的完全乘数。
第六章 联立方程计量经济模型理论方 法
The Theory and Methodology of the Simultaneous-Equations Econometrics
Model(SEM)
本章内容
§6.1 联立方程计量经济学模型的提出 §6.2 联立方程计量经济学模型的基本概念 §6.3 联立方程计量经济学模型的识别 §6.4 联立方程计量经济学模型的估计 §6.5 联立方程计量经济学模型的讨论
Ct 0 1Yt 1t
I
t
0
1Yt
2Yt1 2t
Yt Ct I t Gt
• 如果用单方程模型的方法估计某一个方程,将损 失变量信息。
• 为什么?
⒊损失方程之间的相关性信息问题
CI tt
0 1Yt 0 1Yt
1t Y2 t1
2t
Yt Ct I t Gt
⒉例题2
经济学研究中的计量经济学模型建立方法
经济学研究中的计量经济学模型建立方法计量经济学是应用数理统计方法研究经济现象的学科,它是现代经济学的重要组成部分。
在经济学研究中,计量经济学模型的建立是一个关键的环节,它能够帮助我们对经济现象进行定量分析和预测。
下面我们将介绍一些常用的计量经济学模型建立方法。
首先,经济学研究中最常见的计量经济学模型是线性回归模型。
线性回归模型假设自变量与因变量之间存在线性关系,并通过最小二乘法来估计模型参数。
在建立线性回归模型时,我们首先需要确定自变量和因变量的选择,然后通过收集相关数据来估计模型参数,并进行假设检验来验证模型的有效性。
其次,有些经济现象可能存在非线性关系,这时我们可以使用非线性回归模型来建立计量经济学模型。
非线性回归模型可以捕捉到因变量和自变量之间的复杂关系,但模型的参数估计通常更加困难。
常见的非线性回归模型包括多项式回归、对数线性模型、指数模型等。
在建立非线性回归模型时,我们需要选择适当的函数形式,并通过非线性最小二乘法来估计模型参数。
此外,为了解决自变量与因变量之间可能存在内生性的问题,我们可以使用工具变量法建立计量经济学模型。
工具变量法利用一个或多个外生变量来代替内生变量进行估计,从而避免内生性引起的估计偏误。
在建立工具变量法模型时,我们需要选择有效的工具变量,并使用合适的估计方法来得到一致的估计结果。
另外,为了适应面板数据的特点,我们可以使用面板数据模型来研究经济现象。
面板数据模型结合了时间序列和横截面数据的特点,可以提供更加准确的估计结果。
常见的面板数据模型包括固定效应模型、随机效应模型和差分法模型等。
在建立面板数据模型时,我们需要考虑时间和个体的固定影响,并使用适当的估计方法进行分析。
此外,为了处理具有序列相关性的时间序列数据,我们可以使用时间序列分析方法建立计量经济学模型。
常见的时间序列分析方法包括自回归移动平均模型(ARMA模型)、自回归条件异方差模型(ARCH模型)和广义自回归条件异方差模型(GARCH模型)等。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
• 经典线性回归模型的估计结果如下:
Yˆ 122 .06 0.065978 X 0.052493 FC
( 21.446)
( 2.2246)
(13.373)
R2=0.84582, F=178.29,拟合的均方误差为11.035。
实际值
拟合值
250 200 150 100
50 0
1 5 9 13 17 21 25 29 33 37 41 45 49 53 57 61 65
• 利用特殊的技术,例如广义刀技术,可以得到用 于边界点估计的边界核。
⒎例题1—模拟例题
• 解列释{ui变}独量立序同列分{x布i}独。立让均xi (匀i=同1,分2,…布3,00随)是机在误[差0,项1]上序 均匀取值相互独立的变量, ui~N(0,0.25) (i=1,2,…300)独立,模型为:
Yi m( X i ) i
• 半参数模型
i 1,, n
Yi
f
(
X
i1 ,
)
m(
X
2 i
)
i
i 1,, n
△既然非参数模型不能将经济活动中变量之间的结 构关系明确地加以描述,那么它是否属于经济数 学模型?
• 非参数模型并不事先假定经济活动中变量之间的 结构关系,而是通过估计获得这种结构关系,而 且具有明确的数学描述。
• 所以它毫无疑问属于经济数学模型,应该将它纳 入计量经济学模型的范围。
△既然非参数模型不能将经济活动中变量之间的结 构关系明确地加以描述,那么它能否用于经济预 测?它的应用价值是什么?
• 它的应用价值在于有更好的拟合效果,可以说是 所有类型经济数学模型中拟合效果最好的。
• 由此而引出的对已经发生的经济活动的推断具有 更高的精度,所得到的反映经济变量之间关系的 结构参数,例如乘数、弹性等,更加反映经济活 动的实际。
• 从这些结构参数出发进行的预测可以得到更加可 靠的结果。
⒉ 模型估计方法
• 局部逼近估计方法
权函数方法
– 核权估计 – 局部线性估计 – K—近邻估计
• 整体逼近估计方法
级数估计(最小二乘估计)
– 正交序列估计 – 多项式样条估计
⒊ 模型估计理论的早期重要发展
• 局部逼近(权函数)估计发展于1980年前后:
叶阿忠博士论文(2002): 非参数联立方程模型的单方
程估计方法研究
• 整体逼近估计方法:级数估计
– I.I.d样本下级数估计量的收敛速度、渐近正态性、一致 收敛速度、模型设定检验的深入研究。
– 弱相依样本(weekly dependent Data)下级数估计量的 研 究 : White and Wooldridge(1991), Chen and Shen(1998)研究渐近性质。
• 不变窗宽和变窗宽 窗宽随xi改变。 核估计效果更好。
⒌核权函数的选择
• 将最佳窗宽代入渐近均分误差公式,可推得最佳 核函数为 :
Kopt (u) 0.75(1 u2)
• 教科书中给出了一般的讨论,上述结果是其中的一 个特例。
⒍边界点的处理
• 由于较少的观测值被利用,估计的偏和方差将增 大。
n
n
min
Wni (x)( yi )2
i 1
Wni (x)( yi mˆ n (x))2
i 1
• 最常用的核函数有: 均匀核:k()是[-1,1] 上的均匀概率密度函数
K1(u) 0.5I (| u | 1)
• I()为显示性函数,当括 号内的不等式成立时,取 值为1,否则取值为0。
孙云博士论文:弱相依样 本下级数估计收敛速度和
模型设定检验研究Biblioteka 二、非参数单方程模型的核估计
⒈核估计是一种权函数估计方法
○ 权函数估计
yi m(xi ) (xi )i
i 1,,n
m(xi ) E( yi | xi )
n
mˆ n (x) Wni (x) yi i 1
Wni (x) Wni (x; X1,, X n )
n
Wni (x) 1
i 1
• 条件回归函数的估计是yi的线性组合,对应所得 到的被解释变量的估计是yi的加权平均,权数利 用了解释变量的信息,且由解释变量的数值来确 定每个yi的权数的大小。
• 不同的选择权函数的方法构成了不同的权估计方 法。
• 核权估计、局部线性估计、k-近邻估计等是其中 常用的方法。
hn2
(mf
2mf 2 f (x)
)( x)
2 (K )
2 (K ) K (u)u 2du
• 渐近方差随着窗宽减少而增大 :
2 (x)
R(K ) nhn f (x)
R(K) K 2 (u)du
f(x)是解释变量的密度函数。
• 在估计的偏和方差中寻求平衡,使得均方误差达 最小。 渐近均方误差=渐近偏2+渐近方差
• 若K()是[-1,1]上的Epanechnikov概率密度函数,则 m对(应x)的的y局i关部于线该性局估部计模就型是的落加在权[x最-h小n,x二+乘hn估]的计xi与。其 当xi越接近x时,对应yi的权数就越大,反之,则 越小。
• 若K()是[-∞,∞]上原点对称的标准正态密度函数,则 m(x)的局部线性估计就是该局部模型的加权最小 二乘估计 。当xi越接近x时,对应yi的权数就越大, 反数之基,本则 上越 为小 零。。当xi落在[x-3hn,x+3hn]之外时,权
yi sin(10 xi ) ui
• 选择
K (u) 0.75(1 u 2 )
hn 0.13n1/ 5
• 数据及其核估计拟合图
2
1
0
0
0.5
1
-1
-2
例题2—我国对外经济联系与国内通货膨胀关
系的非参数估计
• 选定商品进出口总额X和外汇储备FC表示我国对 外经济联系,代表通货膨胀的变量Y则采用居民 消费价格指数。从《中国物价》得到1993年4月 到1998年11月每月与上年同月相比的居民消费价 格指数,再换算成每月与1992年4月相比的居民 消费价格指数,用它作为被解释变量变量y。商品 进出口总额资料来自《海关统计》外汇储备资料 来自《中国金融》。
– Watson和Nadaraja(1964)提出回归模型的核估计。 – Stone(1977)讨论了权函数估计的矩相合性。 – Stone(1977,1980,1982)系统研究了非参数回归模型的局
部多项式拟合。 – Cleveland(1979)提出局部线性拟合的稳健估计。 – Devroye 和Wagner(1980)证明了核估计的相合性。 – Stone(1980,1982)得到非参数估计收敛于实际回归函数的
⒉Nadaraya-Watson核估计
• Nadaraya(1964)及Watson (1964)提出 。 • 选定原点对称的概率密度函数为核函数
K(u)du 1
n
Wni (x) Khn (x xi ) / Khn (x x j ) j 1
Khn (u) hn1K (uhn1)
• 核估计等价于局部加权最小二乘估计均匀核。因为
⒊其它形式的权函数估计
• K –近邻估计
– 用最靠近x的k个观察值进行加权平均 – 适合于解释变量是确定性变量的模型,也适合于解释
变量是随机变量的模型
⒋窗宽的选择
• 核估计是集中x附近一个邻域的样本观测值的加权 平均,该邻域的宽度h称为窗宽。
• 是控制核估计精度的最主要的参数。
• 渐近偏随着窗宽减少而减少:
• 非参数模型采取高斯核估计方法,采用交错鉴定法 选择最佳窗宽为0.25。拟合的均方误差为3.809。
实际值
拟合值
250 200 150 100
50 0
1 5 9 13 17 21 25 29 33 37 41 45 49 53 57 61 65
三、非参数单方程模型的局部线性估计
⒈局部多项式回归
§6.1 非参数计量经济学模型
一、非参数计量经济学模型概述 二、非参数单方程模型的核估计 三、非参数单方程模型的局部线性估计 四、非参数单方程模型的最小二乘估计
一、非参数计量经济学模型概述
⒈概念
△参数模型和非参数模型
• 经典的线性或非线性计量经济模型,首先根据对 研究对象行为的分析,建立包含变量、参数和描 述它们之间关系的理论模型,然后利用变量的样 本观测值,采用适当的方法,估计参数,故称为 参数模型。
• 在现实中,经济变量之间的关系并不是在所有样本 点上都是不变的,或者说不能事先确定某种线性 关系或非线性关系,而是要通过估计才能得到某种 关系,而且随着样本点的不同而不同。这就引出 了非参数模型。
△非参数模型、无参数模型、半参数模型
• 如果所有变量之间的关系都是不明确的,称之为 完全非参数模型,简称非参数模型或者无参数模 型(Nonparametric model);
• 对于非参数回归模型
Y m( X ) u
将m(x)在x0处 进行台劳展开
m(x)
m(
x0
)
m(
x0
)(
x
x0
)
m(
p) (x0 p!
)
(
x
x0
)
p
Yi
m(x0 )
m(x0 )( X i
x0 )
m(p) (x0 ) p!
(Xi
x0 ) p
i
• 该多项式可用加权最小二乘法进行局部拟合。即 最小化
• 如果一部分变量之间的关系是明确的,而另一部 分变量之间的关系是不明确的,称之为半参数模 型(Semiparametric Model)。
• 一般所说的“非参数计量经济学”,既包括非参 数单方程模型,也包括非参数联立方程模型;既 包括完全非参数模型,也包括半参数模型。
