第5章多自由度系统的数值计算方法
合集下载
5-两自由度系统的振动
静平衡位置：
k11 m1 g k2 2
则：
,
k2 2 m2 g k3 3
1 2 1 1 2 2 V k1 x1 k2 ( x1 x2 ) k3 x2 2 2 2
第5章 两个自由度系统的振动 拉格朗日方程
21
d T d x (m1 x1 ) m11 dt x1 dt d T d x (m2 x2 ) m2 2 dt x2 dt
57两自由度系统的强迫振动第5章两个自由度系统的振动68例在两自由度标准mk系统中设m57两自由度系统的强迫振动第5章两个自由度系统的振动6957两自由度系统的强迫振动第5章两个自由度系统的振动70t545图示系统已知x57两自由度系统的强迫振动第5章两个自由度系统的振动71代入数据求得固有频率为28297机车振动频率为0707070718041276利用前面的方法求得振幅为作业
整理写成矩阵形式即可。
第5章 两个自由度系统的振动
拉格朗日方程
24
【T5-30】 用 拉 格 郎 日 方 程
建立系统微振动微分方程。
解：取静平衡位置为坐
x1
标原点和零势能位置
D1
1 2 T (mx12 mx2 ) 2
1 2 1 1 2 2 V kx1 k D1 k D 2 2 2 2
第5章 两个自由度系统的振动 拉格朗日方程
23
代入拉格朗日方程
得
d T T V Qi dt xi xi xi
m1 1 0 (k1 k2 ) x1 k2 x2 F1 (c1 c2 ) x1 c2 x2 x m2 2 0 k2 x1 (k3 k2 ) x2 F2 (c3 c2 ) x2 c2 x1 x
k11 m1 g k2 2
则：
,
k2 2 m2 g k3 3
1 2 1 1 2 2 V k1 x1 k2 ( x1 x2 ) k3 x2 2 2 2
第5章 两个自由度系统的振动 拉格朗日方程
21
d T d x (m1 x1 ) m11 dt x1 dt d T d x (m2 x2 ) m2 2 dt x2 dt
57两自由度系统的强迫振动第5章两个自由度系统的振动68例在两自由度标准mk系统中设m57两自由度系统的强迫振动第5章两个自由度系统的振动6957两自由度系统的强迫振动第5章两个自由度系统的振动70t545图示系统已知x57两自由度系统的强迫振动第5章两个自由度系统的振动71代入数据求得固有频率为28297机车振动频率为0707070718041276利用前面的方法求得振幅为作业
整理写成矩阵形式即可。
第5章 两个自由度系统的振动
拉格朗日方程
24
【T5-30】 用 拉 格 郎 日 方 程
建立系统微振动微分方程。
解：取静平衡位置为坐
x1
标原点和零势能位置
D1
1 2 T (mx12 mx2 ) 2
1 2 1 1 2 2 V kx1 k D1 k D 2 2 2 2
第5章 两个自由度系统的振动 拉格朗日方程
23
代入拉格朗日方程
得
d T T V Qi dt xi xi xi
m1 1 0 (k1 k2 ) x1 k2 x2 F1 (c1 c2 ) x1 c2 x2 x m2 2 0 k2 x1 (k3 k2 ) x2 F2 (c3 c2 ) x2 c2 x1 x
第5章：实用计算方法
x A sin( t )
( D vE ) A 0
代入动力学方程,得标准特征值问题 2 其中 v 1/
A的非零解条件要求方程的系数行列式为零 D vE 0
STDU
DYNAMICS OF STRUCTURES
设
D (d ij ) d11 d12
d n1
STDU
DYNAMICS OF STRUCTURES
T
若取 1 1.8 2 相应得到
1 0.3749 k / m
1.720k R( ) 0.1405k / m 12.24m
与精确解 1 0.3730 k / m 的相对误差为0.5% 如何假设模态呢? 一般地,可以系统的静变形作为假设模态 比如右图,可假设在三个 质点处分别作用有mg, mg, 2mg的力,此时三个 质点的位移分别为 4mg/k, 7mg/k, 8mg/k 因此,可假设模态为 4 7 8
STDU
DYNAMICS OF STRUCTURES
§ 5.1 邓克利法(Dunkerly) 邓克利法计算基频的近似值为实际基频的下限,它 是由邓克利在用实验确定多圆盘的横向振动固有频 率时提出的. Mx Kx 0 自由振动动力学方程为
左乘柔度矩阵F得
令 D FM 自由振动时
FMx x 0 Dx x 0
trD tr(FM ) f ii mi
i 1 n
STDU
DYNAMICS OF STRUCTURES
而特征方程又可以写为
系数
n
(v v1 )(v v2 )
(v vn ) 0
a1 vi
i 1
n
导出
动力计算第五讲-河北建筑工程学院
C1
第一主振型
m1
第二主振型
振动过程中，结构位移形状保持不变的振动形式，称为主振型。 由此可见： （1）多自由度体系如果按某个主振型自由振动，其振动形式保持不变，此时， 多自由度体系实际上是像一个单自由度体系在振动(一个坐标即可表示所有质点 位置）。 （2）按主振型振动的条件： 初位移或初速度与此振型相对应； 实际上，多自由度体系在零时刻的y0或vo通常不能完全与某一振型相对应。
k21
22
1
y1(t)
y1(t)
S1
k11
1
k12
Si Si
m11 S1 0 y m2 2 S2 0 y
S k11 y1 k12 y2
' 1
m1 1 (t ) k11 y1 (t ) k12 y2 (t ) 0 y m2 2 (t ) k21 y1 (t ) k22 y
2 1 2
X1( 2) X1(1)
X 2( 2) X 2 (1)
12 m1 k 11
k 12
2 2 m1 k 11
1 1 10 C1 n 1 2 4
k 12
C2
1 1 9 n 1 2 4
若 n=90 则第一振型和第二振型分别为： 可见当顶端质点的质量和刚度很小时，顶端水平侧移很大。
l /3
EI l /3 1
l /3
依据公式
**
5 ml3 1 可求： 162 EI 1 ml3 2 486 EI
11
21 1 22
12
则有：
1 2
1 EI 5.692 ml3 1 1 EI 22.045 ml3 2
第5章 Hysys模拟换热过程
被指定/计算得到
指定计算热曲线的方式
Individual Heat Curve
参数 区间数（Intervals） 描述 区间的数量
露点/泡点(Dew/Bubble 为相变添加一个露点或泡点到热曲线上（温度为Y Point) 轴，Heat Flow为X 轴) (有相变体系必须选定） 步长类型（Step Type） ������ ������ ������ 独立热曲线 （Individual Heat Curve Details） 等焓（Equal Enthalpy） 等温（Equal Temperature） 自动间隔（Auto Interval.）
逆流换热器 • 当下列假设满足时，可用最简单的表达式确定： 1)两种流体均为定态流动； 2)两种流体以逆流或并流方式流动； 3)在整个换热器内传热总系数保持为常数； 4)每种流体都只有显焓的变化，具有恒定的比热容； 5)热损失可忽略不计。
传热计算方程
Q U A Tm Tm FT f ( R, S ) TLM
四、管程与壳程的确定
第二节 Hysys传热单元模型
• 换热器（Heat Exchanger） – 常规的一股热流与一股冷流的热量交换 • LNG Heat Exchanger – 多股冷流与热流的集中热量交换 • 冷却器/加热器（Cooler/Heater） – 以加热或者冷却工艺物流为目的的热量交换，仅计算 所需热负荷 • 空气冷却器（Air Cooler） – 以空气为冷却介质的热量交换，可计算所需空气量 • 火焰加热炉（加热炉）（Fired Heater (Furnace)） – 可用于计算物料加热或焚烧所需空气量、尾气质量等
二、管壳式换热器的结构
◆管壳式换热器流体的流程
一种流体走管内、称为管程，另一种流体走管外、称为壳程。 管内流体从换热管一端流向另一端一次，称为一程；对U形管换热器， 管内流体从换热管一端经过U形弯曲段流向另一端一次，称为两程.
指定计算热曲线的方式
Individual Heat Curve
参数 区间数（Intervals） 描述 区间的数量
露点/泡点(Dew/Bubble 为相变添加一个露点或泡点到热曲线上（温度为Y Point) 轴，Heat Flow为X 轴) (有相变体系必须选定） 步长类型（Step Type） ������ ������ ������ 独立热曲线 （Individual Heat Curve Details） 等焓（Equal Enthalpy） 等温（Equal Temperature） 自动间隔（Auto Interval.）
逆流换热器 • 当下列假设满足时，可用最简单的表达式确定： 1)两种流体均为定态流动； 2)两种流体以逆流或并流方式流动； 3)在整个换热器内传热总系数保持为常数； 4)每种流体都只有显焓的变化，具有恒定的比热容； 5)热损失可忽略不计。
传热计算方程
Q U A Tm Tm FT f ( R, S ) TLM
四、管程与壳程的确定
第二节 Hysys传热单元模型
• 换热器（Heat Exchanger） – 常规的一股热流与一股冷流的热量交换 • LNG Heat Exchanger – 多股冷流与热流的集中热量交换 • 冷却器/加热器（Cooler/Heater） – 以加热或者冷却工艺物流为目的的热量交换，仅计算 所需热负荷 • 空气冷却器（Air Cooler） – 以空气为冷却介质的热量交换，可计算所需空气量 • 火焰加热炉（加热炉）（Fired Heater (Furnace)） – 可用于计算物料加热或焚烧所需空气量、尾气质量等
二、管壳式换热器的结构
◆管壳式换热器流体的流程
一种流体走管内、称为管程，另一种流体走管外、称为壳程。 管内流体从换热管一端流向另一端一次，称为一程；对U形管换热器， 管内流体从换热管一端经过U形弯曲段流向另一端一次，称为两程.
第5章两自由度系统的振动
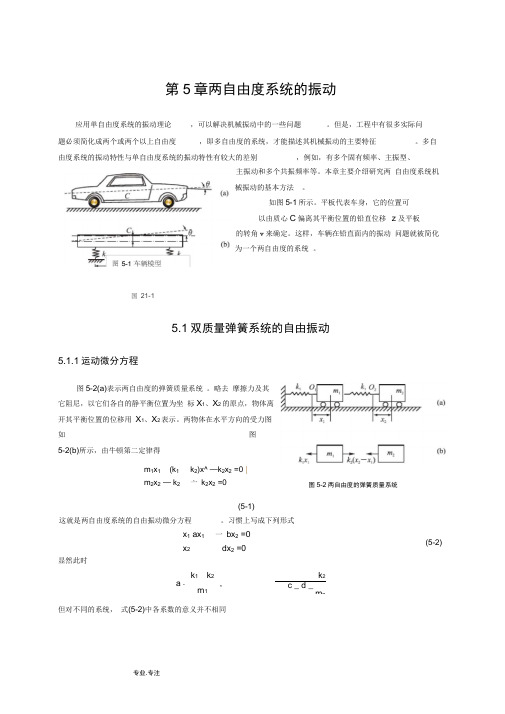
第5章两自由度系统的振动应用单自由度系统的振动理论 ，可以解决机械振动中的一些问题。
但是，工程中有很多实际问题必须简化成两个或两个以上自由度，即多自由度的系统，才能描述其机械振动的主要特征。
多自由度系统的振动特性与单自由度系统的振动特性有较大的差别 ，例如，有多个固有频率、主振型、主振动和多个共振频率等。
本章主要介绍研究两 自由度系统机械振动的基本方法 。
如图5-1所示。
平板代表车身，它的位置可 以由质心C 偏离其平衡位置的铅直位移 z 及平板的转角v 来确定。
这样，车辆在铅直面内的振动 问题就被简化为一个两自由度的系统 。
国 21-15.1双质量弹簧系统的自由振动5.1.1运动微分方程图5-2(a)表示两自由度的弹簧质量系统 。
略去 摩擦力及其它阻尼，以它们各自的静平衡位置为坐 标X 1、X 2的原点，物体离开其平衡位置的位移用 X 1、X 2表示。
两物体在水平方向的受力图如图5-2(b)所示，由牛顿第二定律得m 1x 1 (k 1k 2)x^ —k 2x 2 =0 |m 2x 2 — k 2 亠 k 2x 2 =0(5-1)显然此时k 1 k 2 a -,m 1k 2c _d _m 2但对不同的系统， 式(5-2)中各系数的意义并不相同这就是两自由度系统的自由振动微分方程。
习惯上写成下列形式 x 1 ax 1x 2 一 bx 2 =0dx 2 =0(5-2)图5-2两自由度的弹簧质量系统(5-7)由于式(5-7)确定的p 2的两个正实根仅取决于系统本身的物理性质，与运动的初始条件无关，因此p 称为系统的固有频率。
较小的一个称为第一阶固有频率，较大的一个称为第二阶固有频率5.2.2 主振型将固有频率P 1和P 2分别代入式(5-5)的任一式，可得到对应于它们的振幅比5.1.2固有频率和主振型根据微分方程的理论，设方程(5-2)的解，即两自由度无阻尼自由振动系统的解为 x^ A 1 sin( pt亠二)x 2 = A 2 sin( pt 亠：：£)(5-3)或写成以下的矩阵形式X 1A 1T网 n(pt+ot)(5-4)X 2将式(5-4)代入式(5-2)，可得代数齐次方程组-b-p _| !.A 2(5-5)保证式(5-5)具有非零解的充分必要条件是式(5-5)的系数行列式等于零，即展开后为纠 p 2)=-b d - p 2p 4 -(a d)p 2 ad -be =0(5-6)式(5-6)唯一确定了频率p 满足的条件，通常称为频率分程或特征方程。
多自由度自由振动
2
486 EI
20
3m
例：求图示体系对称振动情况下的频率。 m/2 1 m EI
m m EI 3m m
1
0.25 2 1 0.875
M1
0.5 1
3m
EI 3m
M2
4.5 1.6875 1.125 1 11 0 22 4.5 12 21 M1 , M1 相乘:11 EI EI EI EI 4. m ) ( 4.5 m )2 4(1 3 )m m m 1 ( 11m( 5 22 .6875) 11m1 1.22 2 ) 2 4 (4.51.687521.1252 )2 2 11 22 12 1 1 0相乘 6875 1 1122 MEI 2:1 1.6875( 2 M ,22 22 2 0 2 2 M 10 M2 EI 0 1 M 2 ,.M10相乘或M1 ，M 2 相乘.596 EI , 1 0.943 EI 2 8125 / EI m 0 3 1 2 1 m m 1 2 2 1. /1.125 125m EI 12 21 EI
k21=－k2 ,
k22=k2 ,
k12=－k2
12
3 5 k k 0.38197 2 m m k 2 3 5 k 2 2.61803 2 m m
21
22
2
1 0.61803 2 1.61803
k k
m m
9
求振型： Y11 ω1→第一主振型：
Y21
k 1 k12 2 2k 0.38197 1.618 k k11 1 m1
§10-5 多自由度体系的自由振动
工程中的结构有些可简化为单自由度体系分析 单层工业厂房 水塔 有些不能作为单自由度体系分析，需简化为多自由度体系 进行分析 多层房屋、高层建筑 不等高厂房排架和块式基础
486 EI
20
3m
例：求图示体系对称振动情况下的频率。 m/2 1 m EI
m m EI 3m m
1
0.25 2 1 0.875
M1
0.5 1
3m
EI 3m
M2
4.5 1.6875 1.125 1 11 0 22 4.5 12 21 M1 , M1 相乘:11 EI EI EI EI 4. m ) ( 4.5 m )2 4(1 3 )m m m 1 ( 11m( 5 22 .6875) 11m1 1.22 2 ) 2 4 (4.51.687521.1252 )2 2 11 22 12 1 1 0相乘 6875 1 1122 MEI 2:1 1.6875( 2 M ,22 22 2 0 2 2 M 10 M2 EI 0 1 M 2 ,.M10相乘或M1 ，M 2 相乘.596 EI , 1 0.943 EI 2 8125 / EI m 0 3 1 2 1 m m 1 2 2 1. /1.125 125m EI 12 21 EI
k21=－k2 ,
k22=k2 ,
k12=－k2
12
3 5 k k 0.38197 2 m m k 2 3 5 k 2 2.61803 2 m m
21
22
2
1 0.61803 2 1.61803
k k
m m
9
求振型： Y11 ω1→第一主振型：
Y21
k 1 k12 2 2k 0.38197 1.618 k k11 1 m1
§10-5 多自由度体系的自由振动
工程中的结构有些可简化为单自由度体系分析 单层工业厂房 水塔 有些不能作为单自由度体系分析，需简化为多自由度体系 进行分析 多层房屋、高层建筑 不等高厂房排架和块式基础
理论力学 第5章 小振动
A sin( 0 t )
2. 单自由度系统的小振动
三、复摆系统的自由振动 绕不通过质心的光滑水平轴摆动的刚体
d M mgl sin I 2 d t ( 5 )
d mgl I 2 dt
2
2
M l F
转动正向 O 向外
l
*C
d 2 0 2 dt
2. 单自由度系统的小振动
例2：已知 m, OA=AB=L, 求系统微振动固有频率 解：系统的动能和势能 1 1 1 1 2 2 2 2 T J o mv c J c mv B 2 2 2 2 xc 1.5L cos , yc 0.5L sin , xB 2L cos 1 2 2 2 ~ T ( mL 6mL2 sin 2 ) k 6g 2 3 ~ V 4mgL(1 cos ) m L 2 2 1 1~ 2 ~ 2 m mL mq T m (0) q 3 2 2 1 1~ 2 ~ 2 V (q) V " (0)q k q k 4mgL 2 2
3.1 多自由度系统小振动问题（推导）
ˆ 0 ˆ A ˆ 2M K
本征值问题（求本征值 2 和本征矢量 A ）
f ( 2 ) det k m 2 0
即
k11 m11 2 k21 m21 2 ks1 ms1 2
k12 m12 2
T ——周期，每振动一次所经历的时间。 T
2
0
f —— 频率，每秒钟振动的次数， f = 1 / T 。
0 —— 固有频率，振体在2秒内振动的次数。
反映振动系统的动力学特性，只与系统本身的固有参数有关。
2. 单自由度系统的小振动
2. 单自由度系统的小振动
三、复摆系统的自由振动 绕不通过质心的光滑水平轴摆动的刚体
d M mgl sin I 2 d t ( 5 )
d mgl I 2 dt
2
2
M l F
转动正向 O 向外
l
*C
d 2 0 2 dt
2. 单自由度系统的小振动
例2：已知 m, OA=AB=L, 求系统微振动固有频率 解：系统的动能和势能 1 1 1 1 2 2 2 2 T J o mv c J c mv B 2 2 2 2 xc 1.5L cos , yc 0.5L sin , xB 2L cos 1 2 2 2 ~ T ( mL 6mL2 sin 2 ) k 6g 2 3 ~ V 4mgL(1 cos ) m L 2 2 1 1~ 2 ~ 2 m mL mq T m (0) q 3 2 2 1 1~ 2 ~ 2 V (q) V " (0)q k q k 4mgL 2 2
3.1 多自由度系统小振动问题（推导）
ˆ 0 ˆ A ˆ 2M K
本征值问题（求本征值 2 和本征矢量 A ）
f ( 2 ) det k m 2 0
即
k11 m11 2 k21 m21 2 ks1 ms1 2
k12 m12 2
T ——周期，每振动一次所经历的时间。 T
2
0
f —— 频率，每秒钟振动的次数， f = 1 / T 。
0 —— 固有频率，振体在2秒内振动的次数。
反映振动系统的动力学特性，只与系统本身的固有参数有关。
2. 单自由度系统的小振动
10第十讲：多自由度系统特征值问题求解方法(I)
k 23 k 2 2k1
k3=245MN/m
k 33 k 2 k 3 2k1 2.5k1 4.5k1
2
2015/12/7
第十讲：多自由度系统特征值问题求解方法(I) 第十讲：多自由度系统特征值问题求解方法 (I)
一、特征方程法(Characteristic Equation Method)
φ (3) 1 .000 , 1 . 247 ,
0.802
0 . 555
T
T
节点
k3=245MN/m
频率 方程 为
k11 ω2 j m1 k21 k31
k12 k22 ω2 j m2 k32
k13 k23 0 k33 ω2 m j 3
第十讲：多自由度系统特征值问题求解方法(I) 第十讲：多自由度系统特征值问题求解方法 (I)
频率方程：
K 2 M k1 m1 2 1 k 1 1 0 1 m1 2 3 1. 5 k 1 2 0 2 m 4 . 5 1 .5 1 2 k1 0
x1 : x2 : : xn A1 : A2 : : An
(K i M ) A ( i ) 0
i 1, 2, , n
由于上述方程组的系数行列式为零，该方程是降秩的；对于没有 重根的情况，只有n-1个方程是独立的。
并不随时间而变化，也就是说在任何时刻结构的振动都保持同一形状， 整个结构就像一个单自由度结构一样在振动。这种多自由度结构按任一 自振频率 k 进行的简谐振动称为主振动，与其相应的特定振动形式称为 主振型(振型) 无阻尼自由振动的解为
(2)系统的运动方程由刚度矩阵表示 设系统的广义坐标列向量为x，则运动微分方程为 为二阶齐次方程 按微分方程理论，设齐次方程的特解为 x j A j sin(ωt θ ) j 1,2, ,n
《机械振动》张义民—第5章第9、10、11节ppt
例5.9-1 考虑图5.9-1所示系统，在系统上作用 有激励向量F(t)=[0 F0u(t)]T，u(t)为单位阶跃函数。 求在零初始条件下系统的响应。
解：系统的运动微分方程
1 m 0
0 2
q1 q2
k
2 1
1 q1
2
q2
0
F0u
t
为了用振型分析方法求解，
首先要解特征值问题，得
N t uTF t
F0 m
0.627963 0.325057
u
t
将上式代入方程(5.9-14)，得
1t
0.627963
F0 1
m 1
t 0
u
sin
1
t
d
0.62796312F0 m 1 cos1t
2t 0.325057
F0 1
m 2
t 0
u
sin
2
t
d
0.325057
F0
22
m
F0 1
m 2
t 0
sin
sin
1
t
d
0.325057
F0
22
m
sin
t
2
sin
2t
1
1
2
22
最后，得
q1t
F0 m
0.455295112
sin
t
1
sin
1t
1
1
2
12
0.122009
1
22
sin
t
2
sin
2t
1
1
2
22
q2t
F0 m
0.621945
第5章 多自由度系统振动的运动微分方程
解：系统具有一个
第2页 共20页
2010/9/5 21:47
第5章 多自由度系统振动的运动微分方程
题4-2图
用瞬心法求 ：
/gchzhd/xlxt/class/ch4.htm
自由度，选 为广 义坐标。 半圆柱体在任意位 置的动能为：
故 系统具有理想约束，重力的元功为
图中：kx、m 应反向。方程应为
4-9 为了使结构隔离机器产生的振动，将机器安装在一很大的机座上，机座由弹簧支承，如题4-9图所 示。试求机座在图示平面内的运动方程。
第13页 共20页
2010/9/5 21:47
第5章 多自由度系统振动的运动微分方程
/gchzhd/xlxt/class/ch4.htm
(h) 与运动方程
(i) 两端简支的梁，显然是满足边界条件式(h)的。
4-7 应用拉格朗日方程导出题4-7图所示系统的运动微分方程。
第10页 共20页
题4-7图
2010/9/5 21:47
第5章 多自由度系统振动的运动微分方程
/gchzhd/xlxt/class/ch4.htm
质量矩阵
刚度矩阵 位移列阵 4-8 在地震研究中，建筑物可简化为支承在两弹簧上的质量为m的刚体，其中直线弹簧的弹性系数为k，扭 转弹簧的弹性系数为kT，如题4-8图所示。设IG为建筑物相对质心G的转动惯量，试利用坐标x（相对于平衡位 置的直线运动）及描述建筑物转动的坐标q，求出运动方程。
（b）
运动的分离体图如图（b）所示。 地震中可设q为微小角度，因此
应用动能定理的微分形式
等式两边同除 ，
，等式两边同除 故微分方程为
若为小摆动
，
动的微分方程为
① ，并略去二阶以上微量，上述非线性微分方程可线性化，系统微摆
第2页 共20页
2010/9/5 21:47
第5章 多自由度系统振动的运动微分方程
题4-2图
用瞬心法求 ：
/gchzhd/xlxt/class/ch4.htm
自由度，选 为广 义坐标。 半圆柱体在任意位 置的动能为：
故 系统具有理想约束，重力的元功为
图中：kx、m 应反向。方程应为
4-9 为了使结构隔离机器产生的振动，将机器安装在一很大的机座上，机座由弹簧支承，如题4-9图所 示。试求机座在图示平面内的运动方程。
第13页 共20页
2010/9/5 21:47
第5章 多自由度系统振动的运动微分方程
/gchzhd/xlxt/class/ch4.htm
(h) 与运动方程
(i) 两端简支的梁，显然是满足边界条件式(h)的。
4-7 应用拉格朗日方程导出题4-7图所示系统的运动微分方程。
第10页 共20页
题4-7图
2010/9/5 21:47
第5章 多自由度系统振动的运动微分方程
/gchzhd/xlxt/class/ch4.htm
质量矩阵
刚度矩阵 位移列阵 4-8 在地震研究中，建筑物可简化为支承在两弹簧上的质量为m的刚体，其中直线弹簧的弹性系数为k，扭 转弹簧的弹性系数为kT，如题4-8图所示。设IG为建筑物相对质心G的转动惯量，试利用坐标x（相对于平衡位 置的直线运动）及描述建筑物转动的坐标q，求出运动方程。
（b）
运动的分离体图如图（b）所示。 地震中可设q为微小角度，因此
应用动能定理的微分形式
等式两边同除 ，
，等式两边同除 故微分方程为
若为小摆动
，
动的微分方程为
① ，并略去二阶以上微量，上述非线性微分方程可线性化，系统微摆