解读高斯正十七边形的作法(下)
正十七边形作图

1. 如圖, 以 O 為圓心作圓,過 O 作直徑 AC; 2. 過 O 作 AC 的垂線,交圓於 B; 3. 在 OB、OC 上 分別 截 取 I、D 使 得 OI = 1 1 OA, OD= OA; 4 16 4. 以 D 為 圓 心, DI 為 半 徑 作 圓,分 別 交 OA、OC 於 W1 , W2 ; 5. 以 W1 為 圓 心, W1 I 為 半 徑 作 弧,交 W1 A 於 E1 ; 6. 以 W2 為 圓 心, W2 I 為 半 徑 作 弧,交 W1 A 於 E3 ; P5
m
4. 在邊數不超過 100 的正多邊形中,僅用尺規 作 圖 的 有 24 個 。 它 們 分別 是: 3, 4, 5, 6, 8, 10, 12, 15, 16, 17, 20, 24, 30, 32, 34, 40, 48, 51, 60, 64, 68, 80, 85, 96 邊形。 1
4.3
+
B P4
+ +
P3 P2
+
P7
+
P1 K P8 C P9
+ + + + + + + P11 + P12 + + +
I
+
N5 F
+
O E
N3
+
A
P16
P10
P15
+
P14
P13
3
4.5
正 十 七 邊 形 作 圖 :方法(三 )
1. 如圖, 以 O 為圓心作圓,作兩條彼此正交的直徑 AB 和 CD; 2. 過 A 與 D 分別作切線交於 S; 1 3. 在 AS 上取點 E 使得 AE = AS ; 4 4. 以 E 為圓心, OE 為半徑,作弧交 AS 於 F, F’; 5. 以 F 為圓心, OF 為半徑,作弧交 AS 於 H; 6. 以 F’ 為圓心, OF’ 為半徑,作弧交 AS 於 H’; 7. 過 H 作 AH 的垂線交 OC 的延線於 T; 8. 延長 HT 至 Q, 使得 TQ = AH’; 9. 以 BQ 為直徑,作圓交 CT 於 M; 10. 作 OM 的中垂線, 交圓於 P; 11. 以 P 為圓心, PC 為半徑,在圓周上靠 B 的一邊截取 P1 點; 12. 從 P1 出發在圓周上以 P P1 為半徑截取 P2 , P3 , · · · , P15 作為正十七邊形的各頂點。 B
高斯正十七边形原理

高斯正十七边形原理嘿,朋友们!今天咱来聊聊高斯正十七边形原理。
你说这高斯正十七边形,那可真是数学里的一颗璀璨明珠啊!想象一下,就好像是在数学的大花园里,正十七边形就是那朵最特别、最耀眼的花。
咱平常看到的图形,什么三角形、四边形,那都太常见了。
可这正十七边形,它可不一样。
它就像是一个神秘的密码,等待着我们去解开。
高斯啊,那可是个超级厉害的数学家。
他就像是一个神奇的魔法师,轻轻挥动手中的魔法棒,就把这复杂无比的正十七边形给搞定了。
你说这神奇不神奇?咱普通人可能连想都不敢想能画出正十七边形,可高斯就能做到。
这就好像是别人都还在山脚下徘徊,高斯一下子就登上了山顶,看到了别人看不到的风景。
那这正十七边形原理到底是啥呢?简单来说,就是通过一些巧妙的方法和计算,能精确地画出正十七边形。
这可不是随随便便就能做到的,得有深厚的数学功底和超级厉害的头脑才行。
咱平常过日子,有时候也得有点这种钻研的精神。
遇到难题别退缩,就像高斯面对正十七边形一样,勇往直前,去寻找解决的办法。
你想想看,要是我们都能有高斯这种精神,那还有什么事情是做不到的呢?是不是很多困难都会迎刃而解呢?这高斯正十七边形原理啊,还告诉我们一个道理,那就是别小看任何一个看似不可能的事情。
也许一开始觉得很难,觉得根本没法完成,但只要我们肯下功夫,说不定就能创造奇迹呢!就像高斯,他当初要是觉得正十七边形太难了,就放弃了,那我们现在还能知道这个神奇的原理吗?肯定不能啊!所以啊,朋友们,让我们向高斯学习,向这神秘又美妙的正十七边形原理致敬!在生活中遇到困难时,就想想高斯和他的正十七边形,告诉自己:只要努力,没有什么是不可能的!这就是我想说的,大家觉得有没有道理呢?原创不易,请尊重原创,谢谢!。
高斯17边形原理

高斯17边形原理哎呀,这可真是个有趣的题目。
高斯17边形原理,听起来就挺高大上的,不过别担心,咱们今天就用大白话聊聊这个事儿,就像咱们平时聊天那样。
记得那是一个阳光明媚的下午,我正坐在公园的长椅上,手里拿着一本数学书,心里想着这周末的数学考试。
突然,我的视线被一群小孩儿吸引了,他们在草地上跑来跑去,手里拿着彩色的粉笔,画着各种形状。
我看着他们画的圆圈、三角形、正方形,突然就想到了高斯17边形原理。
这原理是说,用直尺和圆规,你只能画出正多边形,而且这些多边形的边数必须是2的幂次方加1。
比如,3边的三角形,5边的五边形,还有我们今天的主角,17边形。
我当时就想,这帮小孩儿要是知道他们在玩的粉笔游戏,其实和数学大师高斯的发现有联系,他们会怎么想呢?我猜他们可能会觉得这太酷了,或者干脆就是一头雾水。
不过,这正是数学的魅力所在,它无处不在,却又常常被我们忽视。
我看着他们画的17边形,虽然不是很规则,但孩子们的笑声和快乐让我意识到,数学不仅仅是书本上的公式和定理,它也可以是生活中的快乐和创造力。
我甚至开始想象,如果高斯本人看到这一幕,他会不会也和我一样,觉得这场景既温馨又有趣呢?我继续坐在长椅上,看着孩子们的游戏,心里却在想,这个17边形原理,虽然听起来很复杂,但其实它就像是生活中的一个小插曲,不经意间就出现在我们眼前。
就像这些孩子们,他们可能并不知道他们正在画的是一个数学上的伟大发现,但他们的纯真和快乐,却让这个原理变得生动起来。
最后,太阳慢慢下山了,孩子们也陆续被家长叫回家。
我合上书,心里想着,今天的数学学习,似乎比以往任何时候都要轻松愉快。
高斯17边形原理,不再是一个冷冰冰的数学概念,而是变成了我记忆中一个温馨的画面,和孩子们的笑声一起,留在了那个阳光明媚的下午。
所以你看,数学其实也可以很有趣,不是吗?就像高斯17边形原理,它不仅仅是一个数学原理,更是生活中的一个小故事,让我们在忙碌的生活中,偶尔也能发现数学的美。
GAUSS与正十七边形

GAUSS与正十七边形用直尺和圆规作出圆内接正七、正九、正十一、正十三、正十七边形, 是从古希腊以来两千多年悬而未决的著名数学难题; 它困扰了许多著名的数学家,有的甚至为之付出终身的努力,却毫无所获. 但是,此难题却被18岁的高斯在1796年3月30日功克.高斯是18~19世纪最伟大的数学家, 近代数学的奠基人之一. 他被称为〝数学王子〞, 〝数学巨人〞. 假设说世界上有神童的话, 那么高斯就是其中的一位. 听说他三岁就发现了他父亲算帐时出现的错误, 10岁时已表现出超群的数学思想才干.有一次,教员出了一道题: 把1到100的整数全部加起来. 其他同窗都拿起笔来一个一个地加, 高斯却坐在那一动也不动. 教员走到跟前问他为什么不做, 他却立刻报出了答案: 5050. 他的做法是: 把1和100相加得101, 2和99相加也是101, 3和97相加还是101; 如此下去, 共有50个101. 因此, 得数为101×50 = 5050. 教员慨叹地说〝他曾经超越我了, 我没有什么可以教他的了〞.15岁时, 高斯进入了卡罗琳学院, 学习了牛顿, 拉格郎日, 欧拉等人的著作, 很快掌握了微积分实际.18岁时, 高斯进入哥廷根大学. 在一次偶然的阅读中, 他知道了用直尺和圆规作出圆内接正七边形的难题. 这使他十分着迷, 并决计要功克它. 他首先查找出先人的作图方法, 细心研讨他们失败的缘由, 经过半年多的努力, 他终于作出了正七边形; 接着, 正九、正十一、正十三边形都被他逐一克制. 没多久, 正十七边形也被他功克.面对第一次取得的成功, 高斯异常兴奋, 决计把自己的终身献给数学. 1801年, 他宣布了<<算术研讨>>,论述了数论和初等代数的一些效果. 高斯对数学的研讨触及很多方面,除了在复变函数\\统计数学\\椭圆函数论上有突出贡献外, 他在向量剖析\\正态散布的正轨曲线\\质数定理的验算研讨上也取得了效果.在高斯逝世后, 哥廷根大学为他建造了一个以正十七边形棱柱为底座的纪念像, 以纪念他终身中的第一个严重发现.。
正十七边形尺规作图

=24sinacosacos2acos4acos8a
因sina不等于0,两边除sina有: 16cosacos2acos4acos8a=-1
又由2cosacos2a=cosa+cos3a等,有
2(cosa+cos2a+…+cos8a)=-1 注意到 cos15a=cos2a,cos12a=cos5a,
——设有圆O求作内接正十七边 形
设有圆O,要求ቤተ መጻሕፍቲ ባይዱ内接正十七边形。
第1步:作直径AP。 第2步:作半径OB⊥OP。
第3步:在半径OB上取点C,使得OC为四分 之一OB,连接CP。
第4步:在半径OP上取点D,使 得∠OCD为四分之一∠OCP。 第5步:作角∠ECD=π/4,射线CE交半径 OA于点E。 第6步:以EP为直径作圆,交半径OB于K。 第7步:以D为圆心,DK为半径作圆,交 半径OP于Q。 第8步:过Q作射线垂直于半径OP,交圆O于 点R。 第9步:以弧PR在圆上顺次截取,得各个分点, 分圆O为17等份。 第10步:依次连接就得到内切于圆O的正十七 边形。
令 x=cosa+cos2a+cos4a+cos8a
y=cos3a+cos5a+cos6a+cos7a 有: x+y=-1/2
正十七边形的尺规作图存在之证明
又 xy=(cosa+cos2a+cos4a+cos8a)(cos3a+cos5a+cos6a+cos7a)
=1/2(cos2a+cos4a+cos4a+cos6a+…+cosa+cos15a) 经计算知xy=-1
可求cosa之表达式,它是数的加减乘除平方根的组合. 故正17边形可用尺规作出。
解读“数学王子”高斯正十七边形的作法(上)

解读“数学王子”高斯正十七边形的作法江苏省泰州市朱庄中学曹开清225300一、高斯的传奇故事高斯(Carl Friedrich Gauss 1777.4.30~1855.2.23),德国数学家、物理学家、天文学家。
有一天,年幼的高斯在一旁看著作水泥工厂工头的父亲计算工人们的周薪。
父亲算了好一会儿,终于将结果算出来了。
可是万万没想到,他身边传来幼嫩的童音说:“爸爸,你算错了,总数应该是……”父亲感到很惊异,赶忙再算一遍,结果证实高斯的答案是对的。
这时的高斯只有3岁!高斯上小学了,教他们数学的老师布特勒(Buttner)是一个态度恶劣的人,他讲课时从不考虑学生的接受能力,有时还用鞭子惩罚学生。
有一天,布德勒让全班学生计算1+2+3+4+5+……+98+99+100=?的总和,并且威胁说:“谁算不出来,就不准回家吃饭!”布德勒说完,就坐在一旁独自看起小说来,因为他认为,做这样一道题目是需要些时间的。
小朋友们开始计算:“1 + 2 =3,3+3=6,6+4=10,……”数越来越大,计算越来越困难。
但是不久,高斯就拿着写着解答的小石板走到布德勒的身边。
高斯说:“老师,我做完了,你看对不对?“做完了?这么快就做完了?肯定是胡乱做的!”布德勒连头都没抬,挥挥手说:“错了,错了!回去再算!”高斯站着不走,把小石板往前伸了伸说:“我这个答案是对的。
”布德勒抬头一看,大吃一惊。
小石板上写着5050,一点也没有错!高斯的算法是1 +2 +3+……+98+99+100100+99+98+……+3+2+1101+101+101+……+101+101+101=101×100=1010010100÷2=5050高斯并不知道,他用的这种方法,其实就是古代数学家经过长期努力才找出来的求等差数列和的方法,那时他才八岁!1796年的一天,德国哥廷根大学。
高斯吃完晚饭,开始做导师给他单独布置的三道数学题。
前两道题他不费吹灰之力就做了出来了。
正十七边形作法

正十七边形作法
正十七边形是几何图形的一个特殊类型,它是由十七条相等的线段组成的,具有十七个角和十七个边,所以它被称为正十七边形。
由于其外形美丽,受到了艺术家和几何学家的青睐,它出现在许多艺术品,如十九世纪英国著名画家弗兰克拉特勒的《正十七边形》中。
正十七边形的历史可以追溯到古代希腊几何学家,他们发现了一些基础几何知识,其中之一就是正十七边形,而创造出这种图形的人则首先是希腊几何学家厄塞尔罗斯(Eureleos),他展示了这种图形
最早的形式,也就是正十七边形。
正十七边形的制作可以分为三个步骤。
首先,画一个圆,圆心到圆周上任意点A的距离为R,其次,画一个外接圆,圆心到A的距离为2R,同时画一个8R的小圆,圆心到A的距离为21R,然后,以小
圆为半径画一个正多边形,十七边的话就会得到一个正十七边形。
正十七边形的图形具有着不可复制的特点,这是由于它具有特殊的构造,也就是说它的角度和边长是以一定的数量和比例来构成的,不可以随意更改。
正十七边形的比例规律不仅仅出现在角度和边长上,在数学上,它也有许多有趣的特性,例如它有一个主对称轴,即从图形的中心点出发,通过其所有的顶点,可以看出来它是一个非常对称的正十七边形。
正十七边形是一种美丽的几何图形,它常常被用来装饰艺术品或用作图案。
目前,正十七边形已经广泛应用于许多不同的领域,如构图、分配、交互设计等,它在空间结构和构图中也发挥着重要作用。
正十七边形作法是一种古老的设计,它不仅在几何学中具有重要意义,而且在许多其他的领域,例如装饰、建筑等也有重要的地位,它的存在也给人们带来了视觉上的美感,使人们在欣赏这种艺术性的几何结构的同时,也感受到了几何的精确性和完美的美学体验。
解读“数学王子”高斯正十七边形的作法(下)
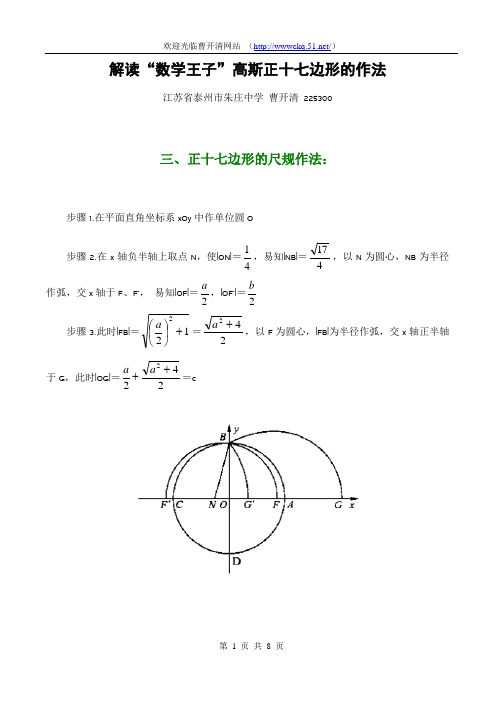
解读“数学王子”高斯正十七边形的作法江苏省泰州市朱庄中学 曹开清 225300三、正十七边形的尺规作法:步骤1.在平面直角坐标系xOy 中作单位圆O步骤2.在x 轴负半轴上取点N ,使|ON|=41,易知|NB|=417,以N 为圆心,NB 为半径作弧,交x 轴于F 、F’, 易知|OF|=2a ,|OF’|=2b 步骤3.此时|FB|=122+⎪⎭⎫ ⎝⎛a =242+a ,以F 为圆心,|FB|为半径作弧,交x 轴正半轴于G ,此时|OG|=2422++a a =c步骤 4.类似地,|F’B|=122+⎪⎭⎫ ⎝⎛b =242+b ,以F’为圆心,|F’B|为半径作弧,交x轴正半轴于点G’,此时|OG’|=2422++b b =e步骤5.以|CG’|为直径作圆,交y 轴正半轴于点H ,易知OH 2=1·e步骤 6.以H 为圆心,21|OG|为半径作弧,交x 轴正半轴于点K ,则有|OK|=222OH OG -⎪⎭⎫ ⎝⎛=222e c -⎪⎭⎫ ⎝⎛=242e c - 步骤7.以K 为圆心,|KH|=21|OG|为半径作弧,交x 轴正半轴于点L ,则|OL|=242e c c -+ 步骤8.取OL 的中点M ,则|OM|=442e c c -+= cos 172π 步骤9.过点M 作y 轴的并行线交单位圆O 于两点A 2和A 17,则Α为正十七边形的第一个顶点,A 2为第二个顶点,A 17为第十七个顶点,从而作出正十七边形。
四、正十七边形边长的表达式在上面得到的一系列等式:a =2171+-,b =2171-- ,c =242++a a , e =242++b b , cos 172π=442e c c -+中 依次求出c =417234171-++-e =417234171++-- 从而求出cos172π的其它表达式:可以验证,它们在数值上是相等的,其中以第二个表达式为最优。
在单位圆中,根据余弦定理,得正十七边形的边长为172cos 22π-,将cos 172π的值代入,即可求出正十七边形的边长。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
e =。
从而求出
cos 的其它表达式:
可以验证,它们在数值上是相等的,其中以第二个表达式为最优。
在单位圆中,根据余弦定理,得正十七边形的边长为 ,将cos 的值代入,即可求出正十七边形的边长。
五、正十七边形的另一种作法
步骤1:
作圆O 的两条互相垂直的直径AC 、BD ;
在OB 上截取OE =14OB ,连接EΑ;
作∠FEO =14∠ΑEO 交OΑ于点F ;
作∠GEF =,边EG 交CO 于点G 。
步骤2:
以GΑ为直径作圆O’,交OB 于点H ;
再以点F 为圆心,经过点H 作圆F ,交AC 于N4和N6两点。
步骤3:
过N4作AC 的垂线交圆O 于点P4,
过G6作AC 的垂线交圆O 于点P6,
那么以圆O 为基准圆,Α为正十七边形的第一个顶点P1,
P4为第四个顶点,P6为第六个顶点。
以12弧P4P6所对的弦为半径,即可在圆O 上截出正十七边形的所有顶点。
注一:
7、9、11边形却未能作出。
让后来数学家为难的是,欧几里德之后的2000多年中,有关正多边形作图仍停留在欧几里德的水平上,未能向前迈进一步。
因此,我们可以想象得到,当1796年年仅19
不过,高斯的结果多少显得有些奇怪。
他没有完成正七边形或正九边形等的作图,却偏偏隔下中间这一些直接完成了正十七边形。
为什么第一个新作出的正多边形是正十七边形而不是正七、九边形呢?在高斯的伟大发现之后,问题仍然存在:正七边形或正九边形等是否可尺规完成?或者更清楚地阐述这个问题:正多边形的边数具有什么特征时,它才能用尺规作出?
在经过继续研究后,高斯最终在1801年对整个问题给出了一个完美的解答。
高斯指出,只用直尺和圆规作圆内接正n 边形,当n 满足如下特征之一时方可作出:
1) n =2m ;〔其中m 为正整数〕
2) 边数n 为质数且形如 n =22t +1〔其中t 为非负整数〕,即n 为质数的费马( Fermat )
数。
3) 边数n具有n=2m p1p2p3……p k的形式〔其中p1,p2,p3,……,p k为互不相同的费马质数〕。
由高斯的结论,具有质数n条边的正多边形可用尺规作出的必要条件是n为费马数。
由于我们目前发现的费马质数只有前五个费马数,因此,边数是费马数的正多边形中,只有正3、5、17、257、65537边形可用尺规作出〔除非你能发现另一个费马质数〕。
进一步,可以作出的有奇数条边的正多边形也就只能通过这五个数组合而得到,这样的组合数只有31种。
而边数为偶数的可尺规作出的正多边形,边数或是2的任意次正整数幂或与这31个数经过组合而得到。
注二:
黎西罗给出了正257边形的尺规作法,写满了整整80页纸。
盖尔梅斯给出了正65537边形的尺规作法,此手稿整整装满了一只手提箱,现存于德国哥廷根大学。
这是有史以来最繁琐的尺规作图。
