近圆轨道遥感卫星星下点轨迹的计算
(西工大)航天器飞行力学7

对于给定仰角值 E,覆盖圈上星下点 B相对P点 的经纬度关系可由图7.2球面三角形 得出(即式7.3)
PN P B
co s ψ − sin ϕ sin L θ = arcco s[ ] co s ϕ co s L
ψ
(7.5) 角是卫星可见覆盖圈的角半径,它的二倍是
卫星的最大可观弧段,决定于卫星高度和仰角。
真近点角由求解开普勒方程得出。
卫星的地理经度等于卫星赤经与格林尼治的恒 星时角之差,即
λ = α − [G 0 + ω e (t − t 0 )]
G0 为起始时刻格林威治的恒星时角;
ω e 为地球自旋转速。
卫星的地心纬度与地理纬度的关系,见图7.1。地球为 椭球模型。扁率为
αe
2
地心纬度和地理纬度的转换式为
如图7.2所示。在平面 OPS内,斜距和仰角为:
ρ = [ R + r − 2rRe cosψ ]
2 e 2
2 e 2
1 2
E = arccos[r sinψ / ( R + r − 2rRe cosψ ) ]
1 2
式中
ψ
角为卫星星下点与观察点之间的地心夹角。
由图7.2的球面三角形
P N PB
,有
(7.13)
7ቤተ መጻሕፍቲ ባይዱ5 发射窗口
根据空间应用要求和飞行任务,在优选卫星的预定轨道 和运载火箭的弹道之后,卫星制导设计的第一项任务是 制定发射窗口。
定义:满足特定飞行任务的卫星发射时刻的集合。 是一个发射时间区间,即发射的日期、时刻及其时 间区间,在该区间内发射卫星能满足飞行任务的若干特 定要求。
航天器发射的三要素是:发射场位置、发射方位角和发 射时刻。 航天器轨道的高度、椭圆度和倾角,与发射时刻无关, 但轨道平面在空间的方位不仅与发射方位角有关,还决 定于航天器脱离地球表面的时刻。
卫星轨道计算课件

04
道的定分 析
哈里斯方法
哈里斯方法是一种用于分析非线性动力系统稳定性的数值 方法。在卫星轨道稳定性分析中,哈里斯方法可用于研究 卫星轨道在受到扰动后的稳定性。
该方法通过计算系统的奇异值来确定系统的稳定性,奇异 值越小,系统越稳定。通过比较不同扰动下的奇异值,可 以评估卫星轨道的稳定性。
李雅普诺夫指数方法
优点 适用于各种复杂轨道和扰动,计算速度快。
缺点 需要选择合适的积分方法和步长,对初值敏感。
03
道的力学型
万有引力
万有引力是影响卫星轨道的主要因素 之一,它使得卫星受到地球的吸引, 产生向心加速度,维持卫星在轨道上 运行。
万有引力的大小与两个物体的质量成 正比,与它们之间的距离的平方成反 比,遵循万有引力定律。
数值模拟方法
数值模拟方法是一种通过数值计算来 模拟动态系统行为的方法。在卫星轨 道稳定性分析中,数值模拟方法可用 于模拟卫星轨道在受到扰动后的演化 过程。
VS
通过数值模拟,可以观察卫星轨道在 不同扰动下的变化情况,从而评估卫 星轨道的稳定性。数值模拟方法还可 以用于预测卫星轨道未来的演化趋势, 为卫星轨道设计和优化提供参考。
优点
直观易懂,适用于简单轨 道分析。
缺点
对于复杂轨道和实时计算 不太适用。
动力法
定义
动力法考虑地球引力、太阳辐射 压和其他天体引力扰动等动力因
素,模拟卫星运动。
优点
能够处理复杂扰动,适用于长期轨 道预测。
缺点
计算量大,需要高精度数值方法。
数值法
1 2 3
定义 数值法采用数值积分方法,对卫星运动方程进行 积分求解。
详细描述
无线电观测是一种常用的卫星轨道观测方法,通过接收卫星发射的无线电信号,测量卫星轨道参数,具有全天候、 全天时的特点,但测量精度受信号质量影响较大。
卫星的近地点和远地点速度公式

卫星的近地点和远地点速度公式
1. 卫星运动的基本原理。
- 根据开普勒第二定律,卫星与中心天体的连线在相等的时间内扫过相等的面积。
设卫星在近地点的速度为v_1,近地点到中心天体的距离为r_1;在远地点的速度为v_2,远地点到中心天体的距离为r_2。
- 由于卫星在运动过程中机械能守恒,其机械能E = (1)/(2)mv^2-(GMm)/(r)(其中m为卫星质量,v为卫星速度,r为卫星到中心天体的距离,G为引力常量,M 为中心天体质量)是一个常量。
2. 近地点和远地点速度公式推导。
- 根据开普勒第二定律可得v_1r_1 = v_2r_2,即v_2=(r_1)/(r_2)v_1。
- 由机械能守恒定律E_1 = E_2,(1)/(2)mv_1^2-(GMm)/(r_1)=(1)/(2)mv_2^2-(GMm)/(r_2)。
- 将v_2=(r_1)/(r_2)v_1代入机械能守恒方程(1)/(2)mv_1^2-
(GMm)/(r_1)=(1)/(2)m((r_1)/(r_2)v_1)^2-(GMm)/(r_2)。
- 化简可得v_1=√(frac{2GM r_2){(r_1 + r_2)r_1}},v_2=√(frac{2GM r_1){(r_1 + r_2)r_2}}。
卫星星下点轨迹计算

卫星星下点轨迹计算1. 前言随着卫星技术的不断发展与应用,卫星星下点轨迹计算越来越重要。
卫星星下点轨迹计算可以帮助我们预测卫星通过的起点、终点以及轨迹。
这对于卫星通信、卫星遥感、导航等应用非常有用。
下面,我们会详细介绍卫星星下点轨迹计算的原理和方法。
2. 卫星星下点轨迹计算的原理卫星星下点轨迹计算就是把卫星的轨道经纬度转化为地面的经纬度。
卫星的轨道是一条椭圆,而卫星的星下点(也就是卫星从地面看到的影子)则在地球的球面上。
因此,我们需要用到球面三角形学来求出卫星星下点的经纬度。
球面三角形学是解决球面上三角形的形状和位置的科学。
3. 卫星星下点轨迹计算的方法3.1 坐标系转换首先,我们需要把卫星的赤道坐标系转化为地心惯性坐标系,然后再把地心惯性坐标系转化为地心地固坐标系。
3.2 椭球体转换我们还需要对卫星的轨道进行椭球体转换。
地球是一个略带扁平的椭球体,因此我们需要用到椭球坐标系来描述卫星的位置。
3.3 计算卫星坐标通过把转换后的卫星轨道信息代入文献中的卫星机轨迹计算公式,我们可以得到任意时刻卫星的坐标。
3.4 计算卫星星下点坐标最后一步是计算卫星星下点的经纬度。
这可以通过球面三角形学中的余弦定理来完成。
根据余弦定理,我们可以通过已知的三角形边长(卫星高度、地球半径和卫星天线到卫星向地球的连线的夹角)求出三角形的角度。
利用这些角度,我们可以通过三角函数算出卫星星下点的经纬度。
4. 结论卫星星下点轨迹计算是卫星应用中的重要环节之一,可以帮助我们预测卫星的轨迹和星下点位置。
这对于卫星通信、卫星遥感、导航等应用非常重要。
通过本文的介绍,我们希望读者能够了解卫星星下点轨迹计算的原理和方法,从而更好地理解卫星应用中的相关内容。
《卫星轨道计算》课件

判据种类
包括周期性判据、频率分析判据、Lyapunov指数判据等。
判据应用
用于预测卫星轨道的变化趋势,评估卫星轨道的寿命。
卫星轨道的摄动分析
摄动定义
01
摄动是指卫星轨道受到外部因素的干扰,导致其偏离理想轨迹
的现象。
摄动分类
02
包括地球非球形摄动、大气阻力摄动、太阳辐射压摄动等。
《卫星轨道计算》ppt课件
目录
• 卫星轨道计算概述 • 卫星轨道的数学模型 • 卫星轨道的力学模型 • 卫星轨道的稳定性分析 • 卫星轨道的观测与测量 • 卫星轨道计算的应用与发展
01
卫星轨道计算概述
卫星轨道的基本概念
01
02
03
卫星轨道
指卫星在空间运行的路径 ,由地球引力、太阳辐射 压和其他天体引力作用维 持。
时间测量
通过测量卫星与地面站之间的 时间差来确定卫星位置。
雷达干涉测量
利用雷达信号干涉原理进行高 精度测量。
星间测量
利用卫星之间的信号传输和干 涉进行高精度测量。
卫星轨道的校准与修正
校准
使用已知精确的卫星轨道数据对观测 数据进行校准,以提高精度。
修正
根据观测数据和计算结果对卫星轨道 进行修正,以实现实时更新。
牛顿万有引力定律
总结词
描述了物体之间的万有引力关系,是卫星轨道计算的基础。
详细描述
牛顿万有引力定律指出任何两个物体都相互吸引,引力的大 小与两个物体的质量成正比,与它们之间的距离的平方成反 比。对于卫星轨道计算,地球对卫星的引力是决定卫星运动 轨迹的关键因素。
地球的引力扰动
总结词
卫星星下点轨迹计算

卫星星下点轨迹计算
卫星星下点轨迹计算是指通过卫星的轨道参数和地球的形状参数,计算出卫星在地球上的投影点的运动轨迹。
这个过程需要考虑到地球的自转、引力场、大气阻力等因素,因此需要进行复杂的数学模型和计算。
我们需要了解卫星的轨道参数。
卫星的轨道通常由半长轴、偏心率、轨道倾角、升交点赤经和升交点赤纬等参数来描述。
这些参数可以通过卫星的发射信息或者卫星测量数据来获取。
我们需要了解地球的形状参数。
地球并不是一个完美的球体,而是一个略带扁平的椭球体。
因此,我们需要知道地球的赤道半径和极半径,以及地球的引力场参数。
接下来,我们需要考虑地球的自转。
地球的自转会导致卫星在地球上的投影点产生运动,因此我们需要考虑地球自转的角速度和卫星的轨道倾角。
我们需要考虑大气阻力对卫星的影响。
大气阻力会导致卫星的轨道逐渐下降,因此我们需要考虑大气密度和卫星的速度等因素。
通过以上的参数和因素,我们可以建立一个复杂的数学模型来计算卫星星下点轨迹。
这个模型需要考虑到各种因素的相互作用,因此需要进行大量的计算和模拟。
同时,由于地球和卫星的运动都是三
维的,因此我们需要进行三维的计算和可视化。
卫星星下点轨迹计算在卫星导航、遥感、气象等领域都有着广泛的应用。
通过计算卫星星下点轨迹,我们可以更加准确地预测卫星的位置和运动轨迹,从而提高卫星的使用效率和精度。
2-2卫星运动轨道及卫星位置计算new.

精度
时间间隔
卫星位置计算方法
预报星历
低
2h 15min
用轨道参数来计算
后处理星历
高
插值
轨道坐标系转换为天球坐标系
• 第一步:绕X’轴顺转角度i,以使Z’轴和Z轴重合 • 第二步:绕Z轴顺转角度Ω ,以使X’轴和X轴重合
x x0 y R R i y 1 0 3 z z0 cos sin 01 R1 i 0 cos i sin i 0 sin i cos i
Es M s es sin Es
Es 0 M s Es1 M s es sin Es 0 Es 2 M s es sin Es1 Esn M s es sin Es n 1
真近点角的计算
as cos Es r cos f s as es a cos f s s cos Es es r cos Es es cos f s 1 e cos E s s 2 1 e s sin Es sin f s 1 e cos E s s
– ftp:///pub/gps/gpsdata – ftp://igs.ensg.ign.fr/pub/igs/ – ftp:///pub/product/
精密星历文件示例
区别
星历类型
获取方法 由导航电文实 时地得到 事后由第三方 提供
预报星历
• 预报星历,是通过卫星发射的含有轨道信息的导航电文传 递给用户的,用户接收机接收到这些信号,经过解码便可 获得所需要的卫星星历,所以这种星历也叫做广播星历。 • 广播星历参数:共有16个,其中包括1个参考时刻,6个对 应参考时刻的开普勒轨道根数和9个反映摄动力影响的参 数。这些参数通过GPS卫星导航电文传递给用户。每两个 小时更新一次;目前广播星历所给出卫星的点位中误差为 5-7m。
卫星轨道参数计算
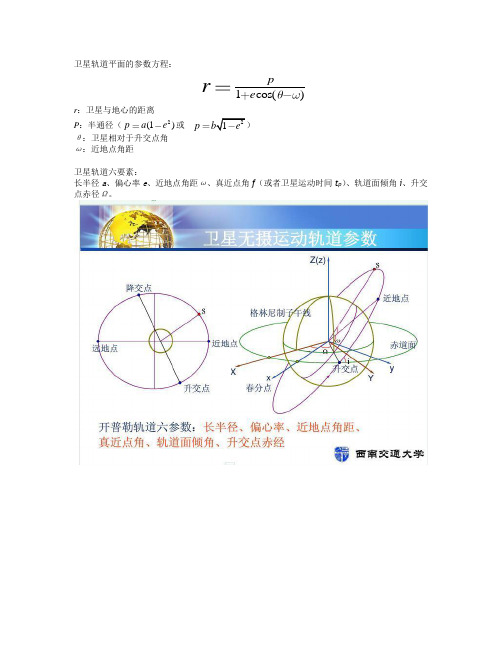
卫星轨道平面的参数方程:1cos()p e rr :卫星与地心的距离P :半通径(2(1)p a e 或21p b e ) θ:卫星相对于升交点角 ω:近地点角距卫星轨道六要素:长半径a 、偏心率e 、近地点角距ω、真近点角f (或者卫星运动时间t p )、轨道面倾角i 、升交点赤径Ω。
OXYZ─赤道惯性坐标系,X轴指向春分点T ;ON─卫星轨道的节线(即轨道平面与赤道平面的交线),N为升交点;S─卫星的位置;P─卫星轨道的近地点;f─真近点角,卫星位置相对于近地点的角距;ω─近地点幅角,近地点到升交点的角距;i─轨道倾角,卫星通过升交点时,相对于赤道平面的速度方向;Ω─升交点赤经,节线ON与X轴的夹角;e─偏心率矢量,从地心指向近地点,长度等于e;W─轨道平面法线的单位矢量,沿卫星运动方向按右旋定义,它与Z轴的夹角为i;a─半长轴;α,δ─卫星在赤道惯性坐标系的赤经、赤纬。
两个坐标系:地心轨道坐标系、赤道惯性坐标系。
地心轨道坐标系Ox0y0z0:以ee1为x0轴的单位矢量,以W为z0轴的单位矢量,y0轴的单位矢量可以由x0轴的单位矢量与z0轴的单位矢量确定,它位于轨道平面内。
赤道惯性坐标系:OXYZ,X轴指向春分点。
由地心轨道坐标系到赤道惯性坐标系的转换:1.先将地心轨道坐标绕W旋转角(-ω),旋转矩阵为R Z(-ω);2.绕节线ON旋转角(-i),旋转矩阵为R X(-i);3.最后绕Z轴旋转角(-Ω),旋转矩阵为R Z(-Ω);经过三次旋转后,地心轨道坐标系和赤道惯性坐标系重合。
在地心轨道坐标系中,卫星的位置坐标是:0 0 0cos sin 0x r f y r fz地心轨道坐标系到赤道惯性坐标系的转换关系是:000()()()cos cos sin cos sin sin cos cos cos sin sin sin cos =cos sincos cos sin sin sincos cos cos sin cos sin sin cos sin cos z x z x x y R R i R y z z i i i r f i i i i ii2sin 0cos sin()sin sin()cos(1)=sin cos()cos sin()cos 1cos sin()sin r f f f i a e f f ie ff i赤道惯性坐标系下的坐标确定后,可与r 、α、δ联系起来,关系式如下:1222()2arctan arctan(1)1cos 1cos y xz x y p a e re fe f若卫星六要素都已知,则可以解出α、δ。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Geosat and ERS21 satellite altimetry [ J ] . Journal of Geophysical Research ,1997 ,102 (B5) :10039210054.
第 18 卷第 4 期 2001 年 12 月
文章编号 :10092427X(2001) 0420257203
测绘学院学报 Journal of Institute of Surveying and Mapping
Vol . 18 No. 4 Dec. 2001
近圆轨道遥感卫星星下点轨迹的计算
张云彬 , 张永生
倾角 ; ae 为地球赤道半径 ;μ = GM 为地心引力常
数 ; J2 为二阶引力位系数 ,取
ae = 6 378 137 m
μ = 3. 986 005 ×1014 m3/ s2
J 2 = 1. 083 ×10- 3 那么 ,卫星升交点相对于经度零点的西退速率 ω′e 为
ω′e = ωe - Ω
(7)
而由地心纬度 φ′转换为大地纬度φ的公式为
tanφ =
(1
1 -
f ) 2tanφ′
(8)
式中 , f = 1/ 298. 257 为地球扁率 。令
⌒
Ω0 S = l
∠SΩ0 D = Ψ
那么 ,在球面三角形 △ΩSΩ0 中 ,根据边的余弦定
收稿日期 :2001203213 ;修回日期 :2001205220 作者简介 :张云彬 (1972 - ) ,男 ,福建福州人 ,博士生 ,主要从事航天遥感工程研究 。
2 58
测绘学院学报
2001 年
理及五元素公式 ,有
cos l = cosω′eΔt ·cos nΔt +
sinω′eΔt ·sin nΔt = sinω′eΔt ·cos nΔt
·cos i
-
-
sin l ·cosΨ
cosω′eΔt ·sin nΔt ·cos i
在球面直角三角形 △Ω0 SD 中 ,有 cos l = cosΔλ·cosφ′
⌒
度 。而卫星相对于 Ω0 的经差Δλ = Ω0 D 。
1 计算原理
设 Ω 为升交点赤经变化率 ,ωe 为地球平均自
转角速度 ,有
ωe = 7. 292 115 ×10- 5 (rad/ s)
(1)
Ω =-
3 2
J2
μ
a2ecos i a7/ 2 (1 - e2)
2
(rad/
s)
(2)
式中 , a 、e 、i 分别为卫星轨道的长半径 、偏心率和
sin l ·cosψ = sinΔλ·cosφ′
因此
sinΔλ·cosφ′= - sinω′eΔt ·cos nΔt + cosω′eΔt ·sin nΔt ·cos i
cosΔλ·cosφ′= cosω′eΔt ·cos nΔt + sinω′eΔt ·sin nΔt ·cos i
(3)
已知卫星平均运动角速度 n 可表示为
μ
n = a3/ 2
(4)
图 1 卫星在地球坐标系中的位置
在球面直角三角形 △ΩSD 中 , ∠SΩD = i , i
为已知的轨道倾角 ,所以有
⌒
⌒
sin SD = sin ΩS ·sin i
(5)
即
sinφ′= sin nin ( sin nΔt ·sin i)
Calculation of Subsatellite Track of Remote Sensing Satellite in Nearly Round Orbit ZHANG Yun2bin ,ZHANG Yong2sheng
图 3 纬度和经度方向的距离偏差与星下点纬度之间的关系
由图 3 中可以看出 ,随着纬度的增加 ,星下点 沿经度变化方向和纬度变化方向的偏差也相应地 在不同程度地增加 ,其中经向偏差略呈线性变化 , 而纬向偏差则在高纬度地区有一个较大的阶跃增 幅 ,文中的星下点算法为了保证计算精度 ,星下点
轨迹从赤道起算外推不得超过 1/ 4 圈 ,其原因正 在于此 。
交点开始逆卫星飞行方向向北外推时 , 取Δt =
- 1 , - 2 , …, - [ T/ 4 ] 。这时星下点地心纬度公式
可改为
φ′= arcsin ( - sin nΔt ·sin i)
(13)
地心经度的计算公式不变 。
地心纬度转换为大地纬度的公式由 (8) 式给
出 。如此可以计算出卫星每秒一点的星下点大地
算得 Ω = 1. 033 107 68 ×10- 6 (rad/ s) ω′e = 7. 188 804 23 ×10- 5 (rad/ s) n = 9. 314 328 65 ×10- 4 (rad/ s) T = 6 745. 72 s 计算了卫星飞行 13 圈中每秒一点的大地经、
(信息工程大学 测绘学院 , 河南 郑州 450052)
摘要 : 根据遥感卫星轨道的特点 , 提出了计算近圆轨道卫星星下点轨迹的算法 , 并对其进行了精度评估 。 结果表明这种算法是快捷和有效的 , 能够满足卫星规划阶段对轨道精度的要求 。 关 键 词 :遥感卫星 ;近圆轨道 ;星下点轨迹 中图分类号 :P228 文献标识码 :A
= - 1 , - 2 , …, - [ T/ 4 ] , 符号“[·]”表示取一个
数的整数部分 ,其代数符号与原数相同 。星下点地
心纬度和地心经度的计算公式由 (7) 和 (10) 式给
出。
已知降交点经度λ0 , 由降交点开始沿卫星飞 行方向向南外推时 ,取Δt = 1 ,2 , …, [ T/ 4 ] , 由降
经 、纬度 。降交点与升交点之间或升交点与前一圈
降交点之间的经差Δλ0 由下式算得 :
Δλ0 = π -
1 2
ω′e T
(14)
这里 ,Δt 的步长亦可取 10 s、30 s 或 60 s , 步长越
小 ,星下点轨迹越平滑 ,但计算量会显著增加 。
3 地面轨迹算例 现给定一组设计的初始轨道根数 a = 7 716 343. 89 m i = 66. 01° λ0 = 107. 010 2°
T = 2π/ n
(12)
其中 , n 为卫星的平均运动角速度 。
这样每次需先从升交点开始向北 、向南各外
推 1/ 4 圈后再转到从降交点开始向南、向北各外
推 1/ 4 圈 ,然后再从下一圈的升交点开始向北 、向
南各外推 1/ 4 圈 , …。如此一圈一圈地计算星下点
轨迹 。
已知升交点经度λ0 , 由升交点开始沿卫星飞 行方向向北外推时 , 取Δt = 1 ,2 …, [ T/ 4 ] ; 由升 交点开始逆着卫星飞行方向向南外推时 , 取Δt
5 小结 相对于从卫星轨道运动方程直接积分求解星
下点轨迹来讲 ,文中所提出的算法更加方便 、快 捷 、实用 。虽然算法本身具有一定的近似性 ,但从 精度评估的结果来看 ,它已能够较好地满足遥感 卫星规划阶段的要求 ,在轨道设计 、覆盖评估等方 面有其实际应用价值 。
参 考 文 献:
[1 ] 王任亭. 军事摄影测量卫星发展现状与应用分析 [J ] . 解放 军测绘研究所学报 ,2000 , (2) 、(3) .
于是
tanΔλ = ( - sinω′eΔt ·cos nΔt + cosω′eΔt ·
sin nΔt ·cos i) / (cosω′eΔt ·cos nΔt +
sinω′eΔt ·sin nΔt ·cos i)
(9)
t 时刻卫星经度λ为
λ = λ0 +Δλ
(10)
这里地心经度与大地经度等同 ,无须转换 。
图 1 中 , X 轴指向国际时间局 (BIH) 定义的经
度零点 。设卫星经过升交点 Ω0 的时刻为 t0 , 经度
为 λ0 。由图 1 可以看出经过Δt = t - t0 时间后升
交点西退至 Ω, 卫星到达 S , 其中 ΩΩ0 = ω′eΔt ,
⌒
⌒
ΩS = nΔt , DS = φ′,φ′为 t 时刻卫星的地心纬
纬度并依此绘制卫星地面轨迹图 。从图 2 中可以 清楚地看到卫星地面轨迹覆盖全球的详细情况 。
图 2 卫星星下点轨迹图
4 精度评估 利用目前国际航天领域优秀的系统分析软件
STK (Satellite Tool Kit) 对该星下点算法的精度进 行评估 。STK 的 HPOP ( High Precision Orbit Propa2 gator) 模块能够精确地预报卫星轨道 ,它包含了影 响地球卫星主要摄动最新的 、高精度的地球引力 模型 ,以及先进的 70 ×70 阶球谐函数展开模型 。 采用美国海军天文台的压缩星历预测日 、月的位 置 。大气阻力采用 Harris Priester 大气模型 ,考虑 了大气周日密度变化和太阳紫外线辐射流量的影
第4期
张云彬等 :近圆轨道遥感卫星星下点轨迹的计算
2 59
响 。采用了 7~8 阶 Runge2Kutta2Fehlberg 方法积 分求解卫星运动方程 。应用表明 ,由 STK/ HPOP 生成的星下点轨迹具有相当高的精度 。
文中以升交点为起点 ,沿卫星飞行方向选取 了 1/ 4 周期的卫星轨道 ,依每 10 s 一点对 STK/ HPOP 生成的数据与本文算法的计算结果进行逐 点的经纬度比较 ,得到了星下点沿纬度变化方向 和沿经度变化方向的距离偏差 (计算时取地球的 几何平均半径为 6 371 000 m) ,该偏差值与卫星纬 度之间的关系分别如图 3 (a) 、( b) 所示 。图中 ,星 下点纬向偏差的平均值为 1. 078 93 km ,偏差的均 方根差为 0. 242 78 km ; 经向偏差的平均值为 1. 672 49 km ,偏差的均方根差为 0. 876 39 km。实际 星下点位置偏差的最大值为 3. 582 22 km ,平均值 为 2. 055 36 km ,偏差的均方根差为 0. 749 78 km。
