竖曲线任意点高程计算例题
竖曲线高程计算

竖曲线高程计算(fx-4800)(1)Lbl 0:H:B:R:I:J:{L}:T=R Abs(J-I) ÷2←C=B-L←I<J=>F=1:≠=>I>J=>F=-1△△←L≦0=>{HRBIJ}:Goto 0≠=>L<B-T=>Z=0:P=I≠=>L<B=>Z=1:P=I:≠=>L<B+T=>Z=1:P=J:≠=>Z=0:P=J△△△G=H-CP+ZF(T-Abs C) ²÷2÷R▲Goto 0说明:H:变坡点高程B:变坡点里程L:线路上所求点里程I:前纵坡J:后纵坡T:竖曲线切线长竖曲线半径本程序可及计算范围(前竖曲线的终点至后竖曲线的起点),当L=0时可重新输入起算要素(H,B,R,I,J)进行下一段竖曲线和直线的高程计算。
边桩及路面以下任意厚度高程计算:变量变为:{LNM }主公式变为:G=H-N-CP+ZF(T-Abs C)²÷2÷R▲V=G+ME▲Goto 0N:路面至各施工层的厚度(m)M:中桩至边桩的距离E:路拱(路面横坡)V:左右边桩高程竖曲线高程计算(2)Lbl 1:{N }:N=1=>Goto 3:≠=>N=2=>Goto 4△←Lbl 2:{L}:T=R Abs(J-I) ÷2←C=B-L←I<J=>F=1:≠=>I>J=>F=-1△△←L<3090=>Goto 1:≠=>L<B-T=>Z=0:P=I:≠=>L<B=>Z=1:P=I:≠=>L<B+T=>Z=1:P=J:≠=>Z=0:P=J△△△G=H-CP+ZF(T-Abs C) ²÷2÷R▲Goto 1←Lbl 3:L≧3090=>H=563.532:B=3860:R=55000:I=0.025:K=4526:L=0.0175←L≧K=>H=580.157:B=4810:R=16000:I=0.0175:K=5503.582:L=-0.018←L≧K=>H=564.137:B=5700:R=10100:I=-0.018:K=6204:L=0.02089←L≧K=>H=579.599:B=6440:R=121193.615:I=0.02089:K=6676:L=0.017←L≧K=>H=589.119:B=7000:R=16000:I=0.017:K=7324:L=-0.0235←Goto 2←Lbl 4:L≧3090=>H=563.532:B=3860:R=56000:I=0.025:K=4649:L=0.0175←L≧K=>H=581.382:B=4880:R=12000:I=0.0175:K=5464.117:L=-0.021←L≧K=>H=564.162:B=5700:R=11100:I=-0.021:K=6204:L=0.0215←L≧K=>H=580.073:B=6440:R=104856.927:I=0.0215:K=6676:L=0.017←L≧K=>H=589.593:B=7000:R=16000:I=0.017:K=7324:L=-0.0235←Goto 2←。
竖曲线要素及变坡点处设计高程计算(1)

竖曲线要素及变坡点处设计高程计算(1)竖曲线要素及变坡点处设计高程计算坡度计算: ①坡度=高差坡长%150.0-67.2553804.0-1==i %220.038.1833967.02==i②竖曲线类型:当1n n i i +-为正值时,为凹型竖曲线;当1n ni i +-为负值时,为凸型竖曲线。
③由厘米坐标纸上,经过反复试坡、调坡, 根据土石方填挖大致平衡和道。
设计规范中最小坡长等设计要求最后确定出变坡点: 变坡点1桩号:67.2550+K ,高程m 9404.0- 变坡点计算①变坡点一:桩号 67.2550+K , %150.0-i 1= %220.0i 2= R=21621.62m 变坡点高程:m 9404.0- A.计算竖曲线要素:=-=1i 2i ω0.37% 此时根据规范可知:该曲线为凹形曲线竖曲线几何要素中曲线长)(m R L 80%37.021621=?=?=ω竖曲线几何要素中切线长m L T 402802===竖曲线几何要素中外距m RTE 037.062.21621240222=?==B.计算竖曲线起终点桩号竖曲线起点桩号:67.2150+K竖曲线起点高程:m 8804.0-%15.0409404.0-=?+ 竖曲线终点桩号:67.2950+K竖曲线终点高程:m 8524.0-%22.0409404.0-=?+计算设计高程由110()H H T X i =-- H=H 1±hH 1:任一点切线的高程 x :计算点到起点的距离 i 1:坡度H:任一点的设计高程曲线段内各点的设计高程: K0+220X=220-215.67=4.33m m Rxy 0004.022==切线高程:-0.8804-4.33×0.15%= -0.8869m 设计高程:-0.8869+0.0004= -0.8865m K0+240X=24.33m m Rxy 0137.022==切线高程:-0.8804-24.33×0.15%= -0.9169m 设计高程:-0.9169+0.0137= -0.9032mK0+260X=35.67m m Rxy 0294.022==切线高程:-0.8524-35.67×0.22%= -0.9309m 设计高程:-0.9309+0.0294= -0.9015m K0+280X=15.67m m Rxy 0057.022==切线高程:-0.8524-15.67×0.22%= -0.8869m 设计高程:-0.8869+0.0057= -0.8812m直线段内各点设计高程见下表:设计高程表桩号高程(m)桩号高程(m)K0+000 -0.56 +240.000 -0.9032 +20.000 -0.59 +260.000 -0.9015 +40.000 -0.62 +280.000 -0.8812 +60.000 -0.65 +300.000 -0.8361 +80.000 -0.68 +320.000 -0.7921 +100.000 -0.71 +340.000 -0.7481 +120.000 -0.74 +360.000 -0.7041 +140.000 -0.77 +380.000 -0.6601 +160.000 -0.80 +400.000 -0.6161 +170.000 -0.83 +420.000 -0.5721 +180.000 -0.86 +440.000 -0.5281 +200.000 -0.89+220.000 -0.8865。
竖曲线任意点标高计算方法

竖曲线任意点标高计算方法一、曲线要素的计算1、转坡角ω=(i1-i2)(上坡取正、下坡取负)2、竖曲线曲线长L = ω×R ( R为曲线半径)3、切线长T = L ÷24、外矢距 E = T2÷2R二、任意点起始桩号、切线标高、改正值的计算1、竖曲线起点桩号=变坡点里程-切线长竖曲线终点桩号=变坡点里程+切线长2、切线标高= 变坡点标高(不考虑竖曲线标高)-(变坡点里程-待求点里程)× i1(所求点位于变坡点后乘i2)3、改正值= (待求点里程-起点里程)2÷(2R)(所求点位于变坡点前)= (待求点里程-终点里程)2÷(2R)(所求点位于变坡点后)4、待求点设计标高= (切线点标高-改正值)三、例:某高速公路变坡点里程为DK555+550,高程为279.866m,前为上坡i1=17.6288‰,后为上坡i2=4.5‰,设计曲线半径R=30000m,试算竖曲线曲线要素及桩号为DK555+450及DK555+680处的设计标高?1、计算曲线要素转坡角ω=(i1-i2)=(17.6288-4.5)‰=0.0131288竖曲线曲线长L = ω×R = 0.0131288×30000 =393.864(m)切线长 T = L ÷2 = 393.864÷2 =196.932(m)外矢距 E = T2÷ 2R = 196.9322÷(2×30000)=0.646(m)2、竖曲线起、始桩号计算起点桩号:(DK555+550)- 196.932 = DK555+353.068终点桩号:(DK555+550)+ 196.932 = DK555+746.9323、DK555+450、DK555+680的切线标高和改正值计算DK555+450切线标高 = 279.866-(DK555+550-DK555+450)×17.6288‰=278.103(m) DK555+450改正值 =(DK555+450-DK555+353.068)2÷(30000×2)=0.157(m)DK555+680切线标高 = 279.866-(DK555+680-DK555+550)×4.5‰=280.451(m)DK555+680改正值 =(DK555+680-DK555+746.932)2÷(30000×2)=0.075(m)4、DK555+450、DK555+680设计标高计算DK555+450设计标高 = 278.103 - 0.157=277.946(m)DK555+680设计标高 = 280.451 -0.075 =280.376(m)。
竖曲线任意点高程计算例题

竖曲线任意点高程计算例题竖曲线是道路设计中常用的一种曲线形式,用于连接不同高程的道路段。
在竖曲线中,曲线是沿垂直方向变化的,通过控制曲率半径和高程变化率来实现。
在竖曲线设计中,一个重要的问题是如何计算曲线上各点的高程。
这需要根据设计要求和道路条件,使用相关的公式和计算方法进行求解。
首先,竖曲线设计中的一个重要参数是曲率半径。
曲率半径是曲线的弯曲程度的测量,在竖曲线中通常使用千分之一切割距(1/k)来表示。
常用的曲率半径有200、250、300等。
一般情况下,设计中需要根据道路的标准、设计速度等因素来确定曲率半径。
其次,竖曲线设计中需要考虑的另一个关键参数是纵坡。
纵坡是曲线的高程变化率,通常以百分比表示。
纵坡的选择需要考虑到各种因素,如舒适度、引导视线、排水等。
在设计中,一般规定了最大纵坡和最小纵坡范围,并根据道路的标准来选择合适的纵坡。
竖曲线设计中高程计算的基本方法是使用上拱曲线理论。
根据路线的设计要求和曲率半径,可以计算出曲线上各点的高程。
具体计算方法如下:1. 确定曲线起点和终点的高程,以及曲线起点的坡度。
在竖曲线设计中,通常规定曲线的起点和终点的高程,以及曲线起点的坡度。
这些信息是计算曲线高程的基础。
2. 将曲线分成若干段,并计算各段的水平长度和垂直位移。
根据曲线的设计要求和曲率半径,可以将曲线分成若干段,计算每段的水平长度和垂直位移。
3. 计算各点的高程。
根据曲线起点和终点的高程,以及曲线起点的坡度,可以计算出曲线上各点的高程。
4. 检查设计是否符合要求。
计算完成后,需要对设计进行检查,确保满足各种要求,如最大纵坡、最小纵坡、曲线长度等。
在竖曲线设计中,还可以使用各种软件进行高程计算。
常用的软件有AutoCAD、Civil 3D等,它们提供了方便快捷的计算功能,可以根据输入的参数自动生成曲线的高程。
总结起来,竖曲线任意点高程计算是道路设计中的重要一环。
通过确定曲率半径、计算水平长度和垂直位移,以及根据曲线起点高程和坡度计算各点高程,可以得到合理的竖曲线设计。
竖曲线设计原理及高程计算(新人必看)

竖曲线设计原理及高程计算(新人必看)竖曲线设计纵断面上相邻两条纵坡线相交的转折处,为了行车平顺用一段曲线来缓和,这条连接两纵坡线的曲线叫竖曲线。
竖曲线的形状,通常采用平曲线或二次抛物线两种。
在设计和计算上为方便一般采用二次抛物线形式。
纵断面上相邻两条纵坡线相交形成转坡点,其相交角用转坡角表示。
当竖曲线转坡点在曲线上方时为凸形竖曲线,反之为凹形竖曲线。
一、竖曲线如图所示,设相邻两纵坡坡度分别为i1 和i2,则相邻两坡度的代数差即转坡角为ω= i1-i2,其中i1、i2为本身之值,当上坡时取正值,下坡时取负值。
当 i1- i2为正值时,则为凸形竖曲线。
当 i1 - i2 为负值时,则为凹形竖曲线。
(一)竖曲线基本方程式我国采用的是二次抛物线形作为竖曲线的常用形式。
其基本方程为:若取抛物线参数P为竖曲线的半径 R,则有:(二)竖曲线要素计算公式1、切线上任意点与竖曲线间的竖距h通过推导可得:2、竖曲线曲线长: L = Rω3、竖曲线切线长:4、竖曲线的外距:5、竖曲线上任意点至相应切线的距离:式中:x —为竖曲任意点至竖曲线起点(终点)的距离, m;R—为竖曲线的半径,m。
二、竖曲线的最小半径(一)竖曲线最小半径的确定1.凸形竖曲线极限最小半径确定考虑因素(1)缓和冲击汽车行驶在竖曲线上时,产生径向离心力,使汽车在凸形竖曲线上重量减小,所以确定竖曲线半径时,对离心力要加以控制。
(2)经行时间不宜过短当竖曲线两端直线坡段的坡度差很小时,即使竖曲线半径较大,竖曲线长度也有可能较短,此时汽车在竖曲线段倏忽而过,冲击增大,乘客不适;从视觉上考虑也会感到线形突然转折。
因此,汽车在凸形竖曲线上行驶的时间不能太短,通常控制汽车在凸形竖曲线上行驶时间不得小于3秒钟。
(3)满足视距的要求汽车行驶在凸形竖曲线上,如果竖曲线半径太小,会阻挡司机的视线。
为了行车安全,对凸形竖曲线的最小半径和最小长度应加以限制。
2.凹形竖曲线极限最小半径确定考虑因素(1)缓和冲击:在凹形竖曲线上行驶重量增大;半径越小,离心力越大;当重量变化程度达到一定时,就会影响到旅客的舒适性,同时也会影响到汽车的悬挂系统。
竖曲线计算
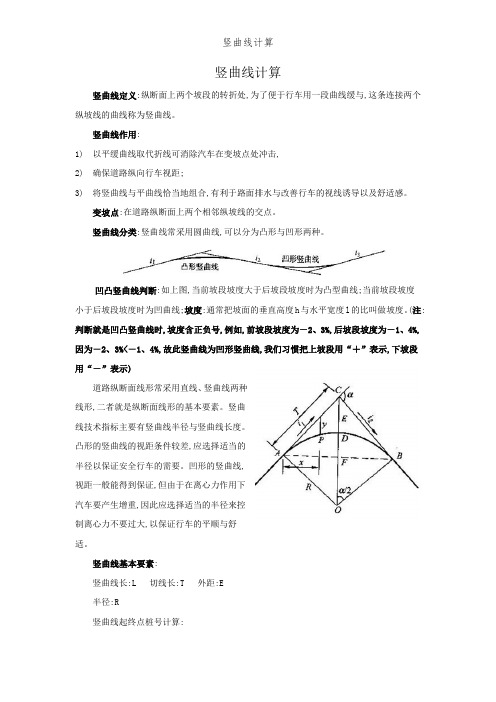
竖曲线计算竖曲线定义:纵断面上两个坡段的转折处,为了便于行车用一段曲线缓与,这条连接两个纵坡线的曲线称为竖曲线。
竖曲线作用:1)以平缓曲线取代折线可消除汽车在变坡点处冲击,2)确保道路纵向行车视距;3)将竖曲线与平曲线恰当地组合,有利于路面排水与改善行车的视线诱导以及舒适感。
变坡点:在道路纵断面上两个相邻纵坡线的交点。
竖曲线分类:竖曲线常采用圆曲线,可以分为凸形与凹形两种。
凹凸竖曲线判断:如上图,当前坡段坡度大于后坡段坡度时为凸型曲线;当前坡段坡度小于后坡段坡度时为凹曲线;坡度:通常把坡面的垂直高度h与水平宽度l的比叫做坡度。
(注:判断就是凹凸竖曲线时,坡度含正负号,例如,前坡段坡度为-2、3%,后坡段坡度为-1、4%,因为-2、3%<-1、4%,故此竖曲线为凹形竖曲线,我们习惯把上坡段用“+”表示,下坡段用“-”表示)道路纵断面线形常采用直线、竖曲线两种线形,二者就是纵断面线形的基本要素。
竖曲线技术指标主要有竖曲线半径与竖曲线长度。
凸形的竖曲线的视距条件较差,应选择适当的半径以保证安全行车的需要。
凹形的竖曲线,视距一般能得到保证,但由于在离心力作用下汽车要产生增重,因此应选择适当的半径来控制离心力不要过大,以保证行车的平顺与舒适。
竖曲线基本要素:竖曲线长:L 切线长:T 外距:E半径:R竖曲线起终点桩号计算:竖曲线起点桩号:变坡点桩号-T竖曲线终点桩号:变坡点桩号+T如右图所示,两个相邻的纵坡为i1与i2,竖曲线半径为R,则测设元素为:曲线长L=R ×α由于竖曲线的转角α很小,故可以认为:α=i1-i2;所以L=R(i1-i2)切线长T=Rtan 2α 因为α很小,tan2α=2α;所以可以推出: T=R ·2α=2L =21R(i1-i2) 又因为α很小,可以认为:DF=E;AF=T根据三角形ACO与三角形ACF相似,根据相似三角形“边角边”定理得出:R:T=T:2E; 于就是如上图外距E=RT 22, 同理可导出竖曲线上任意一点P距切线纵距的计算公式:y =Rx 22式中:x —竖曲线上任意一点P 到竖曲线起点或终点的水平距离Y —值在凹形竖曲线中为正号,在凸形竖曲线中为负号。
曲线计算

、竖曲线上高程计算第一坡度与第二坡度差大于0.5%需设计竖曲线已知:①第一坡度:i1(上坡为“+”,下坡为“-”)②第二坡度:i2(上坡为“+”,下坡为“-”)③变坡点桩号:SZ④变坡点高程:HZ⑤竖曲线的切线长度:T⑥待求点桩号:S计算过程:竖曲线计算竖曲线计算的目的是确定设计纵坡上指定桩号的路基设计标高,其计算步骤如下:(1)计算竖曲线的基本要素:竖曲线长:L;切线长:T;外距:E。
(2)计算竖曲线起终点的桩号:竖曲线起点的桩号= 变坡点的桩号-T竖曲线终点的桩号= 变坡点的桩号+T(3)计算竖曲线上任意点切线标高及改正值:切线标高= 变坡点的标高±()i ;y=X2/2R(4)计算竖曲线上任意点设计标高某桩号在凸形竖曲线的设计标高= 该桩号在切线上的设计标高-y某桩号在凹形竖曲线的设计标高= 该桩号在切线上的设计标高+ y〔例4-1〕:某山岭区二级公路,变坡点桩号为K3+030 .00,高程为427 .68 ,前坡为上坡,i1= +5%,后坡为下坡,i2 = -4%,竖曲线半径R=2000m。
试计算竖曲线诸要素以及桩号为K3+000.00 和K3+100.00处的设计标高。
(1)计算竖曲线要素ω= i1 - i2 = 5% -(-4%) =0.09 所以该竖曲线为凸形竖曲线曲线长:L = R ω=2000 ×0.09 = 180 m切线长:T = L/2 =180 / 2 = 90m 外距:E = m(2)竖曲线起、终点桩号竖曲线起点桩号=(K3+030.00)-90 = K2+940.00竖曲线终点桩号= (K3+030.00) + 90 = K3 +120.00(3)K3+000.00、K3+100.00的切线标高和改正值K3+000.00的切线标高= 427.68 -(K3+030.00-K3+000.00)×5%= 426.18mK3+000.00的改正值=K3+100.00的切线标高=427.68 -(K3+100.00-K3+030.00)×4%= 424.88mK3+100.00的改正值=4)K3+000.00和K3+100.00的设计标高K3+000.00的设计标高= 426.18 -0.9 = 425.28mK3+100.00的设计标高= 424.88 -0.1 =424.78 m超高缓和过渡段的横坡计算已知:如图,第一横坡:i1第二横坡:i2过渡段长度:L待求处离第二横坡点(过渡段终点)的距离:x 求:待求处的横坡:i解:d=x/Li=(i2-i1)(1-3d2+2d3)+i1六、匝道坐标计算已知:①待求点桩号:K②曲线起点桩号:K0③曲线终点桩号:K1④曲线起点坐标:x0,y0⑤曲线起点切线方位角:α0⑥曲线起点处曲率:P0(左转为“-”,右转为“+”)⑦曲线终点处曲率:P1(左转为“-”,右转为“+”)求:①线路匝道上点的坐标:xy②待求点的切线方位角:αT计算过程:注:sgn(x)函数是取符号函数,当x0时sgn(x)=1,当x=0时sgn(x)=0。
竖曲线任意点高程计算例题

竖曲线任意点高程计算例题在地理和土木工程中,计算竖曲线上任意点的高程是一个常见的问题。
竖曲线是指一条道路或铁路的纵向剖面曲线,它用于平滑地连接两个不同的高程点,以确保交通的安全和舒适。
在进行竖曲线的高程计算时,我们需要知道以下几个参数:1. 起点高程:即曲线的起始点的高程值。
2. 终点高程:即曲线的终点的高程值。
3. 曲线长度:即曲线的水平长度。
4. 曲线半径:即曲线的曲率半径。
下面举一个例子来说明如何计算竖曲线上任意点的高程。
假设我们有一条道路,起点高程为100米,终点高程为150米,曲线长度为500米,曲线半径为1000米。
我们想要计算曲线上距离起点100米的点的高程。
首先,我们可以通过计算曲线的坡度来确定曲线的整体高程变化。
坡度可以通过起点和终点高程差除以曲线长度得到:坡度 = (终点高程 - 起点高程) / 曲线长度= (150 - 100) / 500= 0.1然后,我们可以使用曲线半径和距离起点100米的水平距离来计算该点的纵坐标变化。
纵坐标变化可以通过距离起点的水平距离除以曲线半径得到:纵坐标变化 = 距离起点的水平距离 / 曲线半径= 100 / 1000= 0.1最后,我们可以将曲线的坡度和纵坐标变化相加,得到距离起点100米的点的高程变化:高程变化 = 坡度 + 纵坐标变化= 0.1 + 0.1= 0.2最终,我们可以将高程变化与起点高程相加,得到距离起点100米的点的高程:高程 = 起点高程 + 高程变化= 100 + 0.2= 100.2米因此,在距离起点100米的点的高程为100.2米。
除了这个例子,竖曲线的高程计算还涉及到其他参数和公式,如切线长、中线长和横坡等。
根据具体情况,我们可以选择不同的计算方法和公式来求解竖曲线上任意点的高程。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
竖曲线任意点高程计算例题
竖曲线是公路设计中非常重要的一部分,它涉及到道路的纵向变化和高程的计算。
在竖曲线设计中,计算任意点的高程是一个关键步骤。
本文将通过一个例题来演示竖曲线任意点高程的计算方法。
假设有一条公路,起点高程为100米,终点高程为200米,道路总长度为1000米。
现在我们需要计算出道路上每隔100米的点的高程。
首先,我们需要确定竖曲线的类型。
常见的竖曲线类型有:凸型、直线型和凹型。
我们会根据具体情况选择适合的竖曲线类型。
在本例中,我们选择凸型竖曲线。
接下来,我们需要确定竖曲线的参数。
竖曲线的参数包括:起点高程、终点高程、公路长度、曲线长度、曲率半径和过渡曲线长度等。
在这个例子中,起点高程为100米,终点高程为200米,公路长度为1000米。
我们需要计算出曲线长度、曲率半径和过渡曲线长度。
首先,我们来计算曲线长度。
曲线长度可以根据起点高程和终点高程的差值来计算。
在本例中,曲线长度为200米。
接下来,我们需要计算曲率半径。
曲率半径是曲线最高点的曲率半径,它影响曲线的陡峭程度。
在凸型曲线中,曲率半径的计算公式为:R = (L^2 + H^2) / (2H),其中R表示曲率半径,L表示曲线长度,H表示起点高程和终点高程的差值。
在本例中,曲率半径为200米。
最后,我们需要计算过渡曲线长度。
过渡曲线长度是指曲线从平缓过渡到陡峭的长度。
在凸型曲线中,过渡曲线长度的计算公式为:T = (L^2) / (24R),其中T表示过渡曲线长度,L表示曲线长度,R表示曲率半径。
在本例中,过渡曲线长度为
16.67米。
现在我们已经计算出了曲线长度、曲率半径和过渡曲线长度,接下来我们可以计算出道路上每隔100米的点的高程。
首先,我们计算出每个100米点的距离。
在本例中,道路总长度为1000米,所以我们需要计算出10个100米点的高程。
然后,我们根据距离和曲线参数来计算每个点的高程。
在本例中,起点高程为100米,曲线长度为200米,曲率半径为200米,过渡曲线长度为16.67米。
根据曲线参数,我们可以将曲线分为两段:过渡段和曲线段。
过渡段是指曲线从平缓过渡到陡峭的部分,曲线段是指曲线最陡峭的部分。
首先,我们计算出过渡段的高程。
过渡段的高程可以根据距离和过渡曲线长度来计算。
在本例中,过渡段的高程计算公式为:E = H + (T^2 - X^2) / (2T),其中E表示过渡段的高程,H表示
起点高程和终点高程的差值,T表示过渡曲线长度,X表示距离。
然后,我们计算出曲线段的高程。
曲线段的高程可以根据距离、曲率半径和曲线长度来计算。
在本例中,曲线段的高程计算公式为:E = H + R - sqrt(R^2 - (L/2 - X)^2),其中E表示曲线段
的高程,H表示起点高程和终点高程的差值,R表示曲率半径,L表示曲线长度,X表示距离。
通过以上计算,我们可以得到道路上每隔100米的点的高程。
根据计算结果,我们可以绘制出竖曲线图,并在图上标注出每个点的高程。
在竖曲线设计中,高程的计算是一个非常重要的环节。
通过合理的计算方法和准确的参数,我们可以得到道路上每个点的高程,从而保证公路的安全和舒适性。
