2019年5月初三九年级初中数学复习资料锐角三角函数知识点加练习题及详细解析
最新初三年级锐角三角函数知识点总结、典型例题、练习[精选]
![最新初三年级锐角三角函数知识点总结、典型例题、练习[精选]](https://img.taocdn.com/s3/m/78ed1ec4ec3a87c24128c427.png)
最新初三年级锐角三角函数知识点总结、典型例题、练习[精选]锐角三角函数知识点总结1、勾股定理:直角三角形两直角边a 、b 的平方和等于斜边c 的平方. 222c b a =+2、如下图,在Rt △ABC 中,∠C 为直角,则∠A 的锐角三角函数为(∠A 可换成∠B):定 义表达式取值范围关 系正弦 斜边的对边A A ∠=sin c aA =sin 1sin 0<<A (∠A 为锐角)B A cos sin =B A sin cos =1cos sin 22=+A A余弦 斜边的邻边A A ∠=cos c bA =cos 1cos 0<<A (∠A 为锐角) 正切 的邻边的对边A tan ∠∠=A A b aA =tan 0tan >A (∠A 为锐角)3、任意锐角的正弦值等于它的余角的余弦值;任意锐角的余弦值等于它的余角的正弦值.4、0°、30°、45°、60°、90°特殊角的三角函数值(重要) 三角函数 0° 30°45°60°90° αsin 0 21 22 23 1 αcos1 23 2221 0 αtan33 1 3-5、正弦、余弦的增减性:当0°≤α≤90°时,sin α随α的增大而增大,cos α随α的增大而减小. 6、正切的增减性:当0°<α<90°时,tan α随α的增大而增大,7、解直角三角形的定义:已知边和角(两个,其中必有一边)→所有未知的边和角. 依据:①边的关系:222c b a =+;②角的关系:A+B=90°;③边角关系:三角函数的定义.(注意:尽量避免使用中间数据和除法))90cos(sin A A -︒=)90sin(cos A A -︒=BA cos sin =BA sin cos =A90B 90∠-︒=∠︒=∠+∠得由B A对边邻边斜边 ACBba c8、应用举例:(1)仰角:视线在水平线上方的角;俯角:视线在水平线下方的角.仰角铅垂线水平线视线视线俯角(2)坡面的铅直高度h和水平宽度l的比叫做坡度(坡比).用字母i表示,即hil=.坡度一般写成1:m的形式,如1:5i=等.把坡面与水平面的夹角记作α(叫做坡角),那么tanhilα==.3、从某点的指北方向按顺时针转到目标方向的水平角,叫做方位角.如图3,OA、OB、OC、OD的方向角分别是:45°、135°、225°.4、指北或指南方向线与目标方向线所成的小于90°的水平角,叫做方向角.如图4,OA、OB、OC、OD的方向角分别是:北偏东45°(东北方向) , 南偏东45°(东南方向), 南偏西45°(西南方向), 北偏西45°(西北方向).类型一:直角三角形求值例1.已知Rt△ABC中,,12,43tan,90==︒=∠BCAC求AC、AB和cos B.例2.已知:如图,⊙O的半径OA=16cm,OC⊥AB于C点,⋅=∠43sin AOC求:AB及OC的长.:i h l=hlα例3.已知A∠是锐角,178sin=A,求Acos,Atan的值对应训练:1.在Rt△ABC中,∠ C=90°,若BC=1,AB=5,则tan A的值为A.55B.255C.12D.22.在△ABC中,∠C=90°,sin A=53,那么tan A的值等于().A.35B.45C.34D.43类型二. 利用角度转化求值:例1.已知:如图,Rt△ABC中,∠C=90°.D是AC边上一点,DE⊥AB于E点.DE∶AE=1∶2.求:sin B、cos B、tan B.例2.如图,直径为10的⊙A经过点(05)C,和点(00)O,,与x轴的正半轴交于点D,B是y 轴右侧圆弧上一点,则cos∠OBC的值为()A.12B.32C.35D.45对应训练:3.如图,O⊙是ABC△的外接圆,AD是O⊙的直径,若O⊙的半径为32,2AC=,则sin B的值是()DCBAOyx第8题图A.23B.32C.34D.434. 如图4,沿AE折叠矩形纸片ABCD,使点D落在BC边的点F处.已知8AB=,10BC=,AB=8,则tan EFC∠的值为 ( )A.34B.43C.35D.45A DECBF类型三. 化斜三角形为直角三角形例1 如图,在△ABC中,∠A=30°,∠B=45°,AC=23,求AB的长.例2.已知:如图,在△ABC中,∠BAC=120°,AB=10,AC=5.求:sin∠ABC的值.对应训练1.如图,在Rt△ABC中,∠BAC=90°,点D在BC边上,且△ABD是等边三角形.若AB=2,求△ABC 的周长.(结果保留根号)2.已知:如图,△ABC中,AB=9,BC=6,△ABC的面积等于9,求sin B.3. △ABC中,∠A=60°,AB=6 cm,AC=4 cm,则△ABC的面积是A.23 cm2B.43 cm2C.63 cm2D.12 cm2类型四:利用网格构造直角三角形例1 如图所示,△ABC的顶点是正方形网格的格点,则sinA的值为()A.12B.55C.1010D.255对应训练:1.如图,△ABC的顶点都在方格纸的格点上,则sin A =_______.2.正方形网格中,AOB∠如图放置,则tan AOB∠的值是()A.55B.2 55C.12D. 2类型五:取特殊角三角函数的值1).计算:︒-︒+︒60tan45sin230cos2.2)计算:︒-︒+︒30cos245sin60tan2.3)计算:3-1+(2π-1)0-33tan30°-tan45°4).计算:30tan2345sin60cos221⎪⎪⎭⎫⎝⎛︒-︒+︒+.5).计算:tan45sin301cos60︒+︒-︒;CBAABO类型六:解直角三角形的实际应用例1.如图,从热气球C处测得地面A、B两点的俯角分别是30°、45°,如果此时热气球C 处的高度CD为100米,点A、D、B在同一直线上,则AB两点的距离是()A.200米B.200米C.220米D.100()米例2.已知:如图,在两面墙之间有一个底端在A点的梯子,当它靠在一侧墙上时,梯子的顶端在B点;当它靠在另一侧墙上时,梯子的顶端在D点.已知∠BAC=60°,∠DAE=45°.点D到地面的垂直距离m 23=DE,求点B到地面的垂直距离BC.例3如图,一风力发电装置竖立在小山顶上,小山的高BD=30m.从水平面上一点C测得风力发电装置的顶端A的仰角∠DCA=60°,测得山顶B的仰角∠DCB=30°,求风力发电装置的高AB的长.对应训练:1..如图,小聪用一块有一个锐角为30︒的直角三角板测量树高,已知小聪和树都与地面垂直,且相距33米,小聪身高AB为1.7米,求这棵树的高度.2.如图,为测量某物体AB的高度,在D点测得A点的仰角为30°,朝物体AB方向前进20米,到达点C,再次测得点A的仰角为60°,则物体AB的高度为()ABCDEA . 10米B . 10米C . 20米D .米类型七:三角函数与圆:例1. 如图,直径为10的⊙A 经过点(05)C ,和点(00)O ,,与x 轴的正半轴交于点D ,B 是y轴右侧圆弧上一点,则cos∠OBC 的值为( ) A .12 B .32 C .35D .45例2. 已知:在⊙O 中,AB 是直径,CB 是⊙O 的切线,连接AC 与⊙O 交于点D, (1) 求证:∠AOD=2∠C (2) 若AD=8,tanC=34,求⊙O 的半径.对应训练:1.如图,DE 是⊙O 的直径,CE 与⊙O 相切,E 为切点.连接CD 交⊙O 于点B,在EC 上取一个点F,使EF=BF.(1)求证:BF 是⊙O 的切线; (2)若54C cos , DE =9,求BF 的长.DB OACD C B A Oyx第8题图CFDOBECB A作业: 1.已知21sin =A ,则锐角A 的度数是( ) A .75︒B .60︒C .45︒D .30︒ 2.在Rt△ABC 中,∠ C =90°,若BC =1,AB =5,则tan A 的值为( )A .55 B .255 C .12D .2 3.在△ABC 中,∠C =90°,sin A=53,那么tan A 的值等于( ).A .35B . 45C . 34D . 434. 若sin α=32,则锐角α= . 5.将∠α放置在正方形网格纸中,位置如图所示,则tan α的值是A .21B .2C .25D .5526.如图,AB 为⊙O 的弦,半径OC ⊥AB 于点D ,若OB 长为10,3cos 5BOD ∠=, 则AB 的长是A . 20 B. 16 C. 12 D. 87.在Rt△ABC 中,∠C=90°,如果cosA=54,那么tanA 的值是( ) A .53 B .35 C .43 D .348. 如图,在△ABC 中,∠ACB =∠ADC= 90°,若sin A =35,则cos∠BCD 的值为 .9.计算:︒-︒+︒60tan 45sin 230cos 210.计算︒+︒-︒-︒45tan 30tan 345cos 260sin 2.αDCBA11.计算:22sin 604cos 30+sin 45tan 60-⋅oooo.12.已知在Rt△ABC 中,∠C=90°,a=64,b=212.解这个直角三角形13. 已知:在⊙O 中,AB 是直径,CB 是⊙O 的切线,连接AC 与⊙O 交于点D, (3) 求证:∠AOD=2∠C (4) 若AD=8,tanC=34,求⊙O 的半径.14.如图,某同学在楼房的A 处测得荷塘的一端 B 处的俯角为30︒,荷塘另一端D 处C 、B 在 同一条直线上,已知32AC =米,16CD =米, 求荷塘宽BD 为多少米?(结果保留根号)15.如图,一艘海轮位于灯塔P 的南偏东45°方向,距离灯塔100海里的A 处,它计划沿正北方向航行,去往位于灯塔P 的北偏东30°方向上的B 处.(1)B 处距离灯塔P 有多远?(2)圆形暗礁区域的圆心位于PB 的延长线上,距离灯塔200海里的O 处.已知圆形暗礁区域的半径为50海里,进入圆形暗礁区域就有触礁的危险.请判断若海轮到达B 处是否有触礁的危险,并说明理由.DBOAC。
最新初三锐角三角函数知识点总结、典型例题、练习(精选)
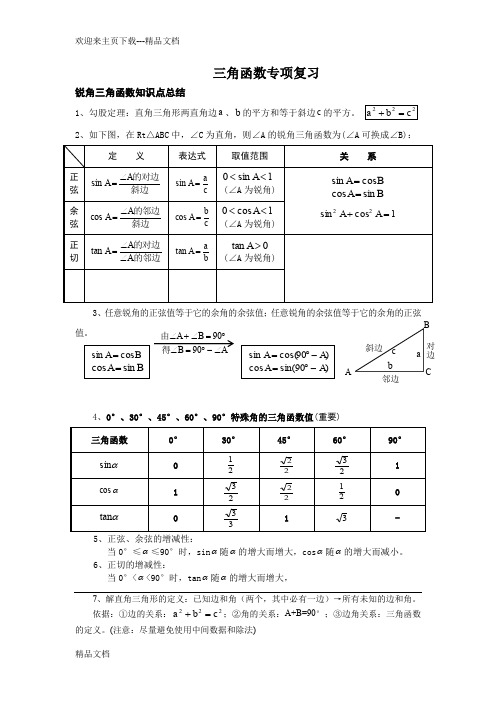
三角函数专项复习锐角三角函数知识点总结1、勾股定理:直角三角形两直角边a 、b 的平方和等于斜边c 的平方。
222c b a =+2、如下图,在Rt △ABC 中,∠C 为直角,则∠A 的锐角三角函数为(∠A 可换成∠B):定 义表达式取值范围关 系正弦 斜边的对边A A ∠=sin c aA =sin 1sin 0<<A (∠A 为锐角)B A cos sin =B A sin cos =1cos sin 22=+A A余弦 斜边的邻边A A ∠=cos c bA =cos 1cos 0<<A (∠A 为锐角) 正切 的邻边的对边A tan ∠∠=A A b aA =tan 0tan >A (∠A 为锐角)3、任意锐角的正弦值等于它的余角的余弦值;任意锐角的余弦值等于它的余角的正弦值。
4、0°、30°、45°、60°、90°特殊角的三角函数值(重要) 三角函数 0° 30°45°60°90° αsin 0 21 22 23 1 αcos1 23 2221 0 αtan33 1 3-5、正弦、余弦的增减性:当0°≤α≤90°时,sin α随α的增大而增大,cos α随α的增大而减小。
6、正切的增减性:当0°<α<90°时,tan α随α的增大而增大,7、解直角三角形的定义:已知边和角(两个,其中必有一边)→所有未知的边和角。
依据:①边的关系:222c b a =+;②角的关系:A+B=90°;③边角关系:三角函数的定义。
(注意:尽量避免使用中间数据和除法) )90cos(sin A A -︒=)90sin(cos A A -︒=BA cos sin =BA sin cos =A90B 90∠-︒=∠︒=∠+∠得由B A对边邻边斜边 ACBba c8、应用举例:(1)仰角:视线在水平线上方的角;俯角:视线在水平线下方的角。
初三数学锐角三角函数含答案
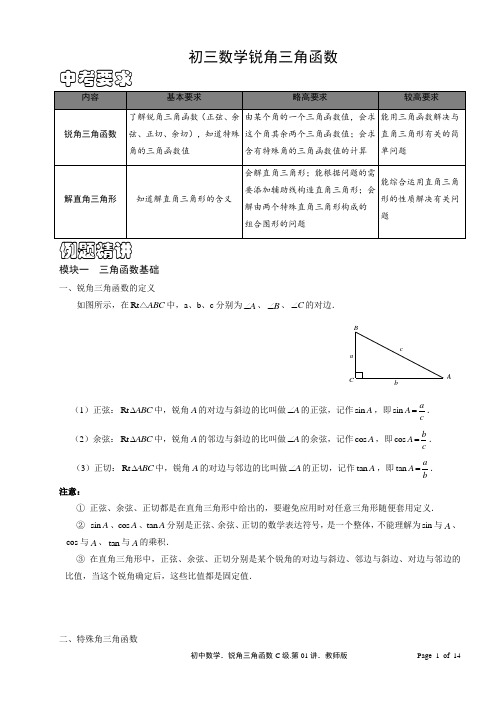
初三数学锐角三角函数中考要求例题精讲模块一 三角函数基础一、锐角三角函数的定义如图所示,在Rt ABC △中,a 、b 、c 分别为A ∠、B ∠、C ∠的对边.(1)正弦:Rt ABC ∆中,锐角A 的对边与斜边的比叫做A ∠的正弦,记作sin A ,即sin aA c=. (2)余弦:Rt ABC ∆中,锐角A 的邻边与斜边的比叫做A ∠的余弦,记作cos A ,即cos b A c =. (3)正切:Rt ABC ∆中,锐角A 的对边与邻边的比叫做A ∠的正切,记作tan A ,即tan a A b=. 注意:① 正弦、余弦、正切都是在直角三角形中给出的,要避免应用时对任意三角形随便套用定义. ② sin A 、cos A 、tan A 分别是正弦、余弦、正切的数学表达符号,是一个整体,不能理解为sin 与A 、cos 与A 、tan 与A 的乘积.③ 在直角三角形中,正弦、余弦、正切分别是某个锐角的对边与斜边、邻边与斜边、对边与邻边的比值,当这个锐角确定后,这些比值都是固定值.二、特殊角三角函数a A这些特殊角的三角函数值一定要牢牢记住! 三、锐角三角函数的取值范围在Rt ABC ∆中,90C ∠=︒,000a b c a c b c >>><<,,,,,又sin a A c =,cos b A c =,tan aA b=,所以 0sin 10cos 1tan 0A A A <<<<>,,. 四、三角函数关系 1.同角三角函数关系: 22sin cos 1A A +=,sin tan cos AA A= 2.互余角三角函数关系:(1) 任意锐角的正弦值等于它的余角的余弦值:()sin cos 90A A =︒-;(2) 任意锐角的余弦值等于它的余角的正弦值:()cos sin 90A A =︒-; (3) 任意锐角的正切值等于它的余角的余切值:()tan cot 90A A =︒-. 3.锐角三角函数值的变化规律:(1)A 、B 是锐角,若A >B ,则sin A >sin B ;若A <B ,则sin A <sin B(2) A 、B 是锐角,若A >B ,则cos A <cos B ;若A <B ,则cos A >cos B (3) A 、B 是锐角,若A >B ,则tan tan A B >;若A <B ,则tan tan A B < 【例1】 已知在ABC △中,A B ∠∠、是锐角,且5sin tan 22913A B AB cm ===,,,则ABC S =△ . 【解析】过C 作CD AB ⊥于D ,这样由三角函数定义得到线段的比:5sin tan 213CD CDA B AC BD====,, 设5132CD m AC m CD n BD n ====,,,,解题的关键是求出m n 、值.51222CD BD n m AD m ====, 所以529122922AB AD BD m m m =+=+==所以12101452ABC m CD S AB CD ===⋅=,,△ 小结:设ABC △中,a b c 、、为A B C ∠∠∠、、的对边,R 为ABC △外接圆的半径,不难证明:与锐角三角函数相关的几个重要结论:(1)111sin sin sin 222ABC S bc A ac B ab C ===△;(2)2sin sin sin a b c R A B C===. 【答案】145【巩固】如图,点A 在半径为R 的O 上,以A 为圆心,r 为半径作A ,设O 的弦PQ 与A 相切,求证PA QA ⋅为定值.【答案】证明线段乘积为定值,联想到三角形的面积,可以和三角函数联系起来.∵1sin 2APQ S PA QA A =⋅△,12APQ S r PQ =⋅△, ∴sin PA QA A r PQ ⋅⋅=⋅.在APQ △中,sin 2PQ A R =,∴2PQPA QA r PQ R⋅=⋅÷,∴2PA QA Rr ⋅=为定值.【例2】 求tan1tan2tan3tan89︒⋅︒⋅︒⋅⋅︒的值【答案】∵tan cot 1αα=,tan cot(90)αα=︒-∴tan1tan89tan1cot11︒︒=︒︒=,tan2tan88tan2cot 21︒︒=︒︒=, tan44tan46tan44cot 441︒︒=︒︒=,而tan451︒=,∴tan1tan2tan3tan891︒⋅︒⋅︒⋅⋅︒=.【巩固】化简:22sin cos sin 1tan sin cos αααααα++-- 【解析】原式()2222cos sin cos sin cos sin sin cos αααααααα+=+--22cos sin sin cos cos sin αααααα-==--. 【答案】sin cos αα-【例3】已知tan α1)221cos sin cos 1sin cos sin a ααααα-+-+(2090α︒<<︒).【答案】⑴221cos sin cos 1sin cos sin a ααααα-+-+()()222222sin sin sin sin cos sin sin cos sin cos cos 3cos cos cos sin cos cos cos sin cos sin sin αααααααααααααααααααααα⎛⎫+ ⎪++⎝⎭====+⎛⎫++ ⎪⎝⎭,1sin 2cos αα-=OQPA【巩固】已知tan 2α=,求4sin 2cos 5cos 3sin αααα-+.【答案】4sin 2cos 5cos 3sin αααα-+4sin 24226cos 3sin 532115cos αααα-⨯-===+⨯+.【例4】 已知α为锐角,且22sin 5cos 10αα-+=,求α的度数. 【答案】∵22sin cos 1αα+=∴22(1cos )5cos 10αα--+=,即:22cos 5cos 30αα+-=. ∴(2cos 1)(cos 3)0αα-+=. 解得:cos 3α=-或1cos 2α=. ∵0cos 1α≤≤,∴1cos 2α=,∴60α=︒. 【巩固】若α为锐角,且22cos 7sin 50αα+-=,求α的度数.【答案】由α为锐角,可知0sin 1α<<. 又由22cos 7sin 50αα+-=,22sin cos 1αα+=可知22sin 7sin 30αα-+=,解之得1sin 302αα=⇒=︒. 【例5】已知sin cos αα+(α为锐角),求作以1sin α和1cos α为两根的一元二次方程. 【解析】∵sin cos αα+=,两边平方得:22sin cos 2sin cos 2αααα++=又∵22sin cos 1αα+=,∴1sin cos 2αα⋅=.∴11sin cos sin cos sin cos αααααα++==112sin cos αα⋅= ∴以1sin α和1cos α为两根的一元二次方程为:220x -+=【答案】220x -+=【巩固】若方程222210x ax a -+-=的一个根是sin α,则它的另一个根必是cos α或cos α-. 【答案】不妨设方程的另一根为m ,由一元二次方程的根系关系可知sin m a α+=,21sin 2a m α-=, 故2(sin )1sin 2m m αα+-=,整理可得22sin (sin )1m m αα=+-,即22sin 1m α+=,又22sin cos 1αα+=,故cos m α=±.【巩固】已知:ABC △中,方程2(sin sin )(sin sin )(sin sin )0B A x A C x C B -+-+-=的两根相等,求证60B <︒. 【答案】两根相等则判别式为0,但是观察系数的规律,是否有其他的好办法呢?∵此方程系数之和为0,∴1x =必为此方程的根.又∵此方程两根相等,∴121x x ==,∴12sin sin 1sin sin C Bx x B A-==-.又由正弦定理,有c b b a -=-,∴2c ab +=. 再由余弦定理,有22222222()3()26212cos 22882c a a c c a ba c ca ca ca B caca ca ca ++-+-+--====≥.∴60B ︒≤,且等号不会成立,否则方程就不存在了.【巩固】在ABC △中,60A =︒,最大边与最小边的边长分别是方程2327320x x -+=的两个根,求ABC △的外接圆半径和内切圆的面积.【答案】题目中涉及到边长的关系,以及外接圆半径,这为正弦定理提供了便利条件.∵60A =︒,且显然此三角形有两边不等(即以已知方程为根的两边), ∴ABC △中,A 既不是最大角也不是最小角,不防设b 为最大边,c 为最小边, 由韦达定理,有3293b c bc +==,, 又由余弦定理,有:2222cos a b c bc A =+-222()3b c bc b c bc =+-=+- 813249=-=.∴7a =(7a =-舍去)又由正弦定理,有2sin aR A===∴7916a b c ++=+=. 1sin 2S bc A P r ==⋅(其中2a b cP ++=,r 为内切圆半径)即132822r =⨯,∴r =∴内切圆面积21ππ3S r ==.【例6】 若0°<θ<30°,且1sin 3km θ=+(k 为常数,且k <0),则m 的取值范是 . 【答案】∵0°<θ<30°∴sin 0°<sin θ<sin 30°,即0<sin θ<12∴0<13km +<12,所以1136km -<<,又因为0k <∴1163m k k<<-. 模块二 解直角三角形一、解直角三角形的概念根据直角三角形中已知的量(边、角)来求解未知的量(边、角)的过程就是解直角三角形.二、直角三角形的边角关系如图,直角三角形的边角关系可以从以下几个方面加以归纳: (1)三边之间的关系:222a b c += (勾股定理) (2)锐角之间的关系:90A B ∠+∠=︒(3)边角之间的关系:sin cos ,cos sin ,tan a b aA B A B A c c b=====三、解直角三角形的四种基本类型(1)已知斜边和一直角边(如斜边c ,直角边a ),由sin aA c=求出A ∠,则90B A ∠=︒-∠,b =; (2)已知斜边和一锐角(如斜边c ,锐角A ),求出90B A ∠=︒-∠,sin a c A =,cos b c A =; (3)已知一直角边和一锐角(如a 和锐角A ),求出90B A ∠=︒-∠,tan b a B =,sin ac A=; (4)已知两直角边(如a 和b ),求出c =tan aA b=,得90B A ∠=︒-∠. 具体解题时要善于选用公式及其变式,如sin a A c =可写成sin a c A =,sin a c A=等. 四、解直角三角形的方法解直角三角形的方法可概括为:“有斜(斜边)用弦(正弦,余弦),无斜用切(正切,余切),宁乘毋除,取原避中”.这几句话的意思是:当已知或求解中有斜边时,就用正弦或余弦;无斜边时,就用正切或余切; 当所求的元素既可用乘法又可用除法时,则用乘法,不用除法;既可由已知数据又可用中间数据求得时,则用原始数据,尽量避免用中间数据. 五、解直角三角形的技巧及注意点在Rt ABC ∆中,90A B ∠+∠=︒,故sin cos(90)cos A A B =︒-=,cos sin A B =.利用这些关系式,可在解题时进行等量代换,以方便解题. 六、如何解直角三角形的非基本类型的题型对解直角三角形的非基本类型的题型,通常是已知一边长及一锐角三角函数值,可通过解方程(组)来转化为四种基本类型求解;(1)如果有些问题一时难以确定解答方式,可以依据题意画图帮助分析;(2)对有些比较复杂的问题,往往要通过作辅助线构造直角三角形,作辅助线的一般思路是:①作垂线构成直角三角形;②利用图形本身的性质,如等腰三角形顶角平分线垂直于底边等. 七、直角三角形中其他重要概念(1)仰角与俯角:在视线与水平线所成的角中,视线在水平线上方的叫做仰角,在水平线下方的叫做俯角.如图⑴.(2)坡角与坡度:坡面的垂直高度h 和水平宽度l 的比叫做坡度(或叫做坡比),用字母表示为hi l=,坡面与水平面的夹角记作α,叫做坡角,则tan hi lα==.坡度越大,坡面就越陡.如图⑵. cb aC BA(3)方向角(或方位角):方向角一般是指以观测者的位置为中心,将正北或正南方向作为起始方向旋转到目标的方向线所成的角(一般指锐角),通常表达为北(南)偏东(西)××度.如图⑶.八、解直角三角形应用题的解题步骤及应注意的问题:(1)分析题意,根据已知条件画出它的平面或截面示意图,分清仰角、俯角、坡角、坡度、水平距离、垂直距离等概念的意义;(2)找出要求解的直角三角形.有些图形虽然不是直角三角形,但可添加适当的辅助线,把它们分割成一些直角三角形和矩形(包括正方形);(3)根据已知条件,选择合适的边角关系式解直角三角形;(4)按照题目中已知数据的精确度进行近似计算,检验是否符合实际,并按题目要求的精确度取近似值,注明单位.【例7】 如图,某高层楼房与上海东方明珠电视塔隔江想望,甲、乙两学生分别在这楼房的A B ,两层,甲在A 层测得电视塔塔顶D 的仰角为α,塔底C 的俯角为β,乙在B 层测得塔顶D 的仰角为θ,由于塔底的视线被挡住,乙无法测得塔底的俯角,已知A B ,之间的高度差为a ,求电视塔高CD (用含a αβθ,,,的代数式表示)【解析】作AE CD ⊥于E ,BF CD ⊥于F ,设DE x = 在Rt ADE ∆中,由tan DE AE α=,得tan tan DE xAE αα==, 在Rt DBF ∆中,由tan DFBFθ=,得 tan tan DF x aBF θθ+==,因为AE BF =, 所以tan tan x x a αθ+=,解得tan tan tan a x αθα⋅=-,从而tan tan aAE θα=- 在Rt AEC ∆中,由tan EC AE β=,得tan tan tan tan a EC AE ββθα=⋅=- 所以()tan tan tan tan tan tan tan tan tan tan a a a CD DE EC αβαβθαθαθα+=+=+=--- 【答案】()tan tan tan tan a αβθα+-【例8】 一座建于若干年前的水库大坝的横断面如图所示,其中背水面的整个坡面是长为90米、宽为5图(3)图(2)图(1)俯角仰角视线视线水平线铅垂线米的矩形. 现需将其整修并进行美化,方案如下:① 将背水坡AB 的坡度由1:0.75改为;② 用一组与背水坡面长边垂直的平行线将背水坡面分成9块相同的矩形区域,依次相间地种草与栽花 .(1)求整修后背水坡面的面积;(2)如果栽花的成本是每平方米25元,种草的成本是每平方米20元,那么种植花草至少需要多少元?【答案】(1)作AE BC ⊥于E .∵ 原来的坡度是1:0.75,∴ 140.753AE EB == . 设4AE k =,3BE k =, ∴ 5AB k =, 又 ∵ 5AB =米, ∴1k =,则4AE =米 .设整修后的斜坡为AB ',由整修后坡度为,有AE EB =',∴∠AB E '=30°, ∴ 28AB AE '==米 . ∴ 整修后背水坡面面积为908720⨯=米2 . (2)将整修后的背水坡面分为9块相同的矩形,则每一区域的面积为80米2 .解法一:∵ 要依次相间地种植花草,有两种方案:第一种是种草5块,种花4块,需要20×5×80+25×4×80=16000元; 第二种是种花5块,种草4块,需要20×4×80+25×5×80=16400元 . ∴ 应选择种草5块、种花4块的方案,需要花费16000元 .解法二:∵ 要依次相间地种植花草,则必然有一种是5块,有一种是4块,而栽花的成本是每平方米25元,种草的成本是每平方米20元,∴ 两种方案中,选择种草5块、种花4块的方案花费较少 . 即:需要花费20×5×80+25×4×80=16000元 .【例9】 如图,在某海域内有三个港口A 、D 、C .港口C 在港口A 北偏东60︒方向上,港口D 在港口A北偏西60︒方向上.一艘船以每小时25海里的速度沿北偏东30︒的方向驶离A 港口3小时后到达B 点位置处,此时发现船舱漏水,海水以每5分钟4吨的速度渗入船内.当船舱渗入的海水总量超过75吨时,船将沉入海中.同时在B 处测得港口C 在B 处的南偏东75︒方向上.若船上的抽水机每小时可将8吨的海水排出船外,问此船在B 处至少应以怎样的航行速度驶向最近的港口停靠,才能保证船在抵达港口前不会沉没(要求计算结果保留根号)?并指出此时船的航行方向.DCBA【解析】连结AC、AD、BC、BD,延长AT,过B作BT AT⊥于T,AC与BT交于点E.过B作BP AC⊥于点P.由已知得90BAD∠=︒,30BAC∠=︒,32575AB=⨯=(海里),在BEP∆和AET∆中,90BPE ATE∠=∠=︒,AET BEP∠=∠,∴30EBP EAT∠=∠=︒.∵60BAT∠=︒,∴30BAP∠=︒,从而17537.52BP=⨯=(海里).∵港口C在B处的南偏东75︒方向上,∴45CBP∠=︒.在等腰Rt CBP∆中,BC==,∴BC<AB.BAD∆是Rt∆,∴BD AB>.综上,可得港口C离B点位置最近.∴此船应转向南偏东75︒方向上直接驶向港口C.设由B驶向港口C船的速度为每小时x海里,548)5÷⨯-<7,解不等式,得x>.答:此船应转向沿南偏东75︒的方向向港口C航行,且航行速度至少不低于每小时能保证船在抵达港口前不会沉没.【答案】此船应转向沿南偏东75︒的方向向港口C航行,且航行速度至少不低于每小时证船在抵达港口前不会沉没.【巩固】海面上B处有一货轮正在向正南方向航行,其航行路线是当它到达正南方C时,在驶向正西方的目的地A处,且200CA CB==海里,在AB中点O处有一客轮,其速度为货轮的一半,现在客轮要截住货轮取一件货物,于是选择某一航向行驶去截住货轮,那么当客轮截住客轮时至少航行了多少海里,它所选择了怎样的方向角?(路程保留整数海里,角度精确到度)【解析】如图,由题意可知,ABC∆为等腰直角三角形,假设客轮截住货轮的地点在BC边上时,过OD BC⊥于D,OD为客轮到达BC边的最短距离,即客轮航行的路程为OD,由货轮速度为客轮的2倍可知,货轮航行的距离为2OD BC=,即货轮此时到达了C点,∴客轮截住货轮的地点不可能在BC边上.∴客轮截住货轮的地点在AC 边上.设在AC 边上的F 点两船相遇,设客轮航行的距离为x ,即OE x =,则2BC CE x +=, ∴2200CE x =-,过O 作OF AC ⊥于F ,则11002OF BC ==海里,11002FC AC ==海里, ∴3002EF x =-在Rt DEF ∆中,222OF EF OE +=, 即222100(3002)x x +-=,解得x =1282x ≈,2118x ≈∴141OE OA ≤=∴1282x ≈不符合题意,∴118x ≈ 即当客轮截住货轮时,航行了118海里. 在Rt OEF ∆中,100cos 0.8475118EOF ∠=≈ ∴32EOF ∠=︒∴客轮的航行方向应为南偏东32︒.【答案】客轮的航行方向应为南偏东32︒课堂检测1. (辽宁竞赛)如图,湖心岛上有一凉亭,现欲利用湖岸边的开阔平整地带,测量凉亭顶端到湖面所在平面的高度AB (见示意图),可供使用的工具有测倾器、皮尺.(1)请你根据现有条件,设计一个测量凉亭顶端到湖面所在平面的高度AB 的方案,画出测量方案的平面示意图,并将测量的数据标注在图形上(所测的距离用m ,n 表示,角用α,β表示,测倾器高度忽略不计);(2)根据你所测量的数据,计算凉亭到湖面的高度AB (用字母表示).F EDOC BA【解析】(1)如图所示,在点C 测得ACB α∠=,在点D 测得ADB β∠=,测得DC m =(2)在Rt ABC ∆中,设AB x =,tan x BC α=在Rt ABD ∆中,tan xBD β= BD BC m -=, 即tan tan x xm βα-= 解得tan tan tan tan x m αβαβ⋅=-【答案】(1)DC m =;(2)tan tan tan tan m αβαβ⋅-2. 化简:222tan1tan 2....tan89sin 1sin 2...sin 89︒⋅︒︒︒+︒++︒【解析】tan1tan2....tan89tan451︒⋅︒︒=︒=()()22222222sin 1sin 2...sin 89sin 1cos 1sin 2cos 2...sin 45︒+︒++︒=︒+︒+︒+︒++︒1894422=+=,故原式289=. 【答案】2893. 如图1、图2,是一款家用的垃圾桶,踏板AB (与地面平行)或绕定点P (固定在垃圾桶底部的某一位置)上下转动(转动过程中始终保持''AP A P BP B P ==,).通过向下踩踏点A 到'A (与地面接触点)使点B 上升到点'B ,与此同时传动杆BH 运动到''B H 的位置,点H 绕固定点D 旋转(DH 为旋转半径)至点'H ,从而使桶盖打开一个张角'HDH ∠.如图3,桶盖打开后,传动杆''H B 所在的直线分别与水平直线AB DH 、垂直,垂足为点M C 、,设''H C B M =.测得6cm 12cm '8cm AP PB DH ===,,.要使桶盖张开的角度'HDH ∠不小于60︒,那么踏板AB 离地面的高度至少等于多少cm ?(结果保留两位有效数字)【解析】过点'A 作'A N AB ⊥垂足为N 点,在Rt 'H CD ∆中, 若'HDH ∠不小于60︒, 则'3sin 60'H C H D ≥︒=, 即3''43H C H D ≥=, ∴''43B M H C =≥, ∵Rt 'Rt 'A NP B MP ∆∆∽ ∴''''A N A PB M B P=, ∴''643'23 3.5cm 'A P B M A N B P ⋅⨯=≥=≈,∴踏板AB 离地面的高度至少等于3.5cm .【答案】踏板AB 离地面的高度至少等于3.5cm课后作业1. 化简求值:1sin 1sin 1cos 1cos 1sin 1sin 1cos 1cos αααααααα⎛⎫⎛⎫-+-+-- ⎪⎪ ⎪⎪+-+-⎝⎭⎝⎭(090α︒<<︒) 【解析】原式()()()()222222221sin 1sin 1cos 1cos 1sin 1sin 1cos 1cos αααααααα⎡⎤⎡⎤-+-+⎢⎥⎢⎥=-⋅-⎢⎥⎢⎥----⎣⎦⎣⎦由090α︒<<︒可知,0cos 1α<<,0sin 1α<<.故原式1sin 1sin 1cos 1cos cos cos sin sin αααααααα-+-+⎛⎫⎛⎫=-- ⎪⎪⎝⎭⎝⎭2sin 2cos 4cos sin αααα--=⋅=. 图3图2C MAA'P BB'HDH'H'DHB'BPA'A(图1)NCMA'PBB'HDH'【答案】42. 若045α︒<<︒,且sin cos αα=sin α的值. 【解析】方法1:由2263sin cos sin cos 256αααα==,结合22sin cos 1αα+=,可得 2226397sin (1sin )sin 2561616ααα-=⇒=或. 由045α︒<<︒可知221sin sin 452α<︒=,故27sin sin 16αα=⇒=. 方法2:由sin cos 2sin cos αααα=,结合22sin cos 1αα+=,可得sin cos αα+==cos sin αα-=,故sin α.3. (2011甘肃兰州)通过学习三角函数,我们知道在直角三角形中,一个锐角的大小与两条边长的比值相互唯一确定,因此边长与角的大小之间可以相互转化.类似的,可以在等腰三角形中建立边角之间的联系.我们定义:等腰三角形中底边与腰的比叫做顶角的正对(sad ).如图①在ABC △中,AB AC =,顶角A 的正对记作sadA ,这时=BCsadA AB=底边腰.容易知道一个角的大小与这个角的正对值也是相互唯一确定的.根据上述角的正对定义,解下列问题: (1)60sad ︒= .(2)对于0180A ︒<<︒,∠A 的正对值sadA 的取值范围是 . (3)如图②,已知3sin 5A =,其中A ∠为锐角,试求sadA 的值.【解析】(1)1(2)02sadA <<(3)设53AB a BC a ==,,则4AC a =.在AB 上取4AD AC a ==,作DE AC ⊥于点E . 则312416164sin 4cos 44555555DE AD A a a AE AD A a a CE a a =⋅=⋅==⋅=⋅==-=,,,CD =图②图①C BAC B A∴CDsadAAC==EDCBA。
(word完整版)初中数学九年级锐角三角函数知识点总结,文档

【苏教版】初中数学九年级知识点总结28 锐角三角函数一、知识框架二、知识点、看法总结 1.Rt △ ABC 中(1) ∠ A 的对边与斜边的比值是∠A 的正弦,记作 sinA =∠ A 的对边斜边(2) ∠ A 的邻边与斜边的比值是∠A 的余弦,记作 cosA =∠ A 的邻边斜边∠ A 的对边(3) ∠ A 的对边与邻边的比值是∠ A 的正切,记作 tanA = ∠ A 的邻边∠ A 的邻边(4) ∠ A 的邻边与对边的比值是∠ A 的余切,记作 cota = ∠ A 的对边2. 特别值的三角函数:a sina cosa tana cota1 3 3 30°232345°2 2 121260°3 1 322333. 互余角的三角函数间的关系sin(90°- α)=cos α, cos(90°- α)=sinα,tan(90°- α)=cotα, cot(90°- α)=tanα.4.同角三角函数间的关系平方关系:sin2( α)+cos2( α)=1tan 2( α)+1=sec2(α)cot 2( α)+1=csc2(α)积的关系:sin α=tan α· cosαcosα=cot α· sin αtan α=sin α· secαcot α=cosα· cscαsecα=tan α· cscαcscα=secα· cot α倒数关系:tan α· cot α=1sin α· cscα=1cosα· secα=15.三角函数值(1 〕特别角三角函数值(2 〕0°~ 90°的任意角的三角函数值,查三角函数表。
(3 〕锐角三角函数值的变化情况(i 〕锐角三角函数值都是正当(ii 〕当角度在 0°~ 90°间变化时,正弦值随着角度的增大〔或减小〕而增大〔或减小〕余弦值随着角度的增大〔或减小〕而减小〔或增大〕正切值随着角度的增大〔或减小〕而增大〔或减小〕余切值随着角度的增大〔或减小〕而减小〔或增大〕(iii 〕当角度在 0°≤∠ A≤90°间变化时,0≤sin α≤ 1, 1 ≥cosA≥0,当角度在0°<∠A<90°间变化时,tanA>0, cotA>0.6.解直角三角形的根本种类解直角三角形的根本种类及其解法以下表:种类条件解法两边两直角边 a、 b c=a2b2, tanA=a,∠ B=90 ° -∠ A b素来角边 a,斜边 c b=c2a2, sinA= a,∠ B=90 ° -∠ A c一边一锐角素来角边 a,锐角 A a∠B=90 °-∠ A ,b=a· cotA ,c=sin A斜边 c,锐角 A∠B=90 °-∠ A ,a=c· sinA ,b=c· cosA7.仰角、俯角当我们进行测量时,在视线与水平线所成的角中,视线在水平线上方的角叫做仰角,在水平线下方的角叫做俯角.〔参照教材:初中数学九年级人教版〕。
初三锐角三角函数知识点总结、典型例题附带部分答案、练习(精选)
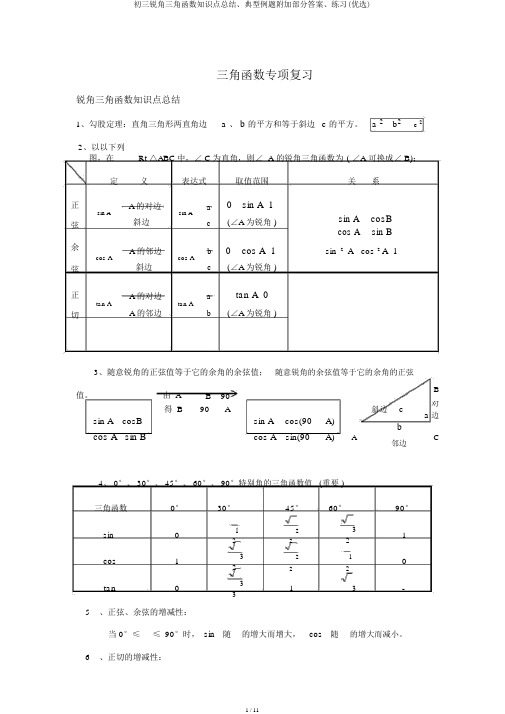
三角函数专项复习锐角三角函数知识点总结1、勾股定理:直角三角形两直角边 a 、 b 的平方和等于斜边 c 的平方。
a 2 b 2c 22、以以下列图,在Rt △ABC 中,∠ C 为直角,则∠ A 的锐角三角函数为 ( ∠A 可换成∠ B):定 义 表达式取值范围关系正A 的对边 a 0 sin A 1sin A 斜边sin A(∠A 为锐角 )sin A cosB 弦ccos Asin B余A 的邻边 b 0 cos A 1sin 2 A cos 2 A 1cos A 斜边cos A(∠A 为锐角 )弦c正A 的对边atan A 0tan Atan A(∠A 为锐角 )切A 的邻边b3、随意锐角的正弦值等于它的余角的余弦值; 随意锐角的余弦值等于它的余角的正弦值。
由 A B 90 B得 B90A斜边c对a 边sin A cosBsin Acos(90A)bcos A sin Bcos A sin(90A)AC邻边4、 0°、 30°、 45°、 60°、 90°特别角的三角函数值 (重要 )三角函数0° 30°45°60°90°sin0 1 2 3 1 222cos13 2 1 02 22tan0 3 13-35 、正弦、余弦的增减性:当 0°≤≤ 90°时, sin 随 的增大而增大, cos 随的增大而减小。
6 、正切的增减性:当 0° < <90°时, tan随的增大而增大,7、解直角三角形的定义:已知边和角(两个,此中必有一边)→全部未知的边和角。
依照:①边的关系:a2b2c2;②角的关系:A+B=90°;③边角关系:三角函数的定义。
( 注意:尽量防范使用中间数据和除法)8、应用举例:(1)仰角:视野在水平线上方的角;俯角:视野在水平线下方的角。
初三下学期锐角三角函数知识点总结及经典例题
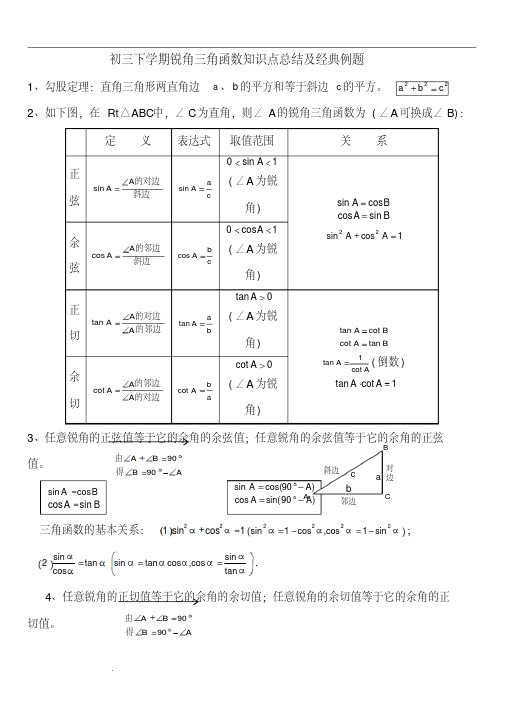
1、勾股定理:直角三角形两直角边 a 、 b 的平方和等于斜边 c 的平方。 a 2 b 2 c 2 2、如下图,在 Rt△ABC中,∠ C为直角,则∠ A的锐角三角函数为 ( ∠A 可换成∠ B):
定义
正
sin A
弦
A的对边 斜边
余
cos A
弦
A的邻边 斜边
1
1
60°
3 2 1 2
3
3 3
90° 1 0
不存在 0
当 0°≤ ≤90°时, sin 随 的增大而增大, cos 随 的增大而减小。 7 、正切、余切的增减性:
当 0°< <90°时, tan 随 的增大而增大, cot 随 的增大而减小。
8、应用举例: (1) 仰角:视线在水平线上方的角;俯角:视线在水平线下方的角。
)A. 2 B . 2 2 C . 1
3
3
3
D. 10
3
4. 等腰三角形的边长为 6,8,则底角的余弦是( 和3
8
)A.2 B .3 C .4 D .2
3
8
3
3
5. 某市在旧城改造中,计划在市内一
块如图 1 所示三角形
空地上种植草皮以美化环境,已知
A 20米
150°
30米
售价 a 元,则购买这种草皮至少需要 B
么重叠部分(阴影)
的面积是(
).
A. 1 D. 1
cos
B. 1
sin
C.
1 sin2
10. 如图 5,在高楼前 D 点测得楼顶的仰角为
30°,向高楼前 进 60 米到 C 点,又测得仰角为 45°,则该高楼的高度大
人教版九年级数学下册锐角三角函数知识点及例题整理
28. 锐角三角函数知识点一: 正弦的定义及其表示方法1. 在直角三角形中,一个锐角的对边与斜边的比叫做这个锐角的正弦,如:∠A 的正弦记作sinA ,即sinA = ∠A 的对边斜边 = a c.2. 求锐角的正弦值,要以正弦的概念为依据,在直角三角形中求解。
若题目中给出的角不是在直角三角形中,应先构造直角三角形再求解。
3. 画出符合题意的图形,弄清所求角的对边与斜边。
4. 没有直接给出对边与斜边的题目,一般先根据勾股定理,求出所需的边长再求解。
例1:判断:在Rt△ABC 中,∠A 的正弦,记作cosA.______(填”对”或“错”) 例2:判断:在Rt△ABC 中,∠A 的正弦都等于∠A 的邻边与对边的比.______(填”对”或“错”)例3:Rt△ABC 中,∠C=90°,a 、b 、c 分别是∠A、∠B、∠C 的对边,下列式子中,正确的是( )A. a=b ⋅sinA ;B. a=c ⋅sinA ;C. b=a ⋅sinA ;D. c=b ⋅sinA ; 例4:下列说法中,不正确的有______个.①直角三角形中,锐角的正弦为对边比斜边②直角三角形中,锐角的正弦为斜边比对边③直角三角形中,锐角的正弦为一条直角边比另一条直角边④直角三角形中,锐角的正弦为任意一条直角边比斜边例5:下列说法中,正确的有______个.①一个锐角的正弦值是一个无单位的量②某一锐角的正弦值与这个锐角所在的三角形的大小无关③sinA 既是一个完整的符号,同时也可以表示为sin×A 的乘积关系④在所有的ΔABC中,都可以计算出sinA= BC AB【答案】1.错; 2.错; 3.B; 4. 3; 5. 2;知识点二:余弦的定义及其表示方法1.如图,在直角三角形中,∠C=90°,我们把锐角A的邻边b与斜边c的比叫做∠A的余弦,记作cos A,即cos A =∠A的邻边斜边=bc.2.注意:(1)余弦也是建立在直角三角形中的,当锐角度数一定时,不论直角三角形的大小,它的邻边与斜边的比是一个固定值,换句话说,余弦值只与锐角的大小有关。
九年级数学《锐角三角函数》知识点总结归纳
一、三角函数的定义1. 正弦函数sinx:对于任意实数x,将x的终边与x轴正方向的夹角的终点的纵坐标就是sinx。
2. 余弦函数cosx:对于任意实数x,将x的终边与x轴正方向的夹角的终点的横坐标就是cosx。
3. 正切函数tanx:对于任意实数x,将sinx除以cosx就是tanx。
4. 余切函数cotx:对于任意实数x,将cosx除以sinx就是cotx。
5. 正割函数secx:对于任意实数x,将1除以cosx就是secx。
6. 余割函数cscx:对于任意实数x,将1除以sinx就是cscx。
二、三角函数的性质1. 基本关系式:sin^2x + cos^2x = 12. 周期性:sin(x+2kπ) = sinx,cos(x+2kπ) = cosx,其中k为任意整数。
3. 奇偶性:奇函数有sinx、tanx和cotx,偶函数有cosx、secx和cscx。
4. 正函数和负函数:在单位圆上,sinx和cscx为正函数,cosx和secx为负函数。
5. 三角函数的范围:sinx、cosx和tanx的范围是[-1,1],cotx、secx和cscx的范围是(-∞,∞)。
三、特殊角的三角函数值1.0°、30°、45°、60°和90°的三角函数值。
2.30°、45°、60°和90°的三角函数值的推导。
四、角度的度量转换1.度和弧度之间的转换:π弧度=180°,1°=π/180弧度。
2.角度的换算:1°=60',1'=60''。
五、倍角、半角和三倍角公式1. 倍角公式:sin2x = 2sinxcosx,cos2x = cos^2x - sin^2x,tan2x = 2tanx / (1 - tan^2x)。
2. 半角公式:sin(x/2) = ±√[(1-cosx)/2],cos(x/2) =±√[(1+cosx)/2],tan(x/2) = ±√[(1-cosx) / (1+cosx)]。
初三锐角三角函数知识点与典型例题
4. 已知 A 是锐角, sin A 8 ,求 cos A , tan A 的值 17
对应训练:
(西城北) 3.在 Rt△ ABC中,∠ C=90°,若 BC= 1, AB= 5 ,则 tan A 的值为
高,已知小聪和树都与地面垂直,且相距 3 3 米,小聪身高 AB
为 1.7 米,求这棵树的高度 .
A
D
B
E
例 5.已知:如图,河旁有一座小山,从山顶 A 处测得河对岸点 C的俯角为 30°,测得岸边 点 D的俯角为 45°,又知河宽 CD为 50m.现需从山顶 A 到河对岸点 C拉一条笔直的缆绳 AC, 求山的高度及缆绳 AC的长 ( 答案可带根号 ) .
A. 0 °< A < 60° B. 30°< A < 60° C. 60 °< A < 90 ° D. 30 °< A < 90 °
例 4. 三角函数在几何中的应用
...
.
1.已知:如图,在菱形 ABCD中, DE⊥AB于 E,BE= 16cm, sin A 12 13
求此菱形的周长.
2.已知:如图, Rt△ ABC中,∠ C= 90°, AC BC
A. 200 米
B. 200 米
C. 220 米
D. 100(
)米
例 2.已知:如图,在两面墙之间有一个底端在
A 点的梯子,当它靠在一侧墙上时,梯子的
顶端在 B 点;当它靠在另一侧墙上时, 梯子的顶端在 D点.已知∠ BAC= 60°,∠ DAE=45°.点
D到地面的垂直距离 DE 3 2m ,求点 B 到地面的垂直距离 BC.
九年级数学下学期期末知识点复习:锐角三角函数
九年级数学下学期期末知识点复习:锐角三角函数
2019学年九年级数学下学期期末知识点复习:
锐角三角函数
知识点在不断更新的同时也需要及时的归纳总结,才能更好的掌握,接下来查字典大学网初中频道给大家整理九年级数学下学期期末知识点复习,供大家参考阅读。
锐角角A的正弦(sin),余弦(cos)和正切(tan),余切(cot)以及正割(sec),(余割csc)都叫做角A的锐角三角函数。
正弦等于对边比斜边
余弦等于邻边比斜边
正切等于对边比邻边
余切等于邻边比对边
正割等于斜边比邻边
余割等于斜边比对边
正切与余切互为倒数
它的本质是任意角的集合与一个比值的集合的变量之间的映射。
通常的三角函数是在平面直角坐标系中定义的,其定义域为整个实数域。
另一种定义是在直角三角形中,但并不完全。
现代数学把它们描述成无穷数列的极限和微分方程的解,将其定义扩展到复数系。
由于三角函数的周期性,它并不具有单值函数意义上的反函数。
它有六种基本函数(初等基本表示):。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
12、在 △ th 中, sin A. 锐角三角形 B. 直角三角形 C. 等边三角形 D. 钝角三角形
二、填空题
t sin tt h ,则 △ th 为( )
1、已 知 直 角 三 角 形 的 一 个 锐 角 的 余 弦 值 为 , 则 它 的 正 弦 值 也
为
。
2、在 △ ABC 中 , 若 tan A h
1、已知直角三角形的两直角边之比为 th , ∠ 是它的一个锐角,则 ∠ 的 正切值为( )。
A.
h
B. h
C. 或 h
h
D. 不能确定
2、如图,在 t △ th 中, 函数表示正确的是( )。
, t h , th h ,则下列三角
A. sin h B. cos h C. tan h D. tan t h 3、已知等腰三角形底角的余弦值为 ,则三角形顶角的余弦值为( )。
锐角三角函数
概念:
正 弦 : 在 Rt △ ABC 中 , ∠ C=900 , 我 们 把 锐 角 A 的 对 边 与 斜 边 的 比 叫 ∠A 的正弦,记作 sinA。
余弦:在 Rt△ABC 中,∠C=900 ,我们把锐角 A 的邻边与斜边的比叫做 ∠A 的正 弦,记作 cosA。
正切:在 Rt△ABC 中,∠C=900 ,我们把锐角 A 的对边与邻边的比叫 ∠A 的正切,记作 tanA。
解析:本题主要考查完全平方公式和勾股定理。
由完全平方公式的概念“两数和(或差)的平方,等于它们的平方和,加上
(或减去)它们的积的 倍”可知,
h⇒
h⇒
h ,即满足勾股定理,所以三角形应为直角三角形,故 C
项符合题意。
7、【答案】C
解析:本题主要考查等腰三角形的判定和勾股定理的逆定理。
如果一个三角形两边的平方和等于第三边的平方,那么这个三角形是直角三
〱 h ,那么这个三
角形是( )。
A. 锐角三角形
B. 直角三角形 C. 钝角三角形 D. 无法确定
10、在 △ th 中, t h , h h , th h A. 锐角三角形 B. 直角三角形 C. 钝角三角形 D. 等腰直角三角形
,则该三角形为( )。
11、在一个三角形中,若 ∠ h ∠t ∠h ,则 △ th 是( )。 A. 直角三角形 B. 锐角三角形 C. 钝角三角形 D. 以上都不对
为
。
, sin B h
, 则 △ ABC
3、已知直角三角形的斜边 AB 与一直角边 BC 的比为 7t ,则 ∠B 的余
弦值为
。
4、身高 . m 的小丽用一个两锐角分别为 和 的三角尺测量一棵
树的高度,已知她与树之间的距离为 m ,那么这棵树高大约为
。
三、计算题 1、如图,一艘海轮位于灯塔 的北偏东 650 方向,距离灯塔 海里的
角形。由题意知,
h
,所以该三角形为直角三角形。因为三角形
中有两边相等,因此该三角形为等腰直角三角形。
8、【答案】A
个顶点, sin , cos t 是方程 h 〱
h 的两个不相等的实数根,
求 〱 的值及 ∠ 和 ∠t 的大小。
3、如图,防洪大堤的横截面是梯形 th ,其中
,h
,
汛期来临前对其进行了加固,改造后的背水面坡角
。若原坡长 t h
〱 ,求改造后的坡长 t 。(结果保留根号)(10 分)
4、已知 〱 , , 为一个直角三角形的三边长,且有 〱 h ,求三角形三边长分别为多少。
勾股定理的逆定理可知, △ th 是直角三角形。
5、【答案】C
解析:本题主要考查三角形的基本概念和三角形内角和定理。
因为三角形三个内角的比为 t t ,则不妨设三角形的三个内角分别为
, , 。因为三角形的内角和为
,则
h
,解
得 h 。因此三角形的三个内角分别为 , , ,即该三角形
为直角三角形。
6、【答案】C
A 项正确。 3、【答案】A 解析:本题主要考查角的正弦值和余弦值。
因为等腰三角形底角的余弦值为 ,所以底角为 ,所以顶角为 ,
所以顶角的余弦值为 。 4、【答案】B
解析:本题主要考查勾股定理的逆定理。
由题意可知,
h,
h , h h ,即 h , h ,
h h ,因为
h h h , h h ,即
h ,由
A.
B.
C. D. 4、已知 、 、 是三角形的三边长,如果满足 ,则三角形的形状是( )。
t th
h
A. 等腰三角形 B. 直角三角形 C. 锐角三角形 D. 钝角三角形 5、若三角形三个内角的比为 t t ,则这个三角形是( )。 A. 钝角三角形 B. 锐角三角形 C. 直角三角形 D. 等腰直角三角形 6、三角形的三边长分别为 、 、 ,且满足等式 则此三角形是( )。 A. 锐角三角形 B. 钝角三角形 C. 直角三角形 D. 等腰直角三角形
h,
7、已知一个三角形的三边长分别为 〱 , 〱 和 〱 ,则这个三角形是
( )。
A. 等腰三角形
B. 直角三角形
C. 等腰直角三度数的比为 t th ,则这个三角形是( )。
A. 锐角三角形
B. 直角三角形
C. 钝角三角形
D. 等边三角形
9、如果三角形的三边 , 〱 , 满足 〱
特殊三角函数值
A
sinA
cosA
tanA
300
1
3
3
2
2
3
450
2
2
1
2
2
600
3
1
2
2
3
解直角三角形及其应用:
解直角三角形:由直角三角形已知元素求出其他未知元素的过程。 勾股定理:直角三角形两直角边 a、b 的平方和等于斜边 c 的平方 a2+b2=c2。 解直角三角形的基本类型及其方法
一、选择题
答案
一、选择题
1、【答案】C 解析:本题主要考查角的正切值。 因为只知道 ∠ 是锐角,所以根据正切的定义,可得 ∠ 的正切值为
h
或h。 2、【答案】A
解析:本题主要考查三角函数。
在 t △ th 中,根据勾股定理可得, h h t th h
h
,则 sin h , cos h , tan h , tan t h ,故只有
处,它沿正南方向航行一段时间后,到达位于灯塔 的南偏东 450 方向上的 t 处,这时,海轮所在的 t 处距离灯塔 有多远?(结果用非特殊角的三角函 数及根式表示即可)
2、对于钝角 ,定义它的三角函数值如下:
,
。
(1)求
,
,
的值。
(2)若一个三角形的三个内角的比是 t th , , t 是这个三角形的两
