多阀同步振动台解耦控制的
解耦控制2

相对增益矩阵的一般求法(1)
• 对于已知的多输入多输出系统的静态特性矩阵形式为
Y=MU 式中Y=[y1,y2,……..,ym]T;U=[u1,u2,……..,um]T
y1 u 1 . M . ym u1
u
..... . .
y1 um . .
u
ym ..... um
1 detM
其中,Δij为M矩阵中对应元素的代数余子式。
相对增益矩阵的一般求法(3)
• 从矩阵C的形式可以看出,相对放大系数阵列表的每 一行(或每一列),都是行列式M对应行(或列)的 展开式并除以M的行列式。这个结果必然导致相对增 益矩阵每一行(或每一列)的元素相加等于1。 • 可以利用这个结果来减少求相对放大系数的次数。如 一个2×2的耦合系统只需要计算一次相对增益,一个 3×3的耦合系统只需要计算4次相对增益,其他相对放 大系数皆可由这些相对放大系数求出来。
K13 K 23 K 33 Q1 0.311 102 R3 Q2 0.155 102 R3 Q3 0.722 102 R3
Q1 0.746103 R1 0.124103 R2 0.311102 R3 Q2 0.249103 R1 0.258103 R2 0.155102 R3 Q3 0.124103 R1 0.311102 R2 0.722102 R3
3×3耦合对象(5)
• 使用与二阶系统相同的方法,可求得本3×3系统的 相对增益矩阵为:
K11 K 22 K 33 K 23 K 32 K 21 K12 K 33 K13 K 32 K 31 K12 K 23 K 22 K13 K12 K 21 K 33 K 23 K 31 K 22 K11 K 33 K13 K 31 K 32 K11 K 32 K 21 K13 K13 K 32 K 21 K 22 K 31 K 23 K11 K 32 K 31 K12 K 33 K11 K 22 K12 KRelative gain )
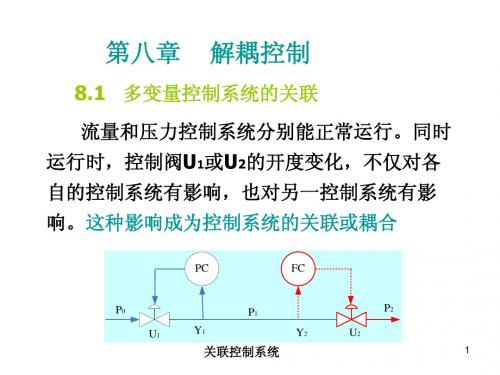
第八章 解耦控制
3
控制系统之间的耦合(关联)程度可用传递函数矩阵表示。 控制系统之间的耦合(关联)程度可用传递函数矩阵表示。
Y( s ) = G ( s ) U( s )
Y1 (s) G 11 (s) G 12 (s) U1 (s) Y (s) = G (s) G (s) U (s) 22 2 21 2
确定各变量之间耦合程度的分析方法有直接法和相对增 确定各变量之间耦合程度的分析方法有直接法和相对增 益法。直接法是采用解析法得到各变量之间的传递函数 益法。直接法是采用解析法得到各变量之间的传递函数 关系,从而确定过程中每个变量相对每个控制作用的耦 关系, 合程度。相对增益法是一种通用的耦合特性分析工具, 合程度。相对增益法是一种通用的耦合特性分析工具, 通过相对增益矩阵,不仅可以确定变量之间的耦合程度, 通过相对增益矩阵,不仅可以确定变量之间的耦合程度, 相对增益矩阵 并且以此去设计解耦控制系统。 并且以此去设计解耦控制系统。
同理
u2
= k11
= k 21,p22 = ∂y2 ∂u2 = k 22
7
p12 =
∂y1 ∂u2
u1
= k12,p21 =
∂y2 ∂u1
u2
u1
第二增益系数 qij 输入 u j 对输出 yi 的第二增益系数指其它控制回路 均为闭环( Y ( s) = 0, k ≠ j ) 该通道的增益,用
k
∂yi qij = ∂u j
17
v22
vn 2
消除和减弱耦合的方法
(1)被控变量(输出变量)与操纵变量(输入变量) )被控变量(输出变量)与操纵变量(输入变量) 间的正确匹配 若相对增益矩阵为单位阵,则表明过程通道之间没 有静态耦合,系统的每一个通道均可以构成单回路控制。 如果控制系统的相对增益矩阵中有一个相对增益
5 第5章 解耦控制

D 11 ( s ) D 22 ( s ) 1
D 12 ( s ) G 11 ( s ) 1 G 21 ( s )
G 12 ( s ) G 22 ( s ) 0
D 12 ( s ) D 21 ( s )
第三节 串接解耦装置的设计
3. 前馈补偿法
只规定对角线以外的元素为零,并且规定某几 个 Dij(s) 为适当的数值
各条通道的传递函数一般不再是原来的Gii(s), 如取某几个 Dij(s) =1 在通道数目不多时,用常规仪表也容易实现, 称之为简化的解耦方案
第三节 串接解耦装置的设计
双通道,取
假设系统 2 闭环后接近理想控制,Y2(s)=0
Y1 ( s ) G 11 ( s ) 0 G 21 ( s ) G 12 ( s ) U 1 ( s ) G 22 ( s ) U 2 ( s )
第一节 系统的关联分析 一.系统的关联
Y1 ( s ) G 11 ( s ) 0 G 21 ( s ) G 12 ( s ) U 1 ( s ) G 22 ( s ) U 2 ( s )
由方程2
G 21 ( s )U 1 ( s ) G 22 ( s )U 2 ( s ) 0
k 11 k 22 k 12 k 21 k 22
11
y1 / u 1 |u y1 / u 1 | y
k 11 k 22 k 11 k 22 k 12 k 21
第一节 系统的关联分析 二.相对增益
2. 相对增益阵
λ11 λ 21
解耦控制

ij
pij q ij
pij 第一放大系数(开环增益) qij 第二放大系数(闭环增益)
过程控制 青海大学
2014-1-17
17
3.2.2
相对增益与相对增益矩阵
第一放大系数pij (开环增益) – 指耦合系统中,除Uj到Yi通道外,其它通 道全部断开时所得到的Uj到Yi通道的静态 增益; – 即,调节量 Uj 改变了 Uj 所得到的 Yi的变 化量Yi与Uj之比,其它调节量 Uk(k≠j) 均不变。 – pij可表示为:
2014-1-17
过程控制 青海大学
10
3.2.1
耦合过程及其要解决的问题
耦合程度分析方法
– 直接法
解析法
– 相对增益法
求相对增益矩阵的计算方法
2014-1-17
过程控制 青海大学
11
3.2.1
耦合过程及其要解决的问题
直接法
– 借助耦合系统的方框图,直接解析地导出各 变量之间的函数关系,从而确定过程中每个 被控量相对每个调节量的关联程度。
PC FC
u1
PT
FT
u2
图 6-8 关联严重的控制系统
2014-1-17
过程控制 青海大学
4
3.2.1
耦合过程及其要解决的问题
控制回路间的关联
控制回路间的耦合
– 单回路控制系统 – 多回路控制系统 – 各回路间的耦合
一个调节量影响多个被控变量;
R1
U1 Gc1 Gp1 Y1
Rn
Yn Gcn Un Gpn
Yi qij U j
2014-1-17
Yk const
Uj → Yi的增益 (不仅Uj → Yi通道投运,其 他通道也投运)
周丽多电机总线网络技术与同步解耦控制策略研究精讲

二、多电机总线网络技术
PROFIBUS现场总线通讯协议包括三个主要部分: • PROFIBUS-DP:主站和从站之间采用轮循的通讯
方式,主要应用于自动化系统中单元级和现场级通 信。 • PROFIBUS-PA:电源和通信数据通过总线并行传 输,主要用于面向过程自动化系统中单元级和现场 级通讯。 • PROFIBUS-FMS:定义了主站和主站之间的通讯 模型,主要用于自动化系统中系统级和车间级的过 程数据交换。
二、多电机总线网络技术
PROFIBUS是目前国际上通用的现场总 线标准之一,是不依赖于生产厂家的、开 放式的现场总线,各种各样的自动化设备 均可以通过同样的接口交换信息。 PROFIBUS用于分布式I/O设备、传动装 置、PLC和基于PC的自动化系统.
二、多电机总线网络技术
90年代初,PROFIBUS由西门子引入中 国,开始被国内所接受。到中德两国政府有 关部门支持及西门子大力推广,PROFIBUS 中国发展势头良好,目前,PROFIBUS我国 已拥有众多用户,如上海扬树蒲电厂、西安 扬森制药厂、云南玉溪卷烟厂、青岛啤酒厂、 海尔冰箱生产线。
二、多电机总线网络技术
现场总线有以下优点: 1、一对N的结构,一对传输线,可以对应多台现场数
字仪表,也可采用多种网络拓扑结构,简化了工程 设计,降低了工程费用; 2、现场总线采用数字信号传输;实现远程监控;综合 多种功能,以微处理器为基础的数字仪表具有多种 功能; 3、数字调节阀直接从现场总线接收数字调节信号,在 现场总线上就可以构成回路,把原来的DCS站的功 能下放到现场仪表,实现彻底地分散,提高系统的 可靠性 。
无忧PPT整理发布
代表全世界1200 多家会员公司的 PROFIBUS 国际组织推出了基于实时工业以 太网的PROFINET 自动化解决方案。该技术 为当前的用户提供了一套完整高性能可伸缩的 升级至工业以太网平台的解决方案PROFINET 是一项重大的并具有战略性的技术创新,它不 仅能为PROFIBUS,而且能为其它现场总线网 络系统提供以太网移植服务。
7.1-3 解耦控制Decouple

过程控制/ Process Control2010 by解耦控制/Decouple系统的耦合相对增益解耦系统Condition Number过程控制/ Process Control Inputs and Outputs 2010 byUp to now, we have relied on our intuition about a process to decide how to connect sensors to actuators, but there area few problems that can arise:(1)Sometimes these parings can be difficult to determine(2)Sometimes it is difficult to distinguish between pairings(3)Sometimes the parings we think will work don’t work(4)Sometimes there are no pairings that will work Questions:•Are there other, data driven ways to see if asystem can be decoupled?•How can we evaluate the best pairing in a more objective way?Four terms:1) SISO : Single input, single output. Simplest to design, uses data from one sensor to control one thing.PID controller TC v12) SIMO : Single input, multiple output. Uses data from one sensor to control multiple things.#1 PID controllerTCv1#2 PID controllerTCv23) MISO:Multiple input, single output. More complex as it uses data from multiple sensors to control one thing. E.g. cascade control#1 PID controllerTCv1FC#2 PID controllerSet point4) MIMO:Multiple Input, Multiple Output. Hardest to design as it integrates multiple sensor data to coordinate multiple actuators MIMOcontroller TCv2FCv1v3General strategy:•MIMO controllers are more complex, and as such designers often try to avoid them.•Process design attempts to minimize cross-talk between sensors and actuators if possible.•Even if there is significant cross talk, can we get away with a simpler controller by finding approximate pairings?Note: MIMO controllers are generally not PID, and as such are often designed for each particular case.Questions:•CN?•RGA?如上图示,两个调节量,两个被调量;K ij为静态增益,g ij为动态向量;任一调节量的变化将影响所有被调量;若K21/g21=0,K12/g12=0,则蜕化成下图.即调节量对被控量的影响是各自独立的,相互之间没有耦合K11/g11K22/g22y1y2μ1μ2K11/g11K21/g21K12/g12K22/g22y1y2μ1μ2用方框图描述过程控制/ Process Control2010 by概述一个生产过程甚至一个对象中有两个或两个以上的被调参数、调节参数(多变量控制系统),而这些参数之间又是相互关联或耦合的。
解耦控制系统
接计算第二放大系数, 从而得到相对增益矩 阵。
10
相对增益系数的计算方法1
输入输出稳态方程
u1(s)
y1(s) y1 K11u1 K12u2
u2(s)
y2(s) y2 K21u1 K22u2
0
0 Gp22 (s)
Gp11(s)Gp22
(s)
1
Gp12
(s)Gp21(s)
Gp22 (s) Gp21(s)
Gp12 (s)Gp11(s)
Gp11(s)
0
0 Gp22 (s)
Gp11(s)Gp22 (s)
G
p11
(
s)G
p
22
(s)
G
p12
(
s)G
p
21
(s)
Gp11(s)Gp21(s)
G
p11
(
s)G
p
22
(s)
G
p12
(
s)G
p
21
(s)
Gp22 (s)Gp12 (s)
G
p11
(
s)G
p
22
(s)
G
p12
(
s)G
p
21
(s)
Gp11(s)Gp22 (s)
G
p11
(
s)G
p
22
(s)
G
p12
(
s)G
p
21
(s)
29
3.解耦控制系统设计
R1
Gc1(s) Uc1 Gp11(s) Y1
基于动力学耦合模型的超冗余振动台解耦控制-概述说明以及解释
基于动力学耦合模型的超冗余振动台解耦控制-概述说明以及解释1.引言1.1 概述概述部分的内容可以包括以下方面:超冗余振动台是一种由多自由度振动台组成的复杂系统,在众多工业领域具有广泛的应用。
然而,由于振动台中的自由度较多,各自由度之间存在耦合效应,使得振动台的运动受到相互影响,导致控制困难。
为了克服这些问题,引入动力学耦合模型成为解耦控制的有效手段。
本文主要研究了基于动力学耦合模型的超冗余振动台的解耦控制方法。
首先,对振动台的动力学行为进行建模和分析,考虑了各自由度之间的耦合效应。
其次,提出了一种基于解耦控制的策略,通过分析振动台的动力学特性,将其分解为多个子系统来进行控制,从而实现各自由度之间的独立控制。
最后,设计了相应的解耦控制算法,并通过实验验证了其有效性。
本文的研究意义在于提出了一种针对超冗余振动台的解耦控制方法,有力地解决了多自由度系统中的耦合效应问题。
通过将振动台分解为多个子系统进行独立控制,不仅保证了振动台的正常运行,并且提高了系统的控制精度和效率。
该方法为超冗余振动台的控制与应用提供了一种新思路和技术支持。
下一部分将介绍本文的组织结构。
1.2文章结构文章结构部分的内容应该包括该篇文章的主要分节和每个分节的内容概述。
可以参考以下例子进行编写:1.2 文章结构本文分为三个主要部分:引言、正文和结论。
在引言部分,首先概述了本文的研究背景和目的,引出了使用动力学耦合模型对超冗余振动台解耦控制进行研究的需求。
在正文部分,首先介绍了动力学耦合模型的基本原理和方法,包括系统的数学描述和参数估计方法。
接着,详细阐述了超冗余振动台的解耦控制策略,包括对控制系统的设计和分析。
通过分析和实验验证,展示了该方法的有效性和可行性。
最后,在结论部分,对本文的研究内容进行总结,并展望了未来进一步深入研究的方向和可能的应用领域。
通过以上组织结构,本文将系统地介绍基于动力学耦合模型的超冗余振动台解耦控制。
每个部分将清晰地展示研究内容,使读者能够快速了解本文的主要观点和研究方法。
第七章 解耦控制
(yi j ) | ur (yi j ) | yr
越大, pij与qij相差越大, 说明别的
回路的闭合与否对yi和µ控制通道影响越大, 即µ对yi的控制 j j 作用越弱。
20
相对增益与耦合程度
◆当通道的相对增益接近于1, 例如0.8<λij <1.2, 则表明其它通 道对该通道的关联作用很小; 无需进行解耦系统设计。 ◆当相对增益小于零或接近于零时, 说明使用本通道调节器不 能得到良好的控制效果. 或者说, 这个通道的变量选配不适当, 应重新选择. ◆当相对增益0.3<λ<0.7或λ>1.5时, 则表明系统中存在着非 常严重的耦合. 需要考虑进行解耦设计或采用多变量控制系统 设计方法.
PC QC
h t/40 - 1 例3. P152例7-1 μ1 p0 p1 h p p2 0 p1 - p2 p1 p0 p2
p1
PT
h
DT
μ2 p1 - p2 p0 p2 p0 p1 p0 p2
p0
p2
μ1
μ2
14
2. 矩阵法 由第一放大系数经过计算得到第二放大系数从而得到相对增 益矩阵
y2为定值, µ 2是变化的
y1 第一放大系数 p11 u1
K11
u2
y2 K 21u1 y1 K11u1 K12 K 22
第二放大系数
相对增益
11
1 K12 K 21 1 K11 K 22
12
相对增益ij的计算,直接根据定义得
p11 K11 K 22 q11 K11 K 22 K12 K 21 p12 K12 K 21 12 q12 K12 K 21 K11 K 22 p K12 K 21 21 21 q21 K12 K 21 K11 K 22 p22 K11 K 22 22 q22 K11 K 22 K12 K 21
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
积;yp 为活塞输出位移;Vt 为液压缸容积;Eh 为体积弹性模量;
(3)活塞及负载的动力学方程可表示为:
Ap
pL
=m
d2 yp dt 2
+
B
p
dyp dt
+ KL yp
+ FL
其中,m、Bp表示活塞及振动台架等负载的总质量和粘性阻尼系数;
KL表示负载的弹簧刚度;FL表示作用在活塞上的外负载力。
3.多阀同步振动台仿真分析
图 3 振动中心对位移波形的影响 (3)活塞输出位移最大值分析 在振动台中,活塞输出位移最大幅值越大,液压缸推力越大,通过 引入振动中心,可减弱因激振频率提高对幅值的急剧衰减作用,增加液 压缸的输出力。 位移最大值 yr由激振频率、幅值和振动中心共同决定,仿真分析 f= 100Hz,不同滑阀开口下,转阀轴向开口与激振波形振幅间的关系如图 4 所示。 由于 yr受振动中心和振幅的联合作用,yr随转阀开口的增大先减小 再增大,滑阀开口越小,yr 的增大、减小速率越显著。当转阀开口较小 (如 5%)时,振动的最大幅值主要受滑阀的影响,滑阀开口越大,yr越大, 随着转阀轴向开口逐渐增大,流经转阀进入液压缸的油液比例增大,流 经滑阀的油液比例减小,振动中心作用减弱,振动中心的减小程度大于 转阀开口对幅值的增大程度,因此 yr继续减小;当转阀开口大于某一临 界值后,yr 开始随转阀开口的增大而增大,这是由于此时转阀开口对幅 值的增大程度大于振动中心对最大振动幅值的削减程度。
图 2 转阀轴向开口与幅值的关系 (2)振动中心对位移波形的影响 激振频率为 50Hz,转阀轴向开口最大,不同滑阀轴向开口的活塞 位移波形如图 3 所示。滑阀关闭时,振动波形中心为零、与液压缸中心 重合;通过改变滑开口大小可实现不同位置的振动中心,开口越大振动 中心偏移液压缸中心越远,当滑阀开口大于某一临界值后,波峰处将出 现流量饱和现象。
0.引言 振动台是一种提供典型振动条件以检验和评价各类工程装置机械 力学性能的标准试验设备,尤其是电液振动台因其大推力大位移,在航 空航天、汽车等行业具有广泛的应用前景,因此研究振动台的位移波形 具有重要的理论及实际工程意义。 在传统的电液伺服系统中,一般采用力马达滑阀式或喷嘴-挡板式 电液激振器,可通过叠加信号构成闭环的方法实现对振动台输出位移 波形的控制,早在上世纪 70 年代已提出将振动控制理论应用于振动试 验。 受频响特性限制,传统滑阀或马达构成的电液振动台频率难于提 高至一较高的水平,本文提出采取双自由度转阀与一三位四通滑阀共 同作用于对称液压缸的方式构建多阀同步振动台,不仅可获得较高的 激振频率,更可通过对振动幅值和振动中心的联合控制提高活塞位移 最大值,补偿因频率提高对幅值的削弱,增加在较高频率时的振动台输 出力。 1.多阀同步振动台工作原理 本文构建多阀同步电液振动台原理如图 1 所示,转阀与电液数字 滑阀并联,共同作用于双出杆对称液压缸,驱动活塞围绕某一平衡位置 (即振动中心)作周期性往复运动,利用转阀阀芯的旋转运动和轴向滑 动分别实现振动台频率和幅值的独立控制,利用滑阀的轴向滑动实现 振动波形中心位置的控制[1]。 转阀同时具有径向旋转和轴向滑动两个自由度,其阀芯轴向均布 四个台肩,每个台肩周向均布四个圆心角为α的沟槽,通过与阀套上的 窗口沟通形成阀口,随着阀芯的旋转,阀口面积呈三角波周期变化,进 出液压缸油液的大小和方向也呈周期性变化,从而驱动活塞杆作往复 运动,一旦转阀结构固定,振动台频率为阀芯转速与每转阀芯沟槽与阀 套窗口之间沟通次数的乘积,易于实现高频激振,并能很好地保持电液 激振所固有的较大激振推力特性。通过调整转阀阀芯的轴向位移 xv1可 改变阀口面积梯度,进而改变振动幅值;通过改变并联滑阀的轴向节流 开口 xv2的大小实现不同的振动中心,从而实现了对多阀同步振动台输 出位移最大值的准确控制,达到提高振动台输出力的目标。
图 1 多阀同步振动台工作原理
2.数学模型建立
转阀与滑阀的阀口节流面积分别为 Av1 - Av4 和 A1 - A4 ,皆按匹 配-对称结构设计,根据流体动力学和系统动力学理论构建数学模型[2]。
(1)流量方程
转阀负载流量为:
QL1 = Cd Av2
ps - pL ρ
- Cd Av1
ps + pL ρ
振动台输出位移波形的频率、幅值及振动中心分别由转阀阀芯连
续旋转转速、转阀轴向位移及与滑阀轴向位移来实现开环或闭环控制,
三者相互耦合,故建立 Simulink 模型仿真分析如下[3,4]:
(1)振动幅值分析
仿真分析滑阀关闭,不同频率下振动幅值随转阀开口变化情况如
图 2 所示。从图中可知,当激振频率较低(如 5Hz)、阀芯轴向开口较小
基金项目:本文系杭州职业技术学院 2012 年度院级项目:《振动台多阀同步系统解耦控制的研究》,项目编号:ky201211。
— 16 —
科技信息
根据转阀与滑阀并联的原理实现激振频率提高、输出力增大的目 标,搭建振动台,实验装置见图 5。
图 6 为实测的活塞输出位移幅值随滑阀轴向开口变化的曲线。实 测曲线和仿真结果基本吻合,即可实现对振幅的准确控制。
时,幅值 Ay(p 最大值为 Aypm)与阀芯开口间呈线性关系,活塞位移幅值随 阀芯轴向开口的增大而线性增大,上升斜率与频率大小有关,频率越大
斜率越小;当阀芯轴向开口增大到某一值时,出现流量饱和现象,幅值
达最大值;在激振频率较高时,幅值衰减严重,不存在流量饱和现象,位
移波形幅值与阀芯轴向开口基本保持线性关系增大。
滑阀流量为:
QL2 = Cd A2
ps - pL ρ
- Cd A1
ps + pL ρ
振动台流量为:QL = QL1 + QL2
其中,Cd 、ρ 为液压油液的粘度系数和密度;
(2)液压缸流量连续性方程可写成:
QL
- ki
pL
-
ke 2
pL
= Ap
dyp dt
&#压缸内,外泄漏系数;Ap 液压缸活塞的有效面
科技信息
多阀同步振动台解耦控制的研究
杭州职业技术学院友嘉机电学院 丁媛媛
[摘 要]为获得高频大推力电液振动台,本文提出构建双自由度转阀并联一滑阀的多阀同步振动台,通过转阀结构大幅提高激振频 率,建立系统非线性模型,解耦分析频率、转阀与滑阀开口对振幅的联合控制,提高液压缸活塞位移最大值,进而提高振动台输出 力。搭建实验平台,分析实际位移波形验证理论分析的准确性。研究结果表明:理论分析与实验结果一致,即可获得较高的激振频 率和较大输出力。 [关键词]振动台 解耦控制
