一元一次方程数字问题
北师大版七上第五章一元一次方程 之应用:表格数字、日历类专项训练(含答案)

一元一次方程之应用:表格数字、日历类专项训练1.将连续的偶数2,4,6,8,…,排成如下表,并用一个十字形框架框住其中的五个数,请你仔细观察十字形框架中的数字的规律,并回答下列问题:(1)十字框中的五个数的和等于;(2)若将十字框上下左右移动,可框住另外的五个数,设中间的数为x,用代数式表示十字框中的五个数的和是;(3)在移动十字框的过程中,若框住的五个数的和等于2020,这五个数从小到大依次是,,,,;(4)框住的五个数的和能等于2019吗?答:(回答“能”或“不能”)理由是:.2.探索规律:将连续的偶2,4,6,8,…,排成如表:(1)请你求出十字框中的五个数的和;(2)设中间的数为x,请你用含x的式子表示十字框中的五个数的和;(3)若将十字框上下左右移动,可框住另外的五个数,这五个数的和能等于2018吗?如能,写出这五个数,如不能,请说明理由.3.每年的开学初,学校都会把这一学期的日历按周全部排列出来,称为校历,然后根据校历来安排工作.例如:如图就是某年校历的一部分.(示意图)(1)小张一家外出旅游5天,这5天的期之和是20小张旅游的最后一天是号.(2)如果用一个长方形方框任意框出3×3个数,从左下角到右上角的“对角线上的3个数字的和为27,那么这个长方形方框中最中间的日期是号.(3)在一张校历中,框出了这样的九个数,设中间的一个为数x,左下角的一数为y,请你用含有x的式子来表示y,或说明x,y之间的数量关系.4.如图,将连续的奇数1,3,5,7……排成如下的数表,用十字形框框出5个数.探究规律一:设十字框中间的奇数为x,则框中五个奇数的和用含x的整式表示为,这说明被十字框框中的五个奇数的和一定是正整数n(n>1)的倍数,这个正整数n是;探究规律二:落在十字框中间且位于第二列的一组奇数是21,39,57,75,…,则这一组数可以用整式表示为18m+3(m为序数),同样,落在十字框中间且位于第三列的一组奇数可以表示为;(用含m的式子表示)运用规律:(1)已知被十字框框中的五个奇数的和为2025,则十字框中间的奇数是,这个奇数落在从左往右第列;(2)被十字框框中的五个奇数的和可能是2020吗?若能,请求出这五个数:若不能,请说明理由.5.把正整数1,2,3,4,…排列成如图所示的一个表.(1)用一正方形在表中随意框住4个数,把其中最大的数记为x,另三个数用含x的式子表示出来,从大到小依次是,,;(2)在(1)的前提下,当被框住的4个数之和等于984时,x位于该表的第几行第几列?6.如图的数阵由全体正奇数排成:(1)图中平行四边形框内的9个数的和与中间数41有什么关系?(2)设中间数为a,将平行四边形框上下左右移动,框内的9个数的和与a之间还有这种规律吗?说明理由;(3)这9个数的和能等于2016吗?如果能,写出这9个数中最小的一个;如果不能,说明理由.7.在左边的日历中,用一个正方形任意圈出二行二列四个数,如若在第二行第二列的那个数表示为a,其余各数分别为b,c,d.(1)分别用含a的代数式表示b,c,d这三个数.(2)求这四个数的和.(用含a的代数式表示,要求合并同类项化简)(3)这四个数的和会等于51吗?如果会,请算出此时a的值,如果不会,说明理由.8.把正整数1,2,3,4,…,2019排列成如图所示的一个表(1)用一个正方形在表中随意框住4个数,把其中最小的数记为x,另三个数用含x的式子表示出来,从小到大依次是,,.(2)在(1)的前提下,当被框住的4个数之和等于416时,x的值是多少?9.把2018个正整数1,2,3,4,…,2018按如图方式排列成一个表;(1)用如图方式框住表中任意4个数,记左上角的一个数为x,则另三个数用含x的式子表示出来,从小到大依次是、、(请直接填写答案)(2)用(1)中方式被框住的4个数之和可能等于2019吗?如果可能,请求出x的值;如果不可能,请说明理由.10.将连续奇数1,3,5,7,9……排成如下数表:(1)十字框中5个数字和与23这个数字有何关系?(2)设中间数为a,用a的代数式表示这5个数字之和;(3)十字框中5个数字之和可以等于2008吗?若能,写出这5个数;若不能,说明为什么?11.将连续的奇数1,3,5,7,排成如下表:如图所示,图中的T字框框住了四个数字,若将T字框上下左右移动,按同样的方式可框住另外的四个数.(1)设T字框内处于中间且靠上方的数是整个数表当中从小到大排列的第n个数,请你用含n的代数式表示T字框中的四个数的和;(2)若将T字框上下左右移动,框住的四个数的和能等于2018吗?如能,写出这四个数,如不能,说明理由.12.将正整数1至2019按照一定规律排成下表:记a ij表示第i行第j个数,如a14=4表示第1行第4个数是4.(1)直接写出a42=,a53=;(2)①如果a ij=2019,那么i=,j=;②用i,j表示a ij=;(3)将表格中的5个阴影格子看成一个整体并平移,所覆盖的5个数之和能否等于2027.若能,求出这5个数中的最小数,若不能说明理由.13.小明是个爱动脑筋的同学,在发现教材中的用方框在月历中移动的规律后,突发奇想,将连续的偶数2,4,6,8,…,排成如图:并用一个十字形框架框住其中的五个数,请你仔细观察十字形框架中的数字的规律,并回答下列问题:(1)十字框中的五个数的和与中间的数16有什么关系?(2)设中间的数为x,用代数式表示十字框中的五个数的和;(3)若将十字框上下左右移动,可框住另外的五位数,其它五位数的和能等于2015吗?如能,写出这五位数,如不能,说明理由.14.将连续的奇数1,3,5,7,9,…,排成如图所示的数阵.(1)设中间数为a,用式子表示十字框中五数之和并化简.(2)若将十字框上下左右移动,可框住另外五个数,这五个数的和还有这种规律吗?十字框中五数之和能等于2005吗?若能,请写出这五个数,若不能,说明理由.15.将整数1,2,3……,2016按下列方式排列成数表,用斜十字框“X”框出任意的5个数,如果用a,b,c,d,m(m处于斜十字的中心)表示类似“X”框中的五个数.如图中的a=10,b=12,c=24,d=26,m=18.(1)若a+b+c+d=252,求m的值.(2)框中的a、b、c、d的和能为364吗?若能,求出m的值;若不能,请说明理由.参考答案1.解:(1)6+14+16+18+26=80,故答案为:80;(2)设中间的数为x,则另四个数分别为:x﹣10,x+10,x﹣1,x+1,∴x﹣10+x+10+x﹣1+x+1+x=5x,故答案为:5x;(3)根据题意得:5x=2020,解得:x=404,∴另四个数分别为:394,403,405,414,故答案为:394,403,404,405,414;(4)根据题意可得5x=2019,解得:x=403.8,∴2019不能被5整除,∴这五个数之和不能为2019.故答案为:不能,2019不能被5整除2.解:(1)十字框框出5个数的和为:6+14+16+18+26=80;(2)根据题意得:x上边的数字为:x﹣10,x下边的数字为:x+10,x左边的数字为:x﹣2,x右边的数字为:x+2,则十字框中的五个数字之和为:(x﹣10)+(x+10)+(x﹣2)+(x+2)+x=5x,即用含x的代数式表示十字框框住的5个数字之和为5x;(3)设中间的数为m,根据题意得:5m=2018,解得:m=403.6,m不是整数,即不能框住五个数,和等于2018.3.解:(1)设中间的一天是x号.根据题意,得x﹣2+x﹣1+x+x+1+x+2=20解得x=4.x+2=6.答:最后一天是6号.故答案为6.(2)设最中间的日期为x号.根据题意,得x+6+x+x﹣6=27解得x=9.答:最中间的日期是9号.故答案为9.(3)y=x+6.答:y与x之间的数量关系为y比x大6.4.解:探究规律一:根据题意,得设十字框中间的奇数为x,则框中其它五个奇数为x﹣2,x+2,x﹣18,x+18.所以x+x﹣2+x+2+x﹣18+x+18=5x五个奇数的和一定是正整数n(n>1)的倍数,这个正整数n是5.故答案为5x、5.探究规律二:因为第二列的一组奇数是21,39,57,75,…21=1×18+339=2×18+357=3×18+375=4×18+3所以这一组数可以用整式表示为18m+3(m为序数).所以落在十字框中间且位于第三列的一组奇数可以表示为(18m+5).故答案为(18m+5)(1)根据题意,得5x=2025x=405所以十字框中间的奇数是405.因为18m+9=405,解得m=22,所以405这个奇数落在从左往右第五列.故答案为405、五(2)十字框框中的五个奇数的和可以是2020.理由如下:5x=2020x=404,x﹣2=402,x+2=406,x﹣18=396,x+18=422.答:这五个数为404、402、406、396、422.5.解:(1)用一正方形在表中随意框住4个数,把其中最大的数记为x,另三个数用含x 的式子表示出来,从大到小依次是:x﹣1;x﹣7;x﹣8;故答案为:x﹣1;x﹣7;x﹣8;(2)依据题意可得:x+x﹣1+x﹣7+x﹣8=984,解得:x=250,250=35×7+5,答:x位于第36行第5列.6.解:(1)图中平行四边形框内的九个数的和为: 23+25+27+39+41+43+55+57+59=369,369÷41=9,所以图中平行四边形框内的九个数之和是中间的数的9倍;(2)在数阵图中任意作一类似(1)中的平行四边形,这九个数之和还有这种规律.理由如下:设数阵图中中间的数为a,则其余的8个数为a﹣18,a﹣16,a﹣14,a﹣2,ax+2,a+14,a+16,a+18,这九个数的和为:a﹣18+a﹣16+a﹣14+a﹣2+a+a+2+a+14+a+16+a+18=9a,所以图中平行四边形框内的九个数之和是中间的数的9倍;(3)根据题意,得9x=2016,解得x=224,∵数阵是由全体奇数排成,∴数阵图中中间的数为224不合题意.答:这9个数的和不能等于2016.7.解:(1)观察日历表可知:右边的数比左边的数大1,下面的数比上面的数大7,∵在第二行第二列的那个数表示为a,则b=a﹣7,c=a﹣7﹣1=a﹣8,d=a﹣1.(2)这四个数的和为a+b+c+d=a+a﹣7+a﹣8+a﹣1=4a﹣16.(3)这四个数的和不会等于51,理由如下:假设这四个数的和等于51,由(2)知4a﹣16=51,解得:a=16,∵16不是正整数,∴假设不成立,∴这四个数的和不会等于51.8.解:(1)设其中最大的数记为x,则另外三个数分别为x+1、x+7、x+8.故答案为:x+1;x+7;x+8.(2)根据题意得:x+(x+1)+(x+7)+(x+8)=416,解得:x=100.9.解:(1)设左上角的一个数为x,由图表得:其他三个数分分别为:x+8,x+16,x+24.(2)由题意,得x+x+8+x+16+x+24=2019,解得:x=492.75,因为2018是正整数,所以被框住的4个数之和不可能等于2019.故答案为:x+8,x+16,x+24.10.解:(1)∵7+21+23+25+39=115,23×5=115,∴十字框中5个数字和是23的5倍.(2)设中间数为a,则另外四个数分别为(a﹣16),(a﹣2),(a+2),(a+16),∴5个数字之和=(a﹣16)+(a﹣2)+a+(a+2)+(a+16)=5a.(3)不可以,理由如下:5a=2008,解得:a=401,∵a=401不是整数,∴十字框中5个数字之和不可以等于2008.11.解:(1)由题意,设T字框内处于中间且靠上方的数为2n﹣1,则框内该数左边的数为2n﹣3,右边的为2n+1,下面的数为2n﹣1+10,∴T字框内四个数的和为:2n﹣3+2n﹣1+2n+1+2n﹣1+10=8n+6.故T字框内四个数的和为:8n+6.(2)由题意,令框住的四个数的和为2018,则有:8n+6=2018,解得n=251.5由于n必须为正整数,因此n=251.5不符合题意.故框住的四个数的和不能等于2018.12.解:(1)∵前面3行一共有8×3=24个数,=26;∴第4行的第1个数为25,则第4行的第2个数为26,即a42∵前面4行一共有8×4=32个数,=35.∴第5行的第1个数为33,则第5行的第3个数为35,即a53故答案为:26;35.(2)①∵2019=252×8+3,∴2019是第253行的第3个数,∴i=253,j=3.故答案为:253;3.②根据题意,可得a ij=8(i﹣1)+j.故答案为8(i﹣1)+j.(3)设这5个数中的最小数为x,则其余4个数可表示为x+4,x+9,x+11,x+18,依题意,得:x+x+4+x+9+x+11+x+18=2027,解得x=397.∵397=49×8+5,∴397是第50行的第5个数,而此时x+4=401是第51行的第1个数,与397不在同一行,∴将表格中的5个阴影格子看成一个整体并平移,所覆盖的5个数之和不能等于2027.13.解:(1)∵6+14+16+18+26=80=16×5,∴十字框中的五个数的和是中间的数16的5倍.(2)设中间的数为x,则另外四个数分别为x﹣10、x﹣2、x+2、x+10,∴(x﹣10)+(x﹣2)+x+(x+2)+(x+10)=5x.(3)不能,理由如下:设中间的数为x,根据题意得:5x=2015,解得:x=403.∵403不是偶数,∴框住的五个数的和不能等于2015.14.解:(1)设中间数为a,则另外四个数分别为a﹣10、a﹣2、a+2、a+10,∴十字框中五数之和为(a﹣10)+(a﹣2)+a+(a+2)+(a+10)=5a.(2)无论如何移动,这五个数的和还有这种规律,十字框中五数之和不能等于2005,理由如下:设中间数为x时,五数之和为2005,根据题意得:5x=2005,解得:x=401,∵401为第201个奇数,且201=40×5+1,∴401为第40行的第一个数,∴401不能为中间数,∴十字框中五数之和不能等于2005.15.解:(1)观察图形,可知:a=m﹣8,b=m﹣6,c=m+6,d=m+8,∴(m﹣8)+(m﹣6)+(m+6)+(m+8)=252,解得:m=63.答:m的值为63.(2)不能,理由如下:根据题意,得:(m﹣8)+(m﹣6)+(m+6)+(m+8)=364,解得:m=91.∵91=7×13,∴91为第一列的数,∴m=91不符合题意,舍去,∴框中的a、b、c、d的和不能为364.。
实际问题与一元一次方程问题(5)数字与等积变形问题

1,-3,9,-27,81,-243,…
其中某三个相邻数的和是 -1701,这三个数各是多 少?
后一个数=前一个数×(-3)
分
探究1 有一列数,按 一定规律排列成:
析
问题2:如果设相邻
三个数中第一个数为x,
你能否表示出另两个数
吗?如果设第二个数或
1,-3,9,-27,81,-243,…
第三个数呢?
思考:
(1)在三位数345中,3,4,5是这个三位数的什么? (2)如果a ,b ,c 分别表示百位数字、十位数字、个 位数字,这个三位数能不能写成abc形式?为什么?
用一元一次方程分析和解决实际问题的基本过程如下:
实际问题
列方程
数学问题
(一元一次方程) 解 方 程
实际问题 的答案
数学问题的解
检验 (x=a)
义务教育课程标准实验教科书
七年级上册
辽源市灯塔中学 徐广清
学习目标
1、掌握数字问题,能熟练地利用相等关系列 方程; 2、掌握等积变形问题,能熟练地利用变形前 后的体积相等的关系列方程; 3、提高学生分析实际问题中数量关系的能力。
分
探究1 有一列数,按 一定规律排列成:
析
问题1:你能看出这 列数有什么规律吗?
第一个 第二个 第三个 第一种 第二种 x -x/3 -3x x 9x -3x
其中某三个相邻数的和是 -1701,这三个数各是多 少?
第三种
x/9
-x/3
x
练
习
1. 三个连续奇数的和93,求这三个数。
2. 有一个两位数,它的两个数字之和是8,把
这个两位数的数字交换位置后所得的数乘以原来的 数就得到1855,求原来的两位数。
初一数学一元一次方程应用题(完整版)
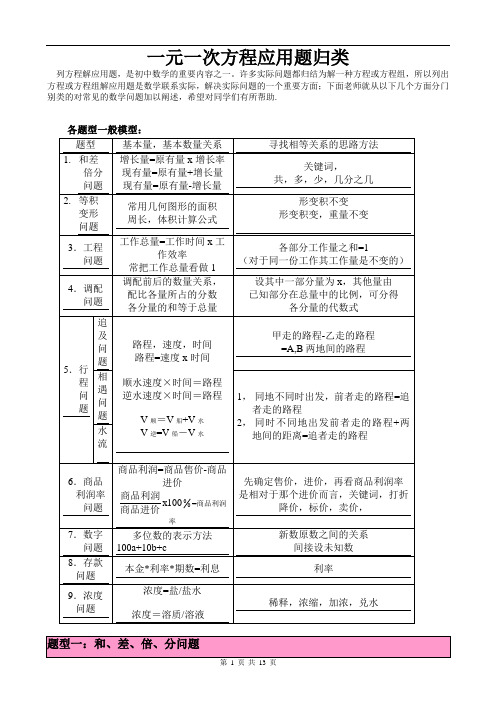
一元一次方程应用题归类列方程解应用题,是初中数学的重要内容之一。
许多实际问题都归结为解一种方程或方程组,所以列出方程或方程组解应用题是数学联系实际,解决实际问题的一个重要方面;下面老师就从以下几个方面分门别类的对常见的数学问题加以阐述,希望对同学们有所帮助.各题型一般模型:(1)倍数关系:通过关键词语“是几倍,增加几倍,增加到几倍,增加百分之几,增长率……”来体现。
(2)多少关系:通过关键词语“多、少、和、差、不足、剩余……”来体现。
根据2001年3月28日新华社公布的第五次人口普查统计数据,截止到2001年11月1日0时,全国每10万人中具有小学文化程度的人口为35701人,比1990年7月1日减少了3.66%,1990年6月底每10万人中约有多少人具有小学文化程度?分析:等量关系为:1、某石油进口国这个月的石油进口量比上个月减少了5%,由于国际油价上涨,这个月进口石油的费用反而比上个月增加了14%,求这个月的石油价格相对上个月的增长率。
2、某县城为鼓励居民节约用水,对自来水用户按分段计费方式收取水费:若每月用水不超过7m³,则按每立方米1元收费;若每月用水超过7m³,则超过部分按每立方米2元收费。
如果某居民今年5月缴纳了17元水费,那么这户居民今年5月的用水量为多少m³?3、芜湖供电公司分时电价执行时段分为平、谷两个时段,平段为8:00-22:00,14个小时;谷段为22:00-次日8:00,10个小时。
平段用电价格在原销售电价基础上每千瓦时上浮0.03元,谷段电价在原销售电价基础上每千瓦时下浮0.25元。
小明家5月份实用平段电量40千瓦时,谷段电量60千瓦时,按分时电价付费42.73元。
(1)问小明该月支付的平段、谷段电价每千瓦时各为多少元?(2)如不使用分时电价结算,5月份小明家将多支付电费多少元?4、某工厂食堂第三季度一共节煤7400斤,其中八月份比七月份多节约20%,九月份比八月份多节约25%,问该厂食堂九月份节约煤多少公斤?“等积变形”是以形状改变而体积不变为前提。
20道一元一次方程应用题

列一元一次方程解应用题一、数字问题1、一个两位数十位上的数字与个位上的数字之和是6,把这个两位数加上18后,正好等于这个两位数的十位数字与个位数字对调后的两位数,请问这个两位数是多少?2、有一个三位数,其各位数字之和为16.,十位数字是个位数字与百位数字的和,若把百位与个位数字对调,那么新数比原数大594,求原数。
二、等积变形问题cm.求原来3、一块正方形铁皮,四角截去4个一样的小正方形,折成底面边长是50cm的无盖长方体盒子,容积是450003正方形铁皮的边长。
4、用直径为4cm的圆钢,锻造一个重0.62kg的零件毛坯,如果这种钢每立方厘米重7.8g,应截圆钢多长?5、把直径6cm,长16cm的圆钢锻造成半径为4cm的圆钢。
求锻造后的圆钢的长。
6、用长7.2m的木料做成如图所示的“日”字形窗框,窗的高比宽多0.6m。
求窗的高和宽。
(不考虑木料加工时损耗)7、直径为30厘米,高为50厘米的圆柱形瓶里存满了饮料,现把饮料倒入底面直径为10厘米的圆柱形小杯中,刚好倒满20杯,求小杯子的高。
三、利润率问题8、丽丽的妈妈到百盛商场给她买一件漂亮毛衣,售货员说:“这毛衣前两天打八折,今天又在八折的基础上降价10%,只卖144元,丽丽很快算出了这件毛衣的原标价,你知道是多少元吗?9、一种商品,甲提出按原价降低10元后卖掉,用售价的10%作积累;乙提出将原价降低20元卖掉,用售价的20%仍做积累,经测算两种积累一样多.则这种商品的原价是多少?10、某种商品因换季准备打折出售,如果按定价的七五折出售,将赔25元,而按定价的九折出售,将赚20元,这种商品的定价为多少元?11、某商品的进价是2000元,标价为3000元,商店要求以利润率不低于5%的售价打折出售,售货员最低可以打几折出售此商品?四、调配问题12、某厂一车间有64人,二车间有56人。
现因工作需要,要求第一车间人数是第二车间人数的一半。
问需从第一车间调多少人到第二车间?13、甲乙两车间各有工人若干,如果从乙车间调100人到甲车间,那么甲车间的人数是乙车间剩余人数的6倍;如果从甲车间调100人到乙车间,这时两车间的人数相等,求原来甲乙车间的人数。
5.3 实际问题与一元一次方程(7)——比例、年龄、数字问题
5.3
1
课前预习
2
3
分层检测
课堂学练
5.3 实际问题与一元一次方程(7)——比例、
年龄、数字问题
课前预习
1. 小明买笔、笔记本、文具盒所花的钱之比是2∶3∶5,总共花了40元,则
买笔花
8
元,买笔记本花
12
元,买文具盒花
2. 小明今年10岁,他爸爸今年38岁, x 年前,小明
所以个位数字为8- x =3,
原来的两位数为53.
答:原来的两位数为53.
1
2
3
4
5
6
7
8
9
10
11
12
5.3 实际问题与一元一次方程(7)——比例、
年龄、数字问题
课堂学练
6. 一个两位数,个位数字是十位数字的2倍,交换十位数字与个位数字
后,新的两位数比原数大27.求原来的两位数.
解:设原来两位数的十位数字为 x ,则个位数字为2 x ,
由题意得10 x + x +1+10(x+1)+ x =33,
解得 x =1, x +1=1+1=2.
1×10+2=12.
答:这个两位数是12.
1
2
3
4
5
6
7
8
9
10
11
12
5.3 实际问题与一元一次方程(7)——比例、
年龄、数字问题
分层检测
10. 有一列数,按一定规律排成1,-2,4,-8,16,-32,…,其中
1
2
3
4
5
6
7
8
9
10
11
一元一次方程应用题6----比例问题、数字问题QQQ

----比例、数字问题
小虎钓了4条鲫鱼,小华钓了5条鲫鱼,鱼的大 小差不多。 游客留了18元表示感谢,他们各分多少才比较 合理?
一足球由黑白两种皮子缝制而成共32块,
已知黑白皮子数的比为3:5,求各多少块?
按比例分配的应用题的设元和找相等关系
各有什么特点? 设元是间接设元,一般设其中的一份为x, 必要时要求连比 相等关系一般是总量等于部分量的和或 找题中的话,也可以是整个题中始终不变的量
答 :原两位数是84。
课本P97 练习1、2 例7 :一个两位数的十位上的数是个位上的数的两倍,若把两个数字 对调,则新得到的两位数比原两位数小36,求原两位数。 分析 :题中数量关系如下表 (若设原数的个位数字为X)
十位数字 原两位数 新两位数 个位数字 X 本数
可知相等关系为: 原两位数+36=新两位数 解 :设原两位数的个位数字为X,则其十位数字为2X。
3.4.7实际问题与一元一次方程导学案(存款、数字问题)

3.4.7实际问题与一元一次方程----存款、数字问题学习目标:1、会用一元一次方程解决实际问题的存款和数字问题;2、在解决实际的过程中,提高分析问题、解决问题的能力。
重点难点:存款、数字问题中的一元一次方程建模。
学习过程:预备知识:1、存款问题中各量之间的关系:利息=本金×年利率×存款年数本息和=本金+利息税后利息=利息-利息税利息税=利息×20%2、数字问题:(1)多位数的表示方法:①若一个两位数的个位上的数字为a,十位上的数字为b,则这个两位数是_______;②若一个三位数的个位上的数字为a,十位上的数字为b,百位上的数字为c,则这个三位数是_______________;③四、五…位数依此类推。
(2)日历上的数字:在日历中用长方形框9个数字,设正中间的数为a,请填写右表中其他8个数。
探究1:小张前年存了一种年利率为2.43%的二年期定期储蓄,今年到期后,扣除利息税(利息税=利息×20%),所得利息为97.2元,问小张前年存了多少钱?探究2:某两位数,数字之和为8,将这个两位数的数字位置对换,得到的新两位数比原两位数小18,求原来的两位数。
探究3:用正方形圈出日历中的4个的和是76,这4天分别是几号?巩固练习:1、三个连续奇数的和为69,则这三个数分别是多少?2、一个两位数,个位上的数是十位上的数的2倍,如果把十位与个位上的数对调,那么所得到的两位数比原来两位数大36,则原两位数是多少?3、你假期外出旅行一周,这一周各天的日期之和是84,那么旅行社是_____号送你回家的.4、日历中同一竖列相邻三个数的和可以是()A .78 B.26 C.21 D. 45 ;5、你能在日历中圈出一个竖列上相邻的3个数,使得它们的和是40吗?为什么?小结:作业:课后反思:。
一元一次方程的应用(7)日历数字问题同步培优题典(解析版)

七年级数学上册同步培优题典一元一次方程的应用(7)日历数字问题姓名:__________________ 班级:______________ 得分:_________________注意事项:本试卷满分100分,试题共24题.答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级等信息填写在试卷规定的位置.一、选择题(本大题共10小题,每小题3分,共30分)在每小题所给出的四个选项中,只有一项是符合题目要求的.1.(2019秋•道里区校级期中)在一张日历上,在同一行或同一列上任意圈出三个相邻的数,它们的和不可能是()A.60B.39C.40D.57【分析】列出代数式并化简,以选项中的数是3的倍数确定选项.【解析】如果三个数在同一列上时,设第二个数为x,则第一个数为x﹣7,第三个数为x+7.三个数字之和是x+x﹣7+x+7=3x.∵x是正整数,∴三个数的和是3的倍数.如果三个数在同一行上时,设第二个数为x,则第一个数为x﹣1,第三个数为x+1.三个数字之和是x+x﹣1+x+1=3x.∵x是正整数,∴三个数的和是3的倍数.综上所述:三个数的和是3的倍数.选项中的60、39、57都是3的倍数,而40不是3的倍数,故选:C.2.(2019秋•定州市期末)在如图所示的月历表中,任意框出表中竖列上的三个相邻的数,这三个数的和不可能是()A.72B.65C.51D.27【分析】设中间的数为x,从而可知三个数的和为3x,分别求出x的值即可判断.【解析】设中间的数为x,由表格可知:从上至下三个数分别为x﹣7,x,x+7,∴这三个数为:x﹣7+x+x+7=3x,当3x=72时,此时x=24,当3x=65,时,此时x=653,不符合题意,当3x=51时,此时x=17,当3x=27时,此时x=9,故选:B.3.(2019春•晋江市期末)小明在某月的日历上圈出了三个数a、b、c,并求出了它们的和为39,则这三个数在日历中的排位位置不可能的是()A.B.C.D.【分析】日历中的每个数都是整数且上下相邻是7,左右相邻差1,根据题意列方程可解.【解答】解;A:设最小的数是x,则x+(x+1)+(x+2)=39,解得:x=12,故本选项不符合题意;B:设最小的数是x,则x+(x+1)+(x+8)=39,解得x=10,故本选项不符合题意;C:设最小的数是x,则x+(x+8)+(x+16)=39,解得x=5,故本选项不符合题意;D:设最小的数是x,则x+(x+8)+(x+14)=39,解得x=173,故本选项符合题意.故选:D.4.(2018秋•蔡甸区期末)一个两位数,十位上的数比个位上的数的3倍大1,个位上的数与十位上的数的和等于9,这个两位数是()A.54B.72C.45D.62【分析】设个位数字为x,则十位数字是(3x+1).根据“个位上的数与十位上的数的和等于9”列出方程并解答.【解析】设个位数字为x,则十位数字是(3x+1),依题意得:x+(3x+1)=9,解得x=2,则3x+1=3×2+1=7,即所求的两位数是72.故选:B.5.(2020•盐城)把1~9这9个数填入3×3方格中,使其任意一行,任意一列及两条对角线上的数之和都相等,这样便构成了一个“九宫格”.它源于我国古代的“洛書”(图①),是世界上最早的“幻方”.图②是仅可以看到部分数值的“九宫格”,则其中x的值为()A.1B.3C.4D.6【分析】根据任意一行,任意一列及两条对角线上的数之和都相等,可得第三行与第三列上的两个数之和相等,依此列出方程即可.【解析】由题意,可得8+x=2+7,解得x=1.故选:A.6.(2019秋•黄陂区期末)在2020年1月的月历表中,用如图所示的“S”型框任意框出表中四个数,这四个数的和可能是()A.28B.34C.58D.82【分析】设四个数中最小的数为x,则另外三个数分别为(x+1),(x+6),(x+7),根据四个数的和,可得出关于x的一元一次方程,解之即可得出x的值,逐一分析各x值即可得出结论.【解析】设四个数中最小的数为x,则另外三个数分别为(x+1),(x+6),(x+7),依题意,得:x+(x+1)+(x+6)+(x+7)=28或x+(x+1)+(x+6)+(x+7)=34或x+(x+1)+(x+6)+(x+7)=58或x+(x+1)+(x+6)+(x+7)=82,解得:x=72或x=5或x=11或x=17.x=72不是整数,舍去;x=5在第一列,无法框出“S”型框,舍去;x=11在第七列,无法框出“S”型框,舍去.故选:D.7.(2019秋•北海期末)在排成每行七天的日历表中取下一个3×3的方块(如图),若方块中所有日期之和为207,则n的值为()A.23B.21C.15D.12【分析】先求出这九个日期之和,列出方程可求解.【解析】这九个日期分别为:n﹣8,n﹣7,n﹣6,n﹣1,n,n+1,n+6,n+7,n+8,∴所有日期之和=9n,由题意可得9n=207,∴n=23,故选:A.8.(2019秋•张家港市期末)小淇在某月的日历中圈出相邻的三个数,算出它们的和是19,那么这三个数的位置可能是()A.B.C.D.【分析】日历中的每个数都是整数且上下相邻是7,左右相邻相差是1.根据题意可列方程求解.【解析】A、设最小的数是x.x+x+7+x+7+1=19x=4 3故本选项不符合题意;B、设最小的数是x.x+x+6+x+7=19,x=2.故本选项符合题意.C、设最小的数是x.x+x+1+x+8=19,x=10 3,故本选项不符合题意.D、设最小的数是x.x+x+1+x+7=19,x=11 3,故本选项不符合题意.故选:B.9.(2019秋•霸州市期末)如图,表中给出的是某月的月历,任意选取“H”型框中的7个数(如阴影部分所示),请你运用所学的数学知识来研究,发现这7个数的和不可能的是()A.63B.70C.96D.105【分析】设“H”型框中的正中间的数为x,则其他6个数分别为x﹣8,x﹣6,x+﹣1,x+1,x+6,x+8,表示出这7个数之和,然后分别列出方程解答即可.【解析】设“H”型框中的正中间的数为x,则其他6个数分别为x﹣8,x﹣6,x﹣1,x+1,x+6,x+8,这7个数之和为:x﹣8+x﹣6+x﹣1+x+1+x+x+6+x+8=7x.由题意得A、7x=63,解得:x=9,能求得这7个数;B、7x=70,解得:x=10,能求得这7个数;C、7x=96,解得:x=967,不能求得这7个数;D、7x=105,解得:x=15,能求得这7个数.故选:C.10.(2019秋•武安市期末)如图是某月份的日历表,任意框出同一列上的三个数,则这三个数的和不可能是()A.39B.43C.57D.66【分析】可设中间的数为x,根据竖列上相邻的数相隔7可得其余2个数,相加等于各选项中数字求解即可.【解析】A、设中间的数为x,则最小的数为x﹣7,最大的数为x+7.x+(x﹣7)+(x+7)=39,解得:x=13,故此选项错误;B、设中间的数为x,则最小的数为x﹣7,最大的数为x+7.x+(x﹣7)+(x+7)=43,解得:x=433,故此选项符合题意;C、设中间的数为x,则最小的数为x﹣7,最大的数为x+7.x+(x﹣7)+(x+7)=57,解得:x=19,故此选项错误;D、设中间的数为x,则最小的数为x﹣7,最大的数为x+7.x+(x﹣7)+(x+7)=66,解得:x=22,故此选项错误;故选:B.二、填空题(本大题共8小题,每小题3分,共24分)请把答案直接填写在横线上11.(2020•孝感)有一列数,按一定的规律排列成13,﹣1,3,﹣9,27,﹣81,….若其中某三个相邻数的和是﹣567,则这三个数中第一个数是﹣81.【分析】设这三个数中的第一个数为x,则另外两个数分别为﹣3x,9x,根据三个数之和为﹣567,即可得出关于x的一元一次方程,解之即可得出结论.【解析】设这三个数中的第一个数为x,则另外两个数分别为﹣3x,9x,依题意,得:x﹣3x+9x=﹣567,解得:x=﹣81.故答案为:﹣81.12.(2019秋•越秀区期末)在一张普通的月历中,相邻三行里同一列的三个日期数之和为27,则这三个数分别是2,9,16.【分析】设三个数中最小的数为x,则另外两个数分别为(x+7),(x+14),根据三个日期数之和为27,即可得出关于x的一元一次方程,解之即可得出结论.【解析】设三个数中最小的数为x,则另外两个数分别为(x+7),(x+14),依题意,得:x+x+7+x+14=27,解得:x=2,∴x+7=9,x+14=16.故答案为:2,9,16.13.(2018秋•香坊区校级月考)有一列数,按一定规律排列成1、﹣4、16、﹣64、256…,其中某相邻三个数的和是﹣832,那么这三个数中最大的数是256.【分析】根据题目中的数字,可以发现数字的变化规律,再根据某相邻三个数的和是﹣832,可以列出相应的方程,从而求得最大的数,本题得以解决.【解析】∵有一列数,按一定规律排列成1、﹣4、16、﹣64、256…,∴这列数中每个数都是前面相邻数的﹣4倍,设这三个相邻的数中的中间数为x,则第一个数为−x4,第三个数为﹣4x,−x4+x+(﹣4x)=﹣832,解得:x=256,∴﹣4x=﹣4×256=﹣1024,−x4=−64,∴这三个数﹣64,256,﹣1024,∴这三个数中最大的数是256,故答案为:256.14.(2018秋•万州区期末)《孙子算经》是中国传统数学的重要著作之一,其中记载的“荡杯问题”很有趣.《孙子算经》记载“今有妇人河上荡杯.津吏问曰:‘杯何以多?’妇人曰:‘家有客.’津吏曰:‘客几何?’妇人曰:‘二人共饭,三人共羹,四人共肉,凡用杯七十八.’不知客几何?”译文:“2人同吃一碗饭,3人同吃一碗羹,4人同吃一碗肉,共用78个碗,问有多少客人?”则客人的个数为72.【分析】设共有客人x人,根据“2人同吃一碗饭,3人同吃一碗羹,4人同吃一碗肉,共用78个碗”列出方程即可.【解析】设有x个客人,则x2+x3+x4=78解得,x=72答;有72个客人.故答案是:72.15.(2019秋•黄冈期末)一个两位数,十位数字是个位数字的2倍,将两个数对调后得到的两位数比原来的两位数小36,这个两位数是84.【分析】首先设个位数字为x,则十位数字为2x,则原两位数可表示为10×2x+x,数字对调后所得两位数是(10x+2x),再根据“将两个数对调后得到的两位数比原来的两位数小36”可得方程:10×2x+x﹣(10x+2x)=36,解方程得到个位数,进而可得十位数字.【解析】设个位数字为x,则十位数字为2x,由题意得:10×2x+x﹣(10x+2x)=36,解得:x=4,则2x=8,答:原两位数是84.故答案为84.16.(2015秋•哈尔滨校级月考)一个数的一半,它的三分之一,它的百分之四十,它的六分之一,加起来一共是49,则这个数是35.【分析】设这个数为x,根据“一个数的一半,它的三分之一,它的百分之四十,它的六分之一,加起来一共是49”找到等量关系并列出方程求解即可.【解析】设这个数为x,根据题意得:1 2x+13x+40%x+16x=49,解得:x=35.故答案为:3517.(2019秋•沙坪坝区校级月考)如图是某月的月历,用一个矩形框,每次框住9个数.若这9个数之和是81,则这9个数中最大的数为17,这9个数之和可能会是100吗?不能(填“能”或“不能”)【分析】设中间的数为x,根据框柱的数之间的规律即可求出答案.【解析】设最中间的数为x,则这9个分别是x﹣8,x﹣7,x﹣6,x﹣1,x,x+1,x+6,x+7,x+8,这9个数之和为:x﹣8+x﹣7+x﹣6+x﹣1+x+x+1+x+6+x+7+x+8=9x,∴9x=81,∴x=9,∴最大的数为x+8=17,当9x=100时,此时x=100 9,所以这9个数之和不可能是100,故答案为:17,不能.18.(2019秋•东莞市期末)中国始有历法大约在四千年前每页显示一日信息的叫日历,每页显示一个月信息的叫月历,每页显示全年信息的叫年历如图是2019年1月份的月历,用一个方框圈出任意2×2的4个数,设方框左上角第一个数是x,则这四个数的和为4x+16(用含x的式子表示)【分析】根据同一行中相邻两个数的差为1,同一列中,相邻两个数的差为7列出代数式.【解析】x+x+1+x+7+x+8=4x+16.故答案是:4x+16.三、解答题(本大题共6小题,共46分.解答时应写出文字说明、证明过程或演算步骤)19.(2015秋•吉安月考)生活与数学.(1)小明在某月的日历上象图①样圈了2×2个数,若正方形的方框内的四个数的和是44,那么这四个数是7、8、14、15.(直接写出结果)(2)小莉也在日历上象图②样圈出5个数,呈十字框形,若这五个数之和是60,则中间的数是12.(直接写出结果)(3)小虎说他在日历上向图③样圈了五个数,算了它们的和是65.你认为小虎计算正确吗?说明理由.拓展与推广:若干个偶数按每行8个数排成如图④所示:(1)写出图④中方框内的9个数的和与中间的数的关系是9个数的和是中间的数的9倍.(2)小明说若用图④中所画的方框去框9个数,其和可以是360,你能求出所框的中间一个数是多少吗?(3)小华画了一个如图⑤所示的斜框,小华能用这个斜框框处9个数的和为2016吗?若能,请求出第行中间一个数,若不能,请说明理由.【分析】(1)设第一个数是x,根据日历上的数据规律把所要求的数用代数式表示,用一元一次方程求解即可;(2)设中间的数是x,根据日历上的数据规律把所要求的数用代数式表示,用一元一次方程求解即可;(3)设中间一个为x,根据日历上的数据规律把所要求的数用代数式表示,用一元一次方程求解即可;拓展与推广:设中间的数是x,根据日历上的数据规律把所要求的数用代数式表示,用一元一次方程求解即可.【解析】(1)设第一个数是x,其他的数为x+1,x+7,x+8,则x+x+1+x+7+x+8=44,解得x=7;∴四个数分别为7、8、14、15,故答案为:7、8、14、15;(2)设中间的数是x,则5x=60,解得x=12,故答案为:12;(3)不准确,理由如下:设中间一个为x,则其它数从上到下依次为:x﹣14,x﹣7,x+7,x+14,则x﹣7+x﹣14+x+x+7+x+14=65,解得x=13;所以最上面一个数为x﹣14=﹣1,显然不在日历上,所以小虎计算错误;拓展与推广:①9个数的和是中间的数的9倍.②设中间的数是x,解得x=40;③由图⑤中数据的排列可知224这个偶数排在第14行的最后一个,因此其后的226这个偶数排在第15行第一个数,因此实际上图⑥这个框框不到226这个偶数,因此小华不可能框出9个数据的和为2016.20.(2018秋•宁都县期中)生活中处处有数学,表一是某月的日历表,用一个正方形框出3×3=9个数(如图),(1)在表中框出九个数之和最大的正方形;(2)若一个正方形内九个数字之和是108,求出它中间的数字;(3)将自然数1至2014按表二的方式排列,框出九个数其和能为2016吗?若能,求出该方框中的最小数,若不能,请说明理由.【分析】(1)根据表格容易找到九个数之和最大的正方形,中间数字为22;(2)设中间数字为a,根据九个数之间的联系即可列出方程,解方程即可;(3)和(2)一样,设中间数字为a,根据九个数之间的联系即可列出方程9a=2016,解方程求出x=224,但是224在第7列,由此即可判定这样的九个数不存在.【解析】(1)如图,红颜色框,是九个数之和最大的正方形;(2)设中间数字为a,则9a=108,解得a=12;(3)依题意得9a=2016,∵224÷7=32,∴224在第7列,故这样的九个数不存在.21.(2009秋•沙坪坝区校级月考)下面是2006年12月的日历,仔细观察,你能发现其中有何规律吗?(1)现任意圈出一竖列上相邻的三个数,设中间的一个为a,则用含a的代数式表示这三个数(从小到大排列)分别是a﹣7,a,a+7.(2)用正方形任意框出4个数,设最小的一个为a,则这4个数的和为4a+16.(3)现将连续自然数1至2008按图中的方式排成一个长方形阵列,用一个正方形框出16个数,如图①图中框出的这16个数的和为352;②图中要使一个正方形框出的16个数之和分别等于2000,2006,是否可能?若不可能,试说明理由;若有可能,请求出该正方形框出的16个数中的最小数和最大数.【分析】(1)根据每列中上面一个数比下面的一个数大7即可用中间的一个数表示出上面和下面的那个数;(2)根据框出的四个数的关系,用最小的数表示出来其他的三个数即可求得4个数的和;(3)①设左上角一个为n,然后表示出其他各数,最后即可表示出16个数的和与n的关系,最后将n =10代入求值即可;②令16(n+12)=2000或2006,求得n为正整数就行,否则就不行,【解析】(1)∵设中间一个数为a,则上面的一个数是a﹣7,下面的一个数是a+7,∴三个数按从小到大排列为:a﹣7,a,a+7;(2)设最小的一个为a,则右边一个为a+1,下面一个数是a+7,最后一个为a+8,故四个数的和为:a+(a+1)+(a+7)+(a+8)=4a+16;(3)①设左上角第一个数为n,根据相邻之间的关系可以得到下表:其中最小数为n,最大数为n+24.这16个数的和为16n+192=16(n+12).∴当n=10时,16(n+12)=16×22=352.②设在16(n+12)=2000,n=113,∴存在最小为113,最大为137,16(n+12)=2006,n=113.375,∴不存在.22.(2019秋•文水县期末)在日历上,我们可以发现其中某些数满足一定的规律,图是2020年1月份的日历,我们用如图所示的四边形框出五个数.2020年1月(1)将每个四边形框中最中间位置的数去掉后,将相对的两对数分别相减,再相加,例如:(10﹣8)+(16﹣2)=16,(21﹣19)+(27﹣13)=16.不难发现,结果都是16.若设中间位置的数为n,请用含n的式子表示发现的规律,并写出验证过程.(2)用同样的四边形框再框出5个数,若其中最小数的2倍与最大数的和为56,求出这5个数中的最大数的值.【分析】(1)根据运算法则写出规律即可;(2)设中间位置的数为x,则最小的数为x﹣7,最大的数为x+7.最小数的2倍与最大数的和为56,可得出关于x的一元二次方程,解之取其正值即可得出结论【解析】(1)规律:[(n+1)+(n+7)]+[(n+7)﹣(n﹣7)]=16.验证:[(n+1)+(n+7)]+[(n+7)﹣(n﹣7)]=(n+1﹣n+1)+(n+7﹣n+7)=2+14=16;(2)解:设中间位置的数为x,则最小的数为x﹣7,最大的数为x+7.根据题意得:2(x﹣7)+(x+7)=56.解得x=21.则x+7=28.答:这5个数中最大数的值为28.23.(2019秋•沈河区校级期中)生活与数学(1)莹莹在日历上圈出三个数,呈大写的“一”字,这三个数的和是中间数的3倍,莹莹又在日历上圈出5个数,呈“十”字框形,它们的和是50,则中间的数是10:(2)小丽同学也在某月的日历上圈出如图所示“七”字形,发现这八个数的和是125,那么这八个数中最大数为26:(3)在第(2)题中这八个数之和不能为101(填“能”或“不能”).【分析】(1)根据日历上的数据规律即可得出答案;(2)先根据日历上的数据规律把所要求的数用代数式表示,再用一元一次方程求解即可;(3)根据(2)的规律解得即可.【解析】(1)莹莹在日历上圈出三个数,呈大写的“一”字,这三个数的和是中间数的3倍,莹莹又在日历上圈出5个数,呈“十”字框形,它们的和是50,则中间的数是10;故答案为:3;10(2)设最小的数为x,则其余数分别为:x+6,x+7,x+8,x+14,x+21,x+22,x+23,根据题意得x+(x+6)+(x+7)+(x+8)+(x+14)+(x+21)+(x+22)+(x+23)=125,解得x=3,∴这八个数中最大数为3+23=26.故答案为:26;(3)x+(x+6)+(x+7)+(x+8)+(x+14)+(x+21)+(x+22)+(x+23)=101,解得x=0,但是日历上最小的数是1,所以在第(2)题中这八个数之和不能为101.故答案为:不能24.(2016秋•灌云县校级月考)生活与数学日一二三四五六12345678910111213141516171819202122232425262728293031(1)山姆同学在某月的日历上圈出2×2个数,如图1,正方形的方框内的四个数的和是48,那么这四个数是8,9,15,16.(2)小丽也在上面的日历上圈出2×2个数,如图2,斜框内的四个数的和是46,则它们分别是8,9,14,15.(3)刘莉也在日历上圈出5个数,呈十字框形,如图3,它们的和是55,则中间的数是11.(4)某月有5个星期日的和是75,则这个月中最后一个星期日是29号?【分析】先根据日历上的数据规律把所要求的数用代数式表示,用一元一次方程求解即可;【解析】(1)设第一个数是x,其他的数为x+1,x+7,x+8,则x+x+1+x+7+x+8=48,解得x=8;所以这四个数是:8,9,15,16;故答案为:8,9,15,16;(2)设第一个数是x,其他的数为x+1,x+6,x+7,则x+x+1+x+6+x+7=46,解得x=8.x+1=9,x+6=14,x+7=15;故答案为:8,9,14,15;(3)设中间的数是x,则5x=55,解得x=11;故答案为:11;(4)设最后一个星期日是x,x﹣7,x﹣14,x﹣21,x﹣28,则x+x﹣7+x﹣14+x﹣21+x﹣28=75,解得x=29;故答案为:29.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一元一次方程数字问题
一元一次方程,是指在方程中只包含一个未知数,并且未知数的最
高次数为一。
解一元一次方程常用的方法有逆运算法、加减法消元法
或倍增消元法等。
数字问题是指在解题过程中,涉及到具体数字的计算和推导。
本文
将通过一些实际例子,来探讨一元一次方程的数字问题。
例1:
题目:小明买了一本书,花了50元,剩下的钱是他原来的两倍。
请问小明原来有多少钱?
解析:设小明原来的钱数为x元。
根据题目中的条件,可以列出方程:x-50=2x。
根据方程可以得到:x=50。
因此小明原来有50元。
例2:
题目:一个数字的2倍加上5得到的结果是27,这个数字是多少?
解析:设这个数字为x。
根据题目中的条件,可以列出方程:
2x+5=27。
解方程得:2x=22,即x=11。
因此这个数字是11。
例3:
题目:一个两位数,个位数字比十位数字大3,这个两位数是多少?
解析:设十位数字为x,个位数字为y。
根据题目中的条件,可以
列出方程:10x+y=x+3y。
化简方程得到:9x=2y。
由于题目中要求是两位数,因此x在1至9之间,而y为1至9之间的整数。
通过遍历x和y的组合,可以得到满足方程的两位数为12、24、36、48、60、72、84和96。
综上所述,这个两位数有8个解:12、24、36、48、60、72、84和96。
例4:
题目:一件商品原价100元,现在打8折出售,售价是多少?
解析:设售价为x元。
根据题目中的条件,可以列出方程:0.8 *
100 = x。
解方程可以得到:x = 80。
因此售价是80元。
通过以上几个例子可以看出,在解决一元一次方程数字问题时,关
键是准确地将问题抽象成方程,并通过变量的设定,将具体的数值问
题转化为未知数的运算问题。
这样一来,就可以通过解方程来求解未知数,从而得到问题的答案。
在实际数学运用中,一元一次方程数字问题有着广泛的应用,例如在
商业、市场调研、经济学等领域。
总结起来,解决一元一次方程数字问题的关键是将问题转化为方程,并通过解方程来求解未知数,从而得到问题的答案。
这需要我们熟练
掌握方程计算的基本方法,并善于将问题抽象成数学语言,通过运算
来求解。
掌握这些技巧将有助于提高我们解决实际问题的能力。
