等分面积
9.3.3等分三角形面积模型初步

1 2
S△ACD =2.5
由题意S△FDE=
1 2
S△CDE =1.25
针对训练1
如图所示,在△ABC中,AB=AC=5,BC=6, AD⊥BC于点D,且AD=4,若点P在边AC上移动,求 BP的最小值.
解:根据垂线段最短,可知当BP⊥AC时, BP有最小值.
由△ABC的面积公式可知,
1 AD·BC= 1 BP·AC.
2
2
代入数值,可解得BP=
24 5
Байду номын сангаас
.
方法总结
面积法的应用:若涉及两条高求长度,一般 需结合面积(但不求出面积),利用三角形面积的 两种不同表示方法列等式求解.
二、平行线中的等面积三角形
a
b
F
E
同底等高
1 S△ABC= 2 AB*CF
S△ABD= 1 2
∵CF = DE
AB*DE
∴S△ABC =S△ABD
1
B
DE
C
S△ABD=
BD*AE
2
1
2 S△ACD= CD*AE
DB=CD
三角形的中线将三角形分成面积相等的两部分
等底等高
例1 如图,△ABC的面积等于10,AD是中线,分别求出 △ABD和△ACD的面积。
由题意S△ACD =S△ABD=
1 2
S△ABC
=5
变式一
如图,△ABC的面积等于10,AD是中线,E为AD中点,分别 求出△ABE和△BDE的面积。
E
由题意S△ACD
=S△ABD=
1 2
S△ABC =5
由题意S△ABE =S△BDE=
1 2
S△ABD =2.5
中考25题常考类型------面积均分问题

中考 25 题常考类型 ------ 面积均分问题本节课讲了两种类型,第一种三角形和不规则四边形面积均分问题;第二种特殊的四边形面积均分问题。
在讲三角形面积均分时学生很容易就理解三角形的中线就能均分三角形面积。
但是在具体的题中要求过三角形一边的某一个定点均分三角形面积。
这道题学生觉得有难度,需要老师架一个梯度,帮助学生突破这种过定点等分的情形,其中需要用到蝴蝶模型,所以在讲过定点面积等分问题前给学生铺垫了蝴蝶模型。
即就是平行线剪的三角形面积相等,借助同底等高,不仅可以面积相等,还可以根据平行线做的位置不同转变三角形的位置。
引入:等腰三角形面积等分---一般三角形面积等分得到结论:三角形的中线能够等分三角形的面积。
师:在没有任何条件限制下,等分三角形面积我们知道找三角形中线即可。
那么要是有条件限制呢?比如过三角形ABC一边BC上的一定点P的直线如何等分三角形面积?先抛出问题,引发学生独立思考,再进行小组合作。
师:在解决这个问题前我们先来看一个模型---蝴蝶模型。
引入蝴蝶模型。
小结:我们发现蝴蝶模型存在等积转化的方法,即可以构造平行线,转化面积。
师:我们思考这个问题,已经会用中线等分面积了,那如何使得过定点的直线等分三角形面积?生:(思考中)生:(小组合作中)生:我考虑借助蝴蝶模型进行等积转化。
师:很好,给其他同学也提供了思路,可以朝这个方向思考。
再思考蝴蝶模型在什么线中产生的?生:平行线中产生,所以要构造平行线。
师:很棒,那么我们是等积转化,如何转化?在什么情况下可以转化成等分面积的情形呢?生:在已知中线可以等分面积的基础上,考虑结合中点构造平行线和蝴蝶模型。
生:我连接AP,取BC边上的中点M,连接AM,过M作MD平行于AP交AB于点D,连接DP,构造平行线,得到等积模型,从而得到三角形APM和三角形ADP面积相等,将这两个三角形面积进行转化,得到四边形DPCA的面积等于三角形AMC的面积,即就是四边形DPCA的面积等于三角形ABC的一半,即直线DP即为所求的直线。
举一个例子,将一个饼干分成两半的方法。

举一个例子,将一个饼干分成两半的方法。
在我们日常生活中,我们常常会遇到需要将一个物品分成两部分的情况,比如,我们要和朋友分享一块饼干,但是我们又不希望将它完全分成两半。
那么,有没有一种方法可以很好地解决这个问题呢?答案是肯定的。
下面,我将为大家介绍一种利用几何学原理的方法,将一个饼干分成两半,并且做到平衡和公平。
1. 方法一:通过等分角度进行划分首先,我们需要将饼干放置在一个水平的表面上。
然后,我们需要一把锋利的刀具,先将刀尖放在饼干的中央位置。
接着,我们需要将刀慢慢地旋转,并且用适当的力度将饼干切开。
在这个过程中,我们需要注意力度的掌握,以免刀片切入过深。
当饼干被切成两半时,我们需要确保切口的位置距离饼干的中心点相等。
这样,我们就可以保证饼干的两半在形状和重量上大致相同。
2. 方法二:通过等分面积进行划分除了通过等分角度进行划分,我们还可以通过等分饼干的面积来实现分开。
具体的操作方式如下:首先,我们需要准备一个饼干盘子和一张透明的纸。
将饼干放置在盘子上,然后用纸覆盖住饼干。
接下来,我们需要用一支铅笔或者其他标记工具,在纸上画出饼干的轮廓。
然后,我们将纸剪下来,将其平铺在桌面上。
接着,我们需要将纸对折,再次对折,直到将纸折叠成两半。
最后,我们只需要将纸放置在饼干的中央位置,然后用刀具沿着纸的轮廓进行切割。
通过这种方法,我们可以确保饼干的两半在面积上大致相同。
3. 方法三:通过让对方选择除了几何学原理的方法,我们还可以采用更加公平的方式来分割饼干。
这种方法是当事人选择自己所需的一半。
我们只需要将饼干放在公平的位置上,然后让每一个人都选择自己想要的一半。
这样一来,不仅保证了双方的满意度,还体现了公正和公平的原则。
总结起来,我们可以通过等分角度或者面积的方式将一个饼干分成两半。
如果我们想要做到更加公平和公正,我们可以采用让对方选择的方式。
这些方法都是在日常生活中非常实用的,可以帮助我们解决分割物品的难题。
五年级下册数学-等分思想求面积
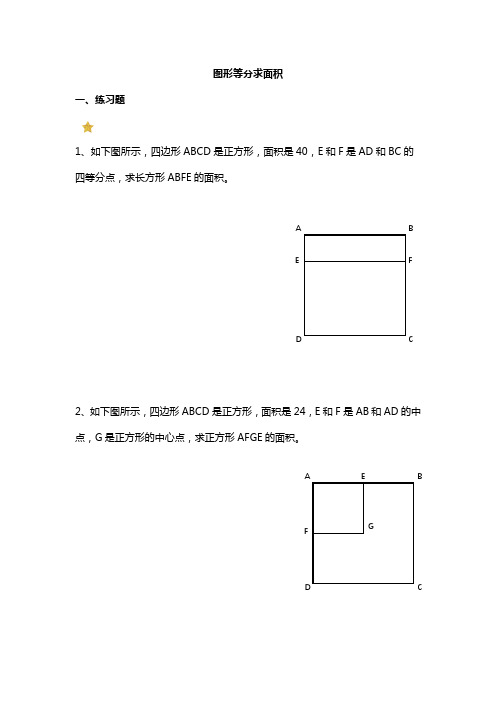
图形等分求面积一、练习题1、如下图所示,四边形ABCD 是正方形,面积是40,E 和F 是AD 和BC 的四等分点,求长方形ABFE 的面积。
2、如下图所示,四边形ABCD 是正方形,面积是24,E 和F 是AB 和AD 的中点,G 是正方形的中心点,求正方形AFGE 的面积。
ACDBE FACDBEGF3、如下图所示,三角形ABC 是等边三角形,面积是12,D 、E 是AB 、AC 边的中点,求三角形ADE 的面积。
4、如下图所示,四边形ABCD 是正方形,面积是36,E 是AB 的中点,求三角形AED 的面积。
ABCDEACDBE5、如下图所示,大正六边形的面积是24,图中阴影部分是一个等边三角形,求阴影部分的面积。
二、答案1、答案解析:如下图,将正方形ABCD 分成完全相同的四个长方形,每个长方形面积相等,所以长方形ABFE 的面积=40÷4=10。
2、答案解析:如下图,将正方形ABCD 分成完全相同的四个小正方形,每个小正方形面积相等,所以正方形AFGE 的面积=24÷4=6。
3、答案解析:如下图,将正三角形分成完全相同的四个小三角形,每个小三角形面积相等,所以三角形ADE 的面积=12÷4=3。
A CDB EFACDBEGFABCDE4、答案解析:如下图,将正方形ABCD 分成完全相同的四个三角形,每个三角形面积相等,所以三角形ADE 的面积=36÷4=9。
5、答案解析:如下图,将正六边形等分成6份,阴影部分有3份,已知大六边形的面积是24,所以一份是24÷6=4,阴影部分的面积是4×3=12。
ACDBE。
等分图形面积

(2)若四边形ABCD是梯形. 点P在BC上什么位置?
A D
点P在线段CS上呢?
M B P S C N
T
P
设MC的中点为S. 点P在线段BS上时, 在线段CD上存在点Q,
设BN的中点为T. 点P在线段TC上时, 在线段AB上存在点Q, 直线PQ将△ABN面积 2等分.
直线PQ将△DMC面积 2等分.
经过边BC上的点P作直线将△ABC分割成 2个面积相等的图形.
A
(1)若点P与点B(或C)重合;
Q
取AC中点Q,连接PQ.
B
PA
C
(2)设BC边中点为M,点P与点M重合.
连接AP.
B
M P
C
(3)设BC中点为M,若点P与点B(C)、点M不重合. 如图,P在BM上.
A
Q
连接AP. 可能是AP吗?
满足条件的直线与三角形边的交 点Q可能在AB上吗?
等分图形面积
如何用直线将一个多边形分割成几个面积相等的图形? n边形 m个面积相等的图形
如何研究这个问题?
从最简单的开始研究. n=3,m=2.
活动1:将△ABC分割成2个面积相等的图形.
A
作法:(1)取BC边中点M; (2)作直线AM. 则直线AM即所求的分割线.
B
M
C
S△ABM= S△ACM(等底同高的三角形面积相等).
X
Y
S△XST= S△YST
T
数量关系
SE
F
XY∥ST
位置关系
过X作XE⊥ST,过Y作XF⊥ST ,垂足为E、F. 因为S△XST= S△YST,所以XE=YF. 所以XE∥YF.
反之,因为XE∥YF, 所以XE=YF.
拓展资源:等分多个圆的面积

等分多个圆的面积
如图所示,有七个完全一样的圆,试画出一条直线将七个圆分成两部分,使得这两部分的面积相等。
仔细观察之后可以发现,上面的4个圆构成的图形Ⅰ和下面的3个圆构成的图形Ⅱ分别都是中心对称图形,并且这两部分合起来即为本题的整个图形。
现在将图形Ⅰ的对称中心与图形Ⅱ的对称中心连接起来,这条直线即为所求直线(如图)。
想一想,根据中心对称策略,还有其他的分割方法吗?(比如,还可以将原图分成左边六个圆和右边一个圆两部分,再分别找出它们的对称中心;或者在原图右侧补上两圆,使之成为九圆图,再分别找出九圆图和补上的两圆的对称中心即可。
但无论怎样进行分割,分割完以后的后续操作与原题解法类似。
)。
等分面积模型
等分面积模型引言在数学中,等分面积模型是一个用来划分一个给定区域的面积为若干个相等部分的模型。
这个模型在实际生活中有着广泛的应用,特别是在城市规划、土地开发和农业领域。
通过等分面积模型,我们可以合理地划分土地、规划城市、分配资源,以实现公平和可持续发展。
基本原理等分面积模型基于数学原理和计算方法,通过将一个给定的区域划分为若干个相等的小区域,从而实现面积的等分。
在等分面积模型中,我们需要考虑以下几个基本原理:1.区域的划分:将一个给定的区域划分为若干个小区域,每个小区域的面积相等。
2.边界条件:在划分过程中,需要考虑区域的边界条件,确保每个小区域都在给定的区域内。
3.划分方法:有多种划分方法可供选择,如网格划分、随机划分、最优划分等,根据具体情况选择合适的方法。
4.精确性:划分的精确性取决于所选择的划分方法和计算精度,需要根据实际需求进行调整。
应用领域等分面积模型在许多领域都有着广泛的应用,以下是一些常见的应用领域:城市规划在城市规划中,等分面积模型可以用来划分土地、规划建筑物和道路的位置。
通过合理地划分土地,可以提高土地利用率和城市的整体效益。
同时,等分面积模型也可以用来规划城市的绿地和公共设施,以满足居民的需求。
土地开发在土地开发中,等分面积模型可以用来划分不同用途的土地,如住宅用地、商业用地和工业用地。
通过合理地划分土地,可以提高土地的利用效率和资源的分配公平性。
同时,等分面积模型还可以用来评估土地的价值和潜力,为土地开发提供科学依据。
农业领域在农业领域,等分面积模型可以用来划分农田和农作物的种植区域。
通过合理地划分农田,可以提高农作物的产量和质量,实现农业的可持续发展。
同时,等分面积模型还可以用来评估农田的肥力和适宜性,为农业生产提供科学指导。
实际案例以下是一些实际案例,展示了等分面积模型在不同领域的应用:案例一:城市规划某城市规划部门使用等分面积模型划分土地,以规划新的城市发展区。
通过将发展区划分为若干个相等的小区域,确保每个小区域的土地利用率相等。
等分面积模型
等分面积模型
等分面积模型是数学中的一种几何模型,用于将一个给定的区域
等分成若干个面积相等的部分。
其方法是通过合理的几何构造和计算,将区域分割成所需的均等面积。
使用等分面积模型可以解决一些实际问题,例如在土地规划和城
市规划中,需要将一块土地或城市区域按照一定的标准划分成相等的
地块或建筑区域,以实现资源的合理利用。
在农田规划中,也可以利
用等分面积模型将农田按照一定面积的要求进行划分,方便农民进行
耕种和管理。
等分面积模型的具体方法有很多种,可以根据不同情况选择相应
的方法。
常见的方法包括使用几何图形(如正方形、三角形、圆形等)进行划分,或者利用数学计算(如积分、代数等)进行面积的计算和
分配。
在进行划分时,需要考虑到区域的形状、面积要求以及实际应
用的要求。
总之,等分面积模型是一种数学工具,可以帮助我们合理地将给
定的区域等分成若干个面积相等的部分。
通过合理的几何构造和计算,可以满足实际问题中对面积均等分配的要求。
初中数学专题---------直线等分面积问题
初中数学专题讲座---------直线等分面积问题一、直线等分常见的一些特殊图形二、直线等分三角形(1)不受限制的等分(2)过一边上一点等分三、直线等分梯形(1)不受限制的等分(2)过一腰上一点等分四、等分基本图形练习:1、作图题,请用学过的知识将下图所示的图形面积分成相等的两部分,请用一条直线把阴影部分的面积两等分.(保留作图痕迹)2、在一个矩形中,把此矩形面积二等分的直线最多有条,这些直线都必须经过此矩形的点(一个矩形只画一条直线,不写画法).3、轴对称图形的对称轴将图形面积二等分,中心对称图形过对称中心的直线将图形面积二等分.请用学过的知识将下图所示的图形面积分成相等的两部分.4、在一个矩形中,把此矩形面积两等分的直线最多有条,这些直线都必须经过该矩形.5、在复习“四边形”时,刘老师出了这样一道题:如图1,已知四边形ABCD、BEFG都是矩形,点G、H分别在AB、CD上,点B、C、E在同一条直线上.(1)当S矩形AGHD=S矩形CEFH时,试画一条直线将整个图形面积2等分.(不写画法)(2)①当S矩形AGHD<S矩形CEFH时,如图3;②当S矩形AGHD>S矩形CEFH时,如图4.画一条直线将整个图形面积2等分,在(1)的基础上,应该如何画图呢?(不写画法,保留作图痕迹或简要的文字说明)(3)小娟和小宇两位同学的画法是图5和图6:刘老师看过之后说这两个图形实质上体现的是一种画法,请你用简要的文字说明两个图形画法的共同点:(把原图形分割或构造成两个矩形,再过这两个矩形对角线的交点画一条直线).6、通过计算几何图形的面积可表示一些代数恒等式7、如图所示,▱ABCD内有一圆,请你画一条直线,同时将圆和平行四边形的周长二等分.(保留画图痕迹,并简要说出画图步骤)8、提出问题:如图,有一块分布均匀的等腰三角形蛋糕(AB=BC,且BC≠AC),在蛋糕的边缘均匀分布着巧克力,小明和小华决定只切一刀将这块蛋糕平分(要求分得的蛋糕和巧克力质量都一样).背景介绍:这条分割直线即平分了三角形的面积,又平分了三角形的周长,我们称这条线为三角形的“等分积周线”.尝试解决:(1)小明很快就想到了一条分割直线,而且用尺规作图作出.请你帮小明在图1中画出这条“等分积周线”,从而平分蛋糕.(2)小华觉得小明的方法很好,所以自己模仿着在图1中过点C画了一条直线CD交AB于点D.你觉得小华会成功吗如能成功,说出确定的方法;如不能成功,请说明理由.(3)通过上面的实践,你一定有了更深刻的认识.请你解决下面的问题:若AB=BC=5cm,AC=6cm,请你找出△ABC的所有“等分积周线”,并简要的说明确定的方法.9、提出问题:如图,在“儿童节”前夕,小明和小华分别获得一块分布均匀且形状为等腰梯形和直角梯形的蛋糕(AD∥BC),在蛋糕的边缘均匀分布着巧克力,小明和小华决定只切一刀将自己的这块蛋糕平分(要求分得的蛋糕和巧克力质量都一样).背景介绍:这条分割直线既平分了梯形的面积,又平分了梯形的周长,我们称这条线为梯形的“等分积周线”.尝试解决:(1)小明很快就想到了一条分割直线,而且用尺规作图作出.请你帮小明在图1中作出这条“等分积周线”,从而平分蛋糕.(2)小华觉得小明的方法很好,所以模仿着在自己的蛋糕(图2)中画了一条直线EF分别交AD、BC于点E、F.你觉得小华会成功吗?如能成功,说出确定的方法;如不能成功,请说明理由.(3)通过上面的实践,你一定有了更深刻的认识.若图2中AD∥BC,∠A=90°,AD<BC,AB=4cm,BC=6cm,CD=5cm.请你找出梯形ABCD的所有“等分积周线”,并简要的说明确定的方法.10、阅读下面问题的解决过程:问题:已知△ABC 中,P 为BC 边上一定点,过点P 作一直线,使其等分△ABC 的面积. 解决:情形1:如图①,若点P 恰为BC 的中点,作直线AP 即可.情形2:如图②,若点P 不是BC 的中点,则取BC 的中点D ,连接AP ,过点D 作DE ∥AP 交AC 于E ,作直线PE ,直线PE 即为所求直线. 问题解决:如图③,已知四边形ABCD ,过点B 作一直线(不必写作法),使其等分四边形ABCD 的面积,并证明.11、如图,把一个等边三角形的顶点放置在正六边形的中心O 点,请你借助这个等边三角形的角,以角为工具等分正六边形的面积,等分的情况分别为 等分. 12、用一条直线把下图分成面积相等的两部分.13、用三种不同的方法把▱ABCD 的面积四等分,并简要说明分法.14、、如图,所示,张家兄弟要平分这块地,请你用一条直线把它分成面积相等的两部分.(至少有两种画法)15、抛物线y=x 2,212y x =-和直线x=a (a >0)分别交于A 、B 两点,已知∠AOB=90°.(1)求过原点O ,把△AOB 面积两等分的直线解析式; (2)为使直线2y x b =+与线段AB 相交,那么b 值应是怎样的范围才适合.16、如图长为2的线段PQ 在x 的正半轴上,从P 、Q 作x 轴的垂线与抛物线y=x 2交于点p '、12题Q′.(1)已知P的坐标为(k,0),求直线OP′的函数解析式;(2)若直线OP′把梯形P′PQQ′的面积二等分,求k的值.17、一条直线过△ABC的内心,且平分三角形的周长,那么该直线分成的两个图形的面积比为()A.2:1 B.1:1 C.2:3 D.3:118、某课题研究小组就图形面积问题进行专题研究,他们发现如下结论:(1)有一条边对应相等的两个三角形面积之比等于这条边上的对应高之比;(2)有一个角对应相等的两个三角形面积之比等于夹这个角的两边乘积之比;…现请你继续对下面问题进行探究,探究过程可直接应用上述结论.(S表示面积)问题1:如图1,现有一块三角形纸板ABC,P1,P2三等分边AB,R1,R2三等分边AC.经探究知=S△ABC,请证明.问题2:若有另一块三角形纸板,可将其与问题1中的拼合成四边形ABCD,如图2,Q1,Q2三等分边DC.请探究与S四边形ABCD之间的数量关系.问题3:如图3,P1,P2,P3,P4五等分边AB,Q1,Q2,Q3,Q4五等分边DC.若S四边形ABCD=1,求.问题4:如图4,P1,P2,P3四等分边AB,Q1,Q2,Q3四等分边DC,P1Q1,P2Q2,P3Q3将四边形ABCD分成四个部分,面积分别为S1,S2,S3,S4.请直接写出含有S1,S2,S3,S4的一个等式.19、阅读下面材料,再回答问题:有一些几何图形可以被某条直线分成面积相等的两部分,我们将“把一个几何图形分成面积相等的两部分的直线叫做该图形的二分线”,如:圆的直径所在的直线是圆的“二分线”,正方形的对角线所在的直线是正方形的“二分线”.解决下列问题:(1)菱形的“二分线”可以是(2)三角形的“二分线”可以是(3)在下图中,试用两种不同的方法分别画出等腰梯形ABCD的“二分线”,并说明你的画法.20、用一条直线将一个直角梯形分成面积相等的两部分,请你在下面的图中分别画出两种不同的分割图形.21、下图所示是一块木板的示意图,能不能用一条直线把这块木板分成面积相等的两部分.(3种画法)22、如图所示的图案是一个轴对称图形,直线l是它的一条对称轴,如果最大圆的半径为2,那么阴影部分面积是()A.π B.2π C.3π D.4π23、如图所示是由7个完全相同的正方形拼成的图形,请你用一条直线将它分成面积相等的两部分.(在原图上作出).24、九条直线中的每一条直线都把正方形分成面积比为2:3的两个四边形.证明:这九条直线中至少有三条经过同一点.抽屉原理.专题:证明题.分析:首先根据抽屉定理证明9条直线中的每一条直线都把正方形分成面积比为2:3的两个四边形中至少有5条直线穿过一对边,然后再根据抽屉原理证明至少必有三点经过同一点.解答:证明:按抽屉原理,9条直线中的每一条直线都把正方形分成面积比为2:3的两个四边形,则至少有5条直线穿过一对边.又2:3≠1:1,根据“梯形的面积等于中位线长乘以高”,可知这5条直线必过正方形的一条对边中点连线上的两定点.故若5个点不全经过一点,则必经过这条直线上的两点,再据抽屉原理,至少必有三点经过同一点.25、一条直线平行于直线y=2x-1,且与两坐标轴围成的三角形面积是4,则直线的解析式是A.y=2x+4 B.y=2x-4 C.y=2x±4 D.y=x+2 ()26、把一个圆心为点O,半径为r的圆的面积四等分,请你尽可能多地设想各种分割方法.如图,如果圆心也是点O的三个圆把大圆O的面积四等分.求这三个圆的半径OB、OC、OD的长.27、已知直线AB与x,y轴分别交于A、B(如图),AB=5,OA=3,(1)求直线AB的函数表达式;(2)如果P是线段AB上的一个动点(不运动到A,B),过P作x轴的垂线,垂足是M,连接PO,设OM=x,图中哪些量可以表示成x的函数?试写出5个不同的量关于x的函数关系式.(这里的量是指图中某些线段的长度或某些几何图形的面积等)28、(1)如图1所示,已知△ABC中,D为BC的中点,请写出图1中,面积相等的三角形:,理由是(2)如图2所示,已知:平行四边形A′ABC,D为BC中点,请你在图中过D作一条线段将平行四边形A′ABC的面积平分,平分平行四边形A′ABC的方法很多,一般地过画直线总能将平行四边形A′ABC的面积平分.(3)如图3所示,已知:梯形ABCA′中,AA′∥BC,D为BC中点,请你在图3中过D作一条线段将梯形的面积等分.(4)如图4所示,某承包人要在自己梯形ABCD(AD∥BC)区域内种两种等面积的作物,并在河岸AD与公路BC间挖一条水渠EF,EF左右两侧分别种植了玉米、小麦,为了提高效益,要求EF最短.①请你画出相应的图形.②说明方案设计的理由.19、如图,抛物线y=ax2-3ax+b经过A(-1,0),C(3,2)两点,与y轴交于点D,与x轴交于另一点B.(1)求此抛物线的解析式;(2)若直线y=kx-1(k≠0)将四边形ABCD面积二等分,求k的值.。
圆的八等分计算公式
圆的八等分计算公式圆是数学中最基本的几何图形之一,它的性质和应用十分广泛。
在圆的研究中,圆的八等分是一个重要的问题。
圆的八等分是指将一个圆分成八个相等的部分,每个部分的角度为45度。
本文将介绍圆的八等分计算公式。
首先我们需要了解一些基本知识。
圆是由无数个点组成的,其中心是圆的重要部分。
圆的半径是从圆心到圆上的任意一点的距离。
圆的直径是通过圆心的一条线段,它等于半径的两倍。
圆的周长是圆上所有点到圆心的距离之和,它等于直径乘以π(圆周率)。
圆的面积是圆内所有点到圆心距离的平均值乘以π的平方。
这些基本知识将为我们后面的计算提供帮助。
圆的八等分计算公式可以分为两个部分:圆的周长和圆的面积。
圆的周长首先我们需要计算圆的周长。
由于我们要将圆分成八等分,因此每个等分的弧度为45度,也就是π/4。
根据圆的周长公式,圆的周长等于直径乘以π。
因此,我们可以得到以下公式:周长 = 直径×π我们需要将直径分成八份,因此每个等分的长度为直径的1/8。
根据这个长度可以计算出每个等分的弧长。
弧长等于圆的周长乘以弧度,因此我们可以得到以下公式:弧长 = 周长×弧度将上面两个公式结合起来,我们可以得到圆的八等分计算公式:圆的周长 = 直径×π每个等分的长度 = 直径的1/8每个等分的弧长 = 直径的1/8 ×π/4圆的八等分的周长 = 直径的1/8 ×π× 8 = 直径×π因此,圆的八等分的周长等于圆的直径乘以π。
圆的面积接下来我们需要计算圆的面积。
由于我们要将圆分成八等分,因此每个等分的角度为45度。
根据圆的面积公式,圆的面积等于圆的半径的平方乘以π。
因此,我们可以得到以下公式:面积 = 半径×π我们需要将半径分成八份,因此每个等分的长度为半径的1/8。
根据这个长度可以计算出每个等分的面积。
每个等分的面积等于扇形面积减去三角形面积。
扇形面积等于圆的面积乘以弧度除以2,三角形面积等于底乘以高除以2。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
初中数学专题讲座---------直线等分面积问题命题人:西安东方中学---卫孝春一、直线等分常见的一些特殊图形二、直线等分三角形(1(2)过一边上一点等分三、直线等分梯形(1)不受限制的等分(2)过一腰上一点等分四、等分基本图形练习:1、作图题,请用学过的知识将下图所示的图形面积分成相等的两部分,请用一条直线把阴影部分的面积两等分.(保留作图痕迹)2、在一个矩形中,把此矩形面积二等分的直线最多有条,这些直线都必须经过此矩形的点(一个矩形只画一条直线,不写画法).3、轴对称图形的对称轴将图形面积二等分,中心对称图形过对称中心的直线将图形面积二等分.请用学过的知识将下图所示的图形面积分成相等的两部分.4、在一个矩形中,把此矩形面积两等分的直线最多有条,这些直线都必须经过该矩形.5、在复习“四边形”时,刘老师出了这样一道题:如图1,已知四边形ABCD、BEFG都是矩形,点G、H分别在AB、CD上,点B、C、E在同一条直线上.(1)当S矩形AGHD=S矩形CEFH时,试画一条直线将整个图形面积2等分.(不写画法)(2)①当S矩形AGHD<S矩形CEFH时,如图3;②当S矩形AGHD>S矩形CEFH时,如图4.画一条直线将整个图形面积2等分,在(1)的基础上,应该如何画图呢?(不写画法,保留作图痕迹或简要的文字说明)(3)小娟和小宇两位同学的画法是图5和图6:刘老师看过之后说这两个图形实质上体现的是一种画法,请你用简要的文字说明两个图形画法的共同点:(把原图形分割或构造成两个矩形,再过这两个矩形对角线的交点画一条直线).6、通过计算几何图形的面积可表示一些代数恒等式7、如图所示,▱ABCD内有一圆,请你画一条直线,同时将圆和平行四边形的周长二等分.(保留画图痕迹,并简要说出画图步骤)8、提出问题:如图,有一块分布均匀的等腰三角形蛋糕(AB=BC,且BC≠AC),在蛋糕的边缘均匀分布着巧克力,小明和小华决定只切一刀将这块蛋糕平分(要求分得的蛋糕和巧克力质量都一样).背景介绍:这条分割直线即平分了三角形的面积,又平分了三角形的周长,我们称这条线为三角形的“等分积周线”.尝试解决:(1)小明很快就想到了一条分割直线,而且用尺规作图作出.请你帮小明在图1中画出这条“等分积周线”,从而平分蛋糕.(2)小华觉得小明的方法很好,所以自己模仿着在图1中过点C画了一条直线CD交AB于点D.你觉得小华会成功吗如能成功,说出确定的方法;如不能成功,请说明理由.(3)通过上面的实践,你一定有了更深刻的认识.请你解决下面的问题:若AB=BC=5cm,AC=6cm,请你找出△ABC的所有“等分积周线”,并简要的说明确定的方法.9、提出问题:如图,在“儿童节”前夕,小明和小华分别获得一块分布均匀且形状为等腰梯形和直角梯形的蛋糕(AD∥BC),在蛋糕的边缘均匀分布着巧克力,小明和小华决定只切一刀将自己的这块蛋糕平分(要求分得的蛋糕和巧克力质量都一样).背景介绍:这条分割直线既平分了梯形的面积,又平分了梯形的周长,我们称这条线为梯形的“等分积周线”.尝试解决:(1)小明很快就想到了一条分割直线,而且用尺规作图作出.请你帮小明在图1中作出这条“等分积周线”,从而平分蛋糕.(2)小华觉得小明的方法很好,所以模仿着在自己的蛋糕(图2)中画了一条直线EF分别交AD、BC于点E、F.你觉得小华会成功吗?如能成功,说出确定的方法;如不能成功,请说明理由.(3)通过上面的实践,你一定有了更深刻的认识.若图2中AD∥BC,∠A=90°,AD<BC,AB=4cm,BC=6cm,CD=5cm.请你找出梯形ABCD的所有“等分积周线”,并简要的说明确定的方法.10、阅读下面问题的解决过程:问题:已知△ABC 中,P 为BC 边上一定点,过点P 作一直线,使其等分△ABC 的面积. 解决:情形1:如图①,若点P 恰为BC 的中点,作直线AP 即可.情形2:如图②,若点P 不是BC 的中点,则取BC 的中点D ,连接AP ,过点D 作DE ∥AP 交AC 于E ,作直线PE ,直线PE 即为所求直线. 问题解决:如图③,已知四边形ABCD ,过点B 作一直线(不必写作法),使其等分四边形ABCD 的面积,并证明.11、如图,把一个等边三角形的顶点放置在正六边形的中心O 点,请你借助这个等边三角形的角,以角为工具等分正六边形的面积,等分的情况分别为 等分. 12、用一条直线把下图分成面积相等的两部分.13、用三种不同的方法把▱ABCD 的面积四等分,并简要说明分法.14、、如图,所示,张家兄弟要平分这块地,请你用一条直线把它分成面积相等的两部分.(至少有两种画法)15、抛物线y=x 2,212y x =-和直线x=a (a >0)分别交于A 、B 两点,已知∠AOB=90°. (1)求过原点O ,把△AOB 面积两等分的直线解析式;(2)为使直线y b =+与线段AB 相交,那么b 值应是怎样的范围才适合.12题16、如图长为2的线段PQ在x的正半轴上,从P、Q作x轴的垂线与抛物线y=x2交于点p 、Q′.(1)已知P的坐标为(k,0),求直线OP′的函数解析式;(2)若直线OP′把梯形P′PQQ′的面积二等分,求k的值.17、一条直线过△ABC的内心,且平分三角形的周长,那么该直线分成的两个图形的面积比为()A.2:1 B.1:1 C.2:3 D.3:118、某课题研究小组就图形面积问题进行专题研究,他们发现如下结论:(1)有一条边对应相等的两个三角形面积之比等于这条边上的对应高之比;(2)有一个角对应相等的两个三角形面积之比等于夹这个角的两边乘积之比;…现请你继续对下面问题进行探究,探究过程可直接应用上述结论.(S表示面积)问题1:如图1,现有一块三角形纸板ABC,P1,P2三等分边AB,R1,R2三等分边AC.经探究知=S△ABC,请证明.问题2:若有另一块三角形纸板,可将其与问题1中的拼合成四边形ABCD,如图2,Q1,Q2三等分边DC.请探究与S四边形ABCD之间的数量关系.问题3:如图3,P1,P2,P3,P4五等分边AB,Q1,Q2,Q3,Q4五等分边DC.若S四边形ABCD=1,求.问题4:如图4,P1,P2,P3四等分边AB,Q1,Q2,Q3四等分边DC,P1Q1,P2Q2,P3Q3将四边形ABCD分成四个部分,面积分别为S1,S2,S3,S4.请直接写出含有S1,S2,S3,S4的一个等式.19、阅读下面材料,再回答问题:有一些几何图形可以被某条直线分成面积相等的两部分,我们将“把一个几何图形分成面积相等的两部分的直线叫做该图形的二分线”,如:圆的直径所在的直线是圆的“二分线”,正方形的对角线所在的直线是正方形的“二分线”.解决下列问题:(1)菱形的“二分线”可以是(2)三角形的“二分线”可以是(3)在下图中,试用两种不同的方法分别画出等腰梯形ABCD的“二分线”,并说明你的画法.20、用一条直线将一个直角梯形分成面积相等的两部分,请你在下面的图中分别画出两种不同的分割图形.21、下图所示是一块木板的示意图,能不能用一条直线把这块木板分成面积相等的两部分.(3种画法)22、如图所示的图案是一个轴对称图形,直线l是它的一条对称轴,如果最大圆的半径为2,那么阴影部分面积是()A.π B.2π C.3π D.4π23、如图所示是由7个完全相同的正方形拼成的图形,请你用一条直线将它分成面积相等的两部分.(在原图上作出).24、九条直线中的每一条直线都把正方形分成面积比为2:3的两个四边形.证明:这九条直线中至少有三条经过同一点.抽屉原理.专题:证明题.分析:首先根据抽屉定理证明9条直线中的每一条直线都把正方形分成面积比为2:3的两个四边形中至少有5条直线穿过一对边,然后再根据抽屉原理证明至少必有三点经过同一点.解答:证明:按抽屉原理,9条直线中的每一条直线都把正方形分成面积比为2:3的两个四边形,则至少有5条直线穿过一对边.又2:3≠1:1,根据“梯形的面积等于中位线长乘以高”,可知这5条直线必过正方形的一条对边中点连线上的两定点.故若5个点不全经过一点,则必经过这条直线上的两点,再据抽屉原理,至少必有三点经过同一点.25、一条直线平行于直线y=2x-1,且与两坐标轴围成的三角形面积是4,则直线的解析式是A.y=2x+4 B.y=2x-4 C.y=2x±4 D.y=x+2 ()26、把一个圆心为点O,半径为r的圆的面积四等分,请你尽可能多地设想各种分割方法.如图,如果圆心也是点O的三个圆把大圆O的面积四等分.求这三个圆的半径OB、OC、OD的长.27、已知直线AB与x,y轴分别交于A、B(如图),AB=5,OA=3,(1)求直线AB的函数表达式;(2)如果P是线段AB上的一个动点(不运动到A,B),过P作x轴的垂线,垂足是M,连接PO,设OM=x,图中哪些量可以表示成x的函数?试写出5个不同的量关于x的函数关系式.(这里的量是指图中某些线段的长度或某些几何图形的面积等)28、(1)如图1所示,已知△ABC中,D为BC的中点,请写出图1中,面积相等的三角形:,理由是(2)如图2所示,已知:平行四边形A′ABC,D为BC中点,请你在图中过D作一条线段将平行四边形A′ABC的面积平分,平分平行四边形A′ABC的方法很多,一般地过画直线总能将平行四边形A′ABC的面积平分.(3)如图3所示,已知:梯形ABCA′中,AA′∥BC,D为BC中点,请你在图3中过D作一条线段将梯形的面积等分.(4)如图4所示,某承包人要在自己梯形ABCD(AD∥BC)区域内种两种等面积的作物,并在河岸AD与公路BC间挖一条水渠EF,EF左右两侧分别种植了玉米、小麦,为了提高效益,要求EF最短.①请你画出相应的图形.②说明方案设计的理由.19、如图,抛物线y=ax2-3ax+b经过A(-1,0),C(3,2)两点,与y轴交于点D,与x轴交于另一点B.(1)求此抛物线的解析式;(2)若直线y=kx-1(k≠0)将四边形ABCD面积二等分,求k的值.。
