自动控制原理第2章 习题及解析
自动控制理论第二章习题答案
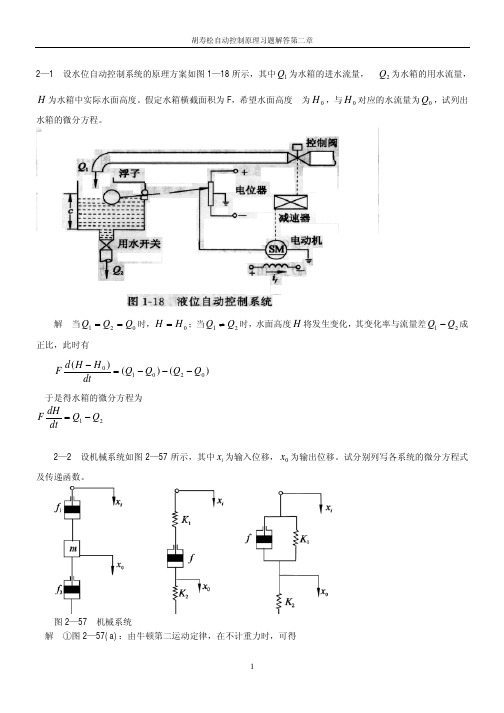
式中 K 为比例常数, P 为阀门前后的压差。若流量 Q 与压差 P 在其平衡点 (Q0 , P0 ) 附近作微小变化,试导出线性化
方程。 解:
设正常工作点为 A,这时 Q0 = K P0
在该点附近用泰勒级数展开近似为:
y
=
f
(
x0
)
+
df (x) dx
x0
(
x
−
x0
)
即 Q − Q0 = K1 (P − P0 )
其中 K1
= dQ dP P=P0
=
1K 2
1 P0
2-7 设弹簧特性由下式描述:
F = 12.65 y1.1
其中,是弹簧力;是变形位移。若弹簧在变形位移附近作微小变化,试推导的线性化方程。 解:
设正常工作点为 A,这时 F0
=
12.65
y1.1 0
在该点附近用泰勒级数展开近似为:
2-3 试证明图2-58(a)的电网络与(b)的机械系统有相同的数学模型。
2
胡寿松自动控制原理习题解答第二章
图 2-58 电网络与机械系统
1
解:(a):利用运算阻抗法得: Z1
=
R1
//
1 C1s
=
R1 C1s
R1
+
1 C1s
=
R1 = R1 R1C1s + 1 T1s + 1
Z2
=
R2
+
1 C2s
(C2
+
2C1 )
du0 dt
+ u0 R
=
C1C2 R
d 2ui dt 2
自动控制原理及其应用_课后习题答案_第二章

自动控制原理及其应用_课后习题答案_第二章黄坚主编自动化专业课程(2-1a)第二章习题课(2-1a)2-1(a)试建立图所示电路的动态微分方程。
u+ci1=i2-ic+d)+uoR1(ui-uo+u1u[R-CR2u]R1+uoui=dtoi2---C解:CCi1R1R2ic+uoi2-duiduo输入量为ui,输出量为uo。
Rui=u1+uoR2ui=uoR1-CdtR1R2+CdtR12+uoR2ducd(ui-uo)uoic=Cidt=dtu1=i1R1duodui2=RuoR1+CdtR1R2+uoR2=R2ui+CdtR1R22黄坚主编自动化专业课程(2-1b)第二章习题课(2-1b)2-1(b)试建立图所示电路的动态微分方程。
ducCLd2uoduoLduoLic==2+CdtR1uL=dtR2dt+uR2dtd2u+uooCCLoR2duou=+uo+Ci1ii2=Rui=u1+uo2dt-R2R2dt2-输入量为ui,输出量为uo。
u1=i1R1i1=iL+icdiLuL=Ldtducd(ui-uo)ic=Cdt=dtuoiL=i2=R2习题课一(2-2)求下列函数的拉氏变换。
(1)f(t)=in4t+co4tf(t)=in4t+co4tw:L解:∵L[inwt]=22w+L[cowt]=22w+ 4+L∴L[in4t+co4t]=2+162+16+4=2+16黄坚主编自动化专业课程(2)f(t)=t3+e4tf(t)=t3+e4t]=3!+:解:L[t3+1(3)f(t)=tneatf(t)=)=t13!1-4=4+-4:解:L[tneat]=n!(-a)n+1(4)f(t)=(t-1)2e2tf(t)=(t-1)2e2t]=e-(-2)2:解:L[(t-1)(-2)3黄坚主编自动化专业课程2-3-1函数的拉氏变换。
F()=(+1)(+3)F()=+1+1A解:A1=(+2)(+1)(+3)+1A2=(+3)(+1)(+3)1F()=+3-+2F()=2=-3=-1=-2=2f(t)=2e-3t-e-2tf(t)=2e黄坚主编自动化专业课程2-3-2函数的拉氏变换。
黄家英自动控制原理第二版第二章习题答案

6 s
部分分式展开 5 1 −4 Y(s) = + + s+3 s+2 s
∴ y (t ) = −4e −3 t + 5e −2t + 1 , t ≥ 0
已知控制系统的微分方程(或微分方程组) B2.9 已知控制系统的微分方程(或微分方程组)为
式中r(t)为输入量,y(t)为输出量, (t)、 (t)和 式中r(t)为输入量,y(t)为输出量,z1(t)、z2(t)和z3(t) r(t)为输入量 为输出量 为中间变量, 均为常数。 为中间变量,τ、β、K1和K2均为常数。 试求: a)各系统的传递函数Y(s)/R(s);(b)各系统含 各系统的传递函数Y(s)/R(s) 试求:(a)各系统的传递函数Y(s)/R(s);(b)各系统含 有哪些典型环节? 有哪些典型环节?
在图B2.4所示的电路中电压u (t)为输入量 B2.4所示的电路中电压 为输入量, B2.4 在图B2.4所示的电路中电压u1(t)为输入量,试以电 (t)或 (t)作为输出量 分别列写该系统的微分方程。 作为输出量, 压u2(t)或uC2(t)作为输出量,分别列写该系统的微分方程。
B 2.4解: u 2作为输出,应用网络的 复阻抗法: 作为输出, 复阻抗法: Q U 2 (s ) = U 1 (s ) 1 R1 1 C1s + R2 + 1 C 2s R1 + C1s 1 (R 2 + ) C 2s
B2.8 设系统的微分方程为
试用拉氏变换法进行求解。 试用拉氏变换法进行求解。
B 2.8解: 进行拉氏变换 & s 2 Y(s) - (sy(0) + y(0)) + 5sY(s) - 5y(0) + 6Y(s) =
自动控制原理(胡寿松)课后习题答案详解
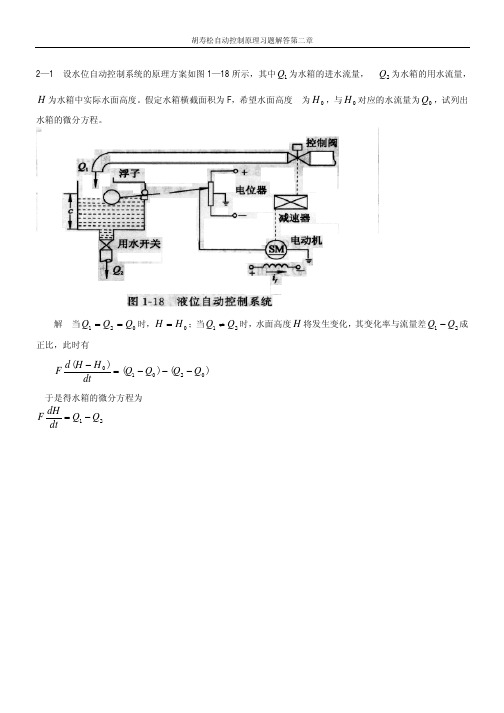
N
G3
G2
1+G1G2H1
-
- C
再进一步化简得:
1+G1G2H1
G1
G2
20
胡寿松自动控制原理习题解答第二章
N
-
G3
G2
C
1+G1G2H1
-
1+G1G2H1
G1
G2
再进一步化简得:
N G2G3-1-G1G2H1 1+G1G2H1
G2
C
G2+G1 (1+G1G2H1)
所以: C(s) =
G2 (G2G3 − 1 − G1G2 H1 )
10 6s + 10
R(s) 1 + G(s)H (s) 1 + 20 10
6s + 10 20s + 5
E(s) =
10
=
10
R(s) 1 + G(s)H (s) 1 + 20 10
6s + 10 20s + 5
=
(6s
200(20s + 5) + 10)(20s + 5) +
200
=
200(20s + 5) 120s 2 + 230s + 250
Z2
=
R2
+
1 C2s
=
1 C2s
(R2C2s + 1) =
1 C2
s
(T2
s
+ 1)
所以: U 0 (s) = Z 2 =
1 C2
s
(T2
s
+
1)
自动控制原理习题2带答案

1.采用负反馈形式连接后 ○ A. 一定能使闭环系统稳定; B. 系统动态性能一定会提高; C. 一定能使干扰引起的误差逐渐减小,最后完全消除; D. 需要调整系统的结构参数,才能改善系统性能。 2. 关于系统传递函数,以下说法不正确的是 ○
A. 是在零初始条件下定义的; B. 只适合于描述线性定常系统; C. 与相应s平面零极点分布图等价; D. 与扰动作用下输出的幅值无关。
3.系统特征方程为 0632)(23ssssD,则系统 ○ A. 稳定; B. 临界稳定; C. 右半平面闭环极点数2Z; D. 型别1v。
4.系统在2)(ttr作用下的稳态误差sse,说明 ○ A. 型别2v; B. 系统不稳定; C. 输入幅值过大; D. 闭环传递函数中有一个积分环节。 5. 对于以下情况应绘制0°根轨迹的是 ○
A. 主反馈口符号为“+”; B. 除*K外的其他参数变化时; C. 非单位反馈系统; D. 根轨迹方程(标准形式)为1)()(sHsG。 6.非最小相角系统 ○ A. 一定是条件稳定的; B. 对应要绘制0°根轨迹; C. 开环一定不稳定; D. 闭环相频的绝对值非最小。
7.对于单位反馈的最小相角系统,依据三频段理论可得出以下结论 ○ A. 低频段足够高,sse就能充分小; B. )(L以-20dB/dec穿越0dB线,系统就能稳定; C. 高频段越低,系统抗干扰的能力越强; D. 可以比较闭环系统性能的优劣。 8.频域串联校正方法一般适用于 ○ A. 单位反馈的非最小相角系统; B. 线性定常系统;
C. 单位反馈的最小相角系统; D. 稳定的非单位反馈系统。 9.离散系统差分方程 )()1(3)(2)1(3)2(kukukckckc
则脉冲传递函数为 ○
A.23132zzz; B.23132zzz; C.23132zzz; D.23132zzz。 10. 适用于描述函数法分析非线性系统的前提条件之一是 ○ A. )(sG必须是二阶的; B. 非线性特性正弦响应中的基波分量幅值占优; C. 非线性特性具有偶对称性;D. )(),(sGAN必须是串联形式连结的。
自动控制第二章习题答案

2-1 解:显然,弹簧力为)(t kx ,根据牛顿第二运动定律有:22)()()(dtt x d m t kx t F =- 移项整理,得机械系统的微分方程为:)()()(22t F t kx dt t x d m =+对上述方程中各项求拉氏变换得:)()()(2s F s kX s X ms =+所以,机械系统的传递函数为:2()1()()X s G s F s ms k==+2-2 (b) 解一:由图易得:11121221()()()()()()()()c c i t R u t u t u t i t R u t du t i t Cdt=-+== 由上述方程组可得无源网络的运动方程为:--2112221()()()()()++=+du t du t C R R u t CR u t dt dt对上述方程中各项求拉氏变换得:1222211()()()()()C R R sU s U s CR sU s U s ++=+所以,无源网络的传递函数为:22112()1()()1()U s CR sG s U s C R R s+==++ 解二(运算阻抗法或复阻抗法):222112121()11()1()++==++++R U s R Cs Cs U s R R CsR R Cs(c) 解一:设总电流为i 1(t ),R 2中的电流为i 2(t ),则由基尔霍夫定律,有12112122222()()()()()()()()()-==-+=u t u t i t R du t Ci t i t dt di t L R i t u t dt消去中间变量i 1(t )和i 2(t ),得22221222121111()()()()(1)()()++++=+d u t du t R du t R L L LC R C u t u t R dt R R dt R dt 对上式进行拉氏变换可得222111212()()()()()+==++++U s Ls R G s U s R LCs R R C L s R R 解二:(运算阻抗法或复阻抗法):222221112122121()1()()1()()()()()++++==++++++++R Ls CsR Ls U s Ls R Cs U s R LCs R R C L s R R R Ls Cs R R Ls Cs2-5 解:按照上述方程的顺序,从输出量开始绘制系统的结构图,其绘制结果如下图所示:依次消掉上述方程中的中间变量,,,321X X X 可得系统传递函数为:)]()()[()()()()()()()()()(1)()()()()()(8743215436324321s G s G s G s G s G s G s G s G s G s G s G s G s G s G s G s G s R s C -+++=(也可由结构图化简方法,求得上述传递函数)2-6 解:① 将)(1s G 与)(1s G 组成的并联环节和)(1s G 与)(1s G 组成的并联环节简化,它们的等效传递函数和简化结构图为:)()()()()()(43342112s G s G s G s G s G s G -=+=② 将)(),(3412s G s G 组成的反馈回路简化便求得系统的闭环传递函数为:2-7 (a )解:由上图可列方程组:)()()()()()()()]()()()([21221s E s G s C s H s R s C s G s H s C s G s E =-=-联列上述两个方程,消掉)(s E ,得传递函数为:121122()()()()1()()()()G s G s C s R s H s G s H s G s =++ 联列上述两个方程,消掉)(s C ,得传递函数为:2211221()()()()1()()()()H s G s E s R s H s G s H s G s +=++2-8 解:将①反馈回路简化,其等效传递函数和简化图为:351125.0*4.01124.0)(1+=+++=s s s s G将②反馈回路简化,其等效传递函数和简化图为:4.39.55.4535)35)(13.0(4.0113.01)(23222++++=++++++=s s s s s s s s s s G将③反馈回路简化便求得系统的闭环传递函数为:3232320.7*(53)()5 4.5 5.9 3.40.7*(53)()15 4.5 5.93 3.5 2.15(4.5 3.5)(5..9 2.1)34.4o i s s s s s s Ks s s s s s K s K s s +Θ+++==+Θ++++++++++2-9 (a )一个前向通道 P 1=G 1G 2, Δ1=1 两个回路 L 1=-G 1H 1,L 2=-G 2H 2 所以1211221=++G G P G H G H(b )两个前向通道 P 1=G 1G 2, Δ1=1P 2=G 3G 2 Δ2=1一个回路 L 1=-G 1G 2H 1 所以213121()1=++G P G G G G H。
(完整版)自动控制原理课后习题及答案

第一章绪论1-1 试比较开环控制系统和闭环控制系统的优弊端.解答: 1 开环系统(1)长处 :构造简单,成本低,工作稳固。
用于系统输入信号及扰动作用能早先知道时,可获得满意的成效。
(2)弊端:不可以自动调理被控量的偏差。
所以系统元器件参数变化,外来未知扰动存在时,控制精度差。
2闭环系统⑴长处:不论因为扰乱或因为系统自己构造参数变化所惹起的被控量偏离给定值,都会产生控制作用去消除此偏差,所以控制精度较高。
它是一种按偏差调理的控制系统。
在实质中应用宽泛。
⑵弊端:主要弊端是被控量可能出现颠簸,严重时系统没法工作。
1-2什么叫反应?为何闭环控制系统常采纳负反应?试举例说明之。
解答:将系统输出信号引回输入端并对系统产生控制作用的控制方式叫反应。
闭环控制系统常采纳负反应。
由1-1 中的描绘的闭环系统的长处所证明。
比如,一个温度控制系统经过热电阻(或热电偶)检测出目前炉子的温度,再与温度值对比较,去控制加热系统,以达到设定值。
1-3试判断以下微分方程所描绘的系统属于何种种类(线性,非线性,定常,时变)?2 d 2 y(t)3 dy(t ) 4y(t ) 5 du (t ) 6u(t )(1)dt 2 dt dt(2) y(t ) 2 u(t)(3)t dy(t) 2 y(t) 4 du(t) u(t ) dt dtdy (t )u(t )sin t2 y(t )(4)dtd 2 y(t)y(t )dy (t ) (5)dt 2 2 y(t ) 3u(t )dt(6)dy (t ) y 2 (t) 2u(t ) dty(t ) 2u(t ) 3du (t )5 u(t) dt(7)dt解答: (1)线性定常(2)非线性定常 (3)线性时变(4)线性时变(5)非线性定常(6)非线性定常(7)线性定常1-4 如图 1-4 是水位自动控制系统的表示图, 图中 Q1,Q2 分别为进水流量和出水流量。
控制的目的是保持水位为必定的高度。
《自动控制原理》第二版课后习题答案
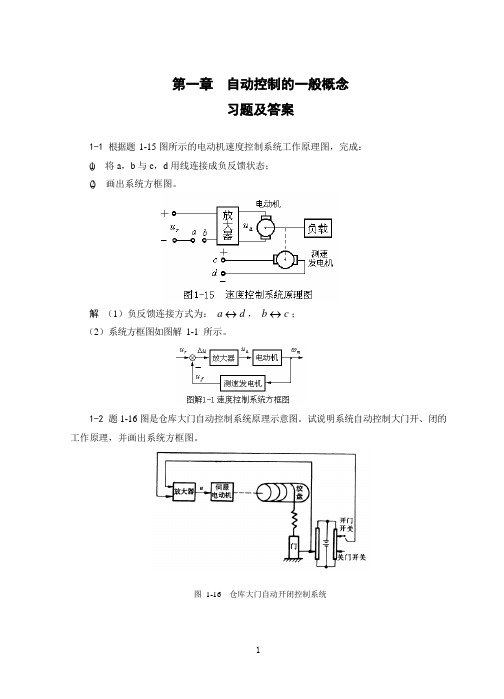
k (x x ) f ( dx1 dy )
(1)
1
1
dt dt
对B点有
f ( dx1 dy ) k y dt dt 2
(2)
联立式(1)、(2)可得:
dy k1k2 y k1 dx dt f (k1 k2 ) k1 k2 dt
电压。
在正常情况下,炉温等于某个期望值T °C,热电偶的输出电压u f 正好等于给定电压ur 。 此时, ue ur u f 0 ,故u1 ua 0 ,可逆电动机不转动,调压器的滑动触点停留在某 个合适的位置上,使uc 保持一定的数值。这时,炉子散失的热量正好等于从加热器吸取的热
量,形成稳定的热平衡状态,温度保持恒定。
第一章 自动控制的一般概念 习题及答案
1-1 根据题 1-15 图所示的电动机速度控制系统工作原理图,完成: (1) 将 a,b 与 c,d 用线连接成负反馈状态; (2) 画出系统方框图。
解 (1)负反馈连接方式为: a d , b c ;
(2)系统方框图如图解 1-1 所示。
1-2 题 1-16 图是仓库大门自动控制系统原理示意图。试说明系统自动控制大门开、闭的 工作原理,并画出系统方框图。
图 1-16 仓库大门自动开闭控制系统
1
解 当合上开门开关时,电桥会测量出开门位置与大门实际位置间对应的偏差电压,偏 差电压经放大器放大后,驱动伺服电动机带动绞盘转动,将大门向上提起。与此同时,和大 门连在一起的电刷也向上移动,直到桥式测量电路达到平衡,电动机停止转动,大门达到开 启位置。反之,当合上关门开关时,电动机带动绞盘使大门关闭,从而可以实现大门远距离 开闭自动控制。系统方框图如图解 1-2 所示。
当炉膛温度T °C 由于某种原因突然下降(例如炉门打开造成的热量流失),则出现以下
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第二章 习题解析2-4 当系统处于零初始条件下时,给系统输入单位阶跃响应信号,其输出响应为2()1t t y t e e --=-+试求该系统的传递函数。
参考解答:2111421()()21(2)(1)s s Y s R s s s s s s s s++=-+==++++ 22()42()()32Y s s s G s R s s s ++==++2-5 某可控硅整流器的输出电压d 2cos U KU αΦ=式中,K 为常数;2U Φ为整流变压器副边相电压有效值;α为可控硅的控制角。
设α在0α附近作微小变化,试将d U 与α的关系式线性化。
参考解答:将非线性微分方程d 2cos U KU αΦ=进行线性化,即在平衡点α0 附近将其展为泰勒级数取一次近似,线性化后用变量增量的线性方程ΔU d = C Δα 代替原来的非线性方程,式中常数2020sin sin dd dU C KU U KU d ααααααΦΦ===-→∆=-∆略去增加量符号“Δ”,上式可简写为20sin d U KU ααΦ=- 2-6 试求图2-70所示电路的传递函数()/()y r U s U s 。
参考解答:图 a)可作出该无源电路的动态结构图(图a-1)亦可作成图(图a-2)所示由结构图等效变换可求得传递函数212()11()()11c r U s R Cs bTs U s R R Cs Ts ++==+++式中21212(),1R T R R C b R R =+=<+ ,该网络称为滞后网络。
图 b)由图(b )网络可作出其动态结构图(b-1),简化为(b-2)即可得传递函数:112221122112212()(1)(1)()()1y r U s R C s R C s U s R C R C s R C R C R C s ++=++++该网络称为滞后-超前网络(滞后-超前电路)。
2-7 试求图2-71所示有源电路的传递函数y r ()/()U s U s 。
参考解答:运算放大器电路的传递函数21()()/()/y r G s U s U s Z Z ==-,式中的负号表示运算放大器电路()()y r U s U s 、间的反相关系, Z 1、Z 2 分别是输入电路和反馈电路的复阻抗。
α)图:22112()()()(1)1y r U s Z R KG s U s Z R R Cs Ts -===-=-++ 图2-71a )所示电路是一个惯性环节。
b )图:2222112112111122211121222''2'11()(1)(1)()()11(1)(1)(1)(1)1()y r R U s Z R C s R C s C s G s U s Z R C s R R C s C s R R C s R C s T s T s K R R C s T sK T s T s+-++===-=-⎛⎫⨯+ ⎪⎝⎭++++=-⨯=-=-++ 2-8 发电机-电动机组如图2-72所示。
发电机激磁电压f u 为输入量,电动机轴的角位移θ为输出量。
f R ,f L 为发电机激磁绕组电阻和电感,f i 为发电机激磁绕组的电流;a R 、a L 分别为发电机和电动机的总电枢电阻和总电枢电感,a i 为电枢电流,a e 为发电机电枢感应电势,b e 为电动机电枢反电势;0ω为发电机电枢转子的恒定转速,M 为电动机所生的主动力矩,J 、f 分别是折算到电动机轴上的转动惯量和粘性摩擦系数。
试画出系统的动态结构图,并求出传递函数()/()f s U s Θ。
参考解答:列写出发电机—电动机组的微分方程组,在零初始条件下进行拉氏变换,可得相应的变换方程组:发电机激磁回路:()()()f f ff f di t u t L R i t dt=+ (1)→ ()()()f f f f f u s L sI s R I s =+发电机—电动机的电枢回路:0()()()a f f f e t K t K i t ω=Φ= (2)→ ()()a f f E s K I s =()()()()a a a a ab di t e t R i t L e t dt=++ (3)→ ()()()()a b a a a a E s E s L sI s R I s -=+ ()()m b bd te t k dtϑ= (4)→ ()()b b E s K s s θ=()()m a M t C i t = (5)→ ()()m a M s C I s =电动机:22()()()()L f d t M t M t M t J dt θ--= (6)→ 2()()()()L fM s M s M s Js s θ--= ()()f d t M t fdtθ= (7)→ ()()f M s fs s θ= 由变换方程组作出系统动态结构图,再求得传递函数()/()f s U s θ∴2/()()1[()()]f fmf f a a a a m b K R C s U s T s s JL s JR fL s fR C K θ=⋅+++++若0a L =,则//()()1[()](1)(1)f ff m f mf f a a m b f m K R K C R C s U s T s s JR s fR C k s T s T s θ=⋅=+++++若a L 不忽略,则432/()()()[()]()f m ff f a f f a f a f a f f m b a f a m b K C R s U s L L Js L T L JR s R JR L fR K C K R f s R R C K sθ=++++++++ 2-9 系统的微分方程如下15211322433()()()()()()()()()()dn x t r t y t K dtx t K x t dx t K x t dtx t x t K n t =-+===-44()()()dc t K x t Ty t dt=+ 其中()r t 为给定输入信号,()n t 为输出量,15~K K 和T 均为正常数。
试画出系统的动态结构图,并求出传递函数()/()Y s R s 和()/()Y s N s 。
参考解答:将系统微分方程组在零初始条件下拉氏变换,由变换方程组作出系统动态结构图。
15152112113223224334334444()()()()()()()()()()()()()()()()()()()()()()()()()()()dn x t r t y t K dt X s R s Y s K SN s x t K x t X s K X s dx t K x t sX s K X s dt X s X s K N s x t x t K n t K X s TsY s Y s dc t K x t T y t dt ⎧=-+⎪=-+⎧⎪=⎪⎪=⎪⎪⎪⎪=⇒=⎨⎨⎪⎪=-=-⎪⎪⎪⎪=+⎩⎪=+⎪⎩令N (s ) = 0124124124124()1()()(1)11K K K K K K Y s s Ts s K K K R s s Ts K K K s Ts ⋅+Φ===+++⋅+令R (s ) = 012534124()()()()(1)N K K K K K s Y s s N s s Ts K K K -Φ==++ 2-11 系统的微分方程组为211112()()()(),()()dx t x t r t y t T K x t x t dt=-=-323223()()()(),()()dy t x t x t K y t T c t K x t dt=-+= 式中,T 1、T 2、K 1、K 2、K 3均为正的常数,系统的输入量为()r t ,输出量为()c t ,试画出动态结构图,并求出传递函数()/()Y s R s 。
参考解答:解:将微分方程组在零初始条件下拉氏变换,由变换方程组作出系统动态结构图(1),也可更详细作成动态结构图(2)。
11211121211323323223223()()()()()()()()()(1)()()()()()()()()(1)()()()()()x t r t y t X s R s Y s dx t T K x t x t T s X s K X s dt X s X s K Y s x t x t K y t T s Y s K X s dy t T y t K x t dt =-⎧⎪=-⎧⎪=-⎪+=⎪⎪⇒⎨⎨=-=-⎪⎪⎪⎪+=⎩+=⎪⎩由系统方框图运算可知,图(1)、(2)有完全相同的传递函数:121222212212312312()()s+1()(1)K K K K Y s R s T T K K K K TT s T T K K T s K K K K ==++++++1231()(s+)+2-13 简化图2-75 所示动态结构图,并求取传递函数Y (s ) / R (s )。
参考解答: 2-13a )图2-13b)图2-14 简化图2-76 所示动态结构图,并求取传递函数Y(s) / R(s) 。
参考解答:2-14a)图2-14b)图2-15 简化图2-77 所示动态结构图,并求取传递函数Y(s) / R(s) 。
参考解答:2-15a)图本题可有不同解法,分别讨论如下解1:分析结构图中信号传递和转换关系,左上方R 经比较点G1 后有三个方向:(1) 到达最右端比较点后输出;(2) 经引出点下左方比较点、环节G2后来至右端比较点后输出;(3) 由G1 后引出点→左下方比较点→环节G2、经引出点后回到右上方比较点形成一个正反馈回路,同理左下方的R 经比较、G 2 后也有类似三个走向。
可将系统结构图改画为图(1),再由图(2)、(3)逐步化简即可求出传递函数Y (s ) / R (s )。
解2:按结构图等效变换法则,将图(1)中G 1 后引出点移至G 1 前面,并与比较点交换,再由图(2)、(3)、(4)、(5)逐步化简即可求出传递函数Y (s ) / R (s )。
解3:本题也可直接用梅逊公式计算传递函数Y (s ) / R (s )()/()Y s R s =11()nk k k G s P p ===∆∆∑图中只有一个单独回路12:aL G G + ∴121G G ∆=-4n = 11p G = 11∆= ; 22p G = 21∆=;312p G G =- 31∆= ; 421p G G =- 41∆=∴ 1212122()()1G G G G Y s R s G G +-=- 相比之下,用梅逊公式计算最简便,但必须正确确定结构图中的单独回路、多种互不接触回路,前向通道及其余之式等。
