静力学-第2章(1) 平面基本力系-PPT课件
合集下载
第二章平面汇交力系及平面力偶系

一、几何法合成(作图法)
1、两力的合成方法——平行四边形法则。
2、多个力的合成。方法——力多边形法 则(依据平行四边形法则)。将汇交
力系各力平行移至首尾相接,起点至
第
终点连线为合力。
一 章
静 力 学 基 础
理论力学教学课件
第一节 平面汇交力系的合成
一、几何法(作图法)
F1
R12
O
F2
F3
R123
同理 :Ry= F1y+ F2y+ F3y
R FX 2 Fy 2
第二节 平面汇交力系合成的解析法
例 用 解 析 法 求 三 力 的 合 力 。 已 知 F1=100N ,
F2=200N,F3=300N 。
F1
45°
O
F2
解:F1X=F1COS45°=71N F1y=F1sin45°=71N F2X=F2=200N
静 力
自行封闭。
学 基
础
第二节 平面汇交力系的合成与 平衡的解析法
一、解析法合成(计算 ) 1、力在直角坐标轴上的投影
y
a’
A
αF
B
b’
oa
b
x
ab:F在x轴上的投影(Fx). a’b’:F在y轴上的投影(Fy)。
Fx=ab=Fsinα
第
一
Fy=a’ b’= - Fcosα
章
静 力 学 基 础
第二节 平面汇交力系合成的解析法
解:据平衡方程:ΣFx=0 ΣFy=0
ΣFy=-P- FD cos30°-FCBsin30°=0 FCB=-74.6 KN (BC杆受压) ΣF x=-FAB - FD sin30°FCBcos30°=0 FAB =54.6 KN (AB杆受拉)
1、两力的合成方法——平行四边形法则。
2、多个力的合成。方法——力多边形法 则(依据平行四边形法则)。将汇交
力系各力平行移至首尾相接,起点至
第
终点连线为合力。
一 章
静 力 学 基 础
理论力学教学课件
第一节 平面汇交力系的合成
一、几何法(作图法)
F1
R12
O
F2
F3
R123
同理 :Ry= F1y+ F2y+ F3y
R FX 2 Fy 2
第二节 平面汇交力系合成的解析法
例 用 解 析 法 求 三 力 的 合 力 。 已 知 F1=100N ,
F2=200N,F3=300N 。
F1
45°
O
F2
解:F1X=F1COS45°=71N F1y=F1sin45°=71N F2X=F2=200N
静 力
自行封闭。
学 基
础
第二节 平面汇交力系的合成与 平衡的解析法
一、解析法合成(计算 ) 1、力在直角坐标轴上的投影
y
a’
A
αF
B
b’
oa
b
x
ab:F在x轴上的投影(Fx). a’b’:F在y轴上的投影(Fy)。
Fx=ab=Fsinα
第
一
Fy=a’ b’= - Fcosα
章
静 力 学 基 础
第二节 平面汇交力系合成的解析法
解:据平衡方程:ΣFx=0 ΣFy=0
ΣFy=-P- FD cos30°-FCBsin30°=0 FCB=-74.6 KN (BC杆受压) ΣF x=-FAB - FD sin30°FCBcos30°=0 FAB =54.6 KN (AB杆受拉)
第2章静力学

yD
=
Jc + yc A
yc
!压力中心 D 恒在平面形心 C 的下方。
为什么?
应用上述公式时应该注意: (1)没有考虑大气压的影响。 (2)在压力中心的计算式中y坐标原点的取法。
将y轴原点取在自由液面上。
[例题2-3] 如图所示,一矩形闸门两面受到水的压力,左 边水深H1 = 4.5m,右边水深 H2 = 2.5m ,闸门与水面成 α = 450
四.流体静压力的两个重要特性:
特性一:静压力方向永远沿着作用面内法线方向
p
τ
证明:
pn m
一方面,流体静止时只有法向力,没有切向力,静压力只 能沿法线方向;
另一方面,流体不能承受拉力,只能承受压力。所以,静 压力唯一可能的方向就是内法线方向。
特性二:静止流体中任何一点上各个方向的静压力
大小相等,与作用面方位无关。
说明: 实压力体(+):压力体内充满液体,垂直分力是向下的; 虚压力体(-):压力体内没有液体,垂直分力是向上的。 压力体液重并不一定是压力体内实际具有的液体重力,只 是一个虚构概念。
综上所述,压力体的画法可归纳为以下几步:
(1)将受力曲面根据具体情况分成若干段; (2)找出各段的等效自由液面。 (3)画出每一段的压力体并确定虚实。 (4)根据虚实相抵的原则将各段的压力体合成,得到最
受压曲面ab的压力体为V=BAabc。 面积Aabc为扇形面积aob与三角形 cob面积之差,所以有
θ
P
Pz
b
Pz = ρ gBAacb
图2-23 例2-4图
Pz = ρ gBAacb
=
ρgB
⎡α
⎢ ⎣
360
(π H )2 − sin α
平面力偶系

F
(A)
第二章 平面基本力系
B
(B)
F
29
力偶系的平衡
思考题:结构如图所示,已知各杆均作用一个主动力偶 M, 确定各个铰链约束力的方向(不计构件自重)
A
M
O
M B
第二章 平面基本力系
30
力偶系的平衡
例:求当系统平衡时,力偶 M1, M2 应满足的关系。
研究BD
研究AC
C
M1 D
B
M1
D
NB
MO (Fn ) Fn h Fnr cos
78.93 N m
解法二
r
或根据合力矩定理,将
O
力Fn分解为圆周力F 和径向 F
力Fr , 则力Fn对轴心O的矩
MO Fn MO (F) MO (Fr ) MO (F) Fnr cos
Fn Fr
第二章 平面基本力系
9
例题
力对点之矩
水平梁AB受三角形分布的载荷作用,如图所示。
载荷的最大集度为q, 梁长l。试求合力作用线的位置。
q
A
Bx
第二章 平面基本力系
10
例题
力对点之矩
F
q A
dx x
h l
第二章 平面基本力系
解: 在梁上距A端为x的微段 dx上,作用力的大小为q’ dx,
其中q’ 为该处的载荷集度 ,
i 1
第二章 平面基本力系
6
三、力矩的解析表达式
Mo(F)= xFy-yFx
x、y是力F作用点A的坐标, 而Fx 、 Fy是力F在x、y轴的投影,
计算时用代数量代入。
合力FR对坐标原点之矩的解析表达式
静力学第二章

§2–3
空间力偶
1、力偶矩以矢量表示,力偶矩矢
空间力偶的三要素 (1) 大小:力与力偶臂的乘积; (2) 方向:转动方向; (3) 作用面:力偶作用面。
F1 F2 F1 F2
力偶矩矢 M rBA F (4–10)
2、力偶的性质
(1)力偶中两力在任意坐标轴上投影的代数和为零 . (2)力偶对任意点取矩都等于力偶矩,不因矩心改变而改变 。 力偶矩
B
A
A O
α
FAB
FBA
B
M1
M2 D
FO
M1 O
M2 D FD
解:杆AB为二力杆。 由于力偶只能与力偶平衡, 则AO杆与BD杆的受力如图所示。 分别写出杆AO和BD的平衡方程: Mi 0 由 得 M1 r ·AB cosα= 0 F
M2 + 2r · BA cosα= 0 F
则得
因为
三式与(2-3)式比较
比较(2-3)、(2-5)、(2-6)、(2-7)式可得
M o ( F ) yFz zFy M x ( F )
x
M o ( F ) zFx xF M y ( F )
y
M o ( F ) xFy yFz M z ( F )
FAB = FBA
M2 = 2 M1
例2-5 如图所示机构的自重不计。圆轮上的销子A放在摇杆BC上的光
滑导槽内。圆轮上作用一力偶,其力偶矩为M1=2 kN· , OA = r =0.5 m。 m
图示位置时OA与OB垂直,角α=30o , 且系统平衡。求作用于摇杆BC上的力偶 的矩 M2 及铰链O,B处的约束力。 先取圆轮为研究对象。 解:
静力学(受力分析)-课件

第一篇 静 力 学
引言
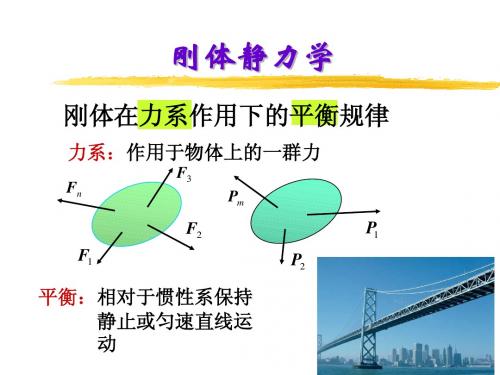
一、静力学:研究物体在力系作用下的平 衡条件的科学
二、静力学研究的主要内容: — 研究力系的合成和简化 —研究受力物体的平衡规律。
三、几个重要的基本概念
1、平衡
物体相对于惯性坐标系(工程中通常指地面)保 持静止或匀速直线运动。
2、力是矢 力的三要素:
量
大小、方向 、作用线
3、力的单位:N(牛顿)、kN(千牛)
实例:
FR
柔索: 实 例
3、光滑圆柱铰链约束
销 钉
圆柱销约束力的分析
FR y
销钉
销
FR
钉 孔
O
FR x
FRy FRx
销钉(铰链)
4、滚动支座
FN
FN
FN
5、固定铰支座
A
FAx FAy
固定铰支座
圆柱铰链和固定铰链支座的进一步说明
C
Ⅰ
Ⅱ
A
C
B
固定铰链支座 圆柱铰链
C
Ⅰ
Ⅱ
A
B
FAy
A
FC y
FRy FRx
FRz
球 股骨
球窝 盆骨
盆骨与股骨之间的球铰连接
(2)止推轴承
FA y
A
ห้องสมุดไป่ตู้A FAz
FAx
§1-3 研究对象、分离体、受力图
受力分析-过程与方法
确定研究对象 取分离体; 根据约束性质确定约束力; 画受力图。
受 力 分 析 示 例 (1)
W
取 分离 体
W
A B
FRA
FRB
画受力图
开丹
公理1:力的平行四边形法则
F2
F RF 1F 2
引言
一、静力学:研究物体在力系作用下的平 衡条件的科学
二、静力学研究的主要内容: — 研究力系的合成和简化 —研究受力物体的平衡规律。
三、几个重要的基本概念
1、平衡
物体相对于惯性坐标系(工程中通常指地面)保 持静止或匀速直线运动。
2、力是矢 力的三要素:
量
大小、方向 、作用线
3、力的单位:N(牛顿)、kN(千牛)
实例:
FR
柔索: 实 例
3、光滑圆柱铰链约束
销 钉
圆柱销约束力的分析
FR y
销钉
销
FR
钉 孔
O
FR x
FRy FRx
销钉(铰链)
4、滚动支座
FN
FN
FN
5、固定铰支座
A
FAx FAy
固定铰支座
圆柱铰链和固定铰链支座的进一步说明
C
Ⅰ
Ⅱ
A
C
B
固定铰链支座 圆柱铰链
C
Ⅰ
Ⅱ
A
B
FAy
A
FC y
FRy FRx
FRz
球 股骨
球窝 盆骨
盆骨与股骨之间的球铰连接
(2)止推轴承
FA y
A
ห้องสมุดไป่ตู้A FAz
FAx
§1-3 研究对象、分离体、受力图
受力分析-过程与方法
确定研究对象 取分离体; 根据约束性质确定约束力; 画受力图。
受 力 分 析 示 例 (1)
W
取 分离 体
W
A B
FRA
FRB
画受力图
开丹
公理1:力的平行四边形法则
F2
F RF 1F 2
第2章 平面力系-平面力对点之矩及平面力偶

即
MO(F) F d
O点为力矩的中心,称为矩心; d 为O点到力F 作用线的垂直
距离,称为力臂。 力矩的正负号:力使物体绕逆时针方向转动时为正,反
之为负。
应注意: 在平面问题中,力对点之矩只取决于力矩的大小及其旋 转方向(力矩的正负),因此它是一个代数量。
力矩的单位: 国际制 N·m,kN·m 工程制 公斤力米(kgf·m)
偶矩的代数和等于零,即 ∑Mi=0
利用这个平衡条件,可以求解一个未知量。
例题
两力偶作用在板上,尺寸如图,已知 F1 = F2=1.5 kN , F3
=F4 = 1 kN, 求作用在板上的合力偶矩。
F 1 180mm
解:由式
F2
M = M1 + M2
F4
则
M =-F1 ·0.18 –F3 ·0.08
FBA
B
A
FAB
M1
FO
O
M2 D
FD
M1 - FABrcosq 0 - M 2 2FBArcosq 0
因为 FAB FBA
所以求得 M 2 2M1
思考题1 一力偶(F1,F1′)作用在Oxy平面内,另一力偶(F2 ,F2′)作用在
Oyz平面内,它们的力偶矩大小相等(如图)。试问此两力偶是否 等效,为什么?
F1
d1
F2 d2
F1′
=
F2′
M1 F1 d1 , M 2 -F2 d2
F22 d F11
F11′
=
F22′
d
FR
FR′
M1 F11 d , M 2 -F22 d
FR F11 - F22 , FR F11 - F22
静力学(第二章)
A FC
C
B
W
①选研究对象; ②去约束,取分离体;③画上主动力;④画出约束反力。
例3 图示结构中各杆重力均不计,所有接触处均为光滑 接触。试画出:构件AO、AB和CD的受力图。
①选研究对象; ②去约束,取分离体;③画上主动力;④画出约束反力。
例4 画出下列各构件的受力图
说明:三力平衡必汇交 当三力平行时,在无限 远处汇交,它是一种特 殊情况。
改变原力系对刚体的作用。
只适于刚体!
静力学基本公理
推理1
力的可传性
作用在刚体上某点的力,可沿其作用线移动, 而不改变它对刚体的作用。
力对刚体的作用决定于:力的大小、方向和作用线。 力是有固定作用线的滑动矢量。
静力学基本公理
根据力的可传性,作D 的受力图, 此受力图是否正确?
分析整个系统平衡时,作用力 是否可沿其作用线移动?
刚体静力学模型
1.3 接触和连接方式的抽象和理想化
自由体:
-约束
其运动没有受到其它物体预加 的直接制约的物体
刚体静力学模型
约束:对非自由体运动起制约作用的周围物体 约束反力:约束作用于被约束物体的力
非自由体:
其运动受到其它物体预加的直接制约的物体
刚体静力学模型 约束反力的特点:
大小:常常是未知的 作用点:接触点 方向:总是与约束所能阻止的物体运动方向相反 F G
工程常见约束与约束反力
2.1 柔性约束
柔性约束只能承受拉力 约束反力: 沿柔索而背离被约束物体,作 用于连接点。
工程常见约束与约束反力
2.1 柔性约束
柔性约束只能承受拉力
约束反力: 沿柔索而背离被约束物体,作用于连接点。
链条约束与约束力
工程力学 (静力学)单辉祖主编PPT课件

y
F
y F
O
x
O
x
(a)
(b)
1-1-2 力的性质
例3:用图解法求合力
(a)
1-1-2 力的性质
例4:用图解法求Fx,Fy,Fz的合力
z Fz
FxxO源自Fyy1-1-2 力的性质
例4:已知系统平衡,画出B、C两点的受力方向
1-1-2 力的性质
例5:已知构件处于平衡状态,求Fc的方向
Fc
(a) (b)
➢ 固体力学研究在外力作用下,可变形固体内部各质点所产生的 位移、运动、应力、应变及破坏等的规律。属于固体力学范畴 的有材料力学、结构力学、弹性力学和塑性力学、复合材料力 学、断裂力学等。
➢ 流体力学的研究对象是气体和液体。研究在力的作用下,流体 本身的静止状态、运动状态及流体和固体间有相对运动时的相 互作用和流动规律等。属于流体力学的有水力学、空气动力学、 环境流体力学等。
据自己的爱好和特长,进一步广泛深入地研究工程力 学相关的其它问题
学习方法与要求
学习要求:
➢ 不可迟到、早退、旷课 ➢ 上课不允许睡觉、做与本课程无关的事、说与上课无关的话 ➢ 积极参与教学过程,认真完成课堂练习 ➢ 按教师要求及时、独立完成课后作业 ➢ 上课带教材、课堂笔记本、练习本、画图工具、计算器
M x M i xM y M i yM z M i z
M= ﹝(∑Mix)2+(Miy)2+(Miz)2 ﹞ ½
n
平面力偶系的简M化:Mi Mi i1
力偶系的平衡条件:
n
M Mi 0
或
i 1
M x M i x 0 M y M i y 0 M z M i z 0
平面力偶系的平衡条件:
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
解:
根据合力投影定理,得合力在轴 x,y上的投影分别为:
F1
60
O
45
30
F F cos 30 F cos 60 F cos 45 F cos 45 R x 1 2 3 4
45
x
F4
11
129 . 3 N
F3
F F cos 60 F cos 30 F cos 45 F cos 45 R y 1 2 3 4 112 . 3 N
F B
O
A
h
21
例题
平面基本力系
例 题 5
R
解: 1. 选碾子为研究对象,受力分析如图b所示。
各力组成平面汇交力系,根据平衡的几何条 件,力G , F , FA和FB组成封闭的力多边形。
F
O
由已知条件可求得 Rh cos 0.866 R 30
再由力多边形图c 中各矢量 的几何关系可得
y
F cos 60 G F cos 30 0 0 , BC
联立求解得
F 5 . 45 kN AB
F 74 .5 kN BC
19
例题
平面基本力系
例 题 4
约束力FAB为负值,说明该力实际指向 与图上假定指向相反。即杆AB实际上受拉力。 解析法的符号法则:当由平衡方程求得
15
例题
平面基本力系
例 题 3
水平梁AB中点C作用着力F,其大小等于2 kN,方向与
梁的轴线成60º 角,支承情况如图a 所示,试求固定铰链 支座A和活动铰链支座B的约束力。梁的自重不计。
60º
A
B
30º
C
a a
(a)
16
例题
平面基本力系
D
例 题 3
解:
1.取梁AB作为研究对象。
F F B sin F G A F B cos
FB FA G F
O
B
A
(a)
h
F
(c)
解得
FB
G
B
A
F FA F 10 kN, F G F cos 11 . 34 kN B A B sin
B
F
B
x
F
D
F F
x y
0, F F cos 45 F cos 0 B D
sin F sin 45 0 0, F D
14 . 03 , 已知:
sin 0 . 243 , cos 0 . 969
联立求解得
F 750 N B
5
动画
第2章 平面基本力系
平面力偶系的合成
6
动画
第2章 平面基本力系
力偶实例
7
动画
第2章 平面基本力系
力偶实例
8
动画
第2章 平面基本力系
力偶实例
9
第 2 章 平面力系的简化 第 3章 平面力系的平衡
例 题
10
例题
平面基本力系
例 题 1
求如图所示平面共点力系的合力。其中:F1 = 200 N,F2 = 300 N,F3 = 100 N,F4 = 250 N。 F2 y
1 4
F
J
I
FD
4 .由力三角形图c可得:
K
FB
(c)
sin 180 F F 750 N B sin
14
例题
平面基本力系
解析法
例 题 2
1.取制动蹬ABD作为研究对象。
y
A
2.画出受力图,并由力的可传性
化为共点力系。 3.列出平衡方程:
FD
O
45°
静力学篇
第 2 章 平面力系的简化 第 3章 平面力系的平衡
1
第 2 章 平面力系的简化 第 3章 平面力系的平衡
动画 例题
2
第 2 章 平面力系的简化 第 3章 平面力系的平衡
动 画
3
动画
第2章 平面基本力系
平面汇交力系合成的几何法
4
动画
第2章 平面基本力系
同平面内力偶等效定理证明
B
A FA
F 60º C (b) E
60º
2.画出受力图。
30º
FB
3.作出相应的力多边形。
FB K
4.由力多边形解出:
FA = F cos30=17.3 kN FB = F sin30=10 kN
17
F
30º
FA
H
(c)
例题
平面基本力系
例 题 4
A 30° 30° C
B
利用铰车绕过定滑轮B 的绳子吊起一货物重 G = 20
例题
平面基本力系
例 题 1
合力的大小:
2 2 F F F 171 . 3N R R x R y
F2
y F1
合力与轴x,y夹角的方向余弦为:
F cos R x 0 . 754 FR cos FR y FR 0 . 656
60
45
O
45
30
x F4
12
F3
49 .01
所以,合力与轴x,y的夹角分别为:
40 .99
例题
平面基本力系
例 题 2
图 a 所示是汽车制动机构的 一部分。司机踩到制动蹬上的
F
A
力F=212 N,方向与水平面成
24cm
O
B D
E
C
6cm
a = 45角。当平衡时,DA铅 直, BC 水平,试求拉杆 BC 所 受 的 力 。 已 知 EA=24 cm , DE=6 cm 点 E 在铅直线 DA 上 ,又 B , C , D 都是光滑铰
某一未知力的值为负时,表示原先假定的
该力指向和实际指向相反。
20
例题
平面基本力系
例 题 5
如图轧路碾子自重G = 20 kN,半 径 R = 0.6 m,障碍物高h = 0.08 m碾 子中心O处作用一水平拉力F,试求:
R
(1)当水平拉力F = 5 kN时,碾子对地
面和障碍物的压力;(2)欲将碾子拉 过障碍物,水平拉力至少应为多大; (3)力F 沿什么方向拉动碾子最省力, 此时力F为多大。
链,机构的自重不计。
(a)
13
例题
平面基本力系
ALeabharlann 例 题 2F解: 几何法
1.取制动蹬ABD作为研究对象, 并画出受力图。 2.作出相应的力多边形。 3. 由图b几何关系得:
OE EA 24 cm
DE 6 tan OE 24
O
B E
FD
(b)
FB
D
arctan 14 . 01
kN , 滑轮由两端铰接的水平
刚杆 AB 和斜刚杆 BC 支持于点 G
B 。不计铰车的自重,试求杆 AB和BC所受的力。
a
18
例题
y
平面基本力系
FBC
例 题 4
解:
x
1.取滑轮 B 轴销作为研究对象。
2.画出受力图。 3.列出平衡方程:
B
30°
30°
FAB
F
G
b
F
cos 30 F F sin 30 0 Fx 0, F BC AB
