哈工大概率论答案-习题七
哈工大理论力学教研室《理论力学Ⅰ》(第7版)课后习题-点的合成运动(圣才出品)

图 7-4 解:以 M 为动点,水轮为动系,牵连运动轨迹为定轴转动,速度分析如图 7-5 所示。
图 7-5 由 va = ve + vr 在 x、y 两个方向上的分量得
va sin 60o = ve + vr sin va cos 60o = vr cos
7 / 42
圣才电子书
图 7-1
图 7-2
7-2 图 7-2 中的速度平行四边形有无错误?错在哪里?
1 / 42
圣才电子书 十万种考研考证电子书、题库视频学习平台
答:都有错误,改正见图 7-3。
图 7-3 7-3 如下计算对不对?错在哪里?
图 7-4 (a)图 7-4(a)中取动点为滑块 A,动参考系为杆 OC,则 ve=ω·OA,va=cosφ (b)图 7-4(b)中 vBC=ve=vacos60°va=ωr 因为 ω=常量,所以,VBC=常量, (c)图 7-4(c)中为了求 aa 的大小,取加速度在 η 轴上的投影式:aacosφ-ac=0 所以 答:(a)不对,va 的速度平行四边形画法不正确,正确图见图 7-5。 (b)加速度的计算不正确。vBC 和 ω 为此瞬时的大小,不是任意时刻的速度和角速度 故不能对时间求导。
其中 ρ 和 φ 是用极坐标表示的点的运动方程,aρ 和 aψ 是点的加速度沿极径和其垂直 方向的投影。
答:如图 7-7 建立直角坐标系.xOy 与极坐标系 ρOφ。 取动点 Q,动系 OA
4 / 42
圣才电子书
加速度合成(图 7-8)
十万种考研考证电子书、题库视频学习平台
aa=aen+aet+ar+ac
大小:?
方向:Hale Waihona Puke √ √ √ √图 7-7
哈工大理论力学第七版课后习题答案

第1章 静力学公理和物体的受力分析1-1 画出下列各图中物体 A ,ABC 或构件 AB ,AC 的受力图。
未画重力的各物体的自 重不计,所有接触处均为光滑接触。
F N1APF N 2(a)(a1)(b)(b1)N 3(c)(c1)F N 2Ax(d)(d1)F AFF BAB(e)(e1)AqB (f) (f1)FBC F CFA(g) (g1)FAyAFCCFAxBP1P2(h) (h1)BFCFCDAFAyFAx(i) (i1)(j) (j1)F(k) (k1)FBAF′(l) (l2) (l3)图1-11-2 画出下列每个标注字符的物体的受力图。
题图中未画重力的各物体的自重不计,所有接触处均为光滑接触。
N22(a) (a1)B FN 1CP2P1FAyAFN 2FAx Ax(a2)N 3(b) (b1)′N 3N(b2) (b3)FFAxN12(c) (c1)N2AxN12(c2) (c3)(d) (d1)C D y(d2) (d3)FCx ByBxB′y (e) (e1) (e2) (e3)ByAx(f) (f1)BxAxF F′Bx (f2) (f3)FB(g) (g1)F′BCx(g3)F1FB′BDFCyCFBF2FCxBFAyA F Ax(h) (h1) (h2)FFAxF(i) (i1) (i2)A FCFOyOEFOxFDFByBFBx B (i3) (i4)FAyFFCy (j) (j1) (j2)2FFE′x FDxEyT 3C y(j3) (j4) (j5)EBD F′BC yD E(k) (k1)BBCx (k2) (k3)FA(l) (l1) (l2)F1F2DBA C EFAFCFE(l3) (l4)或FDxC Ey Ey(l2)’(l3)’(l4)’FA′D AFCyCFCxF1B(m) (m1)FADDEFEH F2FHFFA′D(m2) (m3)FN B (n)q(n2)FB D FFCFEA GA C E F G(o) (o1)B DBF FAFB′ C C D(o2) (o3) (o4)图1-2= ) 2 2F 第2章 平面汇交力系与平面力偶系2-1 铆接薄板在孔心 A ,B 和 C 处受 3 个力作用,如图 2-1a 所示。
概率论与数理统计第七章习题答案

解:(1)已知ξ ~N (µ, σ 2 ),取统计量U = ξ − µ ,则有U ~ N (0,1),于给定的置信概率1−α ,
n
σ/ n
可求出uα
+ (4 − 0.8)2 ×1] = 0.831.
14.设ξ1,ξ2,……,ξn是取自总体ξ的一个样本,n ≥ 2,ξ ~ B(1, p),其中p为未知,0 < p < 1, 求证:
(1)ξ12是p的无偏估计; (2)ξ12不是p2的无偏估计;
(3) ξ1ξ2是p2的无偏估计。
证明:(1)Eξ
2 1
tα /2 (4) = 2.78, S = 11.937, n = 5代入(*),求得µ的置信区间为(1244.185,1273.815).
20.假定到某地旅游的一个游客的消费额ξ~N (µ,σ 2 ),且σ = 500元,今要对 该地每一个游客的平均消费额µ进行估计,为了能以不小于95%的置信概率 确信这估计的绝对误差小于50元,问至少需要随机调查多少个游客?
乐山师范学院化学学院
1.设总体ξ 有分布律
第七章 参数估计部分习题答案
ξ
−1
0
2
p
2θ
θ
1-3θ
其中 0 < θ < 1 为待估参数,求θ 的矩估计。 3
解:总体一阶矩为Eξ = (−1) × 2θ + 0×θ + 2× (1− 3θ ) = −8θ + 2.
用样本一阶矩代替总体一阶矩得ξ = -8θˆ + 2,则θˆ = 1 (2 − ξ ). 8
概率论与数理统计(理工类,第四版)吴赣昌主编课后习题答案第七章

写在前面:由于答案是一个个复制到word rh,比校耗时耗力,故下载收取5分・希望需要的朋友给予理解和支持!PS网上有一些没经我同总就将我的答案整合、转换成pdf,放在文库里的.虽然是免费的.但是窃取f我的劳动成果,希望有心的朋友支持我一下.下载我的原版答案。
第七章假设检验假设检验的基本談念习题1 样木容fin确定后,在一个假设检验中•给定显著水平为*设此第一类错的概率为。
•则必有()•(A)a+p=l; (B)a+p>l; (C)a+p<l; {D)a+p<2.解答: 应选(D)・当样木容Sn确定后.aQ不能同时都很小.即a变小时,p变大:而P变小时• a变大.理论上,自然希望犯这两类错误的概率都很小・但a*的大小关系不能确定.并且这两类错谋不能同时发生,即a=l且p=l不会发生.故选(D).习題2设总休X^(g,a2b其中02已知,着要检验W需川统计a U=X"-gOa/n,(1)若对敢边检验,统计假设为则拒绝区间为(2)若肌边假设为H0:g=g0,Hl:n<^0,则拒绝区间为. (给定显着性水平为4样木均值为X•,样木容fi 为n,且可记ul・a为标准正态分布的(l・a)分位数).解答:由敢侧检验及拒绝的概念即可御到.习題3 如何理解假设检验所作出的〃拒绝原假设H0"和“接受原假设Hcr的判断解答:拒绝H0是有说服力的,接受H0是没有充分说服力的•因为假设检验的方法是概率性质的反证法.作为反证法就是必然要〃推出矛盾r才能得出"拒绝HO"的结论.这是有说服力的・如果“推不出矛盾化这时只能说〃目前还找不到拒绝H0的充分理由W此“不拒绝H0”或〃接受HCr\这并没有肯定H0—定成立•由于样木观察值是随机的• W此拒绝H0.不童味着H0是假的•接受H0也不意味着H0是真的•都存在着错误决策的可能.当原假设H0为真,而作出r拒绝H0的判断,这类决策错谋称为第一类错谋.又叫弃真错洪•显然犯这类错渓的概率为前述的小槪率a:a=P(拒绝HOIHO为真);而原假设HO不真•却作出接受H0的判断•称这类错误为第二类错误,又称取伪错误.它发生的槪率P为P二P(接受HO|H0不真).习題4 犯第一类错误的概率a与犯第二类错谋的概率P之间有何关系一般來说.当样木容g固定时,若减少犯一类错误的槪率.则犯另一类错渓的概率往往会增大•要它们同时减少,只有増加样木容a n.在实际问题中,总是控制犯節一类错误的概率a而使犯第二类错谋的概率尽可能小・a的大小视具体实际问题而定.通常取a弓等tfL 习題5 在假设检验中•如何理解指定的显著水平a 解答:我们希望所作的检验犯两类错谋的槪率尽可能都小・但实际上这是不可能的•当样木容Sn固定时,一般地•减少犯其中一个错谋的槪帑就会增加犯另一个错误的概率• W此,通常的作法是只要求犯第一类错误的概率不大于指定的显著水平6因而根据小概率原理,最终结论为拒绝H0较为可靠,而最终判断力接受H0则不大可靠,«原因是不知道犯第二类错误的概率P处竟有多少.且a小,P就大.所以通常用JW 相容r 〃不拒绝HO"等词语來代替“接受H0".而"不拒绝HO"还包含有再进一步作抽样检验的意思.习题6 在假设检验中•如何确定原假设H0和备择假设H1 解答: 在实际中・通常把那些需要着重考虑的假设视为原假设H0.而与之对应的假设视为备择假设H1.(1)如果问题是要决定新方案是否比原方案好,往往将原方案取假设.而将新方案取为备择假设:(2)若提出一个假设・检验的目的仅仅是为r判断这个假设是否成立.这时直接取此假设为原假设H0即可. 习題7 假设检验的基木步腺有哪些解答:根据反证法的思想和小概率原理•可将假设检验的步骤归纳如下:(1)根据问题的要求.提出原理假设H0和备择假设HL (2)根据检验对紀构造检验统计gT(Xl,X2宀Xn),使肖H0为真时汀有确定的分布.(3)由给定的显著水平6直统计址T所服从的分布表,定出临界值K使P{ 1 T I >A)=a,或P(T>M)=P(T<X2)=a/2,从而求出H0的拒绝域:I T I >入或T>MJ<X2,(4)由样木观察值计算统i|・fi T的观察值t(5)作出判断,将t的值与临界值比较大小作出结论:当tW拒绝域g时,则拒绝H0.否则,不拒绝H0.即认为在显著水平a下,H0与实际悄况差界不显著.习題8 假设检验与区间估il•有何异同解答:假设检验与区间估ii•的提法虽不同,但解决问题的途径是相通的.参数0的a信水平为i・a的a信区间对应于双边假设检验在駄着性水平a下的接受域:参数e的a信水平为1-a的爪侧置信区对应于爪边假设检验在显著性水平a下的接受域.在总休的分布已知的条件下•假设检验与区间估计是从不同的角度回答同一个问題•假设检验是判别原假设H0是否成立,而区间估计解决的是“多少"(或范前者是宦性的.后者是定fi的.习题9 某天开工时,需检验自动包装工作是否正常•根据以往的经验,其装包的质a在正常情况下服从正态分布N(100,仲位:kg).现抽测了9包,其质S为:问这天包装机工作是否正常将这一问题化为假设检验问题.写出假设检验的步驟(am 解答: ⑴提出假设检验问题H0:尸100, Hl:"100;(2)选取检验统il S U:U=X; HO成立时,UW((U);(3)a=,ua/2=,拒绝域W={ 1 u 1 >};(4))f勺I u I =. hM 1 u I <ua/2=,故接受HO,认为包装机.I:作正常.设总休X^(pJbXl,X2/7Xn是取自X的样木.对于假设检验HO:|i=O'Hl:pMO,取显著水平a,拒绝域为W={ i U i >ua/2b其中u=nX-,求:H0成立时,犯第一类错误的槪率aO;(2)十HO不成立时(若"0),犯第二类错的概率p.(l)X^(H4)/X'MM(g,l/n),故nX'=uMM(O,l). a0=P{ I u I >ua/2 I g=0}=l-P{-ua/2<u<ua/2}=1-[<D(ua/2)-(D(-ua/2)]=l-[(l-a2)-a2]=a,即犯第一类错误的概率是显著水平a.(2)F H0不成立.即PMO时.犯第二类错误的概率为P=P{ I U I 30/2 I E(X)=n}=P{・uct/2<u<ua/2 I E(X)=A}=P{-ua/2<nX'<ua/2 I E(X)=|i}=P{-ua/2-nn<n(X'-n)<ua/2-nn I E(X)=n}=(I)(ua/2-niJi)-®(-ua/2-nn),注1 '^1 H T+8或时,PTO.由此可见.当实际均值H偏离原假设校大时,犯第二类错误的概率很小.检验效果较好.注2!勺卩工0但接近于0时.Pdw.Wa很小.故犯第一娄错误的概率很大.检验效果较差.单正态总体的假设检験习题1 已知某炼铁厂铁水含碳量服从正态分布N,・现在测定r 9炉铁水•其平均含碳虽为•如果估计方差没有变化.可否认为现在生产的饮水平均含碳fi仍为(a=解答^ 木问题是在a二下检验假设HO:ns由r a2=已知,所以可选取统计sU=X •在HO 成立的条件下• UW(OJ),且此检验问题的拒绝域为I U 1 = I X •这里 说明U 没有落在拒绝域中.从而接受H0.即认为现在生产之饮水平均含碳S 仍为•习題2要求一种元件平均便用寿命不斜低于1000小肘,生产者从一批这种元件中随机抽取25件,测御其寿命的 平均值为950小时.已知该种元件寿命服从标准差为0=100小时的正态分布,试在显著性水平(1=卜确定 这批元件是否合格设总体均值为卩川未知.即需检验假设H0:H >1000,H1:H <1000.解答:检验假设 HO :n>1000,Hl :n<1000.这是飛边假设检验问题.由于方差02二,故用U 检验法.对于显着性水平a 二,拒绝域为W={X"-1000a/n<-ua.査标准正态分布表•得 又知n=25X=950,故可计算出x'-1000a/n=950-1000100/25=,因为&故在a=下拒绝H0,认为这批元件不合格.习题3 打包机装糖入包,每包标准重为100kg.毎天开工后,要检验所装糖包的总体期望值是否合乎标准 (100kg)•某日开工后.测御9包糖重如下位:kg):打包机装糖的包得服从正态分布•问该天打包机1:作是否正常(a 二 解答: 木问题是在a 二下检验假设HO:p=100,Hl :"100・由于02未知.所以可选取统讣fi T=X--100S/n,在HO 成立的条件下.W(n-1K 且此检验问題的拒绝域为I T I = 1 X'-lOOS/n I >ta/2(n-l).I t 1 =<=(8),即t 未落在拒绝域中・从而接受H0,即可以认为该天打包工作正常.习題4机器包装食盐.假设毎袋盐的净重服从正态分布•规定毎俊标准含fi 为500g,标准差不斜趙过lOg •某天开 工后•随机抽取9袋.测得浄重如下仲位:g):497, 507, 510, 475, 515, 484, 488, 524, 491,I U I =<=ua/2・这里 t=x"-100s/ns :试在駄著性水平a二下检验假设:HO:n=500,Hl:n#500,解答:x'=499,ss:,n=9,t=(x~-|jiO)sn==,a=, (8)=.Will <(8b故接受HO,认为该天每袋平均质a可视为500g・习«5从清凉饮料自动售货机・随机抽样36杯,其平均含g为219(mL),标准差为/在a二的显I?性水平下・试检验假设S HO:A=|I O=222,H1:H<M=222・解答: 设总休X-W(g,a2bX代表自动售货机售出的清凉饮料含S・检验假设H0:n=n0=222(mL), Hl:n<222(mL),由asn=36,査表毎(36・1)弓拒绝域为W={t=x'-nOs/n<-ta(n-l).il•算t值并判断:t=36»习題6 某种寻线的电阻服从正态分布N(x・今从新生产的一批导线中抽取9根・测«电阻•得s=Q,对于a®能否认为这批导线电阴的标准差仍为解答:木问题是在a二下检验假设H0:a2=, Hl:o2匕选取统计fi x2=n-la2S2,在HO成立的条件下,X2^2(n-1),且此检验问題的拒绝域为X2>xa/22(n-l)或x2<xl-a/22(n-l).这里X2==x=,X(8)=,x(8)-落在拒绝域中,从而拒绝HO,即不能认为这批导线电阻的标准差仍为.习题7某厂生产的铜线,要求其折断力的方差不超过16N2.今从某日生产的铜丝中随机抽取容fi为9的样木•测得其折断力如下(飛位:N):289, 286, 285, 286, 285, 284, 285, 286, 298, 292设总体服从正态分布,问该日生产的铜线的折斷力的方差是否符合标准(a二解答: 检验问題为n=9, s2勺X2=8XS216勺am X(8)=・因X2<X(8)s故接受HO,可认为铜丝的折断力的方差不超过16N2.习题8过去经验示.商三学生完成标准考试的时间为一正态变其标准差为6min.若随机样木为20位学生, 其标准差为X,试在显着性水平a= b\检验假设:H0:a>6,Hl:a<6,解答:HO:a>6,Hl:a<6,a=,n-l=19,ssx(19)-拒绝域为W={x2<},i l•算X2值X2=(20-l)x^.因为>■故接受H0,认为a>6.习題9测定某种潯液中的水分・它的10个测定值给出*%,设测定值总体服从正态分布.02为总休方差.02未知,试在a二水平下检验假设:在a= b\拒绝域为W={(n-l)S2a02<xl-a2(9).查X2分布表得X(9)m讣算得(n-l)s2o02=(10-l)x\per)2\per)2^>,未落入拒绝域•故接受H0.取正态总体的假设检越习題1制造厂家宜称•线A的平均张力比线B至少强120N,为证实其说法.在同样情况下测试两种线各50条.线A的平均张力x-=867N,标准差为01=;而线B的平均张力为y・=778N,标准差为o2m在a二的显善性水平下,试检验此制造厂家的说法.解答:H0:nl4l2=120,Hl:pl 屮2<120・am=・W={u=x'-y~-120ol2nl+a22n2<-ua,拒绝域为由x'=867,y'=778,nl=n2=50, 012=2,o22=2,得□=867-778-120250+250^^^,因为&故拒绝H0,认为pl-rx2<120,即厂家的说法不对.习题2 欲知某新血清是否能抑制白血球过多症,选择已患该病的老畝9只•并将其中5只施予此种血清,另外4 只则不热•从实验开始.其存活年限表示如下假设两总体均服从方差相同的正态分布,试在显著性水平a二下检验此种血清是否有效解答^ 设pl- p2分别为老鼠接受和未接受血清的平均存活年限。
哈工大概率论与数理统计期末试卷及标准答案A卷(2007)

概率论与数理统计试卷 (A) 2007姓名: 班级: 学号:题 号 一 二 三 四 总 分得 分一. 选择题(15分,每题3分)1. 对任意事件B A ,,下列结论正确的是 ( ))(A )()()(B A P AB P B A P ⋃≤⋃; )(B )()()()(B A P AB P B P A P ⋃≤+; )(C )()()()(B P A P AB P B A P ≤⋃; )(D )()()()(BA P AB P B P A P +≤+.2. 下列函数中可作为连续型随机变量),(Y X 的联合密度函数是 ( ))(A ⎩⎨⎧≤≤≤≤-=他其,05.00,2/2/,cos ),(1y x x y x f ππ; )(B ⎩⎨⎧≤≤π≤≤π-=他其,010,2/2/,cos ),(2y x x y x f ; )(C ⎩⎨⎧≤≤π≤≤=他其,05.00,0,cos ),(3y x x y x f ; )(D ⎩⎨⎧≤≤π≤≤=他其,010,0,cos ),(4y x x y x f . 3. 设X 服从指数分布)(μE ,Y 服从泊松分布)(λP ,则下列等式不成立的是 ( ))(A λμ+=+2/1)(Y X D ; )(B 2/1)(μ=X D ,λ+λ=22)(Y E ; )(C λμ+=+/1)(Y X E ; )(D λ=)(Y D ,22/2)(μ=X E .4. 设总体),1(~p B X (二项分布),其样本),,,(10021X X X Λ均值为∑==10011001i iXX ,)(x Φ为标准正态分布函数,则下列结论不正确的是 ( ))(A 在概率意义下X 近似等于p ; )(B )()()100(a b b X a P Φ-Φ≈<<;)(C ),100(~100p B X ; )(D p X E =)(,100/)1()(p p X D -=.5. 设正态总体),(~2σμN X ,其中2σ未知,样本容量n 和置信度α-1都不变,则对于不同的样本观察值,总体期望μ的置信区间长度L ( ))(A 变短; )(B 变长; )(C 不变; )(D 不能确定.二. 填空题(15分,每题3分)1. 设两随机事件B A ,满足:,7.0)(=A P ,2.0)(=A B P )()(B A P B A P =,则=)(B A P .2. 10件产品中有3件次品,任取5件,其中次品数X 的分布律(用解析式表达)为. 3. 已知二维随机变量),(Y X 的联合分布函数为),(y x F ,则_______________________________________)1,30(=≤≤<Y X P .4. 设随机变量X 和Y 的期望分别为-1和1,方差分别为1和4,0.5XY ρ=-,则 根据切比雪夫不等式________)3(≤>+Y X P .5. 设),,,(921X X X Λ为来自正态总体),(~2σμN X )(2未知σ的样本,样本均值与方差分别为12=x ,1442=s ,则参数μ的置信度为0.9的置信区间__________下限为.三. 计算题 (共63分,每题9分)1. 设有甲,乙两个相同口袋,甲袋中有4个红球,3个白球,乙袋中有3个红球,2个白 球.先从两口袋中任取一袋;然后再从该口袋中不放回地任取一球,共取二球.(1)已知第一次取的球是红球,求该红球来自甲袋的概率;(2)求第二次取出的是红球的概率.2. 设随机变量X 的分布函数为⎩⎨⎧>-≤+=-03/0,3/)(2x e B x e A x F xx ,,求 (1) 常数,A B ;(2)问X 是否为连续型随机变量?(3))2/11(≤<-X P .3.设随机变量~(0,2)X U (均匀分布),)1(~E Y (指数分布),且它们相互独立.试计算 (1) Y X Z -=的概率密度函数)(z f Z ;(2) )(Y X P >.4.闵行水果店准备进一批南汇水蜜桃,据统计每年这个季节顾客对水蜜桃的需求量X (单位:公斤)服从[100,400]上的均匀分布,若每售出1公斤水蜜桃可盈利1元,但如果售不出则亏损2元. 求要进货多少公斤水蜜桃,才能使收益达到最大?5. 学校要新建宿舍有500学生居住,据统计每人每天傍晚约有10%的时间占用一个水龙 头. 设每人需用水龙头是相互独立的,问该宿舍至少需要安装多少个水龙头,才能以95%以上的概率保证用水需要?6.设总体~X 36(),(0,)()0,(0,)x x x f x x θθθθ-⎧∈⎪=⎨⎪∉⎩,0θ>未知,1(,,)n X X L 为其样本. 求(1)θ的矩估计量ˆθ 和ˆ()D θ;(2)设(1.2,1.5,2.1,2.3)为样本的一个观察值,求θ的矩估计值ˆθ,并求出密度函数()f x .7.设某种电池的工作时间服从正态分布,一批电池要出厂为检查其质量,现抽取了5个电池并观察到五个电池的工作时间(小时)为32 41 42 49 53出厂标准为050μ=(小时),方差2σ未知。
理论力学第七版答案_哈工大编_高等教育出版社出版
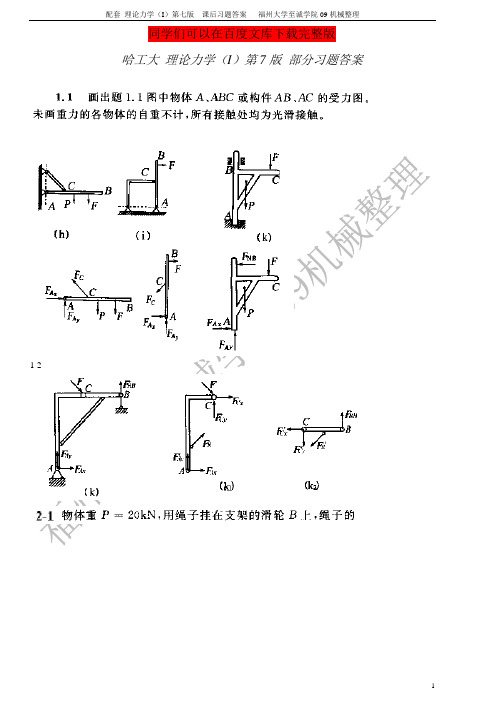
哈工大理论力学(I)第7版部分习题答案1-2两个老师都有布置的题目2-3 2-6 2-14 2- 20 2-30 6-2 6-4 7-9 7-10 7-17 7-21 8-5 8-8 8-16 8-24 10-4 10-6 11-5 11-15 10-3以下题为老师布置必做题目1-1(i,j), 1-2(e,k)2-3, 2-6, 2-14,2-20, 2-306-2, 6-47-9, 7-10, 7-17, 7-21, 7-268-5, 8-8(瞬心后留), 8-16, 8-2410-3, 10-4 10-611-5, 11-1512-10, 12-15, 综4,15,16,1813-11,13-15,13-166-2 图6-2示为把工件送入干燥炉内的机构,叉杆OA=1.5 m在铅垂面内转动,杆AB=0.8 m,A端为铰链,B端有放置工件的框架。
在机构运动时,工件的速度恒为0.05 m/s,杆AB始终铅垂。
设运动开始时,角0=?。
求运动过程中角?与时间的关系,以及点B的轨迹方程。
10-3 如图所示水平面上放 1 均质三棱柱 A ,在其斜面上又放 1 均质三棱柱 B 。
两三棱柱的横截面均为直角三角形。
三棱柱 A 的质量为 mA 三棱柱 B 质量 mB 的 3 倍,其尺寸如图所示。
设各处摩擦不计,初始时系统静止。
求当三棱柱 B 沿三棱柱 A 滑下接触到水平面时,三棱柱 A 移动的距离。
11-4解取A、B 两三棱柱组成 1 质点系为研究对象,把坐标轴Ox 固连于水平面上,O 在棱柱A 左下角的初始位置。
由于在水平方向无外力作用,且开始时系统处于静止,故系统质心位置在水平方向守恒。
设A、B 两棱柱质心初始位置(如图b 所示)在x 方向坐标分别为当棱柱B 接触水平面时,如图c所示。
两棱柱质心坐标分别为系统初始时质心坐标棱柱B 接触水平面时系统质心坐标因并注意到得10-4 如图所示,均质杆AB,长l,直立在光滑的水平面上。
哈工大结构力学题库七章
第七章影响线一判断题1. 图示梁AB与A0B0,其截面C与C0弯矩影响线和剪力影响线完全相同。
(X)题1图题2图2. 图示结构Q E影响线的AC段纵标不为零。
(X)3. 图示梁K截面的M K影响线、Q K影响线形状如图a、b所示。
4. 图示梁的M C影响线、Q C影响线形状如图a、b所示。
5. 图示梁的M C影响线、M B影响线形状如图a、b所示。
1766. 图示结构M B影响线的AB段纵标为零。
7. 图示梁跨中C截面弯矩影响线的物理意义是荷载P=1作用在截面C的弯矩图形。
(X)8. 用静力法作静定结构某量值的影响线与用机动法作该结构同一量值的影响线是不等价的。
(X)9. 求某量值影响线方程的方法,与恒载作用下计算该量值的方法在原理上是相同的。
(√)10. 影响线是用于解决活载作用下结构的计算问题,它不能用于恒载作用下的计算。
(X)11. 移动荷载是指大小,指向不变,作用位置不断变化的荷载,所以不是静力荷载。
(X)12. 用静力法作影响线,影响线方程中的变量x代表截面位置的横坐标。
(X)13. 表示单位移动荷载作用下某指定截面的内力变化规律的图形称为内力影响线。
(√)14. 简支梁跨中截面弯矩的影响线与跨中有集中力P时的M图相同。
(X)15. 简支梁跨中C截面剪力影响线在C截面处有突变。
(√)16. 绝对最大弯矩是移动荷载下梁的各截面上最大的弯矩。
(√)17. 静定结构及超静定结构的内力影响线都是由直线组成。
(X)18. 图示结构Q C影响线的CD段为斜直线。
19. 图示结构K断面的剪力影响线如图b所示。
(√)177178题19图20. 用机动法作得图a 所示Q B 左结构影响线如图b 。
题20图 题21图21. 图示结构a 杆的内力影响线如图b 所示22. 荷载处于某一最不利位置时,按梁内各截面得弯矩值竖标画出得图形,称为简支梁的弯矩包络图。
(X )23. 单位力P=1沿图a 所示桁架上移动,杆K 内力影响线如图b.24. 图为图所示结构Q C右的影响线。
哈工大概率论与数理统计课后习题答案 一
习题一1.写出下列随机试验的样本空间及下列事件中的样本点:(1)掷一颗骰子,记录出现的点数‘出现奇数点’;(2)将一颗骰子掷两次,记录出现点数‘两次点数之和为10’,‘第一次的点数,比第二次的点数大2’;(3)一个口袋中有5只外形完全相同的球,编号分别为1,2,3,4,5;从中同时取出3只球,观察其结果,‘球的最小号码为1’;(4)将a,b两个球,随机地放入到甲、乙、丙三个盒子中去,观察放球情况,‘甲盒中至少有一球’;(5)记录在一段时间(1)其中‘出现i点’,。
(2)(2,1),(2,2),(2,3),(2,4),(2,5),(2,6)(3,1),(3,2),(3,3),(3,4),(3,5),(3,6)(4,1),(4,2),(4,3),(4,4),(4,5),(4,6)(5,1),(5,2),(5,3),(5,4),(5,5),(5,6)(6,1),(6,2),(6,3),(6,4),(6,5),(6,6)};;。
(3)(2,3,5),(2,4,5),(1,3,5)}(4),其中‘’表示空盒;。
(5)。
2.设A,B,C是随机试验E的三个事件,试用A,B,C表示下列事件:(1)仅A发生;(2)A,B,C中至少有两个发生;·1·(3)A,B,C中不多于两个发生;(4)A,B,C中恰有两个发生;(5)A,B,C中至多有一个发生。
解(1)(2)或;(3)或;(4);(5)或;3.一个工人生产了三件产品,以表示第i件产品是正品,试用Ai 表示下列事件:(1)没有一件产品是次品;(2)至少有一件产品是次品;(3)恰有一件产品是次品;(4)至少有两件产品不是次品。
解(1)A(2)(3);1A2A3;;(4)。
4.在电话号码中任取一个电话号码,求后面四个数字全不相同的概率。
解设‘任取一电话号码后四个数字全不相同’,则5.一批晶体管共40只,其中3只是坏的,今从中任取5只,求(1)5只全是好的的概率;(2)5只中有两只坏的的概率。
哈工大概率论与数理统计期末试卷及标准答案A卷(2006)
第1页一、判断题(每小题2分,共10分)1、()0P A =,则A 为不可能事件. ( )2、设X Y 与相互独立,则X Y 与一定不相关. ( )3、µµ12,θθ为θ的两个估计量,µµ12()(),D D θθ<则µ1θ更有效. ( ) 4、A B 与互不相容,则A B 与互不相容.( ) 5、假设检验中,弃真表示事件{接收01H H 真}. ( ) 二、选择题(每小题3分,共15分) 6、设,A B 为两个事件,则“这两个事件至少有一个没发生”可表示为( )()()()()A ABB AB ABC A BD AB U U7、设X Y 与相互独立,()4,()1,D X D Y == 则(23)D X Y -=( )()5()11()7()25A B C D 8、设(0,1),21X N Y X =-:,则Y : ( ) ()(0,1)()(1,4)()(1,3)()(1,1)A N B N C N D N ---9、设总体212(2,4),,,,n X N X X X :L 为X 的样本,则下列结果正确的是( )22()(0,1)()(0,1)416X X A N B N ::-- 2()(0,1)((0,1)2X C N D N ::-10、设2(),()E X D X μσ==,由切比雪夫不等式得{3}P X μσ-≥≤ ( )第2页 1218()()()()339A B C D三、填空题(每小题3分,共15分)11、设X 的概率密度为41,0(),40,0xe xf x x -⎧>⎪=⎨⎪≤⎩则()D X =____________.12、设事件A B 与相互独立,()0.4,()0.7,P A P A B ==U 则()P B A = ______13、设()X πλ:,且{2}{3},P X P X ===则λ=____________.14、设(,)X Y 的概率密度为:,01(,),0,cx x y f x y ≤≤≤⎧=⎨⎩其他则c =_________.15、设(),X t n :则2X :______________.四、计算题(共60分)16、(6分)设()4,10X U :,求关于t 的方程2160t Xt -+=有解的概率.17、(6分)设二维随机变量(,)X Y 的联合分布律如下: 问α,β取何值时, ,X Y 相互独立?……………密………………………………封……………………………………装………………………………订…………………第3页18、(8分)设X 的概率密度为2,01()0,x x f x <<⎧=⎨⎩其他,Y 表示对X 三次独立重复观察事件12X ⎧⎫≥⎨⎬⎩⎭出现的次数.求{}2P Y =.19、(8分)设随机变量(,)X Y 的分布律为求XY ρ.20、(8分)袋中有6只全新的乒乓球,每次比赛取出2只用完之后放回,已知第三次取得的2只球都是新球,求第二次取到的也是2只新球的概率.………………密………………………………封………………级 学号 姓名………………………………装………………………………订………………第4页21、(8分)某保险公司经多年的资料统计表明索赔户中被盗赔户占20%,在随意抽查的10000家索赔户中被盗的索赔户设为随机变量X ,试用中心极限定理估计被盗索赔户在1900户到2100户之间的概率.()()( 2.50.994,20.977,ΦΦ==()0.625Φ0.732)=其中(01)θθ<<为未知参数.已知取得样本值121,2,x x ==31x =,试求θ 的矩估计值. 23、有一批枪弹,出厂时,其初速2(950,10)v N :,经过较长时间储存,取9发进行测试得x =928米/秒.问这批枪弹的初速度是否有显著变化()0.1α=?()0.050.11.645, 1.28u u ==(8分)………………密……………封………………………………线…………………学院 专业 级 学号 姓名………………………………装………………………………订………………………………线…………………第5页一.判断题(5210⨯=分分)× √ × × × 二.选择题(5315⨯=分分)C D B B C三.填空题(5315⨯=分分)11、16 12、0.5 13、3 14、6. 15、(1,)F n四.计算题(共60分)16. 解:因为1,410()60,x f x ⎧<<⎪=⎨⎪⎩其他, (2分)所以{}{}{}102811064088.63P P X P X X dx ∆≥=-≥=≤-≥==⎰或 (4分) 17. 解:因为,X Y 相互独立,所以19=19α+⨯13,118=118β+⨯13 (4分)所以α=29,β=19.(2分)第6页18. 解:因为12011224P X xdx ⎧⎫≥==⎨⎬⎩⎭⎰, (3分)所以1(3,),4Y b :(3分){}2231392.4464P Y C ⎛⎫=== ⎪⎝⎭ (2分) 19. 解: 22()0.6,()0.6,()0.5,()0.5,E X E X E Y E Y ====Q (2分)()0.24,()0.25D X D Y ∴== (2分)()0.1,(,)()()()0.2E XY COV X Y E XY E X E Y =∴=-=-Q (2分)所以3XY ρ∴===- (2分)20. 解:设i A ,i 表示第二次取到只新球0,1,2i =;A 表示第三次取到2只新球.()()()21122244012222666186,,151515C C C C P A P A P A C C C ======()()()222342012222666631|,|,|151515C C C P A A P A A P A A C C C ======.(2分)()16836136151515151515225P A =⨯+⨯+⨯=.(3分)()01611515|.366225P A A ⨯== (3分)21. 解: 因为(10000,0.2)X b :,所以()()2000,1600E X D X ==(4分) 所以{}()200019002100 2.5 2.52 2.510.988.40X P X P Φ-⎧⎫≤≤=-≤≤=-=⎨⎬⎩⎭(4分) 22. 解:()221()122(1)3132E X μθθθθθ==⋅+⋅-+⋅-=- (4分)第7页()11412133A =++=4532,.36θθ∴-==) (4分)23. 解: 提出假设0010:,:H H μμμμ=≠拒绝域为2αμμ≥,2αμ≥(4分)又因为00.05928,950,10,9, 1.645x n μσμ=====,所以26.6,x u u αμ==-≥,所以拒绝0H ,枪弹的初速度有显著变化. (4分)。
哈工大理论力学第七版课后习题答案完整版
FAx (f2)
C FC′x
FC′y F2
FBy
FBx B (f3)
FAy A FAx
FB
C B
(g)
FAy
FAx A
D FT C FCx
(g2)
FB
B
F1
FB′ B
FAy
A
FAx
(h)
(h1)
P (g1)
FC′y
FT
C
FC′x
P (g3)
D
FCy
FB
F2
C FCx
B
(h2)
A FAx
FAy
FCy
FBy
FCy
B
FBx
(j2)
FT′2 E FEx
FEy FT 3 (j4)
FAy FD′y
FE′ y
FAx
C FC′x
A D FD′x
E
FE′x
FC′y (j5)
E
D
(k)
F
FB
C B
θE
D FAy
A
FAx
(k2)
F
FB
CE
FC′x
θ
B
FC′y FD′E (k1)
F FCx
C FCy
90° − θ FDE
( ) FR = (∑ Fx )2 + (∑ Fy )2 = 3 9152 + 3 1072 N = 4 998 N
40°
θ
O
F2
b
FR
F3 c
(a)
(b)
(c)
图 2-2
解 (1)解析法
建立如图 2-2b 所示的直角坐标系 Oxy。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
·90· 习 题 七 1.对某一距离进行5次测量,结果如下: 2781,2836,2807,2765,2858(米).
已知测量结果服从2(,)N,求参数和2的矩估计.
解 的矩估计为ˆX,2的矩估计为22*211ˆ()niiXXSn 1(27812836280727652858)2809.05X,
*215854.01170.845S
所以 2ˆ
2809,1170.8
2.设12,,,nXXX是来自对数级数分布 1(),(01,1,2,)(1)kpPXkpklupk
的一个样本,求p的矩估计. 解 111111ln(1)ln(1)ln(1)1kkkkppppppp (1) 因为p很难解出来,所以再求总体的二阶原点矩 121111ln(1)ln(1)ln(1)kkkxpkkkppkpkpxppp
21ln(1)1ln(1)(1)xppxppxpp
(2)
(1)(2)得 121p 所以 212p 所以得p的矩估计
21221111niiniiXXXnpXn
3.设总体X服从参数为N和p的二项分布,12,,,nXXX为取自X的样本,试求参数N和p的矩估计 ·91·
解 122,(1)()NpNppNp 解之得1/Np, 21(1)pNp
,
即 1Np
,
221
11p
,
所以 N和p的矩估计为 ˆXNp,*21SpX.
4.设总体X具有密度 11(1)1,,(;)0,.CxxCfx
其他
其中参数01,C为已知常数,且0C,从中抽得一个样本,12,,,nXXX,求的矩估计
解 11111111111CCEXCxdxCx
111()11C
CCC
,
解出得
11,C
于是的矩估计为 1CX.
5.设总体的密度为 (1),01,(;)0,.xxfx
其他 ·92·
试用样本12,,,nXXX求参数的矩估计和极大似然估计. 解 先求矩估计: 11
1210011(1),22EXxdxx
解出得 11
12,1
所以的矩估计为 121XX
.
再求极大似然估计: 1121(,,;)(1)(1)()nnniniLXXxxxx
,
1lnln(1)lnniiLnx,
1lnln01niidLnxd
,
解得的极大似然估计:
1(1)lnniinx
.
6.已知总体X在12[,]上服从均匀分布,1nXX是取自X的样本,求12,的矩估计和极大似然估计.
解 先求矩估计: 1212
EX,
2222221121122
2
()()1243EX
解方程组 121
2211222
2
3
得 ·93·
211213(),
221213().
注意到12,得12,的矩估计为 *13XS,*
23XS
.
再求极大似然估计
1121212111(,,;,)()nnn
iLXX
,
1122,,,n
xxx,
由极大似然估计的定义知,12,的极大似然估计为 11(1)min(,,)nXXX;21()max(,,)nn
XXX.
7.设总体的密度函数如下,试利用样本12,,,nxxx,求参数的极大似然估计.
(1)1(),0,(;)0,.xxexfx其它;已知
(2)||1(;),,2xfxex. 解 (1)111111(,,;)()()niiinxxnnniniLXXxexxe
111ln(;)lnln(1)lnnnniiiiLXXnnxx
1ln0niidLnxd
解似然方程
1niinx,
得的极大似然估计
1.niinx
(2)1||||1111(;)22niiinxxnniLXXee
由极大似然估计的定义得的极大似然估计为样本中位数,即 ·94·
1()2()(1)22,1(),.2nnnXnXXn
为奇数,为偶数
8.设总体X服从指数分布 (),,(;)0,.xexfx
其他
试利用样本12,,,nXXX求参数的极大似然估计.
解 1()11(,,;),,1,2,,.niiinxnxniiLXXeexin
1lnniiLnX ln0dLnd
由极大似然估计的定义,的极大似然估计为(1)x 9.设12,,,nXXX来自几何分布 1()(1),1,2,,01kPXkppkp,
试求未知参数p的极大似然估计.
解 1111(,,;)(1)(1)niiinxnxnniLxxppppp
,
1lnln()ln(1),niiLnpXnp
1ln0,1niiXndLndppp
解似然方程
11niinXnpp
,
得p的极大似然估计 1pX。
10.设12,,,nXXX是来自两个参数指数分布的一个样本. ·95·
121
122
1,,(;,)0,.xexfx
其它
其中12,0,求参数1和2的(1)极大似然估计;(2)矩估计。
解 (1)121121121(,,;,),,1,2,,.ixnniiLXXexin
21121lnln()niiLnXn
12ln0Ln
由极大似然估计的定义,得1的极大似然估计为 1(1)
x;
121222ln1()0niiLnXn
解似然方程得2的极大似然估计 2(1)
Xx
(2)112EX 22222212[()]()EXDXEX
解方程组 112222212
,(),
得 22221, 21121
.
所以12,的矩估计为 *
1,XS
*2*2
ˆ
.SS
11.罐中有N个硬币,其中有个是普通硬币(掷出正面与反面的概率各为0.5)其余N个硬币两面都是正面,从罐中随机取出一个硬币,把它连掷两次,记下结果,但不去查看它属于哪种硬币,如此重复n次,若掷出0次、1次、2次正面的次数分别为012,,nnn,利用(1)矩法;(2)极大似然法去估
