结构力学课后习题解答:6位移法习题解答
结构力学课后解答:第7章__位移法
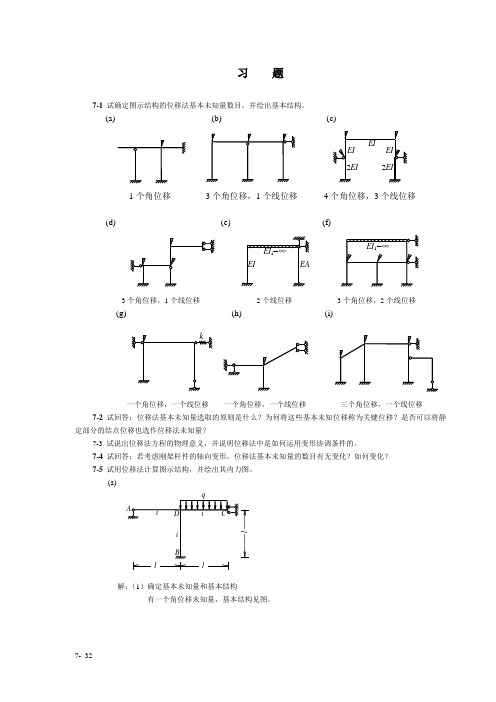
习题7-1 试确定图示结构的位移法基本未知量数目,并绘出基本结构。
(a) (b) (c)1个角位移3个角位移,1个线位移4个角位移,3个线位移(d) (e) (f)3个角位移,1个线位移2个线位移3个角位移,2个线位移(g) (h)(i)一个角位移,一个线位移一个角位移,一个线位移三个角位移,一个线位移7-2 试回答:位移法基本未知量选取的原则是什么?为何将这些基本未知位移称为关键位移?是否可以将静定部分的结点位移也选作位移法未知量?7-3 试说出位移法方程的物理意义,并说明位移法中是如何运用变形协调条件的。
7-4 试回答:若考虑刚架杆件的轴向变形,位移法基本未知量的数目有无变化?如何变化?7-5 试用位移法计算图示结构,并绘出其内力图。
(a)解:(1)确定基本未知量和基本结构有一个角位移未知量,基本结构见图。
l7- 32Z 1M 图(2)位移法典型方程11110p r Z R +=(3)确定系数并解方程iql Z ql iZ ql R i r p 24031831,821212111==-∴-==(4)画M 图M 图(b)解:(1)确定基本未知量1个角位移未知量,各弯矩图如下4m 4m4m7- 341Z =1M 图3EIp M 图(2)位移法典型方程11110p r Z R +=(3)确定系数并解方程1115,352p r EI R ==- 153502EIZ -=114Z EI=(4)画M 图()KN mM ⋅图(c)解:(1)确定基本未知量一个线位移未知量,各种M 图如下6m 6m 9m1M 图243EI 243EI 1243EI p M 图F R(2)位移法典型方程11110p r Z R +=(3)确定系数并解方程1114,243p p r EI R F ==- 140243p EIZ F -=12434Z EI=(4)画M 图94M 图(d)解:(1)确定基本未知量一个线位移未知量,各种M 图如下a 2aa2aaF P7- 3611Z=1111r 252/25EA a 简化图1pR pp M(2)位移法典型方程11110p r Z R +=(3)确定系数并解方程11126/,55p p r EA a R F ==- 126055p EA Z F a -=13a Z EA=(4)画M 图图M(e)解:(1)确定基本未知量两个线位移未知量,各种M 图如下l图1=11211 EA r l r ⎛⇒=⎝⎭1M221EA r l ⎛=⎝⎭图12 0p p p R F R ⇒=-=p M pF(2)位移法典型方程1111221211222200p p r Z r Z R r Z r Z R ++=++= (3)确定系数并解方程11122122121,1,0p p p EA r r r l EA r l R F R ⎛=== ⎝⎭⎛=⎝⎭=-=代入,解得7- 3812p p lZ F EAlZ F EA=⋅=⋅(4)画M 图图M p7-6 试用位移法计算图示结构,并绘出M 图。
结构力学章节习题及参考答案
习题3.1是非判断题
(1) 在使用内力图特征绘制某受弯杆段的弯矩图时,必须先求出该杆段两端的端弯矩。( )
(2) 区段叠加法仅适用于弯矩图的绘制,不适用于剪力图的绘制。( )
(3) 多跨静定梁在附属部分受竖向荷载作用时,必会引起基本部分的内力。( )
(4)习题3.1(4)图所示多跨静定梁中,CDE和EF部分均为附属部分。( )
(7) 习题2.1(6)(a)图所示体系去掉二元体EDF后,成为习题2.1(6) (c)图,故原体系是几何可变体系。( )
习题 2.1(6)图
习题2.2填空
(1) 习题2.2(1)图所示体系为_________体系。
习题2.2(1)图
(2) 习题2.2(2)图所示体系为__________体系。
习题 2-2(2)图
(4)习题5.1(3)图(a)和(b)所示两结构的变形相同。( )
习题7.2填空题
(1)习题5.2(1)图(a)所示超静定梁的支座A发生转角,若选图(b)所示力法基本结构,则力法方程为_____________,代表的位移条件是______________,其中1c=_________;若选图(c)所示力法基本结构时,力法方程为____________,代表的位移条件是______________,其中1c=_________。
(3) 习题7.2(3)图所示刚架各杆的线刚度为i,欲使结点B产生顺时针的单位转角,应在结点B施加的力矩MB=______。
习题 7.2(1)图习题 7.2(2)图 习题 7.2(3)图
(4) 用力矩分配法计算习题7.2(4)图所示结构(EI=常数)时,传递系数CBA=________,CBC=________。
第六章 位移法 视频例题及其答案
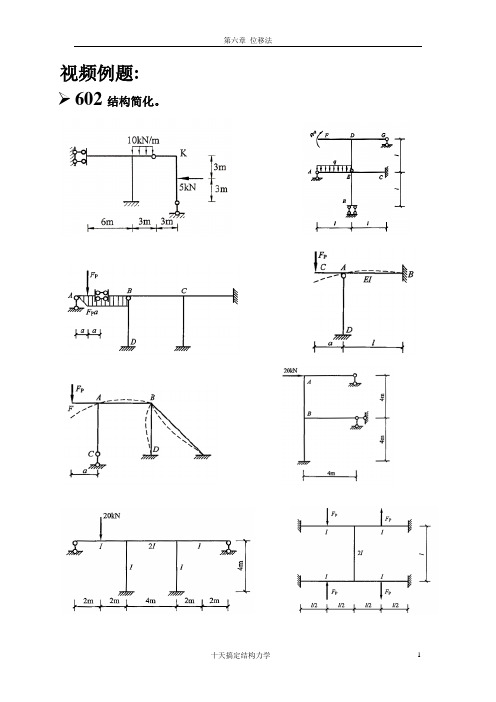
视频例题: ➢602结构简化。
➢603确定未知量。
➢604用位移法求出下列结构的弯矩图。
➢605求出下列结构的弯矩图。
<1>用位移法求下图所示梁的M图。
已知EI=常数,B支座弹簧刚度k=3EI/l3。
<2>下图所示刚架温度变化,各杆截面EI相同,矩形截面高度h=0.5m、宽b=0.3m,
线膨胀系数为α。
试求弯矩图。
➢606求出下图所示有斜杆刚架的位移法方程。
➢607求出下图所示有弹性支座结构的位移法方程。
<1>如下图所示为具有弹性支座的连续梁,kr为弹性抗扭转刚度,
k为弹簧抗侧移刚度。
试列出位移法基本方程。
➢608关于位移法的无穷刚度问题。
<1>用位移法求下图所示结构M图,并校核M图的正确性。
<2>下图所示梁,AB和DE段的抗弯刚度为EI,而BCD段的抗弯刚度为∞,
试用位移法作梁的M图。
<3>下图所示梁,AB和DE段的抗弯刚度为EI,而BCD段的抗弯刚度为∞,
试用位移法作梁的M图。
➢609排架结构或横梁刚度无穷大的刚架问题。
<1>下图所示为一个三跨排架和三跨刚架,杆的轴向变形不计。
(1)试作必要的分析或计算后,分别画出排架和刚架中柱子的弯矩图和剪力图;(2)分别定性地画出两结构在图示荷载作用下的变形图。
结构力学课后答案第7章位移法
解:(1)确定基本未知量
两个位移未知量,各种M图如下
(2)位移法典型方程
(3)确定系数并解方程
代入,解得
(4)求最终弯矩图
(e)
解:(1)确定基本未知量
两个角位移未知量,各种M图如下
(2)位移法典型方程
(3)确定系数并解方程
代入,解得
(4)求最终弯矩图
7-7试分析以下结构内力的特点,并说明原因。若考虑杆件的轴向变形,结构内力有何变化?
(a)
解:(1)利用对称性得:
(2)由图可知:
可得:
(3)求最终弯矩图
(b)
解:(1)利用对称性,可得:
(2)由图可知,各系数分别为:
解得:
(3)求最终弯矩图如下
(c)
解:(1)在D下面加一支座,向上作用1个单位位移,由于BD杆会在压力作用下缩短,所以先分析上半部分,如下图。
D点向上作用1个单位,设B向上移动x个单位,则 ,得 个单位。
习题
7-1试确定图示结构的位移法基本未知量数目,并绘出基本结构。
(a)(b) (c)
1个角位移3个角位移,1个线位移4个角位移,3个线位移
位移3个角位移,2个线位移
(g)(h)(i)
一个角位移,一个线位移一个角位移,一个线位移三个角位移,一个线位移
7-2试回答:位移法基本未知量选取的原则是什么?为何将这些基本未知位移称为关键位移?是否可以将静定部分的结点位移也选作位移法未知量?
(a) (b) (c)
(d) (e) (f)
7-8试计算图示具有牵连位移关系的结构,并绘出M图。
(a)
解:(1)画出 图
由图可得:
由图可知:
(2)列方程及解方程组
结构力学6-位移法

7i 1 6 0
解得
(4)将结点位移代回杆端弯矩表达式。
6 M AB 2i 15 16.72kN m 7i 6 M BA 4i 15 11.57 kN m 7i 6 M BC 3i 9 11.57kN m 7i
M图(kNm)
§7-4
位移法Ⅱ——典型方程法
一、超静定结构计算的总原则:
欲求超静定结构先取一个基本结构,然 后让基本结构在受力方面和变形方面与原 结构完全一样。
力法的特点: 基本未知量——多余未知力; 基本结构——静定结构; 基本方程——位移条件 (变形协调条件)
位移法的特点: 基本未知量—— 独立结点位移 一组单跨超静定梁 基本结构—— ? 基本方程—— 平衡条件
2
F FQ AB 5ql / 8 F FQ BA 3ql / 8
FP A l/2 l/2 B
3FP l/16 A B A
11FP/16 B 5FP/16
M
F AB
3FP l / 16
F FQ AB 11FP l / 16 F FQ BA 5FP l / 16
A
t1 t2 l
A
B
F FQ AB ql F FQ BA 0
FP
A
l/2 l/2
B
3FPl/8
A FP l/8
F M AB 3 FP l / 8 F M BA FP l / 8
FP
B
A
B
F FQ AB FP F FQ BA 0
FP A l B
FPl/2 A FPl/2
F M AB FP l / 2 F M BA FP l / 2
结构力学(5.1.2)--位移法习题及参考答案
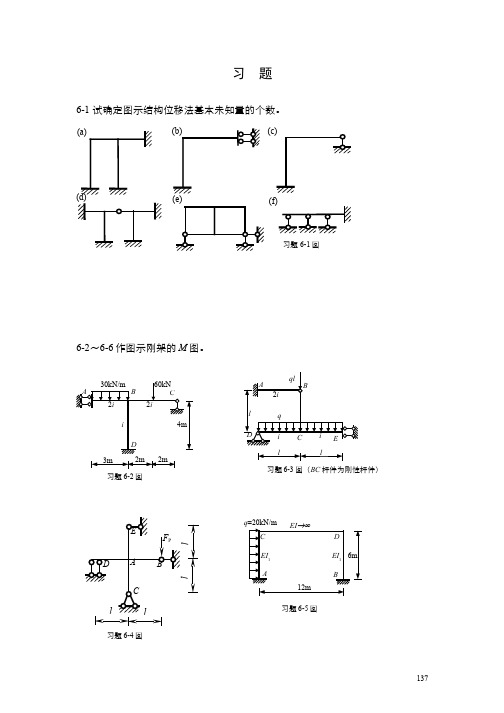
习 题6-1 试确定图示结构位移法基本未知量的个数。
6-2~6-6作图示刚架的M 图。
(a)(f)习题6-1图(d)习题6-2图习题6-5图习题6-3图(BC 杆件为刚性杆件)习题6-4图6-6 试用位移法计算图示结构,并作内力图。
6-7 试用位移法计算图示结构,并作内力图。
6-8 试用位移法计算图示结构,并作内力图。
EI 为常数。
6-9试用位移法计算图示结构,并作弯矩图。
EI 为常数。
6-10 试用位移法计算图示结构,并作弯矩图(提示:结构对称)。
习题6-9图习题6-7图6-11作图示刚架的体系内力图。
6-12 设支座 B 下沉0.5cm B D =,试作图示刚架的M 图。
6-13如图所示连续梁,设支座C 下沉淀1cm ,试作M 图。
6-14图示等截面正方形刚架,内部温度升高+t°C ,杆截面厚度h ,温度膨胀系数为 ,试作M 图。
10 kN/m( a )( b)40 kN习题6-10图BGH习题6-11图(a )(b )q6-15试作图示有弹性支座的梁的弯矩图,332EIk l=,EI =常数。
6-16 试用弯矩分配法计算图示连续梁,并作M 图。
6-176-18 用力矩分配法计算图示结构,并作M 图。
6-19 已知图示结构的力矩分配系数1238/13,2/13,3/13,A A A m m m ===作M 图。
6-20 求图示结构的力矩分配系数和固端弯矩。
已知q=20kN/m,各杆EI 相同。
习题6-17图习题6-13图习题6-14图6-21~6-22 用力矩分配法计算图示连续梁,作M 图,并计算支座反力。
EI=常数。
6-23~6-25用力矩分配法计算图示刚架,作M 图。
EI=常数。
参考答案6.1 (a) 2 (b) 1 (c) 2 (d) 3 (e) 6 (f) 26.2 15BD M =kN·m (右侧受拉)20kN/m 40kN习题6-22图习题6-21图15kN/m习题6-23图F P =10kN 习题6-24图习题6-25图6.321112AB M ql =(上侧受拉)6.4P 0.4AD M F l =(上侧受拉)6.5150AC M =kN·m (左侧受拉)6.651.3AB M =kN·m (左侧受拉)6.780AB M =kN·m (上侧受拉)6.816.9AB M =kN·m (左侧受拉)6.9 (a) 10.43CA M =kN·m (左侧受拉) (b) 56.84CE M =kN·m (下侧受拉)6.10 (a) 8.5AB M =kN·m (上侧受拉) (b) 34.3AC M =kN·m (左侧受拉)6.11 (a) 20.794DC M ql =(右侧受拉) (b) 6.14GD M q =(右侧受拉)6.1223.68AC M =kN·m (右侧受拉)6.1359.3310BA M =ᅲkN·m (上侧受拉)6.142/M EIt h a =(外侧受拉)6.152/32BA M ql =(下侧受拉)6.1617.5CB M =kN·m (下侧受拉)6.1778.75CD M =kN·m (上侧受拉)6.1827/12AB M ql =(上侧受拉)6.191117.95A M =kN·m (上侧受拉)6.200.34AD m =,13.33AD M =kN·m 6.2142.3BA M =kN·m (上侧受拉)6.2217.35BA M =kN·m (上侧受拉)6.2357.4BA M =kN·m (上侧受拉)6.2428.5BA M =kN·m (上侧受拉)6.2573.8BD M =kN·m (左侧受拉)。
《结构力学习题》(含答案解析)

《结构力学习题》(含答案解析)-CAL-FENGHAI.-(YICAI)-Company One120 第三章 静定结构的位移计算一、判断题:1、虚位移原理等价于变形谐调条件,可用于求体系的位移。
2、按虚力原理所建立的虚功方程等价于几何方程。
3、在非荷载因素(支座移动、温度变化、材料收缩等)作用下,静定结构不产生内力,但会有位移且位移只与杆件相对刚度有关。
4、求图示梁铰C 左侧截面的转角时,其虚拟状态应取:A.;; B.D.M C.=1=1=15、功的互等、位移互等、反力互等和位移反力互等的四个定理仅适用于线性变形体系。
6、已知M p 、M k 图,用图乘法求位移的结果为:()/()ωω1122y y EI +。
M kM p 21y 1y 2**ωω( a )M =17、图a 、b 两种状态中,粱的转角ϕ与竖向位移δ间的关系为:δ=ϕ 。
8、图示桁架各杆E A 相同,结点A 和结点B 的竖向位移均为零。
Aa a21 9、图示桁架各杆EA =常数,由于荷载P 是反对称性质的,故结点B 的竖向位移等于零。
二、计算题:10、求图示结构铰A 两侧截面的相对转角ϕA ,EI = 常数。
q l l l /211、求图示静定梁D 端的竖向位移 ∆DV 。
EI = 常数 ,a = 2m 。
a a a 10kN/m12、求图示结构E 点的竖向位移。
EI = 常数 。
l l l l /3 2 /3/3q13、图示结构,EI=常数 ,M =⋅90kN m , P = 30kN 。
求D 点的竖向位移。
P 3m 3m 3m14、求图示刚架B 端的竖向位移。
q15、求图示刚架结点C 的转角和水平位移,EI = 常数 。
q16、求图示刚架中D点的竖向位移。
EI =常数。
l ll/217、求图示刚架横梁中D点的竖向位移。
EI=常数。
18、求图示刚架中D点的竖向位移。
E I = 常数。
qll l/219、求图示结构A、B两截面的相对转角,EI=常数。
同济大学 朱慈勉版 结构力学 课后答案(下)
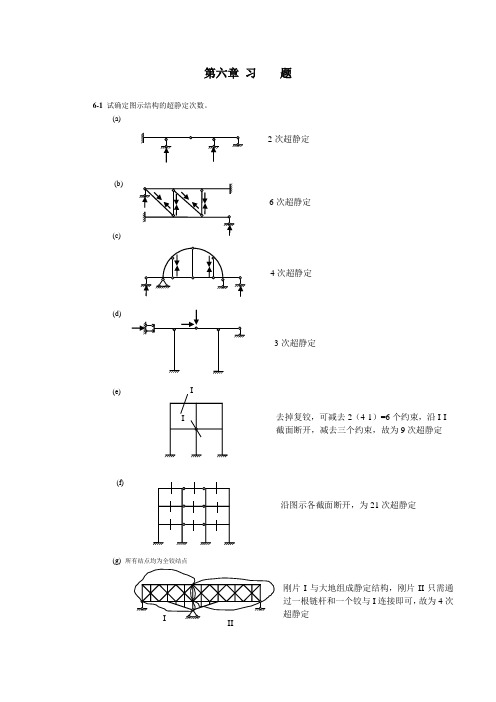
第六章 习 题6-1 试确定图示结构的超静定次数。
(a)(b)(c)(d)(e)(f)(g) 所有结点均为全铰结点2次超静定6次超静定4次超静定3次超静定去掉复铰,可减去2(4-1)=6个约束,沿I-I 截面断开,减去三个约束,故为9次超静定沿图示各截面断开,为21次超静定刚片I 与大地组成静定结构,刚片II 只需通过一根链杆和一个铰与I 连接即可,故为4次超静定(h)6-2 试回答:结构的超静定次数与力法基本结构的选择是否有关?力法方程有何物理意义? 6-3 试用力法计算图示超静定梁,并绘出M 、F Q 图。
(a) 解:上图=l1M p M01111=∆+p X δ其中:EIl l l l l l l EI l l l l EI 8114232332623232333211311=⎪⎭⎫ ⎝⎛⨯⨯+⨯⨯+⨯⨯⨯+⎪⎭⎫ ⎝⎛⨯⨯⨯⨯=δEIl F l lF l lF EI l pp p p817332322263231-=⎪⎭⎫ ⎝⎛⨯-⨯⨯-⨯=∆0817*******=-EIl F X EI l p p F X 211=p M X M M +=11l F p 61l F p 61 2l 3l 3 题目有错误,为可变体系。
+ lF 2 1=1M 图p Q X Q Q +=11p F 21p F 2(b) 解:基本结构为:l1Ml l 2Ml F p 21 p Ml F p 31⎪⎩⎪⎨⎧=∆++=∆++0022221211212111p p X X X X δδδδ p M X M X M M ++=2211p Q X Q X Q Q ++=22116-4 试用力法计算图示结构,并绘其内力图。
(a)l2l 2 l2l l 2Q 图12解:基本结构为:1Mp M01111=∆+p X δ p M X M M +=11(b)解:基本结构为:4a 2a4a4a3m6m 6m810810计算1M,由对称性知,可考虑半结构。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第6章位移法习题解答习题6.1确定用位移法计算习题6.1图所示结构的基本未知量数目,并绘出基本结构。
(除注明者外,其余杆的EI为常数。
)(a) (b) (c) (d)习题6.1图【解】各题基本未知量(取独立未知结点位移为基本未知量)如下:(a)n=4 (b)n=2 (c)n=6 (d)n=8习题6.2是非判断(1)位移法基本未知量的个数与结构的超静定次数无关。
()(2)位移法可用于求解静定结构的内力。
()(3)用位移法计算结构由于支座移动引起的内力时,采用与荷载作用时相同的基本结构。
()(4)位移法只能用于求解连续梁和刚架,不能用于求解桁架。
()【解】(1)正确。
位移法求解时基本未知量是结构的未知结点位移,与结构是否超静定无关。
(2)正确。
无任何结点位移发生的静定结构内力图可利用载常数直接确定;有结点位移发生的静定结构则可利用位移法的一般步骤计算。
(3)正确。
用位移法计算支座位移引起的内力时,可采用与荷载作用相同的基本结构,自由项可根据形常数和支移值确定。
(4)错误。
只要能够取得杆端力与杆端位移之间的函数关系,位移法就可用于求解任何杆系结构。
习题6.3已知习题6.3图所示刚架的结点B产生转角θB =π/180,试用位移法概念求解所作用外力偶M。
习题 6.3图【解】30i π 。
发生转角θB 时,可直接求得结点B 所连的各杆端弯矩,再由结点B 的平衡条件即可得M 。
习题6.4 若习题6.4图所示结构结点B 向右产生单位位移,试用位移法中剪力分配法的概念求解应施加的力F P 。
习题 6.4图【解】315lEI。
结点B 向右产生单位位移时,横梁所连各柱端剪力之和即为F P 。
习题6.5 已知刚架的弯矩图如习题6.5图所示,各杆EI =常数,杆长l =4m ,试用位移法概念直接计算结点B 的转角θB 。
m习题 6.5图【解】由M 图可知,BC 杆上无外荷载,其杆端弯矩为330BC BC B M i θ==-,由此求得40B EIθ=-。
习题6.6 用位移法计算习题6.6图所示连续梁,作弯矩图和剪力图,EI =常数。
(1) (2)习题 6.6图【习题6.6(1)解答】(1)确定基本未知量数目杆段CD 为静定的悬臂梁,可将其简化至C 结点位置。
本题在结点B 上具有一个角位移Z 1。
(2)确定基本体系基本体系如习题解6.6(1) (a)图所示,令EI =6。
kN·m (a)基本体系 习题解6. 6(1)图(3)建立典型方程1111=+P F Z K(4)计算系数项和自由项对基本结构,作1M 、2M 图和M P 图,分别如习题解6.6(1)(b)、(c)图所示。
= 39(b) 1M 图 (c) M P 图(kN.m)习题解6.6(1)图(5)解方程67.85.4391=--=Z (6)根据公式p 11M Z M M +=绘弯矩图,根据弯矩图可绘出剪力图。
结果如下:(d) 弯矩图(kN.m) (e) 剪力图(kN)习题6.6(1)图【习题6.6 (2)解答】(1) 确定基本未知量数目此刚架的基本未知量为结点B 和C 的角位移Z 1和Z 2,即n =2。
(2) 确定基本体系,如习题解6.6(2) (a)图所示。
(a) 基本体系 习题解6.6(2)图(3) 建立典型方程。
根据基本体系每个附加约束处的反力为零的条件,可列出位移法方程如下:0P 2222121P 1212111=++=++F Z k Z k F Z k Z k(4) 求系数和自由项。
分别作出基本结构在Z 1=1、Z 2 =1及荷载单独作用下的1M 图、2M图和M P图,如习题解6.6(2) (b)、(c)、(d)图所示。
= 24(b)1M图(c)2M图(d) M P图(kN.m)习题解6.6(2) 图(5) 解方程,求基本未知量。
将求得的各系数和自由项代入位移法方程,解得Z1=-2,Z2=4(6) 作最后弯矩图。
按P2211MZMZMM++=作出原结构的弯矩图,根据弯矩图可作出剪力图。
结果如下:(e) 弯矩图(kN.m) (f) 剪力图(kN)习题解6.6(2) 图习题6.7用位移法计算习题6.7图所示结构,作弯矩图,EI=常数。
(1) (2)习题 6.7图【习题6.7(1)解答】(1) 确定基本未知量数目。
此刚架的基本未知量为结点B的角位移Z1,即n=1。
(2) 确定基本体系,如习题解6.7(1)(a)图所示。
(a) 基本体系习题解6.7(1) 图(3) 建立典型方程。
根据基本体系每个附加约束处的反力为零的条件,可列出位移法方程如下:0P 1111=+F Z k(4) 求系数和自由项。
分别作出基本结构在Z 1=1及荷载单独作用下的1M 图和M P 图,如习题解6.7(1) (b)、(c)图所示。
1P F =20(b) 1M 图 (c) M P 图(kN.m)习题解6.7(1)图(5) 解方程,求基本未知量。
将求得的各系数和自由项代入位移法方程,解得Z 1 =-2 (6) 作最后弯矩图。
按P 11M Z M M +=作出原结构的弯矩图,根据弯矩图作剪力图,根据剪力图作轴力图。
结果如下:(d) 弯矩图(kN.m) (e) 剪力图(kN) (f) 轴力图(kN)习题解6.7(1)图【习题6.7(2)解答】(1) 确定基本未知量数目。
此刚架的基本未知量为结点A 的角位移Z 1,即n =1。
(2) 确定基本体系,如习题解6.7(2) (a)图所示。
(a) 基本体系 习题解6.7(2)图(3) 建立典型方程。
根据基本体系每个附加约束处的反力为零的条件,可列出位移法方程如下:0P 1111=+F Z k(4) 求系数和自由项。
分别作出基本结构在Z 1=1及荷载单独作用下的1M 图和M P 图,如习题解6.7(2) (b)、(c)图所示。
(b) 1M 图 (c) M P 图(kN.m)习题6.7(2)图(5) 解方程,求基本未知量。
将求得的各系数和自由项代入位移法方程,解得P110F l Z =(6) 作最后弯矩图。
按P 11M Z M M +=作出原结构的弯矩图,然后作剪力和轴力图。
结果如下:(d) 弯矩图 (e) 剪力图 (f) 轴力图习题解6.7(2)图习题6.8 用位移法计算习题6.8图所示各结构,并作弯矩图。
EI =常数。
(1) (2) (3)习题 6.8图【习题6.8(1)解答】(1) 确定基本未知量数目。
此刚架的基本未知量为结点A 和C 的角位移Z 1和Z 2,即n =2。
(2) 确定基本体系,如习题解6.8(1) (a)图所示。
(a) 基本体系 习题解6.8(1)图(3) 建立典型方程。
根据基本体系每个附加约束处的反力为零的条件,可列出位移法方程如下:0P 2222121P 1212111=++=++F Z k Z k F Z k Z k(4) 求系数和自由项。
分别作出基本结构在Z 1=1、Z 2 =1及荷载单独作用下的1M 图、2M 图和M P 图,如习题解6.8(1) (b)、(c)、(d)图所示。
=4.811k =222k1P F = 2020(b) 1M 图 (c) 2M 图 (d) M P 图(kN.m)习题解6.8(1)图(5) 解方程,求基本未知量。
将求得的各系数和自由项代入位移法方程,解得Z 1 =4.530,Z 2 =-0.871 (6) 作最后弯矩图。
按P 11M Z M M +=作出原结构的弯矩图,如习题解6.8(1) (e)图所示。
(e) M 图(kN.m) 习题6.8(1)图【习题6.8 (2)解答】(1) 确定基本未知量数目。
此刚架的基本未知量为结点B 的角位移Z 1和沿BD 方向的线位移Z 2,即n =2。
(2) 确定基本体系,如习题解6.8(2) (a)图所示。
(a) 基本体系 习题解6.8(2)图(3) 建立典型方程。
根据基本体系每个附加约束处的反力为零的条件,可列出位移法方程如下:0P 2222121P 1212111=++=++F Z k Z k F Z k Z k(4) 求系数和自由项。
分别作出基本结构在Z 1=1、Z 2 =1及荷载单独作用下的1M 图、2M 图和M P 图,如习题解6.8(2) (b)、(c)、(d)图所示。
11k =11.41P =76.25(b) 1M 图 (c) 2M 图(d) M P 图(kN.m)习题解6.8(2)图(5) 解方程,求基本未知量。
将求得的各系数和自由项代入位移法方程,解得Z 1 = —3.63,Z 2 =48.46 (6) 作最后弯矩图。
按P 2211M Z M Z M M ++=作出原结构的弯矩图,如习题解6.8(2) (e)图所示。
(e) M (kN.m) 习题解6.8(2)图【习题6.8 (3)解答】(1) 确定基本未知量数目。
此刚架的基本未知量为结点B 和D 的角位移Z 1和Z 2,即n =2。
(2) 确定基本体系,如习题解6.8(3) (a)图所示。
(a) 基本体系 习题解6.8(3)图(3) 建立典型方程。
根据基本体系每个附加约束处的反力为零的条件,可列出位移法方程如下:00P 2222121P 1212111=++=++F Z k Z k F Z k Z k(4) 求系数和自由项。
分别作出基本结构在Z 1=1、Z 2 =1及荷载单独作用下的1M 图、2M 图和M P 图,如习题解6.8(3) (b)、(c)、(d)图所示。
11=11.2=2k 2122k =8=2k 12=1=0= 128F(b) 1M 图(c) 2M 图 (d) M P 图(kN.m)习题解6.8(3)图(5) 解方程,求基本未知量。
将求得的各系数和自由项代入位移法方程,解得Z 1 =13.83,Z 2 =-13.46 (6) 作最后弯矩图。
按P2211M Z M Z M M ++=作出原结构的弯矩图,如习题解6.8(3) (e)图所示。
(e) M 图(kN.m) 习题解6.8(3)图习题6.9 利用对称性计算习题6.9图所示结构,作弯矩图。
EI =常数。
(1) (2)习题 6.9图【习题6.9(1)解答】 (1) 确定基本未知量数目。
选择半结构。
此刚架的基本未知量为结点B 和C 的角位移Z 1和Z 2,即n =2。
(2) 确定基本体系,如习题解6.9(1) (a)图所示。
(a) 基本体系 习题解6.9(1)图(3) 建立典型方程。
根据基本体系每个附加约束处的反力为零的条件,可列出位移法方程如下:0P 1111=+F Z k(4) 求系数和自由项。
分别作出基本结构在Z 1=1及荷载单独作用下的1M 图和M P 图,如习题解6.9(1) (b)、(c)图所示。
11=72F P(b) 1M 图 (c) M P 图习题解6.9(1)图(5) 解方程,求基本未知量。
