版高中数学第二章函数2.2.1一次函数的性质与图象学案新人教B版必修145
《步步高 学案导学设计》2013-2014学年 高中数学 人教B版必修1【配套备课资源】2.2.1

即为所求的图象.
3.正比例函数 y=kx (k 为常数,k≠0)与一次函数 y=kx+b (k, b 为常数,k≠0)的单调性为:当 k>0 时,是增函数;当 k<0 时,是减函数.
3 -2x+8,x≤5, 因此,f(x)= 3x+5,x>3. 5 34 观察 f(x)的图象可知,f(x)min= 5 .
本 课 时 栏 目 开 关
练一练·当堂检测、目标达成落实处
2.2.1
2 1.过点(3,m)、(m,-4)的一次函数的斜率为 ,则实数 m 的 5 本 课 值是 ( D ) 时
填一填·知识要点、记下疑难点
2.2.1
y=kx+b(k≠0) 叫做一次函数,它的 本 1.一次函数的概念:函数 课 定义域为 R ,值域为 R . 时 栏 目 2.一次函数 y=kx+b (k≠0)的图象是 直线 ,其中 k 叫做该直 开 线的 斜率 ,b 叫做该直线在 y 轴上的 截距 .一次函数又叫 关
研一研·问题探究、课堂更高效
2.2.1
跟踪训练 3 对于每个实数 x,设 f(x)取 y=3x+5,y=x+5, y=-2x+8 三个函数中的最大值, 用分段函数写出 f(x)的解 析式,并求出 f(x)的最小值.
本 课 时 栏 目 开 关
解
在同一坐标系内作出 y=3x+5,y=x+5,y=-2x+8
栏 目 开 关
A.2
B.-4
C.0
D.-2
Δy -4-m 2 解析 由Δx= =5,得 m=-2. m-3
练一练·当堂检测、目标达成落实处
2.2.1
k 2.函数 y=kx-1 与 y=-x在同一坐标系中的大致图象可能是 下图中的
本 课 时 栏 目 开 关
人教版B版高中数学必修1一次函数的性质与图象

思想方法技巧Leabharlann 解题技巧 1.解答二次函数问题时,一定要注意根据题设条件的不 同,选取不同形式的解析式.经过三点时,用一般式;已知 顶点时用配方式(即顶点式y=a(x-m)2+n);已知函数与x轴 两交点时,用分解式(即两根式y=a(x-x1)(x-x2))等等. 2.二次函数的单调性、值域(最值)问题,一般都是从开 口方向和对称轴入手讨论,或利用导数讨论.
k+b=1, 2k+b=2,
或k2+k+b=b=2,1,
∴kb==10,, 或kb==-3,1, ∴f(x)=x或f(x)=-x+3, ∴f ′(x)=1或f ′(x)=-1,
∴f ′(-1)=-1或f ′(-1)=1.
答案:D
(2011·浙江文)设函数f(x)=
(2)∵ax2+(b-1)x+1=0(a>0)的两根满足x1<2<x2<4, 设g(x)=ax2+(b-1)x+1,
∴gg24<>00, , 即41a6+ a+24b- b-11++11<>00,, ⇒2ba<>1414. , ∴2a-b>0. 又∵函数f(x)的对称轴为x=x0,∴x0=-2ba>-1.
考点典例讲练
一次函数
[例1] 一次函数f(x)的定义域和值域都是[1,2],f ′(x)
是f(x)的导函数,则f ′(-1)=( )
A.-1
B.4
C.-1或4
D.1或-1
分析:由f(x)为一次函数可设出其解析式,利用其单调
性及定义域和值域都是[1,2]可列出方程组求系数.
解析:设f(x)=kx+b(k≠0),由f(x)的单调性及条件知,
答案:D
(理)如果函数f(x)=x2+bx+c对任意的实数x,都有f(1+x) =f(-x),那么( )
人教B版高中数学必修一2.2.1一次函数的性质与图象课件

目标
1.理解掌握一次函数的概念、图象和性质,提
高学生分析问题的能力,培养数形结合及分类
讨论思想.
2.渗透由特殊到一般由具体到抽象的数学思想
方法。
3.让学生了解数学源于实际,应用于实际,培
养学生的应用意识。
重点
一次函数的性质与图象.
难点 一次函数的性质的应用.
复习导入
A. y=–3x
B. y= –0.5x+1
C. y=√3 x– 4
D. y= –2x-7
2. 一次函数y=(a+1)x+5中,y的值随x的值增大而
a< –1 .
减小,则a满足________
4.探讨一次函数的奇偶性
当b=0时,一次函数变为正比例函数,是奇函数;
当b≠0时,它既不是奇函数,也不是偶函数.
思考:我们如何快速准确的画出一次函数的图像?
当b≠0时,它既不是奇函数,也不是偶函数.
A.-2
B.-1
变式训:1: 已知函数y=2x+b在区间[-1,3]上的最大值是7,求实数b的值.
C.第三象限
D.第四象限
A.第一象限
B.第二象限
②y=3x+6;
1. 下列函数中,y随x的增大而增大的是( C )
=-2x三个函数中的最大值,则f(x)的最小值是
________.
本节课,你有哪些收获?
作业
A组2、3、5
B组1
谢
谢
1 一次函数的性质与图象
即y1=-5x+20.
当k<0时,一次函数y=kx+b在R上是减函数.
1.观察下列函数有什么共同特点:
①y=2x-1;
高中数学第二章函数2.2一次函数和二次函数2.2.1一次函数的性质与图象自我小测新人教B版必修1
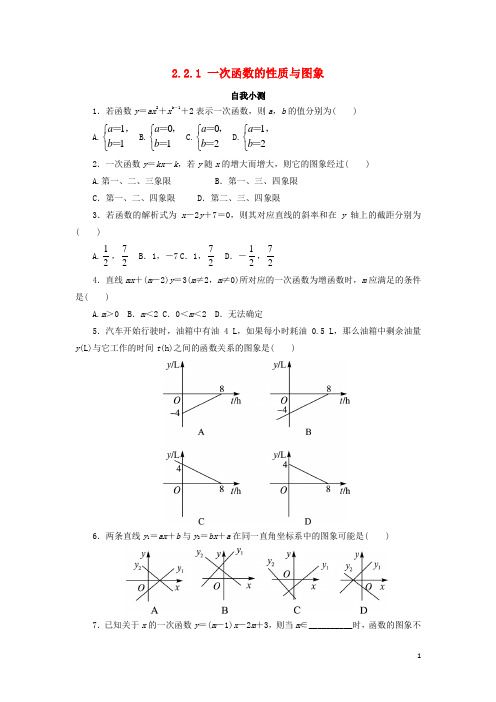
2.2.1 一次函数的性质与图象自我小测1.若函数y =ax 2+xb -1+2表示一次函数,则a ,b 的值分别为( ) A.11a b ⎧⎨⎩=,= B.01a b ⎧⎨⎩=,= C.02a b ⎧⎨⎩=,= D.12a b ⎧⎨⎩=,=2.一次函数y =kx -k ,若y 随x 的增大而增大,则它的图象经过( ) A.第一、二、三象限B .第一、三、四象限C .第一、二、四象限D .第二、三、四象限3.若函数的解析式为x -2y +7=0,则其对应直线的斜率和在y 轴上的截距分别为( ) A.12,72 B .1,-7 C .1,72 D .-12,724.直线mx +(m -2)y =3(m ≠2,m ≠0)所对应的一次函数为增函数时,m 应满足的条件是( )A.m >0 B .m <2 C .0<m <2 D .无法确定5.汽车开始行驶时,油箱中有油4 L ,如果每小时耗油0.5 L ,那么油箱中剩余油量y (L)与它工作的时间t (h)之间的函数关系的图象是()6.两条直线y 1=ax +b 与y 2=bx +a 在同一直角坐标系中的图象可能是()7.已知关于x 的一次函数y =(m -1)x -2m +3,则当m ∈__________时,函数的图象不经过第二象限.8.若一次函数f(x)=(1-m)x+2m+3在[-2,2]上总取正值,则m满足的条件是__________.9.某航空公司规定乘客所携带行李的质量x(kg)与其运费y(元)由如图所示的一次函数确定,求乘客可免费携带行李的最大质量.10.求直线y=x+3和直线y=-x+5以及x轴围成的三角形的面积.参考答案1. 解析:若函数为一次函数,则有011a b ⎧⎨⎩=,-=,即02a b ⎧⎨⎩=,= 答案:C2. 解析:由题意知k >0,所以-k <0,故y =kx -k 的图象经过第一、三、四象限. 答案:B3. 解析:∵x -2y +7=0,∴y =12x +72. ∴斜率k =12,在y 轴上的截距b =72,故选A. 答案:A 4. 解析:把mx +(m -2)y =3整理,得y =2m m --x +32m -.要使得一次函数为增函数,则2m m -->0,解得0<m <2. 答案:C5. 答案:D6. 答案:A解析:函数的图象不过第二象限,如图.所以10230m m >⎧⎨≤⎩-,-+,得1,3.2m m >⎧⎪⎨≥⎪⎩ 故m ≥32. 答案:3,2⎡⎫+∞⎪⎢⎣⎭7. 解析:∵函数f (x )为一次函数,∴m ≠1,要使f (x )在[-2,2]上总取正值,则需()(2)020f f >⎧⎪⎨>⎪⎩-,,即2(1)2302(1)230m m m m >⎧⎨>⎩--++,-++, 解得m >-14. 又∵m ≠1,∴m 满足的条件为m >-14,且m ≠1. 答案:m >-14,且m ≠1 9. 解:设题图中的函数解析式为y =kx +b (k ≠0),其中y ≥0.由题图,知点(40,630)和(50,930)在函数图象上,∴6304093050k b k b ⎧⎨⎩=+,=+,得30570.k b ⎧⎨⎩=,=- ∴函数解析式为y =30x -570.令y =0,得30x -570=0,解得x =19.∴乘客可免费携带行李的最大质量为19 kg.10. 解:设两条直线的交点为A ,y =x +3与x 轴的交点为B ,y =-x +5与x 轴的交点为C ,解35y x y x ⎧⎨⎩=+,=-+得14x y ⎧⎨⎩=,=,即A (1,4),y =x +3与x 轴的交点为B (-3,0),y =-x +5与x 轴的交点为C (5,0),∴|BC |=8,S △ABC =12|BC |·4=12×8×4=16, 即两条直线与x 轴围成的三角形的面积为16.。
2.2.1一次函数的性质和图像

讨论问题一:一次函数的定义
问题:(1)一次函数的定义是什么?
一次函数的定义:函数 y kx bk 0叫做一次函数 .
(2)一次函数的定义域和值域分别是什么?
定义域为R,值域为R.
(3)写出几个一次函数的解析式.
讨论问题二:一次函数的图象
问题:(1)在同一坐标系中画出几个一次函数图象. 观察图象有哪些相同和差异?
高中一年级数学人教B版必修一第二章第二节第一课
2.2.1 一次函数的性质与图象
目录
CONTENTS
一 复习导入
三 典型例题 五 课堂小结
二 新课讨论 四 巩固练习 六 拓展提高
复习 导入
复习导入 初中数学
一次函数
高中数学
函数的概念及 表示方法
函数的单调性 奇偶性
本节
一次函数的性质 与图象
例
例
新课 讨论
一次函数y kx bk 0的图象是直线.
(2)解析式中的字母k和b叫什么?分别代表什么几何意义?
k叫做该直线的斜率, b叫做该直线在 y轴上的截距.
讨论问题三:一次函数的性质
问题:斜率k和截距b的变化对函数图象和性质
有哪些影响呢?
单调性
倾斜程度
奇偶性
图象
8
一次函数的单调性
当 k>0 时,一次函数为 增函数 ; 当 k<0 时,一次函数为 减函数 ;
不等式 ax a 5 0恒成立,则实数a的取值范围是
.
课后作业
56页1
练习A2、3
练习B1题
THANKS
6.讨论函数y a 1x b 5的单调性.
答案
课堂 小结
课堂小结
01 02 03
2016新课标三维人教B版数学必修1 2.2 一次函数和二次函数

一次函数和二次函数2.2.1&2.2.2 一次函数的性质与图象 二次函数的性质与图象(1)什么样的函数是一次函数?其图象和性质是什么?(2)什么样的函数是二次函数?其图象和性质是什么?[新知初探]1.一次函数(1)函数y =kx +b (k ≠0)叫做一次函数,一次函数的图象是直线,其中k 叫做斜率,b 叫做截距,斜率的表达式为:k =y 1-y 2x 1-x 2.(2)一次函数y =kx +b (k ≠0)的图象与性质 k >1k <0b =0 b ≠0b =0b ≠图象定义域 R 值域 R单调性 在R 上是增函数 在R 上是减函数 奇偶性奇函数非奇非偶函数奇函数非奇非偶函数[点睛] 注意k ≠0这一条件,当k =0时,函数为y =b ,它不再是一次函数,其函数图象是平行x 轴或与x 轴重合的一条直线.预习课本P55~60,思考并完成以下问题2.二次函数(1)函数y=ax2+bx+c(a≠0)叫做二次函数,它的定义域是R.(2)二次函数的图象与性质抛物线开口向上,并向上无限延伸抛物线开口向下,并向下无限延伸[点睛]二次项系数a决定了图象的开口方向和在同一直角坐标系中的开口大小.|a|越大,抛物线的开口越小;反之,|a|越小,抛物线的开口越大.[小试身手]1.判断.(正确的打“√”,错误的打“×”)(1)一次函数都具有单调性.()(2)函数y=ax+b是一次函数.()(3)二次函数的特征是未知数的最高次数为2,且二次项系数不能为0.()(4)函数y=ax2(a≠0)在(-∞,0)上递减.()答案:(1)√(2)×(3)√(4)×2.设函数f(x)=2x-1(x<0),则f(x)()A.有最大值B.有最小值C.既有最大值又有最小值D.既无最大值又无最小值答案:D3.二次函数y =1-6x -3x 2的顶点坐标和对称轴方程分别为( ) A .顶点(1,4),对称轴x =1 B .顶点(-1,4),对称轴x =-1 C .顶点(1,4),对称轴x =4 D .顶点(-1,4),对称轴x =4 答案:B4.函数y =3+2x +x 2(0≤x ≤3)的最小值为________. 答案:3一次函数的性质[典例] 已知函数y =(2m -1)x +1-3m ,试求m 为何值时, (1)这个函数为正比例函数; (2)这个函数为一次函数; (3)这个函数是减函数.[解] (1)若y =(2m -1)x +1-3m 是正比例函数,则m 应满足⎩⎪⎨⎪⎧2m -1≠0,1-3m =0.解得m =13.∴当m =13时,这个函数为正比例函数.(2)当2m -1≠0,即m ≠12时,这个函数为一次函数.(3)根据一次函数的性质可知,当2m -1<0, 即m <12时,这个函数是减函数.形如y =kx +b (k ≠0)的函数是一次函数;当k ≠0,b =0时,为正比例函数;当k >0时,函数为增函数,当k <0时,函数为减函数.[活学活用]1.如果一次函数y =kx +b 的图象经过第一、三、四象限,那么( ) A .k >0,b >0 B .k >0,b <0 C .k <0,b >0D .k <0,b <0解析:选B 作出函数图象,由图象可以看出:y 随x 的增大而增大,所以k >0;直线与y 轴的交点在负半轴上,所以b <0.2.若函数y =(a +1)x +2,x ∈R 在其定义域上是增函数,则a 的取值范围是________. 解析:由题意得a +1>0,∴a >-1. 答案:(-1,+∞)二次函数的图象和性质[典例] 已知函数f (x )=3x 2+2x +1. (1)求这个函数图象的顶点坐标和对称轴; (2)已知f ⎝⎛⎭⎫-23=1,不计算函数值求f (0); (3)不直接计算函数值,试比较f ⎝⎛⎭⎫-34与f ⎝⎛⎭⎫154的大小. [解] f (x )=3x 2+2x +1=3⎝⎛⎭⎫x +132+23. (1)顶点坐标为⎝⎛⎭⎫-13,23,对称轴是x =-13. (2)∵f ⎝⎛⎭⎫-23=1,又⎪⎪⎪⎪0-⎝⎛⎭⎫-13=13, ⎪⎪⎪⎪-23-⎝⎛⎭⎫-13=13, 所以结合二次函数的对称性可知 f (0)=f ⎝⎛⎭⎫-23=1. (3)由f (x )=3⎝⎛⎭⎫x +132+23知二次函数图象开口向上,且对称轴为x =-13,所以离对称轴越近,函数值越小.又⎪⎪⎪⎪-34-⎝⎛⎭⎫-13<⎪⎪⎪⎪154-⎝⎛⎭⎫-13, ∴f ⎝⎛⎭⎫-34<f ⎝⎛⎭⎫154.(1)求二次函数图象的对称轴、顶点坐标及最值主要利用配方法,掌握抛物线的顶点坐标⎝⎛⎭⎫-b 2a,4ac -b 24a . (2)比较两个函数值的大小,可以把要比较的两个函数值转化到同一个单调区间上,再利用单调性比较它们的大小;也可以比较两个自变量离对称轴距离的大小关系,结合图象判断函数值的大小关系.[活学活用]1.下列区间中,使函数y =-2x 2+x 为增函数的是( ) A .R B .[2,+∞) C.⎣⎡⎭⎫14,+∞ D.⎝⎛⎦⎤-∞,14 解析:选D 函数y =-2x 2+x =-2⎝⎛⎭⎫x -142+18的图象的对称轴是直线x =14,图象开口向下,所以函数值在对称轴x =14的左边是增加的.2.设abc >0,二次函数f (x )=ax 2+bx +c 的图象可能是( )解析:选D 结合题意,只有D 选项符合,即若a >0,b <0,c <0,则对称轴x =-b2a >0,函数f (x )的图象与y 轴的交点(c,0)在x 轴下方.[典例] 求二次函数f (x )=x 2-2ax +2在[2,4]上的最小值. [解] ∵函数图象的对称轴是x =a , ∴当a <2时,f (x )在[2,4]上是增函数, ∴f (x )min =f (2)=6-4a .当a >4时,f (x )在[2,4]上是减函数, ∴f (x )min =f (4)=18-8a .当2≤a ≤4时,f (x )min =f (a )=2-a 2. ∴f (x )min =⎩⎪⎨⎪⎧6-4a ,a <2,2-a 2,2≤a ≤4,18-8a ,a >4.[一题多变]1.[变设问]在本例条件下,求f (x )的最大值. 解:∵函数图象的对称轴是x =a , ∴当a ≤3时,f (x )max =f (4)=18-8a , 当a >3时,f (x )max =f (2)=6-4a .∴f (x )max =⎩⎪⎨⎪⎧18-8a ,a ≤3,6-4a ,a >3.2.[变设问]在本例条件下,若f (x )的最小值为2,求a 的值. 解:由本例解析知f (x )min =⎩⎪⎨⎪⎧6-4a ,a <2,2-a 2,2≤a ≤4,18-8a ,a >4.当a <2时,6-4a =2,a =1; 当2≤a ≤4时,2-a 2=2,a =0(舍去); 当a >4时,若18-8a =4,a =74(舍去).∴a 的值为1.3.[变条件,变设问]本例条件变为,若f (x )=x 2-2ax +2,当x ∈[2,4]时,f (x )≤a 恒成立,求实数a 的取值范围.解:在[2,4]内,f (x )≤a 恒成立, 即a ≥x 2-2ax +2在[2,4]内恒成立, 即a ≥f (x )max ,x ∈[2,4].而f (x )max =⎩⎪⎨⎪⎧18-8a ,a ≤3,6-4a ,a >3.(1)当a ≤3时,a ≥18-8a ,解得a ≥2,此时有2≤a ≤3. (2)当a >3时,a ≥6-4a ,解得a ≥65,此时有a >3.综上有实数a 的取值范围是[2,+∞).求二次函数最值问题的解题策略(1)确定对称轴,抛物线的开口方向,作图. (2)在图象上标出定义域的位置. (3)观察单调性写出最值.层级一 学业水平达标1.函数的解析式为x -2y +7=0,则其对应直线的斜率与纵截距分别为( ) A.12,72 B .1,-7 C .1,72D .-12,72解析:选A∵x-2y+7=0,∴y=12x+72,∴斜率k=12,纵截距b=72.2.函数y=x2-2x+2在区间[-2,3]上的最大值、最小值分别是()A.10,5B.10,1C.5,1 D.以上都不对解析:选B因为y=x2-2x+2=(x-1)2+1,且x∈[-2,3],所以当x=1时,y min=1,当x=-2时,y max=(-2-1)2+1=10.故选B.3.两条直线y=ax+b与y=bx+a在同一坐标系中的图象可能是下图中的()解析:选A假设B项中直线y=ax+b正确,则a>0,b>0,所以y=bx+a的图象应过第一、二、三象限,而实际图象过第一、二、四象限.∴B错.同理C、D错.故A正确.4.二次函数y=x2+bx+c图象的顶点是(-1,-3),则b与c的值是()A.b=2,c=2 B.b=2,c=-2C.b=-2,c=2 D.b=-2,c=-2解析:选B顶点横坐标x=-b2=-1,得b=2,纵坐标4c-b24×1=4c-44=-3,得c=-2.5.若f(x)=x2+bx+c,且f(-1)=f(3),则()A.f(1)>c>f(-1) B.f(1)<c<f(-1)C.c>f(-1)>f(1) D.c<f(-1)<f(1)解析:选B由题意f(x)的对称轴为x=1,且知(-∞,1]为函数的减区间,故有f(1)<f(0)<f(-1),即f(1)<c<f(-1).6.函数f(x)=-x2+2x+1在[-2,-1]上的最大值是________,最小值是________.解析:f(x)=-(x-1)2+2,则函数f(x)在[-2,-1]上是增函数,当x=-1时,f(x)max=-2;当x=-2时,f(x)min=-7.答案:-2-77.已知函数y=(m2-3m)xm2-2m+2是二次函数,则m=________,此时函数的值域为________.解析:由题意得⎩⎪⎨⎪⎧ m 2-3m ≠0,m 2-2m +2=2,∴⎩⎪⎨⎪⎧m ≠0且m ≠3,m =0或m =2.∴m =2,此时y =-2x 2.故值域为(-∞,0]. 答案:2 (-∞,0]8.如果二次函数f (x )=x 2-(a -1)x +5在区间⎝⎛⎭⎫12,1上是增函数,则实数a 的取值范围为________.解析:∵函数f (x )=x 2-(a -1)x +5的对称轴为x =a -12且在区间⎝⎛⎭⎫12,1上是增函数,∴a -12≤12,即a ≤2. 答案:(-∞,2]9.已知一次函数y =(6+3m )x +(n -4),求: (1)m 为何值时是减函数?(2)m ,n 为何值时,函数图象与y 轴的交点在x 轴下方? 解:(1)∵y =(6+3m )x +(n -4)是减函数, ∴6+3m <0,∴m <-2. (2)当x =0时,y =n -4.当函数图象与y 轴的交点在x 轴下方时,y <0, 得n -4<0,∴n <4.又函数为一次函数,∴6+3m ≠0,即m ≠-2.∴当m ∈R 且m ≠-2,n <4时,函数图象与y 轴的交点在x 轴下方. 10.分别在下列范围内求函数y =x 2-2x -3的最值. (1)0<x <2;(2)2≤x ≤3.解:∵y =x 2-2x -3=(x -1)2-4, ∴顶点坐标为(1,-4).(1)∵x =1在0<x <2范围内,且二次项系数为1>0,∴当x =1时,y 有最小值,y min=-4,无最大值.(2)∵x =1不在2≤x ≤3范围内,∴函数y =x 2-2x -3(2≤x ≤3)的图象是抛物线y =x 2-2x -3的一部分.由二次函数的性质知y =x 2-2x -3在(1,+∞)上单调递增, ∴当x =3时,y max =32-2×3-3=0; 当x =2时,y min =22-2×2-3=-3.层级二 应试能力达标1.若函数y =ax +1在[1,2]上的最大值与最小值的差为2,则实数a 的值是( ) A .2 B .-2 C .2或-2D .0解析:选C 由题意知a ≠0,当a >0时,有(2a +1)-(a +1)=2,解得a =2;当a <0时,有(a +1)-(2a +1)=2,解得a =-2.综上知a =±2.2.若抛物线y =x 2-(m -2)x +m +3的顶点在y 轴上,则m 的值为( ) A .-3 B .3 C .-2D .2解析:选D 因为抛物线y =x 2-(m -2)x +m +3的顶点在y 轴上,所以顶点横坐标--(m -2)2×1=m -22=0,故m =2.3.已知函数y =x 2-2x +3在闭区间[0,m ]上有最大值3,最小值2,则m 的取值范围是( )A .[1,+∞)B .[0,2]C .(-∞,2]D .[1,2]解析:选D f (x )=(x -1)2+2,∵f (x )min =2,f (x )max =3,且f (1)=2,f (0)=f (2)=3,∴1≤m ≤2,故选D.4.当0≤x ≤2时,a <-x 2+2x 恒成立,则实数a 的取值范围是( ) A .(-∞,1] B .(-∞,0] C .(-∞,0)D .(0,+∞)解析:选C 令f (x )=-x 2+2x , 则f (x )=-x 2+2x =-(x -1)2+1. 又∵x ∈[0,2],∴f (x )min =f (0)=f (2)=0. ∴a <0.5.已知函数f (x )=-x 2+4x +a ,x ∈[0,1],若f (x )有最小值-2,则f (x )的最大值为________. 解析:函数f (x )=-x 2+4x +a =-(x -2)2+4+a ,x ∈[0,1],且函数有最小值-2. 故当x =0时,函数有最小值, 当x =1时,函数有最大值.∵当x =0时,f (0)=a =-2,∴f (x )=-x 2+4x -2, ∴当x =1时,f (x )max =f (1)=-12+4×1-2=1. 答案:16.已知-x 2+4x +a ≥0在x ∈[0,1]上恒成立,则实数a 的取值范围是________. 解析:法一:-x 2+4x +a ≥0,即a ≥x 2-4x ,x ∈[0,1],也就是a 应大于或等于f (x )=x 2-4x 在[0,1]上的最大值,函数f (x )=x 2-4x 在x ∈[0,1]的最大值为0,∴a ≥0.法二:设f (x )=-x 2+4x +a ,由题意知⎩⎪⎨⎪⎧f (0)=a ≥0,f (1)=-1+4+a ≥0,解得a ≥0.答案:[0,+∞)7.已知函数f (x )=x 2+2(1-2a )x +6在区间(-∞,-1)上为减函数. (1)求f (2)的取值范围; (2)比较f (2a -1)与f (0)的大小.解:(1)二次函数图象的对称轴为x =2a -1, ∴函数f (x )在(-∞,2a -1]上为减函数. ∴-1≤2a -1. ∴a ≥0.而f (2)=22+2(1-2a )×2+6=-8a +14, ∵a ≥0,∴f (2)=14-8a ≤14.故f (2)的取值范围为(-∞,14].(2)∵当x =2a -1时,函数y =f (x )取最小值, ∴f (2a -1)≤f (0).8.已知函数f (x )=-x 2+2ax +1-a 在x ∈[0,1]时有最大值2,求a 的值. 解:f (x )=-(x -a )2+a 2-a +1, 当a ≥1时,f (x )max =f (1)=a ; 当0<a <1时,f (x )max =f (a )=a 2-a +1; 当a ≤0时,f (x )max =f (0)=1-a .根据已知条件得,⎩⎪⎨⎪⎧ a ≥1,a =2或⎩⎪⎨⎪⎧ 0<a <1,a 2-a +1=2或⎩⎪⎨⎪⎧a ≤0,1-a =2, 解得a =2或a =-1.2.2.3 待定系数法(1)什么是待定系数法?(2)运用待定系数法可求哪些常见函数解析式?[新知初探]待定系数法的定义一般地,在求一个函数时,如果知道这个函数的一般形式,可先把所求函数写为一般形式,其中系数待定,然后再根据题设条件求出这些待定系数.这种通过求待定系数来确定变量之间关系式的方法叫做待定系数法.[点睛] 待定系数法的实质就是方程思想,它把待定的未知数与已知数等同看待来建立等式,即得方程,然后用方程的知识来解决.[小试身手]1.已知一次函数f (x )的图象过点A (1,-1),B (-2,5),则f (x )=( ) A .2x +1 B .2x -1 C .-2x +1 D .-2x -1答案:C2.已知二次函数y =ax 2+bx +1的图象的对称轴是直线x =1,并且通过点A (-1,7),则a ,b 的值分别是( )A .2,4B .2,-4C .-2,4D .-2,-4 答案:B3.二次函数的图象过原点,且顶点为(1,2),那么此二次函数的解析式为________. 答案:f (x )=-2x 2+4x求一次函数及正、反比例函数的解析式预习课本P61~62,思考并完成以下问题[典例] 已知一次函数的图象经过点(-4,15),且与正比例函数的图象交于点(6,-5),求此一次函数和正比例函数的解析式.[解] 设一次函数解析式为y =kx +b (k ≠0),正比例函数解析式为y =k ′x (k ′≠0). 把(6,-5),(-4,15)分别代入y =kx +b ,得⎩⎪⎨⎪⎧ -5=6k +b ,15=-4k +b ,解得⎩⎪⎨⎪⎧k =-2,b =7.∴一次函数的解析式为y =-2x +7. 把(6,-5)代入y =k ′x ,得-5=6k ′, 解得k ′=-56.∴正比例函数的解析式为y =-56x .待定系数法求函数解析式的步骤(1)根据题设条件,设出含有待定系数的函数解析式的恰当形式; (2)把已知条件代入解析式,列出关于待定系数的方程(组);(3)解方程(组),求出待定系数的值(或消去待定系数,从而使问题得到解决). (4)将求得的待定系数的值代回所设的解析式.[活学活用]一次函数在y 轴上的截距是1,且与反比例函数的图象交于点P (1,3),求一次函数与反比例函数的解析式.解:设一次函数与反比例函数分别为 y =k 1x +b (k 1≠0),y =k 2x (k 2≠0), 依题意,得⎩⎪⎨⎪⎧b =1,3=k 1+1,3=k 2,∴b =1,k 1=2,k 2=3.故一次函数的解析式为y =2x +1, 反比例函数的解析式为y =3x .求二次函数的解析式 [典例] 求下列二次函数的解析式.(1)已知y =f (x )是二次函数,且图象过点(-2,20),(1,2),(3,0).(2)已知二次函数的顶点为(-1,-2),且图象经过点(2,25).(3)已知二次函数与x 轴交点为(-2,0),(3,0),且函数图象经过点(-1,8). [解] (1)(一般式)设所求二次函数为y =ax 2+bx +c (a ≠0), 把点(-2,20),(1,2),(3,0)代入解析式,得 ⎩⎪⎨⎪⎧4a -2b +c =20,a +b +c =2,9a +3b +c =0,解得⎩⎪⎨⎪⎧a =1,b =-5,c =6.∴所求函数为y =x 2-5x +6.(2)(顶点式)∵二次函数的顶点为(-1,-2), ∴设二次函数为y =a (x +1)2-2(a ≠0), 又∵图象过点(2,25),∴a (2+1)2-2=25,解得a =3,∴所求函数为y =3(x +1)2-2,即y =3x 2+6x +1. (3)(两根式)∵二次函数与x 轴的交点为(-2,0),(3,0), ∴设所求的二次函数为y =a (x +2)(x -3), 又∵图象过点(-1,8), ∴8=a (-1+2)(-1-3), 解得a =-2,∴所求函数为y =-2(x +2)(x -3), 即y =-2x 2+2x +12.二次函数常见的表达式有三种:一般式、顶点式、两根式,选择合适的表达式能起到事半功倍的效果.(1)一般地,若已知函数经过三点,常设函数的一般式;(2)若题目中出现顶点坐标、最大值、对称轴等信息时,我们可考虑函数的顶点式; (3)若题目中给出函数与x 轴的交点或二次方程ax 2+bx +c =0的两根,可设函数的两根式.[活学活用]1.若二次函数的图象过点(0,1),对称轴为x =2,最小值是-1,则它的解析式为________. 解析:设二次函数的解析式为y =a (x -2)2-1. 将(0,1)代入得1=4a -1, 所以a =12.所以所求函数解析式为y =12(x -2)2-1,即y =12x 2-2x +1.答案:y =12x 2-2x +12.已知f (x )是二次函数,且满足f (0)=1,f (x +1)-f (x )=2x ,求f (x )的解析式. 解:设所求的二次函数解析式为y =ax 2+bx +c (a ≠0). ∵f (0)=1,∴c =1,∴y =ax 2+bx +1. 又∵f (x +1)-f (x )=2x ,对任意x ∈R 成立, ∴a (x +1)2+b (x +1)+1-(ax 2+bx +1)=2x . 整理,得2ax +a +b =2x .∴⎩⎪⎨⎪⎧ 2a =2,a +b =0,∴⎩⎪⎨⎪⎧a =1,b =-1.故所求二次函数的解析式为y =x 2-x +1.待定系数法的综合应用[典例] 如果函数f (x )=x 2+a bx -c (b ,c ∈N +)满足f (0)=0,f (2)=2,且f (-2)<-12,求f (x )的解析式.[解] 由f (0)=0,f (2)=2,可得⎩⎪⎨⎪⎧a-c=0,4+a2b -c =2,∴⎩⎪⎨⎪⎧a =0,2b -c =2,∴f (x )=x 2bx -2b +2.又f (-2)<-12,∴4-4b +2<-12,解不等式得12<b <52.又∵b ∈N +,∴b =1或b =2.又2b -c =2,故当b =1时,c =0,不符合题意. 当b =2时,c =2. ∴f (x )=x 22x -2(x ≠1).函数f (x )中含有a ,b ,c 三个参数,要求a ,b ,c 的值,必须有三个独立的条件,而题目恰有三个独立条件,但由第三个条件得到的结果为不等式,所以还应特别注意b ,c ∈N +这一条件.[活学活用]已知函数f (x )=ax +b x +c (a ,b ,c 是常数)是奇函数,且满足f (1)=52,f (2)=174,求f (x )的解析式.解:∵f (x )为奇函数, ∴f (-x )=-f (x ),∴-ax -b x +c =-ax -bx -c ,∴c =0, ∴f (x )=ax +bx . 又f (1)=52,f (2)=174,∴⎩⎨⎧a +b =52,2a +b 2=174,∴a =2,b =12.∴f (x )=2x +12x.层级一 学业水平达标1.若函数y =kx +b 的图象经过点P (3,-2)和Q (-1,2),则这个函数的解析式为( ) A .y =x -1 B .y =x +1 C .y =-x -1D .y =-x +1解析:选D 把点P (3,-2)和Q (-1,2)的坐标分别代入y =kx +b ,得⎩⎪⎨⎪⎧-2=3k +b ,2=-k +b ,即⎩⎪⎨⎪⎧k =-1,b =1. ∴y =-x +1.2.已知二次函数y =x 2+bx +c 的图象经过(1,0),(2,5)两点,则二次函数的解析式为( )A .y =x 2+2x -3B .y =x 2-2x -3C .y =x 2+2x +3D .y =x 2-2x +6解析:选A 将点(1,0),(2,5)代入y =x 2+bx +c ,可得⎩⎪⎨⎪⎧1+b +c =0,4+2b +c =5.解得b =2,c =-3.3.已知函数f (x )=x 2+px +q ,满足f (1)=f (2)=0,则f (-1)的值是( ) A .5 B .-5 C .6 D .-6解析:选C ∵⎩⎪⎨⎪⎧f (1)=1+p +q =0,f (2)=4+2p +q =0,∴p =-3,q =2. ∴f (x )=x 2-3x +2,∴f (-1)=(-1)2-3×(-1)+2=6.4.若一次函数的图象经过点A (1,6)和B (2,8),则该函数的图象还可能经过的点的坐标为( )A.⎝⎛⎭⎫12,5B.⎝⎛⎭⎫14,4 C .(-1,3)D .(-2,1)解析:选A 设一次函数的解析式为y =kx +b (k ≠0),由该函数的图象经过点A (1,6)和B (2,8),得⎩⎪⎨⎪⎧ k +b =6,2k +b =8,解得⎩⎪⎨⎪⎧k =2,b =4,所以此函数的解析式为y =2x +4,只有A 选项的坐标符合此函数的解析式.故选A.5.已知2x 2+x -3=(x -1)(ax +b ),则a ,b 的值分别为( ) A .2,3 B .3,2 C .-2,3D .-3,2解析:选A (x -1)(ax +b )=ax 2+(b -a )x -b ,因为(x -1)(ax +b )=2x 2+x -3, 所以⎩⎪⎨⎪⎧a =2,b -a =1,-b =-3,解得⎩⎪⎨⎪⎧a =2,b =3.6.反比例函数y =12x的图象和一次函数y =kx -7的图象都经过点P (m,2),则一次函数的解析式为________.解析:因为点P (m,2)在函数y =12x 的图象上,所以2=12m ,m =6,P 点坐标为(6,2).因为一次函数y =kx -7的图象经过点P (6,2),所以6k -7=2,k =32.故所求的一次函数解析式是y =32x -7.答案:y =32x -77.如图是二次函数y =f (x )的图象,若x ∈[-2,1],则函数f (x )的值域为________.解析:依题意设函数f (x )=a (x +3)(x -1),又函数f (x )的图象过点(0,3),代入得a =-1,∴f (x )=-x 2-2x +3.结合题中图形易知函数f (x )在[-2,1]上的最大值为f (-1)=4.又f (-2)=3,f (1)=0,∴函数f (x )在[-2,1]上的最小值为0,∴当x ∈[-2,1]时,函数的值域为[0,4].答案:[0,4]8.已知二次函数f (x )=ax 2+bx +c (a ≠0)的图象经过点A (0,a ),B (1,4)且对称轴为x =-1,则二次函数的解析式为________.解析:由题意得⎩⎪⎨⎪⎧c =a ,a +b +c =4,b =2a .解得⎩⎪⎨⎪⎧a =1,b =2,c =1.∴f (x )=x 2+2x +1. 答案:f (x )=x 2+2x +19.已知二次函数f (x )的图象经过点(4,3),它在x 轴上截得的线段长为2,并且对任意x ∈R ,都有f (2-x )=f (2+x ),求f (x )的解析式.解:∵f (2-x )=f (2+x )对x ∈R 恒成立,∴f (x )的对称轴为x =2.又∵f (x )图像被x 轴截得的线段长为2,∴f (x )=0的两根为1和3.设f (x )的解析式为f (x )=a (x -1)(x -3)(a ≠0).又∵f (x )的图象过点(4,3),∴3a =3,a =1.∴所求f (x )的解析式为f (x )=(x -1)(x -3),即f (x )=x 2-4x +3.10.已知y =f (x )的图象如图所示.(1)求f (x )的解析式; (2)求函数的值域.解:(1)由图象可知①:当0≤x ≤2时,f (x )是一次函数. 设f (x )=kx +b (k ≠0),则⎩⎪⎨⎪⎧ f (0)=b =2,f (1)=k +b =0,即⎩⎪⎨⎪⎧b =2,k =-2.故f (x )=-2x +2. ②当2<x <3时,f (x )=-2.③当3≤x ≤5时,f (x )是一次函数. 设f (x )=mx +n (m ≠0),则⎩⎪⎨⎪⎧f (3)=3m +n =-2,f (5)=5m +n =0, 解得⎩⎪⎨⎪⎧m =1,n =-5,此时f (x )=x -5.综上可知,f (x )的解析式为 f (x )=⎩⎪⎨⎪⎧-2x +2, 0≤x ≤2,-2, 2<x <3,x -5, 3≤x ≤5.(2)由图可知该函数的值域为[-2,2].层级二 应试能力达标1.已知f (x )=ax +b (a ≠0)且af (x )+b =9x +8,则( ) A .f (x )=3x +2 B .f (x )=-3x -4 C .f (x )=3x -4D .f (x )=3x +2或f (x )=-3x -4解析:选D ∵f (x )=ax +b ,af (x )+b =a (ax +b )+b =9x +8, ∴a 2x +ab +b =9x +8,∴⎩⎪⎨⎪⎧ a 2=9,ab +b =8,所以⎩⎪⎨⎪⎧ a =3,b =2,或⎩⎪⎨⎪⎧a =-3,b =-4. ∴f (x )=3x +2或f (x )=-3x -4.2.已知f (x )=x 2+1,g (x )是一次函数且是增函数,若f (g (x ))=9x 2+6x +2,则g (x )的解析式为( )A .g (x )=3x +2B .g (x )=3x +1C .g (x )=-3x +2D .g (x )=3x -1解析:选B 设g (x )=kx +b (k >0),则f (g (x ))=(kx +b )2+1=9x 2+6x +2 ∴k 2x 2+2kbx +b 2+1=9x 2+6x +2, ∴k 2=9,解得k =3或k =-3(舍去), 且2kb =6,∴b =1, ∴g (x )=3x +1.3.二次函数y =ax 2+bx +2(a <0)与x 轴的交点为⎝⎛⎭⎫-12,0,⎝⎛⎭⎫13,0,则a +b 的值是( )A .10B .-10C .14D .-14解析:选D 由题意得⎩⎨⎧14a -12b +2=0,19a +13b +2=0,解得⎩⎪⎨⎪⎧a =-12,b =-2,∴a +b =-14.4.已知某二次函数的图象与函数y =2x 2的图象形状一样,开口方向相反,且其顶点为(-1,3),则此函数的解析式为( )A .y =2(x -1)2+3B .y =2(x +1)2+3C .y =-2(x -1)2+3D .y =-2(x +1)2+3解析:选D 设所求函数的解析式为y =a (x +h )2+k (a ≠0),由题意可知a =-2,h =1,k =3,故y =-2(x +1)2+3.5.已知函数f (x )=x 2+2x +a ,f (bx )=9x 2-6x +2,其中x ∈R ,a ,b 为常数,则a ,b 的值分别为________.解析:∵f (x )=x 2+2x +a ,∴f (bx )=(bx )2+2(bx )+a =b 2x 2+2bx +a . 又∵f (bx )=9x 2-6x +2, ∴b 2x 2+2bx +a =9x 2-6x +2, ∴⎩⎪⎨⎪⎧b 2=9,2b =-6,a =2.∴⎩⎪⎨⎪⎧b =-3,a =2. 答案:2,-36.如图,抛物线y =-x 2+2(m +1)x +m +3与x 轴交于A ,B 两点,且OA =3OB ,则m 的值为________.解析:设A (x 1,0),B (x 2,0), 则x 1=-3x 2. 由⎩⎪⎨⎪⎧x 1+x 2=2m +2,x 1x 2=-m -3,x 1=-3x 2,得3m 2+5m =0, 即m =0或m =-53.由图象知,对称轴x =m +1>0, 即m >-1,因此m =-53不合题意,故m =0.答案:07.已知函数f (x )=xax +b(a ,b 为常数,且a ≠0)满足f (2)=1,且f (x )=x 有唯一解,求函数y =f (x )的解析式和f (f (-3))的值.解:因为f (2)=1,所以22a +b=1,即2a +b =2,① 又因为f (x )=x 有唯一解,即xax +b=x 有唯一解,所以ax 2+(b -1)x =0有两个相等的实数根,所以Δ=(b -1)2=0,即b =1.代入①得a =12.所以f (x )=x 12x +1=2x x +2. 所以f (f (-3))=f ⎝ ⎛⎭⎪⎫-6-1=f (6)=2×66+2=32. [重点选做]8.已知二次函数f (x )满足f (x +1)+f (x -1)=-2x 2+4x . (1)求f (x )的解析式;(2)求当x ∈[a ,a +2]时,f (x )的最大值. 解:(1)设f (x )=ax 2+bx +c (a ≠0),则f (x +1)+f (x -1)=a (x +1)2+b (x +1)+c +a (x -1)2+b (x -1)+c =2ax 2+2bx +2a +2c =-2x 2+4x .由于上式对一切x ∈R 都成立, ∴2a =-2,2b =4,2a +2c =0, ∴a =-1,b =2,c =1, ∴f (x )=-x 2+2x +1.(2)由(1)可知,f (x )=-(x -1)2+2.当a +2≤1,即a ≤-1时,f (x )在[a ,a +2]上单调递增, ∴f (x )max =f (a +2)=-a 2-2a +1;版权所有:中国好课堂 当-1<a <1时,a <1<a +2, f (x )max =f (1)=2;当a ≥1时,f (x )在[a ,a +2]上单调递减, ∴f (x )max =f (a )=-a 2+2a +1.∴f (x )max =⎩⎪⎨⎪⎧ -a 2-2a +1,a ≤-1,2, -1<a <1,-a 2+2a +1, a ≥1.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
金戈出品
学 习 资 料 汇编
2.2.1 一次函数的性质与图象
1.理解一次函数的概念,掌握一次函数的性质.(重点)
2.会用一次函数的图象和性质解题.(难点)
[基础·初探]
教材整理 一次函数的图象与性质
阅读教材P55~P56“练习”以上部分,完成下列问题.
一次函数
定义 函数y=kx+b(k≠0)叫做一次函数
图象
k>0 k
<0
定义域 R
单调性 增函数 减函数
奇偶性 若b=0,奇函数,若b≠0,非奇非偶函数
1.判断(正确的打“√”,错误的打“×”)
(1)函数y=7x是一次函数.( )
(2)函数y=2x+3是单调递增函数.( )
(3)一次函数y=x-1的图象过第一、二、三象限.( )
【答案】 (1)× (2)√ (3)×
2.设函数f(x)=(2a-1)x+b在R上是增函数,则有( )
A.a≥12 B.a≤12
C.a>-12 D.a>12
金戈出品
【解析】 ∵y=f(x)为R上的增函数,∴2a-1>0,∴a>12.
【答案】 D
[小组合作型]
一次函数的概念
(1)已知y=(α+1) xα-1+2是一次函数,则α=______.
(2)已知函数y=3mx+2m+1,试求m为何值时,
①这个函数为正比例函数;
②这个函数为一次函数;
③函数值y随x的增大而减小.
【解析】 (1)由题意得 α+1≠0,α-1=1,解得 α≠-1,α=2,即α=2.
【答案】 2
(2)①若y=3mx+2m+1是正比例函数,则m应满足 m≠0,2m+1=0.
解得m=-12.
∴当m=-12时,这个函数是正比例函数.
②当m≠0时,这个函数为一次函数.
③根据一次函数性质可知,当m<0时,y随x的增大而减小.
对于函数y=kxa+b,当a=1,k≠0时,为一次函数;当a=1,k≠0,b=0时,为正比例函
数.
[再练一题]
1.下列函数:①y=-2x,②y=15-6x,③c=7t-35,④y=1x+2,⑤y=13x,⑥y=x2x,其
中正比例函数是________,一次函数是________.(填序号)
【答案】 ①⑤ ①②③⑤
一次函数的图象
画出函数y=3x+12的图象,利用图象求:
金戈出品
(1)方程3x+12=0的解;
(2)不等式3x+12>0的解集;
(3)当y≤12时,x的取值范围.
【精彩点拨】 求出函数图象与x,y轴的交点坐标,画出函数图象,然后根据函数图象,数
形结合,就可以解决上述问题.
【解】 由函数y=3x+12可知.当x=0时,y=12,当y=0时,x=-4,所以直线y=3
x
+12与x轴、y轴的交点坐标分别为(-4,0),(0,12).
函数图象如图所示:
(1)图象与x轴交点的横坐标是方程3x+12=0的解,即x=-4.
(2)当x>-4时,函数图象位于x轴的上方,所以不等式3x+12>0的解集为{x|x>-4}.
(3)由图象可知,直线与y轴交点的坐标是(0,12),所以y≤12时x的取值范围为{x|x≤0}.
1.一次函数y=kx+b(k≠0)的图象是一条直线,因此k的取值确定了直线的方向,b的取值
确定了直线在y轴上的截距,同时,直线的特征也确定了k,b的取值,总之要达到“数”与“形”
的统一,做到“数中含形,形中蕴数”.
2.(1)作一次函数图象时,常取直线与坐标轴的交点连线.
(2)若图象在x轴的上方,则对应的函数值大于0;反之,则函数值小于0.
[再练一题]
2.本题中解析式不变分别求“图象与坐标轴的两交点的距离”及“与坐标轴围成的三角形的
面积”.
【解】 令x=0,得|OB|=12,令y=0,得|OA|=4.
由勾股定理得|AB|=122+42=410,
由三角形面积公式得S=12×|OA|×|OB|=12×4×12=24.
[探究共研型]
一次函数的性质
已知函数y=x+1,y=2x,y=-x+1,
金戈出品
图221
探究1 上述函数的图象有何特点?
【提示】 图象都为直线.
探究2 观察以上图象,试说明函数的单调性.
【提示】 函数y=x+1,y=2x为增函数,函数y=-x+1为减函数.
已知函数y=(2m-1)x+1-3m,当m为何值时:
(1)这个函数为一次函数;
(2)函数值y随x的增大而减小;
(3)此函数为奇函数;
(4)此函数图象与直线y=x+1的交点在y轴上.
【精彩点拨】 本题主要考查一次函数的概念、奇偶性与单调性,第(1)(2)(3)问易求,对于
第(4)问要重视方程组的作用.
【解】 (1)当2m-1≠0,即m≠12时,此函数为一次函数.
(2)根据一次函数的性质,可知当2m-1<0,即m<12时,函数值y随x的增大而减小.
(3)当2m-1≠0,且1-3m=0,即m=13时,此函数为奇函数.
(4)在y=x+1中,令x=0,y=1,
∴(0,1)是在y=(2m-1)x+1-3m的图象上,
∴m=0,∴当m=0时,两直线的交点在y轴上.
一次函数的值域或一次函数的最大值、最小值,常利用一次函数的单调性来求解.求一次函数
的解析式时,待定系数法是常用的方法.
[再练一题]
3.已知f(x)为一次函数且满足4f(1-x)-2f(x-1)=3x+18,求函数f(x)在[-1,1]上的最
大值,并比较f(2 015)和f(2 016)的大小.
【导学号:60210046】
【解】 设f(x)=kx+b(k≠0).
由已知可得
4[k(1-x)+b]-2[k(x-1)+b]=3x+18.
整理,得-6kx+6k+2b=3x+18.
金戈出品
∴ -6k=3,6k+2b=18,解得 k=-12,b=212.
∴f(x)=-12x+212,易得f(x)在[-1,1]上为减函数(在R上也是减函数).
∴函数f(x)在[-1,1]上的最大值为f(-1)=11且f(2 015)>f(2 016).
1.一次函数y=kx+b(k>0,b<0)的图象不经过( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
【解析】 直线y=kx+b(k>0,b<0)经过点(0,b),在y轴的负半轴上,且y是x的增函
数.
【答案】 B
2.函数y=kx+k2-k过点(0,2)且是减函数,则k的值为( )
A.-2 B.-1
C.-1,2 D.1,-2
【解析】 将点的坐标代入函数关系式,得k2-k=2,即k2-k-2=0,所以k=-1或k=2,
由于一次函数为减函数,即k<0,所以k=-1,故选B.
【答案】 B
3.关于x的一次函数y=(3a-7)x+a-2的图象与y轴的交点在x轴上方,且y随x的增大
而减小,则a的取值范围是________.
【导学号:60210047】
【解析】 由题意得 a-2>0,3a-7<0,
∴ a>2,a<73,∴2<a<73.
【答案】 2,73
4.若一次函数y=(3a-8)x+a-2的图象与两坐标轴都交于正半轴,则a的取值范围是
________.
【解析】 由题意,得 3a-8<0a-2>0,
金戈出品
解之,得2
5.已知y=(m-1)xm2-3m+3+2是一次函数,且为增函数,求m的值.
【解】 ∵函数为一次函数且单调递增,
∴ m2-3m+3=1,m-1>0,
∴ m=1或m=2,m>1.
∴m=2.
敬请批评指正
