吉林省东北师范大学附属中学2015届高考数学第二轮总复习阶段测试卷(第37周)文
吉林省东北师范大学附属中学2015届高三数学(理科)第一轮高考总复习阶段测试卷(第24周)Word版含答案

)
9. 不等式 x 1 x 2 5 的解集为
.
10. 直 线 l 的 参 数 方 程 是 x
y
2
t 2
( 其 中 t 为 参 数 ), 圆 C 的 极 坐 标 方 程 为
2 t 42
2
2 cos(
) ,过直线上的点向圆引切线,则切线长的最小值是
.
4
11. 如图, AB 是⊙ O 的直径, P 是 AB 延长线上的一点,过 P 作⊙ O 的切线,切点为 C ,
时量 120 分钟 总分 150 分
【测试目标:了解外地考卷命题形式】
一、选择题:本大题共 8 小题,每小题 5 分,共 40 分,在每小题给出的四个选项中,只有
一项符合题目要求的 .
1. 如图:给定全集 U 和集合 A,B ,则如图阴影部分表示的集合是(
)
A. A (CU B)
B. (CU A) B
C. CU ( A B) B
D. CU ( A B) A
1
2. 函数 f ( x) ln x 的一个零点所在的区间是(
)
x
AU
A. ( 1,1)
B. (1,2)
C.( 2, e)
1
3. 化简对数式
log 3 1 得到的值为(
log 5 3
15
D. (e,3)
)
AA
AB
A. 1
B. 2
C. - 1
1
D.
则 m=
;
(Ⅱ)令 U (a1, a2, a3 , , an) ,若 V Sn ,则所有 d(U ,V ) 之和为
.
一 选择题:
高三周考 数学 (理科) 答卷
时量 120 分钟 总分 150 分
吉林省东北师范大学附属中学2015届高三数学(文科)第一轮高考总复习阶段测试卷(第27周)(含答案)
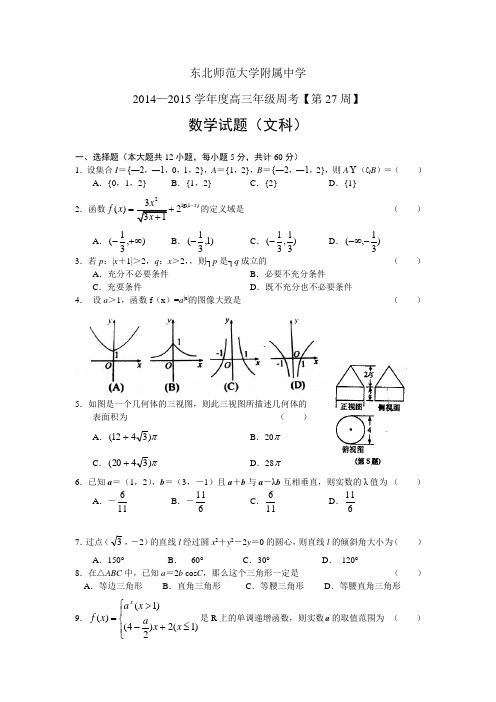
东北师范大学附属中学2014—2015学年度高三年级周考【第27周】数学试题(文科)一、选择题(本大题共12小题,每小题5分,共计60分)1.设集合I ={―2,―1,0,1,2},A ={1,2},B ={―2,―1,2},则A (C I B )=( )A .{0,1,2}B .{1,2}C .{2}D .{1}2.函数2lg(1)()2x f x -=+的定义域是 ( )A .),31(+∞-B .)1,31(-C .)31,31(-D .)31,(--∞3.若p :|x +1|>2,q :x >2,,则┐p 是┐q 成立的 ( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件4. 设a >1,函数f (x )=a |x|的图像大致是 ( )5.如图是一个几何体的三视图,则此三视图所描述几何体的表面积为 ( ) A .π)3412(+ B .20π C .π)3420(+D .28π6.已知a =(1,2),b =(3,-1)且a +b 与a -λb 互相垂直,则实数的λ值为 ( ) A .-116B .-611 C .116 D .6117.过点(3,-2)的直线l 经过圆x 2+y 2-2y =0的圆心,则直线l 的倾斜角大小为( ) A .150° B . 60° C .30° D . 120°8.在△ABC 中,已知a =2b cos C ,那么这个三角形一定是 ( ) A .等边三角形 B .直角三角形 C .等腰三角形 D .等腰直角三角形9.⎪⎩⎪⎨⎧≤+->=)1(2)24()1()(x x ax a x f x 是R 上的单调递增函数,则实数a 的取值范围为 ( )A .(1,+∞)B .[4,8]C .(4,8)D .(1,8)10.2008年3月份开始实施的《个人所得税法》规定:全月总收入不超过2000元的免征个人工资、薪金所得税,超过2000元的部分需征税,设全月总收入金额为x 元,前三级税率如下表:当全月总收入不超过4000元时,计算个人所得税的一个算法框图如上所示,则输出①,输出②分别为 ( ) A .0.05x,0.1x B .0.05x, 0.1x -225C .0.05x -100, 0.1xD .0.05x -100, 0.1x -22511.若不等式组5003x y y a x -+≥⎧⎪≥⎨⎪≤≤⎩表示的平面区域是一个三角形,则a 的取值范围是( )A .5a <B .8a ≥C .5a <或8a ≥D .58a ≤<12.对于任意实数x ,符号[x ]表示x 的整数部分,即[x ]是不超过x 的最大整数,例如[2]=2;[1.2]=2;[2.2-]=3-, 这个函数[x ]叫做“取整函数”,它在数学本身和生产实践中有广泛的应用。
【数学】吉林省东北师范大学附属中学2015届高三(理科)高考总复习阶段测试卷(第36周)

数 学 试 卷(理)第Ⅰ卷一、选择题(本大题共12小题,每小题5分,满分60分.在每小题给出的四个选项中,只有一项是符合题目要求的.)1.等差数列及等比数列中,则当时有( ) A .B .C .D .2. 设点,,直线过点且与线段相交,则的斜率的取值范围是( ) A .或 B . C . D .或3. 若直线和直线关于直线对称,那么直线恒过定点( )A .(2,0)B .(1,-1)C .(1,1)D .(-2,0)4. 设若,则的值为 ( ) A . B. C. D.5. 若函数()3xf x e x =-,x R ∈,则函数的极值点的个数是( )A .0B .1C .2D .36. 已知F 是抛物线2y x =的焦点,,A B 是抛物线上的两点,3AF BF +=,则线段AB 的中点M 到y 轴的距离为( ) A .34B .1C .54D .747. 已知双曲线E 的中心为原点,()3,0F 是E 的焦点,过F 的直线l 与E 相交于,A B 两点,且AB 的中点为()12,15N --,则E 的方程为( )A .22136x y -= B .22145x y -= C .22163x y -= D .22154x y -= 8. 将长方体截去一个四棱锥,得到的几何体如图所示,则该几何体的左视图为( )A.答案AB.答案BC.答案CD.答案D9. 设,a b 为两条直线,,αβ为两个平面,则下列结论成立的是( ){}n a {}n b ,0,02211>=>=b a b a 3≥n n n b a >n n b a =n n b a ≥n n b a ≤(2,3)A -(3,2)B --l (1,1)P AB l k 34k ≥4k ≤-344k -≤≤344k -≤≤4k ≥34k ≤-x k y l )1(2:1-=-2l 1+=x y 2l ,cos sin )cos (sin a a a a f =+21)(=t f t 2±222±22A .若,,a b αβ⊂⊂且//a b ,则//αβB .若,,a b αβ⊂⊂且a b ⊥,则αβ⊥C .若//a α,,b α⊂则//a bD .若,,a b αα⊥⊥则//a b 10.设n S 是等比数列{}n a 的前n 项和,3613S S =,则612SS 等于( ) A.13 B.15 C.18 D.19 11. 在锐角中,若2C B =,则cb的范围( ) A .B .)C .()0,2D .)12. 设()fx 是定义在x R ∈上以2为周期的偶函数,已知(0,1)x ∈,()()12log 1f x x =-,则函数()f x 在(1,2) 上( )A .是增函数且()0f x <B .是增函数且()0f x >C .是减函数且()0f x <D .是减函数且()0f x >第Ⅱ卷本卷包括必考题和选考题两部分.第13题~第21题为必考题,每个试题考生都必须做答.第22~第24题为选考题,考生根据要求做答.二、填空题(本大题共有4小题,每小题5分,共20分,将答案填写在答题卡相应的位置上)13. 将函数的图象向左平移个单位后,得函数的图象,则等于 .14. 设命题:p 22310x x -+≤,命题:q ()221(1)0x a x a a -+++≤.若q 是p 的必要不充分条件,则实数a 的取值范围是________.15.已知各顶点都在同一个球面上的正四棱锥高为3,体积为6,则这个球的表面积是_____. 16.已知直线0x y m ++=与圆222x y +=交于不同的两点A 、B ,O 是坐标原点,OA OB AB +≥,那么实数m 的取值范围是________.三、解答题(要求写出必要的计算步骤和思维过程。
吉林省东北师范大学附属中学2015届高三数学(文科)第一轮高考总复习阶段测试卷(第25周)Word版含答案

高三文科数学阶段质量检测试题[25周]第Ⅰ卷一、选择题(本大题共12小题,每小题5分,满分60分.在每小题给出的四个选项中,只有一项是符合题目要求的.) 1.已知集合}111|{≥-+=x x x M ,集合}032|{>+=x x N ,则=⋂N M C R )(( ) A .(-1,23) B .(-1,23] C .[-1,23) D .[-1,23] 2.已知α是第二象限角,且sin(53)-=+απ,则tan2α的值为( ) A .54B .723-C .724-D .924-3.下列函数中,在其定义域是减函数的是( )A. 12)(2++-=x x x f B. xx f 1)(=C. ||)41()(x x f = D. )2ln()(x x f -=4. 下列函数中,最小正周期为π,且图象关于直线x=3π对称的函数是( ) A .y=2sin(2x+3π) B .y=2sin(2x-6π) C .y=2sin(32π+x ) D .y=2sin(2x-3π)5. 函数xx x f 2)1ln()(-+=的零点所在的大致区间是( ) A .(3,4) B .(2,e ) C .(1,2) D .(0,1)6.已知二次函数4)(2+-=ax x x f ,若)1(+x f 是偶函数,则实数的值为( ) A. -1 B. 1 C. -2 D. 27. 2||,0)(sin(πϕωϕω<>+=x y )的图象的一部分图形如图所示,则函数的解析式为( )A .y=sin(x+3π) B .y=sin(x-3π) C .y=sin(2x+3π)D .y=sin(2x-3π) 8. 设a 为实数,函数f (x )=x 3+ax 2+(a -2)x 的导数是)('x f ,且)('x f 是偶函数,则曲线y =f (x )在原点处的切线方程为( )A .y =-2xB .y =3xC .y =-3xD .y =4x 9. 将函数y=sin(2x+4π)的图象向左平移4π个单位,再向上平移2个单位,则所得图象的函数解析式是( ) A .y=2cos 2(x+8π) B .y=2sin 2(x+8π) C .y=2-sin(2x-4π) D .y=cos2x 10.已知函数⎩⎨⎧≤<+-<≤---=)10(1)01(1)(x x x x x f ,则1)()(->--x f x f 的解集为( )A .(-∞,-1)∪(1,+∞) B. [-1,-21)∪(0,1] C .(-∞,0)∪(1,+∞) D. [-1,-21]∪(0,1) 11.对于任意的实数a 、b ,记max{a,b}=⎩⎨⎧<≥)()(b a b b a a .若F(x)=max{f(x),g(x)}(x ∈R),其中函数y=f(x)(x ∈R)是奇函数,且在x=1处取得极小值-2,函数y=g(x) (x ∈R)是正比例函数,其图象与x ≥0时的函数y=f(x)的图象如图所示,则下列关于函数y=F(x)的说法中,正确的是( ) A .y=F(x)为奇函数 B .y=F(x)有极大值F(-1)C .y=F(x)的最小值为-2,最大值为2D .y=F(x)在(-3,0)上为增函数12.设函数⎪⎩⎪⎨⎧<-≥-=)2(1)21()2()2()(x x x a x f x 是R 上的单调递减函数,则实数a 的取值范围为( )A .(-∞,2)B .(-∞,813] C .(0,2) D .[813,2) 二.填空题:(本大题共4小题,每小题5分。
吉林省东北师范大学附属中学2015届高三数学(文科)第一轮高考总复习阶段测试卷(第25周) Word版含答案

高三文科数学阶段质量检测试题[25周]第Ⅰ卷一、选择题(本大题共12小题,每小题5分,满分60分.在每小题给出的四个选项中,只有一项是符合题目要求的.) 1.已知集合}111|{≥-+=x x x M ,集合}032|{>+=x x N ,则=⋂N M C R )(( ) A .(-1,23) B .(-1,23] C .[-1,23) D .[-1,23]2.已知α是第二象限角,且sin(53)-=+απ,则tan2α的值为( )A .54 B .723- C .724- D .924- 3.下列函数中,在其定义域是减函数的是( ) A. 12)(2++-=x x x f B. x x f 1)(=C. ||)41()(x x f = D. )2ln()(x x f -= 4. 下列函数中,最小正周期为π,且图象关于直线x=3π对称的函数是( ) A .y=2sin(2x+3π) B .y=2sin(2x-6π) C .y=2sin(32π+x ) D .y=2sin(2x-3π)5. 函数xx x f 2)1ln()(-+=的零点所在的大致区间是( ) A .(3,4) B .(2,e ) C .(1,2) D .(0,1)6.已知二次函数4)(2+-=ax x x f ,若)1(+x f 是偶函数,则实数的值为( ) A. -1 B. 1 C. -2 D. 27. 2||,0)(sin(πϕωϕω<>+=x y )的图象的一部分图形如图所示,则函数的解析式为( )A .y=sin(x+3π) B .y=sin(x-3π) C .y=sin(2x+3π)D .y=sin(2x-3π) 8. 设a 为实数,函数f (x )=x 3+ax 2+(a -2)x 的导数是)('x f ,且)('x f 是偶函数,则曲线y =f (x )在原点处的切线方程为( )A .y =-2xB .y =3xC .y =-3xD .y =4x 9. 将函数y=sin(2x+4π)的图象向左平移4π个单位,再向上平移2个单位,则所得图象的函数解析式是( ) A .y=2cos 2(x+8π) B .y=2sin 2(x+8π) C .y=2-sin(2x-4π) D .y=cos2x 10.已知函数⎩⎨⎧≤<+-<≤---=)10(1)01(1)(x x x x x f ,则1)()(->--x f x f 的解集为( )A .(-∞,-1)∪(1,+∞) B. [-1,-21)∪(0,1] C .(-∞,0)∪(1,+∞) D. [-1,-21]∪(0,1) 11.对于任意的实数a 、b ,记max{a,b}=⎩⎨⎧<≥)()(b a b b a a .若F(x)=max{f(x),g(x)}(x ∈R),其中函数y=f(x)(x ∈R)是奇函数,且在x=1处取得极小值-2,函数y=g(x) (x ∈R)是正比例函数,其图象与x ≥0时的函数y=f(x)的图象如图所示,则下列关于函数y=F(x)的说法中,正确的是( ) A .y=F(x)为奇函数 B .y=F(x)有极大值F(-1)C .y=F(x)的最小值为-2,最大值为2D .y=F(x)在(-3,0)上为增函数12.设函数⎪⎩⎪⎨⎧<-≥-=)2(1)21()2()2()(x x x a x f x 是R 上的单调递减函数,则实数a 的取值范围为( )A .(-∞,2)B .(-∞,813] C .(0,2) D .[813,2) 二.填空题:(本大题共4小题,每小题5分。
【数学】吉林省东北师范大学附属中学2015届高三(理科)高考总复习阶段测试卷(第33周)

数学理科周测试卷一、选择题(每小题5分,共40分,每小题给出的四个选项中,只有一项符合题目要求) 1.函数的导数为 ( )A .B .C .D .2.已知等差数列{}n a 的前n 项和为55,5,15n S a S ==,则数列11n n a a +⎧⎫⎨⎬⎩⎭的前100项和为 ( )A .100101 B .99101C .99100D .101100 3.在ABC ∆中,已知:p 三内角A B C 、、成等差数列;:q 60B = .则p 是q 的() A .充分必要条件B .必要不充分条件C . 充分不必要条件D .既不充分也不必要条件4.已知log (1)()(3) 1 (1)a x x f x a x x ≥⎧=⎨--<⎩是定义在R 上的增函数,求a 的取值范围是()A.[2,3)B.(1,3)C.(1,)+∞D.(1,2]5. 连续抛掷两枚骰子得到的点数分别是m 、n ,则向量a =(m ,n )与向量b =(1,1)共线的概率是( ) A .B .C .D . 6. 设P 为曲线C :y=+2x+3上的点,且曲线C 在点P 处切线倾斜角的取值范围为,则点P 横坐标的取值范围为 ( ) A . B .[-1,0] C .[0,1]D .7.实数对(x ,y )满足不等式组20,250,20,x y x y y --≤⎛+-≥ -≤⎝若目标函数3,1z kx y x y =-==在时取最cosx x y 2=xsinx 2cosx x y'2-=sinx x xcosx 2y'2+=sinx x xcosx 2y'2-=sinx x xcosx y'2-=5121316122x [0,]4π1[1,]2--1[,1]2大值,则k 的取值范围是( ) A .1(,)[1,)2-∞-+∞ B .1[,1]2-C .1[,)2-+∞D .(,1]-∞-8..函数)1x x 5(2log y ---=的定义域为()A.{x |-4<x <1}B.{x |x <-1}C.{x |x <1}D.{x |-1<x <1} 二、填空题:(本大题共6小题,每小题5分,满分30分.)9.数列{}n a 满足1(1)21n n n a a n ++-=-,则{}n a 的前60项和为_______.10.一支运动队有男运动员56人,女运动员42人,用分层抽样的方法从全体运动员中抽取一个样本,已知某男运动员被抽中的概率为27,则抽取的女运动员的人数为. 11.定积分⎰+21dx )x1x (的值等于_________________。
吉林省东北师范大学附属中学2015届高三数学(文科)高考总复习阶段测试卷(第32周) Word版含答案
东北师大高三数学周考测试卷【32周】本试卷分为第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.共150分,考试时间120分钟.注意事项:1.各题的答案或解答过程均写在答题纸内的指定处,写在试卷上的无效.2.答题前,考生务必将自己的“姓名”,“班级”和“考号”写在答题纸和答题卡上. 3.考试结束,只交答题纸和答题卡.第Ⅰ卷(选择题 满分60分)一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的). 1.已知I为实数集,2{|20},{|M x x x N y y =-<==,则M N = ( )A .{|01}x x <<B .{|02}x x <<C .{|12}x x ≤<D .∅2.直线04121=+++y m x l )(:与0232=-+y mx l :平行,则m的值为 ( )A .2B .-3C .2或-3D .-2或-33.已知条件3=k p :,条件q :直线2+=kx y 与圆122=+y x 相切,则q p 是的( ) A .充分不必要条件 B .必要不充分条件C .充分必要条件D .既不充分又不必要条件4.在等差数列{}n a 中,若12021062=++a a a ,则93a a + 等于 ( )A .30B .40C .60D .805.已知二次函数)(x f 的图象如图1所示,则其导函数)('x f 的图象大致形状是 ( )6.若ax x x f 2)(2+-=与xax g =)(在区间[]2,1上都是减函数,则a 的取值范围是 ( ) A .)1,0()0,1( - B .)1,0()0,1( - C .(0,1)D . (]10,图1 A B C D7.若直线0301221=+=++y x l y x l :,:,则21l l ,的夹角为 ( )A .030B .)(71arctan - C .71arctanD .7arctan 8.在正三棱锥ABC S -中,E 为SA 的中点,F 为ABC ∆的中心,2==BC SA ,则异面直线BC EF 与与所成的角为( )A . 30B . 45C . 60D . 909.函数b ax x f +=)(和函数(1)2y f x =-+的图象重合.则下面结论正确的是 ( ) A .R b a ∈=,1 B .R b a ∈=,2 C .1==b aD .b a ,取值不确定10.从6双不同颜色的手套中任取4只,其中恰好有两只颜色相同的取法有 ( )A .60B .120C .180D .24011.设圆222)5()3(r y x =+++上有且只有两点到直线234=-y x 的距离等于1,则圆的半径r 的取值范围为( )A .561<<r B .54>rC .5654<<rD .1>r12.若数列{}n a 满足),(111为常数d N n d a a nn ∙+∈=-,则称数列{}n a 为“调和数列”.已知数列⎭⎬⎫⎩⎨⎧n x 1为“调和数列”,且2002021=+++x x x ,则183x x ⋅的最大值为( ) A .50 B .100C .150D .200第Ⅱ卷 (非选择题 满分90分)二、填空题:本大题共4小题,每小题5分,共20分.把答案填写在答题纸相应位置上. 13.圆心在第一象限,半径为1且与两坐标轴都相切的圆的方程为 . 14.若6)1(ax -的展开式中的3x 项的系数为20,则实数a =15.已知N M 、是⎪⎩⎪⎨⎧≥≥≥+-≤+1,1016y x y x y x的取值范围是A1A 1________. 16.若函数x x x f -=331)(在)10,(2a a -上有最小值,则实数a 的取值范围为 . 三、解答题:本大题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤. 17.(本题满分10分)甲乙两个儿童各用一个质地均匀的骰子进行如下游戏,每人各掷一次,规定两个骰子的点数之差的绝对值为1或2时,甲赢。
长春市东北师范大学附属中学届高三高考总复习阶段测试卷数学试题及答案1(理)
吉林省长春市东北师范大学附属中学2015届高三高考总复习阶段测试卷1(理)参考公式:样本数据n x x x ,,21的标准差 锥体体积公式s =13V Sh =其中x 为样本平均数 其中S 为底面面积,h 为高 柱体体积公式 球的表面积,体积公式V Sh = 24S R π= 343V R π=其中S 为底面面积,h 为高 其中R 为球的半径第I 卷一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的.1. 设集合}4,3,2,1{=U ,}05|{2=+-=p x x x M ,若}3,2{=M C U ,则实数p 的值为A. 6-B. 4-C. 4D. 6 2.若复数iia 213++(i R a ,∈为虚数单位)是纯虚数,则实数a 的值为 A. 6- B. 2- C. 4 D. 63.已知}{n a 为等差数列,若π=++951a a a ,则)cos(82a a +的值为A. 21-B. 23- C. 21 D. 234.已知函数,0,)21(0,)(21⎪⎩⎪⎨⎧≤>=x x x x f x则=-)]4([f fA. 4-B. 41- C. 4 D. 6 5.下列命题错误的是A. 命题“若022=+y x ,则0==y x ”的逆否命题为“若y x ,中至少有一个不为0,理科数学试卷 第1页(共6页)则022≠+y x ”;B. 若命题01,:0200≤+-∈∃x x R x p ,则01,:2>+-∈∀⌝x x R x p ;C. ABC ∆中,B A sin sin >是B A >的充要条件;D. 若向量b a ,满足0<⋅b a ,则a 与b 的夹角为钝角.6. 执行如图的程序框图,如果输入30,72==n m ,则输出的n 是A . 12B . 6 C. 3 D . 07. 从5,4,3,2,1中不放回地依次取2个数,事件=A “第一次取到的是奇数”,=B “第二次取到的是奇数”,则=)|(A B P A.51 B. 103 C. 52 D. 218. 函数)sin()(ϕω+=x x f (其中2||πϕ<)的图象如图所示,为了得到x y ωsin =的图象,只需把)(x f y =的图象上所有点A. 向右平移6π个单位长度B. 向右平移12π个单位长度 C. 向左平移6π个单位长度D. 向左平移12π个单位长度 9. 曲线c bx x y ++=2在点))(,(00x f x P 处切线的倾斜角的取值范围为]4,0[π,则点P 到该曲线对称轴距离的取值范围为 A. ]1,0[ B. ]21,0[ C. ]2||,0[b D. ]2|1|,0[-b10. 若圆2221:240,()C x y ax a a R +++-=∈与圆2222:210,()C x y by b b R +--+=∈外切,则a b +的最大值为A. 23-B. 3-C. 3D. 2311.若不重合的四点C B A P ,,,,满足0PA PB PC ++=,AB AC mAP +=,则实数m 的值为A. 2B. 3C. 4D. 512. 函数)(x f y =的最小正周期为2,且)()(x f x f =-.当]1,0[∈x 时,1)(+-=x x f ,那么在区间]4,3[-上,函数)(x f y =的图像与函数||)21(x y =的图像的交点个数是A. 8B. 7C. 6D. 5第Ⅱ卷本卷包括必考题和选考题两部分.第13题~第21题为必考题,每个试题考生都必须做答.第22题~第24题为选考题,考生根据要求做答. 二、填空题:本大题共4小题,每小题5分.13.已知双曲线)0,0(12222>>=-b a by a x 与抛物线x y 82=有一个公共的焦点F ,且两曲线的一个交点为P ,若5||=PF ,则双曲线方程为 . 14.设等比数列}{n a 的前n 项之和为n S ,已知20111=a ,且)(0221∙++∈=++N n a a a n n n ,则=2012S .15.已知不等式组⎪⎩⎪⎨⎧≤-≥≤a x x y x y 表示的平面区域S 的面积为4,点S y x P ∈),(,则y x z +=2 的最大值为 .16. 一个空间几何体的三视图如图所示,且这个空间几何体的所有顶点都在同一个球面上,则这个球的表 面积是 .三、解答题:解答应写出文字说明.证明过程或演算步骤 17.(本小题满分12分)如图,AB 是底部B 不可到达的一个塔型建筑物,A 为塔的最高点.现需在对岸测出塔高AB ,甲、乙两同学各提出了一种测量方法,甲同学的方法是:选与塔底B 在同一水平面内的一条基线CD ,使B D C ,,三点不在同一条直线上,测出DCB ∠及CDB ∠的大小(分别用βα,表示测得的数据)以及D C ,间的距离(用s 表示测得的数据),另外需在点C 测得塔顶A 的仰角(用θ表示测量的数据),就可以求得塔高AB .乙同学的方法是:选一条ED CBA水平基线EF ,使B F E ,,三点在同一条直线上.在F E ,处分别测得塔顶A 的仰角(分别用βα,表示测得的数据)以及F E ,间的距离(用s 表示测得的数据),就可以求得塔高AB .请从甲或乙的想法中选出一种测量方法,写出你的选择并按如下要求完成测量计算:①画出测量示意图;②用所叙述的相应字母表示测量数据,画图时B D C ,,按顺时针方向标注,F E ,按从左到右的方向标注;③求塔高AB .18.(本小题满分12分)如图,四边形DCBE 为直角梯形,90=∠DCB ,CB DE //,2,1==BC DE ,又1=AC , 120=∠ACB , AB CD ⊥,直线AE 与直线CD 所成角为 60.(Ⅰ)求证:平面⊥ACD 平面ABC ; (Ⅱ)求BE 与平面ACE 所成角的正弦值.19.(本小题满分12分) 现有B A ,两个项目,投资A 项目100万元,一年后获得的利润为随机变量1X (万元),根据市场分析,1X 的分布列为:投资B 项目100万元,一年后获得的利润2X (万元)与B 项目产品价格的调整(价格上调或下调)有关, 已知B 项目产品价格在一年内进行2次独立的调整,且在每次调整中价格下调的概率都是)10(<≤p p .FEDCBA20.(本小题满分12分)如图椭圆134:22=+y x C 的右顶点是A ,上下两个顶点分别为D B ,,四边形OANB 是矩形(O 为原点),点M E ,分别为线段AN OA ,的中点.(Ⅰ)证明:直线DE 与直线BM 的交点在椭圆C 上;(Ⅱ)若过点E 的直线交椭圆于S R ,两点,K为R 关于x 轴的对称点(E K R ,,不共线), 问:直线KS 是否经过x 求这个定点的坐标,如果不是,说明理由.21.(本小题满分12分)设函数a aex x f x-++=-)1ln()(,R a ∈.(Ⅰ)当1=a 时,证明)(x f 在),0(+∞是增函数; (Ⅱ)若),0[+∞∈x ,0)(≥x f ,求a 的取值范围.请考生在第22、23、24三题中任选一题做答,如果多做,则按所做的第一题记分.答时用2B 铅笔在答题卡上把所选题目的题号涂黑. 22.(本小题满分10分) 选修4—1;几何证明选讲.如图,A ,B ,C ,D 四点在同一圆上,BC 与AD 的延长线交于点E ,点F 在 BA 的延长线上.(Ⅰ)若21,31==EA ED EB EC ,求AB DC 的值;(Ⅱ)若FB FA EF ⋅=2,证明:CD EF //.23.(本小题满分10分)选修4—4;坐标系与参数方程.在平面直角坐标系xoy 中,曲线1C 的参数方程为⎩⎨⎧==ϕϕsin cos b y a x (0>>b a ,ϕ为参数),在以O 为极点,x 轴的正半轴为极轴的极坐标系中,曲线2C 是圆心在极轴上,且经过极点的圆.已知曲线1C 上的点)23,1(M 对应的参数3πϕ=,射线3πθ=与曲线2C 交于点)3,1(πD .(I )求曲线1C ,2C 的方程; (II )若点),(1θρA ,)2,(2πθρ+B 在曲线1C 上,求222111ρρ+的值.24.(本小题满分10分)选修4—5;不等式选讲.设不等式1|12|<-x 的解集是M ,M b a ∈,. (I )试比较1+ab 与b a +的大小;(II )设max 表示数集A 的最大数.⎭⎬⎫⎪⎩⎪⎨⎧+=b ab ba ah 2,,2max 22,求证:2≥h .答案参考:一、1. C 2.A 3.A 4.C 5.D 6.B 7.D 8.A 9.B 10.D 11.B 12.C 二、13. x 2-y 2/3=1; 14 .0; 15. 6; 16. 16π 三、选甲:示意图1图1 ----------4分 在BCD △中,πCBD αβ∠=--.由正弦定理得sin sin BC CDBDC CBD=∠∠.所以sin sin sin sin()CD BDC s BC CBD βαβ∠==∠+·.在ABC Rt ∆中,)sin(sin tan tan βαβθ+⋅=∠=s ACB BC AB .---------12分选乙:图2图2----------4分在AEF ∆中,αβ-=∠EAF ,由正弦定理得ααβsin )sin(AFEF =-,所以)sin(sin )sin(sin αβααβα-⋅=-⋅=s EF AF .在ABF Rt ∆中,)sin(sin sin sin αββαβ-⋅⋅=⋅=s AF AB .---------12分由直线AE 与直线CD 所成角为 60,得60cos ||||CD AE CD AE =⋅,即3222+=a aa ,解得1=a . ∴)1,1,0(=,)0,21,23(-=CA ,)1,1,0(-=, 设平面ACE 的一个法向量为),,(z y x =n ,则⎪⎩⎪⎨⎧=⋅=⋅0n n ,即⎪⎩⎪⎨⎧=+=-002123z y y x ,取,3=x 则3,3-==z y ,得)3,3,3(n -=,设BE 与平面ACE 所成角为θ,则742sin ==θ,于是BE 与平面ACE 所成角的正弦值为742.---------12分19.(本小题满分12分)【解析】(Ⅰ)1X 的概率分布为则8.1137.1128.11612)(1=⨯+⨯+⨯=X E . 01.031)8.117.11(21)8.118.11(61)8.1112()(2221=⨯-+⨯-+⨯-=X D . ---------4分(Ⅱ)解法1: 由题设得),2(~p B X ,则X 的概率分布为故2X 的概率分布为分解法2: 设i A 表示事件”第i 次调整,价格下调”()2,1=i ,则)0(=X P = 212()()(1)P A P A p =-;)1(=X P =1212()()()()2(1)P A P A P A P A p p +=-; )2(=X P =212()()P A P A p =故2X 的概率分布为(Ⅲ)当3.0=p 时. (12E ,由于01.0)(1=X D . 555.9)(2=X D .所以)()(12X D X D >,当投资两个项目的利润均值相同的情况下,投资B 项目的风险高于A 项目.从获得稳定收益考虑, 当3.0=p 时应投资A 项目. ---------12分20.(本小题满分12分)解:(1)由题意,得)23,2(),0,1(),3,0(),3,0(),0,2(M E D B A -,所以直线DE 的方程33-=x y ,直线BM 的方程为343+-=x y ,------2分 由⎪⎩⎪⎨⎧+-=-=34333x y x y ,得⎪⎪⎩⎪⎪⎨⎧==53358y x ,所以直线DE 与直线BM 的交点坐标为)533,58(,---------------4分因为13)533(4)58(22=+,所以点)533,58(在椭圆134:22=+y x C 上.---------6分 (2)设RS 的方程为)1(-=x k y ,代入134:22=+y x C , 得01248)43(2222=-+-+k x k x k , 设),(),,(2211y x S y x R ,则),(11y x K -,2221222143124,438kk x x k k x x +-=+=+, 直线SK 的方程为)(212122x x x x y y y y --+=-,令,0=y 得121221y y x y x y x ++=,将)1(11-=x k y ,)1(22-=x k y 代入上式得 (9设42)(2212121=-++-=x x x x x x x ,所以直线SK 经过x 轴上的点)0,4(.---------12分21.(本小题满分12分)解:(1))1()1(11)('x e x a e e a x x f x x x ++-=-+=, 当1=a 时, )1()1()('x e x e x f xx ++-=, ---------2分 令x e x g x --=1)(,则1)('-=xe x g ,当),0(+∞∈x 时,01)('>-=xe x g ,所以)(x g 在),0(+∞为增函数, 因此),0(+∞∈x 时,0)0()(=>g x g ,所以当),0(+∞∈x 时,0)('>x f ,则)(x f 在),0(+∞是增函数. ---------6分(2)由)1()1()('x e x a e x f x x ++-=, 由(1)知,,1x e x +≥当且仅当0=x 等号成立. 故)1()1)(1()1()1(1)('x e x a x e x a x x f x x ++-=++-+≥, 从而当01≥-a ,即1≤a 时, 对),0[+∞∈x ,0)('≥x f ,于是对),0[+∞∈∀x 0)0()(=≥f x f .由),0(1≠+>x x e x 得)0(1≠->-x x ex ,从而当1>a 时, )1())(()1(2)1()(22222'x e a a a e a a a e x e a ae e x e a ae a e x f x x x x x x x x x +----+-=++-=+-+-<- 故当))ln(,0(2a a a x -+∈时,0)('<x f , 于是当))ln(,0(2a a a x -+∈时,0)0()(=<f x f ,综上,a 的取值范围是]1,(-∞.---------12分请考生在第(22)、(23)、(24)三题中任选一题做答,如果多做,则按所做的第一题记分.答时用2B 铅笔在答题卡上把所选题目的题号涂黑.22.(本小题满分10分) 选修4—1;几何证明选讲.FE D CBA证明:(1) D C B A ,,,四点共圆,∴EBF EDC ∠=∠,又 AEB CED ∠=∠,∴CED ∆∽AEB ∆,ABDC EB ED EA EC ==∴,21,31==EA ED EB EC , ∴66=AB DC . (2) FB FA EF ⋅=2,∴FE FB FA EF =, 又 BFE EFA ∠=∠,∴FAE ∆∽FEB ∆,∴EBF FEA ∠=∠,又 D C B A ,,,四点共圆,∴EBF EDC ∠=∠,∴EDC FEA ∠=∠,∴CD EF //.23.(本小题满分10分)选修4—4;坐标系与参数方程.解:(I )将)23,1(M 及对应的参数3πϕ=,代入⎩⎨⎧==ϕϕsin cos b y a x ,得⎪⎪⎩⎪⎪⎨⎧==3sin 233cos 1ππb a , 即⎩⎨⎧==12b a , 所以曲线1C 的方程为⎩⎨⎧==ϕϕsin cos 2y x (ϕ为参数),或1422=+y x . 设圆2C 的半径为R ,由题意,圆2C 的方程为θρcos 2R =,(或222)(R y R x =+-). 将点)3,1(πD 代入θρcos 2R =, 得3cos 21πR =,即1=R .(或由)3,1(πD ,得)23,21(D ,代入222)(R y R x =+-,得1=R ), 所以曲线2C 的方程为θρcos 2=,或1)1(22=+-y x .(II )因为点),(1θρA ,)2,(2πθρ+B 在在曲线1C 上,所以1sin 4cos 221221=+θρθρ,1cos 4sin 222222=+θρθρ, 所以45)cos 4sin ()sin 4cos (1122222221=+++=+θθθθρρ.。
吉林省东北师范大学附属中学2015届高三数学(理科)第一轮高考总复习阶段测试卷(第31周)
高三数学理科周测卷[第31周] 第Ⅰ卷(选择题 共60分)一、选择题(本题共有12小题,每小题5分, 共60分,在每小题给出的四个选项中,只有一项是符合题目要求的.)1.下列四个命题中,全称命题是( )A .有些实数是无理数B .至少有一个整数不能被3整除C .任意一个偶函数的图象都关于y 轴对称D .存在一个三角形不是直角三角形 2.函数41lg)(+-=x x x f 的定义域为( )A .{}14<<-x x B .{}41>-<x x x 或 C .{}1<x x D .{}14>-<x x x 或3. 设全集U 是实数集R ,{}2|4M x x =>与{}|31N x x x =≥<或都是U 的子集(如下图所示),则阴影部分所表示的集合为( )A .{}|21x x -≤< B. {}|22x x -≤≤C .{}|12x x <≤D .{}|2x x <4.已知函数)31(12)(≤≤+=x x x f ,则 ( ) A .)1(-x f =)20(22≤≤+x x B .)1(-x f =)42(12≤≤+-x x C .)1(-x f =)20(22≤≤-x x D .)1(-x f =)42(12≤≤-x x5.设12log 3a =,0.213b ⎛⎫= ⎪⎝⎭,132c =,则 ( )A .b c a <<B .a b c <<C .c a b <<D .b a c <<6.若函数)(x f 的唯一一个零点同时在区间(0,16),(0,8),(0,4),(0,2)内,则下列结论中正确的是( )A .)(x f 在区间(0,1)内一定有零点B .)(x f 在区间[)16,2内没有零点C .)(x f 在区间(0,1)或(1,2)内一定有零点D .)(x f 在区间(1,16)内没有零点7.设n S 为数列{}n a 的前n 项和,249n a n =-,则n S 取最小值时,n 的值为 ( ) A .12 B .13 C .24 D .258.“10≤<a ”是“关于x 的方程0122=++x ax 至少有一个负根”的 ( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件9.已知()f x 是R 上的偶函数,对任意∈x R , 都有(6)()(3)f x f x f +=+,且(1)2f =,则(2009)f 的值为( )A .0B .2-C .2D .2009 10.设βα、是方程0622=++-k kx x 的实根,则22)1()1(-+-βα的最小值是( )A .494-B . 8C .18D .14 11.已知函数12)(2++=x x x f ,若存在实数t ,当[]m x ,1∈时,x t x f ≤+)(恒成立,则实数m 的最大值是( )A .6B .5C .4D .312.函数()y f x =的图象是圆心在原点的单位圆的两段弧(如图),则不等式()()f x f x x<-+的解集为 ( )A .⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧≤<<<-15520552x x x 或B .⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧≤<-<<-155551x x x 或C .⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧<<-<<-550551x x x 或D .⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧≠<<-0552552x x x 且第Ⅱ卷(非选择题 共90分)二、填空题(本题共4小题, 每小题5分, 共20分)13.对于实数a (a >0且a ≠1), 函数f (x ) = a x -2-3的图象过定点 . 14.已知数列{}n a 满足nnn a a a a -+==+122,211(∈n N *),则数列{}n a 的第4项是 . 15.若函数)log 2(log 221x y -=的值域是)0,(-∞,则它的定义域是 .16.关于函数xx x f 1lg )(2+=(0≠x ,∈x R ), 有下列命题:①)(x f 的图象关于y 轴对称;②)(x f 的最小值是2lg ;③)(x f 在)0,(-∞上是减函数,在),0(∞+上是增函数; ④)(x f 没有最大值.其中正确命题的序号是 .三、解答题(本题共6小题, 共70分, 解答应写出文字说明、证明过程或演算步骤) 17.(本题满分10分) 若函数()2af x x x=-在定义域(]1,0上是减函数,求实数a 的取值范围. 18.(本题满分12分) 已知函数()2x f x =,1()22x g x =+. (1)求函数()g x 的值域;(2)求满足方程()()0f x g x -=的x 的值.19.(本题满分12分) 设数列{}n a 的前n 项和为n S ,满足22n n n S a =-(∈n N *),令n nn a b 2=. (1)求证:数列{}n b 为等差数列; (2)求数列{}n a 的通项公式.20.(本题满分12分) 某渔业个体户今年年初用96万元购进一艘渔船用于捕捞,规定这艘渔船的使用年限至多为15年. 第一年各种费用之和为10万元,从第二年开始包括维修费用在内,每年所需费用之和都比上一年增加3万元. 该船每年捕捞的总收入为45万元.(1)该渔业个体户从今年起,第几年开始盈利(即总收入大于成本及所有费用的和)? (2)在年平均利润达到最大时,该渔业个体户决定淘汰这艘渔船,并将船以10万元卖出,问:此时该渔业个体户获得的利润为多少万元? (注:上述问题中所得的年限均取整数)21.(本题满分12分) 已知函数)(x f 的定义域为),0(+∞,对于任意正数a 、b ,都有p b f a f b a f -+=⋅)()()(,其中p 是常数,且0>p .1)2(-=p f ,当1>x 时,总有p x f <)(.(1)求)21()1(f f 及(写成关于p 的表达式);(2)判断),0()(+∞在x f 上的单调性,并加以证明;(3)解关于x 的不等式 1)45(2+>+-p x x f .22.(本题满分12分) 已知函数)(1)(a x xa ax x f ≠--+=.(1)证明:对定义域内的所有x ,都有02)()2(=++-x f x a f .(2)当f (x )的定义域为[a +21, a +1]时,求证:f (x )的值域为[]2,3--. (3)设函数g(x ) = x 2+| (x -a ) f (x ) | , 若2321≤≤a ,求g(x )的最小值.理科数学参考答案一、选择题(本题共有12小题,每小题5分, 共60分)1.C 2.D 3.A 4.D 5.B 6.B 7.C 8.A 9.C 10.B 11.C 12.A 二、填空题(本题共4小题, 每小题5分, 共20分)13.)2,2(- 14.6 15.( 0, 2 ) 16.① ② ④三、解答题(本题共6小题, 共70分, 解答应写出文字说明、证明过程或演算步骤) 17.解:(法一)任取12,(0,1]x x ∈且12x x <,由题意知12()()f x f x >, 所以121222a a x x x x ->-,即12212()0a ax x x x -+->,…………………… 4分 所以1212()(2)0a x x x x -+>,只需 1220ax x +<,即122a x x <-. 因为12,(0,1]x x ∈,所以12(0,1)x x ∈,122(2,0)x x -∈-,故2a ≤-.……………………10分 (法二)因为函数()2af x x x=-在定义域(]1,0上是减函数, 所以'220ay x=+≤在(0,1]上恒成立,所以22a x ≤-. 设2()2g x x =-,因为()g x 在(0,1]上的最小值为2-,所以2a ≤-.……………………10分 18.解:(1)11()2()222xxg x =+=+, 因为0x ≥,所以10()12x<≤,即2()3g x <≤,故()g x 的值域是(2,3].…………………5分(2)由()()0f x g x -=得12202xx --=, 当0≤x 时,显然不满足方程,即只有0x >满足12202xx --=,整理得2(2)2210x x -⋅-=,2(21)2x -=,故21x=10分因为20x>,所以21x=2log (1x =. ……………………12分 19.解:(1)因为22n n n S a =-(∈n N *),则*2,n n N ≥∈时,11122n n n S a ---=-,此时,1n n n a S S -=-=11112222222n n n n n n n a a a a ------+=--, 即1122n n n a a --=+. ………………………………………… 4分 由1122a a =-得12a =. 由nn n a b 2=得1112a b ==.…………………6分 当2≥n 时,1n n b b --=1122n n n n a a ---=21222211==---n n nn n a a , 所以{}n b 是首项为1,公差为12的等差数列. ……………………8分 (2)由(1)知,111(1)22n n b n +=+-=,即 2n na =12n +, 所以{}n a 的通项公式为 1(1)2n n a n -=+⋅.……………………12分 20.解:(1)设从今年起,第n 年的盈利额为y 万元,则.96273239632)1(10452-+-=-⎥⎦⎤⎢⎣⎡⨯-+-=n n n n n n y …………………………………3分由0>y 得01927332<+-n n ,∴.3643<<n 又∈n N *,且15≤n ,∴从今年起,第4年开始盈利. ………………………………………………6分 (2)年平均利润为.5.1227396232)9623(2732739623=+⨯-≤+-=+--=n n n n n n n y ……8分当且仅当nn 9623=,即8=n 时年平均利润最大,此时,该渔业个体户共盈利1101085.12=+⨯(万元). (12)分21.解:(1)取a =b =1,则(1)2(1).(1)f f p f p =-=故.……………………2分又p f f f f -+=⨯=)21()2()212()1(,且1)2(-=p f .得:1)1()2()1()21(+=+--=+-=p p p p p f f f .……………………4分(2)设,021x x << 则])()([)()()()(112111212p x f x x f x f x x x f x f x f -+=-⋅=-1()f x -21()x f p x =- 由1,01221><<x x x x 可得,所以 p x xf <)(12,所以 0)()(12<-x f x f ,因此,),0()(+∞在x f 上是减函数. ………………………………………… 8分(3)由1)45(2+>+-p x x f 得 )21()45(2f x x f >+-,又因为),0()(+∞在x f 上是减函数,所以214502<+-<x x .由0452>+-x x 得 1<x 或4>x ;由21452<+-x x 得21152115+<<-x , 因此,不等式的解集为⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧+<<<<-2115412115x x x 或.……………………12分 22.(1)证明:212122)()2(+--+++--+-=++-xa ax x a a a x a x f x a f 02211211=--++--+-=+--++-+-=ax a x a x x a x a a x a x x a ,∴ 结论成立. ……………………………………………………………… 4分 (2)证明:xa x a x a x f -+-=-+--=111)()(.当112,211,211,121-≤-≤--≤-≤---≤-≤--+≤≤+xa x a a x a a x a 时, 2113-≤-+-≤-xa , 即]2,3[)(--的值域为x f .…………………… 8分(3)解:)(|1|)(2a x a x x x g ≠-++=.当a x a x x x g a x a x -++=-++=≠-≥43)21(1)(,122时且; 当.45)21(1)(,122-+-=+--=-<a x a x x x g a x 时因为2321≤≤a ,所以21121≤-≤-a ,则函数)(x g 在),(),1[+∞-a a a 和上单调递增,在)1,(--∞a 上单调递减,因此,当1-=a x 时,g (x )有最小值2)1(-a (12)分。
【数学】吉林省东北师范大学附属中学2015届高三(文科)高考总复习阶段测试卷(第28周)
东北师范大学附属中学2014—2015学年度高三年级周考数学试题(文科)说明:本试卷分为第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.总分150分,考试时间120分钟. 注意事项:1.答第Ⅰ卷前,考生务必将自己姓名、考号、考试科目用2B 铅笔涂写在答题卡上. 2.每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其它答案.3.将第Ⅰ卷选择题的答案涂在答题卡上,第Ⅱ卷每题的答案写在答题纸的指定位置. 4.考试结束,将答题纸和答题卡一并交回,答案写在试卷上视为无效答案. 参考公式:圆锥表面积公式:(是圆锥底面半径,是母线) 圆锥体积公式:(是圆锥底面半径,是高)球体积公式:(R 是球的半径)第Ⅰ卷(选择题 共60分)一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的). 1.已知集合,,则( )A .B .C .D .2.命题“存在R ,0”的否定是( )A .不存在R , >0B .存在R ,0C .对任意的R ,0D .对任意的R , >0()S r r l π=+r l 213V r h π=r h 343R V π={}x x y x M 32+-=={}|||2N x x =>MN ={}|13x x <<{}|03x x <<{}|23x x <<{}32≤<x x 0x ∈02x ≤0x ∈02x0x ∈02x ≥x ∈2x≤x ∈2x3.已知:,则的大小关系为 ( )A .B .C .D .4.有一个几何体的三视图及其尺寸如下(单位:cm ),则该几何体的体积为: ( )A .cm 3B .cm 3C .cm 3D . cm 35.化简( )A .B .C .D .6.已知实数、,则“”是“”的 ( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件7.函数的单调减区间为( )A .B .C .D .8.已知点在曲线上,为曲线在点处的切线的倾斜角,则的取值范围是( )A .B .C .D . 9.已知数列是正项等比数列,是等差数列,且,则( )090711090711...a log .b log .c .===,,a b c ,,c b a <<b c a <<c a b <<b a c <<12π15π36π48π21sin 352sin 20-=1212-1-1a b 2ab ≥224a b +≥()()22log 56f x x x =-+⎪⎭⎫⎝⎛+∞,25()+∞,3⎪⎭⎫ ⎝⎛∞-25,()2,∞-P sin y x =αP α0,4π⎡⎤⎢⎥⎣⎦3,44ππ⎡⎤⎢⎥⎣⎦30,,44πππ⎡⎤⎡⎫⎪⎢⎥⎢⎣⎦⎣⎭3[,)4ππ{}n a {}n b 68a b =A .B .C .D .10.已知向量,,那么=( )A .B .C .D .111.定义两种运算:,,则函数( )A .是奇函数B .是偶函数C .既是奇函数又是偶函数D .既不是奇函数又不是偶函数12.已知定义在上的函数满足,且, ,有穷数列()的前项和等于, 则n 等于( ) A .4 B .5 C .6D .7第Ⅱ卷 (非选择题 共90分)二、填空题(本大题共4小题,每小题5分,共20分.把答案填写在答题纸相应位置上.) 13.函数的定义域为____________________.14.已知m>0,n>0,向量,且,则的最小值是 .7993b b a a +≤+7993b b a a +≥+7993b b a a +>+7993b b a a +<+()cos 75,sin 75a =()cos15,sin15b =a b -21222322b a b a -=⊕2)(b a b a -=⊗()()222xf x x ⊕=-⊗R ()()f x g x 、()()x f x a g x ='()()()'()f x g x f x g x <25)1()1()1()1(=--+g f g f ()()f n g n ⎧⎫⎨⎬⎩⎭n N *∈n 3231()()21log 2f x x =-()()111a m b n ==-,,,a //b 12m n+15.对于函数,在使成立的所有常数中,我们把的最大值-1叫做的下确界,则函数的下确界为 .16.已知中,所对的边长分别为,则下列条件中能推出为锐角三角形的条件是_________. (把正确答案的序号都写在横线上)①. ②.③,. ④.三、解答题(本大题共6小题,共70分,解答应写出文字说明、证明过程或演算步骤) 17.(本题满分10分)设函数,(Ⅰ)不等式的解集为,求的值; (Ⅱ)在(Ⅰ)的条件下,试求不等式的解集. 18.(本题满分12分) 已知函数. (I )求函数的最小正周期;(II )若不等式在上恒成立,求实数的取值范围.19.(本题满分12分)设数列的前项和为,对,都有成立,(Ⅰ) 求数列的通项公式;(Ⅱ)设数列,试求数列的前项和.20. (本题满分12分)如图,在平面直角坐标系中,点在轴的正半轴上,直线()22f x x x =-()f x M ≥M M ()22f x x x =-()()2211x g x x +=+ABC ∆A B C ∠∠∠、、a b c 、、ABC ∆51cos sin =+A A 0<⋅−→−−→−BC AB 33,3==c b30=B 0tan tan tan >++C B A ()()20f x ax a =+<()||6f x <()1,2-a ()12x f x ≥-2()2sin 24f x x x π⎛⎫=+⎪⎝⎭()f x ()1f x m -<64x ππ⎡⎤∈⎢⎥⎣⎦,m {}n a n n S *n N ∈52n n a S =+{}n a 2log n n b a ={}n b n n M xoy A x AB的倾斜角为,,设,. (Ⅰ)用表示;(Ⅱ)若的值.21.(本题满分12分)已知数列的各项都为正数,,前项和满足().(Ⅰ)求数列的通项公式; (Ⅱ)令(),数列的前项和为,若对任意正整数都成立,求实数的取值范围.22. (本题满分12分)已知函数(). (Ⅰ)若,求在上的最大值; (Ⅱ)若,求的单调区间.56π1OB =AOB θ∠=5,26ππθ⎛⎫∈ ⎪⎝⎭θOA tan θ=OA OB ⋅{}n a 11=a n n S 11--+=-n n n n S S S S 2≥n {}n a 11+=n n n a a b *∈N n {}n b n n T n n T a λ≥+1n λ)ln 3(1)(x a xx x f -+-=0>a 1=a )(x f (]1,0)1,0(∈x )(x f参考答案:1.【答案】D【分析】根据集合的含义,把集合具体求出来,再根据集合的运算法则进行计算。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2015年高三年级周测【37周】文科数学试题卷
第I 卷(选择题共50分) 注意事项:
1.考生务必将自己的姓名、班级,试室号,座位号填写在指定位置,
2.本卷必须用黑色水笔(或钢笔)作答,所有答案必须写在答题卷上。
3、本卷不可以使用计算器。
一、选择题(共10小题,每题5分)
1、设全集错误!未找到引用源。
<错误!未找到引用源。
,集合错误!未找到引用源。
,则错误!未找到引用源。
等于( ) A.错误!未找到引用源。
B.错误!未找到引用源。
C.错误!未找到引用源。
D.错误!未找到引用源。
2、在复平面上,复数错误!未找到引用源。
的共轭复数的对应点所在的象限是( ) A .第一象限 B .第二象限 C .第三象限 D .第四象限
3、已知条件错误!未找到引用源。
,条件错误!未找到引用源。
,则错误!未找到引用源。
成立的( )
A .充分不必要条件
B .必要不充分条件
C .充要条件
D .既非充分也非必要条件
4、将正方形(如图1所示)截去两个三棱锥,得到图2所示的几何体,则该几何体的左视图为( )
.
5、命题“设a 、b 、b a bc ac c >>∈则若,,2
2
R ”的逆命题、否命题、逆否命题中真命题共有 ( )A .0个 B .1个 C .2个 D .3个
6、将函数y=sin2x 的图象向右平移错误!未找到引用源。
个单位,再向上平移1个单位,所得函数图象对应的解析式为( )A .错误!未找到引用源。
B .错误!未找到引用源。
C .错误!未找到引用源。
D .错误!未找到引用源。
7、已知(cos 2,sin ),(1,2sin 1),(,)2a b π
ααααπ==-∈若
)
4tan(,52πα+=⋅则b a 的值为( )
A .31
B .71
C . 72
D .32
8、设等比数列
{}n a 中,前n 项和为36789,8,7,n S S S a a a ==++=已知则 ( )
A .18
B .18-
C .57
8
D .55
8
9、函数错误!未找到引用源。
在同一平面直角坐标系内的大致图象为( )
10、设定义在错误!未找到引用源。
上的函数错误!未找到引用源。
满足错误!未找到引用源。
,当错误!未找到引用源。
时,错误!未找到引用源。
;当错误!未找到引用源。
且错误!未找到引用源。
时,错误!未找到引用源。
,则错误!未找到引用源。
与错误!未找到引用源。
的图像在错误!未找到引用源。
上的交点个数是( )
A . 8
B .6
C .4
D .2 第Ⅱ卷(非选择题共100分)
二、填空题(共4小题,每题5分)
11、设a 、b 、c 是单位向量,且a b c +=,则a 与c 的夹角为 。
12、已知实数错误!未找到引用源。
的最小值为 . 13、设
n m ,是不同的直线,α、β、γ是不同的平面,有以下四个命题
①γβγαβα//////⇒⎭⎬⎫;②βαβα⊥⇒⎭⎬⎫⊥m m //;③βαβα⊥⇒⎭⎬⎫⊥//m m ;④αα////m n n m ⇒⎭⎬⎫
⊂;
其中正确的命题是
14、已知y 与100x x ≤()之间的部分对应关系如下表:
x
11 12 13 14 15 … y
2
97 148 295 147 293
…
则x 和y 可能满足的一个关系式是 .
三、解答题(共6小题,计80分,解答题应写出推理、演算步骤)
15、(本小题满分14分) 如右图,已知三棱锥A -BPC 中,AP ⊥PC ,AC ⊥BC ,M 为AB 中点,D 为PB 中点,且△PMB 为正三角形.
(Ⅰ)求证:DM ∥平面APC ; (II )求证:平面ABC ⊥平面APC.
16、(本小题满分12分) 已知A 、B 、C 坐标分别为A (3,0),B (0,3),
C (错误!未找到引用源。
),错误!未找到引用源。
(1)若错误!未找到引用源。
,求角错误!未找到引用源。
的值 (2)若错误!未找到引用源。
,求错误!未找到引用源。
的值
17、(本小题满分12分) 已知直线1l :210x y --=,直线2l
:10ax by -+=,其中a ,
{}
1,2,3,4,5,6b ∈.
(1)求直线
12l l =∅的概率; (2)求直线1l
与2l
的交点位于第一象限的概率.
18、(本小题满分14分) 某产品原来的成本为1000元/件,售价为1200元/件,年销售量为1万件。
由于市场饱和顾客要求提高,公司计划投入资金进行产品升级。
据市场调查,若投入x
万元,每件产品的成本将降低43x 元,在售价不变的情况下,年销售量将减少x 2
万件,按上述
方式进行产品升级和销售,扣除产品升级资金后的纯利润记为)(x f (单位:万元).(纯利润=每件的利润×年销售量-投入的成本) (Ⅰ)求)(x f 的函数解析式;
(Ⅱ)求)(x f 的最大值,以及)(x f 取得最大值时x 的值.
19、(本小题满分14分) 下列关于星星的图案构成一个数列{}n a ,*
()n
a n N ∈对应图中星星
的个数.
(1)写出
56,a a 的值及数列{
}n a 的通项公式;
(2)求出数列1{}
n a 的前n 项和n S ;
(
3)若22911
2n n n b n --=,对于(2)中的n S ,有n n n c S b =⋅,求数列{||}n c 的前n 项和
…
20、(本小题满分14分) 设函数
()x ax x f ln 2
+=.)(R a ∈ (Ⅰ)讨论)(x f 的单调性;
(Ⅱ)已知0<a ,若函数()x f y =的图象总在直线21
-
=y 的下方,求a 的取值范围;
(Ⅲ)记()
f x '为函数()x f 的导函数.若1=a ,试问:在区间[]10,1上是否存在k (k 100<)个正数
321,,x x x …
k
x ,使得
()()()()1232012
k f x f x f x f x ''''++++≥成立?
请证明你的结论.。
