探究各种复摆简谐运动周期的推导方法
摆的周期问题

摆的周期问题通过中学对单摆运动的学习,我们知道单摆的振动周期T 和振幅A 无关,和摆球的质量m 无关,和摆长l 有关,且摆长l 越长,振动越慢,摆动周期T 就越大;和重力加速度g 有关,且重力加速度越大,摆动周期就越小。
我们还得到了单摆的周期公式:gl Tπ2=。
而我们说的单摆只是一种理想化的模型,实际中的摆只要求摆线是不可伸缩的,摆球的直径远小于摆线的长度。
一.下面对几种简单的摆的周期进行推导:例1.如图1,一长为l 的不可拉伸的细线,拴着一个直径远小于l 的质量为m 的钢质小球,小球静止时处于O 处,现把小球轻轻拉离平衡位置O 处至M 处,然后静止释放小球,小球将在MN 之间做来回摆动。
在忽略空气阻尼下,这就是一个传统的单摆模型。
求其摆动周期。
解析 如图1,当摆球处于O 处时,摆球所受到的重力G 和细线拉力T 作用,且两力相平衡,摆球所受合力为零,此处即为单摆运动的平衡位置。
摆球在偏离平衡位置的任意一点P 处,摆球受到的重力G 和细线拉力T 将不再平衡,摆球将在两个力的共同作用下加速靠近平衡位置(或者减速离开平衡位置)。
在P 点,摆球所受到的重力G 沿圆弧切线方向的分力θsin 1mg G =。
这就是提供摆球作为来回摆动的回复力F ,且θs i n 1mg G F==,N GG图 1当偏角θ很小﹝如θ<5°﹞时,lx ≈≈θθs in ,所以单摆受到的回复力xl mg F -=,式中的l 为摆长,x 是摆球偏离平衡位置的位移,负号表示回复力F 与位移x 的方向相反,由于m 、g 、l 都是确定的常数,所以lmg 可以用常数k 来表示,于是上式可写成kx F-=。
因此,在偏角θ很小时,单摆受到的回复力与位移成正比,方向与位移方向相反,单摆作的是简谐运动。
那么回复力F 就可以用公式kx F-=来表示,其中k是比例系数,且k 等于lmg ,x 是位移。
假设在t 时刻(位移是x )小球的加速度为a ,根据牛顿第二运动定律有:kxma F-==,即xmk a-=。
简谐振动弹簧振子和摆锤的周期和频率计算

简谐振动弹簧振子和摆锤的周期和频率计算简谐振动是物理学中研究的一个重要概念,它描述了振动系统在没有外力干扰时的运动规律。
在简谐振动中,周期和频率是计算振动特性的关键参数。
本文将介绍如何计算弹簧振子和摆锤的周期和频率。
1. 弹簧振子的周期和频率计算弹簧振子是一种典型的简谐振动系统,它由一个质点和一个弹簧组成。
当质点受到外力作用而发生位移时,弹簧会产生恢复力,使得质点发生振动。
弹簧振子的周期和频率与弹簧的劲度系数和质点的质量有关。
周期(T)表示振动一次所需要的时间,频率(f)表示单位时间内振动的次数。
它们之间的关系是:T = 2π√(m/k)f = 1/T其中,m表示质点的质量,k表示弹簧的劲度系数。
根据上述公式,我们可以利用给定的质量和劲度系数来计算周期和频率。
2. 摆锤的周期和频率计算摆锤也是一种常见的简谐振动系统,它由一个质量较小的物体(称为锤头)和一根轻而有弹性的线(称为摆线)组成。
当摆线受到外界扰动使得锤头发生摇摆时,摆锤会进行简谐振动。
摆锤的周期和频率与摆线的长度和重力加速度有关。
周期(T)表示摆动一次所需要的时间,频率(f)表示单位时间内摆动的次数。
它们之间的关系是:T = 2π√(l/g)f = 1/T其中,l表示摆线的长度,g表示重力加速度。
根据上述公式,我们可以利用给定的摆线长度和重力加速度来计算周期和频率。
综上所述,我们可以用上述公式计算弹簧振子和摆锤的周期和频率,从而了解它们的振动特性。
这些计算公式在物理学中有着广泛的应用,可以帮助我们更好地理解和分析振动现象。
求振动周期四法 学法指导 不分版本

求振动周期四法杨榕楠(浙江省宁波市效实中学 315012)1. 公式法 如果物体做简谐运动,则它所受的回复力F 与相对于平衡位置的位移x 满足关系kx F -=。
可以证明,这个动力学微分方程的解为)cos(0ϕω+=t A x ,其中ω是振动物体的圆频率,它由系统本身的性质决定,m k =ω,所以简谐运动的周期km T πωπ22==。
利用上式求振动周期,可以进行如下操作:使物体偏离平衡位置一个微小的位移x ,求出此时回复力F 的表达式,若满足kx F -=,则把相应的k 值代入公式,即可求得物体做简谐运动的周期。
这是求振动周期最常用的方法。
例1 设想有一单摆,其摆长l 与地球半径R 相等,试求此单摆在地球表面附近振动时的周期T 。
已知地球半径为R=6370km 。
分析 此单摆的摆长很长,即使摆角很小,摆动过程中摆球相对于地面的位移也很大。
这时摆球受地球引力的方向变化不可忽略。
如图1所示,设单摆的偏角为θ时,它离开平衡位置的位移为x ,偏离地心O 的角度为α,所受地球引力为F',则此时摆球所受回复力为ββcos cos 'mg F F -=-=①图1由图可知2παθβ=++由于θ、α均很小,有Rx l x≈≈αθ,, 代入①可得x R l mg mg mg F )11()()sin(+-≈+-≈+-=αθαθ 可见物体做简谐运动,由周期公式得g R l lR Rl mg m k m T )(2)11(22+=+==πππ 当R l =时,单摆周期8.921037.614.32226⨯⨯⨯⨯==g R T π (min)7.59)(3580==s 。
2. 能量法物体做简谐运动时,任意时刻的动能)(sin 212102222ϕωω+==t A m mv E k 势能)(cos 21210222ϕω+==t kA kx E p机械能为2222121A m kA E E E p k ω==+= 若能求得物体振动中的势能或机械能,且具有形式为222121kA kx 或的表达式,则物体做简谐运动,周期为 p E mx T E mA T 2222222ππωπ===,或。
简谐运动规律

简谐运动规律简谐运动是物体在一个固定的参考点附近,做往复运动的一种运动形式。
它是物理学中一个非常重要的概念,广泛应用于力学、波动、电磁学等领域。
简谐运动有三个基本特征:周期性、稳定性和均匀性。
周期性指的是物体的运动是有规律的,经过一定的时间间隔后会重复出现同样的状态。
稳定性表示物体的运动是稳定的,不受外界干扰的影响。
均匀性则表明物体在简谐运动中的速度和加速度是均匀变化的。
简谐运动的规律可以用如下公式来描述:x = A*cos(ωt + φ)其中,x表示物体的位移,A表示振幅,ω表示角频率,t表示时间,φ表示初相位。
这个公式告诉我们物体在简谐运动中的位移是一个余弦函数,其振幅决定了物体的最大位移,角频率决定了物体振动的快慢,初相位决定了物体运动的起始位置。
简谐运动的周期可以用公式T = 2π/ω来计算,其中T表示周期。
角频率与周期的关系可以通过ω = 2π/T来得到。
简谐运动的速度和加速度也可以通过对位移函数求导来得到。
速度的公式为v = -Aω*sin(ωt + φ),加速度的公式为 a = -Aω²*cos(ωt + φ)。
这两个公式告诉我们物体在简谐运动中的速度和加速度都是正弦函数,并且与位移之间存在一定的相位差。
简谐运动的能量守恒是其重要的特征之一。
在简谐振动中,物体的总机械能保持不变,由势能和动能组成。
势能与位移的平方成正比,动能与速度的平方成正比。
当物体在最大位移处时,动能为零,势能达到最大值;当物体通过平衡位置时,动能达到最大值,势能为零。
简谐运动在生活和科学研究中有着广泛的应用。
例如,钟摆的摆动、弹簧的振动、电磁波的传播等都可以看作是简谐运动。
在工程中,简谐运动的原理被应用于设计和制造各种振动器和传感器。
在医学领域,人体的心脏跳动、呼吸等运动也可以用简谐运动的概念来描述和分析。
简谐运动是物理学中一个重要的概念,它可以描述物体在一个固定点附近做往复运动的规律。
通过对位移、速度和加速度的分析,可以得到简谐运动的各种特征和规律。
复摆的实验报告.doc

复摆的实验报告.doc摘要:本实验通过利用复摆的摆动周期和摆长与摆角度之间的关系,通过多次实验来研究复摆的动力学规律和特性。
实验结果表明,复摆的摆动周期受到重力加速度和摆长的影响,摆长越长,摆臂相对较长,振幅相对小,周期越长。
同时,复摆的摆角度对振幅和周期都产生了影响,当摆角度较小时,振幅较小,周期较长。
关键词:复摆,摆动周期,摆角度,摆长Abstract:In this experiment, the dynamic laws and characteristics of the compound pendulum are studied by utilizing the relationship between the swinging period and the swinging length and swing angle of the compound pendulum. The experimental results show that the swinging period of the compound pendulum is affected by the gravity acceleration and the swinging length. The longer the swinging length, the longer the swinging arm, the smaller the amplitude, andthe longer the period. At the same time, the swinging angle of the compound pendulum affects the amplitude and period. When the swinging angle is small,the amplitude is small and the period is long.Keywords: compound pendulum, swinging period, swinging angle, swinging length实验方案:所用仪器:复摆、计时器、卡尺、直尺、秤。
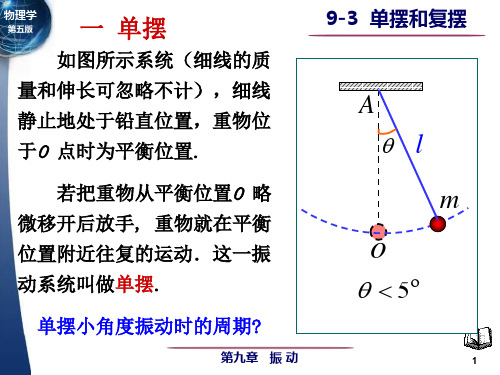
9-3单摆和复摆
dt
θ l
v FT m
o
J = ml
振 动
θ = θ m cos( ω t + ϕ )
T = 2π l g
v P
2
2
第九章
物理学
第五版
二
复摆 (θ < 5 )
o
9-3
单摆和复摆 转动正向
振动时的周期? 振动时的周期
v v v M =l ×F M = −mgl sin θ
d 2θ = Jβ = J 2 dt
第九章 振 动
A
θ
l
m
o
θ <5
o
1
物理学
第五版
动力学分析: 动力学分析:
9-3
单摆和复摆
转动 正向
θ < 5 时 , sinθ ≈ θ M = − mgl sin θ ≈ − mglθ d 2θ − mglθ = J 2
o
A
dθ g g 2 = − θ 令ω = 2 dt l l d 2θ 2 = −ω θ 2 dt
F = − kx 平衡位置 x = 0
d x 2 = −ω x 2 dt
2
x = A cos(ωt + ϕ )
单摆 弹簧振子 ω = k m 由振动系统本身性质决定) (由振动系统本身性质决定)
第九章 振 动
a = −ω x
2
v = − A ω sin( ω t + ϕ )
ω= g l
ω = mgl
π 2
Q0 I 0
O
﹡ π
2π
﹡
(ωt +ϕ)
π q = Q0 cos(ωt +ϕ) i = I0 cos(ωt +ϕ + ) 2
间接推导简谐运动的周期公式

龙源期刊网
间接推导简谐运动的周期公式
作者:马巧枝
来源:《商情》2012年第19期
关键词简谐运动周期公式匀速圆周运动
在讲授《机械运动》一章时,学有余力的学生对简谐运动的周期公式不愿仅局限于死记,很想推导一番。
然而,此公式的推导需要解微分方程,学生是做不了的。
若在教学中采取辅助匀速圆周運动的方法,就可以为这些学生打开一条新的思路,解除他们的困惑,增强学习兴趣,以促进教学。
解微分方程的过程是这样的:一辅助圆周运动。
设一逆时针匀速圆周运动的角速度为ω,半径为A.
在某一时刻物体的纵坐标为:x=Asinωt。
也就是说,物体在x轴的投影也为简谐运动,与我们需要研究的简谐运动等效。
我们恰恰就是要用它的ω来解决问题。
摆动周期的计算公式

摆动周期的计算公式
摆动周期是指一个摆动物体经过一个完整摆动周期所需的时间。
在物理学中,摆动周期通常用符号T表示。
计算摆动周期的公式取决于所考虑的摆动类型,例如简谐摆、物理摆和单摆等。
1.简谐摆:
简谐摆是指一个在弹性势能和重力势能之间进行来回转换的系统,例如一个被悬挂的弹簧、钟摆或弦上的振动等。
简谐摆的周期由下面的公式给出:
T=2π√(l/g)
其中,T是周期,l是摆长(摆动物体到转轴的距离),g是重力加速度(通常取9.8m/s²)。
2.物理摆:
物理摆是指一个由重力作用形成的周期性摆动,例如一个带有质量的物体在被线束悬挂的情况下的摆动。
物理摆的周期由下面的公式给出:T = 2π√(I/mgh)
其中,T是周期,I是物体的转动惯量,m是物体的质量,g是重力加速度,h是物体的重心高度。
3.单摆:
单摆是指一个长度为l的质点由一个与摆节数相等的线束悬挂并在重力作用下进行的来回摆动。
单摆的周期由下面的公式给出:
T=2π√(l/g)
其中,T是周期,l是摆长,g是重力加速度。
注意事项:
1.上述公式假设摆动物体在摆动过程中没有受到其他阻力的影响。
2.这些公式仅适用于小摆角的情况,即当摆动物体的摆角较小且在摆动过程中保持不变时。
3.如果摆动角度较大,则需要考虑非线性项,可以使用级数展开等方法来计算摆动周期。
摆动周期是摆动物体非常重要的一个物理量,它决定了摆动的频率和稳定性。
掌握如何计算摆动周期的公式可以帮助我们更好地理解和应用摆动现象。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
探究各种复摆简谐运动周期的推导方法
复摆简谐运动系统是一个常用的物理学模拟系统,它模拟出现象有多种,如摆、弹簧、钟摆、钢琴琴弦等。
由于其具有复杂的物理性质,当我们需要分析其周期性特征时,会有一定的挑战存在。
本文就介绍探究各种复摆简谐运动周期的推导方法。
首先,我们可以通过一些基础的物理公式来推导各种复摆的周期。
比如我们可
以用牛顿第二定律推出复摆的周期,这是建立在复摆系统处于近似稳定状态的假设之上。
具体而言,我们利用动量守恒定律推导出摆斜坡上的角速度θ。
θ的变化
与复摆杆的动量有关,根据上面的公式可以推出:ω=2π/T=√g/L (T为周期,L
为摆杆的长度,g为地球重力加速度)。
其次,我们可以运用动能定理来求复摆周期。
具体而言,我们可以将复摆系统
的动能分为重力能与弹簧能,根据这两部分能量的积分值,可以计算出复摆的周期T。
T=2π√m/K(m为复摆系统质量,K为弹簧劲度系数)。
再次,通过复摆系统的驱动力分析,也可以求取复摆的周期值。
这种方法适用
于所有复摆系统,无论是固定摆杆摆动还是可调制复摆系统。
根据系统中外力作用守恒定律推导出复摆周期T:T=2π√I/f(I为转动惯量,f为力对摆柄的作用矩)。
此外,我们还可以运用阻尼的概念来求复摆的周期。
此外,我们还可以利用几
何建模的方法来求取复摆简谐运动的周期,例如空气阻力摆的周期,即使空气中充满阻力,由于具有更复杂的几何结构,仍然可以通过几何建模推算出其周期值。
总之,推导各种复摆简谐运动周期的推导方法,主要采用了物理定律、动能定理、转动惯量与驱动力守恒定律以及几何建模等方法,每种方法都有自己的特点,可以用来推导各种复摆的周期特征。
