探索性因子分析
用SPSS做探索性因子分析
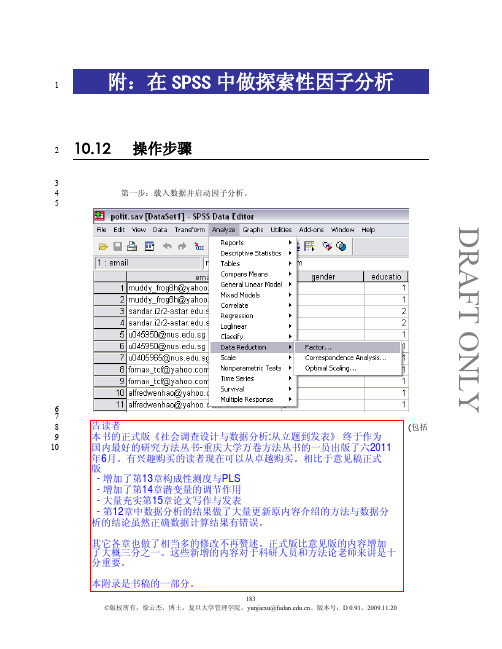
DRAFT ONLY附:在SPSS 中做探索性因子分析110.12操作步骤23 第一步:载入数据并启动因子分析。
4567 第二步:选择因子所对应的测度项。
在这个研究中,我们选择对应于七个变量(包括8 自变量、因变量、与控制变量) 的测度项。
910告读者丗本书的正式版丆《社会调查设计与数据分析:从立题到发表》丆 终于作为国内最好的研究方法丛书-重庆大学万卷方法丛书的一员出版了乮六2011年6月乯。
有兴趣购买的读者现在可以从卓越购买。
相比于意见稿丆正式版丗- 增加了第13章丆构成性测度与PLS•C - 增加了第14章丆潜变量的调节作用 - 大量充实第15章丆论文写作与发表- 第12章中数据分析的结果做了大量更新丆原内容介绍的方法与数据分析的结论虽然正确丆数据计算结果有错误。
其它各章也做了相当多的修改丆不再赘述。
正式版比意见版的内容增加了大概三分之一。
这些新增的内容对于科研人员和方法论老师来讲是十分重要。
本附录是书稿的一部分。
DRAFT ONLY12第三步:设定因子求解办法为主成分分析法。
使用相关系数矩阵,并设定主要因子的34特征根大于1。
5678第四步:设计因子旋转方法为“Varimax”。
然后在“Factor Analysis”窗口中按“ok”开始计算。
910DRAFT ONLY1210.13主成分分析的结果34 对应于27个测度项,主成分分析法一共产生了27个因子。
这是可以产生的因子个数5 的上限。
“Total ”列报告了每一个因子所对应的特征值。
“% of Variance ”表示这个特征6 值在所有特征值和中的比例。
“Extraction Sums of Squared Loadings ”这一列反映了特征根7 大于1的因子。
在这个例子中,我们顺利地得到了7个因子。
相应地,在用碎石坡法对因8 子进行目测时,我们得到的结果是一致的。
请读者参看本章中的相应图例。
值得一提的9 是,第八个因子的特征根为0.967,十分接近1。
CFA and EFA结构方程模型:探索性因子分析与验证性因子分析

F1
F2
F3
1
1
1
X1
1
X2
1
X3
1
X4
1
X5
1
X6
1
X7
1
X8
1
X9
1
e1
e2
e3
e4
e5
e6
e7
e8
e9
验证性因子模型
F1
F2
F3
1
1
1
X1
1
X2
1
X3
1
X4
1
X5
1
X6
1
X7
1
X8
1
X9
1
e1
e2
e3
e4
e5
e6
e7
e8
e9
EFA 特征
• 因子个数可能是从1到可测变量的总数 • 所有可测变量允许与每个因子相关 • 通常需要对EFA的解进行旋转来使得因子 便于解释
– 例如指标之间中度相关
多指标方法
• 多指标方法减少了单个可测变量的总测量 误差对结果精确性的影响。 • 可测变量与潜在的潜变量的区别 • 可测变量与潜变量共同组成测量模型
测量模型的类型
• • • • 探索性 (EFA) 验证性 (CFA) 多特质多方法 (MTMM) 层级CFA
探索性因子模型
结构方程模型: 探索性因子分析与验证性因子分析
科学 追求真理,寻找纷繁复杂的社会现象背后的 原因,找到解决问题的根本办法。
The basic of research process
Deduction(Ex.)
Theory Ideate(形成概念) Summary(假设归纳) Deducting 逻辑推理(Reason)
SPSS探索性因子分析的过程

一.因子分析的定义在现实研究过程中,往往需要对所反映事物、现象从多个角度进行观测。
因此研究者往往设计出多个观测变量,从多个变量收集大量数据以便进行分析寻找规律。
多变量大样本虽然会为我们的科学研究提供丰富的信息,但却增加了数据采集和处理的难度。
更重要的是许多变量之间存在一定的相关关系,导致了信息的重叠现象,从而增加了问题分析的复杂性。
因子分析是将现实生活中众多相关、重叠的信息进行合并和综合,将原始的多个变量和指标变成较少的几个综合变量和综合指标,以利于分析判定。
用较少的综合指标分析存在于各变量中的各类信息,而各综合指标之间彼此是不相关的,代表各类信息的综合指标成为因子。
因子分析就是用少数几个因子来描述许多指标之间的联系,以较少几个因子反应原资料的大部分信息的统计方法。
二.数学模型im im i i i i U F F F F Z +++++=αααα · · · 332211i Z 为第i 个变量的标准化分数;(标准分是一种由原始分推导出来的相对地位量数,它是用来说明原始分在所属的那批分数中的相对位置的。
)m F 为共同因子;m 为所有变量共同因子的数目;i U 为变量i Z 的唯一因素;im α为因子负荷。
(也叫因子载荷,统计意义就是第i 个变量与第m 个公共因子的相关系数,它反映了第i 个变量在第m 个公共因子上的相对重要性也就是第m 个共同因子对第i 个变量的解释程度。
)因子分析的理想情况,在于个别因子负荷im α不是很大就是很小,这样每个变量才能与较少的共同因子产生密切关联,如果想要以最少的共同因素数来解释变量间的关系程度,则i U 彼此间不能有关联存在。
所谓的因子负荷就是因子结构中原始变量与因子分析时抽取出共同因子的相关,即在各个因子变量不相关的情况下,因子负荷im α就是第i 个原有变量和第m 个因子变量间的相关系数,也就是i Z 在第m 个共同因子变量上的相绝对值越大则公共因子和原有变量关系越强。
探索性因子分析(课堂PPT)

目录
1
因子分析介绍
2
探索性因子分析的基本理论
3
探索性因子分析的结构及步骤
4
实例演示
2
因子分析
★ 概念 用于分析影响变量、支配变量的共同因子有几
个且各因子本质为何的一种统计方法。它是一类 降维的相关分析技术,用来考察一组变量之间的 协方差或相关系数结构,并用以解释这些变量与 为数较少的因子之间的关联。
19
因子得分
• 因子得分就是每个观测量的公共因子的值。根 据因子得分系数和原始变量的标准化值,可以 计算每个观测量的各因子的得分数,并可以据 此对观测量进行进一步的分析。
• 计算因子得分的基本思想是将因子变量表现为 原有变量的线性组合,即通过以下的因子得分 函数计算:
F j j 1 x 1 j 2 x 2 jx 3 jx p (j=1,2···p)
• 因子旋转通常分为两类:
➢ 正交旋转
Varimax方差最大旋转,它使每个因子上的具有 最高载荷的变量数最小,可简化对因子的解释。
➢ 斜交旋转
18
因子旋转(二)
• 正交旋转的基本假定是,因子分析中被提 取出来的因子之间是相互独立的,因子间 并不相关。它的目的是要获得因子的简单 结构,即使每个变量在尽可能少的因子上 有较高的负载;而斜交旋转中,因子间的夹 角是任意的,也就是说斜交旋转对因子间 是否相关并无限定,这种因子旋转的结果 就会使各因子所解释的变量的方差出现一 定程度的重叠。
➢公因子的累积方差贡献率
根据累计贡献率达到的百分比确定
12
确定因子个数的方法(二)
• 实际上累积贡献率是一个次要指标 。主要指标是特征值, 在前一指标达 到的情况下,只要累计贡献率不是 太差都可以接受。即使70%也不是 太大的问题。实际处理中,很少碰 到累计贡献率太低的情况,如果问 卷设计和数据收集没有太大问题的 前提下。
探索性因子分析及其在应用中存在的主要问题

探索性因子分析及其在应用中存在的主要问题Ξ孙晓军ΞΞ 周宗奎(华中师范大学心理学院,武汉,430079)摘 要 探索性因子分析的发展非常迅速,已成为教育与社会心理学领域中最常用的统计方法之一。
本文全面介绍了探索性因子分析的基本原理,阐述了其发生的机制及基本过程,对其在教育、心理领域应用中存在的问题进行了总结,并针对应用中样本容量和观测变量数目不够、因子求解方法的误用、因子数目的确定标准及因子旋转中存在的问题、因子值缺乏重复验证性、研究结果呈现形式不规范、过于依赖SPSS 、缺乏主动性等问题提出了一些相应的建议。
关键词:探索性因子分析 因子旋转 因子值 因子分析(Factor Analysis )是通过研究众多变量之间的内部依赖关系,探求观测数据中的基本结构,并用少数几个假想变量(因子)来表示基本的数据结构的方法[1]。
1904年,查尔斯・斯皮尔曼(Charles Spearman )在研究智力时首次采用了因子分析的方法,将因子分析方法运用于实践[2]。
随后,因子分析的理论和数学基础逐步得到发展和完善,特别是50年代以后,随着计算机的普及和各种统计软件的出现,因子分析得到了巨大的发展。
现在,因子分析已成为教育与社会心理学领域研究中最常用的统计方法之一。
但令人遗憾的是,在实际研究的应用中,研究者并不能合理、正确的使用这一方法,导致最后的研究结果缺乏可信度。
本文的目的就是通过对探索性因子分析发生原理、步骤的详细探讨,结合其在应用中存在的问题,希望对心理领域中探索性因子分析的运用提出一些实质性的建议,包括样本大小、因子数目、观测变量数目、因子旋转等等。
1 探索性因子分析的基本原理 探索性因子分析模型(见图1)的一般表达形式为:X 1=w 11F 1+w 21F 2+……w n1F n +w 1U 1+e 1其中,X n 表示观测变量,F M 代表因子分析中最基本的公因子(Common factor ),它们是各个观测变量所共有的因子,解释了变量之间的相关;U n 代表特殊因子(Unique factor ),它是每个观测变量所特有的因子,相当于多元回归分析中的残差项,表示该变量不能被公因子所解释的部分;w M 代表因子负载(Factor loading ),它是每个变量在各公因子上的负载,相当于多元回归分析中的回归系数;而e n 则代表了每一观测变量的随机误差。
spss探索性因子分析

巴特利特球度检验
原假设:所有的变量都是独立的
如果该统计量的观测值比较大,且对应的概率P小 于给定的显著性水平,应拒绝原假设
意味着所有的变量是相互依赖的,原有变量适合做 因子分析。
巴特利特球度检验
拒绝原假设“所有的变量都是独立 的”,即变量是相互依赖的
Kaiser-Meyer-Olkin measure of sampling adequacy (KMO)
累计贡献率 这五个因子可以累计解释 55.478%的变异。
20
⚫ 根据碎石图(Scree Plot)确定因子数量
21
⚫ 每个因子包含哪些测项? ⚫ 因子载荷(factor loadings):因子载荷是变量X
与因子F的相关系数。 ⚫ 因子载荷绝对值越接近1,表明变量X与因子F的相关
性越强。
22
变量名称
INV4 INV3 INV2 INV1
(1)具有描述性的功能:将数目众多的变量浓缩成数 目较少的几个精简变量,这些精简变量即是一般的因子 (factor),以较少的因子(factor)概括所有的观察 测项(item)
(2)探索理论构念的架构:透过因子分析可以将杂乱 无章的变量重新排列组合,理出头绪;此种探索性的功 能有助于建立新的假设、发展新的理论,即为探索性因 子分析(Exploratory Factor Analysis, EFA)
17个测项->有哪些子构念?
构念
技术就绪度
(TRI)
子构念 测项
创新程度
(INNOVATI ON)
乐观程度
(OPTIMISM)
不适应感
(DISCOMFORT)
不安全感
(INSECURITY)
INS5 INS4 INS3 INS2 INS1
SPSS探索性因子分析的过程

现要对长途进修者对教导技巧资本和应用情形进行懂得,设计一个李克特量表,如下图所示:一.因子剖析的界说在实际研讨进程中,往往须要对所反应事物.现象从多个角度进行不雅测.是以研讨者往往设计出多个不雅测变量,从多个变量收集大量数据以便进行剖析查找纪律.多变量大样本固然会为我们的科学研讨供给丰硕的信息,但却增长了数据收集和处理的难度.更重要的是很多变量之间消失必定的相干关系,导致了信息的重叠现象,从而增长了问题剖析的庞杂性.因子剖析是将实际生涯中浩瀚相干.重叠的信息进行归并和分解,将原始的多个变量和指标变成较少的几个分解变量和分解指标,以利于剖析剖断.用较少的分解指标剖析消失于各变量中的各类信息,而各分解指标之间彼此是不相干的,代表各类信息的分解指标成为因子.因子剖析就是用少数几个因子来描写很多指标之间的接洽,以较少几个因子反响原材料的大部分信息的统计办法.二.数学模子iZ 为第i 个变量的尺度化分数;(尺度分是一种由原始分推导出来的相对地位量数,它是用来解释原始分在所属的那批分数中的相对地位的.)mF 为配合因子;m 为所有变量配合因子的数量;iU 为变量i Z 的独一身分;α为因子负荷.(也叫因子载荷,统计意义就是第i个变量与第m个公共因子的相im干系数,它反应了第i个变量在第m个公共因子上的相对重要性也就是第m个配合因子对第i个变量的解释程度.)α不是很大就是很小,如许每个变量因子剖析的幻想情形,在于个体因子负荷im才干与较少的配合因子产生亲密接洽关系,假如想要以起码的配合身分数来解释变量间的关系程度,则i U彼此间不克不及有接洽关系消失.所谓的因子负荷就是因子构造华夏始变量与因子剖析时抽掏出配合因子的相干,α就是第i个原有变量和第m个因子即在各个因子变量不相干的情形下,因子负荷imα绝对变量间的相干系数,也就是i Z在第m个配合因子变量上的相对重要性,是以,im值越大则公共因子和原有变量关系越强.在因子剖析中有两个重要指针:一为“配合性”,二为“特点值”.所为配合性,也称变量配合度或者公共方差,就是每个变量在每个配合因子的负荷量的平方总和(一横列中所有因子负荷的的平方和),也就是个体变量可以被配合因子解释的变异量百分比,这个值是个体变量与配合因子间多元相干的平方.从配合性的大小可以断定这个原始变量与配合因子间的关系程度.假如大部分变量的配合度都高于0.8,则解释提掏出的配合因子已经根本反应了各原始变量80%以上的信息,仅有较少的信息丧掉,因子剖析后果较好.而各变量的独一身分就是1减掉落该变量配合性的值,就是原有变量不克不及被因子变量所能解释的部分.所谓特点值,是每个变量在某一配合因子的因子负荷的平方总和(一向行所有因子负荷的平方和),在因子剖析的的配合因子抽取中,特点值最大的配合因子会最先被抽取,其次是次大者,最后抽取的配合因子的特点值会最小,平日会接近于0.将每个配合因子的特点值除以总题数,为此配合因子可以解释的变异量,因子剖析的目标之一,即在身分构造的简略化,愿望以起码的配合因子能对总变异量做最大的解释,因而抽取的身分越少越好,但抽取的因子的累积变异量越大越好.三.SPSS中实现进程(一)录入数据(二)因子剖析“剖析”|“降维”|“因子剖析”选项卡,打开如图所示“因子剖析”对话框.从原变量量表中选择须要进行因子剖析的变量,然后单击箭头按钮将选中的变量选入“变量”列表中.“变量列表”的变量为要进行因子剖析的的目标变量,变量在区间或比率级别应当是定量变量.分类数据(如:性别等)不合适因子剖析.2.“描写按钮”:重要设定对原始变量的根本描写并对原始变量进行相干性剖析.选中“原始剖析成果”复选框,暗示因子剖析未转轴前之配合性.特点值.变异数百分等到累积百分比,这是一个中央成果,对主成分剖析来说,这些值是要进行剖析变量的相干或协方差矩阵的对角元素.KMO与Bartlett球形度磨练用来磨练适不合适用来做因子剖析.KMO磨练,磨练变量间的偏相干是否很小;巴特利特球形磨练,磨练相干阵是否是单位阵.KMO值越接近1越合适做因子剖析,巴特利特磨练的原假设设为相干矩阵为单位阵,假如Sig值谢绝原假设暗示变量间消失相干关系,是以合适做因子剖析.“抽取”按钮:重要设定提取公共因子的办法和公共因子的个数.办法:主成分剖析法.SPSS默认办法.该办法假定原变量是因子变量的线性组合,第一主成分有最大的方差,后续成分可解释的方差越来越少.这是应用最多的因子提取办法.剖析:相干性矩阵.暗示以相干性矩阵作为提取公共因子的根据,当剖析中应用不合的尺度测量变量时比较合适.输出:未扭转的因子解.显示未扭转时因子负荷量.特点值及配合性.碎石图.暗示输出与每个因子相接洽关系的特点值的图,该图用于肯定应保持的因子个数,平日该图显示大因子的峻峭斜率和残剩因子平缓的尾部之间明显的中止.按特点值大小分列,有助于肯定保存若干个因子.抽取:基于特点值.暗示抽取特点值超出指定值的所有因子,在“特点值大于”输入框中指定值,一般为1.4.扭转:用于设定因子扭转的办法.扭转的目标是为了简化构造,以帮忙解释因子SPSS默认不扭转.办法:最大方差法:是一种正交扭转办法,他使得对每个因子有高负载的变量的数量达到最小,并简化了因子的解释.输出:扭转解.该复选框只有在选择里扭转办法之后才干选择,对于正交扭转会显示已扭转的模式矩阵和因子变换矩阵.5.得分:用于对因子得分进行设置,即盘算因子得分.取默认值,单击持续按钮.6.选项:用于设定对变量缺掉值的处理和系数显示的格局.缺掉值:按列表消除个案.去除所有含缺掉值的个案后再进行剖析.系数显示格局:按大小分列.载荷系数按照数值的大小分列,并组成矩阵,使得在统一因子上具有较高载荷的变量的分列在一路,便于得到结论.(三)成果剖析1.KMO及Bartlett’磨练当KMO值愈大时,暗示变量间的配合因子愈多,愈合适进行因子剖析,根据专家不雅点,假如KMO的值小于0.5时,较不宜进行因子剖析,此处的KMO值为0.695,暗示合适因子剖析.此外Bartkett’s球形磨练的原假设为相干系数矩阵为单位阵,Sig值为0.000小于明显程度0.05,是以谢绝虚无假设,解释变量之间消失相干关系,合适做因子剖析.(Bartkett’s球形磨练的2 为234.438,自由度为45,达到明显,代表母群体的相干矩阵间有配合因子消失,合适进行因子剖析.)2.配合性,显示因子间的配合性成果.在主成分剖析中,有若干个原始变量便有若干个成分,所以配合性会等于1,没有独一身分.所以本成果中央一栏显示初试配合性都为1,则暗示抽取办法为主成分剖析法,最右一栏为题项的配合性.从该表可以得到,因子剖析的变量配合度都异常高,标明变量中的大部分信息均可以或许被因子所提取,解释因子剖析的成果是有用的. 3.整体解释的变异数--------扭转之前的数据.该表给出了因子进献率的成果,表中左侧部分为初始特点值,中央为提取主因子成果,右侧为扭转后的主因子成果.“合计”指因子的特点值,“方差的%”暗示该因子的特点值占总特点值百分比,“累积%”÷10=63.579%.个中自有前三个因子的特点值大于1,并且前三个因子的特点值之和占总特点值的89.366%,是以提取前三个因子作为主因子列于右边,这也是因子剖析时所抽出的公共因子数.因为特点值是由大到小分列,所以第一个公同因子的解释变异量平日是最大者,其次是第二个1.547,再是第三个1.032.扭转后的特点值为 4.389,3.137,1,411,解释变异量为43.885%,31.372%,14.108%,累积的解释变异量为43.885%,75.257%,89.366%.扭转后的特点值不合于转轴前的特点值.4.碎石图.特点值的碎石图.平日该图显示大因子的峻峭斜率和残剩因子平缓的尾部,之间有明显的中止.一般取主因子在异常峻峭的斜率上,而处在平缓斜率上的因子对变异的解释异常小.可以从此碎石图中看出,从第三个身分今后,坡线甚为平展,因而可以保存3个身分较为合适.5.成分矩阵:给出了未扭转的因子载荷.从该表中可以得到应用主成分剖析办法提取的三个因子的载荷量,个中因子负荷量小于0.1的未被显示,因子为了便利解释因子寄义,须要进行因子扭转.6.扭转成份矩阵:给出了扭转后的因子载荷值,个中扭转办法采取的是Kaiser尺度化的正交扭转法.经由过程因子扭转,各个因子有了比较明白的寄义.从图中可以看出:a1,a8,a6,a5,a4位因子1,a10,a9,a7为因子2,a3,a2为因子3.题项在其所属的因子层面次序是按照因子负荷量的高下分列的.7.成份转换矩阵:六.成果解释根据因子的特点值和扭转后的因子矩阵,采取了主成分剖析法抽掏出3个因子作为配合因子,并应用因子扭转办法中的最大方差法,按照从大到小的次序进行分列,使得变量与因子的关系豁然清楚明了,对其做如下表所示的因子剖析摘要表.。
探索性因子分析培训材料

原理与步骤
1. 确定样本和变量
选择适当的样本和测量适当的变量是 进行因子分析的前提。
2. 数据标准化
在进行因子分析之前,需要将原始数 据标准化,即减去平均值并除以其标 准差,以使所有变量具有零均值和单 位方差。
原理与步骤
3. 计算样本相关矩阵
通过计算变量之间的相关系数来创建 样本相关矩阵。
4. 因子提取
案例三:心理学研究数据
总结词
心理学研究数据是探索性因子分析在心理学领域中的重要应用之一,它可以帮助心理学家了解人类行 为的潜在结构和机制。
详细描述
心理学研究数据通常包括被试在各种心理测验和实验中的表现数据,如智力测试、人格测试、行为观 察等。通过探索性因子分析,可以识别出人类行为和心理状态的潜在结构或维度,从而帮助心理学家 更好地理解人类行为的机制和心理过程。
探索性因子分析培训材料
• 引言 • 探索性因子分析概述 • 因子分析的数学基础 • 因子提取与解释 • 因子分析的软件操作 • 案例分析 • 总结与展望
01
引言
培训目标
掌握探索性因子分析 的基本原理和步骤
提高解决实际问题的 能力,能够独立完成 因子分析任务
学会应用探索性因子 分析方法进行数据分 析
04
因子提取与解释
因子提取方法
01
02
03
主成分分析法
通过将原始变量进行线性 组合,得到新的综合变量, 这些变量按照方差依次递 减的顺序排列。
因子分析法
基于变量之间的相关性进 行分组,使得同一组内的 变量高度相关,不同组的 变量相关性较低。
最大似然法
通过迭代算法,使得因子 模型与原始数据的拟合度 最高。
使用各种因子提取方法(如主成分分 析、最小二乘法等)来从相关矩阵中 提取公因子。
