高三数学(文)高考总复习：升级增分训练立体几何 Word版含解析

合集下载

2023届高考数学总复习《立体几何》附答案解析

（2）若点 N 为 BC 的中点，求四面体 A'MNB 的体积．
【解答】证明：（1）连接 BD，设 BD∩EC＝F，连接 MF，
由题意可得四边形 BCDE 为正方形，则 F 为 BD 的中点，
∴MF 为△A′BD 的中位线，可得 MF∥A′B，
又 A′B⊄平面 EMC，MF⊂平面 EMC，
∴A'B∥平面 EMC；
2023 年高考：立体几何复习题及答案
1．如图，已知直角梯形 ABCD，BC∥AD，BC＝CD＝2，AD＝4，∠BCD＝90°，点 E 为 AD 的中点，现将三角形 ABE 沿 BE 折叠，得到四棱锥 A'﹣BCDE，其中∠A'ED＝120°，点 M 为 A'D 的中点．
（1）求证：A'B∥平面 EMC；
第2页共3页
∵BE⊂平面 BEF，∴平面 BEF⊥平面 AMD，结合题意分析知，点 F 在线段 AD 上，连接 MF，过 A 作 AH⊥MF，交 MF 的延长线于点 H，
则结合已知条件得
，解得 AH ，
设 Dt ，
第3页共3页
【解答】解：（1）证明：由题意知 PC2+AC2＝PA2，∴PC⊥AC，同理，PC⊥BC，又 AC∩BC＝C，∴PC⊥平面 ABC， ∵D，E 分别是 AC，PA 的中点，∴DE∥PC， ∴DE⊥平面 ABC，又 DE⊂平面 BDE，∴平面 BDE⊥平面 ABC．（2）在△BDE 中，DE⊥BD，BD＝2 ，DE＝2，∴BE＝4，如图，过 A 作 AM⊥BE 于 M，连接 MD，在△ABE 中，AB＝BE＝4，AE＝2 ，解得 AM ，ME＝1， ∵DM⊂平面 BDE，∴AC⊥DM，在 Rt△ADM 中，AM ，AD＝2，∴DM ， ∴DM2+EM2＝DE2，∴MD⊥BE， ∵AM∩MD＝M，∴BE⊥平面 AMD，

2018届高三数学(理)高考总复习：升级增分训练立体几何含解析

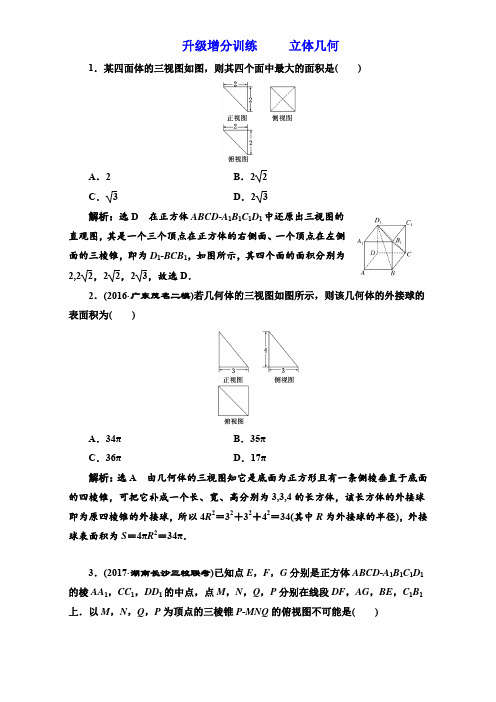
升级增分训练立体几何1．某四面体的三视图如图，则其四个面中最大的面积是()A．2B．2 2C． 3 D．2 3解析：选D在正方体ABCD-A1B1C1D1中还原出三视图的直观图，其是一个三个顶点在正方体的右侧面、一个顶点在左侧面的三棱锥，即为D1-BCB1，如图所示，其四个面的面积分别为2,22，22，23，故选D．2．(2016·广东茂名二模)若几何体的三视图如图所示，则该几何体的外接球的表面积为()A．34π B．35πC．36π D．17π解析：选A由几何体的三视图知它是底面为正方形且有一条侧棱垂直于底面的四棱锥，可把它补成一个长、宽、高分别为3,3,4的长方体，该长方体的外接球即为原四棱锥的外接球，所以4R2＝32＋32＋42＝34(其中R为外接球的半径)，外接球表面积为S＝4πR2＝34π．3．(2017·湖南长沙三校联考)已知点E，F，G分别是正方体ABCD-A1B1C1D1的棱AA1，CC1，DD1的中点，点M，N，Q，P分别在线段DF，AG，BE，C1B1上．以M，N，Q，P为顶点的三棱锥P-MNQ的俯视图不可能是()解析：选C 当M 与F 重合、N 与G 重合、Q 与E 重合、P 与B 1重合时，三棱锥P -MNQ 的俯视图为A ；当M ，N ，Q ，P 是所在线段的中点时，三棱锥P -MNQ 的俯视图为B ；当M ，N ，Q ，P 位于所在线段的非端点位置时，存在三棱锥P -MNQ ，使其俯视图为D ．4．(2017·河南中原名校联考)如图，四棱柱ABCD -A 1B 1C 1D 1是棱长为1的正方体，四棱锥S -ABCD 是高为1的正四棱锥，若点S ，A 1，B 1，C 1，D 1在同一个球面上，则该球的表面积为( )A ．916πB ．2516π C ．4916π D ．8116π 解析：选D 作如图所示的辅助线，其中O 为球心，设OG 1＝x ，则OB 1＝SO ＝2－x ，由正方体的性质知B 1G 1＝22，则在Rt △OB 1G 1中，OB 21＝G 1B 21＋OG 21，即(2－x )2＝x 2＋⎝ ⎛⎭⎪⎫222，解得x ＝78，所以球的半径R ＝OB 1＝98，所以球的表面积为S ＝4πR 2＝8116π．5．(2016·湖南长沙四校一模)某几何体的三视图如图所示，则该几何体的体积为( )A ．1136 B ． 3 C ．533D ．433解析：选B 由三视图知该几何体是一个四棱锥，其直观图如图所示，△PAD 为正三角形，四棱锥的底面是直角梯形，四棱锥的高为3，∴所求体积V ＝13×⎣⎢⎡⎦⎥⎤12×(1＋2)×2×3＝3．6．(2016·湖南郴州模拟)一只蚂蚁从正方体ABCD -A1B 1C 1D 1的顶点A 出发，经正方体的表面，按最短路线爬行到顶点C 1的位置，则下列图形中可以表示正方体及蚂蚁最短爬行路线的正视图的是( )A ．①②B ．①③C ．③④D ．②④解析：选D 由点A 经正方体的表面，按最短路线爬行到达顶点C 1的位置，共有6种路线(对应6种不同的展开方式)，若把平面ABB 1A 1和平面BCC 1B 1展到同一个平面内，连接AC 1，则AC 1是最短路线，且AC 1会经过BB 1的中点，此时对应的正视图为②；若把平面ABCD 和平面CDD 1C 1展到同一个平面内，连接AC 1，则AC 1是最短路线，且AC 1会经过CD 的中点，此时对应的正视图为④．而其他几种展开方式对应的正视图在题中没有出现．7．(2016·福建省质检)在三棱锥P -ABC 中，PA ＝23，PC ＝2，AB ＝7，BC ＝3，∠ABC ＝π2，则三棱锥P -ABC 外接球的表面积为( )A ．4πB ．163π C ．323π D ．16π解析：选D 设三棱锥P -ABC 的外接球的半径为R ，在△ABC 中，因为AB ＝7，BC ＝3，∠ABC ＝π2，所以AC ＝AB 2＋BC 2＝4．在△PAC 中，因为PA ＝23，PC ＝2，AC ＝4，所以PA 2＋PC 2＝AC 2，所以∠APC ＝π2，所以AC 为三棱锥P -ABC 的外接球的直径，所以R ＝2，所以此三棱锥的外接球的表面积S ＝4πR 2＝4π×22＝16π．8．(2016·南宁模拟)设点A ，B ，C 为球O 的球面上三点，O 为球心．球O 的表面积为100π，且△ABC 是边长为43的正三角形，则三棱锥O -ABC 的体积为( )A ．12B ．12 3C ．24 3D ．36 3解析：选B ∵球O 的表面积为100π＝4πr 2，∴球O 的半径为5．如图，取△ABC 的中心H ，连接OH ，连接并延长AH 交BC 于点M ，则AM ＝(43)2－⎝⎛⎭⎪⎫4322＝6，AH ＝23AM ＝4，∴OH ＝OA 2－AH 2＝52－42＝3，∴三棱锥O -ABC 的体积为V ＝13×34×(43)2×3＝123．9．如图，三棱锥V -ABC 的底面为正三角形，侧面VAC 与底面垂直且VA ＝VC ，已知其正视图的面积为23，则其侧视图的面积为________．解析：设三棱锥V -ABC 的底面边长为a ，侧面VAC 的边AC 上的高为h ，则ah ＝43，其侧视图是由底面三角形ABC 边AC 上的高与侧面三角形VAC 边AC 上的高组成的直角三角形，其面积为12×32a×h＝12×32×43＝33．答案：3 310．(2016·南昌一模)正三角形ABC的边长为2，将它沿高AD翻折，使点B 与点C间的距离为2，此时四面体ABCD外接球的表面积为________．解析：由题知，求四面体ABCD的外接球的表面积可转化为求长、宽、高分别为1,1，3的长方体的外接球的表面积，其半径R＝1212＋12＋(3)2＝52，所以S＝4πR2＝5π．答案：5π11．(2016·江西师大附中模拟)已知边长为23的菱形ABCD中，∠BAD＝60°，沿对角线BD折成二面角A-BD-C的大小为120°的四面体，则四面体的外接球的表面积为________．解析：如图1，取BD的中点E，连接AE，CE．由已知条件可知，平面ACE ⊥平面BCD．易知外接球球心在平面ACE内，如图2，在CE上取点G，使CG＝2GE，过点G作l1垂直于CE，过点E作l2垂直于AC，设l1与l2交于点O，连接OA，OC，则OA＝OC，易知O即为球心．分别解△OCG，△EGO可得R＝OC＝7，∴外接球的表面积为28π．答案：28π12．(2017·贵州适应性考试)已知正三棱柱(底面是正三角形，侧棱与底面垂直)的体积为3 3 cm3，其所有顶点都在球O的球面上，则球O的表面积的最小值为________cm2．解析：球O的表面积最小等价于球O的半径R最小．设正三棱柱的底面边长为a，高为b，则正三棱柱的体积V＝34a2b＝33，所以a2b＝12．底面正三角形所在截面圆的半径r＝33a，则R2＝r2＋⎝⎛⎭⎪⎫b22＝⎝⎛⎭⎪⎫33a2＋b24＝13×12b＋b24＝4b＋b24，令f(b)＝4b ＋b 24，0＜b ＜2R ，则f ′(b )＝b 3－82b 2．令f ′(b )＝0，解得b ＝2，当0＜b ＜2时f ′(b )＜0，函数f (b )单调递减，当b ＞2时，f ′(b )＞0，函数f (b )单调递增，所以当b ＝2时，f (b )取得最小值3，即(R 2)min ＝3，故球O 的表面积的最小值为4π(R 2)min ＝12π．答案：12π13．如图1，在直角梯形ABCD 中，AD ∥BC ，∠BAD ＝π2，AB ＝BC ＝1，AD＝2，E 是AD 的中点，O 是AC 与BE 的交点．将△ABE 沿BE 折起到△A 1BE 的位置，如图2．(1)证明：CD ⊥平面A 1OC ；(2)若平面A 1BE ⊥平面BCDE ，求平面A 1BC 与平面A 1CD 的夹角的余弦值．解：(1)证明：在题图1中，因为AB ＝BC ＝1，AD ＝2，E 是AD 的中点，∠BAD ＝π2，所以BE ⊥AC ．即在题图2中，BE ⊥OA 1，BE ⊥OC ，从而BE ⊥平面A 1OC ，又BC ∥DE ，DE ＝1＝BC ，所以四边形BCDE 为平行四边形，所以CD ∥BE ，所以CD ⊥平面A 1OC ．(2)由已知，平面A 1BE ⊥平面BCDE ，又由(1)知，BE ⊥OA 1，BE ⊥OC ，所以∠A 1OC 为二面角A 1-BE -C 的平面角，所以∠A 1OC ＝π2．如图，以O 为原点，建立空间直角坐标系，因为A 1B ＝A 1E ＝BC ＝ED ＝1，BC ∥ED ，所以B ⎝ ⎛⎭⎪⎫22，0，0，E ⎝ ⎛⎭⎪⎫－22，0，0，A 1⎝ ⎛⎭⎪⎫0，0，22，C ⎝ ⎛⎭⎪⎫0，22，0，得BC ―→＝⎝ ⎛⎭⎪⎫－22，22，0，A 1C ―→＝⎝ ⎛⎭⎪⎫0，22，－22，CD ―→＝BE ―→＝(－2，0,0)．设平面A 1BC 的法向量为n 1＝(x 1，y 1，z 1)，平面A 1CD 的法向量为n 2＝(x 2，y 2，z 2)，平面A 1BC 与平面A 1CD 的夹角为θ，则⎩⎪⎨⎪⎧ n 1·BC ―→＝0，n 1·A 1C ―→＝0，得⎩⎨⎧－x 1＋y 1＝0，y 1－z 1＝0，取y 1＝1，得平面A 1BC 的一个法向量为n 1＝(1,1,1)；由⎩⎪⎨⎪⎧n 2·CD ―→＝0，n 2·A 1C ―→＝0，得⎩⎨⎧x 2＝0，y 2－z 2＝0，取y 2＝1，得平面A 1CD 的一个法向量为n 2＝(0,1,1)．从而cos θ＝n 1，n 2＝23×2＝63，即平面A 1BC 与平面A 1CD 的夹角的余弦值为63．。

高中数学立体几何(解析版)

立体几何立体几何一直在高中数学中占有很大的分值，未来的高考中立体几何也会持续成为高考的一个热点，文科高考中立体几何主要考查三视图的相关性质利用，简单几何体的体积，表面积以及外接圆问题.另外选择部分主要考查在点线面位置关系，简单几何体三视图.选择题主要还是以几何体的基本性质为主，解答题部分主要考查平行，垂直关系以及简单几何体的变面积以及体积.本专题针对高考高频知识点以及题型进行总结，希望通过本专题的学习，能够掌握高考数学中的立体几何的题型，将高考有关的立体几何所有分数拿到.【满分技巧】基础知识点考查：一般来说遵循三短一长选最长.要学会抽象问题具体会，将题目中的直线转化成显示中的具体事务，例如立体坐标系可以看做是一个教室的墙角有关外接圆问题：一般图形可以采用补形法，将几何体补成正方体或者是长方体，再利用不在同一个平面的四点确定一个立体平面原理，从而去求.内切圆问题：转化成正方体的内切圆去求.求点到平面的距离问题：采用等体积法.求几何体的表面积体积问题：应注意巧妙选取底面积与高.【考查题型】选择，填空，解答题【限时检测】（建议用时：90分钟）一、单选题AA是1．（2018·上海高考真题）《九章算术》中，称底面为矩形而有一侧棱垂直于底面的四棱锥为阳马，设1AA为底面矩形的一边，则这样的阳正六棱柱的一条侧棱，如图，若阳马以该正六棱柱的顶点为顶点、以1马的个数是（）A．4 B．8 C．12 D．16【答案】D【分析】根据新定义和正六边形的性质可得答案．【详解】根据正六边形的性质，则D1﹣A1ABB1，D1﹣A1AFF1满足题意，而C1，E1，C，D，E，和D1一样，有2×4=8，当A1ACC1为底面矩形，有4个满足题意，当A1AEE1为底面矩形，有4个满足题意，故有8+4+4=16故选D．【点睛】本题考查了新定义，以及排除组合的问题，考查了棱柱的特征，属于中档题．2．（2020·上海虹口区·高三一模）在空间，已知直线l及不在l上两个不重合的点A､B，过直线l做平面α，使得点A､B到平面α的距离相等，则这样的平面α的个数不可能是（）A．1个B．2个C．3个D．无数个【答案】C【分析】分情况讨论可得出.【详解】（1）如图，当直线AB与l异面时，则只有一种情况；（2）当直线AB与l平行时，则有无数种情况，平面α可以绕着l转动；（3）如图，当l过线段AB的中垂面时，有两种情况.故选：C.3．（2020·上海高三一模）如图，在正四棱柱1111ABCD A B C D -中，底面边长2AB =，高14A A =，E 为棱1A A 的中点．设BAD ∠=α、BED θ∠=、1B ED γ∠=，则α、β、γ之间的关系正确的是（）．A ．αγθ=>B ．γαθ>>C ．θγα>>D ．αθγ>>【答案】B 【分析】求出α、β、γ的大小即可求解. 【详解】由题意可得2BAD πα∠==，连接BD ，则BDE 为等边三角形，所以3BED πθ∠==，连接1B D ，则222122426B D =++=22222BE DE ==+=取1B D 的中点O ，连接EO ，则16BO 862EO =-=所以16tan 32B EO ∠==，所以13B EO π∠=，即123B ED πγ∠==，所以γαθ>>.故选：B4．已知长方体1111ABCD A B C D -，下列向量的数量积一定不为0的是（）A ．1AD AB ⋅B ．11AD BC ⋅ C ．1BD BC ⋅ D ．1BD AC ⋅【答案】C【分析】利用正方体几何性质计算出数量积为零的选项，根据长方体的性质证明数量积一定不为零的选项.【详解】当长方体1111ABCD A B C D -为正方体时，根据正方体的性质可知： 1111,,AB AD AD B C BD AC ⊥⊥⊥，所以10AB AD ⋅=、110AD B C ⋅=、10BD AC ⋅=.根据长方体的性质可知：1BC CD ⊥，所以1BD 与BC 不垂直，即1BD BC ⋅一定不为0.故选：C5．（2020·上海高三一模）已知正方体1111ABCD A B C D -，点P 是棱1CC 的中点，设直线AB 为a ，直线11A D 为b .对于下列两个命题：①过点P 有且只有一条直线l 与a 、b 都相交；②过点P 有且只有一条直线l 与a 、b 都成45︒角.以下判断正确的是（）A ．①为真命题，②为真命题B ．①为真命题，②为假命题C ．①为假命题，②为真命题D ．①为假命题，②为假命题【答案】B 【分析】作出过P 与两直线相交的直线l 判断①；通过平移直线a ，b ，结合异面直线所成角的概念判断②．【详解】解：直线AB 与A 1D 1 是两条互相垂直的异面直线，点P 不在这两异面直线中的任何一条上，如图所示：取BB 1的中点Q ，则PQ ∥A 1D 1，且 PQ ＝A 1D 1，设A 1Q 与AB 交于E ，则点A 1、D 1、Q 、E 、P 共面，直线EP 必与A 1D 1 相交于某点F ，则过P 点有且只有一条直线EF 与a 、b 都相交，故①为真命题；分别平移a ，b ，使a 与b 均经过P ，则有两条互相垂直的直线与a ，b 都成45°角，故②为假命题． ∴①为真命题，②为假命题．故选：B ．【点睛】本题考查立体几何图形中直线和平面的相交、平行、垂直的性质，体现了数形结合的数学思想，是中档题．二、填空题6．（2020·上海青浦区·高三一模）圆锥底面半径为1cm ，母线长为2cm ，则其侧面展开图扇形的圆心角θ=___________.【答案】π；【分析】根据圆的周长公式易得圆锥底面周长，也就是圆锥侧面展开图的弧长，利用弧长公式可得圆锥侧面展开图扇形的圆心角的大小.【详解】因为圆锥底面半径为1cm ，所以圆锥的底面周长为2cm π，则其侧面展开图扇形的圆心角22πθπ==，故答案为：π.【点睛】思路点睛：该题考查的是有关圆锥侧面展开图的问题，解题思路如下：（1）首先根据底面半径求得底面圆的周长；（2）根据圆锥侧面展开图扇形的弧长就是底面圆的周长，结合母线长，利用弧长公式求得圆心角的大小. 7．（2020·上海闵行区·高三一模）如图，已知正四棱柱1111ABCD A B C D -的底面边长为2，高为3，则异面直线1AA 与1BD 所成角的大小是_______.【答案】22；【分析】根据11//AA DD ，得到1DD B ∠异面直线1AA 与1BD 所成的角，然后在1Rt DD B △，利用正切函数求解.【详解】因为11//AA DD ，所以1DD B ∠异面直线1AA 与1BD 所成的角，在正四棱柱1111ABCD A B C D -的底面边长为2，高为3，所以1122tan 3BD DD B DD ∠==，因为1(0,)2DD B π∠∈，所以122arctan3DD B ∠=，故答案为：22arctan 38．（2019·上海市建平中学高三月考）某几何体由一个半圆锥和一个三棱锥组合而成，其三视图如图所示（单位：厘米），则该几何体的体积（单位：立方厘米）是________.【答案】12π+2，高为3；半圆锥的底面是半径为1的半圆，高为3；据此计算出该几何体的体积.【详解】由三视图可知，三棱锥的体积：1223132V ⎛=⨯⨯= ⎝⎭；半圆锥体积：()11113232V ππ=⨯⨯⨯⨯⨯=，所以总体积为：12π+. 故答案为12π+.【点睛】本题考查空间几何体的体积计算，难度较易.计算组合体的体积时，可将几何体拆分为几个容易求解的常见几何体，然后根据体积公式完成求解.9．（2020·上海高三其他模拟）如图直三棱柱ABB 1-DCC 1中， BB 1⊥AB ，AB=4，BC=2，CC 1=1，DC 上有一动点P ，则△APC 1周长的最小值是 .【答案】521+试题分析：要求周长的最小值，因边为定值，只要求另两边之和的最小值，因两点直线线段最短，所以的最小值为因此△APC 1周长的最小值是521考点：棱柱的相关知识.10．（2020·上海高三一模）已知母线长为6cm 的圆锥的侧面积是底面积的3倍，则该圆锥的底面半径为________cm ．【答案】2【分析】设底面半径为r ，由两个面积的关系可得底面半径的值．【详解】解：设底面半径为r ，则由题意，可得213262r r ππ=⨯⨯，解得2r ，故答案为：2．【点睛】本题考查圆锥的侧面积及圆的面积公式，属于基础题．11．（2020·上海高三其他模拟）已知圆锥的母线长为l ，过圆锥顶点的最大截面三角形的面积为212l ，则此圆锥底面半径r 与母线长l 的比r l的取值范围是____________．【答案】22【分析】先判断两条母线的夹角=90θ时最大截面三角形的面积为212l 22l r ≤和r l <，最后求出r l 的取值范围即可. 【详解】解：过圆锥顶点的截面三角形的面积：1sin 2S l l θ=⋅⋅（θ为两母线的夹角），因为过圆锥顶点的最大截面三角形的面积为212l ，即两条母线的夹角=90θ时的截面面积，此时底面弦长为2l ，所以22l r ≤，又r l <，所以212r l≤<，故答案为：2[,1)2【点睛】本题考查空间几何体，是基础题.12．（2020·上海青浦区·高三二模）用一平面去截球所得截面的面积为23cm π，已知球心到该截面的距离为1cm ，则该球的表面积是___________2cm ．【答案】16π【分析】由已知求出小圆的半径，然后利用勾股定理求出球的半径，即可求出球的表面积【详解】解：因为用一平面去截球所得截面的面积为23cm π，所以小圆的半径为3cm ，因为球心到该截面的距离为1cm ，所以球的半径为221(3)2+=cm ，所以球的表面积为24216S ππ=⨯=2cm ，故答案为：16π【点睛】此题考查球的截面的半径、球心到截面的距离与球的半径间的关系，属于基础题13．（2020·上海普陀区·高三月考）已知一个半圆柱的高为4，其俯视图如图所示，其左视图的面积为8，则该半圆柱的表面积为______.【答案】1612+π【分析】由圆柱的主视图和左视图知该圆柱的底面直径为4，高为3，由此能求出该几何体的表面积，得到答案.【详解】由题意，其左视图为矩形，其左视图的面积为8，半圆柱的高h 为4，可得半圆的半径r 为2，由于半圆柱的表面积为两个底面半圆面积加侧面展开图形的面积，即2211222224224161222S r rh rh πππππ=⨯⨯++=⨯⨯⨯+⨯⨯+⨯⨯=+.故答案为：1612+π.【点睛】本题主要考查了空间几何体的三视图的应用，以及圆柱的表面积的计算问题，同时考查了圆柱的结构特征的应用，属于基础题.三、解答题14．（2020·上海虹口区·高三一模）如图在三棱锥P ABC -中，棱AB 、AC 、AP 两两垂直，3AB AC AP ===，点M 在AP 上，且1AM =.（1）求异面直线BM 和PC 所成的角的大小；（2）求三棱锥P BMC -的体积.【答案】（1）5（2）3. 【分析】（1）以点A 为坐标原点，AB 、AC 、AP 所在直线分别为x 、y 、z 轴建立空间直角坐标系A xyz -，利用空间向量法可求得异面直线BM 和PC 所成的角的大小；（2）计算出PMC △的面积，并推导出AB ⊥平面PMC ，利用锥体的体积公式可求得三棱锥P BMC -的体积.【详解】（1）由于AB 、AC 、AP 两两垂直，以点A 为坐标原点，AB 、AC 、AP 所在直线分别为x 、y 、z 轴建立空间直角坐标系A xyz -，如下图所示：则()3,0,0B 、()0,0,0A 、()0,3,0C 、()0,0,3P 、()0,0,1M ，()3,0,1BM =-，()0,3,3PC =-，5cos ,101032BM PC BM PC BM PC⋅<>===-⨯⋅，因此，异面直线BM 和PC 所成的角的大小为5arccos 10；（2）AB AC ⊥，AB AP ⊥，AC AP A =，AB ∴⊥平面APC ，AC AP ⊥，1AM =，2PM AP AM ∴=-=，132PMC S PM AC ∴=⋅=△， 1133333B PMC PMC V S AB -=⋅=⨯⨯=△.【点睛】方法点睛：求空间角的常用方法：（1）定义法：由异面直线所成角、线面角、二面角的定义，结合图形，作出所求空间角，再结合题中条件，解对应的三角形，即可求出结果；（2）向量法：建立适当的空间直角坐标系，通过计算向量的夹角（两直线的方向向量、直线的方向向量与平面的法向量、两平面的法向量）的余弦值，即可求得结果.15．（2020·上海青浦区·高三一模）如图，在长方体1111ABCD A B C D -中，1AB AD ==，12AA =，点P 为棱1DD 的中点.（1）证明：1//BD 平面P AC ；（2）求异面直线1BD 与AP 所成角的大小. 【答案】（1）证明见解析；（2）30.【分析】（1）AC 和BD 交于点O ，则O 为BD 的中点．推导出1//PO BD ．由此能证明直线1//BD 平面PAC ；（2）由1//PO BD ，得APO ∠即为异面直线1BD 与AP 所成的角或其补角．由此能求出异面直线1BD 与AP 所成角的大小．【详解】（1）证明：设AC 和BD 交于点O ，则O 为BD 的中点. 连结PO ，又因为P 是1DD 的中点，所以1//PO BD . 又因为PO ⊂平面P AC ，1BD ⊄平面P AC 所以直线1//BD 平面P AC.（2）解：由（1）知，1//PO BD ，所以APO ∠即为异面直线1BD 与AP 所成的角或其补角.因为2PA PC ==，2122AO AC ==且PO AO ⊥，所以212sin 22AO APO AP ∠===. 又(0,90APO ︒︒⎤∠∈⎦，所以30APO ∠=︒ 故异面直线1BD 与AP 所成角的大小为30. 【点睛】方法点睛：异面直线所成的角的求法方法一：（几何法）找→作（平移法、补形法）→证（定义）→指→求（解三角形）方法二：（向量法）cos m n m nα=，其中α是异面直线,m n 所成的角，,m n 分别是直线,m n 的方向向量.16．（2020·上海长宁区·高三一模）如图，已知圆锥的顶点为P ，底面圆心为O ，高为23，底面半径为2.（1）求该圆锥的侧面积；（2）设OA ､OB 为该圆锥的底面半径，且90AOB ∠=︒，M 为线段AB 的中点，求直线PM 与直线OB 所成的角的正切值.【答案】（1）8π；（213【分析】（1）利用圆锥侧面积公式即可；（2）通过中点作辅助线即可．【详解】解：（1）OP ⊥底面OAB 由题意高3h =2r ，所以母线4l圆锥的侧面积S =12lr 12242π=⨯⨯⨯8π= （2）取OA 的中点为N ，因为M 为AB 的中点所以//MN OB ，PMN ∠就是直线PM 与直线OB 所成的角．因为OB OA ⊥，OB OP ⊥，所以OB ⊥平面POA ，MN ⊥平面POA ，MN PN ⊥ 在Rt △PNM 中，22()132rPN h =+=，112MN OB ==．所以PMN ∠的正切值为13．即直线PM 与直线OB 所成的角正切值为13．17．（2020·上海徐汇区·高三一模）如图：在直三棱柱111ABC A B C -中，2AC BC ==，14CC =，90ACB ∠=，E 、F 分别为棱1AA 、AB 的中点．（1）求异面直线1A C 与EF 所成的角的大小（结果用反三角函数值表示）；（2）求五棱锥11C EFBB A -的体积11C EFBB A V -．【答案】（1）5arctan （2）143．【分析】（1）连接1A B ，利用中位线的性质可得出1//A B EF ，由此可得出1BA C ∠（或其补角）就是异面直线1A C 与EF 所成的角，利用解三角形的知识求出1BA C ∠的正切值，即可得解；（2）计算出五边形1EFBB A 的面积，并推导出CF ⊥平面11AA B B ，再利用锥体的体积公式可计算出五棱锥11C EFBB A -的体积11C EFBB A V -. 【详解】（1）连接1A B ，E 、F 分别为1AA 、AB 的中点，所以，1//A B EF ，于是1BA C ∠（或其补角）就是异面直线1A C 与EF 所成的角，在1A BC 中，2BC =，221125AC AA AC =+=，221126A B AA AB =+=，22211A C BC A B ∴+=，所以1BC A C ⊥，所以，1125tan 525BC BAC AC ∠===．所以，异面直线1A C 与EF 所成角的大小为5arctan5；（2）由于111111822722AEFEFBB A ABB A S S S AB AA AE AF =-=⋅-⋅==五边形矩形连接CF ，2AC BC ==，F 为AB 的中点，90ACB ∠=，CF AB ∴⊥，且122CF AB == 1AA ⊥平面ABC ，CF ⊂平面ABC ，1CF AA ∴⊥，1AB AA A ⋂=，CF ∴⊥平面11AA B B ，所以11111114722333C EFBB A EFBB A V S CF -=⋅=⨯⨯=五边形．【点睛】思路点睛：平移线段法是求异面直线所成角的常用方法，其基本思路是通过平移直线，把异面直线的问题化归为共面直线问题来解决，具体步骤如下：（1）平移：平移异面直线中的一条或两条，作出异面直线所成的角；（2）认定：证明作出的角就是所求异面直线所成的角；（3）计算：求该角的值，常利用解三角形；（4）取舍：由异面直线所成的角的取值范围是0,2π⎛⎤⎥⎝⎦，当所作的角为钝角时，应取它的补角作为两条异面直线所成的角．18．（2020·上海大学附属中学高三三模）如图，正四棱锥P ABCD -中.（1）求证：BD ⊥平面PAC ；（2）若2AB =，423P ABCD V -=，求二面角A PB C --的余弦值. 【答案】（1）证明见解析；（2）1arccos 3⎛⎫- ⎪⎝⎭【分析】（1）先证明PO BD ⊥，结合,BD AC ⊥利用线面垂直的判定定理可得结论；（2）由423P ABCD V -=求出棱锥的高，可求得侧棱长，判定侧面的形状后可得二面角的平面角，利用余弦定理可得答案. 【详解】（1）因为P ABCD -是正棱锥，P ∴在面ABCD 内射影是AC 与BD 的交点O ，即PO ⊥面ABCD ，PO BD ∴⊥，又,BD AC PO ⊥与AC 在面PAC 内相交，BD ∴⊥面PAC ；（2）2142233P ABCD V PO -=⨯⨯=， 2PO ∴=，222PB =+=，则PAB △与PBC 为边长是2的正三角形，取PB 的中点E ，连,AE CE ，则AE PB ⊥，CE PB ⊥，AEC ∠是二面角的平面角，3381cos 3233AEC +-∠==-⨯⨯，1cos 3AEC arc ⎛⎫∠=- ⎪⎝⎭【点睛】本题主要考查线面垂直的证明以及二面角的求解，考查了正四棱锥的性质，属于中档题.19．（2019·上海市建平中学高三月考）如图：四面体ABCD 的底面ABC 是直角三角形，AC BC ⊥，3AC =，4BC =，DA ⊥平面ABC ，5DA =，E 是BD 上的动点（不包括端点）.（1）求证：AE 与BC 不垂直；（2）当AE DC ⊥时，求DEEB的值. 【答案】（1）证明见解析；（2）259.【分析】（1）利用反证法，先假设AE 与BC 垂直，然后根据条件推出与题设矛盾的结论，即可证明出AE与BC 不垂直；（2）先作辅助线//EF BC ，利用AE DC ⊥以及BC ⊥平面DAC 得到DC ⊥平面AEF ，由此得到AF DC ⊥，从而确定出F 点位置，再由DE DFEB FC=得到结果. 【详解】（1）假设AE BC ⊥，因为DA ⊥平面ABC ，所以DA BC ⊥，且DA AE A =，所以BC ⊥平面DAE ，又因为AB平面DAE ，所以BC AB ⊥，又因为由条件可知BC AC ⊥，所以BC AB ⊥不成立，故假设不成立，所以AE 与BC 不垂直；（2）过E 作//EF BC ，交DC 于F ，连接AF ，因为AC BC ⊥，DA BC ⊥且DA AC A =，所以BC ⊥平面DAC ，因为//EF BC ，所以EF ⊥平面DAC ，所以EF DC ⊥，又因为AE DC ⊥，EF DC ⊥，EF AE E =，所以DC ⊥平面AEF ，所以DC AF ⊥，又cos 25934AD ADC DC ∠===+，所以cos cos 34DF ADF ADC AD ∠=∠==，所以34DF =，所以34FC =，所以259DF FC =，所以由相似可知259DE DF EB FC ==. 【点睛】本题考查空间中的垂直关系的判断与证明，难度一般.空间中的不平行、不垂直关系的证明，如果正面证明比较麻烦，可采用反证法去证明.20．（2020·上海市七宝中学高三其他模拟）如图，四边形11ABB A 是圆柱1OO 的轴载面，4AB =，12OO =，以圆柱上底面为底面作高为2的圆锥1PO ，C 、1C 分别在AB 、11A B 上，2AOC π∠=，1113AO C π∠=.（1）求这个几何体的表面积和体积；（2）求二面角111O AC C --的余弦值. 【答案】（1）表面积为(1242π+，体积为323π；（23823-. 【分析】（1）计算出圆锥的母线长，利用圆锥的侧面积公式和圆柱的侧面积、底面积公式可计算出几何体的表面积，结合柱体和锥体的体积公式可求得几何体的体积；（2）以点O 为坐标原点，OA 、OC 、OP 所在直线分别为x 、y 、z 轴建立空间直角坐标系O xyz -，利用空间向量法可求得二面角111O AC C --的余弦值. 【详解】（1）由题意可知，圆柱的底面半径为22ABr ==，因为1PO 为圆锥的高，且12PO =，所以，圆锥的母线长为221122PA PO r =+=，又12OO =，因此，该几何体的表面积为(22+2222221242S ππππ=⨯⨯⨯+⨯=+.该几何体的体积为22132222233V πππ=⨯⨯+⨯⨯⨯=；（2）以点O 为坐标原点，OA 、OC 、OP 所在直线分别为x 、y 、z 轴建立如下图所示的空间直角坐标系O xyz -，则点()10,0,2O ，()12,0,2A ，()13,2C ，()0,2,0C ，设平面11A CC 的一个法向量为(),,m x y z =，()113,0AC =-，()12,2,2AC =--，由11100m AC m AC ⎧⋅=⎪⎨⋅=⎪⎩，得302220x x y z ⎧-=⎪⎨-+-=⎪⎩，令3x =1y =，13z =所以，平面11A CC 的一个法向量为(3,1,13m =，易知平面111O AC 的一个法向量为()0,0,1n =，()()22233cos ,82331131m n m n m n⋅<>===⋅-++-⨯，由图象可知，二面角111O AC C --31823--【点睛】本题考查组合体的表面积与体积的计算，同时也考查了利用空间向量法计算二面角的余弦值，考查计算能力，属于中等题.21．（2020·上海高三其他模拟）如图，已知⊙O 的直径AB=3，点C 为⊙O 上异于A ，B 的一点，VC ⊥平面ABC ，且VC=2，点M 为线段VB 的中点.（1）求证：BC ⊥平面VAC ；（2）若直线AM 与平面V AC 所成角为4π.求三棱锥B-ACM 的体积. 【答案】（1））祥见解析；（2）试题分析：（1）由线面垂直得VC ⊥BC ，由直径性质得AC ⊥BC ，由此能证明BC ⊥平面V AC ．（2）首先由（1）作出直线AM 与平面V AC 所成的角：取VC 的中点N ，连接MN ，AN ，则MN ∥BC ，由（I ）得BC ⊥平面VAC ，所以MN ⊥平面V AC ，则∠MAN 为直线AM 与平面V AC 所成的角.即∠MAN=4π，所以MN=AN ；这样就可求出AC 的长，且而求得体积．试题解析：（1）证明：因为VC ⊥平面ABC ，BC ABC ⊂平面，所以VC ⊥BC ，又因为点C 为圆O 上一点，且AB 为直径，所以AC ⊥BC ，又因为VC ，AC ⊂平面V AC ，VC∩AC=C ，所以BC ⊥平面V AC.（2）如图，取VC 的中点N ，连接MN ，AN ，则MN ∥BC ，由（I ）得BC ⊥平面V AC ，所以MN ⊥平面V AC ，则∠MAN 为直线AM 与平面V AC 所成的角.即∠MAN=4π，所以MN=AN ；令AC=a,则29-a ，MN=292a -；因为VC=2，M 为VC 中点，所以21a + 所以，292a -=21a +,解得a=1 因为MN ∥BC,所以考点：1.直线与平面垂直的判定;2. 棱柱、棱锥、棱台的体积;3. 直线与平面所成的角.22．（2020·上海高三其他模拟）已知正方体1111ABCD A B C D -，12AA =，E 为棱1CC 的中点．（1）求异面直线AE 与1DD 所成角的大小（结果用反三角表示）；（2）求C 点到平面ABE 的距离，并求出三锥C ADE -的体积．【答案】（1）1arccos 3；（2）C 点到平面ABE 25，三锥C ADE -的体积为23．【分析】（1）由已知得AEC ∠（或补角）是异面直线AE 与1DD 所成角，求解AEC 可得答案；（2）利用等体积E ABC C ABE V V --=，可求得设C 点到平面ABE 的距离，利用C ADE A CDE V V --=，可求得三锥C ADE -的体积．【详解】解：（1）连接AC ，因为11//CC DD ，所以AEC ∠（或补角）是异面直线AE 与1DD 所成角，在AEC 中，()22221cos 3221EC AEC AE AC EC ∠====++，所以异面直线AE 与1DD 所成角是1arccos 3；（2）设C 点到平面ABE 的距离为h ，因为E ABC C ABE V V --=，即1133ABC ABE S EC S h ⋅=⋅△△，又正方体1111ABCD A B C D -中，AB ⊥面11BB C C ，所以ABE △是Rt ABE △，又2222215BE BC EC =+=+=，所以1111221253232h ⨯⨯⨯⨯=⨯⨯⨯⋅，解得255h =，所以C ADE A CDE V V --=111212332DCE S AD ⎛⎫=⋅=⨯⨯⨯⨯ ⎪⎝⎭△23=.【点睛】本题考查空间中异面直线所成的角，运用等体积法求点到面的距离以及三棱锥的体积，属于中档题.。

2023年高考数学总复习：立体几何及答案解析

又∵已知 E 为 PB 的中点，∴OE∥PD．
∵PD⊄平面 AEC，OE⊂平面 AEC，
∴PD∥平面 AEC．
解：（2）∵
⺁，
⺁，∴
⺁⺁．
又∵PD⊥底面 ABCD，∴ 三棱锥 െ
∵E 是 PB 的中点，∴ 三棱锥 െ
⺁三棱锥 െ
⺁⺁⺁⺁⺁
⺁．
⺁三棱锥 െ
⺁⺁．
2．如图，在四棱锥 P﹣ABCD 中，PA⊥平面 ABC，AD∥BC，∠ABC＝90°，AD＝2，⺁， BC＝6．（1）求证：平面 PBD⊥平面 PAC；（2）PA 长为何值时，直线 PC 与平面 PBD 所成角最大？并求此时该角的正弦值．
第1页共3页
【解答】（1）证明：∵PA⊥平面 ABCD，BD⊂平面 ABCD，∴BD⊥PA，
又㋨๗
，㋨๗
，
∴∠ABD＝30°，∠BAC＝60°，∴∠AEB＝90°，即 BD⊥AC（E 为 AC 与 BD 交点）．
又 PA∩AC，∴BD⊥平面 PAC
又因为 BD⊂平面 PBD，所以平面 PBD⊥平面 PAC．
则๗ ๗
，即 െ ⺁㌳⺁ െ⺁㌳ ൅
，取 x＝1，
⺁得平面 PBD 的一个法向量为๗ （1，，），
所以 cos＜，๗＞
๗
，
๗
쳌㌳⺁
㌳
⺁⺁
㌳⺁㌳⺁
因为㌳⺁㌳⺁
㌳⺁⺁⺁
，当且仅当 t＝2 时等号成立，
所以 cos＜，๗＞
，记直线 PC 与平面 PBD 所成角为θ，
则 sinθ＝|cos＜，๗＞|，故 t๗ ，
即⺁时，直线 PC 与平面 PBD 所成角最大，此时该角的正弦值为．

高考数学一轮复习高考大题增分专项四高考中的立体几何课件文新人教版

2
体 ABCE 与四面体 ACDE 的体积比为 1∶1.
2
-10题型一
题型二
题型三
故 E 为 BD 的中点,从而 E 到平面 ABC 的距离为 D 到平面 ABC
1
1
的距离的 ,四面体 ABCE 的体积为四面体 ABCD 的体积的 ,即四面
2
体 ABCE 与四面体 ACDE 的体积比为 1∶1.
2
-16题型一
题型二
题型三
(2)证明:在△ABD中,AD=1,AB=2,∠BAD=60°,
由余弦定理可得BD= 3 ,
进而∠ADB=90°,即BD⊥AD.
又因为平面AED⊥平面ABCD,BD⊂平面ABCD,平面AED∩平面
ABCD=AD,所以BD⊥平面AED.
能力和空间想象能力,而且对数学运算的要求有加强的趋势.转化
与化归思想贯穿整个立体几何的始终.
-3题型一
题型二
题型三
题型一线线、线面平行或垂直的判定与性质
线线、线面平行或垂直的转化
1.在解决线线平行、线面平行问题时,若题目中已出现了中点,可
考虑在图形中再取中点,构成中位线进行证明.
2.要证线面平行,先在平面内找一条直线与已知直线平行,或找一
个经过已知直线与已知平面相交的平面,找出交线,证明二线平行.
3.要证线线平行,可考虑公理4或转化为线面平行.
4.要证线面垂直可转化为证明线线垂直,应用线面垂直的判定定
理与性质定理进行转化.
-4题型一
题型二
题型三
例1如图,在四棱锥P-ABCD中,侧面PAD为等边三角形且垂直于底
1
面ABCD,AB=BC= 2 AD,∠BAD=∠ABC=90°.

高考数学文一轮分层演练：第8章立体几何第1讲 Word版含解析

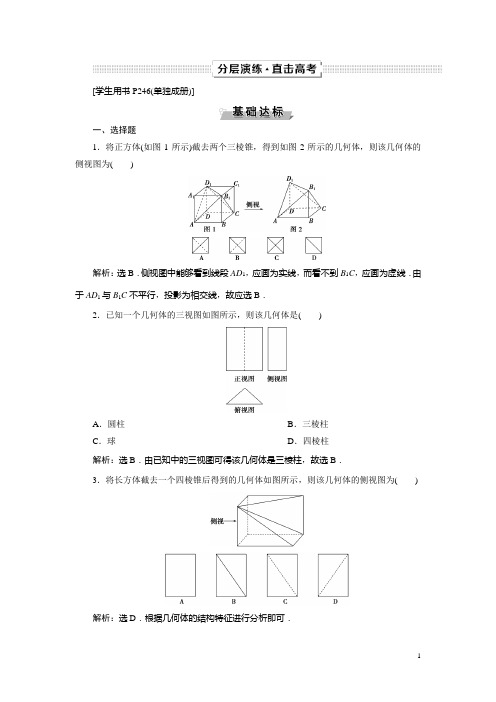
[学生用书P246(单独成册)]一、选择题1．将正方体(如图1所示)截去两个三棱锥，得到如图2所示的几何体，则该几何体的侧视图为()解析：选B．侧视图中能够看到线段AD1，应画为实线，而看不到B1C，应画为虚线．由于AD1与B1C不平行，投影为相交线，故应选B．2．已知一个几何体的三视图如图所示，则该几何体是()A．圆柱B．三棱柱C．球D．四棱柱解析：选B．由已知中的三视图可得该几何体是三棱柱，故选B．3．将长方体截去一个四棱锥后得到的几何体如图所示，则该几何体的侧视图为()解析：选D．根据几何体的结构特征进行分析即可．4．若某几何体的三视图如图所示，则这个几何体的直观图可以是()解析：选D ．A ，B 的正视图不符合要求，C 的俯视图显然不符合要求，故选D ． 5．如图，网格纸上小正方形的边长为1，粗实线画出的是某几何体的正视图(等腰直角三角形)和侧视图，且该几何体的体积为83，则该几何体的俯视图可以是( )解析：选C ．由正视图和侧视图及体积易得几何体是四棱锥P -ABCD ，其中ABCD 是边长为2的正方形，P A ⊥平面ABCD ，且P A ＝2，此时V P ABCD ＝13×22×2＝83，则俯视图为Rt△P AB ，故选C ．6．(2018·兰州适应性考试)如图，在正方体ABCD -A 1B 1C 1D 1中，点P 是线段A 1C 1上的动点，则三棱锥P -BCD 的俯视图与正视图面积之比的最大值为( )A ．1B ． 2C ． 3D ．2解析：选D ．正视图，底面B ，C ，D 三点，其中D 与C 重合，随着点P 的变化，其正视图均是三角形且点P 在正视图中的位置在边B 1C 1上移动，由此可知，设正方体的棱长为a ，则S正视图＝12×a 2；设A 1C 1的中点为O ，随着点P 的移动，在俯视图中，易知当点P 在OC 1上移动时，S 俯视图就是底面三角形BCD 的面积，当点P 在OA 1上移动时，点P 越靠近A 1，俯视图的面积越大，当到达A 1的位置时，俯视图为正方形，此时俯视图的面积最大，S 俯视图＝a 2，所以S 俯视图S 正视图的最大值为a 212a 2＝2，故选D ．二、填空题7．如图，一个水平放置的平面图形的直观图是一个底角为45°，腰和上底长均为1的等腰梯形，则该平面图形的面积为________．解析：直观图的面积S ′＝12×(1＋1＋2)×22＝2＋12．故原平面图形的面积S ＝S ′24＝2＋2．答案： 2＋ 28．一个圆台上、下底面的半径分别为3 cm 和8 cm ，若两底面圆心的连线长为12 cm ，则这个圆台的母线长为________cm ．解析：如图，过点A 作AC ⊥OB ，交OB 于点C ．在Rt △ABC 中，AC ＝12 cm ，BC ＝8－3＝5(cm)．所以AB ＝122＋52＝13(cm)．答案：139．已知正四棱锥V -ABCD 中，底面面积为16，一条侧棱的长为211，则该棱锥的高为________．解析：如图，取正方形ABCD 的中心O ，连接VO ，AO ，则VO 就是正四棱锥V -ABCD 的高．因为底面面积为16，所以AO＝22．因为一条侧棱长为211，所以VO＝VA2AO2＝44－8＝6．所以正四棱锥V-ABCD的高为6．答案：610．如图是一个几何体的三视图，则该几何体任意两个顶点间距离的最大值是________．解析：作出直观图如图所示，通过计算可知AF、DC最长且DC＝AF＝BF2＋AB2＝33．答案：3 3三、解答题11．如图，在四棱锥P-ABCD中，底面为正方形，PC与底面ABCD垂直，如图为该四棱锥的正视图和侧视图，它们是腰长为6 cm的全等的等腰直角三角形．(1)根据图中所给的正视图、侧视图，画出相应的俯视图，并求出该俯视图的面积；(2)求P A．解：(1)该四棱锥的俯视图为(内含对角线)边长为6 cm的正方形，如图，其面积为36 cm2．俯视图(2)由侧视图可求得PD ＝PC 2＋CD 2＝62＋62＝6 2 (cm)．由正视图可知AD ＝6 cm ，且AD ⊥PD ，所以在Rt △APD 中， P A ＝PD 2＋AD 2＝（62）2＋62＝6 3 (cm)．12．如图所示的三个图中，上面是一个长方体截去一个角所得多面体的直观图，它的正视图和侧视图如图所示(单位：cm)．(1)在正视图下面，按照画三视图的要求画出该多面体的俯视图； (2)按照给出的尺寸，求该多面体的体积．解：(1)如图．(2)所求多面体的体积 V ＝V 长方体－V 正三棱锥＝4×4×6－13×(12×2×2)×2＝2843(cm 3)．。

2023届高考数学总复习：立体几何附答案解析

第1页共2页
（1）求证：C1F∥平面 ABE；（2）求三棱锥 A﹣BCE 的体积．
【解答】（1）证明：取 AB 的中点 G，连接 EG，FG， ∵E，F，G 分别是 A1C1，BC，AB 的中点，
∴FG∥AC，且 FG ࡐAC，EC1 ࡐA1C1，
∵AC∥A1C1 且 AC＝A1C1，∴GF∥EC1 且 GF＝EC1，
又 AB⊥AC，B1C∩AC＝C，
所以 AB⊥平面 AB1C，AB⊂ABB1A1；
所以平面 AB1C⊥平面 ABB1A1；
（Ⅱ）解：设 BC1∩B1C＝O，作 OE⊥AB1 于 E，连结 BE，
∵平面 AB1C⊥平面 ABB1A1 于 AB1，∴OE⊥平面 ABB&1A1，
∴∠EBO 为 BC1 与平面 ABB1A1 所成角；
∴四边形 FGEC1 为平行四边形，得 C1F∥EG，
又∵EG⊂平面 ABE，C1F⊄平面 ABE，∴C1F∥平面 ABE；
（2）解：∵AA1＝AC＝2，BC＝1，AB⊥BC，∴AB
ࡐ
∴三棱锥 A﹣BEC 的体积 V＝VA﹣BEC＝VE﹣ABC
ࡐ
．
ࡐ
ࡐ．
第2页共2页
由已知 AB＝AC＝2，
ࡐ ，得 B1C＝2，
ࡐ ࡐ，
∴t
ࡐ tࡐ ，
在等腰直角△AB1C 中，t㤵 ࡐࡐ，
所以 th 㤵 t
t㤵 t
ࡐ，即 BC1 与平面 ABB1A1 所成角的正弦值为
ࡐ ．
2．如图，在直三棱柱 ABC﹣A1B1C1 中，AB⊥BC，AA1＝AC＝2，BC＝1，E，F 分别是 A1C1， BC 的中点．
2023 年高考：立体几何复习题及答案
1．在斜三棱柱 ABC﹣A1B1C1 中，AB⊥AC，B1C⊥平面 ABC，且 AB＝AC＝2，AA1＝2 ．（Ⅰ）求证：平面 AB1C⊥平面 ABB1A1；（Ⅱ）求直线 BC1 与平面 ABB1A1 所成角的正弦值．

高考数学二轮专题升级训练解答题专项训练(立体几何)文(含解析)新人教A版

高考数学二轮专题升级训练解答题专项训练 ( 立体几何 )文（含分析）新人教A版1.下列图是一个几何体的直观图及它的三视图( 此中正 ( 主 ) 视图为直角梯形, 俯视图为正方形, 侧 ( 左 )视图为直角三角形, 尺寸如下图) .(1)求四棱锥 P-ABCD的体积;(2)若 G为 BC的中点,求证: AE⊥ PG.2. (2013 ·吉林通化模拟 ,19) 如图 , 在四棱锥P-ABCD中 , 底面ABCD为平行四边形 , N是PB的中点 ,过 A, N, D三点的平面交 PC于点 M.(1)求证 : PD∥平面ANC;(2)求证 : M是PC的中点 ;(3)若 PD⊥底面 ABCD,PA=AB,BC⊥ BD,证明:平面 PBC⊥平面 ADMN.3.如图 , AA1, BB1为圆柱OO1的母线 , BC是底面圆O的直径, D, E 分别是 AA1, CB1的中点, DE⊥平面 CBB1.(1)证明 : DE∥平面ABC;(2)求四棱锥 C-ABB1A1与圆柱 OO1的体积比 .4.如下图 , 平面ABCD⊥平面ABEF,ABCD是正方形 , ABEF是矩形 , 且AF=AD=2, G是EF的中点.(1)求证 : 平面AGC⊥平面BGC;(2)求三棱锥 A-GBC的体积 .5.已知正四周体ABCD(图1),沿 AB, AC, AD剪开,展成的平面图形正好是( 图 2) 所示的直角梯形A1A2A3D(梯形的极点A1, A2, A3重合于四周体的极点A) .(1)证明 : AB⊥CD;(2)当 A1D=10, A1A2=8时,求四周体 ABCD的体积 .6.如图 , 已知三棱锥P-ABC中, PA⊥平面 ABC,AB⊥ AC, PA=AC=AB,N为 AB上一点, AB=4AN, M, D, S 分别为 PB, AB, BC的中点 .(1)求证 : PA∥平面CDM;(2)求证 : SN⊥平面CDM.7.如图 , 在三棱柱ABC-A1B1C1中,侧棱与底面垂直,∠ABC=90°,AB=BC=BB12, M, N分别是AB, A1C的中点.(1 ) 求证 : MN∥平面BCC1B1;( 2) 求证 : MN⊥平面A1B1C;(3)求三棱锥 M-A1B1C的体积 .8 .一个多面体的直观图和三视图如下图, 此中,分别是, 的中点.M G AB DF(1)求证 : CM⊥平面FDM;(2)在线段 AD上(含 A, D端点)确立一点 P,使得 GP∥平面 FMC,并给出证明 .##1.解 : (1) 由几何体的三视图可知 , 底面 ABCD是边长为 4 的正方形 ,PA⊥面 ABCD,PA∥ EB,且PA=4,BE=2, AB=AD=CD=CB=4,所以 V P-ABCD=PA·S正方形ABCD=×4×4×4=.(2)证明 : 连结 BP.由于 , ∠ EBA=∠ BAP=90°,所以△ EBA∽△ BAP,所以∠ PBA=∠AEB,所以∠ PBA+∠ BAE=∠ BEA+∠ BAE=90°, 所以 PB⊥ AE.由题易证 BC⊥平面 APEB,所以 BC⊥ AE.又由于 PB∩ BC=B,所以 AE⊥平面 PBC,由于 PG? 平面 PBC,所以 AE⊥ PG.2. 解 : 证明 (1) 连结 BD,AC, 设 BD∩ AC=O,连结 NO.∵ ABCD是平行四边形,∴O是 BD的中点 .在△ PBD中 ,又 N 是 PB 的中点 , ∴ PD∥NO.又 NO? 平面 ANC,PD?平面 ANC,∴PD∥平面 ANC.(2)∵底面 ABCD为平行四边形 ,∴AD∥BC.∵BC?平面 ADMN,AD? 平面 ADMN,∴BC∥平面 ADMN.∵平面 PBC∩平面 ADMN=MN,∴BC∥MN.(3) ∵ PA=AB,N是 PB 的中点 , ∴ PB⊥ AN.∵BC⊥BD,AD∥ BC,∴ AD⊥BD.∵PD⊥底面 ABCD,AD? 底面 ABCD,∴PD⊥AD.∵ PD∩ BD=D,∴AD⊥平面 PBD.∴ PB⊥ AD.∵AD∩AN=A,∴ PB⊥平面 ADMN.∵PB? 平面 PBC,∴平面 PBC⊥平面 ADMN.3. 解 :(1) 证明 :连结 EO,OA.∵E,O 分别为 B1C,BC 的中点 ,∴EO∥BB1.又 DA∥ BB1, 且 DA=EO=BB1.∴四边形 AOED是平行四边形,即 DE∥ OA.又 DE?平面 ABC,AO? 平面 ABC,∴DE∥平面 ABC.(2) 解 : 由题意知 DE⊥平面 CBB1, 且由 (1) 知 DE∥OA,∴AO⊥平面 CBB1, ∴ AO⊥ BC,∴AC=AB.因 BC是底面圆 O的直径 , 得 CA⊥ AB.而 AA1⊥ CA,AA1∩ AB=A,∴ CA⊥平面 AA1 B1B, 即 CA 为四棱锥的高 .设圆柱高为h, 底面半径为r,则 V 柱 =π r 2h,V 锥 =h(r) ·(r)=hr2,∴V锥∶V柱=.4. 解 :(1) 证明 : ∵G是矩形 ABEF的边 EF的中点 , ∴ AG=BG==2,222进而得 :AG +BG=AB, ∴ AG⊥ BG.又∵平面 ABCD⊥平面 ABEF,平面 ABCD∩平面 ABEF=AB,且 BC⊥AB,∴BC⊥平面 ABEF.∵ AG? 平面 ABEF,∴BC⊥AG.∵BC∩BG=B,∴ AG⊥平面 BGC,∵AG? 平面 AGC,∴平面 AGC⊥平面 BGC.(2) 解 : 由 (1) 得 BC⊥平面 ABEF,∴CB是三棱锥A-GBC的高 .而 S△ABG=×2×2=4,∴V A -GBC=V C-ABG=×4×4=.5.解 :(1) 证明 : 在四周体 ABCD中 , ? AB⊥平面 ACD? AB⊥ CD.(2)解 : 在题图 2 中作 DE⊥ A2A3于点 E.∵A1A2=8,∴DE=8.又∵ A1D=A3D=10, ∴ EA3=6,A 2A3=10+6=16.又 A2C=A3C,∴ A2C=8.即题图 1 中 AC=8,AD=10,由 A1A2=8,A 1B=A2B 得题图 1 中 AB=4.∴S△ACD=DE·A3C=×8×8=32.又∵ AB⊥面 ACD,∴ V B-ACD=×32×4=.6. 解 : 证明 : (1) 在三棱锥P-ABC中 , 由于 M,D 分别为 PB,AB 的中点 ,所以 MD∥ PA.由于 MD? 平面 CMD,PA?平面 CMD,所以 PA∥平面 CMD.(2) 由于 M,D 分别为 PB,AB 的中点 , 所以 MD∥PA.由于 PA⊥平面 ABC,所以 MD⊥平面 ABC.又 SN? 平面 ABC,所以 MD⊥ SN.在△ ABC中 , 连结 DS,由于 D,S 分别为 AB,BC的中点 , 所以 DS∥AC且 DS=AC.又 AB⊥ AC,所以∠ ADS=∠BAC=90°.由于 AC=AB,所以 AC=AD,所以∠ ADC=45°, 所以∠ CDS=45°.又 AB=4AN,所以 DN=AD=AC,即 DN=DS,故SN⊥CD. 又 MD∩ CD=D,所以 SN⊥平面 CMD.7.解:( 1)证明:连结BC1,AC1.由题知点N在AC1上且为AC1的中点.∵M是 AB的中点 ,∴MN∥BC1.又∵ MN?平面 BCC1B1,∴MN∥平面 BCC1B1.(2)证明 : ∵三棱柱 ABC-A1B1C1中, 侧棱与底面垂直 , ∴四边形 BCC1B1是正方形 ,∴BC1⊥ B1C,∴ MN⊥ B1 C.连结 A1M,由∠ ABC=∠ MAA1=90°,BM=AM,BC=AA1得△ AMA1≌△ BMC∴. A1M=CM又. N 是 A1C的中点, ∴ MN⊥ A1C.∵B1C 与 A1C 订交于点 C, ∴ MN⊥平面 A1B1C.(3) 解 : 由 (2) 知 MN是三棱锥M-A1B1C的高 . 在直角△ MNC中 ,MC=,NC=,∴MN=.又 =2, ∴MN·.8. 解 : 由三视图可得直观图为直三棱柱且底面ADF中 AD⊥ DF,DF=AD=a.(1) 证明 : ∵ FD⊥平面 ABCD,CM? 平面 ABCD,∴FD⊥CM.在矩形 ABCD中 ,CD=2a,AD=a,M 为 AB 的中点 ,DM=CM=a,∴ CM⊥ DM.∵FD? 平面 FDM,DM? 平面 FDM,FD∩ DM=D,∴CM⊥平面 FDM.(2) 点 P在 A点处.证明 : 取 DC中点 S, 连结 AS,GS,GA,∵G是 DF的中点 , ∴ GS∥FC.又 AS∥ CM,AS∩AG=A,∴平面 GSA∥平面 FMC.而 GA? 平面 GSA,∴GP∥平面 FMC.。

高三数学立体几何复习(可编辑修改word版)

2009 数学专题立体几何 [基础自测] 一、平行关系与垂直

1. 空间三条直线互相平行,由每两条平行线确定一个平面,则可确定平面的个数为 B A．3 B．1 或 3 C．1 或 2 D．2 或 3 2. 若 a、b 为异面直线，直线 c∥a，则 c 与 b 的位置关系是 D A．相交 B．异面 C．平行 D．异面或相交 3. 下面表述正确的是（ C ） A、空间任意三点确定一个平面 B、分别在不同的三条直线上的三点确定一个平面C、直线上的两点和直线外的一点确定一个平面 D、不共线的四点确定一个平面 4. 直线 a 与 b 垂直， b 又垂直于平面，则 a 与的位置关系是（ D ） A、 a  B、 a // C、 a  D、 a  或 a //

5. 若 m, n 表示直线，表示平面，则下列命题中，正确命题的个数为（ C ） m // n 

m m m //

① m   n ；② n   m // n ；③ n //  m  n ；④ m  n

 n 

   

A、1 个 B、2 个 C、3 个 D、4 个6．若 a，b 是异面直线，P 是 a，b 外的一点，有以下四个命题： ①过 P 点可作直线 k 与 a，b 都相交;②过 P 点可作平面与 a，b 都平行; ③过 P 点可作直线与 a，b 都垂直;④过 P 点可作直线 k 与 a，b 所成角都等于 50  . 这四个命题中正确命题的序号是（ D ） A．①、②、③ B．②、③、④ C．② D．③、④

7. 直线 a  平面，直线b  ，且// ,则 a 与 b 的位置关系为平行或异面。

8. 设α、β、γ为平面，给出下列条件：（1） a,b 为异面直线，a  α,b  β,a∥β,b∥α；（2） α内距离为 d 的平行直线在β内的射线仍为两条距离为 d 的平行线；（3） α内不共线的三点到β的距离相等；（4） α⊥γ,β⊥γ 其中，能使α∥β成立的条件个数为：A

2018届高三数学(文)二轮复习专题集训：专题五立体几何5.2 Word版含解析

A级1．设α，β是两个不同的平面，m是直线且m⊂α，“m∥β”是“α∥β”的()A．充分而不必要条件B．必要而不充分条件C．充分必要条件D．既不充分也不必要条件解析：当m∥β时，过m的平面α与β可能平行也可能相交，因而m∥β⇒/ α∥β；当α∥β时，α内任一直线与β平行，因为m⊂α，所以m∥β.综上知，“m∥β”是“α∥β”的必要而不充分条件．答案： B2．(2017·全国卷Ⅰ)如图，在下列四个正方体中，A，B为正方体的两个顶点，M，N，Q为所在棱的中点，则在这四个正方体中，直线AB与平面MNQ不平行的是()解析：B选项中，AB∥MQ，且AB⊄平面MNQ，MQ⊂平面MNQ，则AB∥平面MNQ；C选项中，AB∥MQ，且AB⊄平面MNQ，MQ⊂平面MNQ，则AB∥平面MNQ；D选项中，AB∥NQ，且AB⊄平面MNQ，NQ⊂平面MNQ，则AB∥平面MNQ.故选A.答案： A3．(2017·新疆第二次适应性检测)设m，n是不同的直线，α，β，γ是不同的平面，有以下四个命题：①若α∥β，α∥γ，则β∥γ②若α⊥β，m∥α，则m⊥β③若m⊥α，m∥β，则α⊥β④若m∥n，n⊂α，则m∥α其中正确命题的序号是()A．①③B．①④C．②③D．②④解析：对于①，因为平行于同一个平面的两个平面相互平行，所以①正确；对于②，当直线m位于平面β内，且平行于平面α，β的交线时，满足条件，但显然此时m与平面β不垂直，因此②不正确；对于③，在平面β内取直线n平行于m，则由m⊥α，m∥n，得n ⊥α，又n⊂β，因此有α⊥β，③正确；对于④，直线m可能位于平面α内，显然此时m与平面α不平行，因此④不正确．综上所述，正确命题的序号是①③，选A.答案： A4．如图，在三棱锥P-ABC中，不能证明AP⊥BC的条件是()A．AP⊥PB，AP⊥PCB．AP⊥PB，BC⊥PBC．平面BPC⊥平面APC，BC⊥PCD．AP⊥平面PBC解析：A中，因为AP⊥PB，AP⊥PC，PB∩PC＝P，所以AP⊥平面PBC，又BC⊂平面PBC，所以AP⊥BC，故A正确；C中，因为平面BPC⊥平面APC，BC⊥PC，所以BC⊥平面APC，AP⊂平面APC，所以AP⊥BC，故C正确；D中，由A知D正确；B中条件不能判断出AP⊥BC，故选B.答案： B5．在正方体ABCD-A1B1C1D1的侧面ABB1A1内有一动点P到直线A1B1与直线BC的距离相等，则动点P所在的曲线的形状为()解析：由题意可知点P到点B的距离等于到直线A1B1的距离，根据抛物线的定义可知，动点P的轨迹是以点B为焦点，以A1B1为准线的过点A的抛物线的一部分．A选项中的图象为直线，排除A.C选项中点B不是抛物线的焦点，排除C.D选项中的图象不过A点，排除D.故选B.答案： B6．如图，在空间四边形ABCD 中，M ∈AB ，N ∈AD ，若AM MB ＝ANND ，则直线MN 与平面BDC 的位置关系是________．解析：由AM MB ＝ANND ，得MN ∥BD .而BD ⊂平面BDC ，MN ⊄平面BDC ，所以MN ∥平面BDC . 答案：平行7．已知α，β表示两个不同的平面，m ，n 表示两条不同的直线，且m ⊥β，α⊥β，给出下列四个结论：①∀n ⊂α，n ⊥β； ②∀n ⊂β，m ⊥n ； ③∀n ⊂α，m ∥n ； ④∃n ⊂α，m ⊥n .则上述结论正确的为________．(写出所有正确结论的序号)解析：由于m ⊥β，α⊥β，所以m ⊂α或m ∥α.∀n ⊂α，则n ⊥β或n ⊂β或n ∥β或n 与β斜交，所以①不正确；∀n ⊂β，则由直线与平面垂直的性质，知m ⊥n ，②正确；∀n ⊂α，则m ∥n 或m ，n 相交或m ，n 互为异面直线，③不正确；当m ⊂α或m ∥α时，∃n ⊂α，m ⊥n ，④正确．答案： ②④ 8.如图，P A ⊥圆O 所在的平面，AB 是圆O 的直径，C 是圆O 上的一点，E 、F 分别是点A 在PB 、PC 上的正投影，给出的下列结论正确的是________．①AF ⊥PB ；②EF ⊥PB ； ③AF ⊥BC ；④AE ⊥平面PBC .解析：由题意知P A ⊥平面ABC ，所以P A ⊥BC . 又AC ⊥BC ，P A ∩AC ＝A ，所以BC ⊥平面P AC . 所以BC ⊥AF .因为AF ⊥PC ，BC ∩PC ＝C ，所以AF ⊥平面PBC ，PB ⊂平面PBC ，所以AF ⊥PB ，又AE ⊥PB ，AE ∩AF ＝A ，所以PB ⊥平面AEF ，所以PB ⊥EF . 故①②③正确．答案： ①②③9．(2017·惠州市第三次调研考试)在如图所示的多面体ABCDE 中，已知ABCD 是边长为2的正方形，平面ABCD ⊥平面ABE ，∠AEB ＝90°，AE ＝BE .(1)若M 是DE 的中点，试在AC 上找一点N ，使得MN ∥平面ABE ，并给出证明； (2)求多面体ABCDE 的体积．解析： (1)连接BD ，交AC 于点N ，则点N 即为所求，证明如下： ∵ABCD 是正方形，∴N 是BD 的中点，又M 是DE 的中点，∴MN ∥BE ， ∵BE ⊂平面ABE ，MN ⊄平面ABE ， ∴MN ∥平面ABE .(2)取AB 的中点F ，连接EF ，∵△ABE 是等腰直角三角形，且AB ＝2， ∴EF ⊥AB ，EF ＝12AB ＝1，∵平面ABCD ⊥平面ABE ，平面ABCD ∩平面ABE ＝AB ， EF ⊂平面ABE ，∴EF ⊥平面ABCD ，即EF 为四棱锥E -ABCD 的高， ∴V 四棱锥E -ABCD ＝13S 正方形ABCD ·EF ＝13×22×1＝43.10．如图，过底面是矩形的四棱锥F -ABCD 的顶点F 作EF ∥AB ，使AB ＝2EF ，且平面ABFE ⊥平面ABCD ，若点G 在CD 上且满足DG ＝GC .(1)求证：FG ∥平面AED ； (2)求证：平面DAF ⊥平面BAF .证明： (1)因为DG ＝GC ，AB ＝CD ＝2EF ，AB ∥EF ∥CD ，所以EF ∥DG ，EF ＝DG .所以四边形DEFG 为平行四边形，所以FG ∥ED .又因为FG ⊄平面AED ，ED ⊂平面AED ，所以FG ∥平面AED .(2)因为平面ABFE ⊥平面ABCD ，平面ABFE ∩平面ABCD ＝AB ，AD ⊥AB ，AD ⊂平面ABCD ，所以AD ⊥平面BAF ，又AD ⊂平面DAF ，所以平面DAF ⊥平面BAF .B 级1．(2017·成都市第二次诊断性检测)把平面图形M 上的所有点在一个平面上的射影构成的图形M ′称为图形M 在这个平面上的射影．如图，在长方体ABCD -EFGH 中，AB ＝5，AD ＝4，AE ＝3.则△EBD 在平面EBC 上的射影的面积是( )A ．234B ．252C ．10D ．30解析：连接HC ，过D 作DM ⊥HC ，连接ME ，MB ，因为BC ⊥平面HCD ，又DM ⊂平面HCD ，所以BC ⊥DM ，因为BC ∩HC ＝C ，所以DM ⊥平面HCBE ，即D 在平面HCBE 内的射影为M ，所以△EBD 在平面HCBE 内的射影为△EBM ，在长方体中，HC ∥BE ，所以△MBE 的面积等于△CBE 的面积，所以△EBD 在平面EBC 上的射影的面积为12×52＋32×4＝234，故选A.答案： A2．(2017·惠州市第三次调研考试)如图是一几何体的平面展形图，其中四边形ABCD 为正方形，E ，F 分别为P A ，PD 的中点，在此几何体中，给出下面4个结论：①直线BE 与直线CF 异面； ②直线BE 与直线AF 异面； ③直线EF ∥平面PBC ； ④平面BCE ⊥平面P AD . 其中正确的有( ) A ．1个 B ．2个 C ．3个D ．4个解析：将展开图还原为几何体(如图)，因为E ，F 分别为P A ，PD 的中点，所以EF ∥AD ∥BC ，即直线BE 与CF 共面，①错；因为B ∉平面P AD ，E ∈平面P AD ，E ∉AF ，所以BE 与AF 是异面直线，②正确；因为EF ∥AD ∥BC ，EF ⊄平面PBC ，BC ⊂平面PBC ，所以EF ∥平面PBC ，③正确；平面P AD 与平面BCE 不一定垂直，④错．故选B.答案： B3．如图所示，平行四边形ABCD 中，∠DAB ＝60°，AB ＝2，AD ＝4.将△CBD 沿BD 折起到△EBD 的位置，使平面EBD ⊥平面ABD .(1)求证：AB ⊥DE ；(2)求三棱锥E -ABD 的侧面积和体积．解析： (1)证明：在△ABD 中，因为AB ＝2，AD ＝4，∠DAB ＝60°，所以BD ＝AB2＋AD2－2AB·AD cos ∠DAB＝23，所以AB2＋BD2＝AD2，所以AB⊥BD.又平面EBD⊥平面ABD，平面EBD∩平面ABD＝BD，AB⊂平面ABD，所以AB⊥平面EBD.又DE⊂平面EBD，所以AB⊥DE.(2)由(1)知AB⊥BD.因为CD∥AB，所以CD⊥BD，从而DE⊥BD.在Rt△DBE中，因为DB＝23，DE＝DC＝AB＝2，所以S△EDB＝12BD·DE＝2 3.因为AB⊥平面EBD，BE⊂平面EBD，所以AB⊥BE.因为BE＝BC＝AD＝4，所以S△EAB＝12AB·BE＝4.因为DE⊥BD，平面EBD⊥平面ABD，平面EBD∩平面ABD＝BD，所以DE⊥平面ABD，而AD⊂平面ABD，所以DE⊥AD，故S△EAD＝12AD·DE＝4.故三棱锥E-ABD的侧面积S＝S△EDB＋S△EAB＋S△EAD＝8＋2 3. 因为DE⊥平面ABD，且S△ABD＝S△EBD＝23，DE＝2，所以V三棱锥E-ABD＝13S△ABD×DE＝13×23×2＝433.4．在多面体ABCDEF中，底面ABCD是梯形，四边形ADEF是正方形，AB∥DC，AB ＝AD＝1，CD＝2，AC＝EC＝ 5.(1)求证：平面EBC⊥平面EBD；(2)设M为线段EC上一点，且3EM＝EC，试问在线段BC上是否存在一点T，使得MT ∥平面BDE，若存在，试指出点T的位置；若不存在，请说明理由．解析：(1)证明：因为AD＝1，CD＝2，AC＝5，所以AD2＋CD2＝AC2，所以△ADC为直角三角形，且AD⊥DC.同理，因为ED＝1，CD＝2，EC＝5，所以ED2＋CD2＝EC2，所以△EDC 为直角三角形，且ED ⊥DC . 又四边形ADEF 是正方形，所以AD ⊥DE ，又AD ∩DC ＝D ，所以ED ⊥平面ABCD .又BC ⊂平面ABCD ，所以ED ⊥BC .在梯形ABCD 中，过点B 作BH ⊥CD 于点H ，故四边形ABHD 是正方形，所以∠ADB ＝45°，BD ＝ 2. 在Rt △BCH 中，BH ＝CH ＝1，所以BC ＝2，故BD 2＋BC 2＝DC 2，所以BC ⊥BD .因为BD ∩ED ＝D ，BD ⊂平面EBD ，ED ⊂平面EBD ，所以BC ⊥平面EBD ，又BC ⊂平面EBC ，所以平面EBC ⊥平面EBD .(2)在线段BC 上存在一点T ，使得MT ∥平面BDE ，此时3BT ＝BC .连接MT ，在△EBC 中，因为BT BC ＝EM EC ＝13，所以MT ∥EB .又MT ⊄平面BDE ，EB ⊂平面BDE ，所以MT ∥平面BDE .。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

1 升级增分训练立体几何 1．某四面体的三视图如图，则其四个面中最大的面积是( )

A．2 B．22 C．3 D．23 解析：选D 在正方体ABCD-A1B1C1D1中还原出三视图的直观图，其是一个三个顶点在正方体的右侧面、一个顶点在左侧面的三棱锥，即为D1-BCB1，如图所示，其四个面的面积分别为2,22，22，23，故选D． 2．(2016·广东茂名二模)若几何体的三视图如图所示，则该几何体的外接球的表面积为( )

A．34π B．35π C．36π D．17π 解析：选A 由几何体的三视图知它是底面为正方形且有一条侧棱垂直于底面的四棱锥，可把它补成一个长、宽、高分别为3,3,4的长方体，该长方体的外接球即为原四棱锥的外接球，所以4R2＝32＋32＋42＝34(其中R为外接球的半径)，外接球表面积为S＝4πR2＝34π．

3．(2017·湖南长沙三校联考)已知点E，F，G分别是正方体ABCD-A1B1C1D1

的棱AA1，CC1，DD1的中点，点M，N，Q，P分别在线段DF，AG，BE，C1B1

上．以M，N，Q，P为顶点的三棱锥P-MNQ的俯视图不可能是( ) 2

解析：选C 当M与F重合、N与G重合、Q与E重合、P与B1重合时，三棱锥P-MNQ的俯视图为A；当M，N，Q，P是所在线段的中点时，三棱锥P-MNQ的俯视图为B；当M，N，Q，P位于所在线段的非端点位置时，存在三棱锥P-MNQ，使其俯视图为D． 4．(2017·河南中原名校联考)

如图，四棱柱ABCD-A1B1C1D1是棱长为1的正方体，四棱锥S-ABCD是高为1的正四棱锥，若点S，A1，B1，C1，D1在同一个球面上，则该球的表面积为( )

A．916π B．2516π

C．4916π D．8116π

解析：选D 作如图所示的辅助线，其中O为球心，设OG1＝x，则OB1＝SO＝2－x，

由正方体的性质知B1G1＝22，则在Rt△OB1G1中， OB21＝G1B21＋OG21，

即(2－x)2＝x2＋222，解得x＝78，所以球的半径R＝OB1＝98， 3

所以球的表面积为S＝4πR2＝8116π．

5．(2016·湖南长沙四校一模)某几何体的三视图如图所示，则该几何体的体积为( )

A．1136 B．3 C．533 D．433 解析：选B 由三视图知该几何体是一个四棱锥，其直观图如图所示，△PAD为正三角形，四棱锥的底面是直角梯形，四棱锥

的高为3，∴所求体积V＝13×12×1＋2×2×3＝3． 6．(2016·湖南郴州模拟)一只蚂蚁从正方体ABCD-A1B1C1D1的顶点A出发，经正方体的表面，按最短路线爬行到顶点C1的位置，则下列图形中可以表示正方体及蚂蚁最短爬行路线的正视图的是( )

A．①② B．①③ C．③④ D．②④ 解析：选D 由点A经正方体的表面，按最短路线爬行到达顶点C1的位置，共有6种路线(对应6种不同的展开方式)，若把平面ABB1A1和平面BCC1B1展到同一个平面内，连接AC1，则AC1是最短路线，且AC1会经过BB1的中点，此时对应的正视图为②；若把平面ABCD和平面CDD1C1展到同一个平面内，连接AC1，则AC1是最短路线，且AC1会经过CD的中点，此时对应的正视图为④．而其他几种展开方式对应的正视图在题中没有出现． 4

7．(2016·福建省质检)在三棱锥P-ABC中，PA＝23，PC＝2，AB＝7，BC＝3，∠ABC＝π2，则三棱锥P-ABC外接球的表面积为( )

A．4π B．163π

C．323π D．16π

解析：选D 设三棱锥P-ABC的外接球的半径为R，在△ABC中，因为AB＝7，BC＝3，∠ABC＝π2，所以AC＝AB2＋BC2＝4．在△PAC中，因为PA＝

23，PC＝2，AC＝4，所以PA2＋PC2＝AC2，所以∠APC＝π2，所以AC为三棱锥P-ABC的外接球的直径，所以R＝2，所以此三棱锥的外接球的表面积S＝4πR2＝4π×22＝16π．

8．(2016·南宁模拟)设点A，B，C为球O的球面上三点，O为球心．球O的表面积为100π，且△ABC是边长为43的正三角形，则三棱锥O-ABC的体积为( ) A．12 B．123 C．243 D．363

解析：选B ∵球O的表面积为100π＝4πr2，∴球O的半径为5．如图，取△ABC的中心H，连接OH，连接并延长AH

交BC于点M，则AM＝432－4322＝6，AH＝23AM＝4，∴OH＝OA2－AH2＝52－42＝3， ∴三棱锥O-ABC的体积为V＝13×34×(43)2×3＝123． 9．如图，三棱锥V-ABC的底面为正三角形，侧面VAC与底面垂直且VA＝VC，已知其正视图的面积为23，则其侧视图的面积为________．解析：设三棱锥V-ABC的底面边长为a，侧面VAC的边AC上的高为h，

则ah＝43，其侧视图是由底面三角形ABC边AC上的高与侧面三角形VAC边AC上的高组成的直角三角形， 5

其面积为12×32a×h＝12×32×43＝33．答案：33

10．(2016·南昌一模)正三角形ABC的边长为2，将它沿高AD翻折，使点B与点C间的距离为2，此时四面体ABCD外接球的表面积为________．解析：由题知，求四面体ABCD的外接球的表面积可转化为求长、宽、高分别

为1,1，3的长方体的外接球的表面积，其半径R＝12 12＋12＋3 2＝52，所以S＝4πR2＝5π．答案：5π 11．(2016·江西师大附中模拟)已知边长为23的菱形ABCD中，∠BAD＝60°，沿对角线BD折成二面角A-BD-C的大小为120°的四面体，则四面体的外接球的表面积为________．解析：如图1，取BD的中点E，连接AE，CE．由已知条件可知，平面ACE⊥平面BCD．易知外接球球心在平面ACE内，如图2，在CE上取点G，使CG＝2GE，过点G作l1垂直于CE，过点E作l2垂直于AC，设l1与l2交于点O，连接OA，OC，则OA＝OC，易知O即为球心．分别解△OCG，△EGO可得R＝OC＝7，∴外接球的表面积为28π．

答案：28π 12．(2017·贵州适应性考试)已知正三棱柱(底面是正三角形，侧棱与底面垂直)的体积为33 cm3，其所有顶点都在球O的球面上，则球O的表面积的最小值为________cm2．解析：球O的表面积最小等价于球O的半径R最小．设正三棱柱的底面边长

为a，高为b，则正三棱柱的体积V＝34a2b＝33，所以a2b＝12．底面正三角形所在截面圆的半径r＝33a，则R2＝r2＋b22＝33a2＋b24＝13×12b＋b24＝4b＋b24，令f(b) 6

＝4b＋b24，0＜b＜2R，则f′(b)＝b3－82b2．令f′(b)＝0，解得b＝2，当0＜b＜2时f′(b)＜0，函数f(b)单调递减，当b＞2时，f′(b)＞0，函数f(b)单调递增，所以当b＝2时，f(b)取得最小值3，即(R2)min＝3，故球O的表面积的最小值为4π(R2)min＝12π．答案：12π

13．如图1，在直角梯形ABCD中，AD∥BC，∠BAD＝π2，AB＝BC＝1，AD＝2，E是AD的中点，O是AC与BE的交点．将△ABE沿BE折起到△A1BE的位置，如图2．

(1)证明：CD⊥平面A1OC； (2)若平面A1BE⊥平面BCDE，求平面A1BC与平面A1CD的夹角的余弦值．解：(1)证明：在题图1中，因为AB＝BC＝1，AD＝2，E是AD的中点，∠

BAD＝π2，所以BE⊥AC．即在题图2中，BE⊥OA1，BE⊥OC，从而BE⊥平面A1OC，又BC∥DE，DE＝1＝BC，所以四边形BCDE为平行四边形，所以CD∥BE，所以CD⊥平面A1OC． (2)由已知，平面A1BE⊥平面BCDE，又由(1)知，BE⊥OA1，BE⊥OC，所以∠A1OC为二面角A1-BE-C的平面角，

所以∠A1OC＝π2．如图，以O为原点，建立空间直角坐标系，因为A1B＝A1E＝BC＝ED＝1，BC∥ED，

所以B22，0，0，E－22，0，0，

A10，0，22，C0，22，0， 7

得BC―→＝－22，22，0，A1C―→＝0，22，－22， CD―→＝BE―→＝(－2，0,0)．设平面A1BC的法向量为n1＝(x1，y1，z1)，平面A1CD的法向量为n2＝(x2，y2，z2)，平面A1BC与平面A1CD的夹角为θ，

则 n1·BC―→＝0，n1·A1C―→＝0，得 －x1＋y1＝0，y1－z1＝0，取y1＝1，得平面A1BC的一个法向量为n1＝(1,1,1)；

由 n2·CD―→＝0，n2·A1C―→＝0，得 x2＝0，y2－z2＝0，取y2＝1，得平面A1CD的一个法向量为n2＝(0,1,1)．从而cos θ＝n1，n2＝23×2＝63，

即平面A1BC与平面A1CD的夹角的余弦值为63．