【KS5U首发】山东省2013年高二暑假作业(二)理科数学
13级高二数学暑假作业2试卷及答案

高三数学高考模拟练习题第一部分 (选择题 共60分)一、选择题:本大题共12小题,每题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的,请将正确的答案填在后面的括号内1.设全集U =R ,集合}14|{2<=x x A ,}1|1||{<-=x x B ,则=B A ( ) (A )}20|{<<x x (B )}10|{<<x x (C )}210|{<<x x (D )}410|{<<x x2.复数31ii-化简为( )(A )i --1 (B )i -1 (C )i +-1 (D )i +13.函数)0(,1log )(2>=x xx f 的反函数的大致图像为( )(A ) (B ) (C ) (D ) 4.抛物线24x y =的焦点到准线的距离为( ) (A )4 (B )2 (C )41 (D )815.设变量y x ,满足约束条件⎪⎩⎪⎨⎧≥≤+≥-0302y y x y x ,则式子y x -的最小值等于( )(A )1- (B )0 (C )1 (D )26.已知函数⎩⎨⎧<+≥=)0(,)0(,2)(x c x x x f x ,“函数)(x f 在R 上递增”是“函数)(x f 在R 上连续”的( )(A )充分不必要条件 (B )必要不充分条件 (C )充要条件 (D )既不充分也不必要条件 7.在ABC ∆中,角C B A ,,所对边长分别为c b a ,,,且满足=-+-)2sin (sin )2sin (sin A B b B A aC c sin ,则C sin 的值为( )(A )21 (B )41 (C )23 (D )4158.已知m l ,是两条不同的直线,βα,是两个不同的平面,在下列条件中,能成为m l ⊥的充分条件的是( )(A )l =βα ,m 与βα、所成角相等 (B )m l ,在α内的射影分别为//,m l ,且//m l ⊥ (C )l =βα ,αβ⊥⊂m m , (D )βα⊥,βα//,m l ⊥9.已知函数)(,|ln |1ln )(R k x x k x f ∈+=,且1)75(tan = f ,则)15(tanf 的值等于( )(A )1- (B )1 (C )0 (D )与k 有关10.已知P 是正四面体S-ABC 表面SAB 内任意一点,P 到点S 的距离为1d ,P 到直线AB 的距离为2d ,P 到面ABC 的距离为3d ,若321,,d d d 成等差数列,则P 的轨迹为( )(A )圆的一部分 (B )椭圆的一部分 (C )抛物线的一部分 (D )双曲线的一部分 11.从集合}3,2,1,0,1,2,3{---=A 中,任取2个元素y x ,作向量),(y x OP =,从这些向量中任取两个向量,两个向量为一对,则互相垂直的向量共有( )对 (A )66 (B )60 (C )54 (D )4812.定义在),1[+∞上的函数)(x f 满足)2(2)(x f x f =,当]2,1[∈x 时,|32|44)(--=x x f ,设函数)(x f 在)(],2,2[*1N n x n n ∈∈-上的极大值为n a ,则数列}{n a 的所有项之和为( ) (A )2 (B )4 (C )8 (D )16第二部分 (非选择题 共90分)二、填空题:本大题共4小题,每题4分,共16分,把答案填在题中的横线上 13.在6)12(xx -的展开式中,常数项为 .14.半径为R 的球面上有三点A 、B 、C ,任意两点的球面距离都等于π,且球心到平面ABC 的距离为R 36,则该球的表面积为 .15.已知直线2=+by ax 经过点)(),sin ,(cos R P ∈ααα,则2211ba+的最小值等于 .16.已知单位向量j i ,的夹角为)0(πθθ<<,若j y i x a +=则),(y x 叫做向量a 的][θ坐标,记作θ),(y x a =,有以下命题: ①已知60)1,2(-=a ,则5||=a ;②若θθ),(,),(2211y x b y x a ==,则=+b a θ),(2121y y x x ++; ③若θθ),(,),(2211y x b y x a ==,则=⋅b a 2121y y x x +;④向量θ),(11y x OA =,θθ),(,),(3322y x OC y x OB ==,若C B A ,,三点共线,则)(,)1(213R x x x ∈-+=λλλ上述命题中正确的有 .(将你认为正确的都写上) 三、解答题:本大题共6小题,共74分 17.(12分)已知函数)0(),3sin(cos 4)(>-⋅=ωπωωx x x f 的图像的相邻两条对称轴的距离为2,(1)求函数)(x f 的最大值及相应的x 的值;(2)若函数)(x f 按向量),(k h a =平移后得奇函数)(x g y =,求当||a 最小时的a 的坐标.18.某学科共开设有必修一、必修二、选修一和选修二共四门课程,要求必修一、二都要合格,且选修一和选修二至少有一门合格,则才能修得该学科的学分,现有甲、乙、丙三位同学报名参加该学科的学习,每一位同学对这四门课程考试是否合格相互独立,其合格的概率均相同,(见下表),且每一门课程是否合格相互独立,(1(2)记ξ表示三位同学中能修得该学科学分的人数,求ξ的分布列及数学期望ξE .19.(12分)在三棱锥ABC S -中,⊥SA 平面ABC ,60,1,2,2=∠===CAB AC AB SA ,E D ,分别为AB 、SB 上的点,且AD AB SE SB 4,2==,(1)证明:BC SC ⊥;(2)求二面角E AC S --的大小; (3)求点A 到平面CDE 的距离.20.(12分)定义在),0(+∞上的函数)(x f 满足对任意的正数b a ,都有bb f aa f abab f )()()(+=,且1)2(-=f ,记数列)21(nn f a =,(1)证明数列}2{n na ⋅为等差数列,并求数列}{n a 的通项公式;(2)设数列}{n a 的前n 项和为n S , 证明1<n S .BCASDE21.(12分)已知椭圆)0(12222>>=+b a by ax 的离心率为21,焦点到对应准线的距离为3,斜率为1的直线l 与椭圆相交于不同两点21,P P ,O 为坐标原点, (1)若7321-=⋅OP OP ,求直线l 的方程;(2)以21P P 为直径作圆,P 是圆上任意一点,求||OP 的最大值.22.(14分)已知函数)1ln()(+=x x f ,x x g 21)(=,(1)求函数)()(x g x f y -=的极值; (2)不等式2)(++>x t x x f )(*N t ∈,当1≥x 时恒成立,求t 的值;(3)证明:852ln )]1(3)2([3213+<--<∑=n k f k f n nk .参考答案:一、选择题1.C ,提示:142<x 的解集为)21,21(-,1|1|<-x 的解集为)2,0(,故)21,0(=B A 2.D ,提示:i ii i ii ii +=--=--=-1)1(11233.B ,提示:x x xxx f 212122logloglog1log)(=-===-,所以xx f)21()(1=-4.D ,提示:抛物线)0(,22>=p py x 焦点到准线的距离为p 5.A ,提示:画出可行域得2,1==y x 时,y x -取最小值1-6.B ,提示:当1≤c 时,函数)(x f 在R 上递增,当1=c 时,函数)(x f 在R 上连续 7.C ,提示:由正弦定理得ab cb a ca b b b a a =-+⇒=-+-2222)2()2(,由余弦定理得21cos =C ,故23sin =C8.C ,提示:因为αβ⊥⊂m m ,,所以l m ⊥9.A ,提示:)(|ln |1ln )1(x f x xk x f -=+-=,又75t a n 115t a n =,1)75tan 1()15(tan -==∴f f10.D ,提示:3122d d d += ,由正四面体ABC S -得23322d d =,所以2123222d d d +=,化简得),1(322221+∞∈-=d d11.B ,提示:设),(),,(2211y x b y x a ==互相垂直,当都不含0时,必有一向量的横纵坐标同号,故分三类,第一类:021==y x ,共有3666=⨯对,第二类:0,011>>y x ,共有12223=⨯A 对,第三类:0,011<<y x ,共有12223=⨯A 对,12.C ,提示:函数)(x f 当)(],2,2[*1N n x n n ∈∈-时,|]32)21(|1[)21()(13--=--x x f n n ,所以函数在1223-⋅=n x 的取得极大值,且3)21(-=n n a ,所以数列}{n a 的所有项之和为811=-=qa S二、填空题13.60,提示:2366626612)1()1()2(r r rr r rrr r xC xx C T ----+⋅-=-=,所以4=r 时得常数项 14.π36,提示:由题意知ABC O -为正四面体(O 是球心),所以33=⇒=R R ππ15.4,提示:即直线2=+by ax 与圆122=+yx 有公共点,所以111222≤+ba16. ②④,提示:若60)1,2(-=a,则360cos 414||=⋅-+==a ;若θθ),(,),(2211y x b y x a ==,j y y i x x j y i x j y i x b a )()(21212211+++=+++=+, θcos )()()(122121212211y x y x y y x x j y i x j y i x b a +++=+⋅+=⋅若θ),(11y x OA =,θθ),(,),(3322y x OC y x OB ==,则θ),(2121y y x x BA --=, θ),(2323y y x x BC --=,所以)(2123x x x x -=-λ三、解答题17.解(1)32cos 32sin ]cos 23sin 21[cos 4)(--=-=x x x x x x f ωωωωω3)32sin(2)(--=∴πωx x f …………………….3分由条件知函数周期为4,即2422πωωπ=⇒= …………………….5分所以函数的最大值为32-,其中)(,265Z k k x ∈+= ……………………6分(2)函数3)3sin(2)(--=ππx x f 按向量),(k h a =平移后得:k h x x g +---=3]3)(sin[2)(ππ为奇函数, …………………….8分即0)0(=g ,所以3),(,3=∈=--k Z n n h πππ …………………….10分 当||a 最小时,3,31=-=k h ,即)3,31(-=a …………………….12分18.解:(1)分别记甲对这四门课程考试合格为事件D C B A ,,,,则“甲能修得该学学分”的概率为)()()(D C AB P D ABC P ABCD P ++ ………….3分 事件D C B A ,,,相互独立,)()()(D C AB P D ABC P ABCD P +++⋅⋅⋅=21323243+⋅⋅⋅2132324312521313243=⋅⋅⋅ …………….6分 (2)303)127()0(C P ==ξ, 2113)127()125()1(C P ==ξ1223)127()125()2(C P ==ξ 333)125()3(C P ==ξ …………….8分因为)125,3(~B ξ ……………10分 所以451253=⨯=ξE …………….12分19.解法一:(1)在ABC ∆中,60,1,2=∠==CAB AC AB 由余弦定理得:3=BC ,即AC BC ⊥ …………………….2分又⊥SA 平面ABC ,所以AC 为SC 在平面ABC 内的射影, BC SC ⊥∴ …………………….4分 (2)分别取AC SC ,中点G F ,,连接EG FG EF ,,由(1)知⊥EF 平面SAC ,且AC FG ⊥,所以AC EG ⊥, 即EGF ∠为所求二面角的平面角, …………………….6分 在EFG ∆中,22,23==FG EF ,26tan ==∠∴FGEF EGF所以所求二面角大小为26arctan …………………….8分BCA SDEFG(3)在SBC ∆中,E 是SB 中点,且3==SC BC ,CE SB ⊥∴在ABC ∆中,由平几知识得AB CD ⊥,所以CD SB ⊥所以⊥SB 平面CDE ,即BE 为点B 到平面CDE 的距离,且26=BE …………………….10分又因为点A 到平面CDE 的距离是点B 到平面CDE 的距离的31所以点A 到平面CDE 的距离为66 …………………….12分解法二:(1)同解法一, ……………………4分 (2)如图建立空间直角坐标系)22,23,21(),0,3,1(),2,0,0(),0,0,1(E B S C ∴设平面ACE 的法向量为),,(1z y x n =由⎪⎩⎪⎨⎧=+=⇒⎪⎩⎪⎨⎧⊥⊥02223011z y x AE n AC n ,令1-=z 得)1,36,0(1-=n …………………….5分 取平面SAC 的法向量)0,1,0(2=n …………………….6分 所以510,cos 21>=<n n …………………….8分(3)同理取平面CDE 的法向量为)2,3,1(-=n ,…………………….10分6661||===∴d …………………….12分20.解(1)令21,)21(1==-b a n 得:21)21(21)21(21)21(11f f f n n n n+=--,即)21(22211f a a n n n n =---再令2,21==b a 得:2)2()21(21)1(f f f +=,又0)1(1)1(1)1(1)1(=⇒+=f f f f ,所以41)21(=f ……………………2分 21)21(22211==-∴--f a a n n n n ,记}2{n na 是以21为公差,21为首项的等差数列……………4分1)21(+⋅=∴n n n a …………………….6分(2)132)21()21(2)21(1+⋅++⋅+⋅=n n n S243)21()21(2)21(121+⋅++⋅+⋅=n n n S 相减得2132)21()21(1)21(1)21(121++⋅-⋅++⋅+⋅=n n n n S …………………….10分 21)21()21(1)21(1)21(1)21(212132-⋅-⋅++⋅+⋅+=⇒++n n n n S化简得1212111<⋅--=+n nn n S ……………………12分21. 解答:(1)由已知得椭圆方程为13422=+yx…………………….2分设直线m x y l +=:, 设),(),,(22111y x P y x P联立0124871342222=-++⇒⎪⎩⎪⎨⎧=++=m mx x yx m x y 78,712421221m x x m x x -=+-=∴,所以7123)(22212121-=+++=m m x x m x x y y37324773222121=⇒-=-⇒-=+mmy y x x ,…………………….4分又702<⇒>∆m3:±=∴x y l …………………….5分(3)设21P P 中点为M ,即M 为圆心,||||||MP OM OP +≤∴||21||21P P OM += ……………………6分设m x y l P P +=:21,由椭圆的对称性不妨设0≥m联立0124871342222=-++⇒⎪⎩⎪⎨⎧=++=m mx x yx mx y 由韦达定理得)73,74()2,2(2121mm M y y x x M -⇒++75)2()2(||221221m y y x x OM =+++=∴ …………………….7分 由弦长公式得7762||21221m P P -⋅= ……………………8分≤∴||OP ||21||21P P OM +776252m m -⋅+= 令)20(,sin 7παα<<=m 所以)sin(77cos 422sin 7576252ϕααα+=+=-+m m ………………10分所以当1)sin(=+ϕα时,7777776252==-⋅+m m 所以7||max =OP …………………….12分 22.证明(1)102111/=⇒=-+=x x y , …………………….1分 且当11<<-x 时,0/>y ,当1>x 时,0/<y 所以212ln -=极大值y …………………….3分 (2)x x x t x tx x f -++<⇒++>)1ln()2(2)(令x x x x h -++=)1ln()2()(, 则0)1ln(111)1ln(12)(/>+++=-++++=x x x x x x h ,(1≥x )…………5分所以12ln 3)(min -=x h ,即)2,0(12ln 3∈-<t …………………6分 1=∴t …………………….7分(3)因为)11ln()1(3)2(333k k k f k f ++=-- ……………………8分 当1>x 时,由(1)知212ln 21)1ln(-+<+x x , ………………9分 由(2)知21)1ln(++>+x x x ………………10分 所以当2≥k 时,])1)(1(1[212ln 2ln 21)11ln(333+-+<+<++∴k k k k k k ])1(1)1(1[412ln +--+<k k k k852ln )]1(3)2([13+<--∴∑=n k f k f nk ………………12分 另一方面,321312)11ln(3333>++>++∴k k k k ,即n k f k f n k 32)]1(3)2([13>--∑=综上得原不等式成立 ………………14分。
山东省高二数学暑假作业(三)理
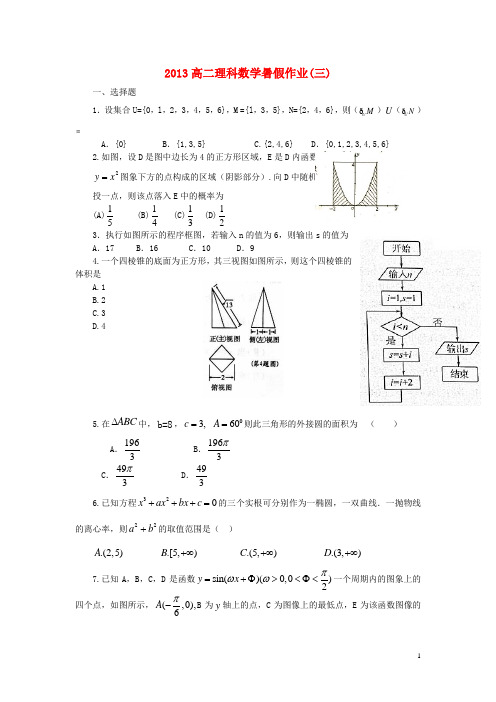
2013高二理科数学暑假作业(三)一、选择题1.设集合U={0,l ,2,3,4,5,6},M ={l ,3,5},N={2,4,6},则(U M ð)U (U N ð)﹦A .{0}B .{1,3,5} C.{2,4,6} D .{0,1,2,3,4,5,6} 2.如图,设D 是图中边长为4的正方形区域,E 是D 内函数2x y =图象下方的点构成的区域(阴影部分).向D 中随机投一点,则该点落入E 中的概率为 (A)51 (B)41 (C)31 (D)21 3.执行如图所示的程序框图,若输入n 的值为6,则输出s 的值为 A .17 B .16 C .10 D .94.一个四棱锥的底面为正方形,其三视图如图所示,则这个四棱锥的体积是A.1B.2C.3D.45.在ABC ∆中,b=8,3,c = 060A =则此三角形的外接圆的面积为 ( )A .1963B .1963πC .493πD .4936.已知方程320x ax bx c +++=的三个实根可分别作为一椭圆,一双曲线.一抛物线的离心率,则22a b +的取值范围是( ).(2,5)A .[5,)B +∞ .(5,)C +∞ .(3,)D +∞7.已知A ,B ,C ,D 是函数sin()(0,0)2y x πωω=+Φ><Φ<一个周期内的图象上的四个点,如图所示,(,0),6A π-B 为y 轴上的点,C 为图像上的最低点,E 为该函数图像的一个对称中心,B 与D 关于点E 对称,CD uuu r 在x 轴上的投影为12π,则,ωΦ的值为A.2,3πω=Φ= B .2,6πω=Φ= C. 1,23πω=Φ= D .1,26πω=Φ= 8.各项为正的等比数列{}n a 中,4a 与14a 的等比中项为22,则7112a a +的最小值为( )A .16B .8C .22D .49.已知x,y 满足条件020x y x x y k ≥⎧⎪≤⎨⎪++≤⎩(k 为常数),若目标函数3z x y =+的最大值为8,则k=A.16-B.6-C.83-D.610.已知抛物线的顶点在原点,焦点在x 轴的正半轴上,若抛物线的准线与双曲线5x 2-y 2= 20的两条渐近线围成的三角形的面积等于54,则抛物线的方程为A .y 2=4xB .y 2=8xC .x 2=4yD .x 2=8y11设正实数x,y,z x 2-3xy+4y 2-z=0.则当xyz取得最大值时,212x y z +-为 (A )0 (B )1 (C ) 94(D )312.若函数()y f x =的导函数...在区间[,]a b 上是增函数,则函数()y f x =在区间[,]a b 上的图象可能是( )二、填空题13.已知0,0x y >>且满足281x y+=,则x y +的最小值为14.某校高三年级的学生共1000人,一次测验成绩的分布直方图如右图所示,现要按右图所示的4个分数段进行分层抽样,抽取50人了解情况,则在80~90分数段应抽取人数为 。
山东省2013年高二暑假作业(二)理科数学

2013高二理科数学暑假作业(二)一、选择题 1.复数11ii+-(i 是虚数单位)的共轭复数的虚部为 A.1-B.0C.1D.22.已知不同的直线m ,n ,l ,不重合的平面,αβ,则下列命题正确的是 A .m//α,n∥α,则m∥nB .m//α,m//β,则α//βC .m⊥l ,n⊥l ,则m∥nD .m⊥α,m⊥β,则α// 3. 曲线33y x x =-和y x =围成的面积为( ).4A .8B .10C .9D4.已知0)](log [log log 237=x ,那么21-x 等于( )A.31B.63C.33D.425.某车间为了规定工时定额,需要确定加工零件所花费的时间,为此进行了5次试验,根据收集到的数据(如下表),由最小二乘法求得回归直线方程0.6854.6y x =+表中有一个数据模糊不清,请你推断出该数据的值为A .68B . 68.2C .69D .756.函数)1(1)(xx n x f -=的图象是7.如果n a a )13(32-的展开式中各项系数之和为128,则展开式中2a 的系数是 ( )A .-2835 B.2835 C.21 D.-21 8.下列四个判断: ①2,10x R x x ∃∈-+≤;②已知随机变量X 服从正态分布N (3,2σ),P (X ≤6)=0.72,则P (X ≤0)=0.28; ③已知21()nx x+的展开式的各项系数和为32,则展开式中x 项的系数为20;④11e dx x>⎰⎰其中正确的个数有:A .1个B .2个C .3个D .4个9.已知ABC ∆中,三个内角A ,B ,C 的对边分别为a,b,c ,若ABC ∆的面积为S ,且()222,tan S a b c C =+-则等于A.34B.43C.43-D.34-10 . 把正整数按一定的规则排成了如图所示的三角形数表.设*(,)ij a i j N ∈ 是位于这个三角形数表中从上往下数第i 行,从左 往右数第j 个数,若2013ij a =, 则i 与j 的和为( )A .105B .103C .82D .81 11.要得到函数()sin(2)3f x x π=+的导函数'()f x 的图象,只需将()f x 的图象( )A .向左平移2π个单位,再把各点的纵坐标伸长到原来的2倍(横坐标不变) B .向左平移2π个单位,再把各点的纵坐标缩短到原来的12倍(横坐标不变)C .向左平移4π个单位,再把各点的纵坐标伸长到原来的12倍(横坐标不变)D .向左平移4π个单位,再把各点的纵坐标伸长到原来的2倍(横坐标不变)12.等差数列{}n a 前n 项和为n S ,已知310061006(1)2013(1)1,a a -+-=124753121086911131517141618202224310081008(1)2013(1)1,a a -+-=-则A.2013100810062013,S a a => B .2013100810062013,S a a =< C.2013100810062013,S a a =-> D .2013100810062013,S a a =-< 二、填空题 13.若x,y 满足⎩⎨⎧≥+-≤+-,22,0y x y x 则的最大值y x C )(log 21+=为 .14.以椭圆192522=+y x 的焦点为焦点,离心率为2的双曲线方程为15.已知函数()f x 在实数集R 上具有下列性质:①直线1x =是函数()f x 的一条对称轴;②()()2f x f x +=-;③当1213x x ≤<≤时,()()()21f x f x -⋅()210,x x -<则()2012f 、()2013f 从大到小的顺序为_______.16. 已知2()(0)f x ax bx c a =++≠,且方程()f x x =无实数根,下列命题: ①方程[()]f f x x =也一定没有实数根;②若0a >,则不等式[()]f f x x >对一切实数x 都成立; ③若0a <,则必存在实数0x ,使00[()]f f x x >④若0a b c ++=,则不等式[()]f f x x <对一切实数x 都成立. 其中正确命题的序号是 . 三、解答题17. 已知向量2(3sin,1),(cos ,cos ).444x x xm n ==记()f x m n =⋅. (Ⅰ)若3()2f α=,求2cos()3πα-的值; (Ⅱ)在△ABC 中,角A 、B 、C 的对边分别是a 、b 、c ,且满足(2)cos cos a c B b C -=,若13()f A +=,试判断△ABC 的形状. 18.已知函数)0()221(1)(2>-+=a ax x ax n x f .(Ⅰ)若的一个极)(是函数21x f x =值点,求a 的值; (Ⅱ)求证:当0<a ≤2时,f(x)在⎪⎭⎫⎢⎣⎡∞+,21上是增函数;(Ⅲ)若对任意的)2,1(∈a ,总存在]2,1[0∈x ,使不等式)1()(20a m x f ->成立,求实数m的取值范围.19.由世界自然基金会发起的“地球1小时”活动,已发展成为最有影响力的环保活动之一,今年的参与人数再创新高.然而也有部分公众对该活动的实际效果与负面影响提出了疑问.对此,某新闻媒体进行了网上调查,所有参与调查的人中,持“支持”、“保留”和“不支持”态度的人数如下表所示:(1)在所有参与调查的人中,用分层抽样的方法抽取个人,已知从“支持”态度的人中抽取了45人,求n 的值;(2)在持“不支持”态度的人中,用分层抽样的方法抽取5人看成一个总体,从这5人中任意选取2人,求至少有1人20岁以下的概率;20.(本小题满分13分)如图,椭圆22122:1(0)x y C a b a b +=>>的离心率为2,x 轴被曲线22:C y x b =-截得的线段长等于1C 的短轴长。
山东省2013年高二暑假作业(二)理科数学.pdf

2013高二理科数学暑假作业(二) 一、选择题 1.复数(i是虚数单位)的共轭复数的虚部为 A.B.0C.1D.2 2.已知不同的直线m,n,l,不重合的平面,则下列命题正确的是 A.m//,n∥,则m∥n B.m//,m//,则// C.m⊥,n⊥,则m∥n D.m⊥,m⊥,则//和围成的面积为( ) 4.已知,那么等于( ) A. B. C. D. 5.某车间为了规定工时定额,需要确定加工零件所花费的时间,为此进行了5次试验,根据收集到的数据(如下表),由最小二乘法求得回归直线方程 表中有一个数据模糊不清,请你推断出该数据的值为 A.68 B. 68.2 C.69 D.75 的图象是 7.如果的展开式中各项系数之和为128,则展开式中的系数是 ( ) A.-2835 B.2835 C.21 D.-21 8.; ②已知随机变量X服从正态分布N(3,),P(X≤6)=0.72,则P(X≤0)=0.28; ③已知的展开式的各项系数和为32,则展开式中x项的系数为20; ④ 其中正确的个数有: A.1个 B.2个 C.3个 D.4个 9.已知中,三个内角A,B,C的对边分别为a,b,c,若的面积为S,且等于 A.B.C.D. 10 . 把正整数按一定的规则 排成了如图所示的三角形数表.设是位于这个三角形数表中从上下数第行从左往右数第个数若,则与的和( )A. B.10C. D.的导函数的图象,只需将的图象( ) A.向左平移个单位,再把各点的纵坐标伸长到原来的2倍(横坐标不变) B.向左平移个单位,再把各点的纵坐标缩短到原来的倍(横坐标不变) C.向左平移个单位,再把各点的纵坐标伸长到原来的倍(横坐标不变) D.向左平移个单位,再把各点的纵坐标伸长到原来的2倍(横坐标不变) 12.等差数列前项和为,已知 则 A. B. C. D. 二、填空题 13.若x,y满足则为 . 14.以椭圆的焦点为焦点,离心率为2的双曲线方程为 15.已知函数在实数集R上具有下列性质:①直线是函数的一条对称轴;②;③当时, 、从大到小的顺序为_______. 16. 已知,且方程无实数根,下列命题: ①方程也一定没有实数根; ②若,则不等式对一切实数都成立; ③若,则必存在实数,使 ④若,则不等式对一切实数都成立. 其中正确命题的序号是 . 三、解答题 17. 已知向量记. (Ⅰ)若,求的值; (Ⅱ)在△ABC中,角A、B、C的对边分别是、、,且满足,若,试判断△ABC的形状. 18.已知函数. (Ⅰ)若值点,求a的值; (Ⅱ)求证:当0。
山东省2013年高二暑假作业(一)理科数学含答案

2013高二理科数学暑假作业(一)一.选择题1.复数z 满足(z-3)(2-i)=5(i 为虚数单位),则z 的共轭复数为( D ) A. 2+i B.2-i C. 5+i D.5-i2. 函数xxx f +=1cos )(在)1,0(处的切线方程是( ) A .01=-+y x B .012=-+y x C .012=+-y x D .01=+-y x 3.“x x 22-<0”是“22<-x ”的(A)充分条件 (B)充分而不必要条件 (C)必要而不充分条件 (D)既不充分也不必要条件4.如图,在棱长为1的正方体ABCD -A 1B 1C 1D 1中,M 、N 分别为A 1B 1和BB 1的中点,那么直线AM 与CN 所成的角的余弦值为( )A.32B.1010C.35 D.255.用数学归纳法证明不等式()1111n 1>2322n n N *-++++∈,第二步由k 到k+1时不等式左边需增加( )A.12k B.111212k k-++ C.1111121222k k k --++++ D.1111121222k k k --+++++ 6.利用如图所示程序框图在直角坐标平面上打印一系列点,则打印的点落在坐标轴上的个数是( )A.0B.1C.2D.37.若x x f x f x f ln 4)1(')2(2)(-+-=,则)1(f 等于( )A.2-B.4-C.2D. 08.己知等差数列{a n }的首项为a 1,公差为d ,其前n 项和为S n ,若直线y = a 1x 与圆(x -2)2+ y 2=1的两个交点关于直线x+y+d=0对称,则S n =A . n 2B .-n 2C .2n -n 2D .n 2-2n9.点P 到图形C 上每一个点的距离的最小值称为点P 到图形C 的距离,那么平面内到定圆C 的距离与到定点A 的距离相等的点的轨迹不可能...是( ) A .圆 B .椭圆 C .双曲线的一支 D .直线 10.已知f (x )=41x 2+sin ⎪⎭⎫⎝⎛+x 2π,f '(x )为f (x )的导函数,则f '(x )的图像是11.下列几个命题:①方程0)3(2=+-+a x a x 有一个正实根,一个负实根,则a<0; ②函数2211x x y -+-=是偶函数,但不是奇函数;③函数)(x f 的定义域是[-2,2],则函数)1(+x f 的定义域为[-1,3];④一条曲线23x y -=和直线y=a(a R ∈)的公共点个数是m ,则m 的值不可能是1.其中真命题的个数是(A)1 (B)2 (C)3 (D)412.设函数()sin()cos()(0,)2f x x x πωϕωϕωϕ=+++><的最小正周期为π,且()()f x f x -=,则( )A.()f x 在0,2π⎛⎫⎪⎝⎭单调递减 B.()f x 在3,44ππ⎛⎫⎪⎝⎭单调递减 C.()f x 在0,2π⎛⎫⎪⎝⎭单调递增D.()f x 在3,44ππ⎛⎫⎪⎝⎭单调递增二.填空题 13.若423401234(2x a a x a x a x a x =++++,则2202413()()a a a a a ++-+______=14.已知向量AB 与AC 的夹角为120,且||3,||2,AB AC ==若,AP AB AC λ=+且AP BC ⊥,则实数λ的值为15.如图所示,一个三棱锥的三视图是三个直角三角形,则该三棱锥的外接球的表面积为 。
山东省高二数学暑假作业(五)理

2013高二数学(理)暑假作业(五)一、选择题1.已知全集}{1,2,3,4U =,集合{}{}1,2,2,4A B ==,则()U B B =ð(A ){}1,2 (B ){}2,3,4 (C ){}3,4 (D ){}1,2,3,42. 设全集R U =,集合{}2|l g (1)M x y x ==-,{}|02N x x =<<,则()U NM =ðA .{}|21x x -≤<B .{}|01x x <≤C .{}|11x x -≤≤D .{}|1x x < 3.已知3cos ,05ααπ=<<,则tan 4πα⎛⎫+= ⎪⎝⎭ A.15B.17C.1-D.7-4.由直线12x =,x=2,曲线1y x=及x 轴所围图形的面积为 A .154 B .174 C .1ln 22D .2ln 25. 设,,(,0),a b c ∈-∞则111,,a b c b c a+++( )A.都不大于2-B.都不小于2-C .至少有一个不大于2- D.至少有一个不小于2-6.(2013山东卷)给定两个命题p 、q ,若﹁p 是q 的必要而不充分条件,则p 是﹁q 的 (A )充分而不必条件 (B )必要而不充分条件(C )充要条件 (D )既不充分也不必要条件7.若二项式(x x-θsin )6展开式的常数项为20,则θ的值为 (A))(22Z k k ∈+ππ (B) )(22Z k k ∈-ππ (C)2π-(D)2π 8.若直线x -y =2被圆(x -a)2+y 2=4所截得的弦长为22,则实数a 的值为 A.-1或 3 B .1或3 C.-2或6 D .0或4 9.已知{}n a 为等差数列,若34899,a a a S ++==则 (A )24 (B )27 (C )15 (D )54 10.有四个关于三角函数的命题:1p :∃x ∈R, 2sin 2x +2cos 2x =122p : ∃x 、y ∈R, sin(x-y)=sinx-siny 3p : ∀x ∈[]0,π=sinx 4p : sinx=cosy ⇒x+y=2π右焦点的连线交C 1于第一象限的点M.若C 1在点M 处的切线平行于C 2的一条渐近线,则p=12.2013年第12届全国运动会将在沈阳举行,某校4名大学生申请当A ,B ,C 三个比赛项目的志愿者,组委会接受了他们的申请,每个比赛项目至少分配一人,每人只能服务一个比赛项目,若甲要求不去服务A 比赛项目,则不同的安排方案共有(A )20种 (B )24种 (C )30种 (D )36种 二、填空题13. 某程序框图如右图所示,若3a =,则该程序运行后,输出的x 值为 ;14.函数22y x x =-+与x 轴相交形成一个闭合图形,则该闭合图形的面积是__________.15. 若曲线4y x =的一条切线l 与直线480x y +-=垂直,则l 的方程为________。
2013高二数学暑假作业答案
2013年高二数学暑假作业答案【快乐暑假】2013年高二数学暑假作业答案一.填空题1.A.2.3.3.(1)(4)..5.212cm4.(1)(2)..6.(2)(4).7.300..8.90°.9.①与③.10.④.11.30.12.2:1.13.3.14.若②③④则①.二.解答题15.S=60+42;V=52-38=314816.证明:作PO,,PEABPFAC,垂足分别为,,OEF,连结,,OEOFOA,∵,PEABPFACPAEPAFRtPAERtPAFAEAFPAPA,POABPOAB,又∵ABPE,∴AB平面PEO,∴ABOE.同理ACOF.在RtAOE和RtAOF,,AEAFOAOA,∴RtAOE RtAOF,∴EAOFAO,即点P在平面上的射影在BAC的平分线上.17.证明:(1)因为E,F分别是11AB,AC的中点,所以EF//BC,又EF面ABC,BC面ABC,所以EF∥ABC平面;(2)因为直三棱柱111ABCABC,所以1111BBABC面,11BBAD,又11ADBC,所以111ADBCC面B,又11ADAFD面,所以111AFDBBCC平面平面.18.证明:(1)连结11AC,设11111ACBDO连结1AO,1111ABCDABCD是正方体11AACC是平行四边形11ACAC且11ACAC,又1,OO分别是11,ACAC的中点,11OCAO且11OCAO11AOCO是平行四边形.111,COAOAO面11ABD,1CO面11ABD1CO面11ABD.(2)证明:////''''''ABDCDCABCDABDCDC是平行四边形'//'''''''BCADBCABDADABD平面平面'//'''//'''''BCABDCDABDBCCDC平面同理,平面平面'//CDB平面''ABD.19.(本小题满分14分)(1)证明: E.P分别为AC.A′C的中点,EP∥A′A,又A′A平面AA′B,EP平面AA′B∴即EP∥平面A′FB(2)证明:∵BC⊥AC,EF⊥A′E,EF∥BC∴BC⊥A′E,∴BC⊥平面A′ECBC平面A′BC∴平面A′BC⊥平面A′EC(3)证明:在△A′EC中,P为A′C的中点,∴EP⊥A′C,在△A′AC中,EP∥A′A,∴A′A⊥A′C由(2)知:BC⊥平面A′EC又A′A平面A′EC∴BC⊥AA′∴A′A⊥平面A′BC20.解:(1)证明:在DD1上取一点N使得DN=1,连接CN,EN,显然四边形CFD1N是平行四边形,所以D1F//CN,同理四边形DNEA是平行四边形,所以EN//AD,且EN=AD,又BC//AD,且AD=BC,所以EN//BC,EN=BC,所以四边形CNEB是平行四边形,所以CN//BE,所以D1F//BE,所以1,,,EBFD四点共面.(2)因为GMBF所以BCF∽MBG,所以MBBGBCCF,即2332MB,所以MB=1,因为AE=1,所以四边形ABME是矩形,所以EM⊥BB1又平面ABB1A1⊥平面BCC1B1,且EM在平面ABB1A1内,所以EM面11BCCB.精心整理,仅供学习参考。
2013高二数学暑假作业答案
2013年高二年数学暑假作业答案一、填空题:本大题共14小题。
每小题5分。
共计70分.请把答案填写在答题纸相应位置上1.命题“R,≥”的否定是.2.直线的倾斜角为.3.抛物线的焦点坐标是.4.双曲线的渐近线方程是.5.已知球的半径为3,则球的表面积为.6.若一个正三棱锥的高为5,底面边长为6,则这个正三棱锥的体积为.7.函数在点(1,)处的切线方程为.8.若直线与直线平行,则实数的值等于.9.已知圆与圆相内切,则实数的值为.10.已知直线和圆相交于,两点,则线段的垂直平分线的方程是。
11.已知两条直线和都过点(2,3),则过两点,的直线的方程为.12.已知是椭圆的左焦点,是椭圆上的动点,是一定点,则的最大值为.13.如图,已知(常数),以为直径的圆有一内接梯形,且,若椭圆以,为焦点,且过,两点,则当梯形的周长最大时,椭圆的离心率为.14.设函数,,若的图象与的图象有且仅有两个不同的公共点,则当时,实数的取值范围为.二、解答题:本大题共6小题,共计90分.请在答题纸制定区域内作答,解答时应写出文字说明、证明过程或演算步骤.15.(本小题满分14分)如图,在正方体中,,分别为棱,的中点.(1)求证:∥平面;(2)求证:平面⊥平面.16.(本小题满分l4分)已知圆经过三点,,.(1)求圆的方程;(2)求过点且被圆截得弦长为4的直线的方程.17.(本小题满分14分)已知,命题≤,命题≤≤.(1)若是的必要条件,求实数的取值范围;(2)若,“或”为真命题,“且”为假命题,求实数的取值范围.18.(本小题满分l6分)现有一张长80厘米、宽60厘米的长方形铁皮,准备用它做成一只无盖长方体铁皮盒,要求材料利用率为l00%,不考虑焊接处损失.方案一:如图(1),从右侧两个角上剪下两个小正方形,焊接到左侧中闻,沿虚线折起,求此时铁皮盒的体积;方案二:如图(2),若从长方形的一个角上剪下一块正方形铁皮,作为铁皮盒的底面,用余下材料剪拼后作为铁皮盒的侧面,求该铁皮盒体积的最大值,并说明如何剪拼?。
山东省2013年高二暑假作业(五)文科数学.pdf
2013高二数学暑假作业(五) 一、选择题 1.“a=2”是“直线2x+ay-1=0与直线ax+2y-2=0平行”的( ) A.充要条件 B.充分不必要条件 C.必要不充分条件 D.既不充分也不必要条件 2直线经过点A(2,1)、B(1,) (两点,那么直线的倾斜角的范围是( ) A. B. C. D. 3若双曲线-=1的焦点到其渐近线的距离等于实轴长,则该双曲线的离心率为( ) A. B.5 C. D.2 4已知圆的方程为x2+y2-2x+6y+8=0,那么下列直线中经过圆心的直线方程为( ) A.2x-y+1=0 B.2x+y+1=0 C.2x-y-1=0 D.2x+y-1=0 5、直线l过抛物线y2=2px(p>0)的焦点F,且与抛物线交于A、B两点,若线段AB的长是8,AB的中点到y轴的距离是2,则此抛物线方程是( ) A.y2=12x B.y2=8x C.y2=6x D.y2=4x 6定义:平面内横坐标为整数的点称为“左整点”.过函数y=图象上任意两个“左整点”作直线,则倾斜角大于45°的直线条数为( ) A.10 B.11 C.12 D.13 7设双曲线-=1的一个焦点为(0,-2),则双曲线的离心率为( ) A. B.2 C. D.2 8椭圆+y2=1的焦点为F1,F2,点M在椭圆上,·=0,则M到y轴的距离为( ) A. B. C. D. 9已知双曲线的两个焦点为F1(-,0),F2(,0),M是此双曲线上的一点,且·=0,||·||=2,则该双曲线的方程是( ) A.-y2=1 B.x2-=1C.-=1D.-=1 10设圆C的圆心在双曲线-=1(a>0)的右焦点上,且与此双曲线的渐近线相切,若圆C被直线l:x-y=0截得的弦长等于2,则a=( ) A. B. C. D.2 11直线y=kx+3与圆(x-3)2+(y-2)2=4相交于M,N两点,若|MN|≥2,则k的取值范围是( ) A. B.∪[0,+∞) C. D. 12已知双曲线-=1(a>0,b>0)的两条渐近线均和圆C:x2+y2-6x+5=0相切,且双曲线的右焦点为圆C的圆心,则该双曲线的方程为( ).A.-=1B.-=1C.-=1D.-=113.已知曲线C:y=2x2,点A(0,-2)及点B(3,a),从点A观察点B,要使视线不被曲线C挡住,则实数a的取值范围是( ) A.(4,+∞) B.(-∞,4] C.(10,+∞) D.(-∞,10] 两圆C1:与C2:的公共弦所在直线方程是 ______________,公共弦的长等于 . 15到直线的距离与到定点的距离之比为的点的轨迹方程是 . 16已知两点、,则线段MN的垂直平分线的方程为______________. 17已知点(x0,y0)在直线ax+by=0(a,b为常数)上,则的最小值为________. 18.已知:圆C:x2+y2-8y+12=0,直线l:ax+y+2a=0. (1)当a为何值时,直线l与圆C相切; (2)当直线l与圆C相交于A、B两点,且AB=2时,求直线l的方程. 19.如图,直线l:y=x+b与抛物线C:x2=4y相切于点A. (1)求实数b的值; (2)求以点A为圆心,且与抛物线C的准线相切的圆的方程. 20.设椭圆C:+=1(a>b>0)的离心率为,过原点O斜率为1的直线与椭圆C相交于M,N两点,椭圆右焦点F到直线l的距离为. (1)求椭圆C的方程; (2)设P是椭圆上异于M,N外的一点,当直线PM,PN的斜率存在且不为零时,记直线PM的斜率为k1,直线PN的斜率为k2,试探究k1·k2是否为定值?若是,求出定值;若不是,说明理由.1.B2.B3.A4.B5.B6.B7.A8.B9.A 10.C 11.A 12.A 13.D 二、填空题 14. ; 15. 16. 17. 三、解答题 18.解:将圆C的方程x2+y2-8y+12=0配方得标准方程为x2+(y-4)2=4,则此圆的圆心为(0,4),半径为2. (1)若直线l与圆C相切,则有=2. 解得a=-. (2)过圆心C作CD⊥AB,则根据题意和圆的性质, 得 解得a=-7,或a=-1. 故所求直线方程为7x-y+14=0或x-y+2=0. 19.解:(1)由得x2-4x-4b=0,(*) 因为直线l与抛物线C相切, 所以Δ=(-4)2-4×(-4b)=0,解得b=-1. (2)由(1)可知b=-1,故方程(*)为x2-4x+4=0. 解得x=2,代入x2=4y,得y=1,故点A(2,1). 因为圆A与抛物线C的准线相切, 所以圆A的半径r就等于圆心A到抛物线的准线y=-1的距离,即 r=|1-(-1)|=2, 所以圆A的方程为(x-2)2+(y-1)2=4. 20.解:(1)设椭圆的焦距为2c(c>0),焦点F(c,0),直线l:x-y=0, F到l的距离为=,解得c=2, 又∵e==,∴a=2,∴b=2. ∴椭圆C的方程为+=1. (2)由解得x=y=,或x=y=-, 不妨设M,N,P(x,y), ∴kPM·kPN=·=, 由+=1,即x2=8-2y2,代入化简得k1·k2=kPM·kPN=-为定值.。
山东省高二数学暑假作业(一)文
2013高二文科数学暑假作业(一)一、选择题 1.复数22()i i+= A .34i -- B .34i -+ C .34i - D .34i +2.设全集U 是自然数集N ,集合{}{}1,2,3,1A B x N x ==∈≤,则如图所示的阴影部分的集合为 A.{}0,1B.{}1,2C.{}2,3D.{}0,1,23. 已知x 0 1 23 y 1 35 7则y 与x 的线性回归方程+=a x b y 必过点( ) A.(1.5 ,4) B. (2,2) C.(1.5 ,0) D.(1,2)4. 曲线⎪⎩⎪⎨⎧+-=++-=λλλλ11132y x (λ为参数)与y 坐标轴的交点是( ) A .,0( )52 B .,0( )51 C .,0( )4- D .,0( )95 5.在同一坐标系中,将曲线x y 3sin 2=变为曲线x y sin =的伸缩变换公式是( )⎪⎩⎪⎨⎧==''23.A yy x x ⎪⎩⎪⎨⎧==y y xx 23.B ''⎪⎩⎪⎨⎧==y y xx 213.C ''6. 已知抛物线24y x =的准线与双曲线()2221,0x y a a-=>交于A,B 两点,点F 为抛物线的焦点,若FAB ∆为直角三角形,则双曲线的离心率是 A.3B.6C.2D.37.如图,某几何体的正视图与侧视图都是边长为1的正方形且体积为12,则该几何体的俯视图可以是8.过点M(2,0)作圆221x y +=的两条切线MA ,MB (A ,B 为切点),则MA MB ⋅=u u u r u u u rA .532 B . 52 C .332 D .329.函数f (x )=e x-1x的零点所在的区间是( )A.⎝ ⎛⎭⎪⎫0,12B.⎝ ⎛⎭⎪⎫12,1C.⎝ ⎛⎭⎪⎫1,32D.⎝ ⎛⎭⎪⎫32,2 10.如果上述程序运行的结果为S =132,那么判断框中应填入( ) A. k≤11? B .k≥11? C.k≤10? D .k≥10?11.已知动点(,)P x y 在椭圆2212516x y +=上,若A 点坐标为(3,0),||1AM =u u u u r ,且0PM AM ⋅=u u u u r u u u u r ,则||PM u u u u r的最小值是( )A.2B.3C.2D.3 12.已知函数()f x 满足:当()()()()211;12,log 7x x f x f x x f x f ≥=-==时,当<时,则A.72B.74C.78D.716二、填空题13.已知某几何体的三视图如图所示,若该几何体的体积为24, 则正(主)视图中a 的值为 .14.在复平面内,记复数3i +对应的向量为OZ uuu r ,若向量OZ uuu r绕坐标原点逆时针旋转60o得到向量'OZ u u u u r所对应的复数为___________________.15.已知实数[]0,10x ∈,执行如右图所示的程序框图,则输出的x 不小于47的概率为16.记123k k k kk S n =+++⋅⋅⋅+,当1,2,3,k =⋅⋅⋅时,观察下列等式可以推测A-B=_______________ 三、解答题 17.若函数4)(3+-=bx ax x f .当2=x 时,函数)(x f 取得极值4-3. (1)求函数的解析式;(2)若函数k x f =)(有3个解,求实数k 的取值范围. 18.(本小题满分12分)如图所示,直角梯形ACDE 与等腰直角ABC ∆所在平面互相垂直,F 为BC 的中点, 90BAC ACD ∠=∠=︒,AE ∥CD ,22DC AC AE ===.(1)求证:平面BCD ⊥平面ABC ; (2)求证:AF ∥平面BDE ; (3)求四面体B CDE -的体积.19、己知等比数列{}n a 所有项均为正数,首11a =,且435,3,a a a 成等差数列.(I)求数列{}n a 的通项公式;(II)数列{}1n n a a λ+-的前n 项和为n S ,若*21()n n S n N =-∈,求实数λ的值.20.(本小题满分12分) 已知函数21()(21)2ln ()2f x ax a x x a =-++∈R . (1)若曲线()y f x =在1x =和3x =处的切线互相平行,求a 的值; (2)求()f x 的单调区间;(3)设2()2g x x x =-,若对任意1(0,2]x ∈,均存在2(0,2]x ∈,使得12()()f x g x <,求a 的取值范围.2013高二文科数学暑假作业(一)答案1-5 ACABC 6-10 BADBD 11-12BB 13. 6 14. 2i 15.1/216.41 17. (1)2'()3f x ax b =- 所以'(2)0f =,4(2)3f =-.即12048243a b a b -=⎧⎪⎨-+=-⎪⎩,由此可解得13a =,4b =(2)31()443f x x x =-+ 2'()4(2)(2)f x x x x =-=-+所以()f x 在2x =-处取得极大值283,在2x =处取得极小值43-所以42833k -<< 18.(1)∵面ABC ⊥面ACDE ,面ABC I 面ACDE AC =,CD AC ⊥,∴DC ⊥面ABC ,又∵DC ⊂面BCD ,∴平面BCD ⊥平面ABC . (2)取BD 的中点P ,连结EP 、FP ,则FP 12DC , 又∵EA12DC ,∴EA FP , ∴四边形AFPE 是平行四边形,∴AF ∥EP ,又∵EP ⊂面BDE 且AF ⊄面BDE ,∴AF ∥面BDE .(3)∵BA ⊥AC ,面ABC I 面ACDE =AC , ∴BA ⊥面ACDE .∴BA 就是四面体B CDE -的高,且BA =2. ∵DC =AC =2AE =2,AE ∥DC , ∴11(12)23,121,22ACE ACDE S S ∆=+⨯==⨯⨯=梯形 ∴312,CDES ∆=-= ∴1422.33E CDE V -=⨯⨯=19.(Ⅰ)设数列{}n a 的公比为q ,由条件得423,3,q q q 成等差数列,所以4326q q q +=解得2,3=-=q q 或由数列{}n a 的所有项均为正数,则q =2 数列{}n a 的通项公式为n a =12n -(*)n N ∈(Ⅱ)记n n n a a b λ-=+1,则112)2(22---=⋅-=n n n n b λλ 若0,0,2===n n S b λ不符合条件;若2≠λ, 则21=+nn b b ,数列{}n b 为等比数列,首项为λ-2,公比为2, 此时)12)(2()21(21)2(--=---=n n n S λλ又n S =21(*)n n N -∈,所以1=λ20.解:2()(21)f x ax a x'=-++(0)x >. (1)(1)(3)f f ''=,解得23a =. (3)(1)(2)()ax x f x x--'=(0)x >.①当0a ≤时,0x >,10ax -<,在区间(0,2)上,()0f x '>;在区间(2,)+∞上()0f x '<,故()f x 的单调递增区间是(0,2),单调递减区间是(2,)+∞.②当102a <<时,12a >,在区间(0,2)和1(,)a +∞上,()0f x '>;在区间1(2,)a上()0f x '<,故()f x 的单调递增区间是(0,2)和1(,)a +∞,单调递减区间是1(2,)a.③当12a =时,2(2)()2x f x x -'=, 故()f x 的单调递增区间是(0,)+∞.④当12a >时,102a <<,在区间1(0,)a 和(2,)+∞上,()0f x '>;在区间1(,2)a上()0f x '<,故()f x 的单调递增区间是1(0,)a 和(2,)+∞,单调递减区间是1(,2)a.(Ⅲ)由已知,在(0,2]上有max max ()()f x g x <. 由已知,max ()0g x =,由(Ⅱ)可知,①当12a ≤时,()f x 在(0,2]上单调递增,故max ()(2)22(21)2ln 2222ln 2f x f a a a ==-++=--+,所以,222ln 20a --+<,解得ln 21a >-,故1ln 212a -<≤.②当12a >时,()f x 在1(0,]a 上单调递增,在1[,2]a上单调递减,故max 11()()22ln 2f x f a a a==---.由12a >可知11ln ln ln 12ea >>=-,2ln 2a >-,2ln 2a -<,所以,22ln 0a --<,max ()0f x <,综上所述,ln 21a >-.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2013高二理科数学暑假作业(二)一、选择题 1.复数11ii+-(i 是虚数单位)的共轭复数的虚部为 A.1-B.0C.1D.22.已知不同的直线m ,n ,l ,不重合的平面,αβ,则下列命题正确的是 A .m//α,n∥α,则m∥nB .m//α,m//β,则α//βC .m⊥l ,n⊥l ,则m∥nD .m⊥α,m⊥β,则α// 3. 曲线33y x x =-和y x =围成的面积为( ).4A .8B .10C .9D4.已知0)](log [log log 237=x ,那么21-x 等于( )A.31 B.63 C.33D.425.某车间为了规定工时定额,需要确定加工零件所花费的时间,为此进行了5次试验,根据收集到的数据(如下表),由最小二乘法求得回归直线方程0.6854.6y x =+u r r表中有一个数据模糊不清,请你推断出该数据的值为 A .68 B . 68.2 C .69 D .756.函数)1(1)(xx n x f -=的图象是7.如果n a a )13(32-的展开式中各项系数之和为128,则展开式中2a 的系数是 ( )A .-2835 B.2835 C.21 D.-21 8.下列四个判断: ①2,10x R x x ∃∈-+≤;2②已知随机变量X 服从正态分布N (3,2σ),P (X ≤6)=0.72,则P (X ≤0)=0.28; ③已知21()nx x+的展开式的各项系数和为32,则展开式中x 项的系数为20;④11e dx x>⎰⎰其中正确的个数有:A .1个B .2个C .3个D .4个9.已知ABC ∆中,三个内角A ,B ,C 的对边分别为a,b,c ,若ABC ∆的面积为S ,且()222,tan S a b c C =+-则等于A.34B.43C.43-D.34-10 . 把正整数按一定的规则排成了如图所示的三角形数表.设*(,)ij a i j N ∈ 是位于这个三角形数表中从上往下数第i 行,从左 往右数第j 个数,若2013ij a =, 则i 与j 的和为( )A .105B .103C .82D .81 11.要得到函数()sin(2)3f x x π=+的导函数'()f x 的图象,只需将()f x 的图象( ) A .向左平移2π个单位,再把各点的纵坐标伸长到原来的2倍(横坐标不变) B .向左平移2π个单位,再把各点的纵坐标缩短到原来的12倍(横坐标不变)C .向左平移4π个单位,再把各点的纵坐标伸长到原来的12倍(横坐标不变)D .向左平移4π个单位,再把各点的纵坐标伸长到原来的2倍(横坐标不变)12.等差数列{}n a 前n 项和为n S ,已知310061006(1)2013(1)1,a a -+-=310081008(1)2013(1)1,a a -+-=-则A.2013100810062013,S a a => B .2013100810062013,S a a =< C.2013100810062013,S a a =-> D .2013100810062013,S a a =-< 二、填空题 13.若x,y 满足⎩⎨⎧≥+-≤+-,22,0y x y x 则的最大值y x C )(log 21+=为 .124753121086911131517141618202224314.以椭圆192522=+y x 的焦点为焦点,离心率为2的双曲线方程为15.已知函数()f x 在实数集R 上具有下列性质:①直线1x =是函数()f x 的一条对称轴;②()()2f x f x +=-;③当1213x x ≤<≤时,()()()21f x f x -⋅()210,x x -<则()2012f 、()2013f 从大到小的顺序为_______.16. 已知2()(0)f x ax bx c a =++≠,且方程()f x x =无实数根,下列命题: ①方程[()]f f x x =也一定没有实数根;②若0a >,则不等式[()]f f x x >对一切实数x 都成立; ③若0a <,则必存在实数0x ,使00[()]f f x x >④若0a b c ++=,则不等式[()]f f x x <对一切实数x 都成立. 其中正确命题的序号是 . 三、解答题17. 已知向量2(3sin ,1),(cos ,cos ).444x x x m n ==u v v 记()f x m n =⋅u v v . (Ⅰ)若3()2f α=,求2cos()3πα-的值;(Ⅱ)在△ABC 中,角A 、B 、C 的对边分别是a 、b 、c ,且满足(2)cos cos a c B b C -=,若13()f A +=,试判断△ABC 的形状. 18.已知函数)0()221(1)(2>-+=a ax x ax n x f . (Ⅰ)若的一个极)(是函数21x f x =值点,求a 的值; (Ⅱ)求证:当0<a ≤2时,f(x)在⎪⎭⎫⎢⎣⎡∞+,21上是增函数;(Ⅲ)若对任意的)2,1(∈a ,总存在]2,1[0∈x ,使不等式)1()(20a m x f ->成立,求实数m的取值范围.19.由世界自然基金会发起的“地球1小时”活动,已发展成为最有影响力的环保活动之一,今年的参与人数再创新高.然而也有部分公众对该活动的实际效果与负面影响提出了疑问.对此,某新闻媒体进行了网上调查,所有参与调查的人中,持“支持”、“保留”和“不支持”态度的人数如下表所示:4(1)在所有参与调查的人中,用分层抽样的方法抽取个人,已知从“支持”态度的人中抽取了45人,求n 的值;(2)在持“不支持”态度的人中,用分层抽样的方法抽取5人看成一个总体,从这5人中任意选取2人,求至少有1人20岁以下的概率;20.(本小题满分13分)如图,椭圆22122:1(0)x y C a b a b +=>>,x 轴被曲线22:C y x b =-截得的线段长等于1C 的短轴长。
2C 与y 轴的交点为M ,过坐标原点O 的直线l 与2C 相交于点A B 、,直线,MA MB 分别与1C 相交于点D E 、。
(1)求1C 、2C 的方程; (2)求证:MA MB ⊥。
(3)记,MAB MDE ∆∆的面积分别为12S S 、,若12S S λ=,求λ的取值范围。
2013高二理科数学暑假作业(二)参考答案一、选择题1-5ADBDA 6-10BAACD 11-12DC 二、填空题13. 2- 14. 112422=-y x 15. )2013(f ,)2012(f ,)2011(f 16.①②④ 三、解答题. 17.解:211()cos cos cos 4442222x x x x x f x =+=++1sin 262x π⎛⎫=++ ⎪⎝⎭……2分 (I ) 由已知32f ()α=得13sin 2622απ⎛⎫++= ⎪⎝⎭,于是24,3k k παπ=+∈Z ,5∴ 22241333cos()cos k πππαπ⎛⎫-=--= ⎪⎝⎭……6分 (Ⅱ) 根据正弦定理知:()2cos cos (2sin sin )cos sin cos a c B b C A C B B C -=⇒-= ......8分12sin cos sin()sin cos 23A B B C A B B π⇒=+=⇒=⇒=∵1()2f A +=……10分 ∴11sin 2622263A A πππ⎛⎫++=⇒+= ⎪⎝⎭或23π3A π⇒=或π 而203A π<<,所以3A π=,因此∆ABC 为等边三角形.……………12分18.解:2'212()22()2.11122a ax x aa f x x a ax ax --⋅=+-=++ (Ⅰ)由已知得:'1()0,2f =且220,2a a-≠220,0. 2.a a a a ∴--=>∴=Q ………………3分(Ⅱ)当02a <≤时,22212(2)(1)02222a a a a a a a a----+-==≤Q ,212,22a a -∴≥故当12x ≥时,220.2a x a--≥又'20,()0,1ax f x ax >∴≥+故()f x 在1,2⎡⎫+∞⎪⎢⎣⎭上是增函数. ……………7分 (Ⅲ)当()1,2a ∈时,由(2)知,()f x 在[]1,2上的最小值为11(1)ln()1,22f a a =++-故问题等价于:对任意的()1,2a ∈,不等式211ln()1(1)022a a m a ++-+->恒成立.……8分 记211()ln()1(1),(12)22g a a a m a a =++-+-<<, 则[]'1()122(12),11a g a ma ma m a a=-+=--++6当0m ≤时,'2120,()0,()ma m g a g a -+<∴<∴在区间()1,2上递减,此时,()(1)0,g a g <=0m ∴≤时不可能使()0g a >恒成立,故必有0,m > …………10分.'21()(1).12ma g a a a m ⎡⎤∴=--⎢⎥+⎣⎦若111,2m ->可知()g a 在区间1(1,min 2,1)2m ⎧⎫-⎨⎬⎩⎭上递减,在此区间上,有()(1)0,g a g <=与()0g a >恒成立矛盾,故111,2m-≤此时'()0,g a >()g a 在(1, 2) 上递增,且恒有()(1)0,g a g >=满足题设要求,0,1112m m >⎧⎪∴⎨-≤⎪⎩即14m ≥,即实数m 的取值范围为1[,)4+∞. ……………13分19.解:(1)由题意得n30015010020045080045100800+++++=+, 所以100=n . (2)设所选取的人中,有m 人20岁以下,则5300200200m=+,解得2=m .也就是20岁以下抽取了2人,另一部分抽取了3人,分别记作A1,A2;B1,B2,B3, 则从中任取2人的所有基本事件为 (A1,B1),(A1, B2),(A1, B3),(A2 ,B1),(A2 ,B2),(A2 ,B3),(A1, A2),(B1 ,B2),(B2 ,B3),(B1 ,B3)共10个. 其中至少有1人20岁以下的基本事件有7个:(A1, B1),(A1, B2),(A1, B3),(A2 ,B1),(A2 ,B2),(A2 ,B3),(A1, A2), 所以从中任意抽取2人,至少有1人20岁以下的概率为107. 20.(1)2222c a b a == (1分)又2b =,得1b =22221:1,:12x C y x C y ∴=-+= (2分)(2)设直线1122:,(,),(,)AB y kx A x y B x y =则22101y kxx kx y x =⎧⇒--=⎨=-⎩ (3分)211221212(,1)(,1)(1)()1MA MB x y x y k x x k x x ⋅=+⋅+=++++u u u r u u u r=0MA MB ∴⊥ (5分) (3)设直线1212:1;:1,1MA y k x MB y k x k k =-=-=-71121122110,(,1)111x k y k x x A k k y y k y x ==-⎧⎧=⎧⎪∴-⎨⎨⎨=-=-=-⎪⎩⎩⎩解得或,同理可得222(,1)B k k -11212S MA MB k == (8分) 1212111222221112141120421,(,)11212211212k x y k x k x k k D x y k k k y y k ⎧==-⎧⎪+=⎧-⎪⎪∴⎨⎨⎨=-++-+=⎩⎪⎪=⎩⎪+⎩解得或 同理可得2222222421(,)1212k k E k k -++212S MD ME ∴==(11分) 2122211212152()(12)(12)9161616k S k k k S λ++++===≥。
