(7份试卷合集)上海市静安区XX名校高中2020届数学高二下学期期末模拟试卷.doc
上海市静安区2019-2020学年高二下学期期末2份数学考试试题
同步测试一、选择题:本题共12小题,在每小题给出的四个选项中,只有一项是符合题目要求的。
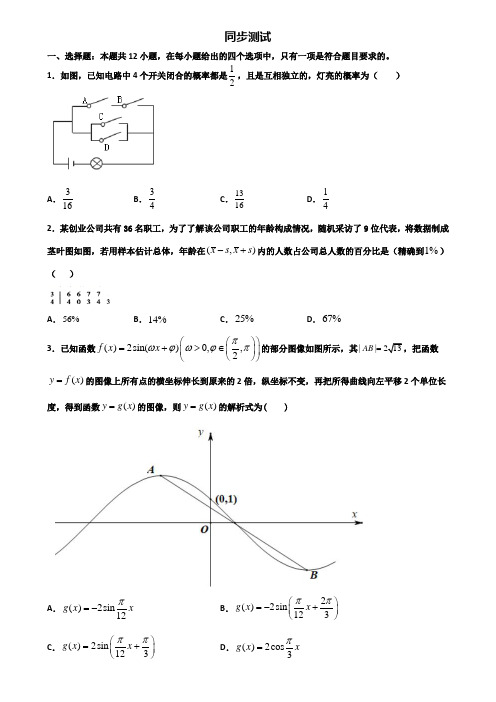
1.如图,已知电路中4个开关闭合的概率都是12,且是互相独立的,灯亮的概率为( )A .316B .34C .1316D .142.某创业公司共有36名职工,为了了解该公司职工的年龄构成情况,随机采访了9位代表,将数据制成茎叶图如图,若用样本估计总体,年龄在(,)x s x s -+内的人数占公司总人数的百分比是(精确到1%)( )A .56%B .14%C .25%D .67%3.已知函数()2sin()0,,2f x x πωϕωϕπ⎛⎫⎛⎫=+>∈⎪ ⎪⎝⎭⎝⎭的部分图像如图所示,其||213AB =,把函数()y f x =的图像上所有点的横坐标伸长到原来的2倍,纵坐标不变,再把所得曲线向左平移2个单位长度,得到函数()y g x =的图像,则()y g x =的解析式为( )A .()2sin12g x x π=-B .2()2sin 123g x x ππ⎛⎫=-+⎪⎝⎭C .()2sin 123g x x ππ⎛⎫=+⎪⎝⎭D .()2cos3g x x π=4.点(,)P x y 是椭圆222312x y +=上的一个动点,则2x y +的最大值为( ) AB .22CD .45.在复平面上,复数2ii+对应的点在( ) A .第一象限B .第二象限C .第三象限D .第四象限6.过点(,)e e -作曲线x y e x =-的切线,则切线方程为( ) A .2(1)y e x e =--+ B .2(1)y e x e =-- C .12(1)e e y e x e ++=--D .1(1)e e y e x e +=--7.定义在{|,1}x x R x ∈≠上的函数()()11f x f x -=-+,当1x >时, ()12xf x ⎛⎫= ⎪⎝⎭,则函数()()11cos 22g x f x x π⎛⎫=-+ ⎪⎝⎭(35x -≤≤)的所有零点之和等于( )A .2B .4C .6D .88.在某项测量中测量结果()2~3,(0)X N σσ>,若X 在(3,6)内取值的概率为0.3,则X 在(0,)+∞内取值的概率为( ) A .0.2B .0.4C .0.8D .0.99.—个盒子里装有相同大小的红球、白球共30个,其中白球4个.从中任取两个,则概率为1102264264230C C C C C +的事件是( ). A .没有白球 B .至少有一个白球 C .至少有一个红球D .至多有一个白球10.已知数列{}a n 的前n 项和为n S ,且()*2120n n n a a a n N +++-=∈,若16182024aa a ++=,则35S =( ) A .140B .280C .70D .42011.已知双曲线222:14x y C a -=的一条渐近线方程为230x y +=,1F ,2F 分别是双曲线C 的左,右焦点,点P 在双曲线C 上,且1 6.5PF =,则2PF 等于( ). A .0.5B .12.5C .4或10D .0.5或12.512.已知i 为虚数单位,则复数21ii-+对应复平面上的点在第( )象限. A .一B .二C .三D .四二、填空题:本题共4小题13.求经过点()43-,,且在x 轴上的截距是在y 轴上的截距2倍的直线方程为________. 14.若函数1()sin 22asin 3f x x x x =--在(),-∞+∞上单调递增,则a 的取值范围是_______. 15.过点()3,1P 的直线l 与圆()()22:224C x y -+-=相交于,A B 两点,当弦AB 的长取最小值 时,直线l 的倾倒角等于___________.16.样本中共有5个个体,其值分别为1-,0,1,2,1.则样本方差为________. 三、解答题:解答应写出文字说明、证明过程或演算步骤。
上海市中学2020年高二数学理下学期期末试卷含解析

上海市中学2020年高二数学理下学期期末试卷含解析一、选择题:本大题共10小题,每小题5分,共50分。
在每小题给出的四个选项中,只有是一个符合题目要求的1. 设数列{a n}的前n项和为S n,a4=7且4S n=n(a n+a n+1),则a5等于()A.8 B.9 C.10 D.11参考答案:B【考点】8H:数列递推式.【分析】利用已知条件逐步求解即可.【解答】解:4S n=n(a n+a n+1),可得4S2=2(a2+a3),4S1=a1+a2,a2=3a1,a3=5a1,从而36a1=3(5a1+7),a1=1,a2=3,a3=5,a4=7,4S4=4(a4+a5),解得a5=9.故选:B.2. =()A.B.C.D.参考答案:D【考点】D4:排列及排列数公式.【分析】根据排列数公式计算即可.【解答】解: ===.故选:D.3. 某单位为了落实“绿水青山就是金山银山”理念,制定节能减排的目标,先调查了用电量y(单位:千瓦·时)与气温x(单位:℃)之间的关系,随机选取了4天的用电量与当天气温,并制作了以下对照表:由表中数据得线性回归方程:,则由此估计:当某天气温为2℃时,当天用电量约为()A. 56千瓦·时B. 62千瓦·时C. 64千瓦·时D. 68千瓦·时参考答案:A【分析】根据回归直线方程经过样本中心点,求得,代入回归直线可求得;代入回归方程后,可预报当气温为℃时,当天的用电量。
【详解】代入回归直线方程,求得所以回归直线方程为当温度为2℃时,代入求得千瓦·时所以选A【点睛】本题考查了回归方程的简单应用,注意回归直线方程一定经过样本的中心点,而不是样本的某个点,属于基础题。
4. 复数z=(1﹣i)(4﹣i)的共轭复数的虚部为()A.﹣5i B.5i C.﹣5 D.5参考答案:D【考点】A5:复数代数形式的乘除运算.【分析】直接利用复数代数形式的乘除运算化简,进一步求得的答案.【解答】解:∵z=(1﹣i)(4﹣i)=3﹣5i,∴,则复数z=(1﹣i)(4﹣i)的共轭复数的虚部为5.故选:D.5. 若等于()A.2 B.-2 C.D.参考答案:D略6. 设f n(x)是等比数列1,﹣x,x2,…,(﹣x)n的各项和,则f2016(2)等于()A.B.C.D.参考答案:C【考点】数列的求和.【分析】利用等比数列的求和公式即可得出.【解答】解:∵f n(x)是等比数列1,﹣x,x2,…,(﹣x)n的各项和,x≠﹣1时,∴f n(x)=.∴f2016(2)==.故选:C.7. 已知集合,,则()A. B. C.D.参考答案:C8. 动点到点及点的距离之差为,则点的轨迹是()A.双曲线 B 双曲线的一支 C. 两条射线 D. 一条射线参考答案:D略9. 设函数,若数列是单调递减数列,则实数a的取值范围为()A.(-,2)B.(-,C.(-,)D.参考答案:B略10. 双曲线的渐近线的方程和离心率分别为( )A. B.C. D.参考答案:D二、填空题:本大题共7小题,每小题4分,共28分11. 已知log2a+log2b≥1,则3a+9b的最小值为_______.参考答案:1812. 由直线,,与曲线所围成的封闭图形的面积为 .参考答案:略13. 已知实数满足则的最小值是.参考答案:-514. 某单位有甲、乙、丙三个部门,分别有职员27人、63人和81人,现按分层抽样的方法从各部门中抽取组建一个代表队参加上级部门组织的某项活动;其中乙部门抽取7人,则该单位共抽取__________人。
上海市2020〖人教版〗高二数学下册期末复习试卷高二下)数学期末试卷

上海市2020年〖人教版〗高二数学下册期末复习试卷高二(下)数学期末试卷一、 选择题1、函数f (x )=x 3-3x +1在闭区间[-3,0]上的最大值、最小值分别是( )A .1,-1B .3,-17C .1,-17D .9,-192、已知f (x )=x 3+ax 2+(a +6)x +1有极大值和极小值,则a 的取值范围为( ))(A -1<a <2 )(B -3<a <6 )(C a <-1或a >2 )(D a <-3或a >63、0()0f x '=是函数()f x 在点0x 处取极值的 ( ))(A 充分不必要条件 )(B 必要不充分条件)(C 充要条件 )(D 既不充分又不必要条件4、设函数f (x )=kx 3+3(k -1)x 22k -+1在区间(0,4)上是减函数,则k 的取值范围是 ( )(A )13k <(B ) 103k <≤(C ) 103k ≤< (D )13k ≤ 5、下列说法正确的是( )A .直线a 平行于平面M ,则a 平行于M 内的任意一条直线B .直线a 与平面M 相交,则a 不平行于M 内的任意一条直线C .直线a 不垂直于平面M ,则a 不垂直于M 内的任意一条直线D .直线a 不垂直于平面M ,则过a 的平面不垂直于M6、设P 是平面α外一点,且P 到平面α内的四边形的四条边的距离都相等,则四边形是( )A .梯形B .圆外切四边形C .圆内接四边形D .任意四边形7、平面α与正四棱柱的四条侧棱AA 1、BB 1、CC 1、DD 1分别交于E 、F 、G 、H.若AE=3,BF=4,CG=5,则DH 等于( )A .6B .5C .4D .38、正方体ABCD-A ’B ’C ’D ’中,面对角线BC ’与对角面BB ’D ’D 所成的角为α,tan α=( ) A 1 B 3 C 33 D 32 9、|→a |=|→b |=4,〈→a ,→b 〉=60°,则|→a -→b |=( ) A. 4 B. 8 C. 37 D. 1310、如图,棱锥P-ABCD 的高PO =3,截面积A ’B ’C ’D ’平行于底面ABCD ,PO 与截面交于O ’,且OO ’=2。
[合集3份试卷]2020上海市高二数学下学期期末检测试题
![[合集3份试卷]2020上海市高二数学下学期期末检测试题](https://img.taocdn.com/s3/m/74561eb94a7302768f993950.png)
同步测试一、选择题:本题共12小题,在每小题给出的四个选项中,只有一项是符合题目要求的。
1.阅读如图所示的程序,若执行循环体的次数为5,则程序中a 的取值范围为( )A .56a ≤≤B .56a <<C .56a ≤<D .56a <≤2.某射手射击所得环数ξ的分布列如下:ξ7 8 9 10Px0.1 0.3y已知ξ的数学期望()8.9E ξ=,则y 的值为( ) A .0.2B .0.4C .0.6D .0.83.设0.3log 0.6m =,21log 0.62n =,则( ) A .m n m n mn ->+> B .m n mn m n ->>+ C .m n m n mn +>->D .mn m n m n >->+4.用数学归纳法证明“当n 为正奇数时,n n x y +能被x y +整除”,第二步归纳假 设应该写成( )A .假设当()n k k N *=∈时,k k x y +能被x y +整除B .假设当2()n k k N *=∈时,k k x y +能被x y +整除C .假设当21()n k k N *=+∈时,k k x y +能被x y +整除D .假设当21()n k k N *=-∈时,2121k k x y --+能被x y +整除 5.在△ABC 中,AD 为BC 边上的中线,E 为AD 的中点,则EB =A .3144AB AC - B .1344AB AC - C .3144+AB ACD .1344+AB ACA .充分而不必要条件B .充要条件C .必要而不充分条件D .既不充分也不必要条件7.已知函数()sin()(0)3f x x πωω=->,若函数()f x 在区间3(,)2ππ上为单调递减函数,则实数ω的取值范围是( ) A .211[,]39B .511[,]69C .23[,]34D .25[,]368.设3log 43a -=,12b a -=,2log c a =,则( ) A .a b c >> B .b a c >> C .b c a >> D .c b a >>9.在26(1)(2)x x --的展开式中,含3x 的项的系数是( ) A .-832 B .-672 C .-512D .-19210.对变量有观测数据,得散点图(1);对变量有观测数据(,得散点图(2),由这两个散点图可以判断( )A .变量与正相关,与正相关B .变量与正相关,与负相关C .变量与负相关,与正相关D .变量与负相关,与负相关11.ABC △的内角A B C ,,的对边分别为a ,b ,c ,若ABC △的面积为2224a b c+-,则C =A .π2B .π3C .π4D .π612.函数()2cos()3f x x π=-的单调递增区间是( )A .42233k k ππππ⎡⎤++⎢⎥⎣⎦,()k Z ∈ B .22233k k ππππ⎡⎤-+⎢⎥⎣⎦,()k Z ∈ C .22233k k ππππ⎡⎤-+⎢⎥⎣⎦,()k Z ∈ D .242233k k ππππ⎡⎤-+⎢⎥⎣⎦,()k Z ∈ 二、填空题:本题共4小题13.为调査某高校学生对“一带一路”政策的了解情况,现采用分层抽样的方法抽取一个容量为500的样本.其中大一年级抽取200人,大二年级抽取100人.若其他年级共有学生2000人,则该校学生总人数是14.81xx⎛⎫+⎪⎝⎭的展开式中21x的系数为______.15.已知某程序框图如图所示,则执行该程序后输出的结果是_____16.若从甲乙丙丁4位同学中选出3位同学参加某个活动,则甲被选中的概率为__________.三、解答题:解答应写出文字说明、证明过程或演算步骤。
2023-2024学年上海中学高二下学期数学期末试卷及答案(2024.06)

1上海中学2023-2024学年第二学期高二年级数学期末2024.06一、填空题(每题3分,共36分)1.已知事件A 满足()0.3P A =,则()P A =___________.2.将4封不同的信投入3个不同的信箱,则不同的投递方式共有___________种.3.已知3223n n C P =,则n =___________.4.在()101x +的展开式中,3x 的系数为.___________(以数字作答)5.函数()242f x lnx x x =−−的驻点为___________.6.若随机变量X 服从正态分布()1,3,21N Y X =+,则[]D Y =___________.7.集合A 是{}12,3,4,5,6,7,8,9,10,的子集,且A 中的元素有完全平方数,则满足条件的集合A 共有___________个.8.从正方体的12条棱中选择两条,这两条棱所在直线异面直线的概率为___________. 9.若不等式x e ax ≥对任意1x ≥−成立,则a 的取值范围是___________.10.对于在定义域上恒大于0的函数()f x ,令()()g x lnf x =.已知()f x 与()g x 的导函数满足关系式()()()f x f x g x ′=′.由此可知,函数()2x f x x =在1x =处的切线方程为___________.11.甲、乙、丙、丁、戊乘坐高铁结伴出行并购买了位于同一排座位的五张车票,因此他们决定自行安排这些座位.高铁列车的座位安排如图,甲希望坐在靠窗的座位上,乙不希望坐在B 座,丙和丁希望坐在相邻的座位上(中间不能隔着过道),则满足要求的座位安排方式共有___________种.12.将1,2,3,4,5,6的所有排列按如下方式排序:首先比较从左至右第一个数的大小,较大的排列在后;若第一个数相同,则比较第二个数的大小,较大的排列在后,依此类推.按这种排序2方式,排列2,3,4,5,6,1的后一个排列是___________. 二、选择题(每题4分,共16分) 13.设()2f x sin x =,则()f x ′=( )(A)2cos x (B)2cos x − (C)22cos x (D)22cos x −14.某班级共有40名同学,其中15人是团员.现从该班级通过抽签选择10名同学参加活动,定义随机变量X 为其中团员的人数,则X 服从( )(A)二项分布 (B)超几何分布 (C)正态分布 (D)伯努利分布 15.将一枚硬币连续抛掷三次,每次得到正面或反面的概率均为12,且三次抛掷的结果互相独立.记事件A 为“至少两次结果为正面”,事件B 为“第三次结果为正面”,则()P B A =∣( ) (A)12 (B)23 (C)34 (D)7816.现有编号分别为()1,2,,*n n N …∈的小球各两个,每个球的大小与质地均相同.将这2n 个球排成一列,使得任意编号相同的球均不相邻,记满足条件的排列个数为n a ,则( ) ①对任意,*n n N a ∈都是偶数;②()()()11212n n a n n a n −>−−≥.(A)①②都是真命题 (B)①是真命题,②是假命题 (C)①是假命题,②是真命题 (D)①②都是假命题 三、解答题(本大题共5题,共48分,解答各题须写出必要的步骤) 17.(本题8分)求函数()()231x f x e x x =⋅−+的单调区间.18.(本题8分)某公司对购买其产品的消费者进行了调研,已知这些消费者在一年内再次购买产品的概率为33%,且这些消费者可以分为A B C、、三类.其中A类消费者占30%,其在一年内再次购买产品的概率为60%;B类消费者占40%,其在一年内再次购买产品的概率为30%;C类消费者占比x%,其在一年内再次购买产品的概率为y%.(1)求x与y的值.(2)若一名消费者在一年内再次购买了产品,求其是B类消费者的概率.19.(本题10分)某学校举办知识竞赛,该竞赛共有三道问题,参赛同学须回答这些问题,以其答对的问题的得分之和作为最终得分.每个问题的得分与参赛同学答对的概率如下表(每次回答是否正确相互独立).定义随机变量X为最终得分.(1)求()50P X=.(2)求[]D X.E X与[]3420.(本题10分)设函数()()()1f x x x x a =−−,其中1a >.且()f x 在0x =与x a =处的切线分别为12,l l .(1)若1l 与2l 平行,求a 的值.(2)记(1)中a 的值为0a .当0a a >时,记12,l l 与x 轴围成的三角形面积为S .当S 取到最小值时,求a 的值.21.(本题12分)仿照二项式系数,可以定义“三项式系数”k n T 为()21nx x ++的展开式中kx 的系数()02k n ≤≤,即()201122221.nn n n n n n x x T T x T x T x ++++++其中0122,,,,n n n n n T T T T Z …∈. (1)求234333,,T T T 的值:(2)对于给定的*n N ∈,计算以下两式的值:20n knk T =∑与20nk n k k T =∑(3)对于*n N ∈,记0122,,,,n n n n n T T T T …中偶数的个数为n a ,奇数的个数为n b .是否存在n 使得2024n n a b −≥?若存在,请给出一个满足要求的n 并说明理由;若不存在,请给出证明.5参考答案一、填空题1.0.7;2.81;3.11;4.120;5.1;6.12;7.896;8.411;9.1,e e−; 10.210x y −−=; 11.11 12.2,3,4,6,1,5二、选择题13.C 14.B 15.C 16.A 三.解答题17.(1)增区间为()(),1,2,−∞−+∞,减区间为[]1,2− 18.(1)30,10x y == (2)123319.(1)0.36 (2)[]57E X =,[]853D X = 20.(1)2 (221.(1)234333676,,T T T ===(2)203nnk nk T ==∑,203n nk n k k T n ==⋅∑ (3)1024n =。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2019年高二下学期数学(理科)期末模拟试卷 注意事项: 1. 答题前,考生先将自己的姓名、准考证号填写清楚,将条形码准确粘贴在考生信息条形码粘贴区。 2.选择题必须使用2B铅笔填涂;非选择题必须使用0.5毫米黑色字迹的签字笔书写,字体工整、笔迹清楚。 3.请按照题号顺序在各题目的答题区域内作答,超出答题区域书写的答案无效;在草稿纸、试题卷上答题无效。 4.保持卡面清洁,不要折叠,不要弄破、弄皱,不准使用涂改液、修正带、刮纸刀。
一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.已知21zii,则复数z( ) A.13i B.13i C.3i D.3i 2.用反证法证明某命题时,对结论:“自然数,,abc中恰有一个偶数”正确的假设为( ) A.,,abc都是奇数 B.,,abc都是偶数 C.,,abc中至少有两个偶数 D.,,abc中至少有两个偶数或都是奇数 3.在极坐标系中,若圆C的方程为2cos,则圆心C的极坐标是( )
A.1,2 B.1,2 C.1,0 D.1, 4.下列推理属于演绎推理的是( ) A.由圆的性质可推出球的有关性质 B.由等边三角形、等腰直角三角形的内角和是180°,归纳出所有三角形的内角和都是180° C.某次考试小明的数学成绩是满分,由此推出其它各科的成绩都是满分 D.金属能导电,金、银、铜是金属,所以金、银、铜能导电
5.对于,abR,2abab(大前提),112xxxx(小前提),所以12xx(结论).以上推理过程中的错误为( ) A.大前提 B.小前提 C.结论 D.无错误 6.函数lnyxx的单调递减区间是( ) A.1,e1,e B.1,e C.10,e D.,e 7.22sincosxxdx的值为( ) A.0 B.2 C.2 D.4 8.已知随机变量服从正态分布23,N,则3P等于( ) A.15 B.14 C.13 D.12 9.投掷一枚均匀硬币和一枚均匀骰子各一次,记“硬币正面向上”为事件A,“骰子向上的点数是3”为事件B,则事件,AB中至少有一件发生的概率是( )
A.512 B.12 C.712 D.34 10.现安排甲、乙、丙、丁、戊5名同学参加上海世博会志愿者服务活动,每人从事翻译,导游,礼仪,司机四项工作之一,每项工作至少有一人参加.甲,乙不会开车但能从事其他三项工作,丙,丁,戊都能胜任四项工作,则不同的安排方案的种数是( ) A.54 B.90 C.126 D.162
11.用数学归纳法证明4221232nnnL,则当1nkn*N时,等式左边应在nk的基础上加上( ) A.21k B.21k
C.42112kk D.22221231kkkkL 12.已知函数2lnxxbfxbxR,若存在1,22x,使得0fxxfx,则实数b的取值范围是( ) A.9,4 B.,0 C.,2 D.3,2 第Ⅱ卷(共90分) 二、填空题(每题5分,满分20分,将答案填在答题纸上) 13.某学校为了制定治理学校门口上学、放学期间家长接送孩子乱停车现象的措施,对全校学生家长进行了问卷调查.根据从中随机抽取的50份调查问卷,得到了如下的列联表: 同意限定区域停车 不同意限定区域停车 合计 男 20 5 25 女 10 15 25 合计 30 20 50 则认为“是否同意限定区域停产与家长的性别有关”的把握约为 .
附:22nadbcKabcdacbd,其中nabcd. 2PKk
0.050 0.005 0.001
k 3.841 7.879 10.828
14.82112xxx的二项展开式中常数项是 .(用数字作答) 15.安排5名歌手的演出顺序时,要求甲歌手不第一个出场,另一名歌手乙不最后一个出场,不同的排法种数是 .(用数字作答)
16.①回归分析中,相关指数2R的值越大,说明残差平方和越大; ②对于相关系数r,r越接近1,相关程度越大,r越接近0,相关程度越小; ③有一组样本数据1122,,,,,,nnxyxyxyL得到的回归直线方程为ˆybxa,那么直线ˆybxa
必经过点,xy; ④2K是用来判断两个分类变量是否有关系的随机变量,只对于两个分类变量适合; 以上几种说法正确的序号是 . 三、解答题 (本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.)
17. 已知曲线14cos:3sinxtCyt(t是参数),28cos:3sinxCy(是参数). (1)化12,CC的方程为普通方程,并说明它们分别表示什么曲线; (2)若1C上的点P对应的参数为2t,Q为2C上的动点,求PQ中点M到直线332:2xtCyt(t是参数)距离的最小值. 18. 某电脑公司有6名产品推销员,其工作年限与推销金额数据如下表: 推销员编号 1 2 3 4 5 工作年限x/年 3 5 6 7 9 推销金额y/万元 2 3 3 4 5
(1)求年推销金额y关于工作年限x的线性回归方程; (2)若第6名推销员的工作年限为11年,试估计他的年推销金额. 附:线性回归方程ˆˆˆybxa中,1221ˆniiiniixynxybxnx,ˆˆaybx,其中,xy
为样本平均值.
19. 甲、乙两人各射击一次,击中目标的概率分别是23和34.假设两人射击是否击中目标,相互之间没有影响;每次射击是否击中目标,相互之间没有影响. (1)求甲射击4次,至少1次未击中目标的概率; (2)求两人各射击4次,甲恰好击中目标2次且乙恰好击中目标3次的概率. 20. 有一次购物抽奖活动中,假设某10张奖券中有一等奖券1张,可获价值为50元的奖品;有二等奖卷3张,每张可获价值为10元的奖品;其余6张没有奖.某顾客从此10张券中任抽2张,求: (1)该顾客中奖的概率; (2)该顾客获得的奖品总价值X(元)的概率分布列和期望. 21. 数列na满足2nnSnan*N. (1)计算123aaa、、,并猜想na的通项公式; (2)用数学归纳法证明(1)中的猜想. 22.已知函数21ln2fxxax. (1)若1a,求函数fx的极值,并指出是极大值还是极小值; (2)若1a,求证:在区间1,上,函数fx的图象在函数323gxx的图象的下方.
高二理科数学参考答案 一、选择题 1-5:BDCDB 6-10:CCDCC 11、12:DA 二、填空题 13.99.5% 14.-42 15.78 16.②③④ 三、解答题
17.解:(1)221:431Cxy,222:1649xyC,
1C为圆心是4,3,半径是1的圆.
2C为中心是坐标原点,焦点在x轴上,长半轴长是8,短半轴长是3的椭圆;
(2)当2t时,4,4P,8cos,3sinQ,
故324cos,2sin2M, 3C为直线270xy,
M到3C的距离54cos3sin135d,
从而当4cos5,3sin5时(可省略), d取得最小值855.
18.解:(1)设所求的线性回归方程为ˆˆˆybxa
,
则5152110ˆ0.520iiiiixxyybxx, ˆˆ0.4aybx
,
∴年推销金额y关于工作年限x的线性回归方程为ˆ0.50.4yx; (2)当11x时,ˆ0.50.40.5110.45.9yx(万元). ∴可以估计第6名推销员的年推销金额为5.9万元. 19.解:(1)设“甲射击4次,至少1次未击中目标”为事件A,
则其对立事件A为“4次均击中目标”, 则426511381PAPA; (2)设“甲恰好击中目标2次且乙恰好击中目标3次”为事件B, 则22242133PBC334311448C. 20.解:(1)设“该顾客中奖”为事件A, 26210
15211453CPAC,
即该顾客中奖的概率为23; (2)X的所有可能值为0,10,20,50,60, 26210
110153CPXC,
1136210
2105CCPXC,
23210
12015CPXC,
1116210
25015CCPXC,
1113210
16015CCPXC.
故X的分布列为: X 0 10 20 50 60
P 13 25 115 215 115
从而期望121010203515EX215060161515.
21.解:(1)当1n时,1112aSa, ∴11a; 当2n时,122222aaSa, ∴232a; 当3n时,1233323aaaSa, ∴374a;
