侧位停车数学建模
数学建模汽车停车距离问题教学实例分析

数学建模汽车停车距离问题教学实例分析发布时间:2021-04-07T11:21:27.893Z 来源:《教育研究》2021年2月作者:黄高湧[导读] 数学建模就是建立数学模型解决实际问题的过程,《普通高中数学课程标准(2017版)》把“数学建模”定义为是对现实问题进行数学抽象,用数学语言表达问题,用数学方法构建模型解决问题的过程,如果问题没有得到很好的解决,还需要重复进行建模过程.龙湾区教师发展中心黄高湧 3250241核心素养数学建模的内涵数学建模就是建立数学模型解决实际问题的过程,《普通高中数学课程标准(2017版)》把“数学建模”定义为是对现实问题进行数学抽象,用数学语言表达问题,用数学方法构建模型解决问题的过程,如果问题没有得到很好的解决,还需要重复进行建模过程. 2007年,Blum提出建模七阶段循环过程,即把整个建模过程分为七个环节,六个状态:现实问题情景模型现实模型数学模型数学结果数学世界现实世界;主要为(1)理解“现实问题”构造“情景模型”;(2)简化“情景模型”构造“现实模型”;(3)数学化,即用数学的语言描述“现实模型”从而构造“数学模型”;(4)应用数学方法得到数学结果;(5)根据现实问题解释数学结果获得现实结果;(6)结合原来的情景验证结果,如果结果差强人意,则重新进行建模过程;(7)介绍问题解决方案,并与他人交流.数学建模是一个过程,而最重要也是学生感觉最困难的是“现实问题数学模型”这一过程,为了更好地提高学生的数学建模能力寻找好的数学建模问题是关键. 2核心素养数学建模实例分析案例《汽车停车距离问题》教学设计2.1教学内容与核心素养解析本案例选自《普通高中数学课程标准(2017版)》,通过让学生思考汽车急刹车过程,折出影响汽车停车距离的主要因素,初步建立急刹车的停车距离模型:停车距离=反应距离+刹车距离,而后借助数据收集、画散点图、函数拟合、物理分析、讨论验证等环节得到汽车停车距离的函数模型,并应用该模型解决实际问题.数学建模是利用数学方法解决实际问题的一种实践.即通过抽象、简化、假设、引进变量等处理过程,将实际问题用数学方式表达,建立起数学模型,然后运用数学方法及计算技术进行求解的过程,本案例力图让学生经历数学建模的一般过程,进一步形成和发展学生数学建模的核心素养,培养和提高学生发现与提出问题、分析与解决问题的能力.2.2汽车停车距离问题教学设计1)实际引入,提出问题问题1 (播放汽车追尾事故视频) 在我国道路交通安全条例第80条中规定,高速公路车速超过100公里每小时时,应当与同车道前车保持100米以上的车距.这个“100米以上”的依据是什么?设计意图:(1)以新闻视角的形成引出课题,吸引学生的注意力,思考追尾事故多发的社会问题,从而引导抽象出数学问题,让学生自然的体会数学抽象的过程,引导学生关注社会实际情况.(2)通过交通法规的相关规定,给出实际问题提出“保持100以上”的依据是什么问题,从而引出汽车停车距离问题,引起学生的思维冲突与关注,激发学生探究问题的兴趣.2)联系实际,分析问题问题2 影响汽车停车距离的因素是什么?其中最关键因素是什么?设计意图:汽车停车距离问题是一个多变量问题,研究不同物理量对安全停车距离的影响,使学生明白研究问题的角度可以多样化,要关注到各种因素.但是在研究分析问题时为了更准确的分析关系,采用控制变量的方式,控制其它因素不变,从而分析实际问题.3)建立数学模型问题3 如何建立汽车停车距离关于行驶速度之间的函数关系?设计意图:汽车停车距离问题,先从物理角度分析得出确定的函数模型,而且它的运动状态对于具有一定物理基础的高中学生是容易推导得出的.但也要让学生明白,很多实际生活中的问题是没有确定的模型,那么就要先收集数据,分析数据特点,然后从散点图拟合的角度去拟合函数模型。
停车场泊车位设计的数学建模

对每一排停车位, 其一边为通道,另一边则可以是另一排停车位或者是停车场的 边缘。所以停车排数 PC 最多只能是通道数 P 1 的两倍,即:
PC 2P 1 (2)
如果按照一排停车位,一条通道,一排停车位这样三排一组的形式加以组合,依 次排列,确实也可以达到 PC 2P 1 。即(2)式中的等号是可以成立的。此时, 车位数可以达到停车位位置的最大值,排列情况同样可以见图 9 100 米宽的停车场的一边可以当作足够长的边来看待, 将 300 米为一排来设计小 轿车的车位, 即每排车位与矩形的短边平行。 在理想情况下, 根据 4.1 讨论可知, 最佳设计下的车位长度为:
我们假定小轿车的最外端在半径为c1的原周上行驶且此时轿车的最内端在半径为c2的原周上随之移动然后以角度进入停车位所以通道的最小宽度每辆车均以角度停放用w表示小轿车停车位的宽度l表示停车位的长度这的最上方并没有渠道最下端是考虑到车身以外的区域可以留给对面停车位使用l0表示停车位末端的距离易知他们分别是停车角的函数且有
1 L C1 sin Cw cos 3.3sin 69.94 1.4cos 69.94 3.580(米) 2
停车场通道宽度为:
R C1 C2 cos 4 2cos 69.94 3.314(米)
所以,理想情况下的一组(即两排车位中间加一条行通车道)的宽度 X 约为:
X 2L R 10.474(米)
则 100 米宽的停车场能够考虑设计 9 组这样的车位, 现在在考虑从出入口到最里 面靠墙这一段与横向垂直通道 R ' 的情况,即有一组里面有一排车位数是完整的, 也就是说其余的 8 组以及剩下一组的两排车位数是一样缺少出入口通道 R ' 所占 的数目。显然,横向通道 R ' =6.1 米较合理,而理想条件下相邻车尾末端的距离 是 L0
停车场-数学建模

停车场-数学建模停车场泊车位模型摘要现如今随着机动车辆的增加,车辆停放困难的问题逐渐加重,我们现在就来讨论New England的一个镇上的某停车场为场景的数学模型。
对单个停车位进行分析得出车位最佳角度,然后对整个停车区域进行规划得出车位布局,再用模糊评判来进行停车位效度评价,比较好的解决了问题。
在对停车场泊车位优化设计的模型中,我们考虑一种把车间距空间并入车辆所在的空间的方式,形成一个矩形,因其可以在空间无间隙密铺从而简化分析过程。
通过分析单个车辆进入泊车位的车辆状态得到车辆的最小转弯半径,再通过非整数规划得到单个车位最佳设计角度,然后拓展到整个规划区域,最后得出停车场泊车位的整个规划,最终的设计方案总共能够提供98个泊车位,空间时间利用效率较高。
对停车场的车位效度评价,采用模糊评价模型,从停车场的安全性、便捷性和效率性三个方面来建立效度评价指标体系,得到三个一级指标,再从进出停车场、进出停车位和停车场内行车等方面考虑建立二级指标,得出比较全面的效度评价指标体系,最后再根据指标体系用层次分析法和模糊评价来进行车位效度评价。
关键词:层次分析模糊评价转弯半径停车角度1、问题的叙述在New England的一个镇上,有一位于街角处面积100 200平方英尺的停车场,场主请你代为设计停车车位的安排方式,即设计在场地上划线的方案。
容易理解,如果将汽车按照与停车线构成直角的方向,一辆紧挨一辆地排列成行,则可以在停车场内塞进最大数量的汽车,但是对于那些缺乏经验的司机来说,按照这种方式停靠车辆是有困难的,它可能造成昂贵的保险费用支出。
为了减少因停车造成意外损失的可能性,场主可能不得不雇佣一些技术熟练的司机专门停车;另一方面,如果从通道进入停车位有一个足够大的转弯半径,那么,看来大多数的司机都可以毫无困难地一次停车到位。
当然通道越宽,场内所容纳的车辆数目也越少,这将使得场主减少收入。
2、问题分析一般来说,想尽可能的把车塞进停车场,最好的办法就是以垂直停靠的方式将车一辆挤一辆地排成行,但是这样停放的后果就是车辆不能自由出入,只有后进入的车辆全部先出去了,先进入的车才可以离开停车场,显然不符合实际的需求。
停车问题模型结构论文

问题二:首先建立了在停车位宽度一定的情况下,车辆与街边车辆距离 y、 与停车位长度 lw 的数学模型,并利用 MATLAB 画出车辆与街边车辆距离 y 变换对 停车位长度 lw 的影响,并总结出最小空位长度 L 的值为 6546mm。
图1-2-1:步骤一
图1-2-2:步骤二
如图1-2-1和图1-2-2所示,在车辆平行泊车过程中,令步骤一结束时后车轮泊车
轨迹的转角弧度为1 ,车轴与水平方向的夹角为1t ,步骤二结束时,车轮泊车
轨迹的转角弧度为2 ,车轴与水平方向的夹角为2t ,此时2t 0 。
步骤一:先右打方向盘,使车神沿后车轴以半径 r1 旋转1 ,其中泊车“一个
三、符号说明
1.y为车子与停靠在街边车辆的距离 2.x为汽车开到超过空位的距离 3. l 为车长 4. w 为车宽 5. lw 为车位长 6. cw 为车位宽
7. zj 为轴距
8. r 为转弯半径 9. 为转弯角度
四、模型假设
1.假设汽车在行驶的公路是平坦的,并且摩擦因子是稳定的。小车的各项部件的 灵敏度是稳定不变的,且各项系数的性度良好,安全度较高。 2.汽车在行驶过程中能做到以稳定的速度运动,排除人的干扰作用。 3.本文中只讨论最佳情况“二次泊车”。 4.车子的运动轨迹为光滑的曲线。 5.平行泊车完成:车辆已完全泊入指定停车位,车身与竖直方向夹角不大于 5 度, 且车辆中轴与停车位中轴间水平距离不大于 100mm。这种状态下,即使泊车结果 不是很理想,驾驶员也可在泊车入位后,轻松的把车辆调整到理想位置。 6.泊车一个步骤:改变方向转动一次方向盘的泊车过程称为“泊车一个步骤", 也叫“一次泊车"。 7.本文中的车辆为普通小轿车。
车位分配问题 数学建模
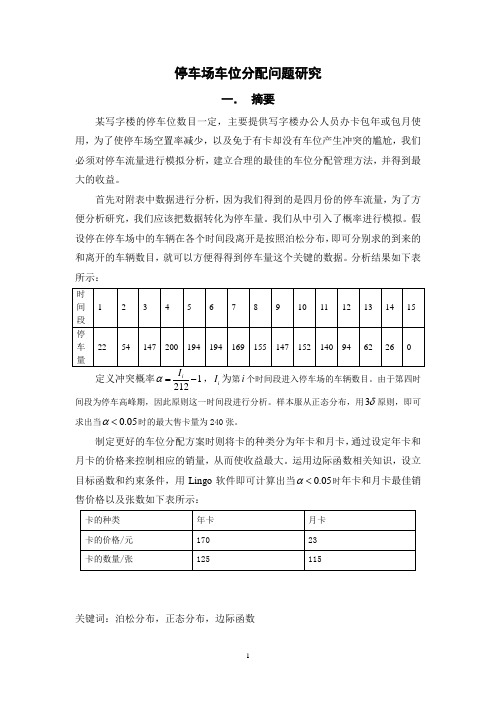
停车场车位分配问题研究一. 摘要某写字楼的停车位数目一定,主要提供写字楼办公人员办卡包年或包月使用,为了使停车场空置率减少,以及免于有卡却没有车位产生冲突的尴尬,我们必须对停车流量进行模拟分析,建立合理的最佳的车位分配管理方法,并得到最大的收益。
首先对附表中数据进行分析,因为我们得到的是四月份的停车流量,为了方便分析研究,我们应该把数据转化为停车量。
我们从中引入了概率进行模拟。
假设停在停车场中的车辆在各个时间段离开是按照泊松分布,即可分别求的到来的和离开的车辆数目,就可以方便得得到停车量这个关键的数据。
分析结果如下表所示:定义冲突概率1212iα=-,i I 为第i 个时间段进入停车场的车辆数目。
由于第四时间段为停车高峰期,因此原则这一时间段进行分析。
样本服从正态分布,用3δ原则,即可求出当0.05α<时的最大售卡量为240张。
制定更好的车位分配方案时则将卡的种类分为年卡和月卡,通过设定年卡和月卡的价格来控制相应的销量,从而使收益最大。
运用边际函数相关知识,设立目标函数和约束条件,用Lingo 软件即可计算出当0.05α<时年卡和月卡最佳销售价格以及张数如下表所示:关键词:泊松分布,正态分布,边际函数二.问题分析与重述问题一:题目要求模拟附表中停车流量,分析停车量的统计规律。
停车流量与停车量是两个不同的概念,要分析停车量的统计规律就必须弄清楚来到停车场的车辆数目以及离开停车场的车辆数目。
而题目所给的条件中我们只知道停车流量,也就是车离开与来到的总的次数,因此我们假设车的离开服从泊松分布,运用概率来求出单位时间内车辆离开的数目,这样也就可以知道单位时间内车辆到来的数目,它们两者的差值也就是我们所要求的停车量。
α=情形下,计算最大售卡量。
问题二:定义冲突概率,求若冲突概率低于0.05根据附表中停车流量数据,以及上题对停车量的分析,我们可以知道在第四个时间段,即早上9:00—10:00停车量是最多的,也就是在这段时间产生冲突的概率是最大的,为了计算最大售卡量,我们就取这段时间进行分析。
讲给老婆的侧方停车和倒车入库模型

掉头
8.6m
1.15 m
一次掉头的距离等效 为2个车身长度
L=2.603m 车身长度:4.49m
:5.35m
侧方位倒车入库 正车出库
后车轮与停着的车距离最近时(约1m)开始反向打死 此时车与停着的车角度60°
1.2m 5m
1.8m
1.0m
1.1m 6.7m
前车轮与停着的车 车头对齐时开始打死
停车位长度为1个半车身长度
倒车入库 正车出库
车头在转向过程 会在车尾处最突出
车尾和相邻车头中心对齐开始打死
4.4m 约为1个车身长度
1.15 m
1m 车头超出2.1m
正车入库 倒车出库
车身中央与停车的车头中心对齐 开始打死
1.9m
1.2m 1.7m
侧方位正车入库
车身中央与停车车头对齐时打死
1.2m 1.7m
9.5m
驾驶人与停车车身外侧平齐时反 向打死
停车位长度应略大于2个车身长度
数学建模停车位规划与评价
. . .. . .承诺书我们仔细阅读了中国大学生数学建模竞赛的竞赛规则.我们完全明白,在竞赛开始后参赛队员不能以任何方式(包括、电子、网上咨询等)与队外的任何人(包括指导教师)研究、讨论与赛题有关的问题。
我们知道,抄袭别人的成果是违反竞赛规则的, 如果引用别人的成果或其他公开的资料(包括网上查到的资料),必须按照规定的参考文献的表述方式在正文引用处和参考文献中明确列出。
我们重承诺,严格遵守竞赛规则,以保证竞赛的公正、公平性。
如有违反竞赛规则的行为,我们将受到严肃处理。
我们参赛选择的题号是(从A/B/C/D中选择一项填写): B我们的参赛报名号为(如果赛区设置报名号的话):所属学校(请填写完整的全名):参赛队员(打印并签名) :1. 肯2. 蔡春婷3. 王露指导教师或指导教师组负责人(打印并签名):日期:2011年08月25 日赛区评阅编号(由赛区组委会评阅前进行编号):某停车场泊位规划与效度评价摘要对于停车位规划问题我们引入了坡度因素,提出了三种模型,分别为“三排斜列坡度式”“斜列交错式”和“两排垂直式”,我们依据空间效率最大化的原则,精确作图,合理分区,最后发现“两排垂直式”能容纳的停车位最多,共100个。
然后我们利用模糊分析法建立了停车场评价系统模型,其中使用了层次分析法确定权系数向量,并创造性地将停车场设计与评语相关联,建立了因素评语表,构建了模糊评价矩阵。
在求解一级、二级综合评价矩阵时,比较了“主因素决定型”“主因素突出型”和“加权平均型”三种计算方法后,发现用“加权平均型”所得的结果最为准确,并判断“两排垂直式”模型的评价为:很好。
由于为露天停车场,且不考虑车位的费用差异,那么车主对于车位的评价,其心理因素应包含防盗、防刮擦、距出入口距离、是否遮阴等。
我们用目标规划的思路,用三个优先级依次递增的指标进行评价。
在筛选车位时我们又使用了决策论中淘汰“次优方案”的思路,根据优先级逐渐把“次劣”泊车位排除,最后发现在我们选用的规划设计中,靠花坛停放的最右侧的两个车位是最劣车位,最不受欢迎。
2016数学建模停车策略论文详解
自动泊车系统数学建模【摘要】随着汽车产业及科技的高速发展,智能驾驶汽车成为了国内外公认的未来汽车重要发展方向之一。
而在汽车智能化进程中,自动泊车是一项非常具有挑战性和实用性的技术。
自动泊车系统可通过各类传感器获取车位相对汽车的距离,通过控制汽车前轮转角和瞬时速度控制车辆行驶。
若考虑系统控制容易性,参考人工倒车入库,当车辆位于与车位垂直的任意位置时,先通过前行或后退到达理想停车起始点后,再确定前进转角和后退转角,使车身与车位在同一直线上后,直接倒车完成入库,即“一进二退”。
这种两段式倒车模式提高了泊车过程中车辆行驶的紧凑性,同时减少了泊车行驶空间。
考虑奇瑞汽车公司的QQ3,长3550mm ,宽1495mm ,轴距2340mm ,前轮距1295mm ,后轮距1260mm ,目标车库为小型汽车库标准大小长6m ,宽2.8m ,车库周围情况如图。
关键字:转乘次数 广度优先算法 查询效率 实时系统一 问题的重述1) 建立模型,按照车辆与车位之间的距离把车辆位置进行分组,给出每一组对应的倒车理想起始点,a=400mm ,b=8000mm ,c=300mm 。
2)建立模型,给出由理想起始点到倒车入库的泊车策略,包括车速、前轮转角、后轮行驶距离。
二 符号说明i L :第i 条公汽线路标号,i=1,2 …10400,当i 520≤时, i L 表示上行公汽路线, 当i 520>时, i L 表示与上行路线i 520L -相对应的下行公汽路线;i ,g S :经过第i 条公汽路线的第g 个公汽站点标号;j T :第j 条地铁路线标号, j=1,2;j ,h D :经过第j 条地铁线路的第h 个地铁站点标号;n L S :转乘n 次的路线;k T :选择第k 种路线的总时间;k N 1:选择第k 种路线公汽换乘公汽的换乘次数;k N 2:选择第k 种路线地铁换乘地铁的换乘次数;k N 3:选择第k 种路线地铁换乘公汽的换乘次数;k N 4:选择第k 种路线公汽换乘地铁的换乘次数;k ,m W :第k 种路线、乘坐第m 辆公汽的计费方式,其中:k,m W 1=表示实行单一票价,k,m W 2=表示实行分段计价;k,m CL :第k 种路线,乘坐第m 辆公汽的费用;k C :选择第k 种路线的总费用;k m MS ,:选择第k 种路线,乘坐第m 辆公汽需要经过的公汽站个点数; k ,n M D :选择第k 种路线,乘坐第n 路地铁需要经过的地铁站个点数;k ,m FS :表示对于第k 种路线的第m 路公汽的路线是否选择步行,k ,m FS 为0-1变量,k,m FS 0=表示不选择步行,k,m F S 1=表示选择步行; k ,n FD :对于第k 种路线的第n 路地铁的路线是否选择步行,k ,n FD 为0-1变量,k,n F D 0=表示不选择步行,k,n FD 1=表示选择步行;三模型假设3.2 其它假设10、查询者转乘公交的次数不超过两次;11、所有环行公交线路都是双向的;12、地铁线T2也是双向环行的;13、各公交车都运行正常,不会发生堵车现象;14、公交、列车均到站停车四问题的分析对于路线的评价,我们可以分别以总行程时间,总转乘次数,总费用为指标,也可以将三种指标标准化后赋以不同权值形成一个综合指标。
2023高教杯数学建模c题
数学建模C题题目为"城市停车问题",是一个具有实际应用背景的问题,涉及到城市交通、土地利用、城市规划等多个方面。
本答案将采用层次分析法(AHP)来解决该问题。
首先,我们需要对问题进行详细的分析。
城市停车问题主要包括两个方面:一是寻找合适的停车位,二是考虑停车场的布局和数量。
针对这两个方面,我们可以从以下几个方面进行建模:1. 确定停车需求:根据城市的人口、车辆数量、交通状况等因素,确定不同区域的停车需求。
2. 确定停车场的布局:根据停车需求和停车场的特点(如占地面积、建设成本等),确定停车场的布局和数量。
3. 建立层次分析模型:将停车需求和停车场布局两个因素作为目标层,将其他相关因素作为准则层,建立层次分析模型。
4. 计算权重:根据层次分析模型,通过计算各因素的权重,为决策者提供参考。
接下来,我们将使用Python语言和相关的数学建模工具来实现上述建模过程。
首先,我们需要导入相关的库和模块,如numpy、scipy等。
假设我们已经收集了相关数据,包括城市的人口、车辆数量、交通状况、土地利用情况等。
我们可以使用这些数据来建立层次分析模型,具体步骤如下:1. 构建层次结构模型:将停车需求和停车场布局作为目标层,将土地利用情况、交通状况、停车场特点等作为准则层。
2. 构造判断矩阵:根据准则层因素对目标层的影响程度,构建判断矩阵。
可以使用专家打分等方法来确定各因素的权重。
3. 计算权重:使用scipy等库中的函数,根据判断矩阵计算各因素的权重。
4. 一致性检验:对判断矩阵进行一致性检验,确保各因素的权重合理。
5. 综合权重:将准则层因素的权重与目标层的权重相乘,得到综合权重。
最终,我们可以根据综合权重来评估不同方案的优劣,为决策者提供参考。
在实际应用中,我们还需要考虑其他因素,如政策支持、经济成本等,综合评估各种方案,选择最优方案来解决城市停车问题。
总之,通过层次分析法可以有效地解决城市停车问题,为决策者提供科学的参考依据。
侧位停车数学建模.
一.问题重述侧位停车是指驾驶员在停车位时利用自身的倒车技巧,使车辆按照一定的行驶轨迹,安全的,在不触碰到两边车辆的前提下,让自己的车停到规定好的停车位上。
侧位停车常常会出现许多两车碰擦的情况,通常时由于驾驶员技术的生疏或者不熟练,亦或是停车位长宽大小建造的不科学。
正确的科学的停车位建设,能在给驾驶员提供充足的停车空间的条件下,尽可能的节约场地,对于当今停车位紧缺的问题具有相当大积极意义。
现在我们根据题中所给的条件,研究停车位宽度一定时,车位长度最小的情况,以及保证车辆正常停车时,停车位长度与车辆可供行驶的道路宽度的关系,建立数学模型解决以下问题:问题(1),在可供行驶的道路宽度足够大时,求车位长度的最小值。
汽车如果可供行驶宽度y足够大,车辆要能够停进这个车位(车辆只能倒车,不能前进),车位长度x最小为多少?假设车辆的初始位置与车位平行,求出车辆的初始位置、倒车入库过程中方向盘位置a的取值变化和车前轮的轨迹。
(2)如果y不是足够大(当然y肯定大于车宽),那么x和y满足什么条件的情况下,车辆只通过倒车就能停进车位(车辆只能倒车不能前进)?(3)设y=2000mm,求出倒车过程中方向盘调整次数最少时x的最小值,以及此时倒车过程中a的取值变化。
二.问题分析城市中建立起愈来愈多住房区,超市,商场,同时又由于人民收入水平的增加,越来越多的人加入到了“有车一族”的行列。
城市建设和有车一族的人们对停车位的需求越来越大。
而城市里的土地资源的紧张,则对我们如何规划一个提高停车位利用率停车位提出了一定的要求。
在此同时,由于一个个新手驾驶员的技术不熟练和内在的不自信,建设的停车位又要能容许他们的操控误差。
针对问题(1),我们考虑到了在停车位宽度一定的情况下,汽车恰好切入停车位的情况(忽略了汽车倒车时速度的大小)。
此时利用一定的几何知识,我们可以求得所求的停车位最小长度。
同时结合汽车的最小转弯半径,我们确定了汽车转弯的圆心,并建立了直角坐标系,求得汽车停车时前轮的运动轨迹。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一.问题重述侧位停车是指驾驶员在停车位时利用自身的倒车技巧,使车辆按照一定的行驶轨迹,安全的,在不触碰到两边车辆的前提下,让自己的车停到规定好的停车位上。
侧位停车常常会出现许多两车碰擦的情况,通常时由于驾驶员技术的生疏或者不熟练,亦或是停车位长宽大小建造的不科学。
正确的科学的停车位建设,能在给驾驶员提供充足的停车空间的条件下,尽可能的节约场地,对于当今停车位紧缺的问题具有相当大积极意义。
现在我们根据题中所给的条件,研究停车位宽度一定时,车位长度最小的情况,以及保证车辆正常停车时,停车位长度与车辆可供行驶的道路宽度的关系,建立数学模型解决以下问题:问题(1),在可供行驶的道路宽度足够大时,求车位长度的最小值。
汽车如果可供行驶宽度y足够大,车辆要能够停进这个车位(车辆只能倒车,不能前进),车位长度x最小为多少?假设车辆的初始位置与车位平行,求出车辆的初始位置、倒车入库过程中方向盘位置a的取值变化和车前轮的轨迹。
(2)如果y不是足够大(当然y肯定大于车宽),那么x和y满足什么条件的情况下,车辆只通过倒车就能停进车位(车辆只能倒车不能前进)?(3)设y=2000mm,求出倒车过程中方向盘调整次数最少时x的最小值,以及此时倒车过程中a的取值变化。
二.问题分析城市中建立起愈来愈多住房区,超市,商场,同时又由于人民收入水平的增加,越来越多的人加入到了“有车一族”的行列。
城市建设和有车一族的人们对停车位的需求越来越大。
而城市里的土地资源的紧张,则对我们如何规划一个提高停车位利用率停车位提出了一定的要求。
在此同时,由于一个个新手驾驶员的技术不熟练和内在的不自信,建设的停车位又要能容许他们的操控误差。
针对问题(1),我们考虑到了在停车位宽度一定的情况下,汽车恰好切入停车位的情况(忽略了汽车倒车时速度的大小)。
此时利用一定的几何知识,我们可以求得所求的停车位最小长度。
同时结合汽车的最小转弯半径,我们确定了汽车转弯的圆心,并建立了直角坐标系,求得汽车停车时前轮的运动轨迹。
针对问题(2)我们根据问题中讨论情况,我们选取汽车恰好能停入停车位的情况,继而求得道路宽度与车位长度之间的关系。
针对问题(3)我们在问题(1)的基础上,选取圆弧轨迹最少的一次,起轨迹变化的次数既是所要求方向盘改变的最小次数。
模型建立2.1车辆初始位置的初步探讨初始位置的确定有几个较重要的条件,分别为:(1)泊车时须保证车身不能和前一车位发生空间碰撞,需确定极限转弯最远点的值;(2)把路旁停车位假想为一个停车库,泊车过程中车身不能和车库的库底发生碰撞,车轮不能和库边发生碰撞。
(3)采用极限转弯半径,即最小转弯半径,来确定最小停车位长度从而约束泊车初始位置。
极限转弯最远点值的确定如图示IV —1所示,F 代表泊车初始位置,MNPQ 代表车位趋势,把方向盘打到极限位置后,以低速稳定车速转弯。
图示IV —1 极限转弯最远点值的计算示意图试验车最小转弯半径r=5500mm ,车宽w=1778mm ,EF=500ram ,车辆中心点距车位角Ⅳ点距离为NE ,可计算得出极限转弯最远点NE 的值。
NE 的确定对泊车初始位置的确定有着实际的意义。
85.263122)17785500(22)(=⨯-=⨯-=w r NE 2.2最短停车位长度的确定如果停车位长度较长,车辆泊车的初始位置较合理,泊车“二个步骤"即可完成泊车。
一般来说,停车位空间较长时,两平行车辆间存在着一最佳水平距离,车辆“两次泊车”即可完成泊入停车位。
图示IV—2所示的最小停车位空间示意图中,车辆“两次泊车"可泊入车位。
显然,车辆初始位置不同,“两次泊车”泊入停车位空间时,所必需的停车位长度是不同的。
当泊车转向角最小时,停车位有一个极限值,称为最小停车位。
泊车入位过程中,当方向盘打死到极限转弯的状态,车辆“两次泊车"完成泊入停车位空间时,所占用的停车位长度最小。
图示IV—2 平行泊车最小停车空间示意图泊车准备时车辆放于F点,逐渐行驶到N点,此时恰好为泊车时内侧车头恰好与前方车辆不碰撞的位置状态。
当车辆到达S点位置时,车身方向角大约为45°左右,此时反打方向盘直至方向盘打死。
当到达T点时,为防止车尾与后方车辆、右车轮与右侧路边相碰撞,取车尾与后车头部、车身与右侧路边最短距离为100mm,最小停车位的约束值为:min2(2)(1100500NP r w=-⋅-+-min100 2QP NE l=++其中,NE的计算见本条中“泊车初始位置的初步探讨,r、l与w分别为车辆最小转弯半径,车辆长度与宽度,500表示在泊车预备时泊车距离车道实线的最小安全距离,单位为mm。
代入试验车相关参数,可得:NP的最小值=2321mm,QP的最小值=5855mm。
经过多次轨迹的仿真,最小停车位的几何参数定为长度5.8m,宽度2.2m。
对于试验车来说,停车位空间不小于5.8m掌2.2m时,车辆可完成泊入停车位。
停车位的长度对于泊车成功与否起着重要的作用,上述的最小停车位长度是一个相对宽松的极限值。
车辆“两次泊车’’可泊入停车位,所需车位长必须大于或等于最小停车位。
在平行泊车过程中,判断泊车能否成功,首先应检测停车位空间大小,使其不小于最小停车位的大小。
2.3普通停车位空间大小的确定停车位空间大小对平行泊车难度系数影响很大,停车位空间由车位长度和车位宽度确定。
车位空间越大,泊车困难程度相对较小;车位空间越小,泊车困难系数就越大。
图示IV—3 平行泊车普通车位空间坐标图如图示IV—3,普通车位大小标记为l*p h,p l代表车位长,p h代表车位p宽,矩形abcd表示试验车,o’代表车辆的几何中心点。
环绕车位的三面标记为BK、FT和SE,为车身方向角,即车身与水平方向的夹角,定义逆时针为正。
泊车时,驾驶员反打方向盘的时刻为,当车身方向角接近于45°时,极少会达到45°。
在实际泊车过程中,大多数驾驶员会潜意识地躲避车位顶点N点(见图示IV—2),很少一开始就把方向盘打死的,基本都是逐渐加大方向盘转角,直到打死;在接近45°至最大车身方向角时,一般维持方向角不变一段时间,保证反打方向盘时车头不会碰撞到N点,才开始反打方向盘;反打方向盘时,逐渐加大角度,直至反向打死。
通过多次平行泊车轨迹计算与仿真,确定停车位长度为7.5 m比较理想。
这样,任意车辆长度不大于5.5 m,最小转弯半径不大于6m的小轿车“两次泊车"即可泊入停车位。
其中,停车位宽度采用标准的路旁停车位宽度2.2所,和NP的最小值=2.2m吻合。
这样,确定普通车位大小为:l=7.5m,p h=2.2mp若有停车位空间满足长度不小于7.5 m,宽度不小于2.2 m,则可认为找到了适合的泊车空间,车辆很容易就能完成泊车。
2.4车辆的运动学模型即运动轨迹建立车辆侧位停车的运动学模型,上文中建立了侧位停车系统中质点的运动学模型。
在此需要求车辆侧位停车时车轮的运动轨迹。
需要建立车辆侧位停车的运动学模型,以推导出车辆侧位停车的运动轨迹方程式,作为后续研究侧位停车系统的理论基础。
下面是侧位停车运动轨迹方程:图示IV —4为车辆泊车的运动学模型,其中(xf ,yf)位前轴中心点坐标,(,r r x y )为后轴中心点坐标,v 为前轴中心点速度,l 为轴距,w 为后轮距,为前轴中心点转向角,为车辆中心轴与水平方向的夹角。
正常情况下泊车速度很低(约≤5km /h),由此假定无滑轮现象产生,后轮轨迹的垂直方向速度为0,其方程式表示如下:'cos 'sin 0r r y x θθ⋅-⋅= …… ①而图示IV —4可知,前后轴中心点坐标关系为:sin cos r f r f x x l y y l θθθθ=+⋅⋅⎧⎨=-⋅⋅⎩ …… ② 对②式进行积分得速度关系式:'''sin '''cos r f r f x x l y y l θθθθ=+⋅⋅⎧⎨=-⋅⋅⎩ …… ③把③式代入①式,得'sin 'cos '0f f x y l θθθ⋅-⋅+⋅= …… ④前后中心点的x ,y 方向速度为:'sin()'cos()r fy v x v θφθφ=⋅+⎧⎨=⋅+⎩ …… ⑤ 将⑤式代入④式,即可求得车辆回转圆角速度为: sin 'v lφθ=⋅ …… ⑥将⑤和⑥同时代入式③,即可求得后轮中心点x ,y 方向速度分别 'cos cos 'sin sin f fx v y v θφθφ=⋅⋅⎧⎨=⋅⋅⎩ …… ⑦ 最后对⑥式求时间积分,并代入⑦式后,在对时间积分即可求得后轴中心点的轨迹方程式:222sin ()cos cos cot sin()sin ()sin sin cot cos()cot (cot )(cot )r r r r v x t v dt l t l v y t v dt l t l l x y l l φθφφφθφφφφφ⋅⎧=⋅⋅⋅=⋅⋅⋅⎪⎪⋅⎪=⋅⋅⋅=-⋅⋅⋅+⋅⎨⎪⎪+-⋅=⋅⎪⎩⎰⎰…… ⑧ 根据图示IV —4中坐标位置的关系,可进一步求出左右轮中心点的运动轨迹方程式:左轮:222sin ()(cot )sin()2sin ()(cot )cos()cot 2(cot )(cot )2rL rL rL rL w v x t l t l w v y t l t l l w x y l l φφφφφφφ⋅⎧=⋅-⋅⋅⎪⎪⋅⎪=-⋅-⋅⋅+⋅⎨⎪⎪+-⋅=⋅-⎪⎩…… ⑨ 右轮:222sin ()(cot )sin()2sin ()(cot )cos()cot 2(cot )(cot )2rR rR rR rR w v x t l t l w v y t l t l l w x y l l φφφφφφφ⋅⎧=⋅+⋅⋅⎪⎪⋅⎪=-⋅+⋅⋅+⋅⎨⎪⎪+-⋅=⋅+⎪⎩…… ⑩ 由式⑨和式⑩知,当低速泊车,且不考虑轮胎侧滑时,后轮的行径轨迹与轮距,轴距及前轴中心点转向角有关,而与泊车速度无关。
以试验车(轴距2548mm ,后轮距1422mm)之相关尺寸参数为例,代入所推导之轨迹方程式中,前轴中心点左转向角为10°,泊车速度为5km/h ,后轮的预测行进轨迹如图示IV —5示:图示IV—5 转向角为10°时后轮倒车轨迹之回转圆三.模型求解对整个泊车过程成功与否影响较大的两点为:1.选准泊车起始位置2.泊车入车位时的切入点。
如图示V—1和图示V—2 所示。
图示V—1 准备泊车图示V—2 调整方向盘I.平行泊车系统模型图示IV—3、图示IV—4、图示IV—5和图示IV—6为平行泊车步骤示意图,其中停车位长度为l w,停车位宽度为c w,车长为l,车宽为w,平行车辆车a与车b问水平距离为d。
