小波分析信号处理(matlab)
小波包分解matlab
小波包分解matlab
小波包分解是一种信号处理方法，它可以将信号分解成若干个小波包，每个小波包包含了不同频率的信号成分。
这个方法在很多领域都有应用，比如图像处理、音频处理、生物信号处理等。
在matlab中，我们可以使用wavedec函数对信号进行小波分解。
而对于小波包分解，matlab也提供了相应的函数，如wpdec和wpcoef。
下面是一个简单的小波包分解的示例代码：
%生成一个随机信号
x=randn(1,256);
%设置小波包分解的参数
wname='db4'; %小波类型
level=3; %分解层数
%进行小波包分解
[wp,tree]=wpdec(x,level,wname);
%提取某个小波包系数
node=[2 1 1]; %小波包节点
coef=wpcoef(wp,tree,node);
%显示分解结果
subplot(2,1,1);
plot(x);
title('原始信号');
subplot(2,1,2);
plot(coef);
title('小波包分解后的信号');
运行上述代码后，我们可以看到分解后的信号包含了不同频率的信号成分，其中第二层第一个小波包内的信号成分最为明显。
需要注意的是，小波包分解需要选择合适的小波类型和分解层数，这个需要根据具体的应用场景进行选择。
同时，小波包分解的结果也可以用于信号压缩和特征提取等方面。
基于MATLAB的小波分析应用(第二版)(周伟)5-13章 (2)
第6章 小波变换与图像处理
2. 图像的小波分解实例 下面通过两个例子说明如何对图像进行单尺度分解和多 尺度分解，并提取多尺度分解的小波系数。 【例6-1】 对图像进行单尺度分解。 在本例中说明如何对图像进行单尺度分解。程序中调用 函数dwt2对图像进行分解，并画出图像分解的低频分量和水 平、垂直和斜线方向的三个高频分量，可以看出低频分量表 现了图像的轮廓，而高频分量表现了图像的细节。 程序代码如下：
第6章 小波变换与图像处理 subplot(231);image(wcodemat(chd2,nbc)); title('尺度2水平方向的高频系数'); subplot(232);image(wcodemat(cvd2,nbc)); title('尺度2垂直方向的高频系数'); subplot(233);image(wcodemat(cdd2,nbc)); title('尺度2斜线方向的高频系数');
第6章 小波变换与图像处理
2. 图像的平稳小波变换实例 下面举例说明函数swt2的用法。 程序代码如下：
%加载图像 load tire; nbc = size(map,1); colormap(pink(nbc)); cod_X = wcodemat(X,nbc); subplot(221)
第6章 小波变换与图像处理
第6章 小波变换与图像处理
C = [ A(N) | H(N) | V(N) | D(N) | ... H(N-1) | V(N-1) | D(N-1) | ... | H(1) | V(1) | D(1) ]
式中，A为低频系数；H为水平高频系数；V为垂直高频系 数；D为斜线高频系数；所有向量均以列向量存储在矩阵C中。
大气奢华2020Matlab中的小波分析工具箱(收藏)
t
2 T
xcjp
33
xcjp
34
课程总结：
均方意义下的时频局部化概念。 Gabor变换。 连续小波变换。
定义，容许性条件，重构定理。 二进小波。
定义，稳定性条件，重构定理。 离散小波变换。
定义，框架与对偶框架，稳定性条件，， 重构定理，正交与半正交小波。
xcjp
35
Hale Waihona Puke 课程总结：多尺度分析的定义。 尺度函数，小波函数，双尺度方程和双尺度序
在多小波变换域，目前，矢值信号的边界处理仅从数量上不增加 和完全重建两个方面来考虑。在此基础上，可进一步研究如何更 好地保持边界的连续性及适合于人的视觉特性。
在静止图像压缩方面，将多小波变换和矢量量化结合起来，是 今后值得探讨的一个方向。同时，多小波在活动图像编码中的应 用，还有待研究。
研究双正交多小波的构造和应用也是富有意义的工作。
xcjp
15
二维信号的多层小波分解：
[A,L]=wavedec2(X,N，’wname’)
[A,L]=wavedec2(X,N,H,G) 其中：A ：各层分量， L：各层分量长度
N：分解层数 X：输入信号。 wname：小波基名称 H：低通滤波器 G：高通滤波器
xcjp
16
其他的二维函数：
对变换信号的伪彩色编码：wcodemat 反变换：idwt2,idwtper2, 重构： upwlev2,waverec2,wrcoef2,
Matlab中的小波分析工具箱
（Wavelet Toolbox,Ver.1.0)
Matlab小波分析工具箱提供了一个可视 化的小波分析工具，是一个很好的算法 研究和工程设计，仿真和应用平台。特 别适合于信号和图像分析，综合，去噪， 压缩等领域的研究人员。
小波图像去噪及matlab分析
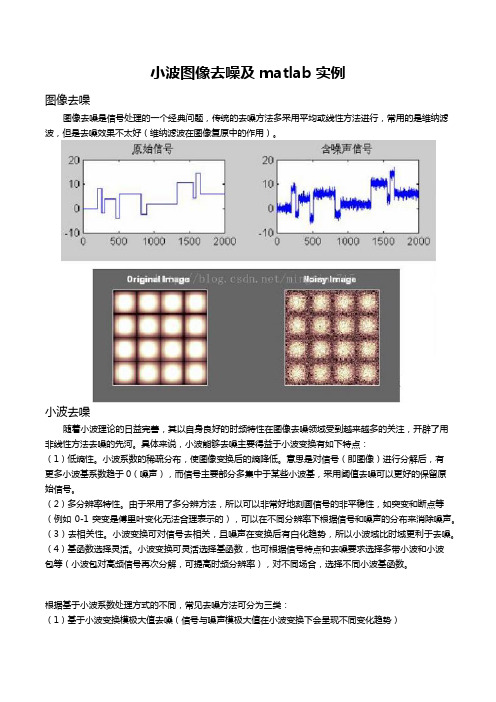
小波图像去噪及matlab实例图像去噪图像去噪是信号处理的一个经典问题，传统的去噪方法多采用平均或线性方法进行，常用的是维纳滤波，但是去噪效果不太好（维纳滤波在图像复原中的作用）。
小波去噪随着小波理论的日益完善，其以自身良好的时频特性在图像去噪领域受到越来越多的关注，开辟了用非线性方法去噪的先河。
具体来说，小波能够去噪主要得益于小波变换有如下特点：（1）低熵性。
小波系数的稀疏分布，使图像变换后的熵降低。
意思是对信号（即图像）进行分解后，有更多小波基系数趋于0（噪声），而信号主要部分多集中于某些小波基，采用阈值去噪可以更好的保留原始信号。
（2）多分辨率特性。
由于采用了多分辨方法，所以可以非常好地刻画信号的非平稳性，如突变和断点等（例如0-1突变是傅里叶变化无法合理表示的），可以在不同分辨率下根据信号和噪声的分布来消除噪声。
（3）去相关性。
小波变换可对信号去相关，且噪声在变换后有白化趋势，所以小波域比时域更利于去噪。
（4）基函数选择灵活。
小波变换可灵活选择基函数，也可根据信号特点和去噪要求选择多带小波和小波包等（小波包对高频信号再次分解，可提高时频分辨率），对不同场合，选择不同小波基函数。
根据基于小波系数处理方式的不同，常见去噪方法可分为三类：（1）基于小波变换模极大值去噪（信号与噪声模极大值在小波变换下会呈现不同变化趋势）（2）基于相邻尺度小波系数相关性去噪（噪声在小波变换的各尺度间无明显相关性，信号则相反）（3）基于小波变换阈值去噪小波阈值去噪是一种简单而实用的方法，应用广泛，因此重点介绍。
阈值函数选择阈值处理函数分为软阈值和硬阈值，设w是小波系数的大小，wλ是施加阈值后小波系数大小，λ为阈值。
（1）硬阈值当小波系数的绝对值小于给定阈值时，令其为0，而大于阈值时，保持其不变，即：（2）软阈值当小波系数的绝对值小于给定阈值时，令其为0，大于阈值时，令其都减去阈值，即：如下图，分别是原始信号，硬阈值处理结果，软阈值处理结果。
MATLAB中的时频分析与小波变换技巧
MATLAB中的时频分析与小波变换技巧引言时频分析是信号处理中的一项关键技术，可以帮助我们在时域和频域上同时展示信号的特征。
其中，小波变换作为一种时频分析方法在MATLAB中得到广泛应用。
本文将介绍MATLAB中的时频分析和小波变换技巧，以帮助读者更好地理解和应用这些技术。
一、时频分析基础时频分析是分析信号在时域和频域上的特性变化。
在MATLAB中，常用的时频分析方法有短时傅里叶变换（Short-Time Fourier Transform，STFT）和小波变换（Wavelet Transform）。
其中，STFT将信号分解为一系列时间上滑动的窗口，并对每个窗口进行傅里叶变换，得到频谱。
小波变换则使用小波函数作为基函数，在不同的尺度和位置上进行信号分析。
二、MATLAB中的STFT分析MATLAB提供了丰富的函数和工具箱，用于进行STFT分析。
其中，常用的函数包括"stft"和"spectrogram"。
通过这些函数，我们可以方便地对信号进行STFT分析，并绘制出时频谱图。
首先，我们需要将信号读取进MATLAB中。
可以使用"audioread"函数读取音频文件，或者使用"load"函数读取其他类型的信号数据。
接着，我们可以使用"stft"函数对信号进行STFT分析，设置合适的窗口长度和重叠比例。
最后，使用频谱绘制函数，如"spectrogram"，将得到的时频谱图展示出来。
三、小波变换的基本原理小波变换是一种局部时频分析技术，对信号的局部特征更为敏感。
与傅里叶变换是基于正弦函数的频域分析方法不同，小波变换使用小波函数作为基函数，在时域和频域上同时分析信号。
MATLAB中的小波变换函数主要有"wavelet"和"cwt"。
其中，"wavelet"函数用于创建小波对象，选择适合信号的小波函数。
matlab 小波相干
matlab小波相干小波相干分析是一种用于信号处理和数据分析的重要方法，在Matlab中也有相应的实现工具。
本文将介绍Matlab中小波相干分析的基本原理和使用方法，帮助读者理解和掌握该方法。
1.小波相干的概念小波相干分析是一种通过分析信号在不同尺度上的相干性来揭示信号的时间-频率结构的方法。
它不仅可以识别信号中的周期性成分，还可以分析信号在不同频段上的相互关系。
相比于传统的时频分析方法，小波相干分析具有更好的局部性和分辨率。
2.小波相干分析的原理小波相干分析的核心是计算信号在不同尺度和不同位置上的小波变换，并通过计算相干函数来评估不同尺度的波动之间的相干性。
相干函数可以用于描述信号之间的线性关系和频率的相似性。
3.Matlab中的小波相干分析工具Matlab提供了丰富的小波相干分析工具，可以方便地进行数据处理和分析。
其中最常用的函数是cwt和waveselect。
cwt函数用于计算小波变换，而waveselect函数用于选择合适的小波基函数。
使用这些函数可以快速计算信号的小波相干，并可视化结果。
4.小波相干分析的应用小波相干分析在信号处理、图像处理、地震学、金融分析等领域都有广泛的应用。
例如，在金融领域中，小波相干分析可以用于分析股票价格的波动性和相关性，帮助投资者进行决策。
在医学领域中，小波相干分析可以用于分析脑电信号和心电信号，帮助医生诊断疾病。
小波相干分析是一种强大的信号处理方法，可以揭示信号的时间-频率结构和相互关系。
Matlab提供了方便的小波相干分析工具，使得该方法更加易于使用和理解。
读者可以根据实际需求，在Matlab中进行小波相干分析，并将其应用于各个领域中。
综上所述，本文介绍了Matlab中小波相干分析的基本原理和使用方法，帮助读者理解和掌握该方法。
希望本文能对读者在信号处理和数据分析方面的研究和实际应用有所帮助。
matlab交叉小波
matlab交叉小波Matlab交叉小波交叉小波是一种用于信号处理和数据分析的数学工具，在Matlab中也有相应的实现。
交叉小波能够在时频领域同时提供时间和频率信息，因此在处理非平稳信号和多尺度分析方面具有很大的优势。
本文将介绍Matlab中交叉小波的基本原理和常见应用。
我们需要了解小波变换的基本概念。
小波变换是一种时频分析方法，通过将信号分解成一系列基函数的线性组合，可以同时提供时间和频率信息。
与傅里叶变换相比，小波变换具有更好的局部性和时频分辨率，可以更好地处理非平稳信号。
在Matlab中，交叉小波可以通过调用Wavelet Toolbox中的函数来实现。
首先，我们需要选择适当的小波基函数，常见的选择包括Morlet小波、Haar小波和Daubechies小波等。
然后，我们可以使用cwt函数对信号进行连续小波变换，得到时频表示。
交叉小波的基本原理是将两个不同尺度的小波基函数进行线性组合，从而得到交叉小波系数。
这样可以同时提供不同尺度下的时间和频率信息，对于非平稳信号的分析非常有用。
在Matlab中，我们可以使用xwt函数来计算交叉小波系数。
交叉小波在信号处理和数据分析中有广泛的应用。
一方面，交叉小波可以用于时频分析，例如分析非平稳信号的瞬态特性、识别信号中的突变点等。
另一方面，交叉小波还可以用于信号的压缩和去噪，例如通过阈值处理交叉小波系数来实现信号的去噪。
除了基本的交叉小波分析，Matlab还提供了许多相关的工具和函数，用于进一步的信号处理和数据分析。
例如，我们可以使用cwtfilterbank函数构建小波滤波器组，用于对信号进行多尺度分析和特征提取。
另外，Matlab还提供了一些交叉小波的图像处理工具，例如对图像进行边缘检测和纹理分析等。
交叉小波是一种强大的信号处理和数据分析工具，在Matlab中有着丰富的实现和应用。
通过使用Matlab提供的函数和工具，我们可以方便地进行交叉小波分析，并在实际应用中发挥其优势。
精品课件-基于MATLAB的小波分析应用-第5章
第5章 小波变换与信号处理
其中，COEFS为连续小波变换后的返回系数CWTx(a, b)矩 阵，系数以行方式存储在矩阵中。矩阵的行数为小波变换中 尺度的个数，列数为信号采样点的个数，即矩阵的第一行对 应第一个尺度变换后的系数，第二行对应第二个尺度变换后 的系数，依此类推。
第5章 小波变换与信号处理
第5章 小波变换与信号处理
2. 信号的连续小波分解实例 下面以信号noissin为例说明如何对一个信号进行连续小 波分解，信号noissin是一个含噪声的周期性信号。 程序代码如下：
%装载noissin信号 load noissin; x = noissin; figure(1); plot(x); figure(2);
第5章 小波变换与信号处理
plot(cA2); title('尺度2的低频系数'); %提取尺度1的高频系数 cD1 = detcoef(C,L,1); %提取尺度2的高频系数 cD2 = detcoef(C,L,2); figure(3); subplot(2,1,1); plot(cD1);
第5章 小波变换与信号处理
第5章 小波变换与信号处理
2) 多尺度一维离散小波变换 MATLAB中实现多尺度离散小波变换的函数为wavedec，其 调用格式有以下两种： (1) [C, L] = wavedec(X, N, 'wname') (2) [C, L] = wavedec(X, N, Lo_D, Hi_D) 其中，N为尺度，且必须为正整数，'wname'为小波名称， Lo_D和Hi_D分别为分解低通和高通滤波器。输出参数C由[cAj, cDj, cDj-1,…, cD1]组成，L由[cAj的长度，cDj的长度， cDj-1的长度，…，cD1的长度，X的长度]组成。例如，一个 三尺度的分解结构的组织形式如图5.4所示。