4假设检验-研究生
研究生数据分析方法:定量研究与统计分析

研究生数据分析方法:定量研究与统计分析概述研究生阶段是一个重要的学术培养阶段,对于研究者而言,掌握合适的数据分析方法以及统计分析技能是至关重要的。
本文将着重介绍研究生在定量研究中所需的数据分析方法和统计分析技巧。
数据分析方法1. 数据收集与整理合适的数据收集和整理方式是进行有效数据分析的基础。
这包括确定研究目标和问题、选择恰当的样本群体、设计问卷或实验方案等。
2. 描述性统计分析描述性统计是对收集到的数据进行总结和描述,并通过各种图表和指标来展现数据特征。
常用的描述性统计指标包括均值、中位数、方差等。
3. 探索性数据分析(EDA)EDA是一种探索性地检查数据特征,发现模式并提出初步假设的方法。
通过可视化图表、散点图等方式,进行多个变量之间关系的初步判断,并帮助在后续推断性统计中选择合适的模型。
4. 推断性统计分析推断性统计是基于收集到的样本数据,对总体进行推断和验证的一种方法。
它包括假设检验、置信区间估计、相关分析等技术,帮助研究者对研究问题进行验证并得出结论。
5. 回归分析回归分析是一种用于建立变量之间关系的统计方法,用于预测或解释因变量与自变量之间的关系。
线性回归、多元回归、逻辑回归等都是常见的回归分析方法。
统计分析技巧1. 数据可视化数据可视化是展示和传达数据信息的重要方式。
利用直方图、饼图、散点图等可视化手段,可以更直观地呈现数据特征和趋势,并有助于发现规律和异常情况。
2. 统计软件应用掌握合适的统计软件工具(如R、Python等)能够提高数据处理和分析效率。
这些工具包含丰富的函数库和算法模型,能够支持从简单到复杂的数据处理过程。
3. 实验设计与样本容量确定科学合理的实验设计以及合理确定样本容量对于确保研究的可靠性和统计分析结果的准确性至关重要。
4. 非参数统计方法除了传统的参数统计方法,研究生还需了解非参数统计方法。
这些方法不依赖数据的具体分布形式,用于处理离散型数据、有序分类数据和顺序数据等情况。
2011研究生医学统计试题01
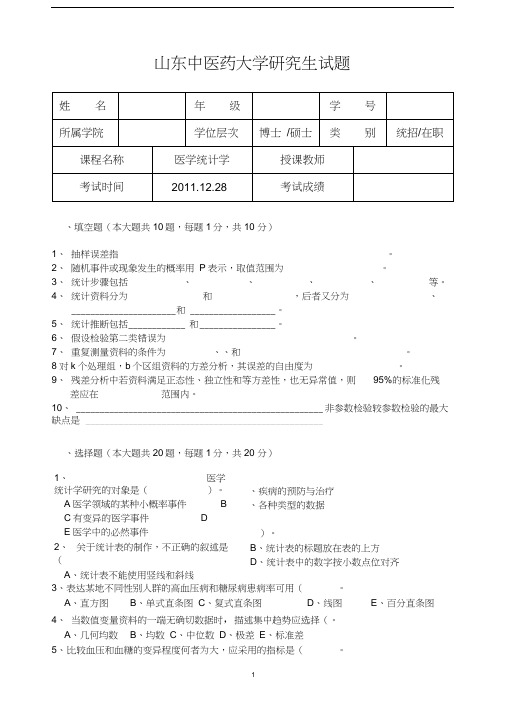
山东中医药大学研究生试题、填空题(本大题共10题,每题1分,共10 分)1、 抽样误差指 。
2、 随机事件或现象发生的概率用 P 表示,取值范围为 。
3、 统计步骤包括 、 、 、 、 等。
4、 统计资料分为 和 ,后者又分为 、______________________ 和 __________________ 。
5、 统计推断包括 ____________ 和 ________________ 。
6、 假设检验第二类错误为 。
7、 重复测量资料的条件为 、、和 。
8对k 个处理组,b 个区组资料的方差分析,其误差的自由度为 。
9、 残差分析中若资料满足正态性、独立性和等方差性,也无异常值,则 95%的标准化残差应在 范围内。
10、 ____________________________________________________ 非参数检验较参数检验的最大缺点是 __________________________________________________ 、选择题(本大题共20题,每题1分,共20 分)3、表达某地不同性别人群的高血压病和糖尿病患病率可用( 。
A 、直方图B 、单式直条图C 、复式直条图D 、线图E 、百分直条图4、 当数值变量资料的一端无确切数据时,描述集中趋势应选择(。
A 、几何均数 B 、均数 C 、中位数 D 、极差 E 、标准差5、 比较血压和血糖的变异程度何者为大,应采用的指标是(。
1、医学统计学研究的对象是()。
A 医学领域的某种小概率事件 B C 有变异的医学事件 DE 医学中的必然事件2、 关于统计表的制作,不正确的叙述是(A 、统计表不能使用竖线和斜线、疾病的预防与治疗 、各种类型的数据 )。
B 、统计表的标题放在表的上方 D 、统计表中的数字按小数点位对齐A、标准差B、四分位数间距C、方差D、极差E、变异系数6、关于相对数,下列不正确的是( )。
研究生数理统计第三章习题答案

习 题 三1.正常情况下,某炼铁炉的铁水含碳量()24.55,0.108XN .现在测试了5炉铁水,其含碳量分别为4.28,4.40,4.42,4.35,4.37.如果方差没有改变,问总体的均值有无显著变化?如果均值没有改变,问总体方差是否有显著变化()0.05α=? 解 由题意知,()24.55,0.108XN ,5n =,511 4.3645i i x x ===∑,0.05α=,()5220110.095265i i s x μ==-=∑.1)当00.108σ=时,①设统计假设0010: 4.55,: 4.55H H μμμμ==≠=. ②当0.05α=时,0.975121.96uu α-==,临界值121.960.0947c α-===, 拒绝域为000{}{0.0947}K x c x μμ=->=->.③004.364 4.550.186x K μ-=-=∈,所以拒绝0H ,接受1H ,即认为当方差没有改变时,总体的均值有显著变化.2)当0 4.55μ=时,①设统计假设2222220010:0.108,:0.108H H σσσσ==≠=. ②当0.05α=时,临界值()()()()222210.02520.975122111150.1662,5 2.566655c n c n n n ααχχχχ-======, 拒绝域为222202122220000{}{2.56660.1662}ssssK c c σσσσ=><=><或或.③202200.095268.16700.108sK σ==∈,所以拒绝0H ,接受1H ,即均值没有改变时,总体方差有显著变化.2.一种电子元件,要求其寿命不得低于1000h .现抽取25件,得其均值950x h =.该种元件寿命()2,100XN μ,问这批元件是否合格()0.05α=?解 由题意知,()2,100XN μ,25n =,950x =,0.05α=,0100σ=.①设统计假设0010:1000,:1000H H μμμμ≥=<=. ②当0.05α=时,0.05 1.65u u α==-,临界值()1.6533c α==-=-, 拒绝域为000{}{33}K x c x μμ=-<=-<-.③00950100050x K μ-=-=-∈,所以拒绝0H ,接受1H ,即认为这批元件不合格. 3.某食品厂用自动装罐机装罐头食品,每罐标准质量为500g ,现从某天生产的罐头中随机抽测9罐,其质量分别为510,505,498,503,492,502,497,506,495〔单位:g1)机器工作是否正常()0.05α=?2)能否认为这批罐头质量的方差为25.5()0.05α=?解 设X 表示用自动装罐机装罐头食品每罐的质量〔单位:g 〕.由题意知()2500,XN σ,方差2σ未知. 9n =,911500.88899i i x x ===∑,0.05α=,()()222111133.6111118nni i i i s x x x x n ===-=-=-∑∑,()52201130.66679i i s x μ==-=∑1)①设统计假设0010:500,:500H H μμμμ==≠=.②()()0.9751218 2.306tn t α--==,临界值()121 2.306 4.4564c n α-=-==,拒绝域为000{}{ 4.4564}K x c x μμ=->=->.③00500.88895000.8889x K μ-=-=∉,所以接受0H ,拒绝1H ,即认为机器工作正常.2)当0500μ=时,①设统计假设2222220010: 5.5,: 5.5H H σσσσ==≠=. ②当0.05α=时,临界值()()()()222210.02520.975122111190.3,9 2.113399c n c n n n ααχχχχ-======,拒绝域为222202122220000{}{2.11330.3}ssssK c c σσσσ=><=><或或.③2022030.66671.013785.5sK σ==∉,所以接受0H ,拒绝1H ,即为这批罐头质量的方差为25.5.4.某部门对当前市场的鸡蛋价格情况进行调查,抽查某市20个集市上鸡蛋的平均售价为()3.399元/500克,标准差为()0.269元/500克.往年的平均售价一直稳定 ()3.25元/500克左右,问该市场当前的鸡蛋售价是否明显高于往年()0.05α=?解 由题意知,()23.25,XN σ,20n =, 3.399x =,0.05α=,0.269s =.①设统计假设0010: 3.25,: 3.25H H μμμμ≤=>=. ②当0.05α=时,()()10.95119 1.729t n t α--==,临界值()11 1.7290.1067c n α-=-==, 拒绝域为000{}{0.1067}K x c x μμ=->=->③003.399 3.250.149x K μ-=-=∈,所以拒绝0H ,接受1H ,即认为市场当前的鸡蛋售价是明显高于往年. 5.某厂生产的维尼纶纤度()2,0.048XN μ,某日抽测8根纤维,其纤度分别为1.32,1.41,1.55,1.36,1.40,,1.50,1.44,1.39,问这天生产的维尼纶纤度的方差2σ是否明显变大了()0.05α=? 解 由题意知()2,0.048XN μ,8n =,811 1.421258i i x x ===∑,0.05α=,()()22211110.0122118nni i i i s x x x x n ===-=-=-∑∑.①设统计假设2222220010:0.048,:0.048H H σσσσ==>=. ②当0.05α=时,临界值()()2210.951117 2.0117c n n αχχ-=-==-,拒绝域为2202200{}{ 2.01}s s K c σσ=>=>.③202200.012215.29950.048s K σ==∈,所以拒绝0H ,接受1H ,即这天生产的维尼纶纤度的方差2σ明显变大了.6.某种电子元件,要求平均寿命不得低于2000h ,标准差不得超过130h .现从一批该种元件中抽取25个,测得寿命均值为1950h ,标准差148s h =.设元件寿命服从正态分布。
中国海洋大学011数学科学学院2023年硕士研究生招生考试大纲

2023年硕士研究生招生考试大纲011 数学科学学院目录初试考试大纲 (2)617 数学分析 (2)856高等代数 (7)432 统计学 (9)复试考试大纲 (13)F1101综合考试(四门科目中任选二门) (13)F1102概率论与数理统计 (19)初试考试大纲617 数学分析一、考试性质数学分析是数学硕士研究生入学初试考试的专业基础课程。
二、考查目标根据教育部颁发的《数学分析》教学大纲的基本要求,力求反映与数学相关的硕士学位的特点,客观、准确、真实地测评考生对数学分析的掌握和运用情况,为国家培养具有良好数学基础素质和应用能力、具有较强分析问题与解决问题能力的高层次、复合型的数学专业人才。
测试考生对一元函数微积分学、多元函数微积分学、级数理论等知识掌握的程度和运用能力。
要求考生系统地理解数学分析的基本概念和基本理论;掌握数学分析的基本论证方法和常用结论;具备较熟练的演算技能和较强的逻辑推理能力及初步的应用能力。
三、考试形式本考试为闭卷考试,满分为150分,考试时间为180分钟。
试卷结构:一元函数微积分学、多元函数微积分学、级数理论及其他(隐函数理论、场论等)考核的比例均约为1/3,分值均约为50分。
四、考试内容(一) 变量与函数1、实数:实数的概念、性质,区间,邻域;2、函数:变量,函数的定义,函数的表示法,几何特征(有界函数、单调函数、奇偶函数、周期函数),运算(四则运算、复合函数、反函数),基本初等函数,初等函数。
(二) 极限与连续1、数列极限:定义(ε-N 语言),性质(唯一性,有界性,保号性,不等式性、迫敛性),数列极限的运算,数列极限存在的条件(单调有界准则(重要的数列极限e n nn =+∞→1)1(lim ),迫敛性法则,柯西收敛准则); 2、无穷小量与无穷大量:定义,性质,运算,阶的比较;3、函数极限:概念(在一点的极限,单侧极限,在无限远处的极限,函数值趋于无穷大的情形(ε-δ, ε-X 语言));性质(唯一性,局部有界性,局部保号性,不等式性,迫敛性);函数极限存在的条件(迫敛性法则,归结原则(Heine 定理),柯西收敛准则);运算;4、两个常用不等式和两个重要函数极限(1sin lim 0=→x x x ,e xx x =+∞→)11(lim ); 5、连续函数:概念(在一点连续,单侧连续,在区间连续),不连续点及其分类;连续函数的性质与运算(局部性质及运算,闭区间上连续函数的性质(有界性、最值性、零点存在性,介值性、一致连续性),复合函数的连续性,反函数的连续性);初等函数的连续性。
管理科学与工程考试:2021应用统计学真题模拟及答案(4)

管理科学与工程考试:2021应用统计学真题模拟及答案(4)共121道题1、按照某一标志,先将总体分成若干组(类),其中每一组(类)称为一层,再在层内按简单随机抽样方法进行抽样,这种抽样方式称为()。
(单选题)A. 类型随机抽样B. 系统随机抽样C. 整群随机抽样D. 多阶抽样试题答案:A2、在假设检验中,不拒绝原假设意味着()。
(单选题)A. 原假设肯定是正确的B. 原假设肯定是错误的C. 没有证据证明原假设是正确的D. 没有证据证明原假设是错误的试题答案:D3、有8名研究生的年龄分别为21,24,28,22,26,24,22,20岁,则他们的年龄中位数为()。
(单选题)A. 24B. 23C. 22D. 21试题答案:B4、在假设检验中,原假设和备择假设()。
(单选题)A. 都有可能成立B. 都有可能不成立C. 只有一个成立而且必有一个成立D. 原假设一定成立,备择假设不一定成立试题答案:C5、在假设检验中,不拒绝原假设意味着()。
(单选题)A. 原假设肯定是正确的B. 原假设肯定是错误的C. 没有证据证明原假设是正确的D. 没有证据证明原假设是错误的试题答案:D6、样本判定系数R2的计算公式是()。
(单选题)A.B.C.D.试题答案:D7、关于两个变量X和Y相关系数的计算,错误的是()。
(单选题)A.B.C.D.试题答案:B8、由49个观测数据组成的随机样本得到的计算结果为∑x=50.3,∑x2=68。
取显著性水平α=0.01,检验假设H0:μ≥1.18,H1:μ<1.18,得到的检验结论是()。
(单选题)A. 拒绝原假设B. 不拒绝原假设C. 可以拒绝也可以不拒绝原假设D. 可能拒绝也可能不拒绝原假设试题答案:B9、由49个观测数据组成的随机样本得到的计算结果为∑x=50.3,∑x2=68。
取显著性水平α=0.01,检验假设H0:μ≥1.18,H1:μ<1.18,得到的检验结论是()。
(单选题)A. 拒绝原假设B. 不拒绝原假设C. 可以拒绝也可以不拒绝原假设D. 可能拒绝也可能不拒绝原假设试题答案:B10、对一部贺岁片收视率进行调查,随机抽取100人,其中有20人没有看过该部贺岁片,则看过该部贺岁片人数比率的点估计值为()。
概率论与数理统计研究生课程

概率论与数理统计研究生课程
概率论与数理统计研究生课程主要包括以下内容:
1. 概率论:概率论是研究随机现象的数学学科。
在概率论中,学生将学习概率空间、随机变量、随机过程、随机模拟等知识,这些知识是理解和分析数据的基础。
2. 数理统计:数理统计是应用概率论对数据进行收集、分析和推断的数学学科。
在数理统计中,学生将学习参数估计、假设检验、回归分析、方差分析、贝叶斯统计等知识,这些知识是解决实际问题的关键。
3. 高级课程:根据学生的专业背景和兴趣,可以选择一些更高级的概率论与数理统计课程,如随机矩阵、非参数统计、时间序列分析、贝叶斯方法等。
4. 编程技能:在现代概率论与数理统计中,编程技能变得越来越重要。
学生需要掌握一门编程语言,如Python、R或MATLAB,以便能够进行数据处理、分析和可视化。
5. 科研项目:最后,学生需要参与一项科研项目,以培养其独立思考和解决问题的能力。
项目可以涉及概率论、数理统计或相关领域的研究课题,如金融数学、生物统计、地理统计等。
总的来说,概率论与数理统计研究生课程是一个全面而深入的学科,旨在培养学生掌握概率论与数理统计的基本理论和方法,并能够运用所学知识解决实际问题。
研究生医学统计学第五版课后答案及解析
研究生医学统计学第五版课后答案及解析示例文章篇一:《研究生医学统计学第五版课后答案及解析》一、第一章课后题答案及解析题目1:简述医学统计学的定义和主要内容。
答案:医学统计学是运用概率论和数理统计的原理与方法,研究医学领域中数据的收集、整理、分析和推断的一门学科。
其主要内容包括统计设计(如实验设计、调查设计等),数据的收集方法(例如抽样方法等),数据的整理(像数据的分组、编码等),数据的分析(包括描述性统计分析,如计算均值、中位数、标准差等,以及推断性统计分析,如假设检验、方差分析、相关与回归分析等)。
解析:医学统计学的定义明确了它是基于概率论和数理统计,并且是专门针对医学领域数据的处理学科。
从内容上看,统计设计就像盖房子的蓝图,如果设计不好,后续的工作都可能出现偏差。
数据收集是基础,好比是获取建筑材料,收集的方法会影响到数据的质量。
整理数据就像是对材料进行分类和初步加工。
而分析数据是核心,描述性统计能让我们初步了解数据的特征,就像观察一块材料的外观和基本性质,推断性统计则能让我们从样本数据推断总体的情况,就像根据一部分材料来推测整座房子的结构和质量。
题目2:举例说明医学研究中为什么需要统计推断。
答案:比如研究一种新的药物对某种疾病的疗效。
我们不可能对所有患有这种疾病的患者进行试验,只能抽取一部分患者作为样本进行药物治疗并观察效果。
假设在这部分样本患者中,有较高比例的患者病情得到了改善。
但是我们不能仅仅根据这个样本的结果就直接说这种药物对所有患者都有效。
因为这只是一个小部分的样本,可能存在偏差。
这时候就需要统计推断,通过样本的数据(如治愈率、好转率等)来推断这种药物对总体患者(所有患这种疾病的人)的疗效,看这个结果是偶然的还是具有普遍性的。
解析:在这个例子里,样本是整体的一小部分,就像从一大锅汤里舀出一小勺尝尝味道。
仅根据这一小勺汤的味道(样本的结果)不能确定整锅汤(总体患者)的味道(疗效)。
统计推断就像是一种科学的推测方法,根据小部分样本的特征,利用概率等知识,来判断这种特征在总体中是不是也存在。
研究生数理统计
研究生数理统计数理统计是数学和统计学的交叉学科,主要研究通过数学方法对统计问题进行建模和分析的科学方法。
数理统计作为一门重要的科学研究方法,具有广泛的应用领域和重要的理论价值。
数理统计的研究内容主要包括:1. 概率论和数理统计基础:概率论和数理统计是数理统计的理论基础。
概率论主要研究随机事件发生的概率和随机变量的分布规律,为数理统计提供了数学工具和方法。
数理统计则将概率论的方法应用到具体的统计问题中,如参数估计、假设检验、回归与相关等。
2. 统计推断:统计推断是数理统计的核心内容,主要研究如何通过样本数据推断总体特征。
经典统计推断方法包括点估计和区间估计,通过样本数据推断总体参数的点估计是数理统计的基本问题。
区间估计则提供了对总体参数估计的不确定性程度的度量。
3. 统计模型:统计模型是数理统计的重要工具,用于描述和分析实际问题中的统计关系。
常用的统计模型有线性回归模型、混合模型、时间序列模型等。
通过对统计模型的建立和参数估计,可以对实际问题进行分析和预测。
4. 多元统计分析:多元统计分析是数理统计的扩展领域,主要研究多个变量之间的关系和数据集的模式。
常用的多元统计分析方法有主成分分析、聚类分析、判别分析等,通过这些方法可以对高维数据进行降维和分类。
5. 实际应用:数理统计方法在各个学科领域都有广泛的应用。
在生物医学领域,数理统计可以用于生物数据的分析和生物实验的设计;在金融领域,数理统计可以用于金融市场的波动性研究和风险管理;在工程领域,数理统计可以用于产品质量控制和工程实验的优化。
总体来说,数理统计作为一门重要的科学研究方法,在理论和应用上都有重要的价值。
通过数理统计的研究,可以提高数据分析和决策的准确性和科学性,对推动科学研究和实际应用都具有重要意义。
高等工程数学
摘要高等工程数学是工程类硕士研究生的一门重要的数学基础课程,在研究生数学素养的训练、创新能力的提高方面具有重要作用。
内容包含矩阵论、数值计算方法和数理统计三部分,其主要内容有:先行空间与线性变换、内积空间、矩阵的标准型、数理统计的基本概念与抽样分布、参数估计、假设检验、回归分析与方差分析。
关键词:线性空间、假设检验、方差分析一、线性空间的综述简单的说,线性空间是这样一种集合,其中任意两元素相加可构成此集合内的另一元素,任意元素与任意数(可以是实数也可以是复数,也可以是任意给定域中的元素)相乘后得到此集合内的另一元素。
线性空间是线性代数最基本的概念之一,也是学习现代矩阵论的重要基础。
1.1 数域的概念设P是一个非空数集,且至少含有非零的数,若P中任意两个数的和、差、积、商(除分母为零外)仍属于该集合,则称P是一个数域。
容易验证有理数集合Q、实数集合R与复数集合C都是数域,分别称为有理数域、实数域与复数域。
1.2 线性空间定义设V是一个非空集合,P是一个数域,如果:(1)在集合V上定义一个二维运算(通常称为加法),即对V中任意两个元素x,y经过这个运算后得到的结果,仍是集合V中唯一确定的元素,该元素称为x 与y的和记作x+y.(2)在数域P与集合V的元素之间还定义了一种运算,叫做数量乘法,即对于P任意数λ与V中任意元素x,经过这一运算后所得到的结果,仍是V中唯一确定的元素,称为唯一确定的元素,称为λ与x的数量乘积,记作λ x。
如果加法和数量乘法还满足下述规则,则称V为数域P上的线性空间。
1.3线性空间的运算(1)对任意x,y∈V,x+y=y+x;(2)对任意x,y,z∈V,(x+y)+z=x+(y+z);(3)V中存在一个零元素,记作θ,对任意x∈V,都有x+θ=x;(4)对任意x∈V,都有y∈V,使得x+y=θ,元素y称为x的负元素,记作-x;(5)对任意x∈V,都有1x=x;对任何λ,μ∈P,x,y∈V。
研究生数学建模题型
研究生数学建模题型
研究生数学建模题型多种多样,包括但不限于以下几种:
1. 最优化问题:研究如何找到一个函数的最大值或最小值,如线性规划、整数规划、非线性规划等。
2. 动力系统问题:研究物理系统或生物系统的运动状态、稳定性和演化情况,如常微分方程组的建模与分析、混沌理论等。
3. 统计问题:研究数据的收集、处理和分析,包括描述性统计、假设检验、方差分析、回归分析等。
4. 随机过程问题:研究随机事件的规律性和统计性质,如马尔可夫链、布朗运动、排队论、随机最优化等。
5. 图论与网络问题:研究图结构和网络的特性、优化和分析,如最短路径问题、最小生成树、网络流、社交网络分析等。
6. 优化调度问题:研究资源的分配、任务调度和排产问题,如作业车间调度、旅行商问题、拓扑排序等。
7. 数据挖掘与机器学习问题:研究从大规模数据中提取有用信息和模式,如聚类分析、分类与预测、人工神经网络等。
8. 组合优化问题:研究在一定规则下,选择最优解的问题,如组合数学、图论等。
9. 数值计算与模拟问题:研究如何通过数值算法和计算模拟来解决实际问题,如差分方程、有限元方法、蒙特卡洛模拟等。
以上仅为常见的研究生数学建模题型,实际上还有很多其他类型的题目。
不同的题目类型要求不同的数学方法和建模技巧。
