方势垒的穿透系数与各因素关系的探究
基于Matlab的势垒贯穿透射系数研究

基于Matlab的势垒贯穿透射系数研究柯常青;丁益民【摘要】粒子在经过一个势垒时,无论粒子能量和势垒高度存在怎样的关系,理论上都有一定的透射.本文用Matlab软件探讨了粒子对于宽度为n*a的势垒和n重宽度为a的势垒进行贯穿时的透射系数.研究结果说明:在E/U>1情况下,宽度为na 的势垒的贯穿透射系数较n重宽度为a的势垒的贯穿系数大;当E/U<1时,情况则相反.【期刊名称】《物理与工程》【年(卷),期】2015(025)001【总页数】3页(P76-77,79)【关键词】Matlab;势垒贯穿;多重势垒贯穿;透射系数【作者】柯常青;丁益民【作者单位】湖北大学物理与电子科学学院,湖北武汉 430062;湖北大学物理与电子科学学院,湖北武汉 430062【正文语种】中文1 问题的提出解薛定谔方程能很容易地得出这样一个结论:当粒子透过势垒时,其透射系数与势垒宽度、粒子能量E和势垒高度U存在着一定的比例关系.若粒子能量与势垒高度保持恒定,粒子穿过势垒时对同样宽度的势垒进行两种透射方式:直接透射和n重依次透射(即让粒子直接透射宽度为n*a的势垒和让粒子依次透射n个宽度均为a的势垒).那么在这两种方式下透射系数有怎样的差别呢?2 问题的分析对于以上两种方式下势垒贯穿透射系数的研究用常规的解析方法比较复杂,且随着透射重数n的增加计算的复杂程度会很明显地加大,这就使得到的结果会出现明显的偏差,不方便对最后结果的比较,为此我们采用Matlab来模拟.从Matlab模拟出的透射图形中可以通过直观地对比得出单重势垒贯穿和多重势垒贯穿的规律.由势垒透射系数D的公式[1]:令为一个假设的量,其量纲与波矢相同)其中,可知:(1)当E>U 时,若满足k2a=nπ,则D=1,此时入射波完全透射,称为共振透射.(2)透射波的振幅在势垒中的衰减并不是线性的,即透射波振幅随势垒宽度的增大呈非线性关系,由此容易看出直接透射和n重透射的透射系数一般情况下并不相同,用数学解析的方法很难比较两种透射方式的透射系数,而用Matlab则很容易解决.3 原理与实现我们知道,在研究势垒贯穿透射系数时,粒子能量与势垒高度的关系可分为以下两种情况:(1)粒子能量高于势垒高度先设定入射波函数的振幅为1,此时的透射系数等于透射波振幅|C|2.反射波振幅为A,透射波振幅为C,则A和C满足以下关系式通过键盘输入,在程序中可设定为m=5.因为下面对于m值的应用都体现在k值上,而k又是与x(x为水平坐标)以积的形式出现,若假定粒子为电子,且其能量以eV形式表述,则k值约为10的9次幂,而在程序中的x是以nm为单位的,刚好产生一个10的-9次幂.ka量纲之积在转化为国际单位制时前面系数刚好为1. (2)粒子能量低于势垒高度反射波的振幅C满足以下方程由透射振幅易知:透射系数随势垒的加宽或加高而急剧减小.4 程序设计(1)设置手动输入量:e=input('请输入粒子能量(E/U0)=');a=input('单个势垒宽度(*10^-9)=');n=input('势垒的重数n=');(2)当粒子能量等于势垒高度时,则利用语句if e=1e=1-eps;将其转化为粒子能量低于势垒高度的情况进行计算.(3)利用式(1),式(2),式(3)运算得出经过宽度为n*a的单个势垒时的透射波振幅C1和n个宽度为a的势垒时的透射波振幅C2.5 模拟结果1)粒子能量大于势垒高度的情况(1)由透射系数的表达式很容易看出:若k2a=nπ时则会出现透射系数为1的情况,即共振透射.运算 Matlab程序:输入e=E/U=2,a=π/5,n=10时,C1=C2=1,即两种情况都出现了共振透射现象.(2)当k2*n*a满足共振透射条件而k2a不满足时,输入e=2,a=π/50,n=10时,C1 =1,C2=0.9424.输出如图1所示.图1 输出图像(图中透射波振幅c分别为1和0.9424)此时可看出其透射系数就存在着明显的差别:n*a势垒仍为共振透射,而n重a 势垒并不完全透射.(3)随机输入两组数据e=3,a=0.1,n=20;e=1.5,a=1,n=25时;得出透射波振幅分别为C1 =0.9798,C2 =0.840 03和C1 =0.972 96,C2=0.549 22.对于上述粒子能量大于势垒高度的3种情况的结果:在E/U>1的情况下,宽度为n*a的势垒的贯穿系数一般较n重宽度为a的势垒的贯穿系数大.2)粒子能量小于势垒高度的情况运算 Matlab程序,输入e=0.5,a=0.1,n=10时,得到C1 =0.058 237,C2 =0.542 05.输入e=0.5,a=0.5,n=10时,得到C1 =4.2045e-8,C2 =1.161 52e-5.输入e=0.1,a=0.1,n=10时,得到C1 =0.010 451,C2 =0.076 23.对于上述粒子能量小于势垒高度的几种情况的结果:在E/U<1的情况下,宽度为n*a的势垒的贯穿系数一般较n重宽度为a的势垒的贯穿系数小(此时透射系数随势垒的加宽或加高而急剧减小).6 结语一般情况下,宽度为n*a的势垒贯穿透射系数与n重宽度为a的势垒贯穿透射系数不同:在E/U>1的情况下,宽度为n*a的势垒的贯穿系数较n重宽度为a 的势垒的贯穿系数大(当两者都满足共振透射条件时相等);在E/U<1的情况下,宽度为n*a的势垒的贯穿系数较n重宽度为a的势垒的贯穿系数小.参考文献【相关文献】[1]周世勋.量子力学教程[M].2版.2012:36-38.[2]周群益,候兆阳,刘让苏.Matlab可视化大学物理学[M].2011:501-506.。
隧道效应及其应用

可以穿过势垒而到达势垒的另一侧,这种现象称为势垒贯穿
或隧道效应。隧道效应只在微观领域才有意义。
则
且
说明
上式表明,透射系数D随势垒的高度U0和宽度
a的增大呈指数性衰减.如:当U0-E=1MeV时,势垒
的宽度为a =10-5 nm时,透射系数D = 10-4;若
下面就两种情况进行讨论;
因为是定态问题方程分别为:
令:
根据边界条件:
在E>U0情况下入射粒子的
∵透射系数:反射系数:
将C , A , A'代入得
可见,:
D与R的和等于1,说明入射粒子一部分反射,一部分透射,不会停留在势垒中。
(2)
隧道效应产生的原理:
光子隧道效应与近场光学显微镜:
将一个同时具有传输激光和接收信号功能的光纤微探针移近样品表面,微探针表面除了尖端部分以外均镀有金属层以防止光信号泄露,探针的尖端未镀金属层的裸露部分用于在微区发射激光和接收信号。当控制光纤探针在样品表面扫描时,探针一方面发射激光在样品表面形成隐失场,另一方面又接收10-100纳米范围内的近场信号。探针接收到的近场信号经光纤传输到光学镜头或数字摄像头进行记录、处理,在逐点还原成图象等信号。近场光学显微镜的其它部分与STM或AFM很相似。
而量子力学认为,描述微观粒子的坐标和动量不
可能同时具有确定的值,势能和动能也不可能同时具
有确定的值,对于微观粒子来说总能量等于动能和势
能之和已不再有明确的意义。
2、隧道效应的应用前景
1、用途:
隧道二极管
半导体
隧道显微镜
光子隧道效应与近场光学显微镜
隧道二极管:
隧道二极管是一种具有负阻特性的半导体二极管。目前主要用掺杂浓度较高的锗或砷化镓制成。其电流和电压间的变化关系与一般半导体二极管不同。当某一个极上加正电压时,通过管的电流先将随电压的增加而很快变大,但在电压达到某一值后,忽而变小,小到一定值后又急剧变大;如果所加的电压与前相反,电流则随电压的增加而急剧变大。因为这种变化关系只能用量子力学中的“隧道效应”加以说明,故称隧道二极管。可用于高频振荡、放大以及开关等电路元件,尤其可以用来提高电子计算机的运算速度。
变质量势垒穿透的研究
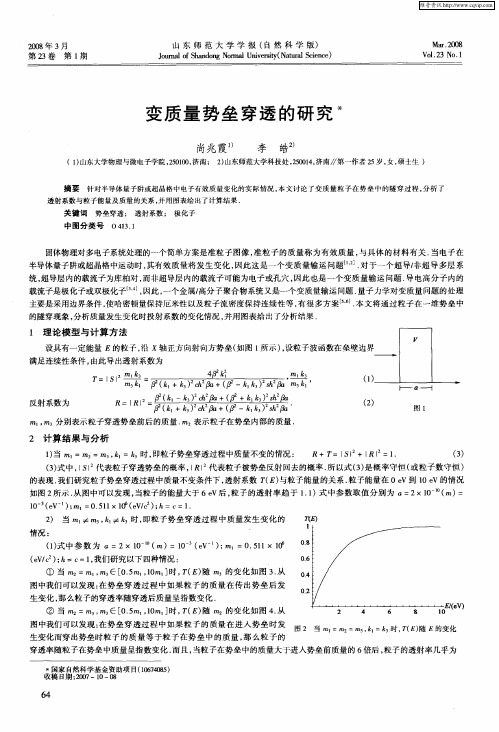
固体物理对 多电子系统处理 的一个简单方案是 准粒 子图像 , 准粒子 的质 量称为有效质 量 , 具体的材料有 关 . 与 当电子在 半导体量子阱或 超晶格 中运动时 , 效质量将发 生变化 , 其有 因此这是一个 变质量输 运问题u J对于一个 超导 } . 超导 多层系 统, 超导层 内的载流子为库柏对 , 而非超导层 内的载流子可能为 电子或孔穴 , 因此也是一个变 质量输运问题 . 导电高分子 内的 载流子是极化子或双极化子 J因此 , 金属/ , 一个 高分子聚合物系统又是一个变质量输运问题 . 量子力学对变质量 问题的处理 主要是采用边界条件 , 使哈密顿量保持厄米性 以及粒子流密度保持连续性等 , 有很多方案 J本文将通 过粒 子在一维势垒 中 . 的隧穿现象 , 分析质量发生变化时投射系数的变化情况 , 并用 图表给 出了分析结果 .
m l 3 ’ k ‘
() 1
— — 一
a
反射系数为
:l J =
() 2
图 1
m , i m 分别表示粒子穿透势垒前后的质量 . 表示粒子在势垒内部 的质量 . m
2 计算 结果 与分析
1 当 ml ) =m =m, k =k 时 , , l , 即粒子势垒穿透过程 中质量不变的情况 : R+T=J +J St J R =1 . () 3 ( ) 中, S 代表粒 子穿透势垒的概率 ,RJ 3式 J J J 代表粒子被势垒反射 回去的概率 . 以式 ( ) 概率守恒 ( 所 3是 或粒 子数守恒 ) 的表现 . 我们研 究粒子势垒穿透过程中质量不变条件下 , 透射系数 ( 与粒子能量的关系 . E) 粒子能量在 0e V到 1 V的情 况 0e 如图2 所示 . 图中可以发现 , 从 当粒子的能量大于 6e , V后 粒子的透射 率趋于 1 1 .)式 中参 数取 值分别为 。=2 0 ( = ×1 。 m)
一维势垒问题总结

一维势垒问题总结
一维势垒问题是指在一维空间中存在一个势能障碍的物理问题。
该问题涉及到粒子的运动和势能的影响,有着广泛的应用。
一维势垒问题的主要特点是势能障碍的存在。
这个势能障碍可以是有限高度的,也可以是无限高度的。
有限高度的势能障碍表示粒子可以跨越势垒,而无限高度的势能障碍表示粒子无法穿越势垒。
在求解一维势垒问题时,需要考虑的主要因素包括粒子的动能和势能。
根据量子力学的原理,粒子在势垒两侧会存在反射和透射两种情况。
对于势能障碍的高度低于粒子的能量,粒子可以自由穿越势垒,这称为透射现象。
透射的概率可以通过隧道效应来描述,隧道效应可以用量子力学中的波函数来解释。
对于势能障碍的高度高于粒子的能量,粒子会发生反射现象。
在经典力学中,反射的概率可以通过粒子的入射能量和势垒高度之间的关系来计算。
对于无限高度的势能障碍,粒子无法穿越势垒,只能发生反射现象。
这种情况下,粒子的能量必须超过势能障碍的高度才能透过。
一维势垒问题在物理学和化学领域都有广泛的应用。
例如,它可以用于解释原子核中的核反应、电子在导体中的传输等。
总之,一维势垒问题是涉及势能障碍的物理问题,涉及粒子的运动和势能的影响。
求解该问题需要考虑粒子的动能和势能,以及透射和反射两种现象。
一维势垒问题在科学研究中具有重要的应用价值。
用WKB方法讨论透射系数和反射系数

用WKB方法讨论透射系数和反射系数
李根小;霍海燕
【期刊名称】《内蒙古石油化工》
【年(卷),期】2007(033)001
【摘要】本文用WKB近似方法讨论了势垒贯穿问题系数T和其透射反射系数R 之和恒等为1,即满足恒等式T+R=1,并进一步得出这一结论不仅适用于一般势垒贯穿而且在方势垒贯穿中也成立,最后讨论了势垒贯穿的几种极限情况,例如,h→0(即经典情况),势垒高度v→∞、v→0,势垒宽度a→∞、a→0,等几种特殊情况下的T及R的取值问题.
【总页数】3页(P35-37)
【作者】李根小;霍海燕
【作者单位】内蒙古农业大学理学院;内蒙古民族高等专科学校
【正文语种】中文
【中图分类】O1
【相关文献】
1.应力的反射系数和透射系数 [J], 黎丹;王兵团
2.同轴射频高功率复反射系数和功率校准装置 [J], 陆翔;周俊孟
3.施瓦希-德希特时空中标量场辐射的反射系数和透射系数 [J], 朱国全
4.球对称稳态时空中标量场辐射的反射系数和透射系数 [J], 郭广海
5.多个平行平面板的反射系数和透射系数 [J], 雷清儒
因版权原因,仅展示原文概要,查看原文内容请购买。
势垒

势能比附近的势能都高的空间区域
01 基本概念
03 贯穿
目录
02 的分类
基本信息
一般在谈到半导体的PN结时,就会到势垒,这涉及半导体的基础内容。简单地说,所谓势垒也称位垒,就是 在PN结由于电子、空穴的扩散所形成的阻挡层,两侧的势能差,就称为势垒。
基பைடு நூலகம்概念
基本概念
势垒(Potential Energy Barrier)是势能比附近的势能都高的空间区域,基本上就是极值点附近的一小 片区域。在众多势垒当中,方势垒是一种理想的势垒。
保持ε和V的乘积不变,缩小ε,并趋于0,V将无穷大。方势垒过渡到δ势垒。在微观物理学中,δ势常作 为一种理想的短程作用来讨论问题。δ势可以看成方势的一种极限情况。事实上,所有涉及δ势的问题,原则上 均可以从方势情况下的解取极限而得以解决。但直接采用δ势来求解,往往要简捷得多。在δ势情况下,粒子波 函数的导数是不连续的,尽管粒子流密度仍然是连续的。
势垒贯穿的根本原因是“测不准原理”,只要你认可测不准原理,就很容易理解势垒贯穿了,并不需要你去 了解复杂的薛定谔方程求解。解释如下:能量E与时间T是不能同时测准的,时间测量越准确(时间范围越短), 相应的能量就会无法很准确测量。这里的测不准并不是技术上的问题,而是“测不准原理”产生的真实的范围变 化。也就是说,微观粒子在极短的时间内,其能量的可能值范围就会变大,因此,虽然微观粒子的能量E小于势垒 U,这里的粒子能量E应该是其可能的能量范围的平均值。在极短的时间内,粒子会有一个较小的几率处于这个能 量范围的高端处(即呈现高能状态),瞬间能量超过了势垒U。如果势垒U的空间跨度非常小,这个只能存在极短 时间的高能粒子将可以越过势垒,越过势垒之后,粒子的能量重新回复到正常大小。简单地说,就是先凭空”借” 来能量,成功穿越后再把“借”来的能量”还”回去,这种凭空的能量“借还”是可以允许的,也并没有违背能 量守恒原理,但必须在极短的时间之内进行,因此势垒贯穿现象能够穿越的距离也就非常小。
方形势垒量子隧穿时间公式的修正
方形势垒量子隧穿时间公式的修正方势垒是一种常见的物理现象,涉及到粒子在势垒中的隧穿现象。
量子隧穿是指当粒子遇到势垒时,即使其能量低于势垒高度,仍有一定概率穿越势垒而传播到势垒的另一侧。
量子隧穿时间是指粒子从势垒的一侧穿越到另一侧所需的时间。
传统的方势垒量子隧穿时间公式是根据WKB近似(Wentzel-Kramers-Brillouin近似)得到的。
这个公式是基于经典力学和量子力学的结合,它给出了一个近似的结果。
然而,这个公式在某些情况下可能会有一定的误差,因此需要修正。
在修正方势垒量子隧穿时间公式时,可以考虑以下几个因素:1. 势垒形状,传统公式通常假设势垒是一个矩形,但实际上势垒的形状可能是复杂的。
修正公式可以考虑势垒的具体形状,例如考虑势垒的斜率、曲率等因素。
2. 势垒高度和宽度,传统公式通常假设势垒高度和宽度是常数,但实际上它们可能是变化的。
修正公式可以考虑势垒高度和宽度的变化对隧穿时间的影响。
3. 粒子的能量,传统公式通常假设粒子的能量是确定的,但实际上能量可能是分布的。
修正公式可以考虑粒子能量的分布对隧穿时间的影响。
4. 量子效应,传统公式是基于经典力学和量子力学的结合得到的,但并没有完全考虑量子效应。
修正公式可以进一步考虑量子效应对隧穿时间的影响,例如考虑波函数的展宽等因素。
总之,修正方势垒量子隧穿时间公式是一个复杂的问题,需要考虑多个因素的影响。
目前还没有一个通用的修正公式,因为具体的修正方法会依赖于具体的势垒形状、粒子能量等因素。
研究者们正在不断努力改进和修正这个公式,以更准确地描述方势垒量子隧穿时间。
一维多阶梯势垒的透射系数
基 础 . 其 分 割 成 一 维 多 阶梯 势 垒 ; 将 然后 , 在推 导一 维 多阶 梯 势 垒透 射 系数 的过 程 中应 用 数 学 处 理 . 简化 推 导过 程 , 而推 导 出一 维 多阶 梯 势 垒 的 透射 系数 ; 后 , 用极 限 方法 , 出连 续 函 数 势 垒 的 进 最 应 得
5 O
数 学教 学研 究
第3 O卷 第 1 期
2 1 年 1月 01
一
维 多阶梯 势垒 的透 射 系数
胡 来喜
( - 西 和 何 坝 职 业技 术 学 校 ,甘肃 西 和 7 2 0 ) i f肃 4 15
摘
要 : 文 对 一 雏 多阶梯 势 垒 的透 射 系数 做 了重 新 推 导 。 主要 方 法 是 : 先 , 本 其 首 以连 续 函 数 势 垒 为
透射波 的几 率流 密瘴 为 吐
由E l1 ) (3 ] (』 ,1得 : k一 (2 + 1 )/是+志.) .
7 爱[ 一 ] D =
一
堕 l ( )a zI 茹 l A
p H
f z
_ 1
() 7
入 射粒子 从左 到右 经 势垒 后 的透射 系 数为 : i P A l 。
对于一般 势 垒 , 解 透 射 系 数 往 往 比方 求 势垒复杂. 用 w. B半 经 典 近 似法 [ 可 应 K. 1
以精确推 导出一 般势 垒的 透射 系数 [ ] 只是 1 , 。 在推导过 程 中要 用 到 比较 高深 的数 学 知识 . 于是 , 有些 文 章将 一 般 势 垒分 成 多个 宽 度 为 A x 的小方 势垒 , 组成 一 维 多阶梯 势垒 , 并有
考寺 - 1 =ix 舞瓮 一.1 A i_ eJ  ̄, - 一。 ( 。 4 。 )
气密性对颗粒物在建筑围护结构缝隙中穿透系数的影响
2017年第3期(总第45卷第313期)建筑节能■保温隔热与材料doi: 10.3969/j.issn. 1673-7237.2017.03.016气密性对颗粒物在建筑围护结构缝隙中穿透系数的影响廖洋洲,邹志军,黄晨(上海理工大学环境与建筑学院,上海200093)摘要:对于没有机械通风的房间,建筑围护结构缝隙的穿透作用是室外颗粒物进入室内的主要途 径。
选取一个房间作为对象,通过示踪气体法得到房间换气次数,采用光散射法监测室内外颗粒物浓度。
第一种方法是分析不同的因素对颗粒物穿透系数的影响,建立通过缝隙尺寸和换气次数计算颗粒物穿透系数的模型。
第二种方法是根据室内外颗粒物质量浓度平衡关系式得到颗粒物在建筑围护结构中的穿透系数。
通过对比2种方法得到的颗粒物穿透系数与换气次数之间的变化关系,得到颗粒物穿透系数随着换气次数的增大而增大,并逐渐趋近于1,换气次数一定时,细颗粒物的穿透系数大于粗颗粒物。
关键词:颗粒物;建筑围护结构;穿透系数;换气次数中图分类号:TU831 文献标志码:A文章编号:1673-7237(2017)03-0069-04The Effect of Air Tightness on the Particle PenetrationThrough Building Envelope LeakageLIAO Yang- zhou,ZOU Zhi- j u n,HUANG Chen(School of Environment and Architecture,University of Shanghai forScience and Technology,Shanghai200093,China)A b stra c t:Outdoor particles,penetrating the building envelope and suspending in indoor air,are themain indoor pollution sources of the building without mechanical ventilation.Tracer gas method was applied to obtain the air change rate of the house,meanwhile,particles concentrations were obtained by light scattering method.The first method,analyzed the different impact factors of particles penetration,then developed a model to calculate the penetration of particle through cracks depend on the cracks dimensions and air change rate.The second one,the particles penetration were calculated by the mass balance equation of indoor- outdoor particles concentrations.According to the two methods,when the air change rate increases,particles penetrations become bigger then appear 1,and the penetrations of fine particles were higher than coarse particles as the same air change rate.Keywords :particles;building envelope;penetrations;air change rate0引言随着社会的飞速发展,人们越来越多的时间会在 室内度过[|-2],研究表明,室内颗粒物污染严重影响 人体健康[3-4]。
势垒穿透填空题(一)
势垒穿透填空题(一)势垒穿透什么是势垒穿透势垒穿透是指电子在电子势垒中能量低于势垒高度,从n型掺杂材料穿过p-n结向另一侧扩散的现象。
在势垒穿透过程中,电子需要克服势垒高度,从而形成电流流动。
势垒穿透的填空题1.势垒穿透是指电子在电子势垒中能量低于势垒高度,从_______扩散的现象。
–答案:n型掺杂材料–解析:势垒穿透是指电子从n型掺杂材料扩散到p-n结的另一侧。
2.在势垒穿透过程中,电子需要克服_______。
–答案:势垒高度–解析:电子需要克服势垒高度才能从n型掺杂材料穿透到p-n结的另一侧。
3.势垒穿透现象中形成的是_______。
–答案:电流流动–解析:当电子通过势垒进行穿透并到达p-n结的另一侧时,形成的是电流流动。
4.势垒穿透要求电子的能量低于_______。
–答案:势垒高度–解析:势垒穿透要求电子的能量低于势垒高度,才能克服势垒并穿透到p-n结的另一侧。
5.势垒穿透是一种_______现象。
–答案:能量量子化–解析:势垒穿透过程中电子的能量受到量子化限制,因此是一种能量量子化现象。
6.势垒穿透的可能性与_______呈指数关系。
–答案:势垒宽度–解析:势垒穿透的可能性与势垒宽度之间呈指数关系,势垒宽度越小,穿透的可能性越大。
7.势垒穿透的概率与电子的_______呈指数关系。
–答案:动能–解析:势垒穿透的概率与电子的动能之间呈指数关系,动能越大,穿透的概率越高。
8.势垒穿透是量子力学的_______。
–答案:波粒二象性–解析:势垒穿透现象涉及到电子的粒子性和波动性,是量子力学的波粒二象性体现之一。
9.势垒穿透现象发生时,电子的波函数在势垒两侧是_______的。
–答案:不连续–解析:在势垒穿透过程中,电子的波函数在势垒两侧是不连续的,存在波函数突变现象。
10.势垒穿透现象在_______尺度下可以发生。
–答案:纳米尺度–解析:势垒穿透现象在纳米尺度下具有显著的效应,可应用于纳米电子器件等领域。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
方势垒的穿透系数与各因素关系的探究
方势垒的穿透问题引入:
设具有一定能量E的粒子,沿着x轴正方向射向方势垒如下图:
axVxaxxV0,
0,,0
0
)(
按照经典力学观点,若0VE,则粒
子不能进入势垒,将会被弹回去。若
0
VE
,则粒子将穿过势垒。但是从量子
力学观点来看,考虑到粒子的波动性,此
问题与波透过一层介质(厚度为a)相似,
有一部分波穿过,一部分波被反射回去。
因此,按波函数的统计诠释,粒子有一部分概率穿过势垒,并有一定
的概率被反射回去。
一、考虑0VE情况:
在势垒之外(axx,0),薛定谔方程为
/2,
2
2
2
mEkkdxd
在势垒内部(ax0),薛定谔方程为
/)(2,
0
2
2
2
EVmkdxd
根据它们的解,可以求得透射系数为
1200)1(11
ashVEVET
现在我们对透射系数做一个简单的估算,设1a,此时
121aeash
,则T可以近似表示成
)(22exp)(16)(16000222222EVm
a
V
EVE
ekkT
a
可以看出来T与势垒宽度),(,0EVa以及粒子质量m的依赖关系
都很敏感。随势垒宽度a和粒子质量m增大,T将指数衰减,maeT。
所以,宏观实验中,不容易观测到粒子穿透势垒的现象。
下面我用Matlab编程,来探究透射系数T与它们几个的关系
(1)透射系数T与势垒宽度a的关系示意图
程序如下:
E=1;
V=2;
a=linspace(1*10^(-10),8*10^(-10),1000);
h=1.6*10^(-19)*(4.14*10^(-15))/(2*pi);
m=0.9*10^(-30);
T=16*E*(V-E)*exp(-2*a/h*(2*m*1.6*10^(-19)*(V-E))^(1/2))/V ;
p=plot(a,T);
grid on
set(p,'linewidth',2);
alabel('势垒宽度 a','Fontsize',14);
ylabel('透射系数 T','Fontsize',14);
title('透射系数T与势垒宽度a的关系示意图','Fontsize',14);
运行程序得到的示意图如下图:
(2)透射系数T与粒子质量m的关系示意图
程序如下:
E=1;
V=2;
a=2*10^(-10);
h=1.6*10^(-19)*(4.14*10^(-15))/(2*pi);
m=linspace(0.9*10^(-30),0.9*20*10^(-30),1000);
T=16*E*(V-E)*exp(-2*a/h*m.^(1/2)*(2*1.6*10^(-19)*(V-E))^(1/2))/V
p=plot(m,T);
grid on
set(p,'linewidth',2);
xlabel('粒子质量 m','Fontsize',14);
ylabel('透射系数 T','Fontsize',14);
title('透射系数T与粒子质量m的关系示意图','Fontsize',14);
运行程序得到的示意图如下图:
(3)透射系数T与V - E的关系示意图(V - E > 0)
程序如下:
E=1;
V=linspace(1,20,1000);
S=V-E;a=2*10^(-10);
h=1.6*10^(-19)*(4.14*10^(-15))/(2*pi);
m=0.9*10^(-30);
T=16*E*S.*exp(-2*a/h*(2*m*1.6*10^(-19))^(1/2)*S.^(1/2))./V ;
p=plot(S,T);
grid on
set(p,'linewidth',2);
xlabel('V - E','Fontsize',14);
ylabel('透射系数 T','Fontsize',14);
title('透射系数T与V-E的关系示意图','Fontsize',14);
运行程序得到的示意图如下图:
二、考虑0VE情况:
这时:
)(sin)(4111''22''kkakkkkkT
现在我们再看“透射系数T”与各个因素的关系:
(1)“透射系数T”与势垒宽度a的关系示意图
程序如下:
E=1;
V=-1;
S=V-E;
a=linspace(1*10^(-10),8*10^(-10),1000);
h=1.6*10^(-19)*(4.14*10^(-15))/(2*pi);
m=0.9*10^(-30);
T=(1-V^2/(S*E)*(sin(a.*(-2*1.6*10^(-19)*S*m)^(1/2)/h)).^2).^(-1);
plot(a,T);
运行程序结果如下:
(2)“透射系数T”与粒子质量m的关系示意图
程序如下:
E=1;
V=-1;
S=V-E;
a=2*10^(-10);
h=1.6*10^(-19)*(4.14*10^(-15))/(2*pi);
m=linspace(0.9*10^(-30),0.9*20*10^(-30),1000);
T=(1-V^2/(S*E)*(sin(a*(-2*1.6*10^(-19)*m.*S).^(1/2)/h)).^2).^(-1);
plot(m,T);
运行程序结果如下:
(3)“透射系数T”与V - E的关系示意图(V - E < 0)
程序如下:
E=1;
V=linspace(-50,-1,1000);
S=V-E;
a=2*10^(-10);
h=1.6*10^(-19)*(4.14*10^(-15))/(2*pi);
m=0.9*10^(-30);T=(1-V.^2/(S.*E)*(sin(a*(-2*1.6*10^(-19)*S.*m).^(1/2)./h)).^2).^(-1);
plot(V,T);
运行程序结果如下:
