第1章解三角形单元复习练习
(练习) 必修5第一章解三角形检测

必修5第一章解三角形检测一、选择题1.△ABC 的内角A 、B 、C 的对边分别为a 、b 、c ,若c =2,b =6,B =120°,则a等于( ) A.6 B .2 C.3 D. 22.在△ABC 中,角A 、B 、C 的对边分别为a 、b 、c ,已知A =π3,a =3,b =1,则c=A .1B .2 C.3-1 D. 33.△ABC 的三边分别为2m +3,m 2+2m ,m 2+3m +3(m >0),则最大内角度数为( )A .150°B .120°C .90°D .135°4.在△ABC 中,若cos A cos B =b a ,且cos B cos C =cb,则△ABC 是( )A .直角三角形B .等腰三角形C .等腰三角形或直角三角形D .正三角形5.在△ABC 中,关于x 的方程(1+x 2)sin A +2x sin B +(1-x 2)sin C =0有两个不等的实数根,则A 为( )A .锐角B .直角C .钝角D .不存在6.在△ABC 中,A =45°,b =4,c =2,那么cos B =( )A.31010 B .-31010C.55 D .-557.等腰△ABC 底角B 的正弦与余弦的和为62,则它的顶角是( )A .30°或150°B .15°或75°C .30°D .15°8.△ABC 三边长分别是3,4,6,则它的较大锐角的平分线分三角形的面积比是( )A .1 1B .1 2C .1 4D .4 39.在△ABC 中,若|AB →|=2,|AC →|=5,AB →·AC →=-5,则S △ABC =( )A.532B. 3C.52D .510.关于x 的方程x 2-x cos A ·cos B -cos 2C2=0有一个根为1,则此三角形为( )A .等腰三角形B .直角三角形C .锐角三角形D .钝角三角形11.若△ABC 的三边为a 、b 、c ,它的面积为a 2+b 2-c243C 等于( )A .30°B .45°C .60°D .90°12.在△ABC 中,∠A 、∠B 的对边分别是a 、b ,且∠A =2∠B ,若a =xb ,则x 的取值范围是( )A .(0,3)B .(1,2) C.⎝⎛⎭⎫12,1D .(0,2) 二、填空题(本大题共4个小题,每个小题4分,共16分.将正确答案填在题中横线上) 13.三角形一边长为14,它对的角为60°,另两边之比为8 5,则此三角形面积为________.14.已知△ABC 外接圆半径是2 cm ,∠A =60°,则BC 边长为__________. 15.在四边形ABCD 中,AB =6,BD =33,BC =4,∠ADB =∠CBD ,A =60°,则△BCD 面积为__________.三、解答题(本大题共6个小题,共74分,解答应写出文字说明,证明过程或演算步骤) 17.(本小题满分12分)在△ABC 中,a ,b ,c 分别是角A 、B 、C 的对边,若tan A =3,cos C =55.(1)求角B 的大小; (2)若c =4,求△ABC 面积.18.(本小题满分12分)在△ABC 中,∠A >∠B >∠C ,且A =2C ,b =4,a +c =8,求a ,c 的长.20.(本小题满分12分)已知∠A 、∠B 满足条件b -b cos A =a -a cos B ,若∠A 、∠B 是△ABC 的内角,且∠A 的对边是a ,∠B 的对边是b .试确定△ABC 的形状.。
高三数学第一章解三角形专项练习(带答案)

高三数学第一章解三角形专项练习〔带答案〕高三的同学要多练习,特殊是高三数学解三角形的题。
三个方面下面是学习啦我整理了高三数学第一章解三角形专项练习(带答案),供你参考。
高三数学第一章解三角形专项练习(带答案)一、选择题1.在△ABC中,sinA=sinB,那么△ABC是( )A.直角三角形B.锐角三角形C.钝角三角形D.等腰三角形答案 D2.在△ABC中,sinA=34,a=10,那么边长c的取值范围是( )A.152,+B.(10,+)C.(0,10)D.0,403答案 D 解析∵csinC=asinA=403,c=403sinC.3.在△ABC中,假设acosA=bcosB=ccosC,那么△ABC是( )A.直角三角形B.等边三角形C.钝角三角形D.等腰直角三角形答案 B解析由正弦定理知:sinAcosA=sinBcosB=sinCcosC,tanA=tanB=tanC,A=B=C.4.在△ABC中,a=2bcosC,那么这个三角形确定是( )A.等腰三角形B.直角三角形C.等腰直角三角形D.等腰或直角三角形答案 A解析由a=2bcosC得,sinA=2sinBcosC,sin(B+C)=2sin Bcos C,sin Bcos C+cos Bsin C=2sin Bcos C,sin(B-C)=0,B=C.5.在△ABC中,(b+c)∶(c+a)∶(a+b)=4∶5∶6,那么sin A∶sin B∶sin C等于( )A.6∶5∶4B.7∶5∶3C.3∶5∶7D.4∶5∶6答案 B解析∵(b+c)∶(c+a)∶(a+b)=4∶5∶6,b+c4=c+a5=a+b6.令b+c4=c+a5=a+b6=k (k0),那么b+c=4kc+a=5ka+b=6k,解得a=72kb=52kc=32k.sinA∶sinB∶sinC=a∶b∶c=7∶5∶3.6.三角形面积为14,外接圆面积为,那么这个三角形的三边之积为( )A.1B.2C.12D.4答案 A解析设三角形外接圆半径为R,那么由R2=,得R=1,由S△=12absinC=abc4R=abc4=14,abc=1.二、填空题7.在△ABC中,角A,B,C的对边分别为a,b,c,A=60,a=3,b=1,那么c=________.答案 2解析由正弦定理asinA=bsinB,得3sin60=1sinB,sinB=12,故B=30或150.由ab,得AB,B=30,故C=90,由勾股定理得c=2.8.在△ABC中,a=32,cosC=13,S△ABC=43,那么b=________.答案23解析∵cosC=13,sinC=223,12absinC=43,b=23.9.在单位圆上有三点A,B,C,设△ABC三边长分别为a,b,c,那么asinA+b2sinB+2csinC=________.答案7解析∵△ABC的外接圆直径为2R=2,asinA=bsinB=csinC=2R=2,asinA+b2sinB+2csinC=2+1+4=7.10.在△ABC中,A=60,a=63,b=12,S△ABC=183,那么a+b+csinA+sinB+sinC=________,c=________.答案12 6解析a+b+csinA+sinB+sinC=asinA=6332=12.∵S△ABC=12absinC=126312sinC=183,sinC=12,csinC=asinA=12,c=6.三、解答题11.在△ABC中,求证:a-ccosBb-ccosA=sinBsinA.证明由于在△ABC中,asinA=bsinB=csinC=2R,所以左边=2RsinA-2RsinCcosB2RsinB-2RsinCcosA=sin(B+C)-sinCcosBsin(A+C)-sinCcosA=sinBcosCsinAcosC=sinBsin A=右边.所以等式成立,即a-ccosBb-ccosA=sinBsinA.12.在△ABC中,a2tanB=b2tanA,试推断△ABC的样子.解设三角形外接圆半径为R,那么a2tanB=b2tanAa2sinBcosB=b2sinAcosA4R2sin2AsinBcosB=4R2sin2BsinAcosAsinAcosA=sinBcosBsin2A=sin2B2A=2B或2A+2B=A=B或A+B=2.△ABC为等腰三角形或直角三角形.力气提升13.在△ABC中,B=60,最大边与最小边之比为(3+1)∶2,那么最大角为( )A.45B.60C.75D.90答案 C解析设C为最大角,那么A为最小角,那么A+C=120,sinCsinA=sin120-AsinA=sin120cosA-cos120sinAsinA=32tanA+12=3+12=32+12,tanA=1,A=45,C=75.14.在△ABC中,a,b,c分别是三个内角A,B,C的对边,假设a=2,C=4,cosB2=255,求△ABC的面积S.解cosB=2cos2B2-1=35,故B为锐角,sinB=45.所以sinA=sin(-B-C)=sin34-B=7210.由正弦定理得c=asinCsinA=107,所以S△ABC=12acsinB=12210745=87.1.在△ABC中,有以下结论:(1)A+B+C=;(2)sin(A+B)=sin C,cos(A+B)=-cos C;(3)A+B2+C2=2;(4)sin A+B2=cos C2,cos A+B2=sin C2,tan A+B2=1tan C2.2.借助正弦定理可以进展三角形中边角关系的互化,从而进展三角形样子的推断、三角恒等式的证明.。
浙教版2021年八年级上册第1章《三角形的初步认识》单元复习题【含答案】

浙教版2021年八年级上册第1章《三角形的初步认识》单元复习题一.选择题1.下列各组长度的三条线段能组成三角形的是( )A.4cm,5cm,9cm B.4cm,4cm,8cmC.5cm,6cm,7cm D.3cm,5cm,10cm2.下列图形具有稳定性的是( )A.B.C.D.3.为使由五根木棒组成的架子不变形,至少还要在架子上钉上的木棒根数是( )A.0根B.1根C.2根D.5根4.下列命题是真命题的是( )A.五边形的内角和是720°B.三角形的任意两边之和大于第三边C.内错角相等D.三角形的重心是这个三角形的三条角平分线的交点5.如图,在△ABC中,∠B=50°,∠C=70°,直线DE经过点A,∠DAB=50°,则∠EAC的度数是( )A.40°B.50°C.60°D.70°6.如图,点B,F,C,E共线,∠B=∠E,BF=EC,添加一个条件,不能判断△ABC≌△DEF的是( )A.AB=DE B.∠A=∠D C.AC=DF D.AC∥FD7.如图,△ABC≌△DEC,B、C、D在同一直线上,且CE=5,AC=7,则BD长( )A.12B.7C.2D.148.在△ABC中,∠A=x°,∠B=(2x+10)°,∠C的外角大小(x+40)°,则x的值等于( )A.15B.20C.30D.40二.填空题9.只用 的直尺和 进行的作图称为尺规作图.10.如图,在△ABC中,∠A=30°,∠B=50°,CD平分∠ACB,则∠ADC的度数是 .11.如图,AC=AD,∠1=∠2,要使△ABC≌△AED,应添加的条件是 .(只需写出一个条件即可)12.如图,△ABC≌△DEF,点B、F、C、E在同一条直线上,AC、DF交于点M,若BE=7,CF=3,则BF= .13.如图,若AB,CD相交于点E,若△ABC≌△ADE,且点B与点D对应,点C与点E对应,∠BAC=28°,则∠B的度数是 °.14.如图,AD平分∠EAC,∠B=70°,∠C=60°,求∠CAD= .三.解答题15.已知△ABC的三边长分别为3、5、a,化简|a+1|﹣|a﹣8|﹣2|a﹣2|.16.已知,△ABC的三边长为4,9,x.(1)求△ABC的周长的取值范围;(2)当△ABC的周长为偶数时,求x.17.在△ABC中,CD平分∠ACB交AB于点D,AH是△ABC边BC上的高,且∠ACB=70°,∠ADC=80°,求:(1)∠BAC的度数.(2)∠BAH的度数.18.如图,在△ABC中,点D是边BC的中点,过点C作直线CE,使CE∥AB,交AD的延长线于点E.试说明AD=ED的理由.解:因为CE∥AB(已知),所以∠BAD= ( ).因为点D是边BC的中点,所以 ,在△ABD和△ECD中,,所以△ABD≌△ECD( ),所以AD=ED( ).19.如图,AD是△ABC的高,E为AC上一点,BE交AD于点F,若有BF=AC,FD=CD,试探究BE 与AC的位置关系.20.如图,D是△ABC的边AB上一点,CF∥AB,DF交AC于E点,DE=EF.(1)求证:△ADE≌△CFE;(2)若AB=5,CF=4,求BD的长.21.如图,点E在AB上,△ABC≌△DEC,求证:CE平分∠BED.22.如图,直线MN与直线PQ相交于O,∠POM=30°,点A在射线OP上运动,点B在射线OM上运动,AC、BC分别是∠BAO和∠ABO的角平分线.(1)若∠BAO=50°,试求出∠ACB的度数.(2)点A、B在运动的过程中,∠ACB的大小是否会发生变化?若发生变化,请说明理由;若不发生变化,试求出∠ACB的度数.(3)在(2)的条件下,在△ABC中,如果有一个角是另一个角的2倍,请直接写出∠BAC的度数.23.△ABC中,三个内角的平分线交于点O,过点O作∠ODC=∠AOC,交边BC于点D.(1)如图1,若∠ABC=50°,求∠BOD的度数;(2)如图1,若∠ABC=n°,求∠BOD的度数;(3)如图2,作∠ABC外角∠ABE的平分线交CO的延长线于点F.求证:BF∥OD;(4)若∠F=∠ABC=40°,将△BOD绕点O顺时针旋转一定角度α后得△B'OD'(0°<α<360°),B'D'所在直线与FC平行,请直接写出所有符合条件的旋转角度α的值.答案一.选择题1.解:根据三角形的三边关系,A、4+5=9,不能组成三角形,不符合题意;B、4+4=8,不能够组成三角形,不符合题意;C、5+6>7,能组成三角形,符合题意;D、3+5=8<10,不能组成三角形,不符合题意.故选:C.2.解:选项中只有选项A是三角形,故具有稳定性的图形是三角形.故选:A.3.解:如图所示,根据三角形具有稳定性,所以至少还要在架子上钉上的木棒根数是2,故选:C.4.解:A、五边形的内角和为540°,故原命题错误,是假命题,不符合题意;B、三角形的任意两边之和大于第三边,正确,是真命题,符合题意;C、两直线平行,内错角相等,故原命题错误,是假命题,不符合题意;D、三角形的重心是这个三角形的三条边上的中线的交点,故原命题错误,是假命题,不符合题意,故选:B.5.解:∵∠B=50°,∠C=70°,∴∠BAC=180°﹣∠B﹣∠C=180°﹣50°﹣70°=60°,∵∠DAB=50°,∠DAB+∠BAC+∠EAC=180°,∴∠EAC=180°﹣∠DAB﹣∠BAC=180°﹣50°﹣60°=70°,故选:D.6.解:∵BF=EC,∴BF+FC=EC+FC,∴BC=EF,又∵∠B=∠E,∴当添加条件AB=DE时,△ABC≌△DEF(SAS),故选项A不符合题意;当添加条件∠A=∠D时,△ABC≌△DEF(AAS),故选项B不符合题意;当添加条件AC=DF时,无法判断△ABC≌△DEF,故选项C符合题意;当添加条件AC∥FD时,则∠ACB=∠DFE,故△ABC≌△DEF(ASA),故选项D不符合题意;故选:C.7.解:∵△ABC≌△DEC,∴AC=DC,CB=CE,∵CE=5,AC=7,∴CB=5,DC=7,∴BD=DC+CB=7+5=12.故选:A.8.解:∵∠C的外角=∠A+∠B,∴x+40=2x+10+x,解得x=15.故选:A.二.填空题9.解:只用没有刻度的直尺和圆规进行的作图称为尺规作图.故没有刻度的,圆规.10.解:∵∠A=30°,∠B=50°,∠A+∠B+∠ACB=180°,∴∠ACB=180°﹣30°﹣50°=100°,∵CD平分∠ACB,∴∠BCD=∠ACB=×100°=50°,∴∠ADC=∠BCD+∠B=50°+50°=100°,故100°.11.解:∵∠1=∠2,∴∠1+∠BAD=∠2+∠BAD,即∠BAC=∠EAD,∵AC=AD,∴当添加∠B=∠E时,可根据“AAS”判断△ABC≌△AED;当添加∠C=∠D时,可根据“ASA”判断△ABC≌△AED;当添加AB=AE时,可根据“SAS”判断△ABC≌△AED.故答案为∠B=∠E或∠C=∠D或AB=AE.12.解:∵△ABC≌△DEF,∴BC=EF,∴BC﹣FC=EF﹣FC,即BF=EC,∵BE=7,CF=3,∴BF+CE=BE﹣FC=7﹣3=4,∴BF=EC=2,故2.13.解:∵△ABC≌△ADE,且点B与点D对应,点C与点E对应,∴∠B=∠D,AC=AE,∠BAC=∠BAD,∴∠ACE=∠AEC,∵∠ACE+∠AEC+∠BAC=180°,∠BAC=28°,∴∠ACE=∠AEC=(180°﹣∠BAC)=76°,∠BAD=28°,∵∠D+∠CAD+∠ACE=180°,∴∠D=180°﹣∠CAD﹣∠ACE=48°,故答案为48.14.解:∵∠EAC=∠B+∠C,∠B=70°,∠C=60°,∴∠EAC=70°+60°=130°,∵AD是∠EAC的平分线,∴∠CAD=∠EAC=65°,故答案是:65°.三.解答题15.解:∵△ABC的三边长分别为3、5、a,∴5﹣3<a<3+5,解得:2<a<8,故|a+1|﹣|a﹣8|﹣2|a﹣2|=a+1﹣(8﹣a)﹣2(a﹣2)=a+1﹣8+a﹣2a+4=﹣3.16.解:(1)∵三角形的三边长分别为4,9,x,∴9﹣4<x<9+4,即5<x<13,∴9+4+5<△ABC的周长<9+4+13,即:18<△ABC的周长<26;(2)∵△ABC的周长是偶数,由(1)结果得△ABC的周长可以是20,22或24,∴x的值为7,9或11.17.解:(1)∵CD平分∠ACB,∠ACB=70°,∴∠ACD=∠ACB=35°,∵∠ADC=80°,∴∠BAC=180°﹣∠ACD﹣∠ADC=180°﹣35°﹣80°=65°;(2)由(1)知,∠BAC=65°,∵AH⊥BC,∴∠AHC=90°,∴∠HAC=90°﹣∠ACB=90°﹣70°=20°,∴∠BAH=∠BAC﹣∠HAC=65°﹣20°=45°.18.解:因为CE∥AB(已知),所以∠BAD=∠E(两直线平行,内错角相等).因为点D是边BC的中点,所以BD=CD,在△ABD和△ECD中,所以△ABD≌△ECD(AAS),所以AD=ED(全等三角形的对应边相等).故答案为∠E,两直线平行,内错角相等;∠BAD=∠E,对顶角相等,BD=CD;AAS;全等三角形的对应边相等.19.解:∵AD是△ABC的高,∴AD⊥BC,∴∠ADB=∠ADC=90°,在Rt△BDF和Rt△ADC中,,∴Rt△BDF≌Rt△ADC(HL),∴∠FBD=∠CAD,∵∠BFD=∠AFE,∴∠AEF=∠ADB=90°,∴BE⊥AC.20.(1)证明:∵CF∥AB,∴∠ADF=∠F,∠A=∠ECF.在△ADE和△CFE中,,∴△ADE≌△CFE(AAS).(2)∵△ADE≌△CFE,∴AD=CF=4.∴BD=AB﹣AD=5﹣4=1.21.证明:∵△ABC≌△DEC,∴∠B=∠DEC,BC=EC,∴∠B=∠BEC,∴∠BEC=∠DEC,∴CE平分∠BED.22.解:(1)如图1中,∵BC平分∠ABO,AC平分∠BAO,∴∠ABC=∠ABO,∠BAC=∠BAO,∵∠POM=30°,∴∠ABO+∠BAO=180°﹣30°=150°,∴∠CBA+∠CAB=(∠ABO+∠BAO)=×150°=75°,∴∠ACB=180°﹣(∠CBA+∠CAB)=180°﹣75°=105°;(2)∠ACB的大小不变,理由如下:由(1)知:点A、B在运动的过程中,∠ACB=105°;(3)由(2)可知,∠ACB=105°,∠BAC+∠ABC=75°,∵△ABC中有一个角是另一个角的2倍,∴∠ACB=2∠BAC或∠ACB=2∠ABC或∠ABC=2∠BAC或∠BAC=2∠ABC,∴∠BAC=52.5°或22.5°或25°或50°.23.(1)解:∵∠ABC=50°,∴∠BAC+∠BCA=130°,∵△ABC的三个内角的平分线交于点O,∴∠OBD=25°,∠OAC+∠OCA=65°,∴∠AOC=115°,∵∠ODC=∠AOC,∴∠ODC=115°,∵∠ODC是△OBD的一个外角,∴∠BOD=∠ODC﹣∠OBD=115°﹣25°=90°.(2)解:∵∠ABC=n°,∴∠BAC+∠BCA=180°﹣n°,∵△ABC的三个内角的平分线交于点O,∴∠OBD=n°,∠OAC+∠OCA=90°﹣n°,∴∠AOC=180°﹣(90°﹣n°)=90°+n°,∵∠ODC=∠AOC,∴∠ODC=90°+n°,∵∠ODC是△OBD的一个外角,∴∠BOD=∠ODC﹣∠OBD=90°+n°﹣n°=90°.(3)证明:由(2)得,∠BOD=90°,∵BO平分∠ABC,BF平分∠ABE,∴∠ABF=∠ABE,∠ABO=∠ABC,∴∠FBO=∠ABE+∠ABC=90°,由(2)得,∠BOD=90°,∴∠FBO=∠BOD,∴BF∥OD.(4)∵∠F=∠ABC=40°,∠FBO=∠BOD=90°,∴∠OBD=∠OB'D'=20°,∠FOB=50°,∴∠ODB=∠OD'B'=70°,∠DOC=180°50°﹣90°=40°,、如图(1),∵D'B'∥FC,∴∠OD'B'=∠D'OC=70°,∴∠DOD'=∠D'OC﹣∠DOC=70°﹣40°=30°,即α=30°,如图(2),∵D'B'∥FC,∴∠OD'B'=∠D'OF=70°,∴α=∠FOD'+∠FOB+∠DOB=70°+50°+90°=210°,∴旋转角α为30°或210°时,B'D'所在直线与FC平行.。
八年级上册第一章三角形整章复习知识点和对应练习

T ——三角形一、知识梳理:专题一:三角形有关的线段;专题二:三角形有关的角;专题三:多边形及其内角和.二、考点分类专题一:三角形有关的线段考点一:三角形的边1.三角形的概念:由不在同一直线上的三条线段首尾顺次相接所组成的图形.2.三角形分类:(1)按角的关系分类 (2)按边的关系分类⎧⎪⎧⎨⎨⎪⎩⎩直角三角形三角形锐角三角形斜三角形钝角三角形⎧⎪⎧⎨⎨⎪⎩⎩不等边三角形三角形底和腰不相等的等腰三角形等腰三角形等边三角形 3.三角形的三边关系:两边之和大于第三边,两边之差小于第三边.【例1】【类型一】 判定三条线段能否组成三角形以下列各组线段为边,能组成三角形的是( )A .2cm ,3cm ,5cm ;B .5cm ,6cm ,10cm ;C .1cm ,1cm ,3cm ;D .3cm ,4cm ,9cm 解析:选项A 中2+3=5,不能组成三角形,故此选项错误;选项B 中5+6>10,能组成三角形,故此选项正确;选项C 中1+1<3,不能组成三角形,故此选项错误;选项D 中3+4<9,不能组成三角形,故此选项错误.故选B.方法总结:判定三条线段能否组成三角形,只要判定两条较短的线段长度之和大于第三条线段的长度即可.【类型二】 判断三角形边的取值范围一个三角形的三边长分别为4,7,x ,那么x 的取值范围是( )A .3<x <11 ;B .4<x <7 ;C .-3<x <11 ;D .x >3解析:∵三角形的三边长分别为4,7,x ,∴7-4<x <7+4,即3<x <11.故选A.方法总结:判断三角形边的取值范围要同时运用两边之和大于第三边,两边之差小于第三边.有时还要结合不等式的知识进行解决.【类型三】等腰三角形的三边关系已知一个等腰三角形的两边长分别为4和9,求这个三角形的周长.解析:先根据等腰三角形两腰相等的性质可得出第三边长的两种情况,再根据两边和大于第三边来判断能否构成三角形,从而求解.解:根据题意可知等腰三角形的三边可能是4,4,9或4,9,9,∵4+4<9,故4,4,9不能构成三角形,应舍去;4+9>9,故4,9,9能构成三角形,∴它的周长是4+9+9=22.方法总结:在求三角形的边长时,要注意利用三角形的三边关系验证所求出的边长能否组成三角形.【类型四】三角形三边关系与绝对值的综合若a,b,c是△ABC的三边长,化简|a-b-c|+|b-c-a|+|c+a-b|.解析:根据三角形三边关系:两边之和大于第三边,两边之差小于第三边,来判定绝对值里的式子的正负,然后去绝对值符号进行计算即可.解:根据三角形的三边关系,两边之和大于第三边,得a-b-c<0,b-c-a<0,c+a-b>0.∴|a-b-c|+|b-c-a|+|c+a-b|=b+c-a+c+a-b+c+a-b=3c+a-b.方法总结:绝对值的化简首先要判断绝对值符号里面的式子的正负,然后根据绝对值的性质将绝对值的符号去掉,最后进行化简.此类问题就是根据三角形的三边关系,判断绝对值符号里面式子的正负,然后进行化简.考点二:三角形的高、中线与角平分线1.三角形的高:从三角形的一个顶点向它的对边作垂线,顶点和垂足间的线段叫做三角形的高.2.三角形的中线:在三角形中,连接一个顶点和它对边中点的线段叫做三角形的中线.3.三角形的角平分线:三角形的一个角的平分线与这个角的对边相交,连接这个角的顶点与交点的线段叫做三角形的角平分线.【例2】探究点一:三角形的高【类型一】三角形高的画法画△ABC的边AB上的高,下列画法中,正确的是( )解:过点C 作边AB 的垂线段,即画AB 边上的高CD ,所以画法正确的是D.故选D. 方法总结:三角形任意一边上的高必须满足:(1)过该边所对的顶点;(2)垂足必须在该边或在该边的延长线上.【类型二】 根据三角形的面积求高如图所示①,在△ABC 中,AB =AC =5,BC =6,AD ⊥BC 于点D ,且AD =4,若点P 在边AC 上移动,则BP 的最小值为________.解析:根据垂线段最短,可知当BP ⊥AC 时,BP 有最小值.由△ABC 的面积公式可知12AD ·BC =12BP ·AC ,解得BP =245方法总结:解答此题可利用面积相等作桥梁(但不求面积)求三角形的高,这种解题方法通常称为“面积法”.① ② ③ ④ 探究点二:三角形的中线【类型一】 应用三角形的中线求线段的长如图②在△ABC 中,AC =5cm ,AD 是△ABC 的中线,若△ABD 的周长比△ADC 的周长大2cm ,则BA =________.解析:如图,∵AD 是△ABC 的中线,∴BD =CD ,∴△ABD 的周长-△ADC 的周长=(BA +BD +AD )-(AC +AD +CD )=BA -AC ,∴BA -5=2,∴BA =7cm.方法总结:通过本题要理解三角形的中线的定义,解决问题的关键是将△ABD 与△ADC 的周长之差转化为边长的差.【类型二】 利用中线解决三角形的面积问题如图③,在△ABC 中,E 是BC 上的一点,EC =2BE ,点D 是AC 的中点,设△ABC ,△ADF 和△BEF 的面积分别为S △ABC ,S △ADF 和S △BEF ,且S △ABC =12,则S △ADF -S △BEF =________.解析:∵点D 是AC 的中点,∴AD =12AC .∵S △ABC =12,∴S △ABD =12S △ABC =12×12=6.∵EC =2BE ,S △ABC =12,∴S △ABE =13S △ABC =13×12=4.∵S △ABD -S △ABE =(S △ADF +S △ABF )-(S △ABF +S △BEF )=S △ADF -S △BEF ,即S △ADF -S △BEF =S △ABD -S △ABE =6-4=2.故答案为2.方法总结:三角形的中线将三角形分成面积相等的两部分;高相等时,面积的比等于底边的比;底相等时,面积的比等于高的比.探究点三:三角形的角平分线如图④,已知:AD 是△ABC 的角平分线,CE 是△ABC 的高,∠BAC =60°,∠BCE =40°,求∠ADB 的度数.解析:根据AD 是△ABC 的角平分线,∠BAC =60°,得出∠BAD =30°,再利用CE 是△ABC 的高,∠BCE =40°,得出∠B 的度数,进而得出∠ADB 的度数.解:∵AD 是△ABC 的角平分线,∠BAC =60°,∴∠DAC =∠BAD =30°.∵CE 是△ABC 的高,∠BCE =40°,∴∠B =50°,∴∠ADB =180°-∠B -∠BAD =180°-50°-30°=100°.方法总结:通过本题要灵活掌握三角形的角平分线的表示方法,同时此类问题往往和三角形的高综合考查.考点三:三角形的稳定性【例3】要使四边形木架(用4根木条钉成)不变形,至少需要加钉1根木条固定,要使五边形木架不变形,至少需要加2根木条固定,要使六边形木架不变形,至少需要加3根木条固定,…,那么要使一个n 边形木架不变形,至少需要几根木条固定?解析:由于多边形(三边以上的)不具有稳定性,将其转化为三角形后木架的形状就不变了.根据具体多边形转化为三角形的经验及题中所加木条可找到一般规律.解:过n 边形的一个顶点可以作(n -3)条对角线,把多边形分成(n -2)个三角形,所以,要使一个n 边形木架不变形,至少需要(n -3)根木条固定.方法总结:将多边形转化为三角形时,所需要的木条根数,可从具体到一般去发现规律,然后验证求解.专题二:三角形有关的角考点四:三角形的内角1.三角形的内角和定理:三角形的内角和等于180°2.直角三角形的性质:直角三角形两锐角互余【例4】探究点一:三角形的内角和【类型一】 求三角形内角的度数已知,如图①,D 是△ABC 中BC 边延长线上一点,DF ⊥AB 交AB 于F ,交AC 于E ,若∠A =46°,∠D =50°.求∠ACB 的度数.① ② 解析:在Rt △DFB 中,根据三角形内角和定理,求得∠B 的度数,再在△ABC 中求∠ACB 的度数即可.解:在△DFB 中,∵DF ⊥AB ,∴∠DFB =90°.∵∠D =50°,∠DFB +∠D +∠B =180°,∴∠B =40°.在△ABC 中,∵∠A =46°,∠B =40°,∴∠ACB =180°-∠A -∠B =94°. 方法总结:求三角形的内角,必然和三角形内角和定理有关,解决问题时要根据图形特点,在不同的三角形中,灵活运用三角形内角和定理求解.【类型二】 判断三角形的形状一个三角形的三个内角的度数之比为1∶2∶3,这个三角形一定是( )A .直角三角形B .锐角三角形C .钝角三角形D .无法判定解析:设这个三角形的三个内角的度数分别是x ,2x ,3x ,根据三角形的内角和为180°,得x +2x +3x =180°,解得x =30°,∴这个三角形的三个内角的度数分别是30°,60°,90°,即这个三角形是直角三角形.故选A.方法总结:在解决有关比例问题时,通常先设比例系数,然后列方程求解.【类型三】 三角形的内角与角平分线、高的综合运用如图②,在△ABC 中,∠A =12∠B =13∠ACB ,CD 是△ABC 的高,CE 是∠ACB 的角平分线,求∠DCE 的度数.解析:根据已知条件用∠A 表示出∠B 和∠ACB ,利用三角形的内角和求出∠A ,再求出∠ACB ,∠ACD ,最后根据角平分线的定义求出∠ACE 即可求得∠DCE 的度数.解:∵∠A =12∠B =13∠ACB ,设∠A =x ,∴∠B =2x ,∠ACB =3x .∵∠A +∠B +∠ACB =180°,∴x +2x +3x =180°,解得x =30°,∴∠A =30°,∠ACB =90°.∵CD 是△ABC 的高,∴∠ADC =90°,∴∠ACD =180°-90°-30°=60°.∵CE 是∠ACB 的角平分线,∴∠ACE =12×90°=45°,∴∠DCE =∠ACD -∠ACE =60°-45°=15°.方法总结:本题是常见的几何计算题,解题的关键是利用三角形的内角和定理和角平分线的性质,找出角与角之间的关系并结合图形解答.探究点二:直角三角形的性质【类型一】 直角三角形性质的运用如图,CE ⊥AF ,垂足为E ,CE 与BF 相交于点D ,∠F =40°,∠C =30°,求∠EDF 、∠DBC 的度数.解析:根据直角三角形两锐角互余列式计算即可求出∠EDF ,再根据三角形的内角和定理求出∠C +∠DBC =∠F +∠DEF ,然后求解即可.解:∵CE ⊥AF ,∴∠DEF =90°,∴∠EDF =90°-∠F =90°-40°=50°.由三角形的内角和定理得∠C +∠DBC +∠CDB =∠F +∠DEF +∠EDF ,∴30°+∠DBC =40°+90°,∴∠DBC =100°.方法总结:本题主要利用了直角三角形两锐角互余的性质和三角形的内角和定理,熟记性质并准确识图是解题的关键.考点五:三角形的外角1.三角形外角的定义:三角形的一边与另一边的延长线组成的角.2.三角形外角的性质:三角形的外角等于与它不相邻的两内角的和;三角形的一个外角大于与它不相邻的任何一个内角.【例5】探究点:三角形的外角【类型一】 应用三角形的外角求角的度数如图所示,P 为△ABC 内一点,∠BPC =150°,∠ABP =20°,∠ACP =30°,求∠A 的度数.解析:延长BP交AC于E或连接AP并延长,构造三角形的外角,再利用外角的性质即可求出∠A的度数.解:延长BP交AC于点E,则∠BPC,∠PEC分别为△PCE,△ABE的外角,∴∠BPC=∠PEC +∠PCE,∠PEC=∠ABE+∠A,∴∠PEC=∠BPC-∠PCE=150°-30°=120°.∴∠A=∠PEC-∠ABE=120°-20°=100°.方法总结:利用三角形的外角的性质将已知与未知的角联系起来是计算角的度数的方法.【类型二】用三角形外角的性质把几个角的和分别转化为一个三角形的内角和已知:如图为一五角星,求证:∠A+∠B+∠C+∠D+∠E=180°.解析:根据三角形外角性质得出∠EFG=∠B+∠D,∠EGF=∠A+∠C,根据三角形内角和定理得出∠E+∠EGF+∠EFG=180°,代入即可得证.证明:∵∠EFG、∠EGF分别是△BDF、△ACG的外角,∴∠EFG=∠B+∠D,∠EGF=∠A +∠C.又∵在△EFG中,∠E+∠EGF+∠EFG=180°,∴∠A+∠B+∠C+∠D+∠E=180°.方法总结:解决此类问题的关键是根据图形的特点,利用三角形外角的性质将分散的角集中到某个三角形中,利用三角形内角和进行解决.【类型三】三角形外角的性质和角平分线的综合应用如图①,∠ACD是△ABC的外角,BE平分∠ABC,CE平分∠ACD,且BE、CE交于点E.(1)如果∠A=60°,∠ABC=50°,求∠E的度数;(2)猜想:∠E与∠A有什么数量关系(写出结论即可);(3)如图②,点E是△ABC两外角平分线BE、CE的交点,探索∠E与∠A之间的数量关系,并说明理由.解析:先计算特殊角的情况,再综合运用三角形的内角和定理及其推论结合三角形的角平分线概念解决.解:(1)根据外角的性质得∠ACD =∠A +∠ABC =60°+50°=110°,∵BE 平分∠ABC ,CE 平分∠ACD ,∴∠1=12∠ACD =55°,∠2=12∠ABC =25°.∵∠E +∠2=∠1,∴∠E =∠1-∠2=30°;(2)猜想:∠E =12∠A ; (3)∵BE 、CE 是两外角的平分线,∴∠2=12∠CBD ,∠4=12∠BCF ,而∠CBD =∠A +∠ACB ,∠BCF =∠A +∠ABC ,∴∠2=12(∠A +∠ACB ),∠4=12(∠A +∠ABC ).∵∠E +∠2+∠4=180°,∴∠E +12(∠A +∠ACB )+12(∠A +∠ABC )=180°,即∠E +12∠A +12(∠A +∠ACB +∠ABC )=180°.∵∠A +∠ACB +∠ABC =180°,∴∠E +12∠A =90°. 方法总结:对于本题发现的结论要予以重视:图①中,∠E =12∠A ;图②中,∠E =90°-12∠A .考点六:多边形及其内角和多边形1.定义:在同一平面内,由不在同一条直线上的一些线段首尾顺次相接组成的封闭图形.2.相关概念:顶点、边、内角、对角线.3.多边形的对角线:n 边形从一个顶点出发的对角线条数为(n -3)条;n 边形共有对角线n (n -3)2条(n ≥3).4.正多边形:如果多边形的各边都相等,各内角也都相等,那么就称为正多边形. 多边形的内角和与外角和1.性质:多边形的内角和等于(n -2)·180°;多边形的外角和等于360°.2.多边形的边数与内角和、外角和的关系:(1)n 边形的内角和等于(n -2)·180°(n ≥3,n 是正整数),可见多边形内角和与边数n 有关,每增加1条边,内角和增加180°.(2)多边形的外角和等于360°,与边数的多少无关.(3).正n 边形:正n 边形的内角的度数为(n -2)·180°n ,外角的度数为360°n. 【例6】探究点一:多边形的概念【类型一】 多边形及其概念下列图形不是凸多边形的是( )解析:根据凸多边形的概念,如果多边形的边都在任意一条边所在的直线的同旁,该多边形即是凸多边形,否则即是凹多边形.由此可得选项D 的图形不是凸多边形.故选D. 方法总结:多边形可分为凸多边形和凹多边形,辨别凸多边形可有两种方法:(1)画多边形任何一边所在的直线,整个多边形都在此直线的同一侧;(2)每个内角的度数均小于180°.通常所说的多边形指凸多边形.【类型二】 确定多边形的边数若一个多边形截去一个角后,变成十五边形,则原来的多边形的边数可能为( )A .14或15或16B .15或16C .14或16D .15或16或17解析:一个多边形截去一个角后,多边形的边数可能增加了一条,也可能不变或减少了一条,则多边形的边数是14,15或16.故选A. 方法总结:一个多边形截去一个角后,多边形的边数可能增加了一条,也可能不变或减少了一条,解决此类问题可以亲自动手画一下.探究点二:多边形的对角线【类型一】 确定多边形的对角线的条数从四边形的一个顶点出发可画________条对角线,从五边形的一个顶点出发可画________条对角线,从六边形的一个顶点出发可画________条对角线,请猜想从七边形的一个顶点出发有________条对角线,从n 边形的一个顶点出发有________条对角线,从而推导出n 边形共有________条对角线.解析:根据n 边形从一个顶点出发可引出(n -3)条对角线.从n 个顶点出发引出n (n -3)条对角线,而每条重复一次,可得答案.解:从四边形的一个顶点出发可画1条对角线,从五边形的一个顶点出发可画2条对角线,从六边形的一个顶点出发可画3条对角线,从七边形的一个顶点出发有4条对角线,从n 边形的一个顶点出发有(n -3)条对角线,从而推导出n 边形共有n (n -3)2条对角线. 方法总结:(1)多边形有n 条边,则经过多边形的一个顶点的对角线有(n -3)条;(2)多边形有n 条边,对角线的条数为n (n -3)2.【类型二】 根据对角线条数确定多边形的边数从一个多边形的任意一个顶点出发都只有5条对角线,则它的边数是( )A .6B .7C .8D .9解析:设这个多边形是n 边形.依题意,得n -3=5,解得n =8.故这个多边形的边数是8.故选C.【类型三】 根据分成三角形的个数,确定多边形的边数连接多边形的一个顶点与其他顶点的线段把这个多边形分成了6个三角形,则原多边形是( )A .五边形B .六边形C .七边形D .八边形解析:设原多边形是n 边形,则n -2=6,解得n =8.故选D.方法总结:从n 边形的一个顶点出发可引出(n -3)条对角线,这(n -3)条对角线把n 边形分成(n -2)个三角形.探究点三:正多边形的有关概念下列图形中,是正多边形的是( )A .等腰三角形B .长方形C .正方形D .五边都相等的五边形解析:根据正多边形的定义:各个角都相等,各条边都相等的多边形叫做正多边形进行解答.正方形四个角相等,四条边都相等,故选C. 方法总结:解答此类问题的关键是要搞清楚正多边形的定义,各个角相等、各条边相等的多边形是正多边形,这两个条件缺一不可.探究点一:多边形的内角和【类型一】利用内角和求边数一个多边形的内角和为540°,则它是( )A.四边形 B.五边形C.六边形 D.七边形解析:熟记多边形的内角和公式(n-2)·180°设它是n边形,根据题意得(n-2)·180=540,解得n=5.故选B.【类型二】求多边形的内角和一个多边形的内角和为1800°,截去一个角后,得到的多边形的内角和为( )A.1620° B.1800°C.1980° D.以上答案都有可能解析:1800÷180=10,∴原多边形边数为10+2=12.∵一个多边形截去一个内角后,边数可能减1,可能不变,也可能加1,∴新多边形的边数可能是11,12,13,∴新多边形的内角和可能是1620°,1800°,1980°.故选D.方法总结:一个多边形截去一个内角后,边数可能减1,可能不变,也可能加1.根据多边形的内角和公式求出原多边形的边数是解题的关键.【类型三】复杂图形中的角度计算如图,∠1+∠2+∠3+∠4+∠5+∠6+∠7=( )A.450° B.540°C.630° D.720°解析:如图,∵∠3+∠4=∠8+∠9,∴∠1+∠2+∠3+∠4+∠5+∠6+∠7=∠1+∠2+∠8+∠9+∠5+∠6+∠7=五边形的内角和=540°,故选B.方法总结:本题考查了灵活运用五边形的内角和定理和三角形内外角关系.根据图形特点,将问题转化为熟知的问题,体现了转化思想的优越性.【类型四】利用方程和不等式确定多边形的边数一个同学在进行多边形的内角和计算时,求得内角和为1125°,当他发现错了以后,重新检查,发现少算了一个内角,问这个内角是多少度?他求的是几边形的内角和?解析:本题首先由题意找出不等关系列出不等式,进而求出这一内角的取值范围;然后可确定这一内角的度数,进一步得出这个多边形的边数.解:设此多边形的内角和为x,则有1125°<x<1125°+180°,即180°×6+45°<x<180°×7+45°,因为x为多边形的内角和,所以它是180°的倍数,所以x=180°×7=1260°.所以7+2=9,1260°-1125°=135°.因此,漏加的这个内角是135°,这个多边形是九边形.方法总结:解题的关键是由题意列出不等式求出这个多边形的边数.探究点二:多边形的外角和【类型一】已知各相等外角的度数,求多边形的边数正多边形的一个外角等于36°,则该多边形是正( )A.八边形 B.九边形C.十边形 D.十一边形解析:正多边形的边数为360°÷36°=10,则这个多边形是正十边形.故选C.方法总结:如果已知正多边形的一个外角,求边数可直接利用外角和除以这个角即可.【类型二】多边形内角和与外角和的综合运用一个多边形的内角和与外角和的和为540°,则它是( )A.五边形 B.四边形C.三角形 D.不能确定解析:设这个多边形的边数为n,则依题意可得(n-2)×180°+360°=540°,解得n =3,∴这个多边形是三角形.故选C.方法总结:熟练掌握多边形的内角和定理及外角和定理,解题的关键是由已知等量关系列出方程从而解决问题.。
2021-2022学年浙教版九年级数学下册《第1章解直角三角形》期末综合复习训练(附答案)

2021-2022学年浙教版九年级数学下册《第1章解直角三角形》期末综合复习训练(附答案)1.某商场准备改善原有楼梯的安全性能,把坡角由37°减至30°,已知原楼梯长为5米,调整后的楼梯会加长()(参考数据:sin37°≈,cos37°≈,tan37°≈).A.6米B.3米C.2米D.1米2.如图,在一次数学实践活动中,小明同学要测量一座与地面垂直的古塔AB的高度,他从古塔底部点B处前行30m到达斜坡CE的底部点C处,然后沿斜坡CE前行20m到达最佳测量点D处,在点D处测得塔顶A的仰角为30°,已知斜坡的斜面坡度i=1:,且点A,B,C,D,E在同一平面内,小明同学测得古塔AB的高度是()A.(10+20)m B.(10+10)m C.20m D.40m3.如图,在△ABC中,∠ACB=90°,点D在AB的延长线上,连接CD,若AB=2BD,tan∠BCD=,则的值为()A.1B.2C.D.4.如图,△ABC底边BC上的高为h1,△PQR底边QR上的高为h2,则有()A.h1=h2 B.h1<h2 C.h1>h2 D.以上都有可能5.如图,在△ABC中,点O是角平分线AD、BE的交点,若AB=AC=10,BC=12,则tan ∠OBD的值是()A.B.2C.D.6.如图,为了测量某建筑物BC的高度,小颖采用了如下的方法:先从与建筑物底端B在同一水平线上的A点出发,沿斜坡AD行走130米至坡顶D处,再从D处沿水平方向继续前行若干米后至点E处,在E点测得该建筑物顶端C的仰角为60°,建筑物底端B 的俯角为45°,点A、B、C、D、E在同一平面内,斜坡AD的坡度i=1:2.4.根据小颖的测量数据,计算出建筑物BC的高度约为(参考数据:≈1.732)()A.136.6米B.86.7米C.186.7米D.86.6米7.构建几何图形解决代数问题是“数形结合”思想的重要应用,在计算tan15°时,如图.在Rt△ACB中,∠C=90°,∠ABC=30°,延长CB使BD=AB,连接AD,得∠D=15°,所以tan15°====2﹣.类比这种方法,计算tan22.5°的值为()A.+1B.﹣1C.D.8.已知,在△ABC中,∠A=45°,AB=4,BC=5,则△ABC的面积为.9.数学活动小组为测量山顶电视塔的高度,在塔的椭圆平台遥控无人机.当无人机飞到点P处时,与平台中心O点的水平距离为15米,测得塔顶A点的仰角为30°,塔底B点的俯角为60°,则电视塔的高度为米.10.如图,一艘轮船位于灯塔P的南偏东60°方向,距离灯塔50海里的A处,它沿正北方向航行一段时间后,到达位于灯塔P的北偏东45°方向上的B处,此时B处与灯塔P 的距离为海里(结果保留根号).11.如图,某活动小组利用无人机航拍校园,已知无人机的飞行速度为3m/s,从A处沿水平方向飞行至B处需10s.同时在地面C处分别测得A处的仰角为75°,B处的仰角为30°,则这架无人机的飞行高度大约是m(≈1.732,结果保留整数).12.如图1是一台手机支架,图2是其侧面示意图,AB,BC可分别绕点A,B转动,测量知BC=8cm,AB=16cm.当AB,BC转动到∠BAE=60°,∠ABC=50°时,点C到AE的距离为cm.(结果保留小数点后一位,参考数据:sin70°≈0.94,≈1.73)13.如图,我国某海域有A,B两个港口,相距80海里,港口B在港口A的东北方向,点C处有一艘货船,该货船在港口A的北偏西30°方向,在港口B的北偏西75°方向,求货船与港口A之间的距离.(结果保留根号)14.2020年7月23日,我国首次火星探测“天问一号”探测器,由长征五号遥四运载火箭在中国文昌航天发射场发射成功,正式开启了中国的火星探测之旅.运载火箭从地面O 处发射,当火箭到达点A时,地面D处的雷达站测得AD=4000米,仰角为30°.3秒后,火箭直线上升到达点B处,此时地面C处的雷达站测得B处的仰角为45°.O,C,D 在同一直线上,已知C,D两处相距460米,求火箭从A到B处的平均速度.(结果保留整数,参考数据:≈1.732,≈1.414)15.小宸想利用测量知识测算湖中小山的高度.他站在湖边看台上,清晰地看到小山倒映在平静的湖水中,如图所示,他在点O处测得小山顶端的仰角为45°,小山顶端A在水中倒影A′的俯角为60°.已知:点O到湖面的距离OD=3m,OD⊥DB,AB⊥DB,A、B、A′三点共线,A'B=AB,求小山的高度AB.(光线的折射忽略不计;结果保留根号)16.某海域有一小岛P,在以P为圆心,半径r为10(3+)海里的圆形海域内有暗礁.一海监船自西向东航行,它在A处测得小岛P位于北偏东60°的方向上,当海监船行驶20海里后到达B处,此时观测小岛P位于B处北偏东45°方向上.(1)求A,P之间的距离AP;(2)若海监船由B处继续向东航行是否有触礁危险?请说明理由.如果有触礁危险,那么海监船由B处开始沿南偏东至多多少度的方向航行能安全通过这一海域?17.如图,莽山五指峰景区新建了一座垂直观光电梯.某测绘兴趣小组为测算电梯AC的高度,测得斜坡AB=105米,坡度i=1:2,在B处测得电梯顶端C的仰角α=45°,求观光电梯AC的高度.(参考数据:≈1.41,≈1.73,≈2.24.结果精确到0.1米)18.如图,在某小区内拐角处的一段道路上,有一儿童在C处玩耍,一辆汽车从被楼房遮挡的拐角另一侧的A处驶来,已知CM=3m,CO=5m,DO=3m,∠AOD=70°,汽车从A处前行多少米才能发现C处的儿童(结果保留整数)?(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75;sin70°≈0.94,cos70°≈0.34,tan70°≈2.75)19.王刚同学在学习了解直角三角形及其应用的知识后,尝试利用所学知识测量河对岸大树AB的高度,他在点C处测得大树顶端A的仰角为45°,再从C点出发沿斜坡走2米到达斜坡上D点,在点D处测得树顶端A的仰角为30°,若斜坡CF的坡比为i=1:3(点E、C、B在同一水平线上).(1)求王刚同学从点C到点D的过程中上升的高度;(2)求大树AB的高度(结果保留根号).20.一架无人机沿水平直线飞行进行测绘工作,在点P处测得正前方水平地面上某建筑物AB的顶端A的俯角为30°,面向AB方向继续飞行5米,测得该建筑物底端B的俯角为45°,已知建筑物AB的高为3米,求无人机飞行的高度(结果精确到1米,参考数据:≈1.414,≈1.732).21.小明和小华约定一同去公园游玩,公园有南北两个门,北门A在南门B的正北方向,小明自公园北门A处出发,沿南偏东30°方向前往游乐场D处;小华自南门B处出发,沿正东方向行走150m到达C处,再沿北偏东22.6°方向前往游乐场D处与小明汇合(如图所示),两人所走的路程相同.求公园北门A与南门B之间的距离.(结果取整数.参考数据:sin22.6°≈,cos22.6°≈,tan22.6°≈,≈1.732)22.小张早起在一条东西走向的笔直马路上晨跑,他在A处时,D处学校和E处图书馆都在他的东北方向,当小张沿正东方向跑了600m到达B处时,E处图书馆在他的北偏东15°方向,然后他由B处继续向正东方向跑600m到达C处,此时D处学校在他的北偏西63.4°方向,求D处学校和E处图书馆之间的距离.(结果保留整数)(参考数据:sin63.4°≈0.9,cos63.4°≈0.4,tan63.4°≈2.0,≈1.4,≈1.7,≈2.4)23.如图,已知△ABD中,AC⊥BD,BC=8,CD=4,cos∠ABC=,BF为AD边上的中线.(1)求AC的长;(2)求tan∠FBD的值.24.在全民健身运动中,骑行运动颇受市民青睐.一市民骑自行车由A地出发,途经B地去往C地,如图.当他由A地出发时,发现他的北偏东45°方向有一信号发射塔P.他由A地沿正东方向骑行4km到达B地,此时发现信号塔P在他的北偏东15°方向,然后他由B地沿北偏东75°方向骑行12km到达C地.(1)求A地与信号发射塔P之间的距离;(2)求C地与信号发射塔P之间的距离.(计算结果保留根号)25.某天,北海舰队在中国南海例行训练,位于A处的济南舰突然发现北偏西30°方向上的C处有一可疑舰艇,济南舰马上通知位于正东方向200海里B处的西安舰,西安舰测得C处位于其北偏西60°方向上,请问此时两舰距C处的距离分别是多少?26.如图,A,B是海面上位于东西方向的两个观测点,有一艘海轮在C点处遇险发出求救信号,此时测得C点位于观测点A的北偏东45°方向上,同时位于观测点B的北偏西60°方向上,且测得C点与观测点A的距离为25海里.(1)求观测点B与C点之间的距离;(2)有一艘救援船位于观测点B的正南方向且与观测点B相距30海里的D点处,在接到海轮的求救信号后立即前往营救,其航行速度为42海里/小时,求救援船到达C点需要的最少时间.参考答案1.解:在Rt△BAD中,AB=5米,∠BAD=37°,则BD=AB•sin∠BAD≈5×=3(米),在Rt△BCD中,∠C=30°,∴BC=2BD=6(米),则调整后的楼梯会加长:6﹣5=1(米),故选:D.2.解:过D作DF⊥BC于F,DH⊥AB于H,∴DH=BF,BH=DF,∵斜坡的斜面坡度i=1:,∴=1:,设DF=xm,CF=xm,∴CD==2x=20m,∴x=10,∴BH=DF=10m,CF=10m,∴DH=BF=(10+30)m,∵∠ADH=30°,∴AH=DH=×(10+30)=(10+10)m,∴AB=AH+BH=(20+10)m,故选:A.3.解:过点D作DM⊥BC,交CB的延长线于点M,∵∠ACB=∠DMB=90°,∠ABC=∠DBM,∴△ABC∽△DBM,∴==,∵AB=2BD,∴===,在Rt△CDM中,由于tan∠MCD==,设DM=2k,则CM=3k,又∵==,∴BC=2k,AC=4k,∴==2,故选:B.4.解:如图,分别作出△ABC底边BC上的高为AD即h1,△PQR底边QR上的高为PE 即h2,在Rt△ADC中,h1=AD=5×sin55°,在Rt△PER中,h2=PE=5×sin55°,∴h1=h2,故选:A.5.解:如图:作OF⊥AB于F,∵AB=AC,AD平分∠BAC.∴∠ODB=90°.BD=CD=6.∴根据勾股定理得:AD==8.∵BE平分∠ABC.∴OF=OD,BF=BD=6,AF=10﹣6=4.设OD=OF=x,则AO=8﹣x,在Rt△AOF中,根据勾股定理得:(8﹣x)2=x2+42.∴x=3.∴OD=3.在Rt△OBD中,tan∠OBD===.故选:A.6.解:如图作DH⊥AB于H,延长DE交BC于F.在Rt△ADH中,AD=130米,DH:AH=1:2.4,∴DH=50(米),∵四边形DHBF是矩形,∴BF=DH=50(米),在Rt△EFB中,∠BEF=45°,∴EF=BF=50(米),在Rt△EFC中,FC=EF•tan60°,∴CF=50×≈86.6(米),∴BC=BF+CF=136.6(米).故选:A.7.解:在Rt△ACB中,∠C=90°,∠ABC=45°,延长CB使BD=AB,连接AD,得∠D=22.5°,设AC=BC=1,则AB=BD=,∴tan22.5°===﹣1,故选:B.8.解:过点B作AC边的高BD,Rt△ABD中,∠A=45°,AB=4,∴BD=AD=4,在Rt△BDC中,BC=4,∴CD==5,①△ABC是钝角三角形时,AC=AD﹣CD=1,∴S△ABC=AC•BD==2;②△ABC是锐角三角形时,AC=AD+CD=7,∴S△ABC=AC•BD=×7×4=14,故答案为:2或14.9.解:在Rt△APO中,OP=15米,∠APO=30°,∴OA=OP•tan30°=(米),在Rt△POB中,OP=15米,∠OPB=60°,∴OB=(米),∴AB=OA+OB=20(米),故答案为:20.10.解:过P作PC⊥AB于C,如图所示:由题意得:∠APC=30°,∠BPC=45°,P A=50海里,在Rt△APC中,cos∠APC=,∴PC=P A•cos∠APC=50×=25(海里),在Rt△PCB中,cos∠BPC=,∴PB===25(海里),故答案为:25.11.解:过A点作AH⊥BC于H,过B点作BD垂直于过C点的水平线,垂足为D,如图,根据题意得∠ACD=75°,∠BCD=30°,AB=3×10=30m,∵AB∥CD,∴∠ABH=∠BCD=30°,在Rt△ABH中,AH=AB=15m,∵tan∠ABH=,∴BH===15,∵∠ACH=∠ACD﹣∠BCD=75°﹣30°=45°,∴CH=AH=15m,∴BC=BH+CH=(15+15)m,在Rt△BCD中,∵∠BCD=30°,∴BD=BC=≈20(m).答:这架无人机的飞行高度大约是20m.故答案为20.12.解:如图,过点B、C分别作AE的垂线,垂足分别为M、N,过点C作CD⊥BM,垂足为D,在Rt△ABM中,∵∠BAE=60°,AB=16,∴BM=sin60°•AB=×16=8(cm),∠ABM=90°﹣60°=30°,在Rt△BCD中,∵∠DBC=∠ABC﹣∠ABM=50°﹣30°=20°,∴∠BCD=90°﹣20°=70°,又∵BC=8,∴BD=sin70°×8≈0.94×8=7.52(cm),∴CN=DM=BM﹣BD=8﹣7.52≈6.3(cm),即点C到AE的距离约为6.3cm,故答案为:6.3.13.解:过点A作AD⊥BC于D,如图所示:由题意得:∠ABC=180°﹣75°﹣45°=60°,∵AD⊥BC,∴∠ADB=∠ADC=90°,在Rt△ABD中,∠DAB=90°﹣60°=30°,AD=AB•sin∠ABD=80×sin60°=80×=40(海里),∵∠CAB=30°+45°=75°,∴∠DAC=∠CAB﹣∠DAB=75°﹣30°=45°,∴△ADC是等腰直角三角形,∴AC=AD=×40=40(海里).答:货船与港口A之间的距离是40海里.14.解:由题意得,AD=4000米,∠ADO=30°,CD=460米,∠BCO=45°,在Rt△AOD中,∵AD=4000米,∠ADO=30°,∴OA=AD=2000(米),OD=AD=2000(米),在Rt△BOC中,∠BCO=45°,∴OB=OC=OD﹣CD=(2000﹣460)米,∴AB=OB﹣OA=2000﹣460﹣2000≈1004(米),∴火箭的速度为1004÷3≈335(米/秒),答:火箭的速度约为335米/秒.15.解:过点O作OE⊥AB于点E,则BE=OD=3m,设AE=xm,则AB=(x+3)m,A′E=(x+6)m,∵∠AOE=45°,∴OE=AE=xm,∵∠A′OE=60°,∴tan60°==,即=,解得x=3+3,∴AB=3+3+3=(6+3)m.16.解:(1)过点P作PC⊥AB,交AB的延长线于点C,由题意得,∠P AC=30°,∠PBC=45°,AB=20,设PC=x,则BC=x,在Rt△P AC中,∵tan30°===,∴x=10+10,∴P A=2x=20+20,答:A,P之间的距离AP为(20+20)海里;(2)因为PC﹣10(3+)=10+10﹣30﹣10=10(+1)(﹣)<0,所以有触礁的危险;设海监船无触礁危险的新航线为射线BD,作PE⊥BD,垂足为E,当P到BD的距离PE=10(3+)海里时,有sin∠PBE===,∴∠PBD=60°,∴∠CBD=60°﹣45°=15°,90°﹣15°=75°即海监船由B处开始沿南偏东至多75°的方向航行能安全通过这一海域.17.解:过B作BM⊥水平地面于M,BN⊥AC于N,如图所示:则四边形AMBN是矩形,∴AN=BM,BN=MA,∵斜坡AB=105米,坡度i=1:2=,∴设BM=x米,则AM=2x米,∴AB===x=105,∴x=21,∴AN=BM=21(米),BN=AM=42(米),在Rt△BCN中,∠CBN=α=45°,∴△BCN是等腰直角三角形,∴CN=BN=42(米),∴AC=AN+CN=21+42=63≈141.1(米),答:观光电梯AC的高度约为141.1米.18.解:∵CM=3m,OC=5m,∴OM==4(m),∵∠CMO=∠BDO=90°,∠COM=∠BOD,∴△COM∽△BOD,∴,即,∴BD==2.25(m),∴tan∠AOD=tan70°=,即≈2.75,解得:AB=6m,∴汽车从A处前行约6米才能发现C处的儿童.19.解:(1)过点D作DH⊥CE于点H,由题意知CD=2米,∵斜坡CF的坡比为i=1:3,∴,设DH=x米,CH=3x米,∵DH2+CH2=DC2,∴,∴x=2,∴DH=2(米),CH=6(米),答:王刚同学从点C到点D的过程中上升的高度为2米;(2)过点D作DG⊥AB于点G,设BC=a米,∵∠DHB=∠DGB=∠ABC=90°,∴四边形DHBG为矩形,∴DH=BG=2米,DG=BH=(a+6)米,∵∠ACB=45°,∴BC=AB=a(米),∴AG=(a﹣2)米,∵∠ADG=30°,∴,∴,∴a=6+4,∴AB=(6+4)(米).答:大树AB的高度是(6+4)米.20.解:过A作AC⊥PQ,交PQ的延长线于C,如图所示:设AC=x米,由题意得:PQ=5米,∠APC=30°,∠BQC=45°,在Rt△APC中,tan∠APC==tan30°=,∴PC=AC=x(米),在Rt△BCQ中,tan∠BQC==tan45°=1,∴QC=BC=AC+AB=(x+3)米,∵PC﹣QC=PQ=5米,∴x﹣(x+3)=5,解得:x=4(+1),∴BC=4(+1)+3=4+7≈14(米),答:无人机飞行的高度约为14米.21.解:作DE⊥AB于E,CF⊥DE于F,∵BC⊥AB,∴四边形BCFE是矩形,∴BE=CF,EF=BC=150 m,设DF=xm,则DE=(x+150)m,在Rt△ADE中,∠BAD=30°,∴AD=2DE=2(x+150)m,在Rt△DCF中,∠FCD=22.6°,∴CD=≈=xm,∵AD=CD+BC,∴2(x+150)=+150,解得x=250(m),∴DF=250 m,∴DE=250+150=400 m,∴AD=2DE=800 m,∴CD=800﹣150=650 m,由勾股定理得AE===400m,BE=CF===600 m,∴AB=AE+BE=400+600≈1293(m),答:公园北门A与南门B之间的距离约为1293 m.22.解:过D作DM⊥AC于M,设MD=x,在Rt△MAD中,∠MAD=45°,∴△ADM是等腰直角三角形,∴AM=MD=x,∴AD=x,在Rt△MCD中,∠MDC=63.4°,∴MC≈2MD=2x,∵AC=600+600=1200,∴x+2x=1200,解得:x=400,∴MD=400m,∴AD=MD=400,过B作BN⊥AE于N,∵∠EAB=45°,∠EBC=75°,∴∠E=30°,在Rt△ABN中,∠NAB=45°,AB=600,∴BN=AN=AB=300,∴DN=AD﹣AN=400﹣300=100,在Rt△NBE中,∠E=30°,∴NE=BN=×300=300,∴DE=NE﹣DN=300﹣100≈580(m),即D处学校和E处图书馆之间的距离约是580m.23.解:(1)∵AC⊥BD,cos∠ABC==,BC=8,∴AB=10,在Rt△ACB中,由勾股定理得,AC===6,即AC的长为6;(2)如图,连接CF,过F点作BD的垂线,垂足E,∵BF为AD边上的中线,即F为AD的中点,∴CF=AD=FD,在Rt△ACD中,由勾股定理得,AD===2,∵三角形CFD为等腰三角形,FE⊥CD,∴CE=CD=2,在Rt△EFC中,EF===3,∴tan∠FBD===.解法二:∵BF为AD边上的中线,∴F是AD中点,∵FE⊥BD,AC⊥BD,∴FE∥AC,∴FE是△ACD的中位线,∴FE=AC=3,CE=CD=2,∴在Rt△BFE中,tan∠FBD===.24.解:(1)依题意知:∠P AB=45°,∠PBG=15°,∠GBC=75°,过点B作BD⊥AP于D点,∵∠DAB=45°,,∴AD=BD=4,∵∠ABD=∠GBD=45°,∠GBP=15°,∴∠PBD=60°,∵BD=4,∴,∴P A=(4+4)(km);(2)∵∠PBD=60°,BD=4,∴PB=8,过点P作PE⊥BC于E,∵∠PBG=15°,∠GBC=75°,∴∠PBE=60°,∵PB=8,∴BE=4,,∵BC=12,∴CE=8,∴PC==4(km).25.解:过点C作CD⊥BA的延长线于点D,如图.由题意可得:∠CAD=60°,∠CBD=30°=∠DCA,∴∠BCA=∠CAD﹣∠CBD=60°﹣30°=30°.即∠BCA=∠CBD,∴AC=AB=200(海里).在Rt△CDA中,CD=sin∠CAD×AC==100(海里).在Rt△CDB中,CB=2CD=200(海里).故位于A处的济南舰距C处的距离200海里,位于B处的西安舰距C处的距离200海里.26.解:(1)如图,过点C作CE⊥AB于点E,根据题意可知:∠ACE=∠CAE=45°,AC=25海里,∴AE=CE=25(海里),∵∠CBE=30°,∴BE=25(海里),∴BC=2CE=50(海里).答:观测点B与C点之间的距离为50海里;(2)如图,作CF⊥DB于点F,∵CF⊥DB,FB⊥EB,CE⊥AB,∴四边形CEBF是矩形,∴FB=CE=25(海里),CF=BE=25(海里),∴DF=BD+BF=30+25=55(海里),在Rt△DCF中,根据勾股定理,得CD===70(海里),∴70÷42=(小时).答:救援船到达C点需要的最少时间是小时.。
第一章三角形单元测试卷(含解析)
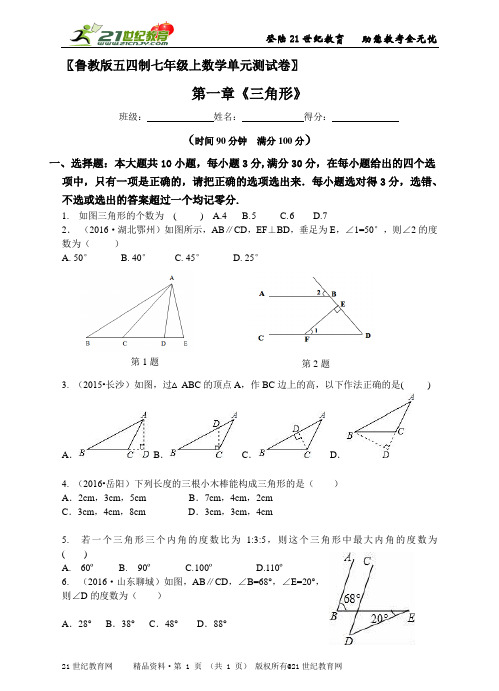
〖鲁教版五四制七年级上数学单元测试卷〗第一章《三角形》班级:姓名:得分:(时间90分钟满分100分)一、选择题:本大题共10小题,每小题3分,满分30分,在每小题给出的四个选项中,只有一项是正确的,请把正确的选项选出来.每小题选对得3分,选错、不选或选出的答案超过一个均记零分.1.如图三角形的个数为() A.4 B. 5 C. 6 D.72.(2016·湖北鄂州)如图所示,AB∥CD,EF⊥BD,垂足为E,∠1=50°,则∠2的度数为()A. 50°B. 40°C. 45°D. 25°第1题第2题3. (2015•长沙)如图,过△ABC的顶点A,作BC边上的高,以下作法正确的是()A.B.C.D.4. (2016•岳阳)下列长度的三根小木棒能构成三角形的是()A.2cm,3cm,5cm B.7cm,4cm,2cmC.3cm,4cm,8cm D.3cm,3cm,4cm5.若一个三角形三个内角的度数比为1:3:5,则这个三角形中最大内角的度数为()A. 60ºB. 90ºC. 100ºD.110º6.(2016·山东聊城)如图,AB∥CD,∠B=68°,∠E=20°,则∠D的度数为()A.28°B.38°C.48°D.88°7. 根据下列条件,不能唯一画出△ABC 的是( )A. AB=12,BC=7,CA=8B. AB=20,BC=30,∠A=50ºC. AB=9, ∠A=60º ,AC=15D. ∠A=50º,∠B=40º,AB=238. (2015•绵阳)如图,在△ABC 中,∠B 、∠C 的平分线BE ,CD 相交于点F ,∠ABC=42°,∠A=60°,则∠BFC=( )A . 118°B . 119°C . 120°D . 121°9. 如图,A 点和B 点之间有一池塘,已知OB=OC ,AC=BD ,若能米尺测出CD=10米,就能知道AB 的距离,它根据( ) A. SAS B. SSS C. ASA D. AAS10. (2015•宜昌)两组邻边分别相等的四边形叫做“筝形”,如图,四边形ABCD 是一个筝形,其中AD=CD ,AB=CB ,詹姆斯在探究筝形的性质时,得到如下结论: ①AC ⊥BD ;②AO=CO=21AC ;③△ABD ≌△CBD ,其中正确的结论有( )A . 0个B . 1个C . 2个D . 3个二、填空题(本大题共4小题,每小题4分,满分16分)11. (2015•江苏盐城)如图,在△ABC 与△ADC 中,已知AD=AB ,在不添加任何辅助线的前提下,要使△ABC ≌△ADC ,只需再添加的一个条件可以是 .12. 小明家的椅子坏了, 小明在学校学习了鲁教版五四制七上数学第一章《三角形》的知识后,正在家里帮爸爸妈妈修理椅子,请你告诉大家聪明的小明应用的数学原理: 。
浙教版八年级数学上《第1章三角形的初步知识》单元检测题含答案

浙教版2022-2023上学期八年级数学(上册)第1章三角形的初步知识检测题(时间:100分钟 满分:120分) 题号 1 2 3 4 5 6 7 8 9 10 答案一、选择题(共10小题 每3分 共30分)1、以长为5cm 和3cm 的线段为边,且第三边为偶数的三角形,可以作 ( )A.1个B.2个C.3个D.4个 2、将三角形面积分成相等两部分的线是( )A.三角形的角平分线B. 三角形的三边垂直平分线C. 三角形的高线D. 三角形的中线3、如图,E D C B A ∠+∠+∠+∠+∠等于( )A.90°B.108°C.180°D.360° 4、不是利用三角形稳定性的是( )A .自行车的三角形车架B .三角形房架C .照相机的三角架D .矩形门框的斜拉条 5、如图,点E ,D 分别在AB ,AC 上,若AB =AC ,BE =CD ,BD =EC ,∠B =32°,∠A =41°, 则∠BOC 度数是( )A .135°B .125°C .115°D .105°6、如图,在△ABC 中,BD 、CE 分别是∠ABC 和∠ACB 的平分线,AM ⊥CE 于P ,交BC 于M ,AN ⊥BD 于Q ,交BC 于N ,∠BAC =110°,AB =6,AC=5,MN =2,结论①AP =MP ;②BC =9;③∠MAN =35°;④AM =AN .其中不正确的有( )A. 4个B. 3个C. 2个D. 1个7、如图,所示某人将一块三角形的玻璃打碎成了四块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的办法是带( )去.A.第①块B.第②块C.第③块D.第④块第7题图第6题图第5题图8、下列命题是真命题的是( )A.一个三角形中至少有两个锐角B. 若A ∠与B ∠是内错角, 则A B ∠=∠C.如果两个角有公共边,那么这两个角一定是邻补角D.如果3.14a b =π,那么a b = 9、如图,∠1=∠2,补充一个条件后仍不能判定△ABC ≌△ADC 是( ) A. AB =AD B. ∠B =∠D C. BC=DC D. ∠BAC =∠DAC10、如图,△ABC 的三边AB 、BC 、CA 的长分别为30、40、15,点P 是三条角平分线的交点,将△ABC 分成三个三角形,则APB S ∆︰BPC S ∆︰CPA S ∆等于( )A.1︰1︰1B. 6︰8︰3C.5︰8︰3D. 4︰5︰3二、填空题(共8小题 每题3分 共24分)11、在△ABC 中,AD 是BC 边上的中线,AB =5cm ,AD =3cm ,则AC 的取值范围是_____________; 12、如图,AB ∥CD ,∠1=42°,∠3=77°,则∠2的度数为( )13、如图,在四边形ABCD 中,AD =AD ,BC =DC ,E 是AC 上的点,则图中共有_______对全等三角形. 14、如图,△ABC 中,DH 是AC 的垂直平分线,交BC 于P ,MN 是AB 的垂直平分线,交BC 于点Q , 连接AP 、AQ ,已知∠BAC =72°,则∠P AQ = 度.15、如图,在△ABC 中,∠C =90°,AC =BC ,BD 平分∠CBA 交AC 于点D ,DE ⊥AB 于点E ,且△DEA 的周长为cm ,则AB = .第15题图第9题图第10题图第13题图第14题图第18题图第16题图16、如图,在△ABC 中,BC =6cm ,AC =2.5cm ,AB =4cm ,∠B =40°,∠C =55°,选择适当数据,画与△ABC 全等的三角形一共有 种选择方法.17、如果一个角的两边与另一个角的两边分别垂直,那么这两个角相等或互补,这个命题的题设 是 ,结论是 .18、如图,在△AB C 中, E 是边A B 上的点,CF ⊥AB 于F ,EG ⊥C B 于G ,若 △CAF ≌△CEF ≌△CEG ≌△BEG ,则∠ACB =______度. 三、解答题(共8题 共66分)19、(满分6分)已知∠α和线段a ,求作△ABC ,使∠A =∠α,∠C =90°,AB =a .20. (满分8分)将推理过程的理由填入括号内:如图,AB =CD ,AD =CB ,O 为BD 上任意一点,过O 点的直线分别交AD 、BC 的延长线于M 、N 点,试说明∠1=∠2.解:在△ABD 和△CDB 中,∴△ABD ≌△CDB ( ),∴∠ADB =∠CBD ( ), ∴ AD ∥BC ( ), ∴∠1=∠2( ).21、(满分8分)如图,点A 、B 、E 、D 在同一直线上, 已知AF ∥DC ,AF =DC ,FE ∥CB .求证:AB DE =.22、(满分6分)如图,在△ABC 中,AF 平分∠BAC ,AC 的垂直平分线交BC 于点E ,∠B =72°,∠F AE =18°,则∠C = 度.( )( ) ( )AB CD AD CB BD DB =⎧⎪=⎨⎪=⎩第21题图第22题图第19题图第20题图23、(满分9分)如图,已知在△ABC 中,∠ACB =90°,CF ⊥AB 于F , 点G 为BC 的中点,E 为AB 上的点,GE 的延长线与CF 的延长线 相交于D ,若CE =BE ,BC =2AC ,则AB =CD .请说明理由.24、(满分8分),如图已知AD 、A D ''分别是边BC 、B C ''上的中线,AB A B ''=,BC B C ''=,AD A D ''=,求证:C C '∠=∠.25、(满分8分)阅读以下材料:对于三个数a 、b 、c ,用}{M a b c ,,表示这三个数的平均数,用}{min a b c ,,表示这三个数中最小的数.例如:}{2121M 21233-++-==,,;}{min 2122-=-,,. 解决下列问题:(1)填空:如果}{M 211358312x x x x +---=-,,,则x 的值为 ; (2)如果}{}{M 3213min 3213a a a a +=+,,,,,求a 的值.26、(满分11分)如图,CD 是经过∠BCA 顶点C 的一条直线,且直线CD 经过∠BCA 的内部,点E ,F 在射线CD 上,已知CA =CB 且∠BEC =∠CF A =∠α.(1)如图1,若∠BCA =80°,∠α=100°,问AF BE EF -=,成立吗?说明理由.(2)将(1)中的已知条件改成∠BCA =∠β,∠α+∠β=180°(如图2),问AF BE EF -=仍成立吗?说明理由.第23题图第24题图答 案一、选择题(共10小题 每3分 共30分) 题号 1 2 3 4 5 6 7 8 9 10 答案BDCCDBCAAB二、填空题(共8小题 每题3分 共24分)11. 1<AC <11 12.∠2=35° 13.3对 14. 36° 15.cm 16.4 三、解答题(共8题 共66分)17.条件:一个角的两边与另一个角的两边分别垂直,结论:这两个角相等或互补 18.90° 19题,作法(1)作∠MAN =∠α, (2)在AM 上截取AB =a ,(3)过点B 作AN 的垂线,垂足为C ,△ABC 为所求作. 20.解:在△ABD 和△CDB 中,AB CDAD CBBD DB =⎧⎪=⎨⎪=⎩(已知)(已知)(公共边) ∴△ABD ≌△CDB (SSS ),∴∠ADB =∠CBD (全等三角形对应角相等), ∴ AD ∥BC (内错角相等两直线平行 ), ∴∠1=∠2( 两直线平行内错角相等). 21.证明:∵AF ∥DC (已知),∴ ∠A =∠D (两直线平行内错角相等).∵FE ∥CB (已知),∴∠1=∠2(两直线平行内错角相等)∵∠F =180-(∠A +∠1),∠C =180-(∠D +∠2)(三角形内角和定理) ∴∠F =∠C (等量代换) 在△AFE 和△DCB 中,A D AF DCF C ∠=∠⎧⎪=⎨⎪∠=∠⎩(已证),(已知),(已证), ∴△AFE ≌△DCB (ASA )∴AE =DB (全等三角形对应边相等). ∴AE -BE =DB -EB (等量减等量差相等). 即AB =DE .第21题图第20题图第19题图22.解:∵DE 是AC 的垂直平分线, ∴EA =EC , ∴∠EAC =∠C , ∴∠F AC =∠EAC +18°, ∵AF 平分∠BAC , ∴∠F AB =∠EAC +18°, ∵∠B +∠BAC +∠C =180°, ∴72°+2(∠C +18°)+∠C =180°, 解得,∠C =24°, 故答案为:24.23.证明:∵G 为BC 的中点(已知), ∴CG =BG (中点定义), ∵BC =2AC (已知), ∴AC =CG (等量代换) 在△ECG 和△EBG 中,CE BE EG EGCG BG =⎧⎪=⎨⎪=⎩(已知),(公共边),(已证), ∴△ECG ≌△EBG (SSS ).∴∠EGC =∠EGB (全等三角形对应角相等). ∵∠EGC +∠EGB =180°(平角定义) ∴∠EGC =∠EGB =90°=∠ACB (等量代换)∵CF ⊥AB (已知),∵∠DFE =∠EGB =90°(垂直定义),∠1=∠2(对顶角相等), ∴∠D =∠B (三角形内角和定理) △ABC 和△CDG 中,B D ACB CGDAC CG ∠=∠⎧⎪∠=∠⎨⎪=⎩(已证),(已证),(已证), ∴△ABC ≌△CDG (AAS )∴AB =CD (全等三角形对应边相等).24.证明:∵AD 、A D ''分别是边BC 、B C ''上的中线(已知), ∴12BD BC =, 12B D BC ''''=(中点定义), ∵BC B C ''=(已知),第23题图第22题图∴BD B D ''=(等量代换).ABD ∆和A B D '''∆中, AB A BBD B DAD A D ''=⎧⎪''=⎨⎪''=⎩(已知),(已证),(已知), ∴ABD ∆≌A B D '''∆(SSS )∴B B '∠=∠(全等三角形对应边相等).ABC ∆和A B C '''∆中, AB A B B BBC B C ''=⎧⎪'∠=∠⎨⎪''=⎩(已知),(已证),(已知), ∴ABC ∆≌A B C '''∆(SAS )∴C C '∠=∠(全等三角形对应边相等). 25.(1)由题意,得2113583123x x x x +---=-+解方程,得2x = (2)由题意,得321333a a +++=,3213213a a a +++=+,321333a aa +++=解这三个方程,都得1a =.26.证明:(1)AF BE EF -=成立,理由如下: ∵∠BCA =80°(已知), ∴∠BCE +∠ACE =80°∵∠BEC =∠α=100°(已知), ∴∠BEF =180°-100°=80°(平角定义). ∴∠B +∠BCE =80°(三角形外角和定理) ∴∠B =∠ACE (等量代换). 在△BCE 和△CAF 中,B ACF BEC CFACB AC ∠=∠⎧⎪∠=∠⎨⎪=⎩(已证),(已知),(已知),∴△BCE ≌△ CAF (AAS )∴BE =CF ,AF =EC (全等三角形对应边相等). ∴EF =CF -CE =BE -AF (等量代换). (2)AF BE EF -=成立,理由如下: ∵∠BCA =∠β,第24题图∴∠BCE+∠ACE=∠β ∵∠BEC =∠α=180°-∠β, ∴∠BEF=180°-∠α=∠β. ∴∠B +∠BCE =∠β. ∴∠B =∠ACE在△BCE 和△CAF 中,B ACF BEC CFACB AC ∠=∠⎧⎪∠=∠⎨⎪=⎩(已证),(已知),(已知),∴△BCE ≌△ CAF (AAS ) ∴BE =CF ,AF =EC ∴EF =CF -CE =BE -AF。
【数学】第一章《解三角形》测试1(苏教版必修5)

第1章 解三角形§1.1正弦定理、余弦定理重难点:理解正、余弦定理的证明,并能解决一些简单的三角形度量问题.考纲要求:①掌握正弦定理、余弦定理,并能解决一些简单的三角形度量问题.经典例题:半径为R 的圆外接于△ABC ,且2R(sin 2A-sin 2C)=(3a-b)sinB .(1)求角C ;(2)求△ABC 面积的最大值.当堂练习:1.在△ABC 中,已知a=5 2 , c=10, A=30°, 则∠B= ( )(A) 105° (B) 60° (C) 15° (D) 105°或15° 2.在△ABC 中,若a=2, b=2 2 , c= 6 + 2 ,则∠A 的度数是 ( )(A) 30° (B) 45° (C) 60° (D) 75° 3.在△ABC 中,已知三边a 、b 、c 满足(a+b+c)·(a+b -c)=3ab, 则∠C=( )(A) 15° (B) 30° (C) 45° (D) 60° 4.边长为5、7、8的三角形的最大角与最小角之和为 ( )(A) 90° (B) 120° (C) 135° (D) 150° 5.在△ABC 中,∠A=60°, a= 6 , b=4, 那么满足条件的△ABC ( )(A) 有 一个解 (B) 有两个解 (C) 无解 (D)不能确定 6.在平行四边形ABCD 中,AC= 3 BD, 那么锐角A 的最大值为 ( )(A) 30° (B) 45° (C) 60° (D) 75° 7. 在△ABC 中,若cos2a A =cos2b B =cos2c C ,则△ABC 的形状是 ( )(A) 等腰三角形 (B) 等边三角形 (C) 直角三角形 (D) 等腰直角三角形 8.如果把直角三角形的三边都增加同样的长度,则这个新的三角形的形状为( )(A) 锐角三角形 (B) 直角三角形 (C) 钝角三角形 (D) 由增加的长度决定 9.在△ABC 中,若a=50,b=25 6 , A=45°则B= .10.若平行四边形两条邻边的长度分别是4 6 cm 和4 3 cm ,它们的夹角是45°,则这个平行四边形的两条对角线的长度分别为 .11.在等腰三角形 ABC 中,已知sinA ∶sinB=1∶2,底边BC=10,则△ABC 的周长是 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第1章解三角形单元复习练习
一、 知识点梳理:
1、正弦定理:在△ABC 中,
R C
c B b A a 2sin sin sin === 注:①R 表示△ABC 外接圆的半径 ②正弦定理能够变形成各种形式来使用
2、余弦定理:在△ABC 中, A bc c b a cos 2222-+= B ac c a b cos 2222-+= C ab b a c cos 2222-+= 也能够写成第二种形式:
bc a c b A 2cos 222-+=,ac b c a B 2cos 222-+=,ab
c b a C 2cos 2
22-+= 3、△ABC 的面积公式,B ac A bc C ab S sin 2
1sin 21sin 21===
二、题组训练: 1、在△ABC 中, a=12,A=060,要使三角形有两解,则对应b 的取值范畴为
2、判定下列三角形的形状
在△ABC 中,已知38,4,3===c b a ,请判定△ABC 的形状。
在△ABC 中,已知C B A 222sin sin sin <+,请判定△ABC 的形状。
在△ABC 中,已知bc a A ==
2,2
1cos ,请判定△ABC 的形状。
在△ABC 中,已知C B bc B c C b cos cos 2sin sin 2222=+,请判定△ABC 的形状。
在△ABC 中,,sin sin 3)sin sin )(sin sin sin (sin C B A C B C B A =-+++请判定△ABC 的形状。
3、在△ABC 中,已知030,4,5===A b a ,求△ABC 的面积。
4、在△ABC 中,若△ABC 的面积为S ,且22)(2c b a S -+=,求tanC 的值。
5、在△ABC 中,已知8
7cos ,6,0222=
==--A a c bc b ,求△ABC 的面积。
6、在△ABC 中,已知,sin sin ,360C B ab ==△ABC 的面积为315,求边b 的长。
7、在△ABC 中,求证:
2222112cos 2cos b a b B a A -=-
三、典型例题 1、设ABC △的内角A B C ,,所对的边长分别为a b c ,,,且3cos cos 5
a B
b A
c -=. (Ⅰ)求B
A tan tan 的值; (Ⅱ)求tan()A
B -的最大值.
2、在ABC △中,内角A B C ,,对边的边长分别是a b c ,,,已知2c =,3
C π=
.
(Ⅰ)若ABC △a b ,;
(Ⅱ)若sin sin()2sin 2C B A A +-=,求ABC △的面积.
3、设ABC △的内角A B C ,,所对的边长分别为a b c ,,,且cos 3a B =,sin 4b A =. (Ⅰ)求边长a ;
(Ⅱ)若ABC △的面积10S =,求ABC △的周长l .
4、在一个特定时段内,以点E 为中心的7海里以内海域被设为戒备水域.点E 正北55海里处有一个雷
达观测站A.某时刻测得一艘匀速直线行驶的船只位于点A 北偏东45且与点A 相距海里的位置
B ,通过40分钟又测得该船已行驶到点A 北偏东45+θ(其中sin θ,090θ<<)且与点A 相
距C .
(I )求该船的行驶速度(单位:海里/小时);
(II )若该船不改变航行方向连续行驶.判定它是否会进入戒备水域,并说明理由.
四、课后练习
1、如图,某住宅小区的平面图呈扇形AOC .小区的两个出入口设置在点A 及点C 处,小区里有两条笔直的小路AD DC ,,且拐弯处的转角为120.
已知某人从C 沿CD 走到D 用了10分钟,从D 沿DA 走到A 用了6分钟.若此人步行的速度为每分钟50米,求该扇形的
半径OA 的长(精确到1米).
2、在ABC △中,5cos 13B =-,4cos 5
C =. (Ⅰ)求sin A 的值;(Ⅱ)设ABC △的面积332ABC S =△,求BC 的长.。
