条件概率的三种求解方法
概率公式从基本概率公式到条件概率的推导

概率公式从基本概率公式到条件概率的推导概率是数学中非常重要的一个概念,用来描述某个事件发生的可能性。
概率公式是计算概率的数学工具,从基本概率公式到条件概率的推导,为我们提供了不同场景下求解概率的方法。
本文将介绍概率公式的推导过程以及它们在实际问题中的应用。
一、基本概率公式在概率理论中,我们用P(A)表示事件A发生的概率,该概率在[0, 1]的范围内。
基本概率公式是计算概率的基础,它由事件A发生的可能性与样本空间Ω中所有事件的可能性之比得出。
P(A) = N(A)/N(Ω)其中,N(A)表示事件A发生的结果数,N(Ω)表示样本空间Ω中所有事件的结果数。
举个例子,假设我们有一副标准扑克牌,其中共有52张牌。
如果我们想知道抽到一张黑桃的概率,可以使用基本概率公式来计算。
假设事件A表示抽到一张黑桃,那么N(A) = 13,因为一副扑克牌中有13张黑桃牌。
样本空间Ω中的结果数为N(Ω) = 52,所以P(A) = 13/52 = 1/4 = 0.25。
二、条件概率的定义与公式条件概率是在已知其他相关事件发生的情况下,求解某个事件发生的概率。
条件概率表示为P(A|B),读作事件B已经发生的条件下,事件A发生的概率。
条件概率的计算方法为:P(A|B) = P(A∩B)/P(B)其中,P(A∩B)表示事件A和B同时发生的概率,P(B)表示事件B发生的概率。
举个例子,假设事件A表示抽到一张黑桃,事件B表示抽到一张红桃。
我们想求解在抽到红桃的情况下,抽到黑桃的条件概率。
假设一副扑克牌中有26张红桃牌和13张黑桃牌。
那么P(B) =26/52 = 1/2。
在红桃已经抽出的情况下,剩下的牌中有13张黑桃牌,所以P(A∩B) = 13/52 = 1/4。
根据条件概率的计算公式,我们可以得到P(A|B) = (1/4) / (1/2) = 1/2。
这表示在已知抽到的牌是红桃的情况下,抽到黑桃的概率为1/2。
三、乘法法则与全概率公式乘法法则是计算多个事件同时发生的概率的方法。
专题17.1 条件概率与全概率公式(精讲精析篇)(原卷版)
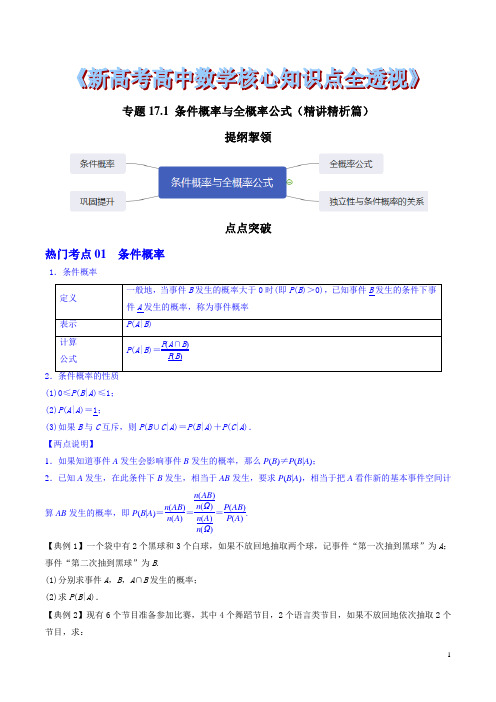
专题17.1 条件概率与全概率公式(精讲精析篇)提纲挈领点点突破热门考点01 条件概率1.条件概率定义一般地,当事件B发生的概率大于0时(即P(B)>0),已知事件B发生的条件下事件A发生的概率,称为事件概率表示P(A|B)计算公式P(A|B)=P(A∩B)P(B)2(1)0≤P(B|A)≤1;(2)P(A|A)=1;(3)如果B与C互斥,则P(B∪C|A)=P(B|A)+P(C|A).【两点说明】1.如果知道事件A发生会影响事件B发生的概率,那么P(B)≠P(B|A);2.已知A发生,在此条件下B发生,相当于AB发生,要求P(B|A),相当于把A看作新的基本事件空间计算AB发生的概率,即P(B|A)=n(AB)n(A)=n(AB)n(Ω)n(A)n(Ω)=P(AB)P(A).【典例1】一个袋中有2个黑球和3个白球,如果不放回地抽取两个球,记事件“第一次抽到黑球”为A;事件“第二次抽到黑球”为B.(1)分别求事件A,B,A∩B发生的概率;(2)求P(B|A).【典例2】现有6个节目准备参加比赛,其中4个舞蹈节目,2个语言类节目,如果不放回地依次抽取2个节目,求:(1)第1次抽到舞蹈节目的概率;(2)第1次和第2次都抽到舞蹈节目的概率;(3)在第1次抽到舞蹈节目的条件下,第2次抽到舞蹈节目的概率.【典例3】在一个袋子中装有10个球,设有1个红球,2个黄球,3个黑球,4个白球,从中依次摸2个球,求在第一个球是红球的条件下,第二个球是黄球或黑球的概率.【总结提升】1.用定义法求条件概率P (B |A )的步骤(1)分析题意,弄清概率模型;(2)计算P (A ),P (A ∩B );(3)代入公式求P (B |A )=P (A ∩B )P (A ). 2.典例2第(3)问给出了两种求条件概率的方法,法一为定义法,法二利用基本事件个数直接作商,是一种重要的求条件概率的方法.3.计算条件概率的方法(1)在缩小后的样本空间ΩA 中计算事件B 发生的概率,即P (B |A ).(2)在原样本空间Ω中,先计算P (A ∩B ),P (A ),再利用公式P (B |A )=P (A ∩B )P (A )计算求得P (B |A ). 4.为了求复杂事件的概率,往往需要把该事件分为两个或多个互斥事件,求出简单事件的概率后,相加即可得到复杂事件的概率(如典例3).利用公式P (B ∪C |A )=P (B |A )+P (C |A )可使条件概率的计算较为简单,但应注意这个性质的使用前提是“B 与C 互斥”.热门考点02 全概率公式1.全概率公式(1)P (B )=P (A )P (B |A )+P (A -)P (B |A -);(2)定理1 若样本空间Ω中的事件A 1,A 2,…,A n 满足:①任意两个事件均互斥,即A i A j =∅,i ,j =1,2,…,n ,i ≠j ;②A 1+A 2+…+A n =Ω;③P (A i )>0,i =1,2,…,n .则对Ω中的任意事件B ,都有B =BA 1+BA 2+…+BA n ,且P (B )=∑ni =1P (BA i )=∑n i =1P (A i )P (B |A i ).2.贝叶斯公式(1)一般地,当0<P (A )<1且P (B )>0时,有P (A |B )=P (A )P (B |A )P (B )=P (A )P (B |A )P (A )P (B |A )+P (A -)P (B |A -). (2)定理2 若样本空间Ω中的事件A 1,A 2,…,A n 满足:①任意两个事件均互斥,即A i A j =∅,i ,j =1,2,…,n ,i ≠j ;②A 1+A 2+…+A n =Ω;③1>P (A i )>0,i =1,2,…,n .则对Ω中的任意概率非零的事件B ,有P (A j |B )=P (A j )P (B |A j )P (B )=P (A j )P (B |A j )∑n i =1P (A i )P (B |A i ). 【拓展】贝叶斯公式充分体现了P (A |B ),P (A ),P (B ),P (B |A ),P (B |A -),P (AB )之间的转化.即P (A |B )=P (AB )P (B ),P (AB )=P (A |B )P (B )=P (B |A )P (A ),P (B )=P (A )P (B |A )+P (A -)P (B |A -)之间的内在联系. 【典例4】甲箱的产品中有5个正品和3个次品,乙箱的产品中有4个正品和3个次品.(1)从甲箱中任取2个产品,求这2个产品都是次品的概率;(2)若从甲箱中任取2个产品放入乙箱中,然后再从乙箱中任取一个产品,求取出的这个产品是正品的概率.【典例5】一项血液化验用来鉴别是否患有某种疾病.在患有此种疾病的人群中,通过化验有95%的人呈阳性反应,而健康的人通过化验也会有1%的人呈阳性反应.某地区此种病的患者仅占人口的0.5%.若某人化验结果为阳性,问此人确实患有此病的概率是多大?【典例6】假定具有症状S ={S 1,S 2,S 3,S 4}的疾病有d 1,d 2,d 3三种,现从20 000份患有疾病d 1,d 2,d 3的病历卡中统计得到下列数字:试问当一个具有S 诊断手段情况下,诊断该病人患有这三种疾病中哪一种较合适?【总结提升】1.以上三例分别代表全概率公式及其应用、贝叶斯公式及其应用及全概率公式与贝叶斯公式的综合应用.2.利用贝叶斯公式求概率的步骤第一步:利用全概率公式计算P (A ),即P (A )=∑ni =1P (B i )P (A |B i ); 第二步:计算P (AB ),可利用P (AB )=P (B )P (A |B )求解;第三步:代入P (B |A )=P (AB )P (A )求解.3.贝叶斯公式实质上是条件概率公式P (B i |A )=P (B i A )P (A ),P (B i A )=P (B i )·P (A |B i ),全概率公式P (A )=∑ni =1P (B i )P (A |B i )的综合应用.4..若随机试验可以看成分两个阶段进行,且第一阶段的各试验结果具体结果怎样未知,那么:(1)如果要求的是第二阶段某一个结果发生的概率,则用全概率公式;(2)如果第二个阶段的某一个结果是已知的,要求的是此结果为第一阶段某一个结果所引起的概率,一般用贝叶斯公式,类似于求条件概率,熟记这个特征,在遇到相关的题目时,可以准确地选择方法进行计算,保证解题的正确高效.【提醒】1.全概率公式P (B )=∑n i =1P (A i )P (B |A i )在解题中体现了化整为零的转化化归思想.2.贝叶斯概率公式反映了条件概率P (B |A )=P (AB )P (A ),全概率公式P (A )=∑n i =1P (B i )P (A |B i )及乘法公式P (AB )=P (B )P (A |B )之间的关系.即P (B j |A )=P (B j A )P (A )=P (B j )P (A |B j )P (A )=P (B j )P (A |B j )∑n i =1P (B i )P (A |B i ). 热门考点03 独立性与条件概率的关系事件的独立性(1)事件A 与B 相互独立的充要条件是P (AB )=P (A )P (B ).(2)当P (B )>0时,A 与B 独立的充要条件是P (A |B )=P (A ).(3)如果P (A )>0,A 与B 独立,则P (B |A )=P (B )成立.P (B |A )=P (AB )P (A )=P (A )P (B )P (A )=P (B ). 【典例7】判断下列各对事件是否是相互独立事件.(1)甲组3名男生,2名女生;乙组2名男生,3名女生.现从甲、乙两组中各选1名同学参加演讲比赛,“从甲组中选出1名男生”与“从乙组中选出1名女生”;(2)容器内盛有5个白乒乓球和3个黄乒乓球,“从8个球中任意取出1个,取出的是白球”与“从剩下的7个球中任意取出1个,取出的还是白球”;(3)掷一颗骰子一次,“出现偶数点”与“出现3点或6点”.【典例8】面对某种流感病毒,各国医疗科研机构都在研究疫苗,现有A ,B ,C 三个独立的研究机构在一定的时期内能研制出疫苗的概率分别是15,14,13.求: (1)他们都研制出疫苗的概率;(2)他们都失败的概率;(3)他们能够研制出疫苗的概率.【典例9】在一段线路中并联着3个自动控制的常开开关,只要其中1个开关能够闭合,线路就能正常工作.假定在某段时间内每个开关能够闭合的概率都是0.7,计算在这段时间内线路正常工作的概率.【规律方法】1.判断事件是否相互独立的方法(1)定义法:事件A,B相互独立⇔P(A∩B)=P(A)·P(B).(2)由事件本身的性质直接判定两个事件发生是否相互影响.(3)条件概率法:当P(A)>0时,可用P(B|A)=P(B)判断.2.求相互独立事件同时发生的概率的步骤(1)首先确定各事件之间是相互独立的;(2)确定这些事件可以同时发生;(3)求出每个事件的概率,再求积.3.使用相互独立事件同时发生的概率计算公式时,要掌握公式的适用条件,即各个事件是相互独立的,而且它们能同时发生.4.求复杂事件的概率一般可分三步进行(1)列出题中涉及的各个事件,并用适当的符号表示它们;(2)理清各事件之间的关系,恰当地用事件间的“并”“交”表示所求事件;(3)根据事件之间的关系准确地运用概率公式进行计算.5.计算事件同时发生的概率常用直接法,当遇到“至少”“至多”问题可以考虑间接法.巩固提升1.有朋自远方来,乘火车、船、汽车、飞机来的概率分别为0.3,0.2,0.1,0.4,迟到的概率分别为0.25,0.3,0.1,0.则他迟到的概率为( )A.0.65 B.0.075C.0.145 D.02.某班学生考试成绩中,数学不及格的占15%,语文不及格的占5%,两门都不及格的占3%.已知一学生数学不及格,则他语文也不及格的概率是( )A.0.2 B.0.33C.0.5 D.0.63.抛掷红、黄两枚质地均匀的骰子,当红色骰子的点数为4或6时,两枚骰子的点数之积大于20的概率是( )A.14B.13C.12D.354.两台机床加工同样的零件,第一台的废品率为0.04,第二台的废品率为0.07,加工出来的零件混放,并设第一台加工的零件是第二台加工零件的2倍,现任取一零件,则它是合格品的概率为( ) A.0.21 B.0.06C.0.94 D.0.955.已知P (A |B )=0.6,P (B |A )=0.3且A ,B 相互独立,则P (AB )等于( )A .0.18B .0.9C .0.3D .无法求解6.抛掷3枚质地均匀的硬币,A ={既有正面向上又有反面向上},B ={至多有一个反面向上},则A 与B 的关系是( )A .互斥事件B .对立事件C .相互独立事件D .不相互独立事件7.把一枚硬币投掷两次,事件A ={第一次出现正面},B ={第二次出现正面},则P (B |A )=________.8.某种元件用满6 000小时未坏的概率是34,用满10 000小时未坏的概率是12,现有一个此种元件,已经用过6 000小时未坏,则它能用到10 000小时的概率为________.9.已知A 与B 相互独立,且P (AB )=58,P (B )=34,则P (A -|B )=________. 10.明天上午李明要参加“青年文明号”活动,为了准时起床,他用甲、乙两个闹钟叫醒自己,假设甲闹钟准时响的概率为0.80,乙闹钟准时响的概率为0.90,则两个闹钟至少有一个准时响的概率是________.11.袋中有10个黑球,5个白球.现掷一枚均匀的骰子,掷出几点就从袋中取出几个球.若已知取出的球全是白球,则掷出3点的概率为________.12.某小组有20名射手,其中一、二、三、四级射手分别有2、6、9、3名.又若选一、二、三、四级射手参加比赛,则在比赛中射中目标的概率分别为0.85、0.64、0.45、0.32,今随机选一人参加比赛,则该小组在比赛中射中目标的概率为________.13.在同一时间内,甲、乙两个气象台独立预报天气准确的概率分别为45和34.在同一时间内,求: (1)甲、乙两个气象台同时预报天气准确的概率;(2)至少有一个气象台预报准确的概率.14.设甲、乙、丙三个地区爆发了某种流行病,三个地区感染此病的比例分别为17,15,14.现从这三个地区任抽取一个人.(1)求此人感染此病的概率;(2)若此人感染此病,求此人来自乙地区的概率.15.某人一周晚上值班2次,在已知他周日一定值班的条件下,求他在周六晚上或周五晚上值班的概率.16.一个家庭中有若干个小孩,假定生男孩和生女孩是等可能的,令A ={一个家庭中既有男孩又有女孩},B ={一个家庭中最多有一个女孩}.对下述两种情形,讨论A 与B 的独立性:(1)家庭中有两个小孩;(2)家庭中有三个小孩.。
例析条件概率问题的四种解法

,
选择题”
则下列结论中正确的是(
A.
P(
A)
=
3
5
C.
P(
B|A )
=
1
2
)
。
3
B.
P(
AB)
=
1
0
1
)
D.
P(
B|A
=
2
解析:
对于 A,
由题意知 不 放 回 地 依 次 随
机抽取 2 道 题 作 答,样 本 空 间 有 5×4=2
0
(
个)等 可 能 的 样 本 点,
n(
A )=3×4=1
青 团”和 2 个 肉 松 馅
。
的“
青团”
(
,求 这 2
1)若 从 甲 箱 中 任 取 2 个 “青 团”
个“
青团”
馅不同的概率;
(
若 先 从 甲 箱 中 任 取 2 个 “青 团 ”放 入
2)
,
乙箱中,
然后再从乙箱 中 任 取 1 个 “青 团”
求
取出的这个“
青团”
是肉松馅的概率。
4
2
0
(
参考答案:
一、定义法
根据条件 概 率 的 定 义,也 就 是 条 件 概 率
的 计 算 公 式,先 求 P (
A )(
P(
A )>0)和
P(
AB)
,
,即 可
再由定义 P (
P(
AB)
B|A )=
(
P A)
。
求解 P (
B|A )
甲、
乙、
丙、
丁 4 名同学报 名 参 加
1.4条件概率及有关公式

23
贝叶斯公式在实际中有很多应用,它 可以帮助人们确定某结果(事件 B)发生 的最可能原因.
24
例 8 某一地区患有癌症的人占0.005,患者 对一种试验反应是阳性的概率为0.95,正常 人对这种试验反应是阳性的概率为0.04,现 抽查了一个人,试验反应是阳性,问此人是 癌症患者的概率有多大? 求解如下: 设 C={抽查的人患有癌症}, A={试验结果是阳性}, 则 C 表示“抽查的人不患癌症”.
设B1,B2,…,Bn互不相容, A Bi ,
i 1
n
P(B )P( A | B )
i 1 i i
n
( k 1,2,..., n)
P ( ABk ) 分析: P ( Bk | A) P ( A) P ( Bk ) P ( A | Bk ) 乘 法 公 式 n P ( Bi ) P ( A | Bi ) 全 概 率 公 式
5
分析: : n个样本点 B: m个样本点 AB: k个样本点 在B已发生的条件下,试验结果为m 中的一个, 这时A发生当且仅当AB中的 某一样本点发生,故 P ( AB ) k k / n P ( A | B) m m/n P( B) 相当于“缩小了样本空间”
6
条件概率的 性质: (1)非负性: 0≤P(A|B)≤1 (2) 规范性: P(|B)=1 (3)可列可加性:若Ak (k=1, 2, …)两两互 斥,则
(3)
11
推广到一般情形中: 若n个事件A1, A2, …, An满足条件: P(A1A2…Ak)>0 (k=1, 2, …, n1), 则: P(A1A2…An)=P(A1)P(A2|A1)P(A3|A1A2) … P(An|A1A2…An1)
条件概率与全概率公式

条件概率与全概率公式
全概率公式定义
全概率公式是求解其中一事件发生的概率的一种统计技术。
全概率公
式又称为贝叶斯概率定理,是比较常见的概率公式之一、全概率公式表述为:设事件B1,B2,...Bn在样本空间S的一致性事件,事件A在样本空间
S中发生的概率为:
P(A)=∑P(A,Bi)P(Bi)
其中P(Bi)是事件B1,B2,...Bn发生的概率;P(A,Bi)是在事件
Bi发生的条件下,事件A发生的概率。
条件概率定义
条件概率是指在其中一条件下事件A发生的概率,它的计算方法是:
在该条件下,事件A发生的概率为:P(A,B)=P(A,B)/P(B)。
其中P(B)是事件B发生的概率;P(A,B)是事件A和B同时发生的概率。
由此可见,条件概率是指在条件B出现的情况下的概率事件A发生的
概率,而全概率公式则是求解其中一事件A的发生概率,即P(A)的值,
以上是全概率公式与条件概率的定义。
全概率公式与条件概率的关系
P(A)=∑P(A,Bi)P(Bi)
=P(A,B1)P(B1)+P(A,B2)P(B2)+···+P(A,Bn)P(Bn)
根据上面的表达式,可以看出,全概率公式实际上是将多个不相关的
结果。
概率与统计中的条件概率知识点总结

概率与统计中的条件概率知识点总结1. 条件概率的定义和计算方法条件概率是指在已知一定条件下,某事件发生的概率。
条件概率可以通过以下公式计算:\[P(A|B) = \frac{{P(A \cap B)}}{{P(B)}}\]其中,\(P(A|B)\)表示在事件B发生的条件下事件A发生的概率,\(P(A \cap B)\)表示事件A和事件B同时发生的概率,\(P(B)\)表示事件B发生的概率。
2. 乘法定理和全概率定理乘法定理是表示两个事件同时发生的概率,可以表示为:\[P(A \cap B) = P(A|B) \cdot P(B)\]全概率定理是表示一个事件发生的概率,可以表示为:\[P(A) = \sum_{i=1}^{n} P(A|B_i) \cdot P(B_i)\]其中,\(B_i\)表示一组互斥且完备的事件。
3. 贝叶斯定理贝叶斯定理是基于条件概率的计算,用于在已知后验概率的情况下求解先验概率。
贝叶斯定理可以表示为:\[P(B|A) = \frac{{P(A|B) \cdot P(B)}}{{P(A)}}\]其中,\(P(B|A)\)表示在事件A发生的条件下事件B发生的概率,\(P(A|B)\)表示在事件B发生的条件下事件A发生的概率,\(P(A)\)表示事件A发生的概率。
4. 独立事件和互斥事件独立事件指的是两个事件之间没有相互影响,可以通过以下条件来判断两个事件是否独立:\[P(A \cap B) = P(A) \cdot P(B)\]互斥事件指的是两个事件不可能同时发生,可以通过以下条件来判断两个事件是否互斥:\[P(A \cap B) = 0\]5. 条件概率与独立性的关系若两个事件A和B满足以下条件:\[P(A|B) = P(A) \quad or \quad P(B|A) = P(B)\]则称事件A和事件B是相互独立的。
以上是概率与统计中的条件概率知识点的总结。
希望对您有所帮助!。
条件概率及全概率公式
与所抽出的球具有相同颜色的
球.
b个白球, r个红球
解: 设Wi={第i次取出是白球}, i=1,2,3,4 Rj={第j次取出是红球}, j=1,2,3,4
于是W1W2R3R4表示事件“连续取四个球,第 一、第二个是白球,第三、四个是红球. ”
用乘法公式容易求出
P(W1W2R3R4)
=P(W1)P(W2|W1)P(R3|W1W2)P(R4|W1W2R3)
解 设A、B、C分别表示抽得产品是甲厂、乙厂、
丙厂生产的,D 表示抽得产品为正品,
则由已知, PA 50%, PB 30%, PC 20% PD | A 95%, PD | B 90%, PD | C 85%
从而任取一件产品为正品的概率可由全概率公式得 到:
例1 掷两颗均匀骰子,已知第一颗掷出6点, 问“掷出点数之和不小于10”的概率是多 少解? : 设A={掷出点数之和不小于10}
B={第一颗掷出6点}
应用定义
解法1: P( A | B) P( AB) 3 36 1 P(B) 6 36 2
解法2: P( A | B) 3 1 62
3. 条件概率的性质(自行验证) 设B是一事件,且P(B)>0,则 1. 对任一事件A,0≤P(A|B)≤1;
2. P (Ω | B) =1 ;
3.设A1,…,An互不相容,则 P[(A1+…+An )| B] = P(A1|B)+ …+P(An|B)
而且,前面对概率所证明的一些重要性质 都适用于条件概率.
=1,2,…,n,
另有一事件B, 它总是与 n
A1, A2, … ,An之一同时发生,即 B Ai ,
《条件概率》课件
公式
联合概率公式
P(A和B) = P(A) * P(B|A)
边缘概率公式
P(A) = ∑[P(A和Bi)], 其中Bi为所 有可能的B事件
条件概率公式
P(A|B) = P(A和B) / P(B)
性质
1 加法法则
P(A或B) = P(A) + P(B) - P(A和B)
3 全概率公式
P(A) = ∑[P(A|Bi) * P(Bi)], 其中Bi为所有可 能的B事件
《条件概率》PPT课件
欢迎大家来到本次关于《条件概率》的PPT课件。今天我们将学习条件概率 的概念、公式、性质以及一些实例应用,让您更深入地了解这个重要的数学 概念。
概念
概率的定义
概率是指在一次随机事件中,某一结果发生的可能性或频率。
条件概率的定义
条件概率是指在给定一定条件下,某一事件发生的概率。
3
桶中含有苹果的概率问题
根据已知条件,计算从一个桶中取出的苹果为某种特定类型的概率。
机器判定眼疾的概率问题
根据机器判定结果和已知数据,评估机器正确判定眼疾的概率。
总结
1 一些注意点
理解条件概率的背后的数学原理以及如何应用条件概率进行问题求解。
2 重点回顾
重要的公式和性质,如联合概率公式、乘法法则、全概率公式和贝叶斯定理。
2 乘法法则
P(A和B) = P(A) * P(B|A) = P(B) * P(A|B)
4 贝叶斯定理
P(B|A) = P(A|B) * P(B) / P(A)
实例应用
1
疾病与人群的关系
了解一个人是否患有某种疾病的概率,基于该人在特定人群中的概率。
2
投骰子的概率问题
条件概率全概率贝叶斯公式
条件概率全概率贝叶斯公式
1、条件概率:
条件概率是指在一定条件下一些事件发生的概率。
条件概率的定义为:设A和B是两个事件,其中条件B发生的概率不为0,条件概率P(A,B)
表示在条件B发生的条件下,事件A发生的概率,即取条件B为客观条件,求解事件A发生的概率,它用来度量在给定条件B发生的情况下A发生的
可能性。
公式表达形式为:P(A,B)=P(AB)/P(B)。
2、全概率:
全概率,即总体事件的概率,是描述总体事件发生的概率,总体事件
是指既蕴涵A,又蕴涵B的事件,全概率指发生总体事件的概率。
全概率
的表达式为:P(A)+P(B)=P(A∪B)。
3、贝叶斯公式:
贝叶斯定理是一种用于求解概率的方法,它基于全概率和条件概率的
概念,用于计算一个随机事件发生的条件概率。
贝叶斯定理的公式表达的
意思为:设A和B是两个事件,P(A,B)为其中一个事件A在另一个事件
B的条件下发生的概率,那么贝叶斯公式可以表达为P(A,
B)=P(AB)/P(B)=P(B,A)*P(A)/P(B)。
条件概率公式
条件概率公式条件概率公式条件概率:设A、B是两个事件,在A事件发生的条件下,B事件发生的概率,其中P(A)>0。
说明A事件发生的概率大于0,表示A事件是必然发生的。
记为:P(B|A)=P(AB)/P(A) 。
注意事件A作为条件,分母必定是条件概率,所以A事件的概率必定在分母上,分子P(AB)表示事件A与B相交的概率,记作P(A∩B)。
举例说明:将一枚硬币抛两次,观察正反面,正面记H,反面记T.样本空间Ω=(HH, HT,TH,TT)设事件A:至少一次为正面,即事件A=(HH,HT,TH)设事件B:两次为同一面,即事件B=(HH,TT)求事件A发生条件下,事件B发生的概率?即求P(B|A)。
(例子来自浙大版概率与统计第四版)从已知条件可知,总样本Ω为4个,A事件有3个,B事件有2个。
所以可以直接求出A的概率与B的概率。
即P(A)=3/4 ,A事件与B事件相交事件只有一个即HH。
即P(AB)=1/4.有公式1可知P(B|A)=P(AB)/P(A)=(1/4)/(3/4)=1/3.1.2 乘法公式:把式1条件概率公式P(B|A)=P(AB)/P(A)把P(AB)相交概率移到式子左边,把P(B|A)条件概率移动式子右边。
即得到乘法公式。
如式P(AB)=P(B|A) P(A)。
全概率公式:在条件概率中引入(A∩B)积事件的概念。
积事件概率表示相交事件的概率只有在A与B事件同事发生情况下才会发生。
P(A∩B)表示A和B相交的概率。
而在全概率公式中将引入∪和事件概念. 有个小窍门,其实可以把积事件理解为数字电路的与门、把和事件理解为数字电路的或门。
比如样本空间S,可以划分样本B1,B2...B6组成,即S=(B1∪B2∪ (6)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
条件概率的三种求解方法:
在概率论中,条件概率表示一个事件发生的条件下另一个事件发生的概率。
常见的三种求解条件概率的方法如下:
1.通过贝叶斯公式求解: 贝叶斯公式是P(A|B) = P(B|A) * P(A) / P(B),其中P(A|B) 表示
条件概率,P(B|A) 表示B 在A 发生的条件下发生的概率,P(A) 表示A 发生的概率,P(B) 表示B 发生的概率。
2.通过乘法公式求解: 乘法公式是P(A and B) = P(A|B) * P(B) = P(B|A) * P(A),其中P(A
and B) 表示A 和B 同时发生的概率。
3.通过联合概率公式求解: 联合概率公式是P(A and B) = P(A) * P(B|A) = P(B) * P(A|B),
其中P(A and B) 表示A 和B 同时发生的概率。
这三种方法都可以求解条件概率,但是要根据具体情况选择使用哪一种方法。
